2013届北京市朝阳区高三第二次模拟考试理综语文试卷

2013年北京市朝阳区高考数学二模试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1. 已知集合M ={0, 1, 3}，N ={x|x =3a, a ∈M}，则M ∪N =( ) A {0} B {0, 3} C {1, 3, 9} D {0, 1, 3, 9}2. 已知∫(10x 2+mx)dx =0，则实数m 的值为（ ） A −13 B −23 C −1 D −23. 执行如图所示的程序框图，若输出的结果是16，则判断框内的条件是（ ）A n >6？B n ≥7？C n >8？D n >9？4. 若双曲线x 2a 2−y 2b 2=1(a >0,b >0)的渐近线与抛物线y =x 2+2有公共点，则此双曲线的离心率的取值范围是( )A [3, +∞)B (3, +∞)C (1, 3]D (1, 3)5.某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）A 16 B 13 C 12 D 16. 某岗位安排3名职工从周一到周五值班，每天只安排一名职工值班，每人至少安排一天，至多安排两天，且这两天必须相邻，那么不同的安排方法有（ ） A 10种 B 12种 C 18种 D 36种7. 已知函数f(x)=a ⋅2|x|+1(a ≠0)，定义函数F(x)={f(x),x >0−f(x),x <0给出下列命题：①F(x)=|f(x)|； ②函数F(x)是奇函数；③当a <0时，若mn <0，m +n >0，总有F(m)+F(n)<0成立， 其中所有正确命题的序号是（ ） A ② B ①③ C ②③ D ①②8. 点P 是棱长为1的正方体ABCD −A 1B 1C 1D 1的底面A 1B 1C 1D 1上一点，则PA →⋅PC 1→的取值范围是( )A [−1, −14] B [−12, −14] C [−1, 0] D [−12, 0]二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上. 9. 设i 为虚数单位，计算3+i1+i =________．10. 若直线l 与圆C:{x =2cosθy =−1+2sinθ（θ为参数）相交于A ，B 两点，且弦AB 的中点坐标是(1, −2)，则直线L 的倾斜角为________．11. 如图，PC 切圆O 于点C ，割线PAB 经过圆心O ，PC =4，PB =8，则tan∠COP =________，△OBC 的面积是________．12. 某公司一年购买某种货物600吨，每次都购买x 吨，运费为3万元/次，一年的总存储费用为2x 万元，若要使一年的总运费与总存储费用之和最小，则每次需购买________吨． 13. 将一个质点随机投放在关于x ，y 的不等式组{3x +4y ≤19x ≥1y ≥1 所构成的三角形区域内，则该质点到此三角形的三个顶点的距离均不小于1的概率是________．14. 数列{2n −1}的前n 项1，3，7，…，2n −1组成集合A n ={1, 3, 7, ..., 2n −1}(n ∈N ∗)，从集合A n 中任取k(k =1, 2, 3,…,n)个数，其所有可能的k 个数的乘积的和为T k （若只取一个数，规定乘积为此数本身），记S n =T 1+T 2+...+T n ，例如当n =1时，A 1={1}，T 1=1，S 1=1；当n =2时，A 2={1, 2}，T 2=1+3，S 2=1+3+1×3=7．则当n =3时，S 3=________；试写出S n =________．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. 在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且f(A)=2cos A2sin(π−A2)+sin 2A2−cos 2A2．(1)求函数f(A)的最大值； (2)若f(A)=0，C =5π12，a =√6，求b 的值．16. 如图，四边形ABCD 是正方形，EA ⊥平面ABCD ，EA // PD ，AD ＝PD ＝2EA ＝2，F ，G ，H 分别为PB ，EB ，PC 的中点．（1）求证：FG // 平面PED ；（2）求平面FGH 与平面PBC 所成锐二面角的大小；（3）在线段PC 上是否存在一点M ，使直线FM 与直线PA 所成的角为π3？若存在，求出线段PM 的长；若不存在，请说明理由．17. 为提高学生学习数学的兴趣，某地区举办了小学生“数独比赛”．比赛成绩共有90分，70分，60分，40分，30分五种，按本次比赛成绩共分五个等级．从参加比赛的学生中随机抽取了30名学生，并把他们的比赛成绩按这五个等级进行了统计，得到如下数据表：（1）根据上面的统计数据，试估计从本地区参加“数独比赛”的小学生中任意抽取一人，其成绩等级为“A 或B”的概率；（2）根据（1）的结论，若从该地区参加“数独比赛”的小学生（参赛人数很多）中任选3人，记X 表示抽到成绩等级为“A 或B”的学生人数，求X 的分布列及其数学期望EX ； （3）从这30名学生中，随机选取2人，求“这两个人的成绩之差大于20分”的概率． 18. 已知函数f(x)=mx x 2+1+1(m ≠0)，g(x)＝x 2e ax (a ∈R)．(Ⅰ)求函数f(x)的单调区间；(Ⅱ)当m >0时，若对任意x 1，x 2∈[0, 2]，f(x 1)≥g(x 2)恒成立，求a 的取值范围． 19. 已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的右焦点为F(1, 0)，短轴的端点分别为B 1，B 2，且FB 1→⋅FB 2→=−a ．(1)求椭圆C 的方程；(2)过点F 且斜率为k(k ≠0)的直线l 交椭圆于M ，N 两点，弦MN 的垂直平分线与x 轴相交于点D ．设弦MN 的中点为P ，试求|DP||MN|的取值范围．20. 已知实数x 1，x 2，…，x n (n ∈N ∗且n ≥2)满足|x i |≤1(i =1, 2,…,n)，记S(x 1，x 2，…，x n )=∑x i 1≤i<j≤n x j ．（1）求S(−1,1,−23)及S(1, 1, −1, −1)的值；（2）当n =3时，求S(x 1, x 2, x 3)的最小值； （3）当n 为奇数时，求S(x 1, x 2,…,x n )的最小值．注：∑x i 1≤i<j≤n x j 表示x 1，x 2，…，x n 中任意两个数x i ，x j (1≤i <j ≤n)的乘积之和．2013年北京市朝阳区高考数学二模试卷（理科）答案1. D2. B3. C4. A5. A6. C7. C8. D9. 2−i 10. π411. 43,185 12. 30 13. 1−π12 14. ,15. 解：(1)f(A)=2cos A2sin A2+sin 2A2−cos 2A2=sinA −cosA =√2sin(A −π4)． 因为0<A <π， 所以−π4<A −π4<3π4，所以当A −π4=π2，即A =3π4时，f(A)取得最大值，且最大值为√2． (2)由题意知f(A)=√2sin(A −π4)=0，所以sin(A −π4)=0． 又知−π4<A −π4<3π4，所以A −π4=0，则A =π4．因为C =5π12，所以A +B =7π12，则B =π3．由asinA=b sinB得，b =asinB sinA=√6⋅sin π3sinπ4=3．16. 证明：因为F ，G 分别为PB ，BE 的中点，所以FG // PE ． 又FG ⊄平面PED ，PE ⊂平面PED ，所以FG // 平面PED ．因为EA ⊥平面ABCD ，所以PD ⊥平面ABCD ，所以PD ⊥AD ，PD ⊥CD ． 又因为四边形ABCD 是正方形，所以AD ⊥CD ． 如图建立空间直角坐标系，因为AD ＝PD ＝2EA ，所以D(0, 0, 0)，P(0, 0, 2)，A(2, 0, 0)， C(0, 2, 0)，B(2, 2, 0)，E(2, 0, 1)．因为F ，G ，H 分别为PB ，EB ，PC 的中点，所以F(1, 1, 1)，G(2, 1, 12)，H(0, 1, 1)．所以GF →=(−1,0,12)，GH →=(−2,0,12)，设n 1→=(x 1,y 1,z 1)为平面FGH 的一个法向量，则{n 1→⋅GF →=0n 1→⋅GH →=0 ，即{−x 1+12z 1=0−2x 1+12z 1=0 ， 再令y 1＝1，得n 1→=(0,1,0)． PB →=(2,2,−2),PC →=(0,2,−2)，设n 2→=(x 2,y 2,z 2)为平面PBC 的一个法向量，则{n 2→⋅PB →=0n 2→⋅PC →=0，即{2x 2+2y 2−2z 2=02y 2−2z 2=0，令z 2＝1，得n 2→=(0,1,1)． 所以|cos <n 1→,n 2→>|=|n 1→⋅n 2→||n 1→|⋅|n 2→|=1×√2=√22． 所以平面FGH 与平面PBC 所成锐二面角的大小为π4．在线段PC 上存在点M ，使直线FM 与直线PC 所成角为60∘证明：假设在线段PC 上存在点M ，使直线FM 与直线PC 所成角为60∘． 依题意可设PM →=λPC →，其中0≤λ≤1． 由PC →=(0,2,−2)，则PM →=(0,2λ,−2λ)． 又因为FM →=FP →+PM →,FP →=(−1,−1,1)， 所以FM →=(−1,2λ−1,1−2λ)．又直线FM 与直线PA 成60∘角，PA →(2,0,−2)， 所以|cos <FM →,PA →>|=12，即12=|−2−2+4λ|2√2⋅√1+2(2λ−1)2，解得：λ=58． 所以PM →=(0,54,−54)，|PM →|=√0+2×(54)2=5√24．所以，在线段PC 上存在点M ，使直线FM 与直线PC 所成角为60∘，此时PM 的长为5√24．17. 解：（1）根据统计数据可知，从本地区参加“数独比赛”的30名小学生中任意抽取一人，其成绩等级为“A 或B”的概率为430+630=13，即从本地区参加“数独比赛”的小学生中任意抽取一人，其成绩等级为“A 或B”的概率为13． （2）由题意知随机变量X 可取0，1，2，3，∴ P(X =0)=C 03 (13)0(23)3=827；P(X =1)=C 13 (13)1(23)2=49；P(X =2)=C 23 (13)2(23)=29；P(X =3)=C 33 (13)3(23)0=127；所以X 的分布列为（必须写出分布列，否则扣1分）故Eξ=0×827+1×49+2×29+3×127=1，所求期望值为1．（3）设事件M ：从这30名学生中，随机选取2人，这两个人的成绩之差大于20分． 设从这30名学生中，随机选取2人，记两个人的成绩分别为m ，n ．则基本事件的总数为C 302， 不妨设m >n ，当m =90时，n =60或40或30，基本事件的数为C 14 （C 110 +C 17 +C 13 ）；当m=70时，n=40或30，基本事件的数为C 16 （C 17 +C 13 ）；当m=60时，n=30，基本事件的数为C 110 C 1 3 ；∴ P(M)=C41(C101+C71+C31)+C61(C71+C31)+C101C31C302=3487．∴ 从这30名学生中，随机选取2人，“这两个人的成绩之差大于20分”的概率为3487．18. 函数f(x)=mxx2+1+1(m≠0)的定义域为R，f′(x)=m(1−x2)(x2+1)2=m(1−x)(1+x)(x2+1)2．①当m>0时，当x变化时，f′(x)，f(x)的变化情况如表：所以，函数f(x)的单调增区间时(−1, 1)，单调递减区间是(−∞, −1)，(1, +∞)．②当m<0时，当x变化时，f′(x)，f(x)的变化情况如表：所以，函数f(x)的单调减区间时(−1, 1)，单调递增区间是(−∞, −1)，(1, +∞)．（2）依题意，对任意当m>0时，对于任意x1，x2∈[0, 2]，f(x1)≥g(x2)恒成立，等价于当m>0时，对于任意x1，x2∈[0, 2]，f(x)min≥g(x)max成立．当m>0时，由(Ⅰ)知，函数f(x)在[0, 1]上单调递增，在[1, 2]上单调递减，因为f(0)＝1，f(2)=2m5+1>1，所以函数f(x)的最小值为f(0)＝1．所以应满足g(x)max≤1．因为g(x)＝x2e ax，所以g′(x)＝(ax2+2x)e ax．③当a＝0时，函数g(x)＝x2，任意x∈[0, 2]，g(x)max＝g(2)＝4，显然不满足g(x)max≤1，故a＝0不成立．④当a≠0时，令g′(x)＝(ax2+2x)e ax＝0得：x1=0,x2=−2a1∘当−2a≥2，即−1≤a<0时，在[0, 2]上g′(x)≥0，所以函数g(x)在[0, 2]上单调递增，所以g(x)max=g(2)=4e2a．由4e2a≤1得，a≤−ln2，所以−1≤a≤−ln2．2∘当0<−2a <2，即a<−1时，在[0,−2a)上g′(x)≥0，在(−2a,2]上g′(x)<0，所以函数g(x)在[0,−2a )上单调递增，在(−2a,2]上单调递减．所以g(x)max =g(−2a)=4a 2e 2．由4a 2e2≤1得：a ≤−2e，所以a <−1．3∘当−2a <0，即a >0时，显然在[0, 2]上g ′(x)≥0， 函数g(x)在[0, 2]上单调递增，且g(x)max =g(2)=4e 2a ． 显然g(x)max =4e 2a ≤1不成立，故a >0不成立． 综上所述，a 的取值范围是(−∞, −ln2]．19. 解：(I)由题意不妨设B 1(0, −b)，B 2(0, b)，则FB 1→=(−1,−b)，FB 2→=(−1,b)． ∵ FB 1→⋅FB 2→=−a ，∴ 1−b 2=−a ，又∵ a 2−b 2=1，解得a =2，b =√3． ∴ 椭圆C 的方程为x 24+y 23=1；(II)由题意得直线l 的方程为y =k(x −1)．联立{y =k(x −1)x 24+y 23=1得(3+4k 2)x 2−8k 2x +4k 2−12=0．设M(x 1, y 1)，N(x 2, y 2)，则x 1+x 2=8k 23+4k2，x 1x 2=4k 2−123+4k 2．∴ 弦MN 的中点P(4k 23+4k 2，−3k3+4k 2)．∴ |MN|=√(1+k 2)[(x 1+x 2)2−4x 1x 2]=√(1+k 2)[64k2(3+4k 2)2−4(4k 2−12)3+4k 2]=12(k 2+1)4k 2+3．直线PD 的方程为y +3k4k 2+3=−1k (x −4k 24k 2+3)． ∴ |DP|=3√k 2(k 2+1)4k 2+3．∴ |DP||MN|=3√k 2(k 2+1)4k 2+312(k 2+1)4k 2+3=14√k 2k 2+1=14√1−1k 2+1．又∵ k 2+1>1，∴ 0<1k 2+1<1，∴ 0<14√1−1k 2+1<14．∴|DP||MN|的取值范围是(0,14)．20. 解：（1）由已知得S(−1,1,−23)=−1+23−23=−1． S(1, 1, −1, −1)=1−1−1−1−1+1=−2． …（2）n =3时，S =S(x 1，x 2，x 3)=∑x i 1≤i<j≤3x j =x 1x 2+x 1x 3+x 2x 3． 固定x 2，x 3，仅让x 1变动，那么S 是x 1的一次函数或常函数，因此S≥min{S(1, x2, x3), S(−1, x2, x3)}．同理S(1, x2, x3)≥min{S(1, 1, x3), S(1, −1, x3)}．S(−1, x2, x3)≥min{S(−1, 1, x3), S(−1, −1, x3)}．以此类推，我们可以看出，S的最小值必定可以被某一组取值±1的x1，x2，x3所达到，于是S≥min{S(x1, x2, x3)}．当x k=±1(k=1, 2, 3)时，S=12[(x1+x2+x3)2−(x12+x22+x32)]=12(x1+x2+x3)2−32．因为|x1+x2+x3|≥1，所以S≥12−32=−1，且当x1=x2=1，x3=−1，时S=−1，因此S min=−1．…（3）S=S(x1，x2，…，x n)=∑x i1≤i<j≤nx j=x1x2+x1x3+...+x1x n+x2x3+...+x2x n+...+x n−1x n．固定x2，x3，…，x n，仅让x1变动，那么S是x1的一次函数或常函数，因此S≥min{S(1, x2, x3, ..., x n), S(−1, x2, x3, ..., x n)}．同理S(1, x2, x3,…,x n)≥min{S(1, 1, x3, ..., x n), S(1, −1, x3, ..., x n)}．S(−1, x2, x3,…,x n)≥min{S(−1, 1, x3, ..., x n), S(−1, −1, x3, ..., x n)}．以此类推，我们可以看出，S的最小值必定可以被某一组取值±1的x1，x2，…，x n所达到，于是S≥min{S(x1, x2, x3, ..., x n)}．当x k=±1(k=1, 2,…,n)时，S=12[(x1+x2+⋯+x n)2−(x12+x22+⋯+x n2)]=12(x1+x2+⋯+x n)2−n2．当n为奇数时，因为|x1+x2+...+x n|≥1，所以S≥−12(n−1)，另一方面，若取x1=x2=⋯=x n−12=1，x n−12+1=x n−12+2=⋯=x n=−1，那么S=−12(n−1)，因此S min=−12(n−1)．…。

北京市朝阳区2013年高考化学一模试卷一、选择题（共7小题，每小题6分，满分42分）1．（6分）（2013•朝阳区一模）关于实现下列物品用途的主要物质的说法，不正确的是（）选项 A B C D物品用途化学能转化为电能吸附水分去除油污光能转化为电能主要物质H2 SO4（aq）是电解质溶液硅酸干凝胶是主要成分硬脂酸钠是主要成分SiO2是转换材料A．A B．B C．C D．D考点：常见化学电源的种类及其工作原理；硅和二氧化硅；硅酸的性质及制法；肥皂、合成洗涤剂．专题：化学应用．分析： A．蓄电池为常见的二次电池；B．硅胶具有疏松多孔的结构；C．肥皂除油污是发生的乳化作用；D．太阳能电池板材料为硅．解答：解：A．蓄电池为常见的二次电池，放电时化学能转化为电能，选择硫酸为电解质，故A正确；B．硅胶具有疏松多孔的结构，具有吸水性，常作干燥剂，故B正确；C．肥皂除油污是肥皂中的硬脂酸钠与油污发生的乳化作用，故C正确；D．太阳能电池板材料为硅，可实现光能转化为电能，故D错误；故选D．点评：本题为小综合，涉及原电池、干燥剂、硅的性质与用途、去污原理等，属于高考中一类常见的冷拼凑试题，各选项之间没有联系，学生应注意思维的及时转换，题目难度不大．2．（6分）（2013•朝阳区一模）下列说法不正确的是（）A．H2N﹣CH2﹣COOH 能与酸、碱反应生成盐B．葡萄糖既能发生银镜反应，又能发生水解反应C．浓硝酸和醋酸铅溶液均可使鸡蛋清溶液中的蛋白质变性D．1 mol油脂完全水解的产物是1 mol甘油和3 mol 高级脂肪酸（或盐）考点：葡萄糖的性质和用途；油脂的性质、组成与结构；氨基酸、蛋白质的结构和性质特点．专题：有机物的化学性质及推断．分析： A．氨基能与酸反应，羧基能与碱反应；B．单糖不能发生水解反应；C．甲醛、强酸、强碱、重金属盐等物质能使蛋白质变性；D．油脂是高级脂肪酸甘油酯．解答：解：A．氨基能与酸反应，羧基能与碱反应，H2N﹣CH2﹣COOH 能与酸、碱反应生成盐，故A正确；B．葡萄糖是单糖，单糖不能发生水解反应，故B错误；C．浓硝酸是强酸；醋酸铅溶液是重金属盐，均可使鸡蛋清溶液中的蛋白质变性，故C正确；D．油脂是高级脂肪酸甘油酯，1 mol油脂完全水解的产物是1 mol甘油和3 mol 高级脂肪酸（或盐），故D正确．故选B．点评：本题考查糖类油脂蛋白质的性质，难度不大，注意油脂是高级脂肪酸甘油酯．3．（6分）（2013•朝阳区一模）Se、Br两种元素的部分信息如图所示，下列说法正确的是（）A．原子半径：Br＞Se＞P B．还原性：S2﹣＞Se2﹣＞Br﹣C．S eO2既有氧化性又有还原性D．在Se2Br2分子中只含有极性键考点：位置结构性质的相互关系应用．专题：元素周期律与元素周期表专题．分析： A．同一周期元素，原子半径随着原子序数增大而减小，不同周期元素，原子的电子层数越多其原子半径越大；B．同一周期元素，阴离子的还原性随着原子序数的增大而减小，同一主族元素，阴离子的还原性随着原子序数的增大而增大；C．中间价态的元素既有氧化性又有还原性，处于最低价态的元素只有还原性，处于最高价态的元素只有氧化性；D．同种非金属元素之间易形成非极性键，不同非金属元素之间易形成极性键．解答：解：A．硒和溴属于同一周期元素，硒的原子序数小于溴，所以原子半径Br＜Se，P处于第二周期，溴处于第四周期，所以原子半径Br＞P，故A错误；B．同一周期元素，阴离子的还原性随着原子序数的增大而减小，同一主族元素，阴离子的还原性随着原子序数的增大而增大，还原性Se2﹣＞S2﹣＞Br﹣，故B错误；C．SeO2中硒处于中间价态，所以既有氧化性又有还原性，故C正确；D．在Se2Br2分子中硒原子间存在非极性键，溴和硒原子之间存在极性键，故D错误，故选C．点评：根据元素周期律来分析解答，易错选项是D，明确Se2Br2的结构是解本题的关键，难度不大．4．（6分）（2013•朝阳区一模）下列解释实验现象的反应方程式不正确的是（）A．新制氯水中滴加NaOH溶液后，黄绿色褪去Cl2+2OH﹣=Cl﹣+ClO﹣+H2OB．向NaHCO3溶液中滴加酚酞溶液，溶液变红HCO3﹣⇌H++CO32﹣C．向Mg（OH）2悬浊液中滴加FeCl3溶液，生成红褐色沉淀3Mg（OH）2+2Fe3+=2Fe（OH）3↓+3Mg2+ D．向少量苯酚稀溶液中逐滴加入饱和溴水，生成白色沉淀考点：离子方程式的书写．专题：离子反应专题．分析： A、新制氯水中滴加NaOH溶液后，氯气和氢氧化钠溶液反应生成氯化钠次氯酸钠和水；B、碳酸氢根离子水解显碱性；C、氯化铁水解显酸性能溶解氢氧化镁，促进铁离子水解，生成氢氧化铁沉淀；D、苯酚和浓溴水发生取代反应反应生成白色沉淀；解答：解：A、新制氯水中滴加NaOH溶液后，黄绿色褪去，是氯气和氢氧化钠反应，反应的离子方程式为：Cl2+2OH﹣=Cl﹣+ClO﹣+H2O；故A正确；B、向NaHCO3溶液中滴加酚酞溶液，溶液变红是因为碳酸氢根离子水解显碱性，反应的离子方程式为：H2O+HCO3﹣⇌OH﹣+H2CO3 ；故B错误；C、向Mg（OH）2悬浊液中滴加FeCl3溶液，生成红褐色沉淀，反应的离子方程式为：3Mg（OH）2+2Fe3+=2Fe（OH）3↓+3Mg2+；故C正确；D、向少量苯酚稀溶液中逐滴加入饱和溴水，生成白色沉淀，反应的化学方程式为；，故D正确；故选B．点评：本题考查了反应离子方程式的正误分析，书写方法，掌握反应实质是解题关键，题目难度中等．5．（6分）（2013•朝阳区一模）如图集气瓶中用滤纸折成的纸蝴蝶上喷洒了一种溶液，通入某种气体后，实验结果与预测的纸蝴蝶颜色变化不一致的是（）A B C D喷洒液酚酞紫色石蕊酸性重铬酸钾酸化的KI﹣淀粉通入的气体NH3Cl2CH3CH2OH（g）O2预测的颜色变化变为红色最终褪色无明显变化变为蓝色A．A B．B C．C D．D考点：氨的化学性质；氯气的化学性质；氯、溴、碘及其化合物的综合应用；乙醇的化学性质．专题：元素及其化合物；化学实验基本操作．分析： A．氨水能使酚酞试液变红；B．次氯酸有漂白性，能使石蕊试液褪色；C．酸性重铬酸钾具有强氧化性，能氧化乙醇而使自身变色；D．淀粉遇碘变蓝色．解答：解：A．氨气溶于水得到氨水，氨水电离出氢氧根离子而使氨水呈碱性，酚酞遇碱变红色，故A不选；B．氯气溶于水生成盐酸和次氯酸，盐酸有酸性而使紫色石蕊试液变红，次氯酸有漂白性而使石蕊试液最终褪色，故B不选；C．酸性重铬酸钾具有强氧化性，能氧化乙醇，而自身被还原，溶液由黄色变为绿色，故C选；D．氧气能氧化酸化的碘化钾生成碘单质，淀粉遇碘变蓝色，故D不选；故选C．点评：本题考查元素化合物的性质，注意次氯酸能使酸碱指示剂褪色，而二氧化硫不能使酸碱指示剂褪色，为易错点．6．（6分）（2013•朝阳区一模）已知：H2（g）+I2（g）⇌2HI（g）△H=﹣14.9kJ/mol．某温度下在甲、乙两个恒容密闭容器中充入反应物，其起始浓度如下表所示．甲中反应达到平衡时，测得c（H2）=0.008mol/L．下列判断正确的（）起始浓度c（H2）/mol/L c（I2）/mol/L c（HI）/mol/L甲0.01 0.01 0乙0.02 0.02 0A．平衡时，乙中H2的转化率是甲中的2倍B．平衡时，甲中混合物的颜色比乙中深C．平衡时，甲、乙中热量的变化值相等D．该温度下，反应的平衡常数K=0.25考点：化学平衡的影响因素；化学平衡常数的含义．专题：化学平衡专题．分析： A、该反应前后气体的体积不变，乙中的浓度为甲中的2倍，乙中压强为甲中2倍，压强不影响平衡移动，二者为等效平衡；B、二者为等效平衡，平衡时乙中c（I2）是甲中的2倍；C、二者为等效平衡，反应物转化率相同，乙中参加反应I2的是甲中的2倍；D、根据平衡时氢气的浓度，利用三段式计算平衡时其它组分的平衡浓度，代入平衡常数表达式计算．解答：解：A、该反应前后气体的体积不变，乙中的浓度为甲中的2倍，乙中压强为甲中2倍，压强不影响平衡移动，二者为等效平衡，平衡时对应各组分的转化率相同，故A错误；B、二者为等效平衡，平衡时乙中c（I2）是甲中的2倍，平衡时乙中颜色更深，故B错误；C、二者为等效平衡，反应物转化率相同，乙中参加反应I2的是甲中的2倍，乙中的热量变化是甲中的2倍，故C错误；D、平衡时氢气的浓度为0.008mol/L，则：H2（g）+I2（g）⇌2HI（g）△开始（mol/L）：0.01 0.01 0变化（mol/L）：0.002 0.002 0.004平衡（mol/L）：0.008 0.008 0.004故该温度下该反应的平衡常数k==0.25，故D正确；故选D．点评：本题考查等效平衡、化学平衡常数的计算、影响化学平衡的因素等，难度中等，注意理解等效平衡规律．7．（6分）（2013•朝阳区一模）室温下，用0.100mol/L NaOH 溶液分别滴定20.00mL 0.100mol/L的盐酸和醋酸，滴定曲线如图所示．下列说法正确的是（）A．Ⅰ、Ⅱ分别表示盐酸和醋酸的滴定曲线B．V（NaOH）=10.00 mL 时C．p H=7时，两种酸所用NaOH溶液的体积相等D．V（NaOH）=20.00 mL 时，c（Cl﹣）＜c（CH3COO﹣）考点：中和滴定．专题：电离平衡与溶液的pH专题．分析： A．根据盐酸和醋酸在滴定开始时的pH来判断；B．醋酸电离大于醋酸根的水解程度；C．醋酸钠水解呈碱性；D．V（NaOH）=20.00 mL 时，二者反应生成氯化钠和醋酸钠．解答：解：A．滴定开始时0.1000mol/L盐酸pH=1，0.1000mol/L醋酸pH＞1，所以滴定盐酸的曲线是图Ⅱ，滴定醋酸的曲线是图Ⅰ，故A错误；B．加入10ml氢氧化钠时，溶液中恰好为同浓度的醋酸和醋酸钠，醋酸电离大于醋酸根的水解程度，故，故B正确；C．醋酸钠水解呈碱性，氯化钠不水解，pH=7时，醋酸所用NaOH溶液的体积小，故C错误；D．V（NaOH）=20.00 mL 时，二者反应生成氯化钠和醋酸钠，醋酸根发生水解，浓度小于氯离子，故D错误．故选B．点评：本题考查NaOH与CH3COOH、盐酸的反应，涉及盐类的水解和溶液离子浓度的大小比较知识，注意利用醋酸电离大于醋酸根的水解程度做题．二、解答题（共4小题，满分58分）8．（12分）（2013•朝阳区一模）工业上常以赤铁矿石（主要成分为Fe2O3）和焦炭为主要原料，在高温下炼铁．焦炭产生CO的反应是：C+O2CO2；C+CO22CO（1）CO还原赤铁矿的化学方程式是Fe2O3+3CO2Fe+3CO2（2）下列说法正确的是aba．为使赤铁矿石充分燃烧，需将其粉碎b．足量的空气能提高炼铁反应速率c．与生铁相比较，纯铁转化为“铁水”的温度低（3）生铁的用途很多，某电镀厂用生铁将废水中的Cr2O72﹣转化为Cr3+，流程图1：①气体A是H2②在上述酸性溶液中，生铁比纯铁产生Fe2+的速率快，原因是生铁中含有C，在硫酸溶液中形成无数微小原电池，加快反应速率③将Cr3+转化为Cr（OH）3的离子方程式是2Cr3++3Ca（OH）2═2Cr（OH）3↓+3Ca2+（4）电解法将一定浓度的酸性废水中的Cr2O72﹣转化为Cr3+，其原理示意图2：①阳极附近溶液中Cr2O72﹣转化为Cr3+的离子方程式是6Fe2++Cr2O72﹣+14H+═6Fe3++2Cr3++7H2O②一段时间后，试管底部出现沉淀．解释生成沉淀的原因：随着电解进行，溶液中c（H+）逐渐减少，c（OH﹣）浓度增大，生成Fe（OH）3和Cr（OH）3沉淀．考点：高炉炼铁；电解原理；金属的回收与环境、资源保护．专题：几种重要的金属及其化合物．分析：（1）根据工业炼铁的原理进行分析；（2）铁矿石需要粉碎，以增大和空气的接触面；浓度越大反应速率越大；合金的熔点低硬度大；（3）①铁与硫酸反应生成H2；②原电池加快反应速率；③Cr（OH）3是沉淀；（4）①铁作阳极，电极本身被氧化，反应式为Fe﹣2e﹣═Fe2+，溶液呈酸性，H+离子在阴极放电生成氢气，反应式为2H++2e═H2↑，生成的Fe2+离子与Cr2O72﹣离子发生氧化还原反应；②随着电解进行，溶液中c（H+）逐渐减少，c（OH﹣）浓度增大；解答：解：（1）一氧化碳和氧化铁在高温的条件下生成铁和二氧化碳，故答案为：Fe2O3+3CO2Fe+3CO2；（2）a、原料铁矿石是固体、空气是气体，为了加快反应速率，所以要将黄铁矿粉碎，增大接触面，提高反应速率，故a正确；b、采用空气过量目的是增大氧气浓度，提高一氧化碳的浓度，提高炼铁反应速率，故b正确；c、生铁是合金，熔点低，故c错误；故答案为：a b；（3）①铁与硫酸反应生成H2，故答案为：H2；②生铁中含有C，铁和碳在硫酸溶液中形成原电池，故答案为：生铁中含有C，在硫酸溶液中形成无数微小原电池，加快反应速率；③Cr3+与石灰乳反应生成Cr（OH）3是沉淀，离子方程式是2Cr3++3Ca（OH）2═2Cr（OH）3↓+3Ca2+，故答案为：2Cr3++3Ca（OH）2═2Cr（OH）3↓+3Ca2+；（4）①铁作阳极，电极本身被氧化，反应式为Fe﹣2e﹣═Fe2+，溶液呈酸性，H+离子在阴极放电生成氢气，反应式为2H++2e═H2↑，Fe2+离子与Cr2O72﹣离子发生氧化还原反应生成Fe3+离子和Cr3+离子，反应离子方程式为6Fe2++Cr2O72﹣+14H+═6Fe3++2Cr3++7H2O，故答案为：6Fe2++Cr2O72﹣+14H+═6Fe3++2Cr3++7H2O；②随着电解进行，c（OH﹣）浓度增大，生成Fe（OH）3和Cr（OH）3沉淀，故答案为：随着电解进行，溶液中c（H+）逐渐减少，c（OH﹣）浓度增大，生成Fe（OH）3和Cr（OH）3沉淀；点评：本题考查较为综合，涉及高炉炼铁、电解、氧化还原反应等问题，题目难度中等，本题电解离子方程式的书写是易错点．9．（14分）（2013•朝阳区一模）燃煤产生的烟气中的氮氧化物NO x（主要为NO、NO2）易形成污染，必须经脱除达标后才能排放．（1）用化学方程式表示NO形成硝酸型酸雨的反应2NO+O2═2NO2、3NO2+H2O═2HNO3+NO（2）能作脱除剂的物质很多，下列说法正确的是aba．用H2O作脱除剂，不利于吸收含氮烟气中的NOb．用Na2SO3作脱除剂，O2会降低Na2SO3的利用率c．用CO作脱除剂，会使烟气中NO2的浓度增加（3）尿素[CO（NH2）2]在一定条件下能有效将NO x转化为N2．Ⅰ．已知可通过下列方法合成尿素：2NH3（g）+CO2（g）⇌H2NCOONH4（s）△H=﹣159.5kJ/molH2NCOONH4（s）⇌CO（NH2）2（s）+H2O（l）△H=+28.5kJ/mol①尿素释放出NH3的热化学方程式是CO（NH2）2（s）+H2O（l）⇌2NH3（g）+CO2（g）△H=+131kJ/mol②写出有利于尿素释放NH3的条件并说明理由升高温度；升高温度有利于平衡向吸热反应方向进行，同时温度升高，氨气的溶解度降低，均有利于向释放氨气的方向进行Ⅱ．CO（NH2）2与某种烟气（主要为N2、NO和O2）中的NO的物质的量比值分别为1：2、2：1、3：1时，NO脱除率随温度变化的曲线如图：①曲线a 对应CO（NH2）2与NO的物质的量比值是3：1．②曲线a、b、c中，800℃～900℃区间内发生主要反应的化学方程式是4NH3+6NO═5N2+6H2O或2CO （NH2）2+6NO═2CO2+4H2O+5N2．③900℃～1200℃区间内脱除率下降，NO浓度上升．发生的主要反应是4NH3+5O2═4NO+6H2O．④曲线a中，NO的起始浓度为6×10﹣4 mg/m3，从A点到B点经过0.8s，该时间段内NO的脱除速率为1.5×10﹣4mg/（m3•s）．考点：氮的氧化物的性质及其对环境的影响；化学平衡的影响因素．专题：氮族元素．分析：（1）一氧化氮不稳定，易和氧气反应生成二氧化氮，二氧化氮和水反应生成硝酸和一氧化氮；（2）a．一氧化氮不易溶于，而二氧化氮易溶于水，反应生成NO；b．亚硫酸钠不稳定，易被氧气氧化；C．用CO作脱除剂，则氮氧化物得电子发生还原反应；（3）Ⅰ．①根据盖斯定律，将两个热化学方程式相加，然后进行颠倒即得目标方程式，其焓变进行相应改变；②尿素释放NH3的反应是吸热反应，根据温度对化学平衡及氨气溶解度的影响进行分析；Ⅱ．①CO（NH2）2的含量越高，NO脱除率越高；②、800℃～900℃区间内NO脱除率增大，NO参加反应，即尿素与NO反应生成N2；③、900℃～1200℃区间内脱除率下降，NO浓度上升，反应中应该生成NO；④、A点到BNO脱除率由0.55变为0.75，故NO的浓度变化量为（0.75﹣0.55）×6×10﹣4 mg/m3=1.2×10﹣4 mg/m3，再利用计算NO的脱除速率．解答：解：（1）一氧化氮不稳定，易和氧气反应生成二氧化氮，二氧化氮和水反应生成硝酸和一氧化氮，故NO形成硝酸型酸雨的反应为：2NO+O2═2NO2、3NO2+H2O═2HNO3+NO，故答案为：2NO+O2═2NO2、3NO2+H2O═2HNO3+NO；（2）a．一氧化氮不易溶于，而二氧化氮易溶于水，反应生成NO，不利于吸收含氮烟气中的NO，故a正确；b．亚硫酸钠不稳定，易被氧气氧化，O2会降低Na2SO3的利用率，故b正确；C．用CO作脱除剂，被氧化，则氮氧化物得电子发生还原反应，不会生成NO2，烟气中NO2的浓度不增加，故c错误；故答案为：ab；（3）①已知：2NH3（g）+CO2（g）⇌H2NCOONH4（s）△H=﹣159.5kJ/molH2NCOONH4（s）⇌CO（NH2）2（s）+H2O（l）△H=+28.5kJ/mol根据盖斯定律，两热化学方程式相加得2NH3（g）+CO2（g）⇌CO（NH2）2（s）+H2O（l）△H=﹣131kJ/mol，故尿素释放出NH3的热化学方程式为：CO（NH2）2（s）+H2O（l）⇌2NH3（g）+CO2（g）△H=+131kJ/mol，故答案为：CO（NH2）2（s）+H2O（l）⇌2NH3（g）+CO2（g）△H=+131kJ/mol；②释放氨气的反应是吸热反应，升高温度，有利于平衡向吸热反应方向进行，同时温度升高，氨气的溶解度降低，均有利于向释放氨气的方向进行，故答案为：升高温度；升高温度有利于平衡向吸热反应方向进行，同时温度升高，氨气的溶解度降低，均有利于向释放氨气的方向进行；Ⅱ．①CO（NH2）2的含量越高，NO的转化率越大，即NO脱除率越高，所以曲线a 对应CO（NH2）2与NO的物质的量比值是3：1，故答案为3：1；②800℃～900℃区间内NO脱除率增大，所以NO是作为反应物参加反应，高温时，尿素分解生成氨气、二氧化碳，氨气和一氧化氮发生氧化还原反应生成氮气，即尿素与NO反应生成N2，同时生成二氧化碳和水，所以反应方程式为：4NH3+6NO═5N2+6H2O 或2CO（NH2）2+6NO═2CO2+4H2O+5N2，故答案为：4NH3+6NO═5N2+6H2O 或2CO（NH2）2+6 NO═2CO2+4H2O+5N2；③900℃～1200℃区间内脱除率下降，所以NO浓度上升，则该反应中应该有NO，尿素分解生成的氨气和烟气中的氧气反应生成一氧化氮和水，导致NO浓度增大，所以反应方程式为：4NH3+5O2═4NO+6H2O，故答案为：4NH3+5O2═4NO+6H2O；④A点到BNO脱除率由0.55变为0.75，故NO的浓度变化量为（0.75﹣0.55）×6×10﹣4 mg/m3=1.2×10﹣4 mg/m3所以NO的脱除速率==1.5×10﹣4mg/（m3．s），故答案为：1.5×10﹣4．点评：本题考查氮的化合物及其性质，注意尿素加热时会分解生成氨气，且尿素是有机氮肥，正确分析图象是解本题的关键，注意图象中的曲线趋向和转折点．10．（16分）（2013•朝阳区一模）实验室制乙烯时，产生的气体能使Br2的四氯化碳溶液褪色，甲、乙同学用下列实验验证．（气密性已检验，部分夹持装置略）．实验操作和现象：操作现象点燃酒精灯，加热至170℃Ⅰ：A中烧瓶内液体渐渐变黑Ⅱ：B内气泡连续冒出，溶液逐渐褪色…实验完毕，清洗烧瓶Ⅲ：A中烧瓶内附着少量黑色颗粒状物，有刺激性气味逸出（1）烧瓶内产生乙烯的化学方程式是（2）溶液“渐渐变黑”，说明浓硫酸具有脱水性性．（3）分析使B中溶液褪色的物质，甲认为是C2H4，乙认为不能排除SO2的作用．①根据甲的观点，使B中溶液褪色反应的化学方程式是CH2=CH2+Br2→CH2Br﹣CH2Br②乙根据现象Ⅲ认为产生了SO2，在B中与SO2反应使溶液褪色的物质是H2O、Br2③为证实各自观点，甲、乙重新实验，设计与现象如下：设计现象甲在A、B间增加一个装有某种试剂的洗气瓶Br2的CCl4溶液褪色乙与A连接的装置如下：D中溶液由红棕色变为浅红棕色时，E中溶液褪色a．根据甲的设计，洗气瓶中盛放的试剂是NaOH溶液b．根据乙的设计，C中盛放的试剂是浓硫酸c．能说明确实是SO2使E中溶液褪色的实验是加热已经褪色的品红溶液，若红色恢复，证明是SO2使品红溶液褪色而不是Br2d．乙为进一步验证其观点，取少量D中溶液，加入几滴BaCl2溶液，振荡，产生大量白色沉淀，浅红棕色消失，发生反应的离子方程式是SO2+2H2O+Br2═4H++2Br﹣+SO42﹣、SO42﹣+Ba2+═BaSO4↓或SO2+2H2O+Br2+Ba2+═4H++2Br﹣+BaSO4↓（4）上述实验得到的结论是乙烯能使Br2的四氯化碳溶液褪色，干燥的SO2不能使Br2的四氯化碳溶液褪色．考点：乙醇的消去反应．专题：有机物的化学性质及推断．分析：（1）乙醇能在一定的条件下发生消去反应生成乙烯；（2）浓硫酸具有脱水性、吸水性和强氧化性；（3）①乙烯可与溴水发生加成反应；②溴单质可以和二氧化硫发生氧化还原反应；③a、氢氧化钠可以和二氧化硫发生反应；b、浓硫酸具有吸水性，可以做干燥剂，并能将乙烯氧化；c、二氧化硫可以使品红褪色，加热后红色会恢复；d、溴单质可以和二氧化硫发生氧化还原反应，硫酸根离子和钡离子反应会生成白色沉淀；（4）乙烯能使Br2的四氯化碳溶液褪色，二氧化硫和溴单质的反应必须在水溶液中进行．解答：解：（1）乙醇能在浓硫酸并加热的条件下发生消去反应生成乙烯，原理方程式为：，故答案为：；（2）浓硫酸具有脱水性，能使乙醇溶液“渐渐变黑”，故答案为：脱水性；（3）①根据甲的观点，溴水可以使B中溶液褪色，反应的化学方程式是CH2=CH2+Br2→CH2Br ﹣CH2Br，故答案为：CH2=CH2+Br2→CH2Br﹣CH2Br；②乙根据现象Ⅲ认为产生了SO2，在B中溴单质可以和二氧化硫发生氧化还原反应，故答案为：H2O、Br2；③a、根据甲的设计，洗气瓶中盛放的试剂是氢氧化钠，可以和二氧化硫反应，吸收二氧化硫，排除二氧化硫的干扰．故答案为：NaOH 溶液；b、根据乙的设计，C中盛放的试剂是，浓硫酸具有吸水性，可以做干燥剂，可将乙烯氧化为二氧化碳，排除在检验二氧化硫时乙烯的干扰，故答案为：浓硫酸；c、二氧化硫可以使品红褪色，加热后红色会恢复原来的红色，故答案为：加热已经褪色的品红溶液，若红色恢复，证明是SO2使品红溶液褪色而不是Br2；d、溴单质可以和二氧化硫发生氧化还原反应，生成硫酸根离子和溴离子，硫酸根离子和钡离子反应会生成白色沉淀，故答案为：SO2+2H2O+Br2═4H++2Br﹣+SO42﹣、SO42﹣+Ba2+═BaSO4↓或SO2+2H2O+Br2+Ba2+═4H++2Br﹣+BaSO4↓；（4）根据实验过程可以知道：乙烯能使Br2的四氯化碳溶液褪色，二氧化硫和溴单质的反应必须在水溶液中进行，故答案为：乙烯能使Br2的四氯化碳溶液褪色，干燥的SO2不能使Br2的四氯化碳溶液褪色．点评：本题考查学生乙醇的化学性质，结合实验考查增加了题目的难度，综合性较强，要求学生具有分析和解决问题的能力．11．（16分）（2013•朝阳区一模）吸水性高分子材料PAA、接枝PAA、用于化妆品的化合物己的合成路线如图：已知：Ⅰ．连在同一个碳原子上的两个羟基之间容易失去一分子水Ⅱ．两个羧酸分子的羧基之间能失去一分子水Ⅲ．请回答：（1）D中的官能团是醛基（2）D→E的化学方程式是（3）F→PAA的化学方程式是（4）①X的结构简式是ClCH2CHO②Y→W所需要的反应条件是氢氧化钠水溶液、加热（5）B为中学常见有机物，甲与FeCl3溶液发生显色反应，丙中的两个取代基互为邻位．①甲→乙的化学方程式是②关于丙的说法正确的是aca．能与银氨溶液发生银镜反应b．与有机物B互为同系物c．不存在芳香醇类的同分异构体（6）丁的核磁共振氢谱只有一种峰，在酸性条件下能水解，水解产物能与NaHCO3反应产生CO2．己的结构简式是．考点：有机物的推断．专题：有机物的化学性质及推断．分析：由接枝PAA的结构可知，PAA的结构简式为，W为HOCH2CH2OH；甲醇催化氧化生成D为HCHO，D发生信息Ⅲ反应生成E，故E为CH2=CHCHO，E与银氨溶液反应、酸化生成F，F为CH2=CHCOOH，CH2=CHCOOH发生加聚反应生成PAA；结构W的结构可知，乙醛与氯气发生取代反应生成X，X为ClCH2CHO，X与氢气发生加成反应生成Y为ClCH2CH2OH，Y水解生成W（HOCH2CH2OH）；乙醛发生催化氧化生成戊，为CH3COOH，丁的核磁共振氢谱只有一种峰，在酸性条件下能水解，水解产物能与NaHCO3反应产生CO2，结构反应信息Ⅱ可知，CH3COOH脱水生成丁为O=C（OCH2CH3）2；由（5）中可知，B为中学常见有机物，甲与FeCl3溶液发生显色反应，故甲中含有酚羟基，结合丙的分子式及结构特点、己的结构特点与反应信息Ⅰ、Ⅲ可知，丙的结构为，己的结构为，故乙为，甲为，B为苯酚，据此解答．解答：解：由接枝PAA的结构可知，PAA的结构简式为，W为HOCH2CH2OH；甲醇催化氧化生成D为HCHO，D发生信息Ⅲ反应生成E，故E为CH2=CHCHO，E与银氨溶液反应、酸化生成F，F为CH2=CHCOOH，CH2=CHCOOH发生加聚反应生成PAA；结构W的结构可知，乙醛与氯气发生取代反应生成X，X为ClCH2CHO，X与氢气发生加成反应生成Y为ClCH2CH2OH，Y水解生成W（HOCH2CH2OH）；乙醛发生催化氧化生成戊，为CH3COOH，丁的核磁共振氢谱只有一种峰，在酸性条件下能水解，水解产物能与NaHCO3反应产生CO2，结构反应信息Ⅱ可知，CH3COOH脱水生成丁为O=C（OCH2CH3）2；由（5）中可知，B为中学常见有机物，甲与FeCl3溶液发生显色反应，故甲中含有酚羟基，结合丙的分子式及结构特点、己的结构特点与反应信息Ⅰ、Ⅲ可知，丙的结构为，己的结构为，故乙为，甲为，B为苯酚，（1）由上述分析可知，D为HCHO，含有醛基，故答案为：醛基；（2）D→E是甲醛与乙醛发生信息Ⅲ反应生成CH2=CHCHO，反应方程式为：，故答案为：；（3）F为CH2=CHCOOH，发生加聚反应生成PAA，反应方程式为：，故答案为：；（4）①由上述分析可知，X为ClCH2CHO，故答案为：ClCH2CHO；②Y→W是ClCH2CH2OH在氢氧化钠水溶液、加热条件下发生水解反应生成HOCH2CH2OH，故答案为：氢氧化钠水溶液、加热；（5）①甲→乙是与氯气在光照条件下发生甲基上的取代反应生成，反应方程式为：，故答案为：；②丙是，含有醛基，能与银氨溶液发生银镜反应，与有机物B（苯酚），含有官能团不完全相同，二者不是同系物，芳香醇类中含有苯环，羟基连接苯环侧链的脂肪烃基上，结合丙的结构可知，苯环侧链不可能可以存在羟基连接苯环侧链的脂肪烃基上的结构，故丙不存在芳香醇类的同分异构体，故ac正确，b错误，故答案为：ac；（6）由上述分析可知，己的结构简式是，故答案为：．点评：本题考查有机物的推断与合成，需要学生对给予的反应信息进行利用，甲醇转化为甲的反应，是难点，中学不涉及，需要学生根据信息、结合丙、丁、己的结构结构推断推断丙，再进行逆推判断，对学生的逻辑推理有较高的要求．。

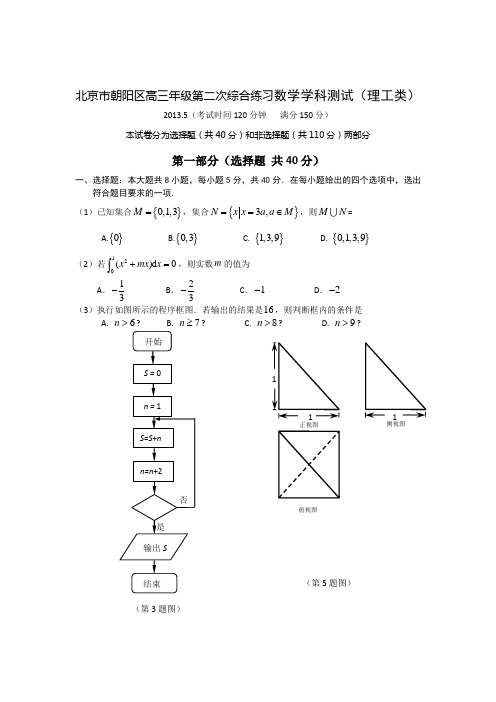
北京市朝阳区高三年级第二次综合练习数学学科测试（理工类）2013.5（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. （1）已知集合{}0,1,3M =，集合{}3,N x x a a M ==∈，则M N =A.{}0B.{}0,3C. {}1,3,9D. {}0,1,3,9 【答案】D【解析】{}3,{0,3,9}N x x a a M ==∈=，所以{0,1,3,9}M N = ，选D.（2）若120()d 0x mx x +=⎰，则实数m 的值为A ．13-B ．23- C ．1- D ．2- 【答案】B 【解析】12321001111()d ()03232x mx x x mx m +=+=+=⎰，解得23m =-，选B.（3）执行如图所示的程序框图．若输出的结果是16，则判断框内的条件是A. 6n >？B. 7n ≥？C. 8n >？D. 9n >？ 【答案】C【解析】第一次循环，1,3S n ==，不满足条件，循环。

第二次循环，134,5S n =+==，不满足条件，循环。

第三次循环，459,7S n =+==，不满足条件，循环。

第四次循环，9716,9S n =+==，满足条件，输出。

所以判断框内的条件是8n >，选C.（4）若双曲线22221(0,0)x y a b a b-=>>的渐近线与抛物线22y x =+有公共点，则此双曲线的离心率的取值范围是A ．[3,)+∞B ．(3,)+∞C ．(1,3]D ．(1,3) 【答案】A【解析】双曲线的渐近线为b y x a =±，不妨取b y x a =，代入抛物线得22b x x a=+，即220b x x a -+=，要使渐近线与抛物线22y x =+有公共点，则2()80ba∆=-≥，即228b a ≥，又22228b c a a =-≥，所以229c a ≥，所以29,3e e ≥≥。

北京市朝阳区2013年高考化学一模试卷一、选择题（共7小题，每小题6分，满分42分）3．（6分）（2013•朝阳区一模）Se、Br两种元素的部分信息如图所示，下列说法正确的是（）向少量苯酚稀溶液中逐滴加入饱和溴水，生成白色沉淀5．（6分）（2013•朝阳区一模）如图集气瓶中用滤纸折成的纸蝴蝶上喷洒了一种溶液，通入某种气体后，6．（6分）（2013•朝阳区一模）已知：H2（g）+I2（g）⇌2HI（g）△H=﹣14.9kJ/mol．某温度下在甲、乙两个恒容密闭容器中充入反应物，其起始浓度如下表所示．甲中反应达到平衡时，测得c（H2）=0.257．（6分）（2013•朝阳区一模）室温下，用0.100mol/L NaOH 溶液分别滴定20.00mL 0.100mol/L的盐酸和醋酸，滴定曲线如图所示．下列说法正确的是（），故二、解答题（共4小题，满分58分）8．（12分）（2013•朝阳区一模）工业上常以赤铁矿石（主要成分为Fe2O3）和焦炭为主要原料，在高温下炼铁．焦炭产生CO的反应是：C+O2CO2；C+CO22CO（1）CO还原赤铁矿的化学方程式是Fe2O3+3CO2Fe+3CO2（2）下列说法正确的是aba．为使赤铁矿石充分燃烧，需将其粉碎b．足量的空气能提高炼铁反应速率c．与生铁相比较，纯铁转化为“铁水”的温度低（3）生铁的用途很多，某电镀厂用生铁将废水中的Cr2O72﹣转化为Cr3+，流程图1：①气体A是H2②在上述酸性溶液中，生铁比纯铁产生Fe2+的速率快，原因是生铁中含有C，在硫酸溶液中形成无数微小原电池，加快反应速率③将Cr3+转化为Cr（OH）3的离子方程式是2Cr3++3Ca（OH）2═2Cr（OH）3↓+3Ca2+（4）电解法将一定浓度的酸性废水中的Cr2O7转化为Cr，其原理示意图2：①阳极附近溶液中Cr2O72﹣转化为Cr3+的离子方程式是6Fe2++Cr2O72﹣+14H+═6Fe3++2Cr3++7H2O②一段时间后，试管底部出现沉淀．解释生成沉淀的原因：随着电解进行，溶液中c（H）逐渐减少，c（OH﹣）浓度增大，生成Fe（OH）3和Cr（OH）3沉淀．2Fe+3CO9．（14分）（2013•朝阳区一模）燃煤产生的烟气中的氮氧化物NO x（主要为NO、NO2）易形成污染，必须经脱除达标后才能排放．（1）用化学方程式表示NO形成硝酸型酸雨的反应2NO+O2═2NO2、3NO2+H2O═2HNO3+NO（2）能作脱除剂的物质很多，下列说法正确的是aba．用H2O作脱除剂，不利于吸收含氮烟气中的NOb．用Na2SO3作脱除剂，O2会降低Na2SO3的利用率c．用CO作脱除剂，会使烟气中NO2的浓度增加（3）尿素[CO（NH2）2]在一定条件下能有效将NO x转化为N2．Ⅰ．已知可通过下列方法合成尿素：2NH3（g）+CO2（g）⇌H2NCOONH4（s）△H=﹣159.5kJ/molH2NCOONH4（s）⇌CO（NH2）2（s）+H2O（l）△H=+28.5kJ/mol①尿素释放出NH3的热化学方程式是CO（NH2）2（s）+H2O（l）⇌2NH3（g）+CO2（g）△H=+131kJ/mol②写出有利于尿素释放NH3的条件并说明理由升高温度；升高温度有利于平衡向吸热反应方向进行，同时温度升高，氨气的溶解度降低，均有利于向释放氨气的方向进行Ⅱ．CO（NH2）2与某种烟气（主要为N2、NO和O2）中的NO的物质的量比值分别为1：2、2：1、3：1时，NO脱除率随温度变化的曲线如图：①曲线a 对应CO（NH2）2与NO的物质的量比值是3：1．②曲线a、b、c中，800℃～900℃区间内发生主要反应的化学方程式是4NH3+6NO═5N2+6H2O或2CO （NH2）2+6NO═2CO2+4H2O+5N2．③900℃～1200℃区间内脱除率下降，NO浓度上升．发生的主要反应是4NH3+5O2═4NO+6H2O．④曲线a中，NO的起始浓度为6×10﹣4 mg/m3，从A点到B点经过0.8s，该时间段内NO的脱除速率为1.5×10﹣4mg/（m3•s）．10．（16分）（2013•朝阳区一模）实验室制乙烯时，产生的气体能使Br 2 的四氯化碳溶液褪色，甲、乙同学用下列实验验证．（气密性已检验，部分夹持装置略）．（1）烧瓶内产生乙烯的化学方程式是（2）溶液“渐渐变黑”，说明浓硫酸具有 脱水性 性． （3）分析使B 中溶液褪色的物质，甲认为是C 2H 4，乙认为不能排除SO 2的作用．①根据甲的观点，使B 中溶液褪色反应的化学方程式是 CH 2=CH 2+Br 2→CH 2Br ﹣CH 2Br②乙根据现象Ⅲ认为产生了SO 2，在B 中与SO 2 反应使溶液褪色的物质是 H 2O 、Br 2a ．根据甲的设计，洗气瓶中盛放的试剂是 NaOH 溶液b ．根据乙的设计，C 中盛放的试剂是 浓硫酸c ．能说明确实是SO 2使E 中溶液褪色的实验是 加热已经褪色的品红溶液，若红色恢复，证明是SO 2使品红溶液褪色而不是Br 2d ．乙为进一步验证其观点，取少量D 中溶液，加入几滴BaCl 2溶液，振荡，产生大量白色沉淀，浅红棕色消失，发生反应的离子方程式是 SO 2+2H 2O+Br 2═4H ++2Br ﹣+SO 42﹣、SO 42﹣+Ba 2+═BaSO 4↓或SO2+2H 2O+Br 2+Ba 2+═4H ++2Br ﹣+BaSO 4↓（4）上述实验得到的结论是 乙烯能使Br 2的四氯化碳溶液褪色，干燥的SO 2不能使Br 2的四氯化碳溶液褪色 ．11．（16分）（2013•朝阳区一模）吸水性高分子材料PAA、接枝PAA、用于化妆品的化合物己的合成路线如图：已知：Ⅰ．连在同一个碳原子上的两个羟基之间容易失去一分子水Ⅱ．两个羧酸分子的羧基之间能失去一分子水Ⅲ．请回答：（1）D中的官能团是醛基（2）D→E的化学方程式是（3）F→PAA的化学方程式是（4）①X的结构简式是ClCH2CHO②Y→W所需要的反应条件是氢氧化钠水溶液、加热（5）B为中学常见有机物，甲与FeCl3溶液发生显色反应，丙中的两个取代基互为邻位．①甲→乙的化学方程式是②关于丙的说法正确的是aca．能与银氨溶液发生银镜反应b．与有机物B互为同系物c．不存在芳香醇类的同分异构体（6）丁的核磁共振氢谱只有一种峰，在酸性条件下能水解，水解产物能与NaHCO3反应产生CO2．己的结构简式是．的结构简式为的分子式及结构特点、己的结构特点与反应信息Ⅰ、Ⅲ可知，丙的结构为，故乙为，甲为，，的分子式及结构特点、己的结构特点与反应信息Ⅰ、Ⅲ可知，丙的结构为，故乙为，甲为，故答案为：反应方程式为：故答案为：乙是与氯气在光照条件下发生甲基上的取代反应生成，反应方程式，故答案为：；，含有醛基，能与银氨溶液发生银镜反应，与有机物）由上述分析可知，己的结构简式是，故答案为：。

北京市朝阳区高三年级第二次综合练习数学学科测试（理工类）2013.5（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. （1）已知集合{}0,1,3M =，集合{}3,N x x a a M ==∈，则MN =A.{}0B.{}0,3C. {}1,3,9D. {}0,1,3,9 【答案】D【KS5U 解析】{}3,{0,3,9}N x x a a M ==∈=，所以{0,1,3,9}MN =，选D.（2）若120()d 0x mx x +=⎰，则实数m 的值为A ．13-B ．23- C ．1- D ．2- 【答案】B【KS5U 解析】123211111()d ()03232x mx x x mx m +=+=+=⎰，解得23m =-，选B. （3）执行如图所示的程序框图．若输出的结果是16，则判断框内的条件是A. 6n >？B. 7n ≥？C. 8n >？D. 9n >？ 【答案】C 【KS5U 解析】第一次循环，1,3S n ==，不满足条件，循环。

第二次循环，134,5S n =+==，不满足条件，循环。

第三次循环，459,7S n =+==，不满足条件，循环。

第四次循环，9716,9S n =+==，满足条件，输出。

所以判断框内的条件是8n >，选C.（4）若双曲线22221(0,0)x y a b a b-=>>的渐近线与抛物线22y x =+有公共点，则此双曲线的离心率的取值范围是A ．[3,)+∞B ．(3,)+∞C ．(1,3]D ．(1,3) 【答案】A【KS5U 解析】双曲线的渐近线为b y x a =±，不妨取b y x a =，代入抛物线得22bx x a=+，即220b x x a -+=，要使渐近线与抛物线22y x =+有公共点，则2()80b a∆=-≥，即228b a ≥，又22228b c a a =-≥，所以229c a ≥，所以29,3e e ≥≥。

北京市朝阳区高三年级第二次综合练习数学学科测试（理工类）2013.5（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.（1）已知集合{}0,1,3M =，集合{}3,N x x a a M ==∈，则M N =A.{}0B.{}0,3C. {}1,3,9D. {}0,1,3,9（2）若120()d 0x mx x +=⎰，则实数m 的值为A ．13-B ．23-C ．1-D ．2- （3）执行如图所示的程序框图．若输出的结果是16，则判断框内的条件是A. 6n >?B. 7n ≥?C. 8n >?D. 9n >?（第5题图）（第3题图）正视图 侧视图 俯视图（4）若双曲线22221(0,0)x y a b a b-=>>的渐近线与抛物线22y x =+有公共点，则此双曲线的离心率的取值范围是A ．[3,)+∞B ．(3,)+∞C ．(1,3]D ．(1,3)（5）某三棱锥的三视图如图所示，则该三棱锥的体积为A ．16B ．13C ．12D ．1 （6）某岗位安排3名职工从周一到周五值班，每天只安排一名职工值班，每人至少安排一天，至多安排两天，且这两天必须相邻，那么不同的安排方法有A ．10种B ．12种C ．18种D ．36种（7）已知函数()21(0)x f x a a =⋅+≠，定义函数(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩ 给出下列命题： ①()()F x f x =； ②函数()F x 是奇函数；③当0a <时，若0mn <，0m n +>，总有()()0F m F n +<成立，其中所有正确命题的序号是A ．②B ．①②C ．③D ．②③（8）点P 是棱长为1的正方体1111ABCD A B C D -的底面1111A B C D 上一点，则1PA PC 的取值范围是A ．1[1,]4-- B ．11[,]24-- C ．[1,0]- D ．1[,0]2- 第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.（9）i 为虚数单位，计算3i 1i +=+ ． （10）若直线l 与圆2cos ,:12sin x C y θθ=⎧⎨=-+⎩（θ为参数）相交于A ，B 两点，且弦AB 的中点坐标是(1,2)-，则直线l 的倾斜角为 ．（11）如图，PC 切圆O 于点C ，割线PAB 经过圆心O ，4,8PC PB ==，则tan COP ∠= ，△OBC 的面积是 ．（12）某公司一年购买某种货物600吨，每次都购买x 吨，运费为3万元/次，一年的总存储费用为2x 万元，若要使一年的总运费与总存储费用之和最小，则每次需购买 吨．（13将一个质点随机投放在关于,x y 的不等式组3419,1,1x y x y +≤⎧⎪≥⎨⎪≥⎩所构成的三角形区域内，则该质点到此三角形的三个顶点的距离均不小于1的概率是 ．（14）数列{21}n -的前n 项1,3,7,,21n -组成集合{1,3,7,,21}()n n A n *=-∈N ，从集合n A 中任取k (1,2,3,,)k n =个数，其所有可能的k 个数的乘积的和为k T （若只取一个数，规定乘积为此数本身），记12n n S T T T =+++．例如当1n =时，1{1}A =，11T =，11S =；当2n =时，2{1,3}A =，113T =+，213T =⨯，213137S =++⨯=.则当3n =时，3S = ；试写出n S = ．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.（15）（本小题满分13分）在△ABC 中， ,,A B C 所对的边分别为,,a b c ，且2()2cos sin()sin 222A A A f A =π-+-2cos 2A . （Ⅰ）求函数()f A 的最大值；（Ⅱ）若()0,,12f A C a 5π===b 的值．（16）（本小题满分14分）如图，四边形ABCD 是正方形，EA ⊥平面ABCD ，EA PD ，22AD PD EA ===，F ，G ， H 分别为PB ，EB ，PC的中点．（Ⅰ）求证：FG 平面PED ； （Ⅱ）求平面FGH 与平面PBC 所成锐二面角的大小；（Ⅲ）在线段PC 上是否存在一点M ,使直线FM 与直线 PA 所成的角为60？若存在，求出线段PM 的长；若 不存在，请说明理由. （17）（本小题满分13分） 为提高学生学习数学的兴趣，某地区举办了小学生“数 A DBC PE FGH（Ⅰ）求2(1,1,)3S --及(1,1,1,1)S --的值；（Ⅱ）当3n =时，求123(,,)S x x x 的最小值；（Ⅲ）求12(,,,)n S x x x 的最小值． 注：1i j i j n x x ≤<≤∑表示12,,,n x x x 中任意两个数i x ,j x （1i j n ≤<≤）的乘积之和. 北京市朝阳区高三年级第二次综合练习数学学科测试答案（理工类）2013.５二、填空题：（注：两空的填空，第一空3分，第二空2分） 三、解答题：（15）（本小题满分13分）解：（Ⅰ）因为22()2cos sin sin cos 2222A A A A f A =+-sin cos )4A A A π=-=-. 因为A 为三角形的内角，所以0A <<π，所以444A ππ3π-<-<.所以当42A ππ-=，即34A π=时，()f A . ………6分（Ⅱ）由题意知())04f A A π=-=，所以sin()04A π-=． 又因为444A ππ3π-<-<，所以04A π-=，所以4A π=． 又因为12C 5π=，所以3B π=．由正弦定理sin sin a b A B =得，sin sin 33sin sin 4a B b A π===π． …………13分（16）（本小题满分14分）（Ⅰ）证明：因为F ,G 分别为PB ，BE 的中点，所以FG PE .又FG ⊄平面PED ，PE ⊂平面PED ，所以FG 平面PED . …………4分（Ⅱ）因为EA ⊥平面ABCD ，EAPD ， 所以PD ⊥平面ABCD ，所以PD AD ⊥，PD CD ⊥.又因为四边形ABCD 是正方形，所以AD CD ⊥.如图，建立空间直角坐标系，因为22AD PD EA ===, 所以D ()0,0,0，P ()0,0,2，A ()2,0,0， C ()0,2,0，B ()2,2,0，(2,0,1)E ．…………5分 因为F ，G ， H 分别为PB ，EB ，PC 的中点，所以F ()1,1,1，G 1(2,1,)2，H (0,1,1). 所以1(1,0,)2GF =-，1(2,0,)2GH =-. 设1111(,,)x y z =n 为平面FGH 的一个法向量，则1100GF GH ⎧⋅=⎪⎨⋅=⎪⎩n n ,即11111021202x z x z ⎧-+=⎪⎪⎨⎪-+=⎪⎩， 再令11y =，得1(0,1,0)=n .(2,2,2)PB =-,(0,2,2)PC =-.设2222(,,)x y z =n 为平面PBC 的一个法向量,则2200PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n ,即222222220220x y z y z +-=⎧⎨-=⎩，令21z =，得2(0,1,1)=n . 所以12cos ,n n =1212⋅⋅n n n n=2. 所以平面FGH 与平面PBC 所成锐二面角的大小为4π. …………9分 （Ⅲ）假设在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为60.依题意可设PM PC λ=,其中01λ≤≤.由(0,2,2)PC =-,则(0,2,2)PM λλ=-.又因为FM FP PM =+,(1,1,1)FP =--，所以(1,21,12)FM λλ=---.因为直线FM 与直线PA 所成角为60，(2,0,2)PA =-， 所以cos ,FM PA =12，即12=58λ=. 所以55(0,,)44PM =-，524PM =. 所以在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为60，此时4PM =. ………………………………………14分（17）（本小题满分13分）解：（Ⅰ）根据统计数据可知，从这30名学生中任选一人，分数等级为“A 或B ”的频率为461013030303+==． 从本地区小学生中任意抽取一人，其“数独比赛”分数等级为“A 或B ”的概率约为13．……………………………………………………………………………………3分 （Ⅱ）由已知得，随机变量X 的可能取值为0，1，2，3．所以0033128(0)()()3327P X C ==⋅=； 112312124(1)()()33279P X C ==⋅==； 22131262(2)()()33279P X C ==⋅==；3303121(3)()()3327P X C ==⋅=． 随机变量X所以80123127272727EX =⨯+⨯+⨯+⨯=． ……………9分 （Ⅲ）设事件M ：从这30名学生中，随机选取2人，这两个人的成绩之差大于20分．设从这30名学生中，随机选取2人，记其比赛成绩分别为,m n ．显然基本事件的总数为230C ．不妨设m n >，当90m =时，60n =或40或30，其基本事件数为111141073()C C C C ⋅++；当70m =时，n =40或30，其基本事件数为111673()C C C ⋅+； 当60m =时，30n =，其基本事件数为11103C C ⋅；所以11111111141073673103230()()34()87C C C C C C C C C P M C ⋅+++⋅++⋅==． 所以从这30名学生中，随机选取2人，这两个人的成绩之差大于20分的概率为3487． ……………13分（18）（本小题满分1 3分）解：（Ⅰ）函数()f x 的定义域为R ，()()()()()()m x m x x f x x x --+'==++2222211111.…………1分 ①当m >0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-11，单调递减区间是(,)-∞-1，(,)+∞1. …………3分②当m <0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-∞-1，(,)+∞1，单调递减区间是(,)-11.……………5分（Ⅱ）依题意，“当m >0时，对于任意12,[0,2]x x ∈，12()()f x g x ≥恒成立”等价于 “当m >0 时，对于任意[0,2]x ∈， min max ()()f x g x ≥成立”.当m >0时，由（Ⅰ）知，函数()f x 在[0,1]上单调递增，在[1,2]上单调递减， 因为(0)1f =，2(2)115m f =+>，所以函数()f x 的最小值为(0)1f =. 所以应满足max ()1g x ≤. ……………………………………………………………6分因为2()e ax g x x =，所以2()(+2)e axg x ax x '=. ……………7分①当0a =时，函数2()g x x =，[0,2]x ∀∈，max ()(2)4g x g ==， 显然不满足max ()1g x ≤，故0a =不成立. ……………8分 ②当0a ≠时，令()0g x '=得，10x =，22x a =-. （ⅰ）当22a-≥，即10a -≤<时， 在[0,2]上()0g x '≥，所以函数()g x 在[0,2]上单调递增，所以函数2max ()(2)4e a g x g ==.由24e 1a ≤得，ln 2a ≤-，所以1ln 2a -≤≤-. ……………10分 （ⅱ）当202a<-<，即1a <-时,在2[0,)a-上()0g x '≥，在2(,2]a-上()0g x '<， 所以函数()g x 在2[0,)a -上单调递增，在2(,2]a-上单调递减， 所以max 2224()()eg x g a a =-=. 由2241e a ≤得，2ea ≤-，所以1a <-. ……………11分 （ⅲ）当20a -<，即0a >时,显然在[0,2]上()0g x '≥， 函数()g x 在[0,2]上单调递增，且2max ()(2)4e a g x g ==.显然2max ()4e 1a g x =≤不成立，故0a >不成立. ……………12分 综上所述，a 的取值范围是(,ln 2]-∞-. ……………13分（19）（本小题满分14分）解：（Ⅰ）依题意不妨设1(0,)B b -，2(0,)B b ，则1(1,)FB b =--，2(1,)FB b =-.由12FB FB a ⋅=-，得21b a -=-.又因为221a b -=，解得2,a b ==. 所以椭圆C 的方程为22143x y +=. ……………4分 （Ⅱ）依题直线l 的方程为(1)y k x =-. 由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩得2222(34)84120k x k x k +-+-=. 设11(,)M x y ，22(,)N x y ，则2122834k x x k +=+，212241234k x x k-=+. …………6分 所以弦MN 的中点为22243(,)3434k k P k k -++. ……………7分所以MN ===2212(1)43k k +=+. ……………9分直线PD 的方程为222314()4343k k y x k k k +=--++， 由0y =，得2243k x k =+，则22(,0)43k D k +，所以DP = …………11分所以224312(1)43DP k k MN k +==++=. ……………12分 又因为211k +>，所以21011k <<+.所以104<<. 所以DP MN的取值范围是1(0,)4. ………………………………………14分（20）（本小题满分13分）解：（Ⅰ）由已知得222(1,1,)11333S --=-+-=-． (1,1,1,1)1111112S --=----+=-． ……………3分（Ⅱ）设123(,,)S S x x x =．当3n =时，12312132313(,,)i j i j S S x x x x x x x x x x x ≤<≤===++∑．若固定23,x x ，仅让1x 变动，此时12132323123()S x x x x x x x x x x x =++=++， 因此2323min{(1,,),(1,,)}S S x x S x x ≥-．同理2333(1,,)min{(1,1,),(1,1,)}S x x S x S x ≥-．2333(1,,)min{(1,1,),(1,1,)}S x x S x S x -≥---．以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的123,,x x x 所达到， 于是12311,2,3min{(,,)}k x k S S x x x =±=≥．当1k x =±（1,2,3k =）时，22221231231[()()]2S x x x x x x =++-++ 212313()22x x x =++-． 因为123||1x x x ++≥，所以13122S ≥-=-，且当121x x ==，31x =-时，1S =-．因此min 1S =-． ……………8分 （Ⅲ）设121(,,,)n i j i j nS S x x x x x ≤<≤==∑121312321n n n n x x x x x x x x x x x x -=++++++++.固定23,,,n x x x ，仅让1x 变动，此时2312321()()n n n n S x x x x x x x x x x -=+++⋅+++++，因此2323min{(1,,,,),(1,,,,)}n n S S x x x S x x x ≥-．同理2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x ≥-． 2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x -≥---．以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的12,,,n x x x 所达到，于是1211,2,,min {(,,,)}k n x k nS S x x x =±=≥．当1k x =±（1,2,,k n =）时，222212121[()()]2n n S x x x x x x =+++-+++2121()22n n x x x =+++-． ①当n 为偶数时，2nS ≥-，若取1221n x x x ====，12221n nn x x x ++====-，则2n S =-，所以min 2nS =-．②当n 为奇数时，因为12||1n x x x +++≥，所以1(1)2S n ≥--，若取12121n x x x -====，1112221n n n x x x --++====-，则1(1)2S n =--，所以min 1(1)2S n =--． …………………………13分。

2013北京市朝阳区高三年级第二次综合练习数学理科北京市朝阳区高三年级第二次综合练习数学学科测试（理工类）2013.5（考试时间120分钟 满分150分） 本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.（1）已知集合{}0,1,3M =，集合{}3,N x x a a M ==∈，则MN=A.{}0B.{}0,3C.{}1,3,9 D. {}0,1,3,9（2）若120()d 0x mx x +=⎰，则实数m 的值为A ．13-B ．23- C ．1- D ．2-（3）执行如图所示的程序框图．若输出的结果是16，则判断框内的条件是 A. 6n >? B. 7n ≥? C. 8n >? D. 9n >?正视图侧视图俯视图D ．36种（7）已知函数()21(0)xf x a a =⋅+≠，定义函数(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩ 给出下列命题：①()()F x f x =； ②函数()F x 是奇函数；③当0a <时，若0mn <，0m n +>，总有()()0F m F n +<成立，其中所有正确命题的序号是 A ．②B ．①②C ．③D ．②③（8）点P 是棱长为1的正方体1111ABCD A B C D -的底面1111A B C D 上一点，则1PA PC 的取值范围是A ．1[1,]4--B ．11[,]24-- C ．[1,0]- D ．1[,0]2- 第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.（9）i 为虚数单位，计算3i1i+=+ ． （10）若直线l 与圆2cos ,:12sin x C y θθ=⎧⎨=-+⎩（θ为参数）相交于A ，B 两点，且弦AB 的中点坐标是(1,2)-，则直线l 的倾斜角为 ．（11）如图，PC 切圆O 于点C ，割线PAB 经过圆心O ，4,8PC PB ==，则tan COP ∠=，△OBC 的面积是 ．（12）某公司一年购买某种货物600吨，每次都购买x 吨，运费为3万元/次，一年的总存储费用为2x万元，若要使一年的总运费与总存储费用之和最小，则每次需购买 吨． （13将一个质点随机投放在关于,x y 的不等式组3419,1,1x y x y +≤⎧⎪≥⎨⎪≥⎩所构成的三角形区域内，则该质点到此三角形的三个顶点的距离均不小于1的概率是 ． （14）数列{21}n-的前n 项1,3,7,,21n -组成集合{1,3,7,,21}()n n A n *=-∈N ，从集合nA 中任取k (1,2,3,,)k n =个数，其所有可能的k 个数的乘积的和为kT （若只取一个数，规定乘积为此数本身），记12nnST T T =+++．例如当1n =时，1{1}A =，11T =，11S=；当2n =时，2{1,3}A=，113T =+，213T=⨯，213137S =++⨯=.则当3n =时，3S = ；试写出nS = ．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. （15）（本小题满分13分）在△ABC 中， ,,A B C 所对的边分别为,,a b c ，且2()2cossin()sin 222A A A f A =π-+-2cos 2A.（Ⅰ）求函数()f A 的最大值；（Ⅱ）若()0,,12f A C a 5π===b 的值．（16）（本小题满分14分）如图，四边形ABCD 是正方形，EA ⊥平面ABCD ，EAPD，22AD PD EA ===，F ，G ， H 分别为PB ，EB ，PC 的中点． （Ⅰ）求证：FG 平面PED ； （Ⅱ）求平面FGH 与平面PBC 所成锐二面角的大小；（Ⅲ）在线段PC 上是否存在一点M,使直线FM 与直线DBCPE F GHPA所成的角为60？若存在，求出线段PM的长；若不存在，请说明理由.（17）（本小题满分13分）为提高学生学习数学的兴趣，某地区举办了小学生“数独比赛”.比赛成绩共有90分，70分，60分，40分，30分五种，按本次比赛成绩共分五个等级．从参加比赛的学生中随机抽取了30名学生，并把他们的比赛成绩按这五个等级进行了统计，得到如下数据表：（Ⅰ）根据上面的统计数据，试估计从本地区参加“数独比赛”的小学生中任意抽取一人，其成绩等级为“A或B”的概率；（Ⅱ）根据（Ⅰ）的结论，若从该地区参加“数独比赛”的小学生（参赛人数很多）中任选3人，记X 表示抽到成绩等级为“A 或B ”的学生人数，求X 的分布列及其数学期望EX ； （Ⅲ）从这30名学生中，随机选取2人，求“这两个人的成绩之差大于20分”的概率．（18）（本小题满分13分）已知函数()mx f x x =++211（m ≠0），2()e ()axg x x a =∈R .（Ⅰ）求函数()f x 的单调区间； （Ⅱ）当m >0时，若对任意12,[0,2]x x∈，12()()f x g x ≥恒成立，求a 的取值范围.（19）（本小题满分14分）已知椭圆2222:1x y C a b+=(0)a b >>的右焦点为F (1,0)，短轴的端点分别为12,B B ,且12FB FBa⋅=-.（Ⅰ）求椭圆C 的方程；（Ⅱ）过点F 且斜率为k (0)k ≠的直线l 交椭圆于,M N 两点，弦MN 的垂直平分线与x 轴相交于点D .设弦MN 的中点为P ，试求DPMN 的取值范围．（20）（本小题满分13分）已知实数12,,,nx x x （2n ≥）满足||1(1,2,3,,)ix i n ≤=，记121(,,,)n i ji j nS x x x x x ≤<≤=∑．（Ⅰ）求2(1,1,)3S --及(1,1,1,1)S --的值； （Ⅱ）当3n =时，求123(,,)S x x x 的最小值；（Ⅲ）求12(,,,)n S x x x 的最小值．注：1i ji j nx x ≤<≤∑表示12,,,nx x x 中任意两个数ix ,jx （1i j n ≤<≤）的乘积之和.北京市朝阳区高三年级第二次综合练习数学学科测试答案（理工类）2013.５一、选择题：二、填空题：（注：两空的填空，第一空3分，第二空2分） 三、解答题：（15）（本小题满分13分）解：（Ⅰ）因为22()2cos sin sincos 2222A A A Af A =+- sin cos )4A A A π=-=-.因为A 为三角形的内角，所以0A <<π，所以444A ππ3π-<-<. 所以当42A ππ-=，即34A π=时，()f A 取得最大值，. ………6分 （Ⅱ）由题意知())04f A A π=-=，所以sin()04A π-=． 又因为444A ππ3π-<-<，所以04A π-=，所以4A π=． 又因为12C 5π=，所以3B π=．由正弦定理sin sin a bA B=得，sin sin 33sin sin 4a Bb Aπ===π． …………13分（16）（本小题满分14分）（Ⅰ）证明：因为F ,G 分别为PB ，BE 的中点，所以FG PE.又FG ⊄平面PED ，PE ⊂平面PED ，所以FG平面PED.…………4分（Ⅱ）因为EA ⊥平面ABCD ，EAPD，所以PD ⊥平面ABCD ， 所以PD AD ⊥，PD CD ⊥. 又因为四边形ABCD 是正方形，所以AD CD ⊥.如图，建立空间直角坐标系，因为22AD PD EA ===,所以D ()0,0,0，P ()0,0,2，A ()2,0,0，C ()0,2,0，B ()2,2,0，(2,0,1)E ．………5分因为F ，G ， H 分别为PB ，EB ，PC 的中点，所以F ()1,1,1，G 1(2,1,)2，H (0,1,1). 所以1(1,0,)2GF =-，1(2,0,)2GH =-.设1111(,,)x y z =n 为平面FGH 的一个法向量，则110GF GH ⎧⋅=⎪⎨⋅=⎪⎩n n ,即11111021202x z x z ⎧-+=⎪⎪⎨⎪-+=⎪⎩，再令11y =，得1(0,1,0)=n .(2,2,2)PB =-,(0,2,2)PC =-.设2222(,,)x y z =n 为平面PBC的一个法向量,则2200PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n ,即222222220220x yz y z+-=⎧⎨-=⎩，令21z=，得2(0,1,1)=n.所以12cos,n n =1212⋅⋅n n n n=2.所以平面FGH 与平面PBC 所成锐二面角的大小为4π. …………9分 （Ⅲ）假设在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为60.依题意可设PM PC λ=,其中01λ≤≤. 由(0,2,2)PC =-,则(0,2,2)PM λλ=-. 又因为FM FP PM=+,(1,1,1)FP =--，所以(1,21,12)FM λλ=---.因为直线FM 与直线PA 所成角为60，(2,0,2)PA =-， 所以cos,FM PA=12，即12=58λ=.所以55(0,,)44PM =-，52PM=.所以在线段PC 上存在一点M ,使直线FM 与直线PA所成角为60，此时PM =.………………………………………14分 （17）（本小题满分13分）解：（Ⅰ）根据统计数据可知，从这30名学生中任选一人，分数等级为“A 或B ”的频率为461013030303+==． 从本地区小学生中任意抽取一人，其“数独比赛”分数等级为“A 或B ”的概率约为13．……………………………………………………………………………………3分 （Ⅱ）由已知得，随机变量X 的可能取值为0，1，2，3．所以0033128(0)()()3327P X C ==⋅=； 112312124(1)()()33279P X C ==⋅==； 22131262(2)()()33279P X C ==⋅==；3303121(3)()()3327P X C ==⋅=．随机变量X 的分布列为所以812610123127272727EX =⨯+⨯+⨯+⨯=． ……………9分（Ⅲ）设事件M ：从这30名学生中，随机选取2人，这两个人的成绩之差大于20分． 设从这30名学生中，随机选取2人，记其比赛成绩分别为,m n ．显然基本事件的总数为230C ．不妨设m n >，当90m =时，60n =或40或30，其基本事件数为111141073()CC C C ⋅++；当70m =时，n =40或30，其基本事件数为111673()C C C ⋅+；当60m =时，30n =，其基本事件数为11103C C ⋅；所以11111111141073673103230()()34()87C C C C C C C C C P M C ⋅+++⋅++⋅==．所以从这30名学生中，随机选取2人，这两个人的成绩之差大于20分的概率为3487．……………13分（18）（本小题满分1 3分） 解：（Ⅰ）函数()f x 的定义域为R，()()()()()()m x m x x f x x x --+'==++2222211111.…………1分①当m >0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-11，单调递减区间是(,)-∞-1，(,)+∞1.…………3分②当m <0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-∞-1，(,)+∞1，单调递减区间是(,)-11.……………5分 （Ⅱ）依题意，“当m >0时，对于任意12,[0,2]x x∈，12()()f xg x ≥恒成立”等价于 “当m >0 时，对于任意[0,2]x ∈， minmax()()f x g x ≥成立”.当m >0时，由（Ⅰ）知，函数()f x 在[0,1]上单调递增，在[1,2]上单调递减，因为(0)1f =，2(2)115mf =+>，所以函数()f x 的最小值为(0)1f =.所以应满足max ()1g x ≤. ……………………………………………………………6分 因为2()e axg x x =，所以2()(+2)e axg x ax x '=. (7)分①当0a =时，函数2()g x x =，[0,2]x ∀∈，max()(2)4g x g ==，显然不满足max ()1g x ≤，故0a =不成立. ……………8分②当0a ≠时，令()0g x '=得，10x=，22xa=-.（ⅰ）当22a -≥，即10a -≤<时，在[0,2]上()0g x '≥，所以函数()g x 在[0,2]上单调递增，所以函数2max()(2)4e ag x g ==.由24e 1a ≤得，ln 2a ≤-，所以1ln 2a -≤≤-. ……………10分（ⅱ）当202a <-<，即1a <-时,在2[0,)a -上()0g x '≥，在2(,2]a -上()0g x '<， 所以函数()g x 在2[0,)a -上单调递增，在2(,2]a-上单调递减，所以max2224()()eg x g a a =-=.由2241e a ≤得，2ea ≤-，所以1a <-. ……………11分（ⅲ）当20a -<，即0a >时,显然在[0,2]上()0g x '≥，函数()g x 在[0,2]上单调递增，且2max ()(2)4e ag x g ==.显然2max ()4e 1a g x =≤不成立，故0a >不成立. ……………12分综上所述，a的取值范围是(,ln 2]-∞-. ……………13分（19）（本小题满分14分）解：（Ⅰ）依题意不妨设1(0,)B b -，2(0,)B b ，则1(1,)FB b =--，2(1,)FB b =-.由12FB FBa⋅=-，得21ba-=-.又因为221ab -=，解得2,a b ==. 所以椭圆C的方程为22143x y +=. ……………4分（Ⅱ）依题直线l 的方程为(1)y k x =-.由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩得2222(34)84120k x k x k +-+-=.设11(,)M x y ，22(,)N x y ，则2122834k x x k +=+，212241234k x x k -=+. …………6分 所以弦MN的中点为22243(,)3434k k P k k-++. ……………7分所以MN ===2212(1)43k k +=+.……………9分直线PD 的方程为222314()4343k k y x k k k +=--++，由0y =，得2243k x k =+，则22(,0)43k D k +，所以DP =.…………11分所以224312(1)43DP k k MN k +==++=. ……………12分又因为211k+>，所以21011k <<+.所以104<<. 所以DP MN的取值范围是1(0,)4. ………………………………………14分（20）（本小题满分13分）解：（Ⅰ）由已知得222(1,1,)11333S --=-+-=-．(1,1,1,1)1111112S --=----+=-．……………3分（Ⅱ）设123(,,)S S x x x =．当3n =时，12312132313(,,)i j i j S S x x x x x x x x x x x ≤<≤===++∑．若固定23,x x ，仅让1x 变动，此时12132323123()S x x x x x x x x x x x =++=++，因此2323min{(1,,),(1,,)}S S x x S x x ≥-．同理2333(1,,)min{(1,1,),(1,1,)}S x x S x S x ≥-．2333(1,,)min{(1,1,),(1,1,)}S x x S x S x -≥---．以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的123,,x x x 所达到，于是12311,2,3min{(,,)}k x k S S x x x =±=≥．当1kx=±（1,2,3k =）时，22221231231[()()]2S x xx x x x =++-++212313()22x x x =++-．因为123||1x xx ++≥，所以13122S ≥-=-，且当121x x ==，31x=-时，1S =-．因此min 1S =-．……………8分 （Ⅲ）设121(,,,)n i ji j nS S x x x x x ≤<≤==∑121312321n n n nx xx x x x x x x x x x -=++++++++. 固定23,,,nx x x ，仅让1x 变动，此时2312321()()n n n n S x x x x x x x x x x -=+++⋅+++++， 因此2323min{(1,,,,),(1,,,,)}n n S S x x x S x x x ≥-．同理2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x ≥-．2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x -≥---．以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的12,,,nx x x 所达到，于是1211,2,,min {(,,,)}k n x k nS S x x x =±=≥． 当1k x =±（1,2,,k n=）时，222212121[()()]2n n S x x x x x x =+++-+++2121()2n x x x =+++-．①当n 为偶数时，2n S ≥-， 若取1221n x xx ====，12221nnn x x x ++====-，则2n S =-，所以min2nS=-．②当n 为奇数时，因为12||1n x xx +++≥，所以1(1)2S n ≥--，若取12121n xx x -====，1112221n n n xx x --++====-，则1(1)2S n =--，所以min 1(1)2S n =--． …………………………13分。

北京市朝阳区高三年级第二次综合练习数学学科测试（理工类）2013.5（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. （1）已知集合{}0,1,3M =，集合{}3,N x x a a M ==∈，则M N =A.{}0B.{}0,3C. {}1,3,9D. {}0,1,3,9 （2）若12()d 0xmx x +=⎰，则实数m 的值为A ．13-B ．23- C ．1- D ．2- （3）执行如图所示的程序框图．若输出的结果是16，则判断框内的条件是A. 6n >?B. 7n ≥?C. 8n >?D. 9n >?（第5题图）（第3题图）111正视图侧视图俯视图（4）若双曲线22221(0,0)x y a b a b-=>>的渐近线与抛物线22y x =+有公共点，则此双曲线的离心率的取值范围是A ．[3,)+∞B ．(3,)+∞C ．(1,3]D ．(1,3) （5）某三棱锥的三视图如图所示，则该三棱锥的体积为A ．16B ．13 C ．12D ．1 （6）某岗位安排3名职工从周一到周五值班，每天只安排一名职工值班，每人至少安排一天，至多安排两天，且这两天必须相邻，那么不同的安排方法有A ．10种B ．12种C ．18种D ．36种（7）已知函数()21(0)xf x a a =⋅+≠，定义函数(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩给出下列命题：①()()F x f x =； ②函数()F x 是奇函数；③当0a <时，若0mn <，0m n +>，总有()()0F m F n +<成立，其中所有正确命题的序号是 A ．②B ．①②C ．③D ．②③（8）点P 是棱长为1的正方体1111ABCD A BC D -的底面1111A B C D 上一点，则1PA PC的取值范围是A ．1[1,]4-- B ．11[,]24-- C ．[1,0]- D ．1[,0]2- 第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上. （9）i 为虚数单位，计算3i1i+=+ ． （10）若直线l 与圆2cos ,:12sin x C y θθ=⎧⎨=-+⎩（θ为参数）相交于A ，B 两点，且弦AB 的中点坐标是(1,2)-，则直线l 的倾斜角为 ．（11）如图，PC 切圆O 于点C ，割线PAB 经过圆心O ，4,8PC PB ==，则tan COP ∠= ，△OBC 的面积是 ．（12）某公司一年购买某种货物600吨，每次都购买x 吨，运费为3万元/次，一年的总存储费用为2x万元，若要使一年的总运费与总存储费用之和最小，则每次需购买 吨．（13将一个质点随机投放在关于,x y 的不等式组3419,1,1x y x y +≤⎧⎪≥⎨⎪≥⎩所构成的三角形区域内，则该质点到此三角形的三个顶点的距离均不小于1的概率是 ．（14）数列{21}n -的前n 项1,3,7,,21n - 组成集合{1,3,7,,21}()n n A n *=-∈N ，从集合n A 中任取k (1,2,3,,)k n = 个数，其所有可能的k 个数的乘积的和为k T （若只取一个数，规定乘积为此数本身），记12n n S T T T =+++ ．例如当1n =时，1{1}A =，11T =，11S =；当2n =时，2{1,3}A =，113T =+，213T =⨯，213137S =++⨯=.则当3n =时，3S = ；试写出n S = ．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. （15）（本小题满分13分） 在△ABC 中， ,,A B C 所对的边分别为,,a b c ，且2()2cossin()sin 222A A A f A =π-+-2cos 2A. （Ⅰ）求函数()f A 的最大值；（Ⅱ）若()0,,12f A C a 5π===b 的值．（16）（本小题满分14分）如图，四边形ABCD 是正方形，EA ⊥平面ABCD ，EA PD ，22AD PD EA ===，F ，G ，H 分别为PB ，EB ，PC 的中点．（Ⅰ）求证：FG 平面PED ；（Ⅱ）求平面FGH 与平面PBC 所成锐二面角的大小； （Ⅲ）在线段PC 上是否存在一点M ,使直线FM 与直线PA 所成的角为60？若存在，求出线段PM 的长；若不存在，请说明理由.（17）（本小题满分13分） 为提高学生学习数学的兴趣，某地区举办了小学生“数独比赛”.比赛成绩共有90分，70分，60分，40分，30分五种，按本次比赛成绩共分五个等级．从参加比赛的学生中随机抽取了30名学生，并把他们的比赛成绩按这五个等级进行了统计，得到如下数据表：A DB CPEFGH（Ⅰ）根据上面的统计数据，试估计从本地区参加“数独比赛”的小学生中任意抽取一人，其成绩等级为“A 或B ”的概率；（Ⅱ）根据（Ⅰ）的结论，若从该地区参加“数独比赛”的小学生（参赛人数很多）中任选3人，记X 表示抽到成绩等级为“A 或B ”的学生人数，求X 的分布列及其数学期望EX ； （Ⅲ）从这30名学生中，随机选取2人，求“这两个人的成绩之差大于20分”的概率．（18）（本小题满分13分）已知函数()mxf x x =++211（m ≠0），2()e ()ax g x x a =∈R . （Ⅰ）求函数()f x 的单调区间；（Ⅱ）当m >0时，若对任意12,[0,2]x x ∈，12()()f x g x ≥恒成立，求a 的取值范围.（19）（本小题满分14分）已知椭圆2222:1x y C a b+=(0)a b >>的右焦点为F (1,0)，短轴的端点分别为12,B B ,且12FB FB a ⋅=-.（Ⅰ）求椭圆C 的方程；（Ⅱ）过点F 且斜率为k (0)k ≠的直线l 交椭圆于,M N 两点，弦MN 的垂直平分线与x 轴相交于点D .设弦MN 的中点为P ，试求DP MN的取值范围．（20）（本小题满分13分）已知实数12,,,n x x x （2n ≥）满足||1(1,2i x i n≤= ，记121(,,,)n i j i j nS x x x x x ≤<≤=∑．（Ⅰ）求2(1,1,)3S --及(1,1,1,1)S --的值； （Ⅱ）当3n =时，求123(,,)S x x x 的最小值； （Ⅲ）求12(,,,)n S x x x 的最小值．注：1i j i j nx x ≤<≤∑表示12,,,n x x x 中任意两个数i x ,j x （1i j n ≤<≤）的乘积之和.北京市朝阳区高三年级第二次综合练习数学学科测试答案（理工类）2013.５一、选择题：二、填空题：（注：两空的填空，第一空3分，第二空2分） 三、解答题： （15）（本小题满分13分） 解：（Ⅰ）因为22()2cossin sin cos 2222A A A Af A =+- sin cos )4A A A π=-=-.因为A 为三角形的内角，所以0A <<π，所以444A ππ3π-<-<. 所以当42A ππ-=，即34A π=时，()f A ………6分（Ⅱ）由题意知())04f A A π=-=，所以sin()04A π-=．又因为444A ππ3π-<-<，所以04A π-=，所以4A π=．又因为12C 5π=，所以3B π=．由正弦定理sin sin a b A B =得，sinsin 33sin sin 4a Bb A π===π． …………13分 （16）（本小题满分14分）（Ⅰ）证明：因为F ,G 分别为PB ，BE 的中点，所以FG PE .又FG ⊄平面PED ，PE ⊂平面PED ，所以FG 平面PED . …………4分 （Ⅱ）因为EA ⊥平面ABCD ，EA PD ，所以PD ⊥平面ABCD ， 所以PD AD ⊥，PD CD ⊥. 又因为四边形ABCD 是正方形， 所以AD CD ⊥.如图，建立空间直角坐标系， 因为22AD PD EA ===,所以D ()0,0,0，P ()0,0,2，A ()2,0,0，C ()0,2,0，B ()2,2,0，(2,0,1)E ．…………5分因为F ，G ， H 分别为PB ，EB ，PC 的中点，所以F ()1,1,1，G 1(2,1,)2，H (0,1,1). 所以1(1,0,)2GF =- ，1(2,0,)2GH =- .设1111(,,)x y z =n 为平面FGH 的一个法向量，则1100GF GH ⎧⋅=⎪⎨⋅=⎪⎩n n ,即11111021202x z x z ⎧-+=⎪⎪⎨⎪-+=⎪⎩， 再令11y =，得1(0,1,0)=n .(2,2,2)PB =- ,(0,2,2)PC =-.设2222(,,)x y z =n 为平面PBC 的一个法向量,则220PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n , 即222222220220x y z y z +-=⎧⎨-=⎩，令21z =，得2(0,1,1)=n .所以12cos ,n n =1212⋅⋅n n n n=2. 所以平面FGH 与平面PBC 所成锐二面角的大小为4π. …………9分 （Ⅲ）假设在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为60.依题意可设PM PC λ=,其中01λ≤≤.由(0,2,2)PC =- ,则(0,2,2)PM λλ=-.又因为FM FP PM =+ ,(1,1,1)FP =-- ，所以(1,21,12)FM λλ=---.因为直线FM 与直线PA 所成角为60，(2,0,2)PA =-，所以cos ,FM PA =12，即12=，解得58λ=.所以55(0,,)44PM =-，PM = 所以在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为60，此时4PM =. ………………………………………14分（17）（本小题满分13分） 解：（Ⅰ）根据统计数据可知，从这30名学生中任选一人，分数等级为“A 或B ”的频率为461013030303+==． 从本地区小学生中任意抽取一人，其“数独比赛”分数等级为“A 或B ”的概率约为13．……………………………………………………………………………………3分 （Ⅱ）由已知得，随机变量X 的可能取值为0，1，2，3．所以0033128(0)()()3327P X C ==⋅=；112312124(1)()()33279P X C ==⋅==；22131262(2)()()33279P X C ==⋅==；3303121(3)()()3327P X C ==⋅=．随机变量X 的分布列为所以80123127272727EX =⨯+⨯+⨯+⨯=． ……………9分 （Ⅲ）设事件M ：从这30名学生中，随机选取2人，这两个人的成绩之差大于20分．设从这30名学生中，随机选取2人，记其比赛成绩分别为,m n ．显然基本事件的总数为230C ． 不妨设m n >，当90m =时，60n =或40或30，其基本事件数为111141073()C C C C ⋅++； 当70m =时，n =40或30，其基本事件数为111673()C C C ⋅+；当60m =时，30n =，其基本事件数为11103C C ⋅； 所以11111111141073673103230()()34()87C C C C C C C C C P M C ⋅+++⋅++⋅==． 所以从这30名学生中，随机选取2人，这两个人的成绩之差大于20分的概率为3487． ……………13分（18）（本小题满分1 3分）解：（Ⅰ）函数()f x 的定义域为R ，()()()()()()m x m x x f x x x --+'==++2222211111.…………1分 ①当m >0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-11，单调递减区间是(,)-∞-1，(,)+∞1. …………3分②当m <0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-∞-1，(,)+∞1，单调递减区间是(,)-11.……………5分（Ⅱ）依题意，“当m >0时，对于任意12,[0,2]x x ∈，12()()f x g x ≥恒成立”等价于 “当m >0时，对于任意[0,2]x ∈， min max ()()f x g x ≥成立”.当m >0时，由（Ⅰ）知，函数()f x 在[0,1]上单调递增，在[1,2]上单调递减， 因为(0)1f =，2(2)115mf =+>，所以函数()f x 的最小值为(0)1f =.所以应满足max ()1g x ≤. ……………………………………………………………6分因为2()e ax g x x =，所以2()(+2)e ax g x ax x '=. ……………7分 ①当0a =时，函数2()g x x =，[0,2]x ∀∈，max ()(2)4g x g ==，显然不满足max ()1g x ≤，故0a =不成立. ……………8分 ②当0a ≠时，令()0g x '=得，10x =，22x a=-. （ⅰ）当22a-≥，即10a -≤<时， 在[0,2]上()0g x '≥，所以函数()g x 在[0,2]上单调递增，所以函数2max ()(2)4e a g x g ==. 由24e1a≤得，ln 2a ≤-，所以1ln 2a -≤≤-. ……………10分（ⅱ）当202a <-<，即1a <-时, 在2[0,)a -上()0g x '≥，在2(,2]a-上()0g x '<，所以函数()g x 在2[0,)a -上单调递增，在2(,2]a -上单调递减，所以max 2224()()eg x g a a =-=.由2241e a ≤得，2e a ≤-，所以1a <-. ……………11分 （ⅲ）当20a-<，即0a >时,显然在[0,2]上()0g x '≥，函数()g x 在[0,2]上单调递增，且2max ()(2)4e a g x g ==.显然2max ()4e 1a g x =≤不成立，故0a >不成立. ……………12分 综上所述，a 的取值范围是(,ln 2]-∞-. ……………13分 （19）（本小题满分14分）解：（Ⅰ）依题意不妨设1(0,)B b -，2(0,)B b ，则1(1,)FB b =-- ，2(1,)FB b =- .由12FB FB a ⋅=- ，得21b a -=-.又因为221a b -=，解得2,a b ==.所以椭圆C 的方程为22143x y +=. ……………4分 （Ⅱ）依题直线l 的方程为(1)y k x =-.由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩得2222(34)84120k x k x k +-+-=.设11(,)M x y ，22(,)N x y ，则2122834k x x k +=+，212241234k x x k -=+. …………6分所以弦MN 的中点为22243(,)3434k k P k k-++. ……………7分所以MN === 2212(1)43k k +=+. ……………9分直线PD 的方程为222314()4343k k y x k k k +=--++， 由0y =，得2243k x k =+，则22(,0)43k D k +，所以DP = …………11分所以224312(1)43DP k k MN k +==++=. ……………12分 又因为211k +>，所以21011k <<+.所以104<<. 所以DP MN的取值范围是1(0,)4. ………………………………………14分（20）（本小题满分13分）解：（Ⅰ）由已知得222(1,1,)11333S --=-+-=-． (1,1,1,1)1111112S --=----+=-． ……………3分 （Ⅱ）设123(,,)S S x x x =．当3n =时，12312132313(,,)i j i j S S x x x x x x x x x x x ≤<≤===++∑．若固定23,x x ，仅让1x 变动，此时12132323123()S x x x x x x x x x x x =++=++， 因此2323min{(1,,),(1,,)}S S x x S x x ≥-．同理2333(1,,)min{(1,1,),(1,1,)}S x x S x S x ≥-．2333(1,,)min{(1,1,),(1,1,)}S x x S x S x -≥---．以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的123,,x x x 所达到， 于是12311,2,3min{(,,)}k x k S S x x x =±=≥． 当1k x =±（1,2,3k =）时，22221231231[()()]2S x x x x x x =++-++ 212313()22x x x =++-． 因为123||1x x x ++≥，所以13122S ≥-=-，且当121x x ==，31x =-时，1S =-． 因此min 1S =-． ……………8分 （Ⅲ）设121(,,,)n i j i j n S S x x x x x ≤<≤==∑121312321n n n n x x x x x x x x x x x x -=++++++++ .固定23,,,n x x x ，仅让1x 变动，此时2312321()()n n n n S x x x x x x x x x x -=+++⋅+++++ ， 因此2323min{(1,,,,),(1,,,,)}n n S S x x x S x x x ≥- ． 同理2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x ≥- ． 2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x -≥--- ． 以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的12,,,n x x x 所达到，于是1211,2,,min {(,,,)}k n x k n S S x x x =±=≥ ． 当1k x =±（1,2,,k n = ）时，222212121[()()]2n n S x x x x x x =+++-+++ 2121()22n n x x x =+++- ． ①当n 为偶数时，2n S ≥-， 若取1221n x x x ==== ，12221nn n x x x ++====- ，则2n S =-，所以min 2n S =-． ②当n 为奇数时，因为12||1n x x x +++≥ ，所以1(1)2S n ≥--， 若取12121n x x x -==== ，1112221n n n x x x --++====- ，则1(1)2S n =--， 所以min 1(1)2S n =--． …………………………13分。

北京市朝阳区高三年级第二次综合练习数学学科测试（理工类）2013.5（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. （1）已知集合{}0,1,3M =，集合{}3,N x x a a M ==∈，则M N =A.{}0B.{}0,3C. {}1,3,9D. {}0,1,3,9 （2）若12()d 0xmx x +=⎰，则实数m 的值为A ．13-B ．23- C ．1- D ．2- （3）执行如图所示的程序框图．若输出的结果是16，则判断框内的条件是A. 6n >?B. 7n ≥?C. 8n >?D. 9n >?（第5题图）（第3题图）111正视图侧视图俯视图（4）若双曲线22221(0,0)x y a b a b-=>>的渐近线与抛物线22y x =+有公共点，则此双曲线的离心率的取值范围是A ．[3,)+∞B ．(3,)+∞C ．(1,3]D ．(1,3) （5）某三棱锥的三视图如图所示，则该三棱锥的体积为A ．16B ．13 C ．12D ．1 （6）某岗位安排3名职工从周一到周五值班，每天只安排一名职工值班，每人至少安排一天，至多安排两天，且这两天必须相邻，那么不同的安排方法有A ．10种B ．12种C ．18种D ．36种（7）已知函数()21(0)xf x a a =⋅+≠，定义函数(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩给出下列命题：①()()F x f x =； ②函数()F x 是奇函数；③当0a <时，若0mn <，0m n +>，总有()()0F m F n +<成立，其中所有正确命题的序号是 A ．②B ．①②C ．③D ．②③（8）点P 是棱长为1的正方体1111ABCD A BC D -的底面1111A B C D 上一点，则1PA PC的取值范围是A ．1[1,]4-- B ．11[,]24-- C ．[1,0]- D ．1[,0]2- 第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上. （9）i 为虚数单位，计算3i1i+=+ ． （10）若直线l 与圆2cos ,:12sin x C y θθ=⎧⎨=-+⎩（θ为参数）相交于A ，B 两点，且弦AB 的中点坐标是(1,2)-，则直线l 的倾斜角为 ．（11）如图，PC 切圆O 于点C ，割线PAB 经过圆心O ，4,8PC PB ==，则tan COP ∠= ，△OBC 的面积是 ．（12）某公司一年购买某种货物600吨，每次都购买x 吨，运费为3万元/次，一年的总存储费用为2x万元，若要使一年的总运费与总存储费用之和最小，则每次需购买 吨．（13将一个质点随机投放在关于,x y 的不等式组3419,1,1x y x y +≤⎧⎪≥⎨⎪≥⎩所构成的三角形区域内，则该质点到此三角形的三个顶点的距离均不小于1的概率是 ．（14）数列{21}n -的前n 项1,3,7,,21n - 组成集合{1,3,7,,21}()n n A n *=-∈N ，从集合n A 中任取k (1,2,3,,)k n = 个数，其所有可能的k 个数的乘积的和为k T （若只取一个数，规定乘积为此数本身），记12n n S T T T =+++ ．例如当1n =时，1{1}A =，11T =，11S =；当2n =时，2{1,3}A =，113T =+，213T =⨯，213137S =++⨯=.则当3n =时，3S = ；试写出n S = ．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. （15）（本小题满分13分） 在△ABC 中， ,,A B C 所对的边分别为,,a b c ，且2()2cossin()sin 222A A A f A =π-+-2cos 2A. （Ⅰ）求函数()f A 的最大值；（Ⅱ）若()0,,12f A C a 5π===b 的值．（16）（本小题满分14分）如图，四边形ABCD 是正方形，EA ⊥平面ABCD ，EA PD ，22AD PD EA ===，F ，G ，H 分别为PB ，EB ，PC 的中点．（Ⅰ）求证：FG 平面PED ；（Ⅱ）求平面FGH 与平面PBC 所成锐二面角的大小； （Ⅲ）在线段PC 上是否存在一点M ,使直线FM 与直线PA 所成的角为60？若存在，求出线段PM 的长；若不存在，请说明理由.（17）（本小题满分13分） 为提高学生学习数学的兴趣，某地区举办了小学生“数独比赛”.比赛成绩共有90分，70分，60分，40分，30分五种，按本次比赛成绩共分五个等级．从参加比赛的学生中随机抽取了30名学生，并把他们的比赛成绩按这五个等级进行了统计，得到如下数据表：A DB CPEFGH（Ⅰ）根据上面的统计数据，试估计从本地区参加“数独比赛”的小学生中任意抽取一人，其成绩等级为“A 或B ”的概率；（Ⅱ）根据（Ⅰ）的结论，若从该地区参加“数独比赛”的小学生（参赛人数很多）中任选3人，记X 表示抽到成绩等级为“A 或B ”的学生人数，求X 的分布列及其数学期望EX ； （Ⅲ）从这30名学生中，随机选取2人，求“这两个人的成绩之差大于20分”的概率．（18）（本小题满分13分）已知函数()mxf x x =++211（m ≠0），2()e ()ax g x x a =∈R . （Ⅰ）求函数()f x 的单调区间；（Ⅱ）当m >0时，若对任意12,[0,2]x x ∈，12()()f x g x ≥恒成立，求a 的取值范围.（19）（本小题满分14分）已知椭圆2222:1x y C a b+=(0)a b >>的右焦点为F (1,0)，短轴的端点分别为12,B B ,且12FB FB a ⋅=-.（Ⅰ）求椭圆C 的方程；（Ⅱ）过点F 且斜率为k (0)k ≠的直线l 交椭圆于,M N 两点，弦MN 的垂直平分线与x 轴相交于点D .设弦MN 的中点为P ，试求DP MN的取值范围．（20）（本小题满分13分）已知实数12,,,n x x x （2n ≥）满足||1(1,2i x i n≤= ，记121(,,,)n i j i j nS x x x x x ≤<≤=∑．（Ⅰ）求2(1,1,)3S --及(1,1,1,1)S --的值； （Ⅱ）当3n =时，求123(,,)S x x x 的最小值； （Ⅲ）求12(,,,)n S x x x 的最小值．注：1i j i j nx x ≤<≤∑表示12,,,n x x x 中任意两个数i x ,j x （1i j n ≤<≤）的乘积之和.北京市朝阳区高三年级第二次综合练习数学学科测试答案（理工类）2013.５一、选择题：二、填空题：（注：两空的填空，第一空3分，第二空2分） 三、解答题： （15）（本小题满分13分） 解：（Ⅰ）因为22()2cossin sin cos 2222A A A Af A =+- sin cos )4A A A π=-=-.因为A 为三角形的内角，所以0A <<π，所以444A ππ3π-<-<. 所以当42A ππ-=，即34A π=时，()f A ………6分（Ⅱ）由题意知())04f A A π=-=，所以sin()04A π-=．又因为444A ππ3π-<-<，所以04A π-=，所以4A π=．又因为12C 5π=，所以3B π=．由正弦定理sin sin a b A B =得，sinsin 33sin sin 4a Bb A π===π． …………13分 （16）（本小题满分14分）（Ⅰ）证明：因为F ,G 分别为PB ，BE 的中点，所以FG PE .又FG ⊄平面PED ，PE ⊂平面PED ，所以FG 平面PED . …………4分 （Ⅱ）因为EA ⊥平面ABCD ，EA PD ，所以PD ⊥平面ABCD ， 所以PD AD ⊥，PD CD ⊥. 又因为四边形ABCD 是正方形， 所以AD CD ⊥.如图，建立空间直角坐标系， 因为22AD PD EA ===,所以D ()0,0,0，P ()0,0,2，A ()2,0,0，C ()0,2,0，B ()2,2,0，(2,0,1)E ．…………5分因为F ，G ， H 分别为PB ，EB ，PC 的中点，所以F ()1,1,1，G 1(2,1,)2，H (0,1,1). 所以1(1,0,)2GF =- ，1(2,0,)2GH =- .设1111(,,)x y z =n 为平面FGH 的一个法向量，则1100GF GH ⎧⋅=⎪⎨⋅=⎪⎩n n ,即11111021202x z x z ⎧-+=⎪⎪⎨⎪-+=⎪⎩， 再令11y =，得1(0,1,0)=n .(2,2,2)PB =- ,(0,2,2)PC =-.设2222(,,)x y z =n 为平面PBC 的一个法向量,则220PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n , 即222222220220x y z y z +-=⎧⎨-=⎩，令21z =，得2(0,1,1)=n .所以12cos ,n n =1212⋅⋅n n n n=2. 所以平面FGH 与平面PBC 所成锐二面角的大小为4π. …………9分 （Ⅲ）假设在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为60.依题意可设PM PC λ=,其中01λ≤≤.由(0,2,2)PC =- ,则(0,2,2)PM λλ=-.又因为FM FP PM =+ ,(1,1,1)FP =-- ，所以(1,21,12)FM λλ=---.因为直线FM 与直线PA 所成角为60，(2,0,2)PA =-，所以cos ,FM PA =12，即12=，解得58λ=.所以55(0,,)44PM =-，PM = 所以在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为60，此时4PM =. ………………………………………14分（17）（本小题满分13分） 解：（Ⅰ）根据统计数据可知，从这30名学生中任选一人，分数等级为“A 或B ”的频率为461013030303+==． 从本地区小学生中任意抽取一人，其“数独比赛”分数等级为“A 或B ”的概率约为13．……………………………………………………………………………………3分 （Ⅱ）由已知得，随机变量X 的可能取值为0，1，2，3．所以0033128(0)()()3327P X C ==⋅=；112312124(1)()()33279P X C ==⋅==；22131262(2)()()33279P X C ==⋅==；3303121(3)()()3327P X C ==⋅=．随机变量X 的分布列为所以80123127272727EX =⨯+⨯+⨯+⨯=． ……………9分 （Ⅲ）设事件M ：从这30名学生中，随机选取2人，这两个人的成绩之差大于20分．设从这30名学生中，随机选取2人，记其比赛成绩分别为,m n ．显然基本事件的总数为230C ． 不妨设m n >，当90m =时，60n =或40或30，其基本事件数为111141073()C C C C ⋅++； 当70m =时，n =40或30，其基本事件数为111673()C C C ⋅+；当60m =时，30n =，其基本事件数为11103C C ⋅； 所以11111111141073673103230()()34()87C C C C C C C C C P M C ⋅+++⋅++⋅==． 所以从这30名学生中，随机选取2人，这两个人的成绩之差大于20分的概率为3487． ……………13分（18）（本小题满分1 3分）解：（Ⅰ）函数()f x 的定义域为R ，()()()()()()m x m x x f x x x --+'==++2222211111.…………1分 ①当m >0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-11，单调递减区间是(,)-∞-1，(,)+∞1. …………3分②当m <0时，当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 的单调递增区间是(,)-∞-1，(,)+∞1，单调递减区间是(,)-11.……………5分（Ⅱ）依题意，“当m >0时，对于任意12,[0,2]x x ∈，12()()f x g x ≥恒成立”等价于 “当m >0时，对于任意[0,2]x ∈， min max ()()f x g x ≥成立”.当m >0时，由（Ⅰ）知，函数()f x 在[0,1]上单调递增，在[1,2]上单调递减， 因为(0)1f =，2(2)115mf =+>，所以函数()f x 的最小值为(0)1f =.所以应满足max ()1g x ≤. ……………………………………………………………6分因为2()e ax g x x =，所以2()(+2)e ax g x ax x '=. ……………7分 ①当0a =时，函数2()g x x =，[0,2]x ∀∈，max ()(2)4g x g ==，显然不满足max ()1g x ≤，故0a =不成立. ……………8分 ②当0a ≠时，令()0g x '=得，10x =，22x a=-. （ⅰ）当22a-≥，即10a -≤<时， 在[0,2]上()0g x '≥，所以函数()g x 在[0,2]上单调递增，所以函数2max ()(2)4e a g x g ==. 由24e1a≤得，ln 2a ≤-，所以1ln 2a -≤≤-. ……………10分（ⅱ）当202a <-<，即1a <-时, 在2[0,)a -上()0g x '≥，在2(,2]a-上()0g x '<，所以函数()g x 在2[0,)a -上单调递增，在2(,2]a -上单调递减，所以max 2224()()eg x g a a =-=.由2241e a ≤得，2e a ≤-，所以1a <-. ……………11分 （ⅲ）当20a-<，即0a >时,显然在[0,2]上()0g x '≥，函数()g x 在[0,2]上单调递增，且2max ()(2)4e a g x g ==.显然2max ()4e 1a g x =≤不成立，故0a >不成立. ……………12分 综上所述，a 的取值范围是(,ln 2]-∞-. ……………13分 （19）（本小题满分14分）解：（Ⅰ）依题意不妨设1(0,)B b -，2(0,)B b ，则1(1,)FB b =-- ，2(1,)FB b =- .由12FB FB a ⋅=- ，得21b a -=-.又因为221a b -=，解得2,a b ==.所以椭圆C 的方程为22143x y +=. ……………4分 （Ⅱ）依题直线l 的方程为(1)y k x =-.由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩得2222(34)84120k x k x k +-+-=.设11(,)M x y ，22(,)N x y ，则2122834k x x k +=+，212241234k x x k -=+. …………6分所以弦MN 的中点为22243(,)3434k k P k k-++. ……………7分所以MN === 2212(1)43k k +=+. ……………9分直线PD 的方程为222314()4343k k y x k k k +=--++， 由0y =，得2243k x k =+，则22(,0)43k D k +，所以DP = …………11分所以224312(1)43DP k k MN k +==++=. ……………12分 又因为211k +>，所以21011k <<+.所以104<<. 所以DP MN的取值范围是1(0,)4. ………………………………………14分（20）（本小题满分13分）解：（Ⅰ）由已知得222(1,1,)11333S --=-+-=-． (1,1,1,1)1111112S --=----+=-． ……………3分 （Ⅱ）设123(,,)S S x x x =．当3n =时，12312132313(,,)i j i j S S x x x x x x x x x x x ≤<≤===++∑．若固定23,x x ，仅让1x 变动，此时12132323123()S x x x x x x x x x x x =++=++， 因此2323min{(1,,),(1,,)}S S x x S x x ≥-．同理2333(1,,)min{(1,1,),(1,1,)}S x x S x S x ≥-．2333(1,,)min{(1,1,),(1,1,)}S x x S x S x -≥---．以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的123,,x x x 所达到， 于是12311,2,3min{(,,)}k x k S S x x x =±=≥． 当1k x =±（1,2,3k =）时，22221231231[()()]2S x x x x x x =++-++ 212313()22x x x =++-． 因为123||1x x x ++≥，所以13122S ≥-=-，且当121x x ==，31x =-时，1S =-． 因此min 1S =-． ……………8分 （Ⅲ）设121(,,,)n i j i j n S S x x x x x ≤<≤==∑121312321n n n n x x x x x x x x x x x x -=++++++++ .固定23,,,n x x x ，仅让1x 变动，此时2312321()()n n n n S x x x x x x x x x x -=+++⋅+++++ ， 因此2323min{(1,,,,),(1,,,,)}n n S S x x x S x x x ≥- ． 同理2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x ≥- ． 2333(1,,,,)min{(1,1,,,),(1,1,,,)}n n n S x x x S x x S x x -≥--- ． 以此类推，我们可以看出，S 的最小值必定可在某一组取值1±的12,,,n x x x 所达到，于是1211,2,,min {(,,,)}k n x k n S S x x x =±=≥ ． 当1k x =±（1,2,,k n = ）时，222212121[()()]2n n S x x x x x x =+++-+++ 2121()22n n x x x =+++- ． ①当n 为偶数时，2n S ≥-， 若取1221n x x x ==== ，12221nn n x x x ++====- ，则2n S =-，所以min 2n S =-． ②当n 为奇数时，因为12||1n x x x +++≥ ，所以1(1)2S n ≥--， 若取12121n x x x -==== ，1112221n n n x x x --++====- ，则1(1)2S n =--， 所以min 1(1)2S n =--． …………………………13分。

20XX年中学测试中学试题试卷科目：年级：考点：监考老师：日期：北京市朝阳区高三理科综合第二次统一考试能力测试试卷化学试题2021.5（考试时间150分钟满分300分）本试卷分第I卷（选择题）和第II卷（非选择题）两部分第I卷（选择题，共120分）本卷共20题，每小题6分，共120分，在下列各题的四个选项中，只有一个选项是符合题目要求的。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 235．氯化铁溶液和氢氧化铁胶体具有的共同性质是A．两种液体都是红褐色B．分散质粒子都能通过半透膜C．分散质粒子大小都在1 nm ~ 100 nm 之间D．加热、蒸干、灼烧后，得到相同的固体6．下列生活中的化学小实验不合理的是A. 用米汤检验加碘盐中的碘酸钾(KIO3)B. 用食用醋除去热水瓶中积存的水垢C. 用纯碱(Na2CO3)溶液洗涤沾有油污的器具D. 用灼烧并闻气味的方法区分化纤织物与纯毛织物7．用N A表示阿伏加德罗常数，下列说法错误的是A. 乙醇的摩尔质量（g / mol）与N A个乙醇分子的质量(g)在数值上相等B. 1mol Mg作为还原剂可提供的电子数为2N AC. 常温常压下，28 g CO中所含碳原子数为0.5N AD. 0.5 L、0.2 mol / L的Fe2(SO4)3溶液中含SO42－个数为0.3 N AZ Y X W其中W的一种原子是3618W，则下列8．四种元素在周期表中相对位置为判断错误的是A．原子半径X＜Y＜ZB．气态氢化物稳定性X＞Y＞ZC．气态氢化物还原性X＞Y＞ZD．最高价氧化物对应水化物的酸性X＞Y＞Z9．将2 mol X和2 mol Y充入2 L密闭容器中发生如下反应:X (气)＋3 Y (气) 2 Z (气) ＋a Q (气)2 min达到平衡时生成0.8 mol Z，测得Q的浓度为0.4 mol / L，下列叙述错误的是A．a的值为2B．平衡时X的浓度为0.2 mol / LC.Y的转化率为60％D.反应速率v(Y)=0.3 mol / (L·min)10.下列离子浓度关系正确的是A. 0.1 mol / L的NH4Cl溶液中c（NH4＋）= c（Cl－）B．同为0.1 mol / L的甲酸和氢氧化钠溶液等体积混合后，c（OH－）= c（H＋）C．向NH4Cl溶液中滴加氨水至pH=7 时，c（NH4＋）＜c（Cl－）D．pH=3的H2SO4和pH=11的NaOH溶液等体积混合后，溶液中c（OH－）= c（H＋）11．在不同条件或不同用量时，下列物质间发生化学反应产物不同的是①AlCl3和NaOH溶液②P和Cl2 ③AgNO3溶液和氨水④C和O2⑤ CO2和NaOH溶液⑥ Fe和浓HNO3⑦乙醇和O2A. ①③⑤⑦B. ②④⑥⑦C. ③④⑤⑥⑦D. 全部12．下表为部分一氯代烷的结构简式和一些性质数据序号结构简式沸点/℃相对密度①CH3Cl －24.2 0.9159②CH3CH2Cl 12.3 0.8978③CH3CH2CH2Cl 46.6 0.8909④CH3CHClCH335.7 0.8617⑤CH3CH2CH2CH2Cl 78.44 0.8862⑥CH3CH2CHClCH368.2 0.8732⑦(CH3)3CCl 52 0.8420下列对表中物质与数据的分析归纳错误的是A.物质①②③⑤互为同系物B.一氯代烷同分异构体的沸点随着支链的增多而升高C.一氯代烷的沸点随着碳数的增多而趋于升高D.一氯代烷的相对密度随着碳数的增多而趋于减小第Ⅱ卷（非选择题共180分）本卷共10道题。