一种面向控制系统解耦的序列决策PID参数整定方法
- 格式:pdf
- 大小:1.07 MB
- 文档页数:10

pid参数的工程整定方法PID控制在工程里可太常见啦,就像一个小管家,管着各种系统的运行呢。
那PID 参数的整定方法也有不少小窍门哦。
最常用的一种是经验试凑法。
这就有点像做菜的时候试味道一样。
对于比例系数P,一开始可以给个比较小的值,就像给菜加一点点盐先尝尝。
如果系统反应很慢,输出老是不能达到目标值,那就可以慢慢增加P的值,让系统反应灵敏点。
但是P也不能太大哦,太大了系统就会像个调皮的小孩,变得很不稳定,晃来晃去的。
积分系数I呢,它主要是用来消除稳态误差的。
要是系统在稳定的时候,输出和目标值还有偏差,就像走路老是走不到目的地一样,这时候就可以调整I啦。
不过I 也不能一下子调得太大,不然系统会变得很“迟钝”,反应超级慢。
微分系数D就像是一个预测小能手。
它可以根据系统的变化趋势来提前调整。
如果系统变化很缓慢,D可以小一点;要是系统变化特别快,像火箭发射似的,那D就可以适当大一点,这样就能让系统更快地稳定下来。
还有一种是临界比例度法。
先把积分和微分关掉,只调整比例系数P,让系统达到临界振荡状态,这时候的比例系数就是临界比例度啦。
然后根据一些经验公式来计算出P、I、D的值。
不过这个方法有点冒险,就像走钢丝一样,一不小心系统就可能振荡得太厉害。
衰减曲线法也挺有趣的。
让系统产生衰减振荡,根据衰减的情况来确定PID参数。
就像看波浪一样,波浪的幅度和衰减速度能告诉我们参数应该怎么调整。
在实际工程里,整定PID参数可不能太死板哦。
要根据具体的系统情况,像系统的特性、负载的变化、干扰的大小这些因素来灵活调整。
有时候可能要多试几次,就像找宝藏一样,要有耐心。
而且不同的工程师可能也有自己独特的小技巧和经验。
毕竟每个工程系统都像是一个独特的小世界,需要我们用心去找到最适合它的PID参数组合,这样系统才能乖乖听话,稳定又高效地运行啦。

PID参数整定方法,大白话,谁都能看懂先来看一段描述:PID控制器(Proportion Integration Differentiation)俗称比例-积分-微分控制器,分别由比例单元(P)、积分单元(I)和微分单元(D)组成。
一般来说,通过调整这三个单元的增益Kp,Ki和Kd来确定PID控制特性。
其实PID控制器是一类控制器,而其实控制器有很多种,比如:P控制器,PI控制器,PD控制器等。
看完这段PID的描述,也许很多人就已经读不下去了,PID控制器到底和我们的现实生活有什么联系啊?怎么能让一个控制小白也很容易地理解这件事呢?那么,让我们来举个通俗易懂的例子,帮助大家更加通俗易懂地理解PID到底是干什么的!先讲个故事,古希腊哲学家芝诺曾提出过一条著名的悖论:阿喀琉斯是古希腊神话中十分善跑的英雄。
在他和乌龟的赛跑竞赛中,他的速度为乌龟十倍,乌龟在前面100米跑,他在后面追,但他不可能追上乌龟。
为什么呢?因为在竞赛中,追者首先必须到达被追者的出发点,当阿喀琉斯追到100米时,乌龟已经又向前爬了10米,于是,一个新的起点产生了;阿喀琉斯必须继续追,而当他追到乌龟爬的这10米时,乌龟又已经向前爬了1米,阿喀琉斯只能再追向那个1米。
就这样,乌龟会制造出无穷个起点,它总能在起点与自己之间制造出一个距离,不管这个距离有多小,但只要乌龟不停地奋力向前爬,阿喀琉斯就永远也追不上乌龟。
看到这里大家是不是感觉到这似乎是一个死循环...这就是鼎鼎有名的芝诺悖论!而该悖论的原理其实是一个时间问题,这里不是我们解释的重点。
▲芝诺悖论那善跑将军阿喀琉斯就永远不会赢吗?借着这个故事,我们可以给阿喀琉斯设计一个PID控制系统,指导阿喀琉斯去追上乌龟,并且还可以一直跟随乌龟,跑过了还可以再跑回来,直到和乌龟保持同一个位置。
在这个过程中,我们相信可以凭借这个“假想”帮助大家很好地理解PID控制的原理及各参数的物理意义。
首先,还是要普及一下基础概念:· PID控制器对反馈系统中的误差进行操作并执行以下操作1. PID控制器计算一个与误差成比例的项- P项;2. PID控制器计算一个与误差积分成比例的项——I项;3. PID控制器计算一个与误差导数成比例的项——D项;4. 这三项——P项、I项和D项——加在一起就产生了应用于被控制系统的控制信号。

pid参数设置方法PID参数设置是控制系统中的一项重要工作,它决定了系统对外界干扰和参考信号的响应速度和稳定性。
PID(比例-积分-微分)控制是一种基本的控制方法,通过调节比例、积分和微分三个参数,可以优化控制系统的性能。
本文将介绍三种常用的PID参数设置方法:经验法、试探法和自整定法。
一、经验法:经验法是一种基于经验和实际运行经验的参数设置方法。
它通常适用于对系统了解较多和试验数据比较丰富的情况下。
经验法的优点是简单易懂,但需要有一定的经验基础。
具体步骤如下:1.比例参数的设置:将比例参数设为一个较小的值,然后通过试验观察系统的响应情况。
如果系统的响应过冲很大,说明比例参数太大;如果响应过于迟缓,则说明比例参数太小。
根据这些观察结果,逐步调整比例参数的大小,直到系统的响应达到理想状态。
2.积分参数的设置:将积分参数设为一个较小的值,通过试验观察系统的响应情况。
如果系统存在静差,说明积分参数太小;如果系统过冲或振荡,说明积分参数太大。
根据这些观察结果,逐步调整积分参数的大小,直到系统的响应达到理想状态。
3.微分参数的设置:将微分参数设为0,通过试验观察系统的响应情况。
如果系统过冲或振荡,说明需要增加微分参数;如果系统响应过缓或不稳定,说明需要减小微分参数。
根据这些观察结果,逐步调整微分参数的大小,直到系统的响应达到理想状态。
二、试探法:试探法是一种通过试验获取系统频率响应曲线,然后根据曲线特点设置PID参数的方法。
具体步骤如下:1.首先进行一系列的试验,改变输入信号(如阶跃信号、正弦信号等)的幅值和频率,记录系统的输出响应。
2.根据试验数据,绘制系统的频率响应曲线。
根据曲线特点,选择合适的PID参数。
-比例参数:根据曲线的峰值响应,选择一个合适的比例参数。
如果曲线的峰值响应较小,比例参数可以增大;如果曲线的峰值响应较大,比例参数可以减小。
-积分参数:根据曲线的静态误差,选择一个合适的积分参数。
如果曲线存在静差,积分参数可以增大;如果曲线没有静差,积分参数可以减小。

PID控制算法精华和参数整定三大招PID是闭环控制算法在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器是应用最为广泛的一种自动控制器。
它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。
PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
因此要实现PID算法,必须在硬件上具有闭环控制,就是得有反馈。
比如控制一个电机的转速,就得有一个测量转速的传感器,并将结果反馈到控制路线上,下面也将以转速控制为例。
PID是比例(P)、积分(I)、微分(D)控制算法但并不是必须同时具备这三种算法,也可以是PD,PI,甚至只有P算法控制。
我以前对于闭环控制的一个最朴素的想法就只有P控制,将当前结果反馈回来,再与目标相减,为正的话,就减速,为负的话就加速。
现在知道这只是最简单的闭环控制算法。
PID控制器结构PID控制系统原理结构框图对偏差信号进行比例、积分和微分运算变换后形成一种控制规律。
“利用偏差,纠正偏差”。
模拟PID控制器模拟PID控制器结构图PID控制器的输入输出关系为:比例(P)、积分(I)、微分(D)控制算法各有作用比例,反应系统的基本(当前)偏差e(t),系数大,可以加快调节,减小误差,但过大的比例使系统稳定性下降,甚至造成系统不稳定;积分,反应系统的累计偏差,使系统消除稳态误差,提高无差度,因为有误差,积分调节就进行,直至无误差;微分,反映系统偏差信号的变化率e(t)-e(t-1),具有预见性,能预见偏差变化的微分,反映系统偏差信号的变化率e(t)-e(t-1),具有预见性,能预见偏差变化的趋势,产生超前的控制作用,在偏差还没有形成之前,已被微分调节作用消除,因此可以改善系统的动态性能。
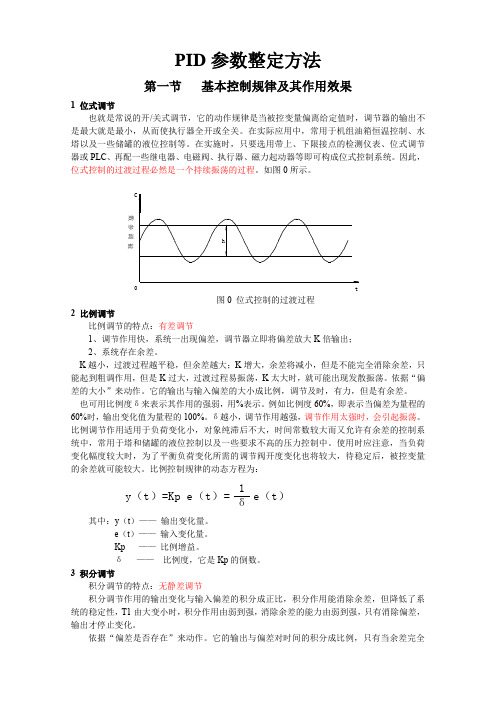
PID 参数整定方法第一节 基本控制规律及其作用效果1 位式调节也就是常说的开/关式调节,它的动作规律是当被控变量偏离给定值时,调节器的输出不是最大就是最小,从而使执行器全开或全关。
在实际应用中,常用于机组油箱恒温控制、水塔以及一些储罐的液位控制等。
在实施时,只要选用带上、下限接点的检测仪表、位式调节器或PLC 、再配一些继电器、电磁阀、执行器、磁力起动器等即可构成位式控制系统。
因此,位式控制的过渡过程必然是一个持续振荡的过程。
如图0所示。
图0 位式控制的过渡过程2 比例调节比例调节的特点:有差调节1、调节作用快,系统一出现偏差,调节器立即将偏差放大K 倍输出;2、系统存在余差。
K 越小,过渡过程越平稳,但余差越大;K 增大,余差将减小,但是不能完全消除余差,只能起到粗调作用,但是K 过大,过渡过程易振荡,K 太大时,就可能出现发散振荡。
依据“偏差的大小”来动作。
它的输出与输入偏差的大小成比例,调节及时,有力,但是有余差。
也可用比例度δ来表示其作用的强弱,用%表示。
例如比例度60%,即表示当偏差为量程的60%时,输出变化值为量程的100%。
δ越小,调节作用越强,调节作用太强时,会引起振荡。
比例调节作用适用于负荷变化小,对象纯滞后不大,时间常数较大而又允许有余差的控制系统中,常用于塔和储罐的液位控制以及一些要求不高的压力控制中。
使用时应注意,当负荷变化幅度较大时,为了平衡负荷变化所需的调节阀开度变化也将较大,待稳定后,被控变量的余差就可能较大。
比例控制规律的动态方程为:其中:y (t )—— 输出变化量。
e (t )—— 输入变化量。
Kp —— 比例增益。
δ —— 比例度,它是Kp 的倒数。
3 积分调节积分调节的特点:无静差调节积分调节作用的输出变化与输入偏差的积分成正比,积分作用能消除余差,但降低了系统的稳定性,T1由大变小时,积分作用由弱到强,消除余差的能力由弱到强,只有消除偏差,输出才停止变化。

PID控制器参数整定及其改进方法【摘要】简要介绍了PID控制器及其参数整定方法中的Z-N法、继电反馈法和基于锁相环的参数整定法。
并且利用计算机辅助设计软件Mablab对典型被控对象进行了仿真。
【关键词】PID控制Z-N法;继电反馈;锁相环;Mablab1.引言PID控制是最早发展起来的控制策略之一[1]。
由于其结构简单,鲁棒性好,可靠性高,是迄今为止最为通用的控制方法。
PID控制实际应用时需要进行参数整定,参数整定值决定了系统的控制效果。
PID控制系统发展至今,提出了许多参数整定方法。
从最早提出的且最具影响力的Ziegler-Nichols PID控制器参数工程整定方法[2],,到现今热门研究方向基于神经网络的参数整定[3]、基于模糊推理的参数整定[4]、基于遗传算法的参数整定[5]等。
本文将介绍在工程实际中被广泛应用的Z-N法及其改进方法。
并且在计算机辅助设计软件Matlab的Simulink仿真环境下对典型被控过程进行仿真。
2.PID控制系统误差信号的比例(Proportional)、积分(Integral)和微分(Derivative)的综合控制称为PID控制。
单输入单输出(SISO)PID控制系统框图如图1所示。
图1 PID控制系统框图系统由PID控制器和被控过程组成,其中,为系统参考输入信号,为系统输出信号。
PID控制器传递函数形式为:(1-1)其中为比例增益,为积分时间常数,为微分时间常数。
过程控制中PID控制器只有在其参数、和得到良好整定的前提下才能达到令人满意的控制效果。
3.Ziegler-Nichols PID控制器参数工程整定方法Z-N法是基于经验的公式整定方法,操作简单方便。
Z-N法利用被控过程响应的特征参数按照整定公式计算PID控制器三个参数,分为基于系统开环阶跃响应和闭环频率响应两类。
由于大部分被控过程模型的响应曲线和一阶系统的响应类似,因此其阶跃响应曲线可由一阶加纯滞后模型(FOPDT)阶跃响应曲线来近似。
PID参数整定公式推导及PID参数整定步骤3 PID参数整定公式推导及PID参数整定步骤3.1 PID参数整定公式推导设单输入单输出离散系统方程为:A(Z-1)r(k)=B(Z-1)Z-dU(K)+N(K)其中:r(k),U(K)分别为被控系统输出和输入量;N(K)为扰动量。
A(z-1)=1+a1z-1+…+anaz-naB(z-1)=1+b1z-1+…+bnbz-nb而PID调节器方程为:U(t)=Kp[e(t)+1/Ti e(t)dt+Td.de(t)/dt> (1) e(t)为偏差;式(1)离散化为:U(k)=Kp[e(k)+Ts/Ti e(j)+Td/TS.(e(k)-e(k-1))> (1a) Ts为采样周期;上式写成增量形式为:ΔU(k)=U(k)-U(k-1) (1b)=Kp[e(k).(1+Td/Ts+Ts/Ti)-(1+2Td/Ts).e(k-1)+e(k-2)Td/Ts>设性能指标为:J=E[e2(k+d) +q.Δe2(k+d) +λ.ΔU2(k)> (2)式中d纯延时;e(k+d)为时刻k预报控制误差,q, λ为加权系数Δ为差分。
ΔU(k)=Δe(k+d)+e(k+d)-e(k+d-1) (3)设控制预报误差模型为:e(k+d)+w(k+d)-w(k)=f0e(k)+f1e(k-1)+…+g0U(k)+g1U(k-1)+…+h0w(k)+h0w(k)+h1w(k-1)+…+r+(4)式中w(k)为参考输入信号,为扰动信号;fi,gi,hi为待辩常数。
又设PID控制算式为U(K)=U(K-1)+P0e(k)+ P1e(k-1)+P2e(k-2) (5)将ΔU(k),Δe(k+d),e(k+d)代入(2)使J?MIN令 U(k)=0得:U(k)=U(k-1)-[(1+q)g0f0e(k)>/[(1+q)g02+λ>-[(1+q)g0f0-g0qf0>e(k-1)/[(1+q)g02+λ>-[(1+q)g0f2-qg0f1>e(k-2)/[(1+q)g02+λ>+ (6)把(6)与(5)比较得:P0=-[(1+q)g0f0>/[(1+q)g02+λ>P1=-[(1+q)g0f1-g0qf0>/[(1+q)g02+λ> P2=-[(1+q)g0f2-qg0f1>/[(1+q)g02+λ> g0,f2,f1,f0为待辩常数。
pid自整定方法PID自整定方法一、引言PID控制器是目前最常用的工业控制器之一,它通过对被控对象的测量值与设定值之间的误差进行反馈调节,实现对被控对象的稳定控制。
PID控制器的参数调节对控制系统的性能至关重要,而PID 自整定方法就是一种用于自动调节PID参数的方法,能够提高控制系统的性能和稳定性。
二、PID控制器及其参数PID控制器由比例项(P项)、积分项(I项)和微分项(D项)组成,其输出值为PID输出信号。
PID控制器的参数包括比例系数Kp、积分时间Ti和微分时间Td,它们的合理选择对系统的控制效果至关重要。
较大的比例系数可以提高系统的响应速度,但可能导致系统过冲和震荡;较大的积分时间可以减小稳态误差,但可能导致系统的超调量增加;较大的微分时间可以提高系统的稳定性,但可能导致系统的响应速度变慢。
三、PID自整定方法1. 经验法经验法是一种常用的PID自整定方法,它基于经验规则来选择PID 参数。
根据被控对象的特性和控制要求,经验法可以通过试错法或专家经验来选择合适的PID参数。
例如,对于快速响应的系统,可以增大比例系数Kp和微分时间Td;对于稳态误差较大的系统,可以增大积分时间Ti。
2. Ziegler-Nichols方法Ziegler-Nichols方法是一种基于系统频率响应的PID自整定方法。
它通过对系统的开环频率响应进行测试,得到临界增益和临界周期,从而计算出PID参数。
具体步骤为:首先将系统的比例增益逐渐增大,直到系统出现持续振荡;然后通过测量振荡的周期和幅度来计算出临界增益和临界周期;最后根据临界增益和临界周期来选择PID参数。
3. Chien-Hrones-Reswick方法Chien-Hrones-Reswick方法是一种基于系统阶跃响应的PID自整定方法。
它通过对系统的阶跃响应进行测试,得到系统的调节时间、超调量和稳态误差,从而计算出PID参数。
具体步骤为:首先对系统施加一个阶跃输入信号,记录系统的响应曲线;然后根据响应曲线计算系统的调节时间、超调量和稳态误差;最后根据调节时间、超调量和稳态误差来选择PID参数。
pid自整定算法
PID自整定算法是用于动态调整PID控制律参数的算法,它可以让系统自动、快速地找到合适的运作参数。
使用PID自整定算法,在获得理想参数之前,系统可以对运行参数的速度和精度进行调节,以达到最佳性能。
PID自整定算法基于一种搜索方法,即穷举法,又称完备搜索。
本质上,它是一个将现有参数搜索并尝试形成最佳参数的演算法。
PID自整定算法开始时,可以选择一个基准设定来作为参数的起点,一般是标准偏差。
然后,它将采用步进调整技术来搜索参数,以定位所需参数的最佳值。
控制器收集不同参数和系统反应之间的数据,并绘制出它们之间的关系图像,从而帮助确定理想的设置。
上述搜索技术不仅可以帮助确定理想参数,而且还可以选择性地更新参数序列,新参数的精度会比以前的参数精度更高。
另外,通过特殊的方法来改善PID自整定算法,可以将得到的控制失调量降至最小,从而得到更加精确和高效的PID参数。
总之,PID自整定算法是一个有效的在线参数调节方法,可以帮助系统迅速达到最佳性能,在行驶过程中快速调节参数,以满足不断变化的应用需求。
同时,它也为不熟悉PID 技术的用户提供了一种简单有效的方式,能够满足从家庭用户到工业级用户不同层次的应用需求。
总的来说,PID自整定算法是控制系统优化运行的有效方法,其可行性及高效性在业界得到广泛认可。
CIESC Journal, 2018, 69(3): 1071-1080 ·1071· 化工学报 2018年 第69卷 第3期 | www.hgxb.com.cn DOI:10.11949/j.issn.0438-1157.20171478 一种面向控制系统解耦的序列决策PID参数整定方法
高月,宿翀,李宏光 (北京化工大学信息科学与技术学院,北京 100029)
摘要:传统的解耦控制方法由于其过于依赖模型辨识等问题难以被实际应用,且存在成熟系统不宜进行控制器再设计等问题,此外,回路解耦控制的专家经验难以提取与传承。因此以等效传函理论为研究基础,提出了一种面向解耦问题的基于序列决策的PID参数整定方法,提取历史数据中经验丰富的操作人员的控制序列。在解决回路之间存在耦合而使控制效果不佳的问题的同时,使工程人员的PID参数整定经验数字化得以传承,辅助初级人员进行操作。最后将所提方法应用于Matlab和Aspen两个仿真平台的耦合回路系统,获得满意结果,并验证所提方法的有效性和正确性。 关键词:过程控制;参数估值;神经网络 中图分类号:TP 29 文献标志码:A 文章编号:0438—1157(2018)03—1071—10
Sequence-decision PID parameter tuning approach towards control system decoupling
GAO Yue, SU Chong, LI Hongguang (College of Information Science & Technology, Beijing University of Chemical Technology, Beijing 100029, China)
Abstract: Traditional decoupling control methods have difficulties in industrial applications as a result of heavily relying on model identification and in controller re-designing as a result of mature system. Besides, it is difficult to extract and inherit expert experience of loops’ decoupling controls. Based on equivalent transfer function theory, sequence-decision PID parameter tuning method was developed, which control sequences of experienced operators were effectively extracted from historical data. When facing poor control performance due to loops’ coupling, junior staff could operate from inheritance of digitalized PID parameter tuning experience of experienced engineers. Method effectiveness and accuracy were verified in two coupling circuit systems in Matlab and Aspen simulation platforms.
Key words: process control; parameter estimation; neural networks
引 言 在化工生产中,存在很多互相干扰的复杂情况,回路中的控制作用会互相干扰,使系统极为不稳定,而且现场的被控对象存在很难控制的因素,如不确
定性,多外扰,大滞后,非最小相位等,很难辨识精确的定常数学模型[1]。而且现场DCS中有很多过
程数据以及操作数据,其中蕴含着操作人员应对耦合问题的经验。针对以上问题,基于传统控制和先进控制的多变量协调控制方法难以奏效,例如①以
2017-07-04收到初稿,2017-07-06收到修改稿。 联系人:宿翀。第一作者:高月(1993—),女,硕士研究生。 基金项目:北京市优秀人才培养项目(2015000020124G041);国家自然科学基金项目(61603023)。
Received date: 2017-07-04. Corresponding author: SU Chong, suchong@mail.buct.edu.cn Foundation item: supported by the Beijing Outstanding Talent Training Project (2015000020124G041) and the National Natural Science Foundation of China (61603023). 化 工 学 报 第69卷 ·1072· 传统频域为代表的解耦控制,如对角阵方法,相对增益分析法,特性曲线分析法,状态变量法,逆奈氏阵列法(INA)等,由于依赖精确的数学模型,现场难以辨识,并且在控制过程中,工作点由于设定值等因素的变换,定常的解耦补偿器难以适应新的模型,很难保证控制品质,甚至导致系统不稳定[2-3]。
②多变量自适应解耦将被控对象的辨识,控制和解耦相结合,可以实现参数未知领域的解耦,属于预测方法,但是实现这种动态解耦控制,依赖于复杂的在线辨识系统,并且设计过程中依赖参考轨迹,很难在DCS上实现[4]。③鲁棒控制的一个分支,鲁棒解耦控制通过设计鲁棒对角控制器来实现解耦,但是鲁棒解耦控制器的设计是针对特定系统讨论特殊的解耦控制问题。内模解耦控制器可以通过设计内模结构来实现解耦,依靠数学模型进行解耦[5]。
以上的控制器设计都需要改变原有的控制器结构或者重新设计控制系统,但是现场DCS系统往往难以进行改动以及成本上不允许重新设计控制系统,故以上的解耦合方法对于实际应用均不合适,而且没有充分利用信息丰富的历史数据,难以将消除耦合现象的经验量化。 在实际操作中,现场的操作人员通常会通过多次调节各回路的控制器参数,根据经验在特定时刻改变控制器参数,来拉开各回路的平衡点来进行协调两个回路的控制质量,通过一系列的参数决策得到理想的控制质量。实施该调节操作的工作人员往往对生产工艺很了解,有很多积累的操作经验。但是,过程数据中蕴含的操作经验难以挖掘,不能够直接指导初级操作人员。因此,从实际化工过程提取人工经验的角度出发,获得人工调节的经验指导,直接通过调节PID参数,以获得期望的控制性能,是现场实施解耦控制的一条有效途径,即将解耦部分与控制部分合二为一来调节控制器参数。文献[6]采用将两者设计为统一的结构,但是设计步骤烦琐。通过调节PID参数的方法,实质上是改变控制回路的传递函数的方法,近年来,很多国内外学者在内模补偿的基础上,提出了一种等效传函的方法(EFE)[7-8],将相对有效增益阵列(ERGA)和相对归
一化增益阵列(RNGA)等方法应用到控制器设计中,避免了内模解耦控制通过补偿方法求解广义逆时产生不稳定极点的问题,并且更适用于控制器结构复杂和维数较高的系统[9],因此采用等效传函的
方法,可以通过整定控制器参数来进行解耦。以上的文献和方法即是整定PID参数解耦控制方法的理
论基础。 近年来,基于过程历史数据挖掘过程信息的研究快速发展,基于神经网络等数据驱动[10-12]的建模
方法[13-21]获得丰硕成果。因此本文基于数据驱动思
想对工程人员的操作历史数据进行经验的提取,模拟工程人员在经验指导下得到控制序列。面向本文非线性、数据关系复杂,数据维度高的耦合回路流程模型时,大多利用智能方法构建软控制器,但未见数据驱动来挖掘PID整定过程中的人工经验。在实际过程中,整定操作为序列决策过程,值得一提的是,序列决策是一种对决策步骤进行建模的方法,通常应用在投资收益分析的决策之中,在生产过程中常用作加工步序规划之中[22],同时,神经网络等
建模方法已被成功应用于序列决策建模领域[23-29]。
因此序列决策思想适合解决此类按照步骤进行的PID整定过程建模。然而,对于耦合回路控制器参数决策中序列决策问题的建模还未见报道。此外,以上的决策模型都属于单点时间序列决策模型,与本文的“复合型决策”不同,本文根据实际的解耦需求,提出了一种决策节点含有多种决策参数的“复合型序列决策”,其决策结果也为多参数组合,更加适用于多回路控制器参数整定过程,并基于提出的序列决策模型,构建了多级神经网络。 受上述讨论启发,本文以等效传函的理论为支撑,提出面向解耦问题的基于NPCA-ANN的序列决策PID参数整定模型,旨在挖掘历史数据中有效的PID调节序列,辅助达到回路解耦控制效果。
1 面向解耦的PID参数整定序列决策模型
1.1 耦合过程描述 工业现场工艺流程复杂,同一个生产质量指标受多变量影响,多个变量在多个回路中作为控制变量,因此有着“牵一发而动全身”的控制效果,在相互耦合的情况下,现场发生变动后,各回路会出现不稳定的情况,以两个相互关联的回路为例,如图1所示。
图1 耦合回路 Fig.1 System with coupling