下载文档原格式
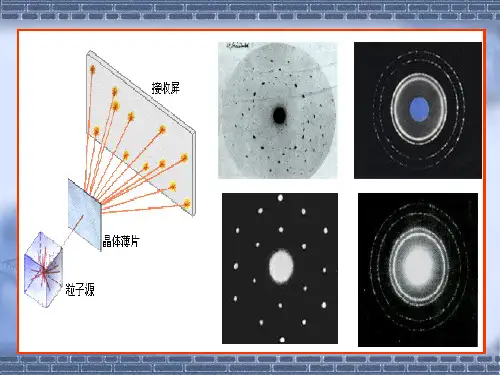
学 习 目 标知 识 脉 络1.知道实物粒子具有波动性．2．知道光波和物质波都是概率波．3．理解德布罗意波，会解释相关现象．(重点、难点)4．知道电子云，了解“不确定性关系”的具体含义.德布罗意波假说及电子衍射[先填空]1．德布罗意波：任何一个实物粒子都和一个波相对应，这种波后来被称为德布罗意波，也称为物质波．2．波长与动量关系：λ＝.3．电子衍射：电子束在晶体上反射可能发生衍射．[再判断]1．电子衍射的发现证明了德布罗意波假说．(√)2．电子不仅会发生衍射，还会发生干涉．(√)3．包括光子在内的一切微观粒子都具有波粒二象性，而实物粒子不具有波粒二象性．(×)[后思考]既然德布罗意提出了物质波的概念，为什么我们生活中却体会不到？【提示】平时所见的宏观物体的质量比微观粒子的质量大得多，运动的动量很大，由λ＝可知，它们对应的物质波波长很小，因此，无法观察到它们的波动性．1．任何物体，小到电子、质子，大到行星、太阳都存在波动性，我们之所以观察不到宏观物体的波动性，是因为宏观物体对应的波长太小的缘故．2．德布罗意波是一种概率波，粒子在空间各处出现的概率受波动规律支配，不要以宏观观点中的波来理解德布罗意波．3．德布罗意假说是光子的波粒二象性的一种推广，使之包括了所有的物质粒子，即光子与实物粒子都具有粒子性，又都具有波动性，与光子对应的波是电磁波，与实物粒子对应的波是物质波．1．下列说法中正确的是( )【导学号：55272058】A．物质波属于机械波B．只有像电子、质子、中子这样的微观粒子才具有波动性C．德布罗意认为，任何一个运动着的物体，小到电子、质子，大到行星、太阳，都有一种波和它对应，这种波叫物质波D．宏观物体运动时，看不到它的衍射或干涉现象，因此宏观物体运动时不具有波动性【解析】物质波是一切运动着的物体所具有的波，与机械波性质不同，A错误；宏观物体也具有波动性，只是干涉、衍射现象不明显，看不出来，B、D错误；德布罗意认为，任何一个运动着的物体，小到电子、质子，大到行星、太阳，都有一种波和它对应，这种波叫物质波，C正确．【答案】C2．如果一个中子和一个质量为10 g的子弹都以103 m/s的速度运动，则它们的德布罗意波的波长分别是多长？(中子的质量为1.67×10－27 kg)【解析】中子的动量为p1＝m1v，子弹的动量为p2＝m2v，据λ＝知中子和子弹的德布罗意波的波长分别为λ1＝，λ2＝hp2联立以上各式解得：λ1＝，λ2＝hm2v将m1＝1.67×10－27 kg，v＝1×103 m/s，h＝6.63×10－34 J·s，m2＝1.0×10－2 kg代入上面两式可解得λ1＝4.0×10－10 m，λ2＝6.63×10－35 m.【答案】 4.0×10－10 m 6.63×10－35 m宏观物体波动性的三点提醒1．一切运动着的物体都具有波动性，宏观物体观察不到其波动性，但并不否定其波动性．2．要注意大量光子、个别光子、宏观物体、微观粒子等相关概念的区别．3．在宏观世界中，波与粒子是对立的概念；在微观世界中，波与粒子可以统一．电子云和不确定性关系[先填空]1．电子云：原子中的电子在原子核的周围运动，在空间各点出现的概率是不同的，当原子处于稳定状态时，电子会形成一个稳定的概率分布．由于历史上的原因，人们常用一些小圆点来表示这种概率分布，概率大的地方小圆点密一些，概率小的地方小圆点疏一些，这样的概率分布图称为电子云．2．不确定性关系：用Δx表示微观粒子位置的不确定性，用Δp 表示微观粒子动量的不确定性，则两者之间的关系为ΔxΔp≥，即不确定性关系．它意味着微观粒子的坐标和动量不可能同时完全精确地确定．[再判断]1．在讨论微观粒子的运动时，只能给出微观粒子在空间各点出现的概率分布，无法给出微观粒子运行的轨迹．(√)2．微观粒子运动的状态，不能像宏观物体的运动那样通过确定的轨迹来描述，而是只能通过概率波作统计性的描述．(√) 3．改进测量技术，不确定性关系可以确定，微观粒子的坐标和动量可以同时确定．(×)[后思考]对微观粒子的运动分析能不能用“轨迹”来描述？【提示】不能．微观粒子的运动遵循不确定关系，也就是说，要准确确定粒子的位置，动量(或速度)的不确定量就更大；反之，要准确确定粒子的动量(或速度)，位置的不确定量就更大，也就是说不可能同时准确地知道粒子的位置和动量．因而不可能用“轨迹”来描述微观粒子的运动．1．粒子位置的不确定性：单缝衍射现象中，入射的粒子有确定的动量，但它们可以处于挡板左侧的任何位置，也就是说，粒子在挡板左侧的位置是完全不确定的．2．粒子动量的不确定性(1)微观粒子具有波动性，会发生衍射．大部分粒子到达狭缝之前沿水平方向运动，而在经过狭缝之后，有些粒子跑到投影位置以外．这些粒子具有与其原来运动方向垂直的动量．(2)由于哪个粒子到达屏上的哪个位置是完全随机的，所以粒子在垂直方向上的动量也具有不确定性，不确定量的大小可以由中央亮条纹的宽度来衡量．3．位置和动量的不确定性关系：ΔxΔp≥h4π由ΔxΔp≥可以知道，在微观领域，要准确地确定粒子的位置，动量的不确定性就更大；反之，要准确地确定粒子的动量，那么位置的不确定性就更大．4．微观粒子的运动没有特定的轨道：由不确定关系ΔxΔp≥可知，微观粒子的位置和动量是不能同时被确定的，这也就决定了不能用“轨迹”的观点来描述粒子的运动．5．经典物理和微观物理的区别(1)在经典物理学中，可以同时用位置和动量精确地描述质点的运动，如果知道质点的加速度，还可以预言质点在以后任意时刻的位置和动量，从而描绘它的运动轨迹．(2)在微观物理学中，不可能同时准确地知道粒子的位置和动量．因而也就不可能用“轨迹”来描述粒子的运动．但是，我们可以准确地知道大量粒子运动时的统计规律．3．对不确定性关系ΔxΔp≥有以下几种理解，其中正确的是( )【导学号：55272059】A．微观粒子的动量不可能确定B．微观粒子的坐标不可能确定C．微观粒子的动量和坐标不可能同时确定D．不确定性关系仅适用于电子和光子等微观粒子，不适用于其他宏观物体【解析】不确定性关系ΔxΔp≥表示确定位置、动量的精确度互相制约，此长彼消，当粒子位置的不确定性变小时，粒子动量的不确定性变大；当粒子位置的不确定性变大时，粒子动量的不确定性变小，故不能同时准确确定粒子的动量和坐标．不确定性关系也适用于其他宏观物体，不过这些不确定量微乎其微．【答案】C4．已知＝5.3×10－35 J·s，试求下列情况中速度测定的不确定量．(1)一个球的质量m＝1.0 kg，测定其位置的不确定量为10－6 m；(2)电子的质量me＝9.0×10－31 kg，测定其位置的不确定量为10－10 m(即在原子的数量级)．【解析】(1)m＝1.0 kg，Δx1＝10－6 m，由ΔxΔp≥，Δp＝mΔv知Δv1≥h4πΔx1m＝m/s＝5.3×10－29 m/s.(2)me＝9.0×10－31 kg，Δx2＝10－10 mΔv2≥＝ m/s＝5.89×105 m/s.【答案】(1)5.3×10－29 m/s (2)5.89×105 m/s对不确定性关系的两点提醒1．不确定性关系ΔxΔp≥是自然界的普遍规律，对微观世界的影响显著，对宏观世界的影响可忽略不计．也就是说，宏观世界中的物体质量较大，位置和速度的不确定范围较小，可同时较精确测出物体的位置和动量．2．在微观世界中，粒子质量较小，不能同时精确地测出粒子的位置和动量，也就不能准确地把握粒子的运动状态了．。
1971年，尼加拉瓜发行了一套十张邮票，题为“改变世界面貌的十个数学公式”，其中第八张邮票中写着这样一个公式：λ=h/mv这就是著名的波粒二象性公式，也称德布罗意定律。
它描述了微观世界中一个非常奇妙的特性：在原子世界里，所有物质既是粒子，也是波！物理学家“亲王”这个公式的提出者是法国物理学家路易·德布罗意。
1892年8月15日，德布罗意出生于法国塞纳河畔的蒂厄浦，他是法国一个贵族家庭的次子，并拥有一个显赫的贵族头衔——“亲王”。
德布罗意家族自17世纪以来，一直在法国的军队、政治、外交等方面颇具盛名。
德布罗意的祖父是法国著名的政治家和国务活动家，1871年当选法国国民议会下院议员，同年担任法国驻英国大使，后来还担任过法国总理和外交部长等职务。
德布罗意从18岁开始，就在巴黎大学学习理论物理。
因为打算以后按其家族传统从事外交活动，他同时兼修历史，并且于1909年获得历史学位。
之后，贵族家庭出身的德布罗意又研究起了中世纪史，据说是因为中世纪史中有着很多神秘的东西吸引着这位年轻人。
第一次世界大战期间，德布罗意在军队服役，并被分配到无线电台工作。
德布罗意的哥哥是个著名的X射线物理学家，拥有设备精良的私人实验室。
1919年，德布罗意突然又一次对物理产生了兴趣。
他来到他哥哥的实验室，开始研究X射线。
1919年是一个科学界急剧动荡着的年代，量子概念早在十几年前就已由普朗克提出，而后被爱因斯坦加以发展。
爱因斯坦指出，光不但是一种电磁波，而且也是一种粒子，即“光量子”。
这是一个很新颖的观点，但并没有完全被当时的物理学界所接受。
从他哥哥那里，德布罗意了解到了普朗克和爱因斯坦关于量子的工作，并产生了浓厚的兴趣。
经过一翻思想斗争之后，德布罗意终于放弃了早先决定的研究历史的计划，选择物理学作为自己的事业。
1920年，他来到了法国物理学界的一派宗师朗之万门下读研究生，希望通过物理学研究获得博士学位。
从此，德布罗意走出了一道足以让任何传奇都黯然失色的人生轨迹。
德布罗意波长最简单解释德布罗意波长啊，这可太有趣啦！你知道吗？德布罗意波长就像是微观世界里的一个小秘密。
想象一下，在我们日常生活里，东西就是东西，粒子就是粒子，波就是波，分得可清楚啦。
可是在微观的世界，那些小小的粒子啊，就像是调皮的小精灵，它们居然还能有波的特性呢。
德布罗意就像是发现了一个超级大宝藏一样，提出了这个概念。
简单来说呢，每一个运动的粒子啊，都可以和一个波联系起来，这个波的波长就是德布罗意波长。
就好比每一个小粒子都给自己披上了一件波的小披风，是不是很有趣呢？这些粒子啊，它们的动量和这个波的波长有着一种奇妙的关系。
动量越大呢，这个德布罗意波长就越小。
这就好像是粒子跑步的速度越快，它身上那件波的小披风就变得越短一样。
从公式的角度来看，德布罗意波长等于普朗克常量除以粒子的动量。
普朗克常量就像是一个神秘的小密码，它在这个微观世界里起着超级重要的作用呢。
你要是把微观粒子想象成一个个小小的球，那它们可不像我们平常看到的球那么简单。
它们一边跑着，一边还散发着波的特性。
这就好像是那些小粒子在微观世界里既有着实体的身体，又有着像幽灵一样的波的影子。
如果我们把德布罗意波长想象成一种信号，那每个粒子都在发出自己独特的信号呢。
这种信号在微观世界里到处传播，影响着周围的一切。
比如说电子，这个小小的电子围绕着原子核转的时候，它的德布罗意波长就在那里默默地发挥着作用。
有时候我就想啊，微观世界就像是一个充满魔法的小天地。
德布罗意波长就像是这个小天地里的一个魔法咒语，一旦我们念出这个咒语，就能看到那些平常看不到的神奇现象。
粒子和波的这种融合，就像是把油和水给混合到一起了，在我们宏观世界里很难想象，但是在微观世界里，这就是真实存在的。
这就告诉我们啊，微观世界有着自己独特的规则，和我们宏观世界是很不一样的呢。
就像我们在生活里遇到一些新奇的事情一样，微观世界的这个德布罗意波长也是科学家们探索未知的一个超级大发现。
它让我们看到了微观世界的复杂性和神奇性，也让我们对这个世界的本质有了更深的认识。
