当前位置：文档之家 › NOI国家集训队论文分类(至2008)(摘抄自C博客)讲解

NOI国家集训队论文分类(至2008)(摘抄自C博客)讲解

  • 格式：doc
  • 大小：58.00 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

国家集训队2003论文集 项荣璟

国家集训队2003论文集 项荣璟

问题三——分析（4）


维护一个表Hlst，表头指针p，表尾指针q。 在递推到第i阶段，bot…top：Si中第bot到第top个元素 （即：lst[bot],lst[bot+1],…,lst[top])都与h联系。 Hlst[k].bot=Hlst[k-1].top+1。
p
H l s t
q
top bot Hlist[k ] h value

问题一——算法分析
for i:=n downto 1 do g(i,1):=f(i,n); ｛边界条件｝ for k:=2 to m do 计算边界g(n-k+1,k); j:=n-k+1; for i:=n-k downto m-k+1 do if f(I,j)<=g(j+1,k-1) then g(i,k):=g(j+1,k-1)｛性质一｝ else if f(i,i)>=g(i+1,k-1) then 【 g(i,k):=f(i,i); j:=i 】 else 【while f(i,j-1)>=g(j,k-1) do j:=j-1; {定si,k} g(i,k):=min{f(i,j),g(j,k-1)} {性质三} if g(i,k)=g(j,k-1) then j:=j-1】 end_for_k 外层每循环一次，j递减的工作量是O(n)。因此总的复杂度O(n２)。

pk q
F (i ) li min Hlst [k ].value
value值不断更新，在求F(n),F(n-1),…,F(0)
时都要察看最小的value。 堆!
问题三——算法分析


国家集训队2009论文集信息学竞赛中概率问题

国家集训队2009论文集信息学竞赛中概率问题
年的NOI中都出现了与概率有关 在05,06,08年的 , , 年的 中都出现了与概率有关 的试题
2 22
全文总览
样本空间 连续型随机变量 随机变量 离散型随机变量
SPOJ RNG SGU Random Shooting SRM 349 LastMarble UVA Randomness
3 22
要用到的定义
1 fi ( [x-Ri, j-Ri+1]x ) = ∫x R i R f i 1 ( t )dt [j-Ri+1,j] [j,x] i
x
P
P
f i1 (t )
f i (x)
19 22
j-Ri j-Ri+1
j j+1
t
j
j+1
x
本题总结
在解决本题的过程中,我们遇到了这样的困难: 在解决本题的过程中,我们遇到了这样的困难: N个随机变量代表着 维空间,较为抽象 个随机变量代表着N维空间 个随机变量代表着 维空间, 两个解法都从N较小的情况开始分析 较小的情况开始分析, 两个解法都从 较小的情况开始分析,发现规律
23 22
用归纳法, 用归纳法,当N=1时,V((0,+∞),x) = x显然 时 显然 符合结论. 符合结论. 设当N=2,3,…,k-1时都有结论成立,那么 时都有结论成立, 设当 时都有结论成立 N=k时,V([0,+∞), [0,+∞),…, [0,+∞),x)就是 时 就是 一个k维锥体的 维体积, 维锥体的k维体积 一个 维锥体的 维体积,椎体的底面面积 是 ( kx 1)! 同时我们知道体积就是截面面积的积分值, 同时我们知道体积就是截面面积的积分值, 而对与锥体的顶点距离为h的截面而言 的截面而言, 而对与锥体的顶点距离为 的截面而言,其 截面面积 (kx 1)! ( h ) 为,所以 所以 x x h 1 x x ( ) dh= ( 0) = V([0,+∞), [0,+∞),…, [0,+∞),x) = ∫ (k 1)! x (k 1)! k k! ■

2008年中国国家集训队选拔考试

2008年中国国家集训队选拔考试

Gn = {1 ,2 , …, n}的全部非空子集排成一个
序列 P1 , P2 , …, P2 n - 1 ,使得对任意的 i ∈{1 ,
2 , …,2 n - 2} ,总有
| Pi ∩Pi + 1 | = 1 ,且 P1 = {1} , P2 n - 1 = Gn .
当 n = 3 时 ,序列{1} ,{1 ,2} ,{2} ,{2 ,3} ,
+
(6 k 2
+4i
+ 1)
=4k
+2i
+1
为蓝色 ,取 an + 1 = 6 k + 4 i + 1 即可.
至此引理 3 证完.
综上三个引理便知结论成立.
2008 年第 7 期
第二天
四 、首先 ,当 n ≥3 时 ,对 n 用数学归纳
法证明下述命题 :
对任意的正整数 n ( n ≥3) ,可以将集合
P′2 k - 4 ∪{ k + 1} , P′2 k - 5 , …, P′3 ,
P′2 ∪{ k + 1} ,{ k + 1} , P′1 ∪{ k + 1} , P′2 ,
P′3 ∪{ k + 1 } , P′4 , …, P′2 k - 2 , ′ P2 k - 1 ∪
{ k + 1}.
q ≥2 p - 1.
三 、引理 1 若正整数集 N+ 中存在一个
无穷的等差数列 ,则结论成立.
事实上 ,设无穷序列 c1 < c2 < …< cn <
…是 一 个 N+ 中 的 红 色 的 等 差 数 列. 则 取
ai = c2 i - 1 ( i ∈N+ ) ,便得到一个满足要求的

国家集训队2004论文集 黄源河

国家集训队2004论文集 黄源河

浅谈图论模型的建立与应用广东省中山市第一中学黄源河【关键字】图论模型、建立、转化【摘要】在近几年的信息学竞赛中，图论题目层出不穷。

图论作为一个新生的数学分支，相比其他数学分支来说，具有许多自有的特性。

利用图论解题，通常具有高效、简洁的便利。

有了这门工具，并不意味就能很好地解决问题，还在于我们能否熟练地识别与建立一系列的图论模型。

本文通过一些实例，简单地介绍一下图论建模的方法。

【正文】引言应用数学知识解题时，首先要通过对实际问题的分析，研究组建用以描述这个问题的数学模型。

使用数学的理论和方法对模型进行分析从而得到结果，再返回去解决现实的实际问题。

图论模型是一类特殊的数学模型，建立图论模型，就是要从问题的原型中，抽取对我们有用的信息和要素，把问题抽象为点、边、权的关系。

经过图论建模之后，杂乱无章的信息变得有规可寻，要素的内在联系体现在了点、边、权的关系。

有不少经典的图论模型可以直接用特定的算法解决，一些复杂的问题，只要能认清问题的本质，把握问题的关键，建立合适的图论模型，往往能转化为我们熟悉的经典问题。

本文要写的，正是我在图论建模方面的一点心得与认识。

例题分析〖例题1〗Place the Robots (ZOJ)[问题大意]有一个N*M(N,M<=50)的棋盘，棋盘的每一格是三种类型之一：空地、草地、墙。

机器人只能放在空地上。

在同一行或同一列的两个机器人，若它们之间没有墙，则它们可以互相攻击。

问给定的棋盘，最多可以放置多少个机器人，使它们不能互相攻击。

[分析]在问题的原型中，草地，墙这些信息不是我们所关心的，我们关心的只是空地和空地之间的联系。

因此，我们很自然想到了下面这种简单的模型：以空地为顶点，有冲突的空地间连边，我们可以得到下面的这个图：那么，问题转化为求图的最大独立集问题。

众所周知，这是NP-完全问题。

看来，建立这样的模型，没有给问题的求解带来任何便利，我们必须建立一个行之有效的新模型。

国家集训队2002论文集-李睿

国家集训队2002论文集-李睿

二分法与统计问题淮阴中学李睿[关键字]线段树二叉树二分法[摘要]我们经常遇到统计的问题。

这些问题的特点是，问题表现得比较简单，一般是对一定范围内的数据进行处理，用基本的方法就可以实现，但是实际处理的规模却比较大，粗劣的算法只能导致低效。

为了解决这种困难，在统计中需要借助一些特殊的工具，如比较有效的数据结构来帮助解决。

本文主要介绍的是分治的思想结合一定的数据结构，使得统计的过程存在一定的模式，以到达提高效率的目的。

首先简要介绍线段树的基础，它是一种很适合计算几何的数据结构，同时也可以扩充到其他方面。

然后将介绍IOI2001中涉及的一种特殊的统计方法。

接着将会介绍一种与线段树有所不同的构造模式，它的形式是二叉排序树，将会发现这种方法是十分灵活的，进一步，我们将略去对它的构造，在有序表中进行虚实现。

目录一线段树1.1 线段树的构造思想1.2 线段树处理数据的基本方法1.3 应用的优势1.4 转化为对点的操作二一种解决动态统计的静态方法2.1 问题的提出2.2 数据结构的构造和设想2.3 此种数据结构的维护2.4 应用的分析三在二叉排序树上实现统计3.1 构造可用于统计的静态二叉排序树3.2 进行统计的方法分析3.3 一个较复杂的例子四虚二叉树4.1 虚二叉树实现的形态4.2 一个具体的例子4.3 最长单调序列的动态规划优化问题[正文]一 线段树在一类问题中，我们需要经常处理可以映射在一个坐标轴上的一些固定线段，例如说映射在OX 轴上的线段。

由于线段是可以互相覆盖的，有时需要动态地取线段的并，例如取得并区间的总长度，或者并区间的个数等等。

一个线段是对应于一个区间的，因此线段树也可以叫做区间树。

1.1线段树的构造思想线段树处理的是一定的固定线段，或者说这些线段是可以对应于有限个固定端点的。

处理问题的时候，首先抽象出区间的端点，例如说N 个端点ti(1≤i ≤N)。

那么对于任何一个要处理的线段（区间）[a,b]来说，总可以找到相应的i,j ，使得ti=a,tj=b,1≤i ≤j ≤N 。

国家集训队2004论文集_林涛

国家集训队2004论文集_林涛

线段树的应用广西柳铁一中林涛【摘要】在竞赛解题中，常遇到与区间有关的操作，比如统计若干矩形并的面积，记录一个区间的最值、总量，并在区间的插入、删除和修改中维护这些最值、总量。

线段树拥有良好的树形二分结构，能够高效的完成这些操作，本文将介绍线段树的各种操作以及一些推广。

本文通过3个例子：《蛇》、《空心长方体》、《战场统计系统》，讲述线段树中基本的插入、删除、查找操作，和不规则的修改和删除操作，以及到二维的推广。

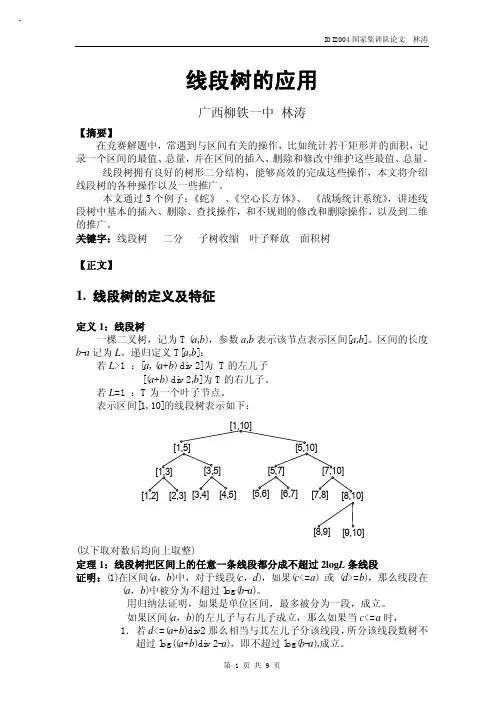
关键字：线段树二分子树收缩叶子释放面积树【正文】1. 线段树的定义及特征定义1：线段树一棵二叉树，记为T (a,b)，参数a,b表示该节点表示区间[a,b]。

区间的长度b-a记为L。

递归定义T[a,b]：若L>1 ：[a, (a+b) div 2]为T的左儿子[(a+b) div 2,b]为T的右儿子。

若L=1 ：T为一个叶子节点。

表示区间[1, 10]的线段树表示如下：(以下取对数后均向上取整)定理1：线段树把区间上的任意一条线段都分成不超过2log L条线段证明：(1)在区间(a，b)中，对于线段(c，d)，如果(c<=a) 或(d>=b)，那么线段在(a，b)中被分为不超过log(b-a)。

用归纳法证明，如果是单位区间，最多被分为一段，成立。

如果区间(a，b)的左儿子与右儿子成立，那么如果当c<=a时，1．若d<=(a+b)div2那么相当与其左儿子分该线段，所分该线段数树不超过log((a+b)div 2-a)，即不超过log(b-a),成立。

2．若d>(a+b) div 2那么相当于该线段被分为它左儿子表示的线段，加上右儿子分该线段，线段数不超过1+log(b-(a+b) div 2),也不超过log(b-a)，成立。

对于d>=b的情况证明类似，不再赘述。

(2)在区间(a,b)中，对于任意线段也用归纳法证明。

对于单位区间，最多分为一段，成立。

2008年noip提高组复赛题解


2015/11/25
北京12中庄燕文
【题目类型】双线程动态规划 【建议编程时间】40分钟。这里的编程时间包括调试时间。 【空间复杂度】约27M，全局变量完全可承受。50*50*50*50*sizeof(int)=2.5*10^7. 【解题分析】 1、 读入矩阵，注意行列。 2、 采用一个四维数组记录当前两条路走到的位置(i1,j1,i2,j2)时取得的最大值，初始化为 0，表示不可能到达。(0,0,0,0)为1，最后减1输出。 3、 一个四重循环枚举两条路分别走到的位置。由于每个点均从上或左继承而来，故内部 有四个if，分别表示两个点从上上、上左、左上、左左继承来时，加上当前两个点所取得 的最大值。例如，f[i][j][k][l] = max{f[i][j][k][l], f[i-1][j][k-1][l] + a[i][j] + a[k][l]}，表示两点均从 上面位置走来。 4、 输出右下角处的最大值f[m][n][m][n]，注意换行。 【编程注意】 1、 在数组边界处特殊处理，避免数组越界。 2、 若待继承的点最大值为零，则停止判断，不能从这里走来。 3、 显然，非矩阵右下角的汇合点，两个位置不能重合（否则路径相交），若重合则最大 值为0，不可达。
2015/11/25
北京12中庄燕文
这道题的错误做法很多,错误做法却能得满分的也很多, 这里就不多说了.直接切入正题,就是即将介绍的这个基 于二分图的算法. 注意到并没有说基于二分 图匹配,因为这个算法和二分图匹配无关.这个算法只是 用到了给一个图着色成二分图. 第一步需要解决的问题是,判断是否有解. 考虑对于任意两个数q1[i]和q1[j]来说,它们不能压入同 一个栈中的充要条件是什么(注意没有必要使它们同时 存在于同一个栈中,只是压入了同一个栈).实际上,这个 条件p是:存在一个k,使得i<j<k且q1[k]<q1[i]<q1[j].

国家集训队2007论文集7.胡伯涛《最小割模型


[Key Words]
Network Flow, Maximum Flow, Minimum Cut, Maximum Weight Closure of a Graph, Finding
a Maximum Density Sub Graph, Minimum Weight Vertex Covering Set and Maximum Weight
第 2 页 共 45 页
[][Library]Thesis
最小割模型在信息学竞赛中的应用
Amber
3.1. 引入 Introduction...........................................................................................................16 3.2. 构造 Construction of Algorithm ....................................................................................17 3.3. 证明 Proof......................................................................................................................17 3.4. 应用 Application............................................................................................................19
knowledge of minimum cut model. The thesis sets focus on researching that is in four aspects: 1. the application based on the

国家集训队2004论文集 韩文韬

模板类的使用carrayint100carraydouble20carraycarrayint1010stl就是建立在模板函数和模板类基础之上的功能强大的库模板函数可以实现一般化的常用算法如统计排序查找等模板类可以实现支持几乎所有类型的容器用来实现常用的数据结构如链表栈队列平衡二叉树等stl头文件一览头文件内容头文件内容iterator迭代器vector向量utility辅助功能deque双头队列memory内存管理list链表algorithm算法set集合与多重集合functional函数对象map映射与多重映射numeric数值运算stackqueue队列与优先队列32迭代器迭代器的定义和种类迭代器iterator实际上是一种一般化的指针类型是对指针类型的抽象
类型 双目 双目 双目 双目 双目 双目 双目 双目 单目 双目 双目 双目 双目 双目 单目
作用 arg1 == arg2 arg1 != arg2 arg1 > arg2 arg1 < arg2 arg1 >= arg2 arg1 <= arg2 arg1 && arg2 arg1 || arg2 !arg arg1 + arg2 arg1 - arg2 arg1 * arg2 arg1 / arg2 arg1 % arg2 -arg
更多关于迭代器的信息
指针类型就是一种特殊的随机迭代器类型. 对于一般的迭代器,这些功能都是通过操 作符重载来实现的.
更多关于迭代器的信息
各种迭代器类型之间的关系:
输出迭代器 前向迭代器 输入迭代器 双向迭代器 随机迭代器
迭代器的作用
访问元素 算法与容器之间的纽带
模板类pair
template<class T1, class T2> struct pair { typedef T1 first_type; typedef T2 second_type; T1 first; T2 second; pair() : first(T1()), second(T2()) { } pair(const T1& x, const T2& y) : first(x), second(y) { } template<class U, class V> pair(const pair<U, V>& p) : first(p.first), second(p.second) { } };

国家集训队2002论文集 李睿


一维序列求和
设序列的元素存储在a[]中,a的下标是 1..n的正整数,需要动态地更新某个a[x] 的值,同时要求出a[x1]到a[y1]这一段所 有元素的和.
对于序列a[1..n],我们设一个数组 C[1..n],C[i]=a[i-2k+1]+…+a[i],其中k为 , i在二进制下末尾0的个数 1001010110010000 k =4 计算C[x]对应的2k LOWBIT(x) 2k =x and (x xor (x-1))
插入一个点x 插入一个点x
procedure INSERT(x) begin now ← 1 repeat SUM[now]←SUM[now]+1 if (V[now]=x) break if (V[now]>x) now←now*2 else now←now*2+1 until false End 其中SUM是记录一棵子树上结点总数 其中 是记录一棵子树上结点总数 删除 的方法是类似的
O(n2)
对P进行特殊的限制,即,在所有等价的决策j 中,P选择a[j]最大的那一个 在处理完a[1..x-1]之后,对于所有长度为M[x]-1 的下降序列,P[x]的决策只跟其中末尾最大的 一个有关. 用另外一个动态变化的数组b,当我们计算完了 a[x]之后,a[1..x]中得到的所有下降序列按照长 度分为L类,每一类中只需要一个作为代表, 这个代表在这个等价类中末尾的数最大,我们 把它记为b[j],1≤j≤L. 处理当前的一个数a[x],我们无需和前面的a[j] (1≤j≤x-1)作比较,只需要和b[j](1≤j≤L)进行 比较.
线段树线段树-一个特殊性质举例
要得到线段树上线段并集的长度,增加 一个数据域 M[v],讨论: C[v]>0,M[v] = E[v]-B[v]; C[v]=0 且v是叶子结点,M[v]=0; C[v]=0 且v是内部结点, M[v]=M[LSON[v]]+M[RSON[v]];
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

NOI国家集训队论文分类（至2008） 摘抄自C博客 组合数学 计数与统计 2001 - 符文杰：《Pólya原理及其应用》 2003 - 许智磊：《浅谈补集转化思想在统计问题中的应用》 2007 - 周冬：《生成树的计数及其应用》 2008 - 陈瑜希《Pólya计数法的应用》 数位问题 2009 - 高逸涵《数位计数问题解法研究》 2009 - 刘聪《浅谈数位类统计问题》 动态统计 2004 - 薛矛：《解决动态统计问题的两把利刃》 2007 - 余江伟：《如何解决动态统计问题》 博弈 2002 - 张一飞：《由感性认识到理性认识——透析一类搏弈游戏的解答过程》 2007 - 王晓珂：《解析一类组合游戏》 2009 - 曹钦翔《从“k倍动态减法游戏”出发探究一类组合游戏问题》 2009 - 方展鹏《浅谈如何解决不平等博弈问题》 2009 - 贾志豪《组合游戏略述——浅谈SG游戏的若干拓展及变形》 母函数 2009 - 毛杰明《母函数的性质及应用》 拟阵 2007 - 刘雨辰：《对拟阵的初步研究》 线性规划 2007 - 李宇骞：《浅谈信息学竞赛中的线性规划——简洁高效的单纯形法实现与应用》 置换群 2005 - 潘震皓：《置换群快速幂运算研究与探讨》 问答交互 2003 - 高正宇：《答案只有一个——浅谈问答式交互问题》 猜数问题 2003 - 张宁：《猜数问题的研究:一题的推广》 2006 - 龙凡：《一类猜数问题的研究》 数据结构 数据结构 2005 - 何林：《数据关系的简化》 2006 - 朱晨光：《基本数据结构在信息学竞赛中的应用》 2007 - 何森：《浅谈数据的合理组织》 2008 - 曹钦翔《数据结构的提炼与压缩》 结构联合 2001 - 高寒蕊：《从圆桌问题谈数据结构的综合运用》 2005 - 黄刚：《数据结构的联合》 块状链表 2005 - 蒋炎岩：《数据结构的联合——块状链表》 2008 - 苏煜《对块状链表的一点研究》 动态树 2006 - 陈首元：《维护森林连通性——动态树》 2007 - 袁昕颢：《动态树及其应用》 左偏树 2005 - 黄源河：《左偏树的特点及其应用》 跳表 2005 - 魏冉：《让算法的效率“跳起来”！——浅谈“跳跃表”的相关操作及其应用》 2009 - 李骥扬《线段跳表——跳表的一个拓展》 SBT 2007 - 陈启峰：《Size Balance Tree》 线段树 2004 - 林涛：《线段树的应用》 单调队列 2006 - 汤泽：《浅析队列在一类单调性问题中的应用》 哈希表 2005 - 李羽修：《Hash函数的设计优化》 2007 - 杨弋：《Hash在信息学竞赛中的一类应用》 Splay 2004 - 杨思雨：《伸展树的基本操作与应用》 图论 图论 2005 - 任恺：《图论的基本思想及方法》 模型建立 2004 - 黄源河：《浅谈图论模型的建立与应用》 2004 - 肖天：《“分层图思想”及其在信息学竞赛中的应用》 网络流 2001 - 江鹏：《从一道题目的解法试谈网络流的构造与算法》 2002 - 金恺：《浅谈网络流算法的应用》 2007 - 胡伯涛：《最小割模型在信息学竞赛中的应用》 2007 - 王欣上：《浅谈基于分层思想的网络流算法》 2008 - 周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》 最短路 2006 - 余远铭：《最短路算法及其应用》 2008 - 吕子鉷《浅谈最短径路问题中的分层思想》 2009 - 姜碧野《SPFA算法的优化及应用》 欧拉路 2007 - 仇荣琦：《欧拉回路性质与应用探究》 差分约束系统 2006 - 冯威：《数与图的完美结合——浅析差分约束系统》 平面图 2003 - 刘才良：《平面图在信息学中的应用》 2007 - 古楠：《平面嵌入》 2-SAT 2003 - 伍昱：《由对称性解2-SAT问题》 最小生成树 2004 - 吴景岳：《最小生成树算法及其应用》 2004 - 汪汀：《最小生成树问题的拓展》 二分图 2005 - 王俊：《浅析二分图匹配在信息学竞赛中的应用》 Voronoi图 2006 - 王栋：《浅析平面Voronoi图的构造及应用》 偶图 2002 - 孙方成：《偶图的算法及应用》 树 树 2002 - 周文超：《树结构在程序设计中的运用》 2005 - 栗师：《树的乐园——一些与树有关的题目》 路径问题 2009 - 漆子超《分治算法在树的路径问题中的应用》 最近公共祖先 2007 - 郭华阳：《RMQ与LCA问题》 划分问题 2004 - 贝小辉：《浅析树的划分问题》 数论 欧几里得算法 2009 - 金斌《欧几里得算法的应用》 同余方程 2003 - 姜尚仆：《模线性方程的应用——用数论方法解决整数问题》 搜索 搜索 2001 - 骆骥：《由“汽车问题”浅谈深度搜索的一个方面——搜索对象与策略的重要性》 2002 - 王知昆：《搜索顺序的选择》 2005 - 汪汀：《参数搜索的应用》 启发式 2009 - 周而进《浅谈估价函数在信息学竞赛中的应用》 优化 2003 - 金恺：《探寻深度优先搜索中的优化技巧——从正方形剖分问题谈起》 2003 - 刘一鸣：《一类搜索的优化思想——数据有序化》 2006 - 黄晓愉：《深度优先搜索问题的优化技巧》 背包问题 2009 - 徐持衡《浅谈几类背包题》 匹配 2004 - 楼天城：《匹配算法在搜索问题中的巧用》 概率 概率 2009 - 梅诗珂《信息学竞赛中概率问题求解初探》 数学期望 2009 - 汤可因《浅析竞赛中一类数学期望问题的解决方法》 字符串 字符串 2003 - 周源：《浅析“最小表示法”思想在字符串循环同构问题中的应用》 多串匹配 2004 - 朱泽园：《多串匹配算法及其启示》 2006 - 王赟：《Trie图的构建、活用与改进》 2009 - 董华星《浅析字母树在信息学竞赛中的应用》 后缀数组 2004 - 许智磊：《后缀数组》 2009 - 罗穗骞《后缀数组——处理字符串的有力工具》 字符串匹配 2003 - 饶向荣：《病毒的DNA———剖析一道字符匹配问题解析过程》 2003 - 林希德：《求最大重复子串》 动态规划 动态规划 2001 - 俞玮：《基本动态规划问题的扩展》 2006 - 黄劲松：《贪婪的动态规划》 2009 - 徐源盛《对一类动态规划问题的研究》 状态压缩 2008 - 陈丹琦《基于连通性状态压缩的动态规划问题》 状态设计 2008 - 刘弈《浅谈信息学中状态的合理设计与应用》 树形DP 2007 - 陈瑜希：《多角度思考创造性思维——运用树型动态规划解题的思路和方法探析》 优化 2001 - 毛子青：《动态规划算法的优化技巧》 2003 - 项荣璟：《充分利用问题性质——例析动态规划的“个性化”优化》 2004 - 朱晨光：《优化，再优化！——从《鹰蛋》一题浅析对动态规划算法的优化》 2007 - 杨哲：《凸完全单调性的加强与应用》 计算几何 立体几何 2003 - 陆可昱：《长方体体积并》 2008 - 高亦陶《从立体几何问题看降低编程复杂度》 计算几何思想 2004 - 金恺：《极限法——解决几何最优化问题的捷径》 2008 - 程芃祺《计算几何中的二分思想》 2008 - 顾研《浅谈随机化思想在几何问题中的应用》 圆 2007 - 高逸涵：《与圆有关的离散化》 半平面交 2002 - 李澎煦：《半平面交的算法及其应用》 2006 - 朱泽园：《半平面交的新算法及其实用价值》 矩阵 矩阵 2008 - 俞华程《矩阵乘法在信息学中的应用》 高斯消元 2002 - 何江舟：《用高斯消元法解线性方程组》 数学方法 数学思想 2002 - 何林：《猜想及其应用》 2003 - 邵烜程：《数学思想助你一臂之力》 数学归纳法 2009 - 张昆玮《数学归纳法与解题之道》 多项式 2002 - 张家琳：《多项式乘法》 数形结合 2004 - 周源：《浅谈数形结合思想在信息学竞赛中的应用》 黄金分割 2005 - 杨思雨：《美，无处不在——浅谈“黄金分割”和信息学的联系》 其他算法 遗传算法 2002 - 张宁：《遗传算法的特点及其应用》 2005 - 钱自强：《关于遗传算法应用的分析与研究》 信息论 2003 - 侯启明：《信息论在信息学竞赛中的简单应用》 染色与构造 2002 - 杨旻旻：《构造法——解题的最短路径》 2003 - 方奇：《染色法和构造法在棋盘上的应用》 一类问题 区间 2008 - 周小博《浅谈信息学竞赛中的区间问题》 序 2005 - 龙凡：《序的应用》 系 2006 - 汪晔：《信息学中的参考系与坐标系》 物理问题 2008 - 方戈《浅析信息学竞赛中一类与物理有关的问题》 编码与译码 2008 - 周梦宇《码之道—浅谈信息学竞赛中的编码与译码问题》 对策问题 2002 - 骆骥：《浅析解“对策问题”的两种思路》 优化 算法优化 2002 - 孙林春：《让我们做得更好——从解法谈程序优化》 2004 - 胡伟栋：《减少冗余与算法优化》 2005 - 杨弋：《从的解法谈算法的优化》 2006 - 贾由：《由图论算法浅析算法优化》 程序优化 2006 - 周以苏：《论反汇编在时间常数优化中的应用》 2009 - 骆可强《论程序底层优化的一些方法与技巧》 语言 C++