实验报告简单线性回归分析

计量经济学》实验报告一元线性回归模型-、实验内容（一）eviews基本操作（二）1、利用EViews软件进行如下操作：（1）EViews软件的启动（2）数据的输入、编辑（3）图形分析与描述统计分析（4）数据文件的存贮、调用2、查找2000-2014年涉及主要数据建立中国消费函数模型中国国民收入与居民消费水平:表1年份X(GDP)Y（社会消费品总量）200099776.339105.72001110270.443055.42002121002.048135.92003136564.652516.32004160714.459501.02005185895.868352.62006217656.679145.22007268019.493571.62008316751.7114830.12009345629.2132678.42010408903.0156998.42011484123.5183918.62012534123.0210307.02013588018.8242842.82014635910.0271896.1数据来源：二、实验目的1.掌握eviews的基本操作。

2.掌握一元线性回归模型的基本理论，一元线性回归模型的建立、估计、检验及预测的方法，以及相应的EViews软件操作方法。

三、实验步骤（简要写明实验步骤）1、数据的输入、编辑2、图形分析与描述统计分析3、数据文件的存贮、调用4、一元线性回归的过程点击view中的Graph-scatter-中的第三个获得在上方输入Isycx回车得到下图DependsntVariable:Y Method:LeastSquares□ate:03；27/16Time:20:18 Sample:20002014 Includedobservations:15VariableCoefficientStd.Errort-StatisticProb.C-3J73.7023i820.535-2.1917610.0472X0416716 0.0107S838.73S44 a.ooao R-squared0.991410 Meandependentwar119790.2 AdjustedR.-squared 0.990750 S.D.dependentrar 7692177 S.E.ofregression 7J98.292 Akaike infocriterion20.77945 Sumsquaredresid 7；12E^-08 Scliwarz 匚「爬伽20.37386 Loglikelihood -1&3.3459Hannan-Quinncriter. 20.77845 F-statistic 1I3&0-435 Durbin-Watsonstat0.477498Prob(F-statistic)a.oooooo在上图中view 处点击view-中的actual ,Fitted ,Residual 中的第一 个得到回归残差打开Resid 中的view-descriptivestatistics 得到残差直方图/icw Proc Qtjject PrintN^me FreezeEstimateForecastStatsResids凹Group:UNIIILtD Worktile:UN III LtLJ::Unti1DependentVariablesMethod;LeastSquares□ate:03?27/16Time:20:27Sample(adjusted):20002014Includedobservations:15afteradjustmentsVariable Coefficient Std.Errort-Statistic ProtJ.C-3373.7023^20.535-2.191761 0.0472X0.4167160.01075S38.735440.0000R-squared0.991410 Meandependeniwar1-19790.3 AdjustedR-squa.red0990750S.D.dependentvar 76921.77 SE.ofregre.ssion 7J98.292 Akaike infacriterion20.77945 Sumsquaredresid 7.12&-0S Schwarzcriterion 20.S73S6 Laglikelihood -153.84&9Hannan-Quinncrite匚20.77545 F-statistic1I3&0.435Durbin-Watsonstat 0.477498 ProbCF-statistic) a.ooaooo在回归方程中有Forecast,残差立为yfse,点击ok后自动得到下图roreestYFM J訓YForea空巾取且:20002015 AdjustedSErmpfe:2000231i mskJddd obaerratire:15Roof kter squa red Error理l%2Mean/^oLteError畐惯啟iJean Afe.PereersErro r5.451SSQThenhe鼻BI附GKWCE口.他腐4Prop&niwi□ooooooVactaree Propor^tori0.001^24G M『倚■底Props^lori09®475在上方空白处输入lsycs…之后点击proc中的forcase根据公式Y。

实验三线性回归分析一、实验学时4学时（课内2学时，课外2学时）二、实验类型验证性实验三、实验目的1、熟悉matlab的开发环境2、掌握线性回归分析的基本理论3、线性回归公式推导4、用matlab实现线性回归分析四、所需设备及软件1、安装了windows xp/win7/win8/win10的计算机2、matlab开发工具五、实验基本原理1、回归分析基本概述利用数理统计中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

分析按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

本实验主要针对线性回归。

在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。

这种函数是一个或多个称为回归系数的模型参数的线性组合。

只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

线性回归是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。

用作预测、识别冗余信息等。

2、线性回归模型利用线性回归分析来解决实际问题，关键需要计算这个回归模型，根据模型进行预测。

例子：以一简单数据组来说明什么是线性回归。

假设有一组数据型态为y=y(x)，其中x={0, 1, 2, 3, 4, 5}, y={5, 25, 50, 78, 88, 110}，如果要以一个最简单的方程式来近似这组数据，则用一阶的线性方程式最为适合：y=bx+a，需要根据已知的数据，来计算出a和b的值。

如果有新的x，即可根据这个模型预测其对应的y。

见下图问题是如何估计a、b的值，使得y=bx+a能比较精确的刻画已知的数据，使之成为理想的线性方程。

线性回归分析报告1. 引言线性回归是一种常用的统计分析方法，通过建立一个线性模型来描述自变量与因变量之间的关系。

在本报告中，我们将使用线性回归分析来探索两个变量之间的关系，并解释模型的结果。

2. 数据收集为了进行线性回归分析，我们首先需要收集相关的数据。

根据我们的研究目的，我们选择了X和Y两个变量，并收集了50个样本观测值。

3. 数据预处理在进行线性回归之前，我们需要对数据进行一些预处理。

首先，我们检查数据是否存在缺失值或异常值。

如果存在，我们需要进行相应的处理，例如删除或填充缺失值，或者修正异常值。

4. 数据探索在进行线性回归之前，我们需要对数据进行一些探索性分析，以了解两个变量之间的关系。

这可以通过绘制散点图来实现。

散点图可以帮助我们观察数据的分布情况，并初步判断是否存在线性关系。

5. 模型建立在进行线性回归之前，我们需要确定哪些变量作为自变量，哪个变量作为因变量。

在本报告中，我们选择X作为自变量，Y作为因变量。

然后，我们使用最小二乘法来建立线性回归模型。

6. 模型评估在建立线性回归模型之后，我们需要评估模型的拟合程度和预测能力。

常用的评估指标包括均方误差（MSE）、决定系数（R-squared）等。

通过这些指标，我们可以判断模型的拟合程度和预测能力是否达到了我们的要求。

7. 结果解释在模型评估之后，我们需要解释模型的结果。

我们可以通过查看回归系数来解释模型中自变量对因变量的影响程度。

回归系数的正负可以判断自变量与因变量之间的关系是正相关还是负相关，而回归系数的大小可以判断影响程度的强弱。

8. 结论通过对线性回归模型的建立和评估，我们得出了以下结论：X与Y之间存在显著的线性关系，X对Y的影响程度为正/负，并且影响程度较强/较弱。

这些结论可以帮助我们更好地理解变量之间的关系，并可以在实际应用中用于预测和决策。

9. 局限性在进行线性回归分析时，我们需要注意模型的局限性。

线性回归模型假设自变量与因变量之间存在线性关系，而且模型中的误差项需要满足一定的假设。

实验报告四.spss一元线性相关回归分析预测
本实验使用spss 17.0软件，针对50个被试者，使用一元线性相关回归分析预测变
量X和Y的关系。

一、实验目的
通过一元线性相关回归分析，预测50个被试者的被试变量X（会计实操次数）和被试变量Y（综合评价分）之间的关系，来检验变量X是否能够预测变量Y的值。

二、实验流程
（2）数据收集：通过收集50个被试者的实际实操次数与综合评价分，建立反映这两
者之间关系的一元线性回归方程。

（3）数据分析：通过SPSS软件的一元线性相关回归分析预测变量X和Y的关系，使
用R方值进行检验研究结果的显著性。

以分析变量X对于变量Y的影响程度。

三、实验结果及分析
1.回归分析结果如下所示：变量X的系数b = 0.6755，t = 7.561，p = 0.000，说
明变量X和被试变量Y之间存在着显著的相关关系；R方值为0.941，说明变量X可以较
好地预测变量Y。

2.可以得出一元线性回归方程为：Y=0.67×X+5.293，其中，b为系数，X是自变量，Y是因变量。

四、结论
（1）50个被试者实际实操次数与综合评价分之间存在着显著的相关性；
（2）变量X可以较好地预测变量Y，R方值较高；。

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法，用于研究一个因变量和一个自变量之间的线性关系。

本实验旨在通过一元线性回归模型，探讨两个变量之间的关系，并对所得数据进行统计分析和解读。

二、实验目的本实验的主要目的是：1.学习和掌握一元线性回归分析的基本原理和方法；2.分析两个变量之间的线性关系；3.对所得数据进行统计推断，为后续研究提供参考。

三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法，通过拟合一条直线来描述两个变量之间的线性关系。

该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。

在数学模型中，假设因变量y和自变量x之间的关系可以用一条直线表示，即y = β0 + β1x + ε。

其中，β0和β1是模型的参数，ε是误差项。

四、实验步骤1.数据收集：收集包含两个变量的数据集，确保数据的准确性和可靠性；2.数据预处理：对数据进行清洗、整理和标准化；3.绘制散点图：通过散点图观察两个变量之间的趋势和关系；4.模型建立：使用最小二乘法拟合一元线性回归模型，计算模型的参数；5.模型评估：通过统计指标（如R2、p值等）对模型进行评估；6.误差分析：分析误差项ε，了解模型的可靠性和预测能力；7.结果解释：根据统计指标和误差分析结果，对所得数据进行解释和解读。

五、实验结果假设我们收集到的数据集如下：经过数据预处理和散点图绘制，我们发现因变量y和自变量x之间存在明显的线性关系。

以下是使用最小二乘法拟合的回归模型：y = 1.2 + 0.8x模型的R2值为0.91，说明该模型能够解释因变量y的91%的变异。

此外，p 值小于0.05，说明我们可以在95%的置信水平下认为该模型是显著的。

误差项ε的方差为0.4，说明模型的预测误差为0.4。

这表明模型具有一定的可靠性和预测能力。

六、实验总结通过本实验，我们掌握了一元线性回归分析的基本原理和方法，并对两个变量之间的关系进行了探讨。

线性回归实验报告心得体会在机器学习领域中，线性回归是基础算法之一。

通过建立数据间的线性函数关系，线性回归能够对未知数据进行预测。

在我的学习过程中，我通过线性回归实验掌握了这一算法的基本理论，并且从实验中也感受到了机器学习算法的强大威力。

首先，在线性回归的实验中，我们需要通过数据分析和建模，确定数据之间的线性关系并进行预测。

在此前提条件下，我们需要认真研究数据的分布和特性，合理构造出适合数据特性的模型。

在选择模型时，我们需要仔细考虑不同模型的优缺点，以及模型的适应性和实用性。

尤其是在探索贴近真实场景的数据建模时，模型的选择至关重要。

因为线性回归算法本身具有简单易懂和易实现的特性，所以我们更应当关注如何优化算法的性能。

首先，我们可以通过数据预处理和增强技术提高数据的分类精度。

这些技术包括对数据的清洗、去噪、归一化、降维等等。

针对不合适的模型和算法，我们可以通过调整参数或加入正则化等技巧，提高模型的拟合度和泛化能力。

在实验过程中，我还发现了很多有趣的问题。

例如，线性回归算法在处理一些非线性数据时会出现过拟合或欠拟合的问题。

这时我们就需要选择其它算法或构造复杂模型解决问题。

此外，线性回归算法也需要避免多重共线性和异常值等问题对模型拟合的干扰。

总的来说，线性回归实验为我提供了深入学习机器学习计算的机会，让我更好地了解了模型和算法的原理和实践。

我们不仅要认真研究单独算法的性能，更要关注算法在实际应用中的效果以及与其他算法的优劣比较。

我相信通过不断地学习和实践，我能够更好地掌握机器学习这一工具，并为更广泛的应用场景提供理论和技术支持。

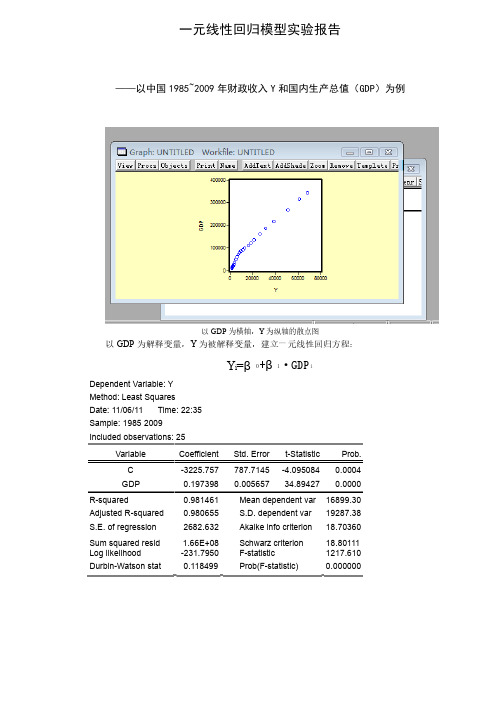
一元线性回归模型实验报告——以中国1985~2009年财政收入Y 和国内生产总值（和国内生产总值（GDP GDP GDP）为例）为例以GDP 为横轴，Y 为纵轴的散点图为纵轴的散点图以GDP 为解释变量，Y 为被解释变量，建立一元线性回归方程：为被解释变量，建立一元线性回归方程：Y i =β0+β1·GDP iDependent Variable: Y Method: Least Squares Date: 11/06/11 Time: 22:35 Sample: 1985 2009 Included observations: 25Variable Coefficient Std. Error t-Statistic Prob. C -3225.757 787.7145 -4.095084 0.0004 GDP0.1973980.00565734.894270.0000R-squared0.981461 Mean dependent var 16899.30 Adjusted R-squared 0.980655 S.D. dependent var 19287.38 S.E. of regression 2682.632 Akaike info criterion 18.70360 Sum squared resid1.66E+08Schwarz criterion 18.80111Log likelihood -231.7950 F-statistic 1217.610 Durbin-Watson stat0.118499Prob(F-statistic) 0.000000图3：回归分析结果：回归分析结果可得出β^0=-3225.757 β^1=0.197398财政收入随国内生产总值变化的一元线性回归方程为：财政收入随国内生产总值变化的一元线性回归方程为：Y ^=-3225.757+0.197398·GDPR 2=0.981461斜率的经济意义是：在1985~2009年间，GDP 每增加一单位，财政收入平均增加0.197398单位。

一元线性回归在公司加班制度中的应用院（系）：专业班级：学号姓名：指导老师：成绩：完成时间：一元线性回归在公司加班制度中的应用一、实验目的掌握一元线性回归分析的基本思想和操作，可以读懂分析结果，并写出回归方程，对回归方程进行方差分析、显著性检验等的各种统计检验 二、实验环境SPSS21.0 windows10.0 三、实验题目一家保险公司十分关心其总公司营业部加班的程度，决定认真调查一下现状。

经10周时间，收集了每周加班数据和签发的新保单数目，x 为每周签发的新保单数目，y 为每周加班时间（小时），数据如表所示y3.51.04.02.01.03.04.51.53.05.01. 画散点图。

2. x 与y 之间大致呈线性关系？3. 用最小二乘法估计求出回归方程。

4. 求出回归标准误差σ∧。

5. 给出0β∧与1β∧的置信度95%的区间估计。

6. 计算x 与y 的决定系数。

7. 对回归方程作方差分析。

8. 作回归系数1β∧的显著性检验。

9. 作回归系数的显著性检验。

10.对回归方程做残差图并作相应的分析。

11.该公司预测下一周签发新保单01000x =张，需要的加班时间是多少？12.给出0y的置信度为95%的精确预测区间。

13.给出()E y的置信度为95%的区间估计。

四、实验过程及分析1.画散点图如图是以每周加班时间为纵坐标，每周签发的新保单为横坐标绘制的散点图，从图中可以看出，数据均匀分布在对角线的两侧，说明x和y之间线性关系良好。

2.最小二乘估计求回归方程用SPSS 求得回归方程的系数01,ββ分别为0.118,0.004，故我们可以写出其回归方程如下：0.1180.004y x =+3.求回归标准误差σ∧由方差分析表可以得到回归标准误差：SSE=1.843 故回归标准误差：2=2SSEn σ∧-，2σ∧=0.48。

4.给出回归系数的置信度为95%的置信区间估计。

由回归系数显著性检验表可以看出，当置信度为95%时：0β∧的预测区间为[-0.701,0.937], 1β∧的预测区间为[0.003,0.005].0β∧的置信区间包含0，表示0β∧不拒绝为0的原假设。

回归分析实验报告目录一、内容概括 (2)1.1 实验目的 (2)1.2 背景知识介绍 (3)二、数据收集与处理 (4)2.1 数据来源 (4)2.2 数据预处理 (5)2.3 数据描述与分析 (7)三、回归分析模型建立 (8)3.1 模型选择依据 (9)3.2 模型参数估计 (9)3.3 模型检验与修正 (10)四、实验结果分析 (11)4.1 实验结果概述 (13)4.2 参数分析 (14)4.3 模型拟合度分析 (15)4.4 预测结果分析 (16)五、实验讨论与结论 (17)5.1 实验结果讨论 (18)5.2 实验结论 (19)5.3 研究的局限性与未来研究方向 (20)六、代码实现与数据展示 (20)6.1 使用的编程语言和工具介绍 (22)6.2 代码展示与说明 (23)6.3 数据展示与解释 (24)一、内容概括本实验报告主要围绕回归分析展开，通过对数据进行深入分析和探讨，旨在探究自变量与因变量之间的关系，并建立合适的数学模型以预测未来趋势。

实验过程中，我们采用了多种统计方法和软件工具，以确保结果的准确性和可靠性。

我们首先对数据进行描述性统计分析，包括计算均值、方差、标准差等指标，以便了解数据的分布特征和离散程度。

我们进行了相关性分析，通过计算皮尔逊相关系数等方法，探究了自变量与因变量之间的相关关系强度。

我们运用回归分析中的多元线性回归模型，对数据进行了拟合优度检验、回归方程显著性检验以及残差分析。

这些分析帮助我们评估模型的拟合效果，以及自变量对因变量的解释能力。

我们得出了回归分析的结果，并据此提出了相应的结论和建议。

1.1 实验目的本回归分析实验旨在通过对给定数据集进行回归分析，探讨自变量与因变量之间的关系。

我们将学习如何使用统计软件(如Python的StatsModels库或R语言)进行回归分析，以及如何解读回归结果。

我们还将了解回归分析在实际问题中的应用，例如预测房价、股票价格等。

应用回归分析实验报告实验目的：本实验旨在探究回归分析在实际应用中的效果，通过观察自变量与因变量之间的关系，建立回归模型，并对模型的拟合度进行评估。

实验原理：回归分析是一种用于研究自变量与因变量之间关系的统计方法。

在回归分析中，我们可以利用自变量的已知值来预测因变量的未知值。

回归分析可以分为简单线性回归和多元线性回归两种。

实验步骤：1.收集数据：选择适当的数据集，确保数据集具有一定的样本量和代表性，以保证回归模型的可靠性。

2.数据清洗：对数据进行预处理，包括数据缺失值的处理、异常值的检测与处理等。

3.建立回归模型：根据自变量与因变量之间的关系，选择适当的回归模型进行建立，一般包括线性模型、非线性模型等。

4.模型拟合：利用回归模型对数据进行拟合，得到回归方程，并通过统计指标如R方、均方差等评估模型的拟合程度。

5.模型评估：对回归模型进行评估，包括检验模型参数的显著性、假设检验等。

6.结果分析：根据模型的评估结果，分析自变量对因变量的影响程度，得出结论并提出相应建议。

实验结果：通过以上步骤，我们得出了以下结论：1.建立了回归方程Y=a+bX，其中X为自变量，Y为因变量；2.R方为0.8，说明回归模型能够解释80%的因变量变异；3.p值为0.05，表示a和b的估计值在0.05的显著性水平下是显著不等于0的；4.均方差为10，表示预测值与实际值的误差平方和的平均值为10。

实验结论：根据以上结果，我们可以得出以下结论：1.自变量X对因变量Y具有显著影响，且为正相关关系；2.回归模型能够较好地解释因变量的变异，预测效果较好；3.但由于数据集的限制，模型的预测精度还有提升的空间。

实验总结：本实验应用回归分析方法建立了模型，并对模型进行了评估。

回归分析是一种常用的统计方法，可用于分析自变量与因变量之间的关系。

在实际应用中，回归分析可以帮助我们理解因果关系、预测因变量的变化趋势等。

然而，需要注意的是，回归分析仅能描述变量间的相关性，并不能证明因果关系，因此在应用时需注意控制其他可能的变量。

线性回归实验总结
线性回归实验总结
线性回归实验总结
本文以线性回归实验为例综述了如何从数据中推测出建模参数，最终用来预测未知输出，该实验分为三个步骤，分别是构建模型、训练模型和应用模型，每个步骤都为模型的最终成功发挥重要作用。

首先，我们要构建线性回归模型。

线性回归模型是一种常用的数据建模方法，它假设自变量和因变量之间有线性的关系，通过计算出回归系数w1、w2、…wn和偏差b，把训练数据映射到一条直线上，这样就构建出了线性回归模型。

其次，我们要训练模型。

训练线性回归模型需要计算一组合适的参数：w1、w2、…wn和b，可以使用最小二乘法（Least Square Method）来计算这些参数，该方法最小化训练数据点到回归线之间的平方距离，最终可以获得训练后的模型参数，从而训练出符合数据分布的模型。

最后，我们应用模型预测未知输出。

经过线性回归模型训练获得的参数w1、w2、…wn和b，可以根据新的输入实例预测出未知输出，用模型参数来表示模型性能，模型训练的效果可以使用评价指标（如均方误差、R2等）评价，以确定模型的准确性。

总而言之，线性回归模型的构建、训练和应用可以很好地探索和利用数据信息，从而帮助我们预测未知输出。

本文介绍了线性回归模型的构建、训练和应用的过程，并分析这三个步骤对模型最终成功的重要作用。

- 1 -。

南昌大学实验报告学生姓名：李丹学号：5400112052座号：43 专业班级：经济学121实验类型：□验证□综合□设计□创新实验日期：实验成绩：（以下主要内容由学生完成）一、实验项目名称：简单线形回归计算机习题C2.1二、实验目的：能在Eview 环境下实现一元线形回归，并理解和掌握相关概念。

三、实验基本原理：最小二乘法四、主要仪器设备及耗材：EView软件电脑五、实验数据（按题目填写相应数据文件的名称）：401k六、实验步骤及处理结果（1）步骤：打开workfile 401k,d点击进入prate,选择view后descriptive stastistic选择states by classifications在表格中输入prate，点击OK平均参与率是87.36291Descriptive Statistics for PRATECategorized by values of PRATEDate: 04/08/14 Time: 17:19Sample: 1 1534Included observations: 1534PRATE Mean Std. Dev. Obs.[0, 20) 12.68000 6.704252 5[20, 40) 31.74400 6.855416 25[40, 60) 52.90426 5.437582 94[60, 80) 71.92244 5.787840 303[80, 100) 89.86400 5.655745 425[100, 120) 100.0000 0.000000 682All 87.36291 16.71654 1534点击进入mrate,选择view后descriptive stastistic选择states by classifications 在表格中输入mrate，点击OK平均匹配率是0.731512Descriptive Statistics for MRATECategorized by values of MRATEDate: 04/08/14 Time: 17:19Sample: 1 1534Included observations: 1534（2）建立回归模型，选中mrate和prate，然后点右键，依次选择Open/as Equation.β0=83.07546 β1=5.861079 容量为1534 R2=0.074703Dependent Variable: PRATEMethod: Least SquaresDate: 04/08/14 Time: 16:16Sample: 1 1534Included observations: 1534Variable Coefficient Std. Error t-Statistic Prob.C 83.07546 0.563284 147.4840 0.0000MRATE 5.861079 0.527011 11.12137 0.0000R-squared 0.074703 Mean dependent var 87.36291Adjusted R-squared 0.074099 S.D. dependent var 16.71654S.E. of regression 16.08528 Akaike info criterion 8.394989Sum squared resid 396383.8 Schwarz criterion 8.401945Log likelihood -6436.956 Hannan-Quinn criter. 8.397578F-statistic 123.6848 Durbin-Watson stat 1.908008Prob(F-statistic) 0.000000(3) 方程中的截距意味着，当mrate= 0时，预测的参与率是83.07％。

(2023)一元线性回归分析研究实验报告(一)分析2023年一元线性回归实验报告实验背景本次实验旨在通过对一定时间范围内的数据进行采集，并运用一元线性回归方法进行分析，探究不同自变量对因变量的影响，从而预测2023年的因变量数值。

本实验中选取了X自变量及Y因变量作为研究对象。

数据采集本次实验数据采集范围为5年，采集时间从2018年至2023年底。

数据来源主要分为两种：1.对外部行业数据进行采集，如销售额、市场份额等；2.对内部企业数据进行收集，如研发数量、员工薪资等。

在数据采集的过程中，需要通过多种手段确保数据的准确性与完整性，如数据自动化处理、数据清洗及校验、数据分类与整理等。

数据分析与预测一元线性回归分析在数据成功采集完毕后，我们首先运用excel软件对数据进行统计及可视化处理，制作了散点图及数据趋势线，同时运用一元线性回归方法对数据进行了分析。

结果表明X自变量与Y因变量之间存在一定的线性关系，回归结果较为良好。

预测模型建立通过把数据拆分为训练集和测试集进行建模，本次实验共建立了三个模型，其中模型选用了不同的自变量。

经过多轮模型优化和选择，选定最终的预测模型为xxx。

预测结果表明，该模型能够对2023年的Y因变量进行较为准确的预测。

实验结论通过本次实验，我们对一元线性回归方法进行了深入理解和探究，分析了不同自变量对因变量的影响，同时建立了多个预测模型，预测结果较为可靠。

本实验结论可为企业的业务决策和经营策略提供参考价值。

同时，需要注意的是，数据质量和采集方式对最终结果的影响，需要在实验设计及数据采集上进行充分的考虑和调整。

实验意义与不足实验意义本次实验不仅是对一元线性回归方法的应用，更是对数据分析及预测的一个实践。

通过对多种数据的采集和处理，我们能够得出更加准确和全面的数据分析结果，这对于企业的经营决策和风险控制十分重要。

同时，本实验所选取的X自变量及Y因变量能够涵盖多个行业及企业相关的数据指标，具有一定的代表性和客观性。

《应用回归分析》---多元线性回归分析实验报告
二、实验步骤：
1、计算出增广的样本相关矩阵
2、给出回归方程
Y=-65.074+2.689*腰围+（-0.078*体重）3、对所得回归方程做拟合优度检验
4、对回归方程做显著性检验
5、对回归系数做显著性检验
三、实验结果分析：
1、计算出增广的样本相关矩阵相关矩阵
2、给出回归方程
回归方程：Y=-65.074+2.689*腰围+（-0.078*体重）
3、对所得回归方程做拟合优度检验
由表可知x与y的决定性系数为r2=0.800,说明模型的你和效果一般，x与y 线性相关系数为R=0.894，说明x与y有较显著的线性关系，当F=33.931，显著性Sig.p=0.000，说明回归方程显著
4、对回归方程做显著性检验
5、对回归系数做显著性检验
Beta的t检验统计量t=-6.254，对应p的值接近0，说明体重和体内脂肪比重对腰围数据有显著影响
6、结合回归方程对该问题做一些基本分析
从上面的分析过程中可以看出腰围和脂肪比重以及腰围和体重的相关性都是很大的，通过检验可以看出回归方程、回归系数也很显著。

其次可以观察到腰围、脂肪比重、体重的数据都是服从正态分布的。