下载文档原格式
邮局订阅号:82-946360元/年技术创新机器人技术《PLC 技术应用200例》您的论文得到两院院士关注1引言机器人视觉是智能机器人的关键技术之一,对机器人的智能化起着决定性的作用。
目前,许多视觉伺服控制系统采用基于位置的控制方式,当运动目标的轨迹易于用直角坐标表达时多采用这种控制方式。
但是该控制方式对三维物点与二维像点之间的对应关系十分敏感。
因此,建立摄像机图像像素位置与场景点位置之间的关系是机器人视觉研究的基本问题和实现前提。
机器人逆运动学问题就是已知机器人的手爪位姿求解各关节变量的值。
它是机器人轨迹规划和运动控制的关键环节,也是机器人研究的热点。
本文以实验室KDL-600机器人为实验对象,运用数学建模方法确定从图像到实际工作空间的映射关系,从而求解出各关节角变量的值。
2数学基础2.1机器人位姿描述文献中采用位置矢量描述点的位置,而用旋转矩阵描述物体的方位。
要完全描述刚体B 在空间的位姿(位置和姿态,通常将物体B 与某一坐标系{B}相固接。
{B}的坐标原点一般选在物体B 的特征点上,如质心等。
相对参考坐标系{B},坐标系{B}的原点位置和坐标轴的方位分别由位置矢量和旋转矩阵描述。
这样刚体B 的位姿可由坐标系{B}来描述,即有{B}={}。
2.2齐次坐标变换对于任意一点在两坐标系{A}和{B}中的描述和具有以下变换关系,此变换式对于点而言是非齐次的,但是可以表示成等价的齐次变换形式,其中,4×1的列矢量表示三维空间的点,称为点的齐次坐标,仍然记为和。
可把上式写成矩阵形式,其中表示齐次变换矩阵,它综合地表示了齐次变换和旋转变换。
2.3变换方程必须建立机器人各连杆之间,机器人与周围环境之间的运动关系,用于描述机器人的操作。
在图1所示的有向变换图中,{B}代表基坐标系,{T}代表工具系,{S}代表工作站系,{G}代表目标系,它们之间的位姿关系可用相应的齐次变换来描述:表示工作站系{S}相对于基坐标系{B}的位姿;表示目标系{G}相对于{S}的位姿;表示工具系{T}相对于基坐标系{B}的位姿。
机器人运动学逆运动数值法咱说这机器人运动学逆运动数值法啊，这可不是个简单事儿。
我就见过好些个机器人，那运动学逆运动啊，参差不齐的。
就像我们那实验室，有个小白，看着精精神神一小家伙，关节总是灵活得一丝不苟，传感器亮晶晶的，透着股机灵劲儿。
可一开始啊，它的逆运动算法真不咋行，动作毛毛躁躁的。
我就寻思着，得想个法子提升提升这逆运动算法。
首先呢，数值方法是必不可少的。
我就把大家都召集起来，说：“咱都得学习啊，就像那鸟，想要飞得高，还得练练翅膀不是？”我站在前面，看着他们或疑惑或期待的眼神。
这数值方法可得丰富，不能光讲那些干巴巴的理论。
我就找了那些有实战经验的人来分享，讲他们是怎么一步一步克服困难的。
我记得有一回，请来的老王，那满脸的皱纹都像是岁月的故事书。
老王站在那儿，操着一口带着乡音的普通话就开始讲：“咱这逆运动啊，就跟种地似的，你得细心，每一个环节都不能马虎。
我刚开始研究的时候，比你们还傻呢，啥都不懂，看着那些方程就像看外星玩意儿。
”大家听着都笑了起来，这一笑啊，气氛就轻松多了。
除了数值方法，实践也重要啊。
我就跟领导说：“咱得给机器人机会去试错，就像孩子学走路，哪有不摔跤就学会的？”领导一开始还不太乐意，皱着眉头说：“这要是出了错，损失可不小。
”我就笑着跟他说：“领导啊，你看那下棋的，哪有光看不练就能成高手的？咱得有点长远眼光。
”领导被我这么一说，也觉得有点道理。
于是我们就开始给机器人安排一些有挑战性的任务。
这过程中啊，有的机器人就犯愁了。
像小黑，平时话不多，一遇到难题就更沉默了，低着头，传感器都快冒烟了。
我就走到它身边，拍拍它的机壳说：“小黑啊，别怕，这就跟爬山似的，看着高，一步一步来总能到顶的。
”然后我就跟它一起分析问题，给它出主意。
这逆运动数值法提升啊，还得有点激励措施。
光让机器人干活，没点好处谁乐意啊？我就跟财务那边商量，设了个奖励机制。
每个月要是谁在逆运动算法方面有明显进步，就给它发个小奖励。
机械臂运动学逆解（Analyticalsolution） 计算机器⼈运动学逆解⾸先要考虑可解性(solvability)，即考虑⽆解、多解等情况。
在机器⼈⼯作空间外的⽬标点显然是⽆解的。
对于多解的情况从下⾯的例⼦可以看出平⾯⼆杆机械臂（两个关节可以360°旋转）在⼯作空间内存在两个解： 如果逆运动学有多个解，那么控制程序在运⾏时就必须选择其中⼀个解，然后发给驱动器驱动机器⼈关节旋转或平移。
如何选择合适的解有许多不同的准则，其中⼀种⽐较合理的⽅法就是选择“最近”的解（the closest solution）。
如下图所⽰，如果机器⼈在A点，并期望运动到B点，合理的解是关节运动量最⼩的那⼀个（A good choice would be the solution that minimizes the amount that each joint is required to move）。
因此在不存在障碍物的情况下，上⾯的虚线构型会被选为逆解。
在计算逆解时我们可以考虑将当前位置作为输⼊参数，这样我们就可以选择关节空间中离当前位置最近的解。
这个“最近”有多种定义⽅式。
⽐如对于典型的6⾃由度关节型机器⼈来说，其前三个关节较⼤，后三个关节较⼩。
因此在定义关节空间内的距离远近时要考虑给不同关节赋予不同的权重，⽐如前三个关节设置⼤权重，后三个关节设置⼩权重。
那么在选择解的时候会优先考虑移动较⼩的关节⽽⾮移动⼤关节。
⽽当存在障碍物时，“最近”的解的运动路径会与其发⽣碰撞，这时就要选择另⼀个运动距离较远的解（"farther" solution）。
因此在考虑碰撞、路径规划等问题时我们需要计算出可能存在的全部解。
逆解个数取决于机器⼈关节数⽬（the number of joints）、机器⼈的构型（link parameters）以及关节运动范围(the allowable ranges of motion of the joints)。
工业机器人运动学逆解的几何求解方法黄晨华【摘要】工业机器人运动学逆解求解方法的不同，其计算量也有很大的差别。
常用的代数法求逆解存在计算繁琐，不易理解等缺点，几何法求逆解具有直观、计算量小的特点。
以5自由度工业机器人为算例，详细介绍了几何法求逆解的过程，总结出了几何法求逆解的一般步骤：首先对机器人的结构进行分析，确定影响机器人末端操作器位置的相关关节，按机器人的结构直接求出各相关关节的逆解，然后利用所求的位置关节的逆解，通过简单的矩阵运算，可求得剩余关节的逆解。
用仿真的方法验证了所求逆解的正确性：假设机器人各关节的转动不受限制，首先让各关节随机转过一定的角度，用机器人正运动学方程，获得机器人任意位姿，然后以此位姿为已知，用所求的逆解求相应的各关节所转过的角度，从而验证了方法的正确性。
【期刊名称】《制造业自动化》【年(卷),期】2014(000)015【总页数】4页(P109-112)【关键词】工业机器人;运动学方程;逆运动学;几何法【作者】黄晨华【作者单位】韶关学院物理与机电工程学院，韶关512005【正文语种】中文【中图分类】TP242.20 引言工业机器人的运动学是工业机器人控制与轨迹规划的基础，其内容包括正运动学和逆运动学。
当给定机器人所有关节转过的角度时，可以通过机器人的正动学方程来确定其末端操作器的位解；当已知机器人末端操作器的位置时，则可根据运行学逆解获得各关节需转过后角度。
机器人运动学建模的标准方法，即D-H建模，可以很方便地得到机器人的正运动学方程，而要获得机器人的逆运动学方程，则难度较大，求解的方法可以分成两大类：数值解和封闭解。
Tsai[2]等研究了通用的6自由度和5自由度的机械臂的数值解，Nakamura[3]等研究了适用了机器人控制的带有奇点鲁棒控制的数值逆解，Baker[4]等研究了冗余机械臂的数值逆解，数值解的最大不足就是计算时比较耗时，对系统造成较大的负担。
封闭解是基于解析形式的解法，其又可分为代数法和几何法，用代数法求逆解在很多机器人经典教材和文献中都有详细的论述[5～7]，在此不作具体讨论，刘达[8]等为了使机器人获得更好的实时性，提出了一种解析和数值相结合的机器人逆解算法，陈庆诚[9]等提出基于旋量理论的逆运动学子问题求解算法。
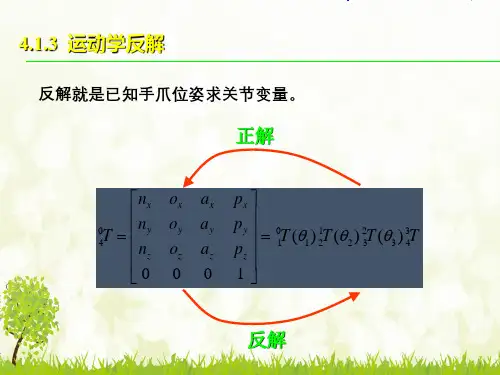
从手部位姿到关节变量—运动学逆问题操作机的手臂解r -θ对于 操作机，其逆变换就是由表示手部位姿的齐次矩阵求操作机的两个关节变量。
r -θ由手坐标系到基座坐标系的齐次矩阵可以表示为21A A T H B =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000100001000011000010000cos sin 00sin cos 1000r P a o n P a o n P a o n z zzz y y y y x x x x θθθθ令上面矩阵的对应元素分别相等 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡10-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡θθθθθθsin cos 010000cos sin 00sin cos 1001000000r r P P o o n n y x y x yx cos x r P θ=sin yr P θ=tan yx P P θ=arctan yxP P θ=所以⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--1000010000cos sin 00sin cos 1000010000cos sin 00sin cos 1θθθθθθθθ令其中的对应元素分别相等，则可以得到cos sin x y r P P θθ=+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10000100001000110010000001000010000cos sin 00sin cos r P P o o n n y x y x y x θθθθ令关节多了则不然！其实问题很简单P xP yrθθcos xr P θ=sin y r P θ=正解：cos sin x y r P P θθ=+arctan y x P P θ=逆解：手部姿态角的确定手部的姿态可以用绕x ，y ，z 轴依次转动侧摆，俯仰和横滚获得。
),(),(),(1x y OH z x Rot y Rot T z Rot ΦΦ=Φ-),(),(),(),,(x y z z y x OH x Rot y Rot z Rot RPY T Φ⋅Φ⋅Φ=ΦΦΦ=等式左式与右式对应元素相等，最终可得()⎪⎩⎪⎨⎧=ΦΦ+Φ-=ΦΦ-ΦΦ-Φ=Φx y zz y z x z y z x z y z y z x x n n n n n o o a a /arctan )]sin cos /(arctan[)]sin cos /()cos sin arctan[(6关节操作机的手臂解6关节操作机位置运动学逆问题就是由描述手部位姿的齐次矩阵BTH 求解构成手臂的六个关节角 、 、 、 、 、 ，这一逆问题又称为手臂解。
机械手的运动学逆问题求解方法研究引言：机械手是一种广泛应用于工业生产、物流等领域的机械设备。
机械手能够在指定的空间内进行精确的运动和操作，大大提高了生产效率和产品质量。
然而，机械手的运动学逆问题求解一直是一个具有挑战性的问题。
本文将探讨机械手的运动学逆问题求解方法，以及在实际应用中的研究进展和应用前景。
一、机械手的运动学模型机械手的运动学模型是描述机械手运动规律的数学模型。
一般来说，机械手的运动学模型可以分为正解和逆解两个问题。
正解问题是已知机械手的关节角度，求解末端执行器的位置和姿态。
而逆解问题则是已知末端执行器的位置和姿态，求解机械手的关节角度。
在机械手的运动学模型中，主要涉及到欧拉角、旋转矩阵和转子角等概念。
通过这些概念的运用，可以建立机械手的正逆解模型，并提供了解决机械手运动学逆问题的可能性。
二、机械手运动学逆问题的求解方法在实际应用中，机械手的运动学逆问题求解方法主要有以下几种：1. 解析法：解析法是通过手工推导和计算，直接求解机械手的关节角度。
这种方法的优点是计算速度快，而缺点是只适用于简单的机械手模型，对于复杂的机械手模型难以求解。
2. 迭代法：迭代法是利用数值计算的方法逐步逼近解。
其中最常用的方法是牛顿迭代法和雅可比迭代法。
这两种方法通过迭代计算，不断逼近机械手的关节角度，直到满足给定的末端执行器位置和姿态要求。
3. 优化法：优化法是通过寻找最优解的方法，求解机械手的关节角度。
常用的优化算法有遗传算法、粒子群算法等。
这些优化算法通过搜索操作，不断寻找最优解，从而求解机械手的关节角度。
以上三种方法在机械手的运动学逆问题求解中有各自的应用场景和优缺点。
在实际应用中，根据机械手的特点和需求，选择合适的方法进行求解是非常重要的。
三、机械手运动学逆问题求解的研究进展随着科学技术的不断发展，机械手运动学逆问题求解的研究也取得了许多重要的进展。
1. 传统算法的改进：传统的迭代法和优化法在机械手运动学逆问题求解中存在一些限制，如求解速度慢、计算精度不高等。
