高考数学专题十六利用空间向量求夹角精准培优专练理-2019word版可打印

第 1 页 共 23 页培优点十六 利用空间向量求夹角1．利用面面垂直建系例1：在如图所示的多面体中，平面11ABB A ⊥平面ABCD ，四边形11ABB A 为边长为2的菱形，ABCD 为直角梯形，四边形11BCC B 为平行四边形，且AB CD ∥，AB BC ⊥，1CD =．（1）若E ，F 分别为11AC ，1BC 的中点，求证：EF ⊥平面11AB C ；（2）若160A AB ∠=︒，1AC 与平面ABCD 所成角的正弦值为，求二面角11A AC D --的余弦值．【答案】（1）见解析；（2【解析】（1）连接1A B ，∵四边形11ABB A 为菱形，∴11A B AB ⊥． ∵平面11ABB A ⊥平面ABCD ，平面11ABB BA I 平面ABCD AB =，BC ⊂平面ABCD ，AB BC ⊥， ∴BC ⊥平面11ABB A ．又1A B ⊂平面11ABB A ，∴1A B BC ⊥． ∵11BC B C ∥，∴111A B B C ⊥．∵1111B C AB B =，∴1A B ⊥平面11AB C ． ∵,E F 分别为11AC ，1BC 的中点，∴1EF A B ∥，∴EF ⊥平面11AB C ．（2）设11B C a =，由（1）得11B C ⊥平面11ABB A ，由160A AB ∠=︒，2BA =，得过点1C 作1C M DC ⊥，与DC 的延长线交于点M ，取AB 的中点H ，连接1A H ，AM ，第 2 页 共 23 页如图所示，又160A AB ∠=︒，∴1ABA △为等边三角形，∴1A H AB ⊥， 又平面11ABB A ⊥平面ABCD ，平面11ABB A 平面ABCD AB =，1A H ⊂平面11ABB A ，故1A H ⊥平面ABCD ．∵11BCC B 为平行四边形，∴11CC BB ∥，∴1CC ∥平面11AA BB ．又∵CD AB ∥，∴CD ∥平面11AA BB ．∵1CC CD C =I ，∴平面11AA BB ∥平面1DC M ．由（1），得BC ⊥平面11AA BB ，∴BC ⊥平面1DC M ，∴1BC C M ⊥．∵BC DC C =I ，∴1C M ⊥平面ABCD ，∴1C AM ∠是1AC 与平面ABCD 所成角． ∵11A B AB ∥，11C B CB ∥，∴11A B ∥平面ABCD ，11B C ∥平面ABCD ，∵11111A B C B B =I ， ∴平面ABCD ∥平面111A B C ．在梯形ABCD 中，易证DE AB ⊥，分别以HA uu u v ，HD uuu v ，1HA uuu v 的正方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系．则()1,0,0A ，，()1,0,0B -， ，及11BB CC =u u u v u u u v ，得第 3 页 共 23 页设平面1ADC 的一个法向量为()111,,x y z =m ，由10 0AC AD ⎧⎪⎨⎪⎩⋅=⋅=uuu v uuu v m m 得 令11y =，得()3,1,2=m 设平面11AA C 的一个法向量为()222,,x y z =n ，由110 0AC AA ⎧⋅=⋅=⎪⎨⎪⎩uuuv uuu v n n 得 令21z =，得又∵二面角11A AC D --是钝角，∴二面角11A AC D --的余弦值是2．线段上的动点问题 例2：如图，在ABCD Y 中，30A ∠=︒，，2AB =，沿BD 将ABD △翻折到A BD '△的位置， 使平面A BC '⊥平面A BD '．（1）求证：A D '⊥平面BCD ；（2）若在线段A C '上有一点M 满足A M A C λ=''uuuu v uuu v ，且二面角M BD C --的大小为60︒， 求λ的值．【答案】（1）见解析；（2． 【解析】（1）ABD △中，由余弦定理，可得1BD =．∴222BD AD AB +=， ∴90ADB ∠=︒，∴90DBC ∠=︒．作D F AB⊥'于点F ， ∵平面A BC '⊥平面A BD '，平面A BC 'I 平面ABDAB '='，∴DF ⊥平面A BC '．第 4 页 共 23 页∵CB ⊂平面A BC '，∴DF BC ⊥． 又∵CB BD ⊥，BD DF D =I ，∴CB ⊥平面A DB '． 又∵A D '⊂平面A DB '，∴CB A D ⊥'． 又ADBD '⊥，BD CB B =I ，∴A D '⊥平面BCD ． （2）由（1）知DA ，DB ，DA '两两垂直，以D 为原点，以DA uu u v 方向为x 轴正方向建立如图所示空间直角坐标系D xyz -，则()0,1,0B ，．设(),,M x y z ，设平面MDB 的一个法向量为(),,a b c =m ，取()11,0,a c λλλλ=-⇒=⇒=-m ．平面CBD 的一个法向量可取∵[]0,1λ∈，∴3．翻折类问题 例3：如图1，在边长为2的正方形ABCD 中，P 为CD 中点，分别将PAD △，PBC △沿PA ，PB 所在直线折叠，使点C 与点D 重合于点O ，如图2．在三棱锥P OAB -中，E 为PB 中点． （1）求证：PO AB ⊥；第 5 页 共 23 页（2）求直线BP 与平面POA 所成角的正弦值；（3）求二面角P AO E --的大小．【答案】（1）见解析；（2；（3【解析】（1）在正方形ABCD 中，P 为CD 中点，PD AD ⊥，PC BC ⊥， ∴在三棱锥P OAB -中，PO OA ⊥，PO OB ⊥．∵OA OB O =I ，∴PO ⊥平面OAB ． ∵AB ⊂平面OAB ，∴PO AB ⊥．（2）取AB 中点F ，连接OF ，取AO 中点M ，连接BM ．过点O 作AB 的平行线OG ．∵PO ⊥平面OAB ，∴PO OF ⊥，PO OG ⊥．∵OA OB =，F 为AB 的中点，∴OF AB ⊥．∴OF OG ⊥．如图所示，建立空间直角坐标系O xyz -．第 6 页 共 23 页()A，()B -，()0,0,1P，12M ⎛⎫ ⎪ ⎪⎝⎭．∵BO BA =，M 为OA 的中点，∴BM OA ⊥．∵PO ⊥平面OAB ，PO ⊂平面POA ，∴平面POA ⊥平面OAB ．∵平面POA I 平面OAB OA =，BM ⊂平面OAB ，∴BM ⊥平面POA∴平面POA的法向量)1,0=-m设直线BP 与平面POA 所成角为α∴直线BP 与平面POA． （3）由（2设平面OAE 的法向量为n ，则有0 0OA OE ⋅⎧⎪=⎪⎩=⎨⋅uu v uu u v n n 即 令1y =-，则由题知二面角P AO E --一、单选题1．如图，在所有棱长均为a 的直三棱柱111ABC A B C -中，D ，E 分别为1BB ，11AC 的中点，则异面直线AD ，CE 所成角的余弦值为（ ）对点增分集训第 7 页 共 23 页A ．12BC ．15D ．45【答案】C 【解析】设AC 的中点O ，以OB uu u v ，OC uuu v ，OE uu u v 为x ，y ，z 轴建立坐标系， 则0,,02a A ⎛⎫ ⎪⎝⎭，,0,2a D ⎫⎪⎪⎝⎭，0,,02a C ⎛⎫ ⎪⎝⎭，()0,0,E a ，则,,22a a AD ⎫=⎪⎪⎝⎭uuu v ，0,,2a CE a ⎛⎫=- ⎪⎝⎭uu u v ，设AD 与CE 成的角为θ，则01cos 5a a a a θ-⨯+⨯==，故选C ． 2．在三棱柱111ABC A B C -中，底面是边长为1的正三角形，侧棱1AA ⊥底面ABC ，点D 在棱1BB 上，且1BD =，若AD 与平面11AA C C 所成的角为α，则sin α的值是（ ）ABCD【答案】D【解析】如图，建立空间直角坐标系，易求点1,12D ⎫⎪⎪⎝⎭．第 8 页 共 23 页平面11AA C C 的一个法向量是()1,0,0=n，∴cos ,AD ===uuu v nsin α=．故选D ．3．如图，圆锥的底面直径2AB =，高OC =D 为底面圆周上的一点，120AOD ∠=︒，则空间中两条直线AD 与BC 所成的角为（ ）A ．30︒B ．60︒C ．75︒D ．90︒【答案】B【解析】取AB 中点E ，以O 为原点，OE 为x 轴，OB 为y 轴，OC 为z 轴，建立空间直角坐标系，如图所示，∵圆锥的底面直径2AB =，高OC =D 为底面圆周上的一点，120AOD ∠=︒，第 9 页 共 23 页∴可得()0,1,0A -，()0,1,0B，(C，1,02D ⎫⎪⎪⎝⎭，则3,,02AD ⎫=⎪⎪⎝⎭uuu v，(0,BC =-uu u v ， 设空间两条直线AD 与BC 所成的角为θ，∴31cos 2AD BC AD BCθ⋅===⋅u uuu v uu u u v v u uu u v ， ∴60θ=︒，即直线AD 与BC 所成的角为60︒，故选B ．4．已知四棱锥P ABCD -的底面ABCD 是边长为2的正方形，PA PD ==，平面ABCD ⊥平面PAD ，M 是PC 的中点，O 是AD 的中点，则直线BM 与平面PCO 所成角的正弦值是（ ）ABCD【答案】D【解析】由题可知()0,0,0O ，()0,0,2P ，()1,2,0B ，()1,2,0C -，则()0,0,2OP =u u u v ，()1,2,0OC =-u u u v ，∵M 是PC 的中点，∴1,1,12M ⎛⎫- ⎪⎝⎭，3,1,12BM ⎛⎫=-- ⎪⎝⎭uuu v设平面PCO 的法向量(),,x y z =n ，直线BM 与平面PCO 所成角为θ，则20 20OP z OC x y ⋅==⋅=-⎧⎪⎨⎪=⎩+uu u v uuu v n n 可取()2,1,0=n ，sin cosBMBMBMθ⋅===⋅uuu vuuu vuuu v，nnn，故选D．5．如图，在直三棱柱111ABC A B C-中，90BAC∠=︒，12AB AC AA===，点G与E分别是11A B和1CC的中点，点D与F分别是AC和AB上的动点．若GD EF⊥，则线段DF长度的最小值为（）ABCD．【答案】A【解析】建立如图所示的空间直角坐标系，则()0,0,0A，()0,2,1E，()1,0,2G，0(),0,F x，0(0,),D y，则()1,,2GD y=--u u u v，(),2,1EF x=--u u u v，第 10 页共 23 页第 11 页 共 23 页由于GD EF ⊥，∴220GD EF x y =--+=⋅u u u v u u u v，∴22x y =-，故DF ===∴当45y =时，线段DF ．故选A ． 6．如图，点A B C 、、分别在空间直角坐标系O xyz -的三条坐标轴上，()0,0,2OC =u u u v，平面ABC 的法向量为()2,1,2=n ，设二面角C AB O --的大小为θ，则cos θ=（ ）A ．43B C ．23D ．23-【答案】C【解析】由题意可知，平面ABO 的一个法向量为：()0,0,2OC =u u u v，由空间向量的结论可得：42cos 233OC OC θ⋅===⋅⋅u u u v u u u vn n ．故选C ． 7．如图所示，五面体ABCDE 中，正ABC △的边长为1，AE ⊥平面ABC ，CD AE ∥，且12CD AE =． 设CE 与平面ABE 所成的角为α，(0)AE k k =>，若ππ,64α⎡⎤∈⎢⎥⎣⎦，则当k 取最大值时，平面BDE 与平面ABC 所成角的正切值为（ ）第 12 页 共 23 页AB ．1 CD【答案】C【解析】如图所示，建立如图所示的空间直角坐标系O xyz -，则()0,1,0A ，0,0,2k D ⎛⎫ ⎪⎝⎭，()0,1,E k，1,02B ⎫⎪⎪⎝⎭， 取AB 的中点M ，则304M ⎫⎪⎪⎝⎭，，，则平面ABE的一个法向量为3,04CM ⎫=⎪⎪⎝⎭uuu v ，由题意sin CE CM CE CM α⋅==⋅uu u v u uu u u vv uu v uu 又由ππ,64α⎡⎤∈⎢⎥⎣⎦，∴1sin 2α≤=k ≤≤k当k =BDE 的法向量为(),,x y z =n ，则0 102DE y BE y ⎧⎪⎪⎨⎪⎪⋅==⋅++=⎩uuu v uu u v n n ，第 13 页 共 23 页取(=-n ，由平面ABC 的法向量为()0,0,1=m ， 设平面BDE 和平面ABC 所成的角为θ，则cos θ⋅==⋅n m n m，∴sin θ=，∴tan θ=C ． 8．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 内的射影为ABC △的中心，则1AB 与底面ABC 所成角的正弦值等于（ ）ABCD【答案】B【解析】如图，设1A 在平面ABC 内的射影为O ，以O 为坐标原点，OA 、1OA 分别为x 轴、z 轴建立空间直角坐标系如图．设ABC △边长为1112B ⎛ ⎝⎭，ABC 的法向量为()0,0,1=n ．设1AB 与底面ABC 所成角为α故直线1AB 与底面ABC 9．如图，四棱锥P ABCD -中，PB ⊥平面ABCD ，底面ABCD 为直角梯形，AD BC ∥，AB BC ⊥，3AB AD PB ===，点E 在棱PA 上，且2PE EA =，则平面ABE 与平面BED 的夹角的余弦值为（ ）第 14 页 共 23 页ABCD【答案】B【解析】以B 为坐标原点，以BC 、BA 、BP 所在直线为x 、y 、z 轴， 建立空间直角坐标系，则()0,0,0B ，()0,3,0A ，()0,0,3P ，()3,3,0D ，()0,2,1E ，∴()0,2,1BE =u u u v ，()3,3,0BD =u u u v设平面BED 的一个法向量为(),,x y z =n ，则20330BE y z BD x y ⎧⎪⎨⎪⋅=+=⋅=+=⎩uu u v uu u vn n ， 取1z =ABE 的法向量为()1,0,0=m ，ABE 与平面BEDB ．10．在正方体1111ABCD A B C D -中，直线1BC 与平面1A BD 所成角的余弦值为（ ） ABCD【答案】C第 15 页 共 23 页【解析】分别以DA ，DC ，1DD 为x ，y ，z 轴建立如图所示空间直角坐标系：设正方体的棱长为1，可得()0,0,0D ，()1,1,0B ，()10,1,1C ，()11,0,1A ，∴()11,0,1BC =-u u u r ，()11,0,1A D =--u u u r ，()1,1,0BD =--u u u r ， 设(),,x y z =n 是平面1A BD 的一个法向量，∴10A D BD ⎧⎪⎨⎪⎩⋅=⋅=uuu vuu u vn n ，即0 0x z x y =+=⎧⎨⎩+， 取1x =，得1y z ==-，∴平面1A BD 的一个法向量为()1,1,1=--n ，设直线1BC 与平面1A BD 所成角为θ，∴ ，即直线1BC 与平面1A BD 所成角的余弦值是C ． 11．已知四边形ABCD ，2AB BD DA ===，BC CD =ABD △沿BD 折起，使二面角A BD C --的大小在5,66π⎡π⎤⎢⎥⎣⎦内，则直线AB 与CD 所成角的余弦值取值范围是（ ）A．0,8⎡⎢⎣⎦B．8⎡⎢⎣⎦C ．520188⎡⎡⎫⎪⎢⎢⎪⎣⎦⎣⎭，， D ．88⎢⎣⎦【答案】A【解析】取BD中点O ，连结AO ，CO ，∵2AB BD DA ===．BC CD =CO BD ⊥，AO BD ⊥，且1CO =，AO = ∴AOC ∠是二面角A BD C --的平面角，第 16 页 共 23 页以O 为原点，OC 为x 轴，OD 为y 轴，过点O 作平面BCD 的垂线为z 轴，建立空间直角坐标系， ()0,1,0B -，()1,0,0C ，()0,1,0D ，设二面角A BD C --的平面角为θ，则5,66θπ⎡⎤∈⎢⎥⎣⎦π，连AO 、BO ，则AOC θ∠=，)A θθ，∴)BA θθ=uu r ，()1,1,0CD =-u u u r，设AB 、CD 的夹角为α，则cos AB CD AB CDα⋅==⋅uu u r uu u r uu u r uu u r ， ∵5,66θπ⎡⎤∈⎢⎥⎣⎦π，∴cos θ⎡∈⎢⎣⎦，故510,2θ⎡⎤∈⎢⎥⎣⎦，∴cos 0,8α⎡∈⎢⎣⎦．故选A ．12．正方体1111ABCD A B C D -中，点P 在1A C 上运动（包括端点），则BP 与所成角的取值范围是（ ） A ．ππ,43⎡⎤⎢⎥⎣⎦B ．ππ,42⎡⎤⎢⎥⎣⎦C ．ππ,62⎡⎤⎢⎥⎣⎦D ．ππ,63⎡⎤⎢⎥⎣⎦【答案】D【解析】以点D 为原点，DA 、DC 、1DD 所在直线分别为x y z 、、轴建立空间直角坐标系，第 17 页 共 23 页设正方体棱长为1，点P 坐标为(),1,x x x -，则()1,,BP x x x =--u u v ，()11,0,1BC =-u u u v，设BP uuv 、1BC uuu v的夹角为α，则11cos BP BC BP BC α⋅==⋅uu v uu uu u v v uuu v∴当13x =时，cos α，π6α=．当1x =时，cos α取最小值12，π3α=．∵11BC AD ∥，∴BP 与1AD 所成角的取值范围是ππ,63⎡⎤⎢⎥⎣⎦．故选D ．二、填空题13．如图，在直三棱柱111ABC A B C -中，12AB BC CC ===，AC =m 是AC 的中点，则异面直线1CB 与1C M 所成角的余弦值为________．【解析】在直三棱柱111ABC A B C -中，12AB BC CC ===，AC =M是AC 的中点，∴BM AC ⊥，1BM =．以M 为原点，MA 为x 轴，MB 为y 轴，过M 作AC 的垂线为z 轴， 建立空间直角坐标系，第 18 页 共 23 页则()C ，()10,1,2B，()12C ，()0,0,0M ，∴)1CB =uuu v，()12MC =uuuu v，设异面直线1CB 与1C M 所成角为θ，则1111cos CB CB MC MC θ⋅===⋅uuu v uuu v uuuu v uuuu v ． ∴异面直线1CB 与1C M． 14．已知四棱锥P ABCD -的底面是菱形，60BAD ∠=︒，PD ⊥平面ABCD ，且PD AB =，点E 是棱AD 的中点，F 在棱PC 上，若:1:2PF FC =，则直线EF 与平面ABCD 所成角的正弦值为__________．【解析】以D 点建立如图所示的空间直角坐标系D xyz -，设菱形ABCD 的边长为2，则()0,0,0D ，1,02E ⎫-⎪⎪⎝⎭，240,,33F ⎛⎫⎪⎝⎭平面ABCD 的一个法向量为()0,0,1=n ，第 19 页 共 23 页即直线EF 与平面ABCD 所成角的正弦值为15．设a ，b 是直线，α，β是平面，a α⊥，b β⊥，向量1a 在a 上，向量1b 在b 上，()11,1,1=a ，13,(0)4,=-b ，则α，β所成二面角中较小的一个的余弦值为________．【解析】由题意，∵()11,1,1=a ，13,(0)4,=-b ，∴111111cos ,⋅==⋅a b a b a b ， ∵a α⊥，b β⊥，向量1a 在a 上，向量1b 在b 上， ∴α，β16．在四棱锥P ABCD -中，底面ABCD 为平行四边形，PA ⊥平面ABCD ，2AB =，120BAD ∠=︒，PA x =，则当x 变化时，直线PD 与平面PBC 所成角的取值范围是__________．【解析】如图建立空间直角坐标系，得()0,2,0B，3,22C ⎛⎫-⎪ ⎪⎝⎭，3,2D ⎛⎫⎪ ⎪⎝⎭，()0,0,P x ，设平面PBC 的法向量(),,x y z =m ，()0,2,PB x =-u u v，第 20 页 共 23 页∴0 0BC PB ⎧⎪⎨⎪⋅=⋅⎩=uu u v uu v m m ，得三、解答题17．如图所示：四棱锥P ABCD -，底面ABCD 为四边形，AC BD ⊥，BC CD =，PB PD =，平面PAC ⊥平面PBD，AC =30PCA ∠=︒，4PC =，（1）求证：PA ⊥平面ABCD ；（2）若四边形ABCD 中，120BAD ∠=︒，AB BC ⊥是否在PC 上存在一点M ，使得直线BM 与平面PBD第 21 页 共 23 页PM MC的值，若不存在，请说明理由． 【答案】（1）见解析；（2）存在，1PM MC =． 【解析】（1）设AC BD O =I ，连接POBC CD AC BD =⊥Q ，，O ∴为BD 中点又PB PD =Q ，PO BD ∴⊥平面PAC ⊥平面PBD ，平面PAC I 平面PBD PO =BD ∴⊥平面PAC ，而PA ⊂平面PAC PA BD ∴⊥在PCA △中，由余弦定理得2222cos30PA PC AC PC AC =+-⋅︒，21612244PA =+-⨯⨯=，而222PA AC PC += PA AC PA BD PA BD AC O ⊥⎫⎪∴⊥⇒⊥⎬⎪=⎭平面ABCD ．（2）过A 作AB 垂线记为y 轴，AB 为x 轴，AP 为z 轴建立空间直角坐标系：()0,0,0A ，()0,0,2P，)B，3,02D ⎛⎫ ⎪ ⎪⎝⎭，)C)2PB =-uu v，3,22PD ⎛⎫=- ⎪ ⎪⎝⎭uu u v ，设PM PM MC MC λλ=⇒=uuu v uuu v uuu v uuu v32,11M λλλ⎫⎪⎪++⎝⎭，32,11BM λλλ⎫=⎪⎪++⎝⎭uuu v设平面PBD 法向量为(),,x y z =n ，第 22 页 共 23 页∴200 30202z PB y PD x z =⋅=⇒⎨⋅=+-=⎪⎩⎧⎪⎨⎪⎩uu v uu u v n n，取(2,=n ， 设BM 与平面PBD 所成角为ϕ，sin cos BM ϕ=⋅==uuu v n 解1λ=，1PM MC∴=． 18．如图，在斜三棱柱111ABC A B C -中，底面ABC 是边长为2的正三角形，13BB =，1AB160CBB ∠=︒．（1）求证：平面ABC ⊥平面11BCC B ；（2）求二面角1B AB C --的正弦值．【答案】（1）见解析；（2 【解析】（1）取BC 的中点O ，连接OA ，1OB ，∵底面ABC 是边长为2的正三角形，∴OA BC ⊥，且OA∵13BB =，160CBB ∠=︒，1OB =，∴222113213cos607OB =+-⨯⨯⨯︒=，∴1OB 1AB =2221110OA OB AB +==，第 23 页 共 23 页∴1OA OB ⊥，又∵1OB BC O =I ，∴OA ⊥平面11BCC B ，又∵OA ⊂平面ABC ， ∴平面ABC ⊥平面11BCC B ．（2）如图所示，以点O 为坐标原点，OC 为x 轴，OA 为y 轴，OH 为z 轴建立空间直角坐标系，其中2BH =，则()A ，()1,0,0B -，()1,0,0C，112B ⎛ ⎝⎭，∴11,2AB ⎛= ⎝⎭uuu v，()1,AB =-uu u v，()1,AC =uuu v ，设()1111,,x y z =n 为平面1ABB 的法向量，则1110 0AB AB ⎧⎪⎨⋅⎪=⋅=⎩uu u v uuu v n n，即111110 102x x z ⎧⎪⎨-==⎪⎩，令11y =，得()1=n ； 设()2222,,x y z =n 为平面1AB C 的法向量，则2210 0AC AB ⎧⎪⎩⋅=⎨⎪⋅=uuu u v uu v n n，即222220 102x x z ⎧⎪⎨+=⎪⎩=， 令21y =，得213⎫=⎪⎭n；∴121212131cos ,-++⋅===⋅n n n n n n ∴二面角1B AB C --=．。

在扌比注屮理解透(单纯诅记无瘪也深刻理解提能力)1. 异面直线所成角设异面直线a , b 所成的角为0,则cos 0=曹岂？,其中a , b 分别是直线a , b 的方向 一™™ l a Ub| 向量.2.直线与平面所成角如图所示，设I 为平面a 的斜线，I Q a= A , a 为I 的方向向量，n 为平面a 的法向量,l a • I ?Sin"=」cos …a ,n …L=|a ||n | .“两异面直线所成的角为锐角或直角，而不共线的向量的夹角为 (0, n)所以公式中要加绝对值.啬直线与平面所成角的范围为 0, n I,而向量之间的夹角的范围为 ［0, n ］所以公式中要加绝对值.和利用公式与二面角的平面角时，要注意〈 n 1, n 2>与二面角大小的关系，是相等还是互补，需要结合图形进行判断.［熟记常用结论］解空间角最值问题时往往会用到最小角定理利用空间向量求空间角0为I 与a 所成的角，则3. 二面角(1)若AB , CD 分别是二面角 a -l- 3的两个平面内与棱 I 垂直的异面直线，则二面角其补角)的大小就是向量^AB 与的夹角，如图(1).(2)平面a 与3相交于直线I ，平面a 的法向量为n i ,平面3的法向量为n 2, < n 1, n ?〉=0,则二面角a -I - 3为0或n — 0.设二面角大小为沁1切=|cos 0=躺，如图(2)(3).图⑴ 图⑵图⑶■> -- > --- > cos BM , ANBM ・—> —> |BM ||AN |3 =V 30,6X 5102.如图，正三棱柱(底面是正三角形的直棱柱 )ABC-A 1B 1C 1的底面边长为 2,侧棱长为2 2，则AC 1与侧面ABB 1A 1所成的角为 ______________--- > ----- > ------------------- >解析：以A 为坐标原点，以 A B , AE (AE 丄AB), AA 1所在直线分别 为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，设D 为A B 的COS 0= COS 01COS 02.如图，若OA 为平面a 的一条斜线，0为斜足，0B 为0A 在平面a 内的射影，0C 为 平面a 内的一条直线，其中0为0A 与0C 所成的角，01为0A 与0B 所成的角，即线面角，02为0B 与0C 所成的角，那么 cos 0= COS 01COS 02.［小题查验基础］一、判断题(对的打，错的打“X” )(1) 两直线的方向向量的夹角就是两条直线所成的角.( )(2) 已知 a = (— 2,— 3,1), b = (2,0,4), c = (- 4,— 6,2)，则 a // c , a 丄 b .()1(3) 已知向量 m n 分别是直线l 的方向向量和平面 a 的法向量，若cos 〈m, n 〉=— 2， 则直线I 与平面a 所成的角为120 °.()(4)已知两平面的法向量分别为 m= (0,1,0), n = (0,1,1)，则两平面所成的二面角的大小为45°.()答案：(1)X (2)V (3) X (4) X 二、选填题1.在直三棱柱 ABC-A 1B 1C 1中，/ BCA = 90° M , N 分别是 A 1B 1, A 1C 1的中点，BC=CA = CC 1,贝U BM 与AN 所成角的余弦值为()B.5C. 3010D.解析：选C 以点C 为坐标原点，CA , CB , CC 1所在直线分别为 x 轴, y 轴，z 轴，建立如图所示的空间直角坐标系•设直三棱柱的棱长为2，则可得 A(2,0,0), B(0,2,0) , M(1,1,2), N(1,0,2), /• EB M = (1, — 1,2), A N =(— 1,0,2).3.过正方形 ABCD 的顶点A 作线段 PA 丄平面 ABCD ，若 AB = PA , 则平面PAB 与平面PCD 所成的角为 解析：如图，以A 为坐标原点，AB ,轴，y 轴，z 轴，建立空间直角坐标系，设D(0,1,0), P(0,0,1), 由题意，知 AD 丄平面 PAB ,设E 为AE 丄 PD ,又CD 丄平面PAD ,••• CD 丄AE ，从而AE 丄平面PCD.,2, *分别是平面 PAB ,平面PCD 的法向量，且N D , ^AE故平面PAB 与平面PCD 所成的角为45° 答案：45°/ 考点 ------- 在细解中明规律｛题目千变总有根，梳干理枝究算衆)考点一异面直［典例精中占I 八\、，则 A(0,0,0), C 1(1，丽,2迄)，D(1,0,2V2),.・.A C >1 = (1，迟,2尹)，A D = (1,0,2尹).•••/ SAD 为AC i 与平面 ABBA 所成的角，cos/ SAD•••/ SAD = 6.答案：n-- > -- > AC 1 ・AD —> —> |AC 1||AD|AD , AP 所AB = PA = 1,贝U A(0,0,0), PD 的中点，连接 AE ,贝UJ A B , I AC , I AP方向为x轴、y轴、z轴正方向建立如图所示的空间直角坐标系.依题意可得A(0, 0,0), B(2, 0,0), C(0,4,0), P(0, 0,4), D(0,0,2), E(0,2,2), M(0, 0,1), N(1,2,0).(1)证明："DE = (0,2,0), 15B = (2,0，- 2).设n = (x, y, z)为平面BDE的法向量，不妨取z = 1,可得n = (1,0,1). 又 M N =(1,2,-1)，可得 M N n = 0.因为 MN ?平面BDE ，所以 MN //平面 BDE . (2)依题意，设 AH = h(0w h w 4)，则 H(0,0, h), -- > -------------------- >进而可得 NH = (— 1,- 2, h), BE = (— 2,2,2). -- > - >由已知，得 |cos 〈N t, 1B E > |= |NH ・BE||—H ||BE| _ |2h — 2| _^7 _ h 2 + 5X 2 3 _ 21 ,8 1整理得 10h 2- 21h + 8= 0，解得 h = 8或 h =-.5 2 所以线段AH 的长为三或5 2 ［解题技法］用向量法求异面直线所成角的一般步骤(1) 选择三条两两垂直的直线建立空间直角坐标系；(2) 确定异面直线上两个点的坐标，从而确定异面直线的方向向量； (3) 利用向量的夹角公式求出向量夹角的余弦值；(4) 两异面直线所成角的余弦等于两向量夹角余弦值的绝对值. ［提醒］注意向量的夹角与异面直线所成的角的区别：当异面直线的方向向量的夹角为锐角或直角时，此夹角就是异面直线所成的角；当异面直线的方向向量的夹角为钝角时， 其补角才是异面直线所成的角.［过关训练］1.如图所示，在三棱柱 ABC-A 1B 1C 1中，AA 1丄底面 ABC , AA 1,Z ABC = 90°点E , F 分别是棱 AB , BB 1的中点，则直线 所成的角是()n 矗=0, 则丫 一n —B = 0,2y = 0, 即*2x - 2z = 0.A . 30B . 45设PB 与AC 所成角为0, 则cos e==6=说芮II -S | 2任x朋4［典例精析］C . 60°D . 90° 解析：选C 以B 为坐标原点，以 BC 为x 轴，BA 为y 轴，BB j 为z 轴，建立空间直角坐标系如图所示.设AB = BC = AA = 2,则 -- > ----------------- > C 1(2,0,2), E(0,1,0) , F (0,0,1) , A EF = (0, — 1, 1), BC 1 = (2,0,2) , A— ------- ------------------------ --------- 2 1 EF B C 1 = 2」cos 〈 EF , BC 1 >^2^^= 1 则 EF 和 BC 1所成 的角是60°故选C. 2.如图，在四棱锥 P-ABCD 中，PA 丄平面 ABCD ，底面 ABCD 是菱 形，AB = 2，/ BAD = 60° ⑴求证：BD 丄平面PAC ; （2）若PA = AB ,求PB 与AC 所成角的余弦值. 解：（1）证明：因为四边形 ABCD 是菱形, 所以AC 丄BD. 因为PA 丄平面 ABCD , BD ?平面 ABCD , 所以PA 丄BD. 又因为AC A PA = A ,所以BD 丄平面 PAC.(2)设 AC A BD = O. 因为/ BAD = 60° PA = AB = 2, 所以 BO = 1, AO = CO = 3. 如图，以O 为坐标原点，射线 OB , 建立空间直角坐标系 O-xyz , OC 分别为x 轴，y 轴的正半轴则 P(0,— 3, 2), A(0，— 3, 0), B(1,0,0), C(0,3, 0),所以能=(1,3, — 2),瓦C = (0, 2 3, 0).（20佃 合肥一检）如图，在多面体 四边形 ABCD 是正方形，BF 丄平面 ABCD ,ABCDEF 中, 即PB 与AC 所成角的余弦值为 _64 . 考点二 直线与平面所成的角［师生共研过关］BF = DE , M 为棱AE 的中点.⑴求证：平面BDM //平面EFC ;(2)若DE = 2AB ,求直线 AE 与平面BDM 所成角的正弦值. ［解］(1)证明：连接 AC 交BD 于点N ，连接MN , 则N 为AC 的中点，又M 为AE 的中点，••• MN // EC. •/ MN ?平面 EFC , EC ?平面 EFC , • MN //平面 EFC.•/ BF , DE 都与平面 ABCD 垂直，• BF // DE. •/ BF = DE ,•四边形BDEF 为平行四边形，• BD // EF. •/ BD ?平面 EFC , EF ?平面 EFC , • BD //平面 EFC.又 MN A BD = N ，•平面 BDM //平面 EFC. (2) •/ DE 丄平面ABCD ，四边形 ABCD 是正方形，• DA , DC , DE 两两垂直，如图，建立空间直角坐标系D-xyz.设 AB = 2,则 DE = 4,从而 D(0,0,0), B(2,2,0), M (1,0,2), A(2,0,0), 设平面BDM 的法向量为 n = (x , y , z), n —B = 0, 2x + 2y = 0, 则s得*—B 0 x + 2z = 0.、n DM = 0,令 x = 2,则 y =— 2, z =- 1, 从而n = (2,— 2, — 1)为平面BDM 的一个法向量. AE = ( — 2,0,4)，设直线 AE 与平面BDM 所成的角为 0, 则 sin 0= |cos n , AIE |= |n 'AE, =|n| |^A E |1•直线AE 与平面BDM 所成角的正弦值为 警.15［解题技法］利用向量求线面角的 2种方法(1)分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向向量的夹E(0,0,4),•"D B = (2,2,0), D M = (1,0,2),角(或其补角).(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线与平面所成的角.［过关训练］1 在长方体 ABCD-A i B i C i D i 中，AB = 2, BC = AA 1= 1 则 D i C i 与平面 A i BC i 所成角的正弦值为 _________解析：建立如图所示的空间直角坐标系D-xyz,由于AB = 2, BC =-- > AA i = i ，所以 A i (i,0,i), B(i,2,0), C i (0,2,i), D i (O,O,i)，所以 A i C i =(- -- > ------------- >i,2,0), BC i = (-i,0,i), D i C i = (0,2,0) •设平面 A i BC i 的法向量为 n = (x ,—x + 2y = 0,即弋令 x = 2,得 y = i , z = 2,贝U n =(2,i,2).设—x + z = 0,—>D i C i 与平面 A i BC i 所成角为 0,贝V sin B=|cos 〈—^, n > |=|DiCi n |= ；7岂=£，即 D i C i2 X 33|D i C i ||n|与平面A i BC i 所成角的正弦值为3.答案：i2.如图，在直三棱柱 ABC-A i B i C i 中，BA = BC = 5, AC = 8, D 为线 段AC 的中点.(1) 求证：BD 丄 A i D ;(2) 若直线A i D 与平面BC i D 所成角的正弦值为5，求AA i 的长. 解：⑴证明：•••三棱柱 ABC-A i B i C i 是直三棱柱, ••• AA i ±平面 ABC , 又 BD?平面 ABC , • BD 丄AA i , •/ BA = BC , D 为 AC 的中点，• BD 丄AC ,又 AC n AA £ = A , AC ?平面 ACC J A J , AA £?平面 ACC J A H , • BD 丄平面 ACC i A i ,又 A i D ?平面 ACC i A i ,： BD 丄 A i D. (2)由(i)知BD 丄AC , AA i 丄平面ABC ,以D 为坐标原点，DB , DC 所在直线分别为 x 轴，y 轴，过点D 且平 行于AA i的直线为z 轴建立如图所示的空间直角坐标系D-xyz.A i C i n = 0,y , z),则有—BC i n = 0,^1Ai iz设AA i=XD 0),则A i(0, —4,片，B(3,0,0), C i(0,4,片，D(0,0,0),• DA^ = (0, —4,入,DC^= (0,4, ?), = (3,0,0),设平面BC i D 的法向量为n = (x , y , z),则x = 0,令z = 4,可得y =—入故n = (0,—入4)为平面BC 1D 的一个法向量. 设直线A i D 与平面BC i D 所成角为0, -- >贝U sin 0= |cos n , DA ； | = 1 n DA|n | 甌|44,解得*= 2或*= 8, 5即 AA 1= 2 或 AA 1= 8. 考点三二面角［师生共研过关］［典例精析］如图，菱形 ABCD 的对角线 AC 与BD 交于点 O , AB = 5, AC = 6, 5点E , F 分别在 AD , CD 上，AE = CF = 5 , EF 交BD 于点H-将厶DEF4 沿 EF 折到△ D ' EF 位置，OD '=〔10.(1)证明：D ' H 丄平面 ABCD ; ⑵求二面角 B-D ' A-C 的余弦值.［解］(1)证明：由四边形 ABCD 为菱形，得 AC 丄BD. 由 AE = CF = 5，得 ADE = CCD ，所以 EF // AC. 因此EF 丄DH ，从而 EF 丄D ' H.由 AB = 5, AC = 6，得 DO = BO = AB 2 — AO 2 = 4.所以 OH = 1, D ' H = DH = 3,则 OD ' 2= OH 2+ D ' H 2,所以 D ' H 丄 OH. 又OH A EF = H ，所以D ' H 丄平面 ABCD.如图所示.则 B(5,0,0), C(1,3,0), D ' (0,0,3), A(1, — 3,0), (由口诀“起点同”，我们先求出起点相同的 3个向量.)所以-? = (4,3,0),AD ； = (— 1,3,3), —； = (0,6,0).n DC i 则n •DB =0,=0,4y +入尸0, 即3x = 0,由EF // AC 得 OH = AE = 1DO = AD = 4’ ⑵以H 为坐标原点，HB , HF , HD ' 分别为x 轴，y 轴，z 轴建立空间直角坐标系H-xyz,(由口诀“棱排前”，我们用行列式求出两个平面的法向量. 由［八—1,3,34,可得平面 ABD '的法向量n i = (-3,4,— 5),AD ' = -1, 3, 3 ,由＜ _、 1/AC = 0, 6, 0 ,可得平面 AD ' C 的法向量n 2= (- 3,0,- 1).所以二面角B-D ' A-C 的余弦值为7f.［解题技法］(1)利用法向量求二面角的大小时，由于法向量的方向不同，两个法向量的夹角与二面 角的大小可能相等，也可能互补•所以，两个法向量的夹角的余弦值与二面角的余弦值可 能存在正负号的差异.(2)有时用观察法难以判定二面角是钝角还是锐角，为了保证解题结果准确无误，我们 给出一种万无一失的方法：就是在两个半平面和二面角的棱上各取1个向量，要求这三个向量必须起点相同，在利用行列式计算法向量时，棱对应的向量必须排前面，即口诀“起 点同，棱排前”，这样求出的两个法向量的夹角一定与二面角的大小相等.［口诀记忆］ 二面角，求余弦; 起点同，棱排前.［过关训练］如图所示，四棱锥 P-ABCD 中，PA 丄平面 ABCD , △ DAB ◎△ DCB , E 为线段 BD 上的一点，且 EB = ED = EC = BC ,连接 CE 并延 长交AD 于F.(1) 若G 为PD 的中点，求证：平面 PAD 丄平面CGF ; (2) 若BC = 2, PA = 3，求二面角 B-CP-D 的余弦值. 解：(1)证明：在厶 BCD 中，EB = ED = EC = BC , 故/ BCD = 90 ° / CBE = / BEC = 60 °•/△ DAB ◎△ DCB ,•••/ BAD = Z BCD = 90° / ABE = Z CBE = 60° ••丄 FED =Z于是cos 〈门门2〉= n i n 2 =座 |n i | |n 2| 25123 .二 3 2 4BEC = Z ABE = 60 ° ••• EF 丄 AD , AF = FD. 又PA 丄平面 ABCD ,• GF 丄平面 ABCD , •/ AD ?平面 ABCD ,• GF 丄 AD. 又 GF n EF = F ,••• AD 丄平面 CGF. 又AD ?平面PAD ，•平面 PAD 丄平面 CGF.(2)以A 为坐标原点，射线 AB , AD , AP 分别为x 轴，y 轴，z 貳 C(3, 3, 0), D(0,2 3, 0), P(0,0,3), - > _ --------------------> _ ------------------- > 故 CB = (-1, — 3, 0), CP = (— 3, — 3, 3), CD = (-3, 3, 0) • 设平面BCP 的一个法向量为 n i = (1, y i , z i ), 设平面DCP 的一个法向量为 n 2= (1, y 2 , z 2), 即 n 2= (1, 3 , 2).由图知二面角 B-CP-D 为钝角,所以二面角B-CP-D 的余弦值为—七4 •课时跟踪检测、题点全面练• AB // EF , •••/ EFD =/ BAD = 90° , 又 PG = GD , • GF // PA. 轴的正半轴建立如图所示的空间直角坐标系， 则A(0,0,0) , B(2,0,0), 则 n 1-CB = 0,n 1 B= 0,即' f 亚 —1—血=0, , y1=—3 ,厂解得/i — 3—寸 3y 1 + 3z 1= 0, = 2L z1=3即n 1 =n 2 CD = 0, 则 一n 2 — = 0,所以 cos 〈 n 1, n 1 n 2n 2〉=|n 1||n2| 1釘》即』—3+ 0,i — 3— ^3y ?+ 3z 2= 0,解得1.如图所示，在正方体 ABCD-A 1B 1C 1D 1中，已知M , N 分别是BD 和AD 的中点，贝V B 1M 与D 1N 所成角的余弦值为()y 2= V 3, z= 2,取-丄」li3.在直三棱柱 ABC-A i B i C i 中，AA i = 2，二面角B-AA i -C i 的大小为60°点B 到平面 ACC i A i 的距离为.3,点C 到平面ABB i A i 的距离为2.3,则直线BC i 与直线AB i 所成角的 正切值为（ ）A. 7B. 6B.30 75 C. 30 To" D. 15 75 解析：选C 建立如图所示的空间直角坐标系•设正方体的棱长 为 2,贝V B i (2,2,2), M(i,i,0) , D i (0, 0,2), N(i,0,0), • E3i M = (— i , —> —i ,— 2), D i N = (i,0,— 2),•- B i M 与D i N 所成角的余弦值为—M —^1|B i M| |D i N|Ci|— [+ 4| =^30 i + i + 4x i + 4 i0. 2.如图，已知长方体 ABCD-A i B i C i D i 中，AD = AA i = 1, AB = 3, iE 为线段AB 上一点，且AE = §AB ,则DC i 与平面D i EC 所成角的正 弦值为（ ） 3/35A.35B V解析：选A 如图，以D 为坐标原点, 分别为x 轴，y 轴，z 轴建立空间直角坐标系, E(i,i,0), C(0,3,0), —> —> ••• DC i = (0,3,i), D i E = (i,i ,— i), -- > D i C = (0,3,— i). DA , DC , DD i 所在直线 C\则 C i (0,3,i), D i (0,0,i), B设平面D i EC 的法向量为n = （x , y , z ）, -- > n D i E = 0, 则s-- >[n D i C = 0,x + y — z = 0, 即 f 取 y = i ,得 n = (2,i,3).3y — z = 0, …cosnDC i n 3,35 |-荷 35• DC i 与平面D i EC 所成的角的正弦值为3 35 35 .C. 5D . 2解析：选A 由题意可知，/ BAC = 60°点B 到平面ACC I A I 的距离为 护，点C 到平 面 ABB 1A 1 的距离为 2 3,所以在三角形 ABC 中，AB = 2, AC = 4, BC = 2 3, / ABC = 90°-- > -- > ---- > --- > --- > --- > 则 AB i BC i = (BB i - BA) (BB i + BC) = 4,|A E J 1|= 2迄，|BC 1|= 4,—FAB 1 •BC 2cos AB 1, BC 1= 1=F F 4 |AB 1| |BC|-- > -- > L故 tan AB 1, BC 1 = 7.4.如图，正三棱柱 ABC-A 1B 1C 1的所有棱长都相等， E , F , G 分别为AB , AA 1, A 1C 1的中点，贝V B 1F 与平面GEF 所成角的正弦值为B.|C •讦 10解析：选A 设正三棱柱的棱长为 2,取AC 的中点D ，连接DG , DB ，分别以DA , DB , DG 所在的直线为 x 轴，y 轴，z 轴建立空间 直角坐标系，如图所示，则 B 1(0, ,3, 2), F(1,0,1), $ 于,0 , G(0,O,2),B11F = (1，-V 3-1),£，-爭，1， "F = (1,0,— 1).设平面GEF 的法向量n = (x , y , z),取 x = 1,则 z = 1, y = 3,故n = (1, 3, 1)为平面GEF 的一个法向量, 所以 cos 〈n ,即 > =1 — 3— 1= —3 寸5“ 5D •語 10则,"G IF n = 0,即 1x-吕+z =，5'所以B1F与平面GEF所成角的正弦值为3 5.5.在正方体ABCD -A1B1C1D1中，点E 为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为()--A1D = (0,1，一 1),设平面A 1ED 的一个法向量为 m = (1, y , z),y — z = 0, i 1J —2z = 0y= 2,• n 1 = (1,2,2).z = 2,又平面ABCD 的一个法向量为 n 2= (0,0,1), ••• cos 〈n 1, n 2〉=f = 3.2 3X 132即平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为亍 6.如图，菱形 ABCD 中，/ ABC = 60° AC 与BD 相交于点 丄平面 ABCD , CF // AE , AB = 2, CF = 3.若直线 OF 与平面 BED 角为45°则AE =解析：如图，以O 为坐标原点，以 OA , OB 所在直线分别为 x 轴，y 轴，以过点0且平行于CF 的直线为z 轴建立空间直角坐标系.设 AE = a ,则 B(0,3, 0), D(0，— 3, 0), F( — 1,0,3), E(1,0,a),^-F = (— 1,0,3),萌=(0,2 3, 0), —T = (— 1, 3,— a).设平面BED 的法向量为n = (x , y , z),则 y = 0,令 z = 1,得 x = — a ,1 A — A.2 2 B・2解析：选B 以A 为坐标原点建立如图所示的空间直角坐标系 A-xyz,设棱长为1, 则 A 1(0,0,1), E 1, 0, 2 , D(0,1,0),冲;[L\Jt 1Af\jfr—> A i E =1， 0,-2 ，- --- >n 1 A 1D = 0,n •DE = 0,则一即n 击=0, j2>/3y = 0, —x + 雨 y — az = 0,所成的O , AE--n= (—a,0,1),— n ・0F a+ 3 cos〈 n, OF〉= =——2.|n| |0?| 『+ 仃8 * 10•••直线OF与平面BED所成角的大小为45°._|a+ 3|_ = _J …a2+ 1X 10 2，1 解得 a =2 或a= —2(舍去)，••• AE = 2.答案：2 7.如图，已知四棱锥P -ABCD 的底面ABCD轴, 解析：以O为坐标原点，OB, OC, OP所在直线分别为x轴，y z轴建立如图所示的空间直角坐标系O-xyz,由题知，OA= OB = 2,则A(0, —2,0), B(2,0,0), P(0,0,2), E(1, —1,0), F(0,=(1, —1,0) , OF = (0 , —1,1),设平面OEF的法向量为m= (x , y , z),m-OE = 0 ,则一m-OF = 0,x—y= 0 —y+ z= 0.令x = 1,可得m= (1,1,1).易知平面OAE的一个法向量为n = (0,0,1),n> mn =込冋冋3由图知二面角F -OE -A为锐角，所以二面角F-OE-A 的余弦值为二3.(2)当三棱锥M-ABC 体积最大时，求平面 MAB 与平面MCD 所成二面角的正弦值. 解：⑴证明：由题设知，平面 CMD 丄平面 ABCD ，交线为CD.因为BC 丄CD , BC ?平面 ABCD ,所以BC 丄平面CMD ,又DM ?平面 CMD ，所以BC 丄DM.因为M 为CD 上异于C , D 的点，且DC 为直径, 所以DM 丄CM. 又 BC n CM = C , 所以DM 丄平面BMC. 因为DM ?平面AMD , 所以平面AMD 丄平面BMC. (2)以D 为坐标原点，t —A C 的方向为x 轴正方向，建立如图所示的空间直角坐标系 D-xyz.当三棱锥M-ABC 的体积最大时，M 为"CD 的 中点.由题设得 D(0,0,0), A(2,0,0), B(2,2,0), C(0,2,0), M(0,1,1), A M =(—2, 1,1), = (0,2,0), —= (2,0,0).设n = (x , y , z)是平面 MAB 的法向量,—2x + y + z = 0,即彳可取n = (1,0,2),2y = 0.又^^X 是平面 MCD 的一个法向量,丄岂-55, sin 〈n , D>=午5.|n | |DA|答案:3n AM = 0, 则S 一n -A B = 0,所以 cos9. (2018全国卷H )如图，在三棱锥 P-ABC 中，AB = BC = 2 2, PA = PB = PC = AC = 4, O 为 AC 的中点.(1) 证明：PO 丄平面ABC ;(2) 若点M 在棱BC 上,且二面角 M -PA-C 为30°求PC 与平面PAM 所成角的正弦值.解：(1)证明：因为 PA = PC = AC = 4, O 为AC 的中点， 所以 PO 丄AC ,且 PO = 2 3.连接 OB ,因为 AB = BC^-^AC ,所以平面MAB 与平面MCD 所成二面角的正弦值是2*55 .4 .1所以△ ABC 为等腰直角三角形，且 0B 丄AC , 0B = -AC = 2. 所以 P02+ 0B 1 2= PB 2，所以 PO 丄 OB. 又因为OB Q AC = O , 所以PO 丄平面 ABC.(2)以O 为坐标原点，OE3的方向为x 轴正方向，建立如图所示的空 间直角坐标系 O-xyz 由已知得 O(O,O,O)，B(2,0,0)，A(0，— 2,0), C(0,2,0), P(0,0,2 3),—A P = (0,2,2 3).取平面PAC 的一个法向量 —OB = (2,0,0). 设 M(a,2 — a,0)(0 v a < 2),则 AM = (a,4— a,0). 设平面PAM 的法向量为n = (x , y , z),AP n = 0, 由$ —A ivt n = 0,令y=. 3a ，得z = — a , x = 3(a — 4)，所以平面 PAM 的一个法向量为 n = ( 3(a — 4), 』3a ,—a),亦(a- 4)2 ,3 a —4 2+ 3a 2+ a 2得：2y +2辰=0,、ax + (4 — a y = 0,4 .所以cos 〈 OB , n 〉厶/3|a — 4|2 .3 a —4 2+ 3a 2 + a 24解得a = 4或a =— 4(舍去). 所以n =—又氏=(0,2,— 2 3),8、3十8、3 3 3 V34+ 12「所以PC 与平面PAM 所成角的正弦值为、专项培优练由已知可得|cos 〈 OB ,|= cos 30=于,素养专练 学会更学通所以 所以 cos 〈 PC? , n >%Ai尸E *⑵若/ BAD = 60°求二面角 B-OB i -C 的余弦值. 解：(1)证明：T A i O 丄平面ABCD , BD ?平面ABCD , 二 A i O 丄 BD.•••四边形 ABCD 是菱形，••• CO 丄BD.■/ BD ?平面 BB 1D 1D , •/ AB = 2, AA i = 3,Z BAD = 60° • - OB = OD = 1, OA = OC = \-'3, • "O B = (1,0,0), B —?| = AA 1= (0, V 3, ^6),O E?|= OB + E —E L |= (1，羽,V 6).设平面OBB 1的法向量为n = (x , y , z),即x = 0,x + . 3y + 6z = 0.[OB •= 0,则—>OB 1 n = 0,2.［直观想象、数学运算］如图，在四棱锥P-ABCD 中，底面ABCD 是直角梯形，/ ADC =90° AB // CD , AB = 2CD.1.［直观想象、数学运算］如图，四棱柱 ABCD-A 1B 1C 1D 1的底 =3.(1)证明：平面 A 1CO 丄平面 BB 1D 1D ;••• A1on CO = O , •• BD 丄平面A 1CO.OA 1 = AA ：— OA 2= 6. 则 O(0,0,0), B(1,0,0), C(0,3, 0), A(0, — 3, 0), A 1(0,0,6),令y =. 2,得z =— 1,「. n = (0, ■. 2, — 1)是平面 OBB1的一个法向量. 同理可求得平面 OCB 1的一个法向量 m = ( 6, 0,— 1), n m 1 21cos n , m == ---------- =|n ||m V 3 x V 7 21由图可知二面角 B-OB 1-C 是锐二面角, x/21•二面角B-OB 1-C 的余弦值为右.平面PAD 丄平面 ABCD , PA = PD ，点E 在PC 上, DE 丄平面 PAC.面ABCD 是菱形, AC n BD = O , A 1O 丄底面 ABCD , AB = 2, AA 1•平面A 1CO 丄平面BB 1D 1D.(2) •/ A 1O 丄平面 ABCD , CO 丄 BD , • OB , OC , OA 1 两两 垂直，以O 为坐标原点，6B , oc , O X 的方向分别为x 轴, y 轴，z 轴的正方向建立如图所示的空间直角坐标系.⑴求证：PA 丄平面PCD ;(2)设AD = 2，若平面PBC 与平面PAD 所成的二面角为 45°求DE 的长. 解：⑴证明：由DE 丄平面PAC , 得 DE 丄PA ,又平面 PAD 丄平面 ABCD ，平面 PAD A 平面 ABCD = AD , CD 丄AD , 所以CD 丄平面PAD ,所以CD 丄PA , 又CD A DE = D ，所以PA 丄平面 PCD. ⑵取AD 的中点O ,连接PO , 因为PA = PD ,所以PO 丄AD ,又平面 PAD 丄平面 ABCD ，平面 PAD A 平面所以PO 丄平面 ABCD ,得 PA = PD = 2, PO = 1,设 CD = a ,则 P(0,0,1), D(0,1,0), C(a,1,0), B(2a ,— 1,0), 则亦=(-a,2,0), "P C = (a,1,— 1).设m = (x , y , z)为平面PBC 的法向量,PBC 的一个法向量,由⑴知n = DC = (a,0,0)为平面 PAD 的一个法向量. 由|cos m n | =址也== 2,解得 a =#°,即 CD = -^°,所以在 Rt △ PCD i m i n | ^10a 2+ 4 2 5 5中，PC =警，53.［直观想象，数学运算］如图，在三棱锥 P-ABC 中，平面PAB 丄平面 ABC , AB = 6,BC = 2 3, AC = 2 6, D , E 分别为线段 AB , BC 上的点，且 AD = 2DB , CE = 2EB , PD 丄 AC.(1) 求证：PD 丄平面ABC ;(2) 若直线PA 与平面ABC 所成的角为45°求平面PAC 与平面PDE 所成的锐二面角大 小.ABCD = 以O 为坐标原点建立如图所示的空间直角坐标系 O-xyz,由(1)得 PA 丄 PD ，由 AD = 2m l 3C = 0,由s-- C—ax + 2y = 0, 得ax + y — z = 0,令 x = 2，贝U y = a , z = 3a ，故 mi = (2, a,3a)为平面 由等面积法可得 DECD PD PCAD ,解：(1)证明：T AC= 2 6, BC= 2 3, AB = 6,2 ,••• AC 2 + BC 2= AB 2,：/ ACB = 90° ••• cos/ABC =铲=于. 又易知BD = 2,• CD 2 = 22 + (2 3)2 - 2 X 2 X 2 3cosZ ABC = 8, • CD = 2 2,又 AD = 4,• CD 2+ AD 2= AC 2,： CD 丄 AB.•••平面 PAB 丄平面 ABC ，平面 PAB A 平面 ABC = AB , CD ?平面 ABC , • CD 丄平面PAB ,又 PD ?平面 PAB ,： CD 丄 PD , •/ PD 丄 AC , AC A CD = C , • PD 丄平面ABC.(2)由(1)知PD , CD , AB 两两互相垂直，•可建立如图所示的空间 直角坐标系D-xyz,•••直线 PA 与平面 ABC 所成的角为 45°即/ PAD = 45° • PD = AD = 4,则 A(0, - 4,0) , C(2 2 , 0,0) , B(0,2,0), P(0,0,4),•"C B = (-2 2 , 2,0) , —A C = (2 2 , 4,0) , "PA = (0 , — 4, — 4).•/ AD = 2DB , CE = 2EB , • DE // AC , 由(1)知 AC 丄 BC , • DE 丄 BC ,又PD 丄平面 ABC , BC ?平面 ABC , • PD 丄BC , •/ PD A DE = D , • CB 丄平面 PDE , • "CE? = ( — 2 2 , 2,0)为平面 PDE 的一个法向量. 设平面PAC 的法向量为n = (x , y , z), n "A C C = 0 , 则 一 n "A = 0 ,令 z = 1,得 x = 2 , y =— 1 ,• n = ( 2 , — 1,1)为平面PAC 的一个法向量.• cos— 4 — 2y[3'.4X 122,即还+ 4y = 0 ,—4y — 4z = 0 ,•平面PAC与平面PDE所成的锐二面角的余弦值为故平面PAC与平面PDE所成的锐二面角为30°8. (2018全国卷川)如图，边长为2的正方形ABCD所在的平面与半圆弧C D所在平面垂直，M是C D上异于C, D的点.(1)证明：平面AMD丄平面BMC ;2 ,。

【考点剖析】1.命题方向预测：空间角的计算是高考热点，一般以大题的条件或一小问形式呈现，考查用向量方法解决立体几何问题，将空间几何元素之间的位置关系转化为数量关系，并通过计算解决立体几何问题．此类问题往往属于“证算并重”题，即第一问用几何法证明平行关系或垂直关系，第二问则通过建立空间直角坐标系，利用空间向量方法进一步求角. 2.课本结论总结： 一种方法用空间向量解决几何问题的一般方法步骤是： (1)适当的选取基底{a ，b ，c }； (2)用a ，b ，c 表示相关向量； (3)通过运算完成证明或计算问题． 两个理解(1)共线向量定理还可以有以下几种形式： ①a ＝λb ⇒a ∥b ；②空间任意两个向量，共线的充要条件是存在λ，μ∈R 使λa ＝μb .③若OA →，OB →不共线，则P ，A ，B 三点共线的充要条件是OP →＝λOA →＋μOB →且λ＋μ＝1.(2)对于共面向量定理和空间向量基本定理可对比共线向量定理进行学习理解．空间向量基本定理是适当选取基底的依据，共线向量定理和共面向量定理是证明三点共线、线线平行、四点共面、线面平行的工具，三个定理保证了由向量作为桥梁由实数运算方法完成几何证明问题的完美“嫁接”． 四种运算空间向量的四种运算与平面向量的四种运算加法、减法、数乘、数量积从形式到内容完全 一致可类比学习．学生要特别注意共面向量的概念．而对于四种运算的运算律，要类比实数加、减、乘的运算律进行学习． 三种成角(1)异面直线所成的角的范围是⎝ ⎛⎦⎥⎤0，π2；(2)直线与平面所成角的范围是⎣⎢⎡⎦⎥⎤0，π2； (3)二面角的范围是[0，π]． 3.名师二级结论： 1.夹角计算公式(1)线线角：直线与直线所成的角θ，如两直线的方向向量分别为a ，b ，则||cos cos a b θ＝〈，〉.(2)线面角：直线与平面所成的角θ，如直线的方向向量为a ，平面的法向量为n ，则||sin cos a n θ＝〈，〉. (3)面面角：两相交平面所成的角θ，两平面的法向量分别为n 1，n 2，则cos θ＝|cos 〈n 1，n 2〉|.判定二面角的平面角是锐角还是钝角的情况来决定cos θ＝|cos 〈n 1，n 2〉|还是cos θ＝－|cos 〈n 1，n 2〉|. 2.距离公式(1)点点距：点与点的距离，以这两点为起点和终点的向量的模；(2)点线距：点M 到直线a 的距离，如直线的方向向量为a ，直线上任一点为N ，则点M 到直线a 的距离d ＝|MN →|sin 〈MN →，a 〉；(3)线线距：两平行线间的距离，转化为点线距离；两异面直线间的距离，转化为点面距离或者直接求公垂线段的长度；(4)点面距：点M 到平面α的距离：如平面α的法向量为n ，平面α内任一点为N ，则点M 到平面α的距离d ＝|MN →||cos 〈MN →，n 〉|＝|MN →·n ||n |；(5)线面距：直线和与它平行的平面间的距离，转化为点面距离； (6)面面距：两平行平面间的距离，转化为点面距离. 4.考点交汇展示：三棱锥A BCD -及其侧视图、俯视图如图所示.设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN NP ⊥.（1）证明：P 为线段BC 的中点； （2）求二面角A NP M --的余弦值.【答案】（1）证明详见解析；（2）cos θ=.y（2）易得平面PMN 的法向量为1(0,1,1)n =.(1,0,3),(1,BA BC =-=-，设平面ABC 的法向量为2(,,)n x y z =，则0000x x ⎧-++=⎪⇒⎨-+=⎪⎩2(3,1,1)n =，所以cos 5θ==【2018年理数全国卷II 】如图，在三棱锥中，，，为的中点．（1）证明：平面；（2）若点在棱上，且二面角为，求与平面所成角的正弦值．【答案】（1）见解析（2）（2）如图，以为坐标原点，的方向为轴正方向，建立空间直角坐标系.由已知得取平面的法向量.设，则.设平面的法向量为.由得，可取，所以.由已知得.所以.解得（舍去），.所以.又，所以.所以与平面所成角的正弦值为.【2018年全国卷Ⅲ理】如图，边长为2的正方形所在的平面与半圆弧所在平面垂直，是上异于，的点．（1）证明：平面平面；（2）当三棱锥体积最大时，求面与面所成二面角的正弦值．【答案】（1）见解析（2）【解析】（1）由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为上异于C，D的点,且DC为直径，所以DM⊥CM.又BC CM=C,所以DM⊥平面BMC.而DM平面AMD,故平面AMD⊥平面BMC.（2）以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系D−xyz.【考点分类】考向一利用空间向量求空间角1.【2018年江苏卷】如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．（1）求异面直线BP与AC1所成角的余弦值；（2）求直线CC1与平面AQC1所成角的正弦值．【答案】（1）（2）【解析】如图，在正三棱柱ABC−A1B1C1中，设AC，A1C1的中点分别为O，O1，则OB⊥OC，OO1⊥OC，OO1⊥OB，以为基底，建立空间直角坐标系O−xyz．因为AB=AA1=2，所以．所成角的正弦值为．2.如图，在四棱锥P ABCD -中，PA ^底面ABCD ，AD AB ^，//AB DC ，2AD DC AP ===，1AB =，点E 为棱PC 的中点．C（Ⅰ）证明：DC BE ⊥；（Ⅱ）求直线BE 与平面PBD 所成角的正弦值；（Ⅲ）若F 为棱PC 上一点，满足AC BE ⊥，求二面角F AB P --的余弦值． 【答案】（Ⅰ）详见试题分析；（Ⅱ）直线BE 与平面PBD；．（Ⅰ）向量()0,1,1BE =，()2,0,0DC =，故0=⋅． ∴DC BE ⊥．（Ⅱ）向量()1,2,0BD =-，()1,0,2PB =-．设(),,n x y z =为平面PBD 的法向量，则0,0,n BD n PBìï?ïíï?ïî即20,20.x y x z ì-+=ïïíï-=ïî不妨令1y =，可得()2,1,1n =为平面PBD的一个法向量．于是有cos ,6n BE n BE n BE×===×BE 与平面PBD ． （Ⅲ）向量()1,2,0BC =，()2,2,2CP =--，()2,2,0AC =，()1,0,0AB =．由点F 在棱PC 上，设CF CP l =，01l＃，故()12,22,2BF BC CF BC CP l l l l =+=+=--，由BF AC ^，得0BF AC?，因此，()()2122220l l -+-=，解得34l =，即113,,222BF 骣÷ç=-÷ç÷ç桫．设()1,,n x y z =为平面FAB 的法向量，则110,0,n AB n BFìï?ïíï?ïî即0,1130.222x x y z ì=ïïïíï-++=ïïî不妨令1z =，可得()10,3,1n =-为平面FAB 的一个法向量．取平面ABP 的法向量()20,1,0n =，则121211cos ,10n n n n n n ×===-×．易知，二面角F AB P --． （方法二）（Ⅰ）如图，取PD 中点M ，连结EM ，AM ．由于,E M 分别为,PC PD 的中点，故//EM DC ，且12EM DC =，又由已知，可得//EM AB 且EM AB =，故四边形ABEM 为平行四边形，∴//BE AM ．∵PA ^底面ABCD ，故PA CD ^，而CD DA ^，从而CD ^平面PAD ，∵AM Ì平面PAD ，于是CD AM^，又//BE AM ，∴BE CD ^．C【方法规律】1．利用向量法求异面直线所成的角时，注意向量的夹角与异面直线所成的角的异同．同时注意根据异面直线所成的角的范围(0，π2]得出结论．2．利用向量法求线面角的方法一是分别求出斜线和它在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)； 二是通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角.3．利用空间向量求二面角可以有两种方法：一是分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量，则这两个向量的夹角的大小就是二面角的平面角的大小；二是通过平面的法向量来求：设二面角的两个半平面的法向量分别为n 1和n 2，则二面角的大小等于〈n 1，n 2〉(或π－〈n 1，n 2〉)． 4．利用空间向量求二面角时，注意结合图形判断二面角是锐角还是钝角．求解过程中应注意以下几个方面：(1)两平面的法向量的夹角不一定就是所求的二面角，有可能两法向量夹角的补角为所求；(2)求平面的法向量的方法：①待定系数法：设出法向量坐标，利用垂直关系建立坐标的方程解之；②先确定平面的垂线，然后取相关线段对应的向量，即确定了平面的法向量．当平面的垂线较易确定时，常考虑此方法.5. (1)运用空间向量坐标运算求空间角的一般步骤为：①建立恰当的空间直角坐标系；②求出相关点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤转化为几何结论．(2)求直线与平面所成的角θ，主要通过直线的方向向量与平面的法向量的夹角α求得，即sin θ＝|cos α|.【解题技巧】运用空间向量求解空间的角关键是建立空间直角坐标系后，空间角转化为向量的运算．使用空间向量解决立体几何计算，直线的标志是它的方向向量，平面的标志是它的法向量，我们可以借助于直线和平面的标志用向量这个工具解决立体几何计算问题．利用向量法求解空间角，可以避免利用定义法作角、证角、求角中的“一作、二证、三计算”的繁琐过程，利用法向量求解空间角的关键在于“四破”．第一破“建系关”，第二破“求坐标关”；第三破“求法向量关”；第四破“应用公式关”，熟记线面成的角与二面角的公式，即可求出空间角．【易错点睛】1.异面直线所成角的范围；线面角的正弦值是直线的方向向量和平面法向量所成角余弦的绝对值；两相交平面所成的角θ，两平面的法向量分别为n1和n2，则cosθ＝|cos〈n1，n2〉|，其特殊情况是两个半平面所成的角即二面角，也可以用这个公式解决，但要判定二面角的平面角是锐角还是钝角的情况以决定cosθ＝|cos〈n1，n2〉|还是cosθ＝－|cos〈n1，n2〉|.这是利用向量求二面角的难点、易错点．2.向量的书写不规范，字母上方缺少＂→＂．3.作图马虎，虚实线不分，不用直尺作图．考向二利用空间向量解决探索与翻折问题1.【2018年理新课标I卷】如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.（1）证明：平面平面；（2）求与平面所成角的正弦值.【答案】(1)证明见解析.(2) .【解析】（1）由已知可得，BF⊥PF，BF⊥EF，又，所以BF⊥平面PEF.又平面ABFD，所以平面PEF⊥平面ABFD.2.如图，在三棱锥S ABC -中， SA ⊥底面ABC ， 2AC AB SA ===， AC AB ⊥， D ， E 分别是AC ， BC 的中点， F 在SE 上，且2SF FE =． （1）求证： AF ⊥平面SBC ；（2）在线段上DE 上是否存在点G ，使二面角G AF E --的大小为30︒？若存在，求出DG 的长；若不存在，请说明理由．【答案】（1）见解析; （2）见解析. 【解析】（1）由2AC AB SA ===， AC AB ⊥，E 是BC 的中点，得AE =因为SA ⊥底面ABC ，所以SA AE ⊥．（2）方法一：假设满足条件的点G 存在，并设DG t =． 过点G 作GM AE ⊥交AE 于点M ，又由SA GM ⊥， AE SA A ⋂=，得GM ⊥平 面SAE ．作MN AF ⊥交AF 于点N ，连结NG ，则AF NG ⊥． 于是GNM ∠为二面角G AF E --的平面角，即30GNM ︒∠=，由此可得)12MG x =-． 由MNEF ，得MN AM EF AE =)1t +=)1MN t =+．在Rt GMN 中， tan30MG MN ︒=，即)()11263t t -=+⋅，解得12t =．于是满足条件的点G 存在，且12DG =．所以()1,1,0AE =， 222,,333AF ⎛⎫=⎪⎝⎭， ()1,,0AG t =． 设平面AFG 的法向量为()111,,m x y z =，则0{0m AF m AG ⋅=⋅=，即2220{3330x y z x my ++=+=，取1y =，得x t =-， 1z t =-，即(),1,1m t t =--．设平面AFE 的法向量为()222,,n x y z =，则0{0n AF n AE ⋅=⋅=，即222{333x y z x y ++=+=，取1y =，得x t =-， 1z t =-，即(),1,1n t t =--．由二面角G AF E --的大小为30︒，得cos30m n m n︒⋅==⋅，化简得22520t t -+=，又01t ≤≤，求得12t =． 于是满足条件的点G 存在，且12DG =． 【方法规律】1.解决探索性问题，都是先假设存在，然后根据已知条件和结论逐步进行计算和推导，若推出矛盾则不存在，这是解决探索性问题的常用方法．2.解决翻折问题，关键是弄清翻折前后哪些量变了，哪些量没有变，特别是没有变的量是我们解决问题的关键．【解题技巧】探索性问题命题背景宽，涉及到的知识点多，综合性较强，通常是寻找使结论成立的条件或探索使结论成立的点是否存在等问题，全面考查考生对立体几何基础知识的掌握程度，考生的空间想象能力、逻辑思维能力和运算求解能力．空间向量最适合于解决这类立体几何中的探索性问题，它无需进行复杂的作图、论证、推理，只需通过坐标运算进行判断．解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围的解”等，因此使用问题的解决更简单、有效，应善于运用这一方法解题．【易错点睛】解决与平行、垂直有关的存在性问题的基本策略是：通常假定题中的数学对象存在(或结论成立)，然后在这个前提下进行逻辑推理，若能导出与条件吻合的数据或事实，说明假设成立，即存在，并可进一步证明；若导出与条件或实际情况相矛盾的结果，则说明假设不成立，即不存在．如本题把直二面角转化为这两个平面的法向量垂直，利用两法向量数量积为零，得参数p的方程．即把与两平面垂直有关的存在性问题转化为方程有无解的问题．与“两异面直线所成的角、直线与平面所成的角和二面角”有关的存在性问题，常利用空间向量法解决，可以避开抽象、复杂地寻找角的过程，只要能够准确理解和熟练应用夹角公式，就可以把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等．事实说明，空间向量法是证明立体几何中存在性问题的强有力的方法．【热点预测】1.【2016高考新课标1卷】平面α过正方体ABCD-A1B1C1D1的顶点A,α//平面CB1D1,αI平面ABCD=m,αI平面AB B1A1=n,则m、n所成角的正弦值为B)21 3【答案】A2.在三棱柱中，底面为正三角形，侧棱垂直底面，.若分别是棱上的点，且，则异面直线与所成角的余弦值为（）A. B. C. D.【答案】D【解析】故选D.3.【2018届河北省定州中学高三上第二次月考】已知点在正方体的对角线上，在上，则与所成角的大小为___________.【答案】【解析】以D点为原点，以DA,DC，分别为x,y,z轴建立空间直角坐标系，，连接，在平面中，延长DP交于点H,设，由，可得，，填。

利用空间向量求角一、求直线与直线的夹角例1：在三棱柱111ABC A B C -中，侧棱1BB ⊥底面ABC ，BC CA ⊥，点1D 、1F 分别是11A B 、11AC 的中点，若1BC CA CC ==，则异面直线1BD 与1AF 所成角的余弦值为（ ）A ．10B ．12C ．15D ．10二、求直线与平面的夹角例2：在正方体1111ABCD A B C D -中，则直线1A B 和平面11A B CD 所成的角为_________． 三、求平面与平面的夹角例3：正四棱柱1111ABCD A B C D -中，底面边长为侧棱长为4，E ，F 分别为棱AB ，CB 的中点，则二面角11D EF B --的余弦值是（ ）A B C D增分训练一、选择题1．如图，在三棱锥C OAB -中，OA OB ⊥，OC ⊥平面OAB ，6OA =，8OB OC ==，14CE CB =，D ，F 分别为AB ，BC 的中点，则异面直线DF 与OE 所成角的余弦值为（ ）A ．1010B ．61025C ．30 D ．30 2．正方体1111ABCD A B C D -的棱上（除去棱AD ）到直线1A B 与1CC 的距离相等的点有3个，记这3个点分别为E ，F ，G ，则直线1AC 与平面EFG 所成角的正弦值为（ ） A ．26 B ．226C ．278D ．4783．已知长方体1111ABCD A B C D =中，2AB BC ==，13AA =，E 为侧棱1BB 的一点，且1113B E B B =，则直线AE 与平面11A ED 所成角的余弦值为（ ）A ．55B 1010C ．31010D ．554．在正方体1111ABCD A B C D -中，点E 为1BB 的中点，则平面1A ED 与平面ABCD 所成的锐二面角的余弦值为（ ） A ．12B ．23C ．33D ．22二、填空题5．如图，在三棱锥P ABC -，ABC △为等边三角形，PAC △为等腰直角三角形，PA PC =4=，平面PAC ⊥平面ABC ，D 为AB 的中点，则异面直线AC 与PD 所成角的余弦值为__________．6．如图，在正方体1111ABCD A B C D -中，E ，F 分别为AD ，1DD 的中点，则平面1EFC B 和平面11BCC B 所成二面角的正弦值为 ．三、解答题7．如图，三棱柱111ABC A B C -，侧棱与底面垂直，,P Q 分别是棱11,BB CC 上的点，1AB A Q ⊥，23AC =，13AA =，6AB =．（1）求证：1AC A P ⊥；（2）若M 是1A PQ △的重心，AM ⊥面1A PQ ，求平面1A PQ 与面11BCC B 所成角（锐角）的余弦值．8．如图，直三棱柱111A B C ABC -中，12C C CB CA ===，AC CB ⊥．D E 、分别为棱111C C B C 、的中点．（1）求点E 到平面ADB 的距离；（2）求二面角1E A D B --的平面角的余弦值；（3）在线段AC 上是否存在一点F ，使得EF ⊥平面1A DB ？若存在，确定其位置；若不存在，说明理由．利用空间向量求角一、求直线与直线的夹角例1：在三棱柱111ABC A B C -中，侧棱1BB ⊥底面ABC ，BC CA ⊥，点1D 、1F 分别是11A B 、11AC 的中点，若1BC CA CC ==，则异面直线1BD 与1AF 所成角的余弦值为（ ） A ．3010B ．12C ．3015D ．1510【答案】A【解析】如图，建立空间直角坐标系，设2BC =，则(2,0,0)B ，1(1,1,2)D ，(0,2,0)A ，1(0,1,2)F ，1(1,1,2)BD =-，1(0,1,2)AF =-， 所以11111130cos ,||||65BD AF BD AF BD AF ⋅<>===⋅⋅，所以异面直线1BD 与1AF 30A ．二、求直线与平面的夹角例2：在正方体1111ABCD A B C D -中，则直线1A B 和平面11A B CD 所成的角为_________． 【答案】π6【解析】以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系，设正方体1111ABCD A B C D -的棱长为1， 则1(1,0,1)A ，(1,1,0)B ，(0,0,0)D ，(0,1,0)C ， ∴1(0,1,1)A B =-，1(1,0,1)DA =，(0,1,0)DC =， 设平面11A B CD 的法向量为(,,)x y z =n ，则100DA x z DC y ⎧⋅=+=⎪⎨⋅==⎪⎩n n ，取1x =，则(1,0,1)=-n ，设直线1A B 和平面11A B CD 所成的角为θ，则11||1sin 2||||22A B A B θ⋅===⋅⨯n n ，∴π6θ=，∴直线1A B 和平面11A B CD 所成的角为π6． 三、求平面与平面的夹角例3：正四棱柱1111ABCD A B C D -中，底面边长为22侧棱长为4，E ，F 分别为棱AB ，CB 的中点，则二面角11D EF B --的余弦值是（ ）A ．217B ．317C ．1317D ．1317【答案】C【解析】以D 为坐标原点，建立如图所示的空间直角坐标系，则1(22,22,4)B ，1(0,0,4)D ，(22,2,0)E ，2,22,0)F ，1(22,2,4)D E =-，1(2,22,4)D F =-，1(0,2,4)B E =--，1(2,0,4)B F =--．设平面1D EF 的一个法向量为(,,1)x y =n ，则1100D E D F ⎧⋅=⎪⎨⋅=⎪⎩n n ，即22402240x x +-=+-=⎧⎪，解得223x =，23y =，所以2222(=n ； 设平面1EFB 的一个法向量为(,,1)x y =m ，则1100B E B F ⋅=⋅⎧⎪⎪⎩=⎨m m ，即240240x -⎧=-=⎪⎨⎪⎩，解得22x =-，2y =- 所以(22,22,1)=--m ，所以881131733cos ,5||||85173--+⋅<>===-m n m n m n ，所以二面角11D EF B --1317．增分训练一、选择题1．如图，在三棱锥C OAB -中，OA OB ⊥，OC ⊥平面OAB ，6OA =，8OB OC ==，14CE CB =，D ，F 分别为AB ，BC 的中点，则异面直线DF 与OE 所成角的余弦值为（ ）A ．1010B ．1025C 30D 30【答案】B【解析】以OA ，OB ，OC 为x 轴，y 轴，z 轴正方向建立空间直角坐标系O xyz -， 则(3,4,0)D ，(0,4,4)F ，(0,2,6)E ，(3,0,4)DF =-，(0,2,6)OE =， ∴610cos ,25||||5210DF OE DF OE DF OE ⋅<>===⋅⋅， ∴异面直线DF 与OE 所成角的余弦值为61025． 2．正方体1111ABCD A B C D -的棱上（除去棱AD ）到直线1A B 与1CC 的距离相等的点有3个，记这3个点分别为E ，F ，G ，则直线1AC 与平面EFG 所成角的正弦值为（ ） A ．2613B ．2613C 278D 478【答案】D【解析】正方体1111ABCD A B C D -的棱上到直线1A B 与1CC 的距离相等的点分别为1D ，BC 的中点，11B C 的四等分点（靠近1B ），假设1D 与G 重合，BC 的中点为E ，11B C 的四等分点（靠近1B ）为F ，以D 为坐标原点，DA ，DC ，1DD 所在直线分别为x ，y ，z 轴，建立空间直角坐标系， 设2AB =，则(1,2,0)E ，3(,2,2)2F ，(0,0,2)G ，(2,0,0)A ，1(0,2,2)C ， ∴1(,0,2)2EF =，3(,2,0)2GF =，1(2,2,2)AC =-． 设平面EFG 的法向量(,,)x y z =n ，则0EF GF ⎧⋅=⎪⎨⋅=⎪⎩n n ，即12023202x z x y ⎧+=⎪⎪⎨⎪+=⎪⎩，取4x =，得(4,3,1)=--n ，设直线1AC 与平面EFG 所成角为θ，则直线1AC 与平面EFG 所成角的正弦值为1478sin |cos ,|AC θ=<>=n ．3．已知长方体1111ABCD A B C D =中，2AB BC ==，13AA =，E 为侧棱1BB 的一点，且1113B E B B =，则直线AE 与平面11A ED 所成角的余弦值为（ ） A 25B 10C 310D ．5 【答案】B【解析】以D 为原点，射线DA ，DC ，1DD 的方向分别为x 轴，y 轴，z 轴正方向建立空间直角坐标系，如图，(2,0,3)A ，(2,2,2)E ，1(0,0,3)D ，(2,0,0)A ， ∴1(0,2,1)A E =-，1(2,2,1)D E =-，(0,2,2)EA =--．设平面11A ED 的一个法向量为(,,)x y z =n ，则110202200A E y z x y z D E ⎧⋅=-=⎧⎪⇒⎨⎨+-=⋅=⎩⎪⎩n n ，取2z =，则(0,1,2)=n ， ∴246310cos ,10||||4414210EA EA EA ⋅---<>====-⋅+⨯+n n n ， 设直线AE 与平面11A ED 所成角大小为θ，则910cos 11010θ=-=．4．在正方体1111ABCD A B C D -中，点E 为1BB 的中点，则平面1A ED 与平面ABCD 所成的锐二面角的余弦值为（ ） A ．12B ．23C ．33D ．22【答案】B【解析】以A 为原点建立如图所示的空间直角坐标系A xyz -，设棱长为1，则1(0,0,1)A ，1(1,0,)2E ，(0,1,0)D ，∴1(0,1,1)A D =-，11(1,0,)2A E =-． 设平面1A ED 的一个法向量为1(1,,)y z =n ，所以有11110A D A E ⎧⋅=⎪⎨⋅=⎪⎩n n ，即01102y z z -=⎧⎪⎨-=⎪⎩，解得22y z =⎧⎨=⎩，∴1(1,2,2)=n ；∵平面ABCD 的一个法向量为2(0,0,1)=n ， ∴1222cos ,313<>==⨯n n ，即平面1A ED 与平面ABCD 所成的锐二面角的余弦值为23．二、填空题5．如图，在三棱锥P ABC -，ABC △为等边三角形，PAC △为等腰直角三角形，PA PC =4=，平面PAC ⊥平面ABC ，D 为AB 的中点，则异面直线AC 与PD 所成角的余弦值为__________．【答案】24【解析】取AC 得中点O ，连接OP ，OB ， 因为PA PC =，所以AC OP ⊥． 因为平面PAC ⊥平面ABC ，平面PAC 平面ABC AC =．所以OP ⊥平面ABC ，又因为AB BC =，所以AC OB ⊥，于是以O 为坐标原点，建立如图所示的空间直角坐标系O xyz -， 结合PAC △为等腰直角三角形，4PA PC ==，ABC △为等边三角形， 则(22,0,0)A ，(2,0,0)C -，(0,0,22)P ，2,6,0)D ， 所以(2,0,0)AC =-，(2,6,2)PD =-， 所以2cos(,4||||424AC PD AC PD AC PD ⋅〉===-⨯，故异面直线AC 与PD所成角的余弦值为24．6．如图，在正方体1111ABCD A B C D -中，E ，F 分别为AD ，1DD 的中点，则平面1EFC B 和平面11BCC B 所成二面角的正弦值为 ．【答案】223【解析】以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系， 设正方体1111ABCD A B C D -的棱长为2，则(1,0,0)E ，(0,0,1)F ，(2,2,0)B ，(1,0,1)EF =-，(1,2,0)EB =．设平面1EFC B 的一个法向量(,,)x y z =n ，则020EF x z EB x y ⎧⋅=-+=⎪⎨⋅=+=⎪⎩n n ，取2x =，得(2,1,2)=-n ；平面11BCC B 的一个法向量(0,1,0)=m ，设平面1EFC B 和平面11BCC B 所成二面角为θ，则||1cos ||||3θ⋅==⋅n m n m ，所以22sin θ=三、解答题7．如图，三棱柱111ABC A B C -，侧棱与底面垂直，,P Q 分别是棱11,BB CC 上的点，1AB A Q ⊥，23AC =，13AA =，6AB =．（1）求证：1AC A P ⊥；（2）若M 是1A PQ △的重心，AM ⊥面1A PQ ，求平面1A PQ 与面11BCC B 所成角（锐角）的余弦值．【答案】（1）证明见解析；（226． 【解析】（1）由已知1AA AB ⊥，1AB A Q ⊥又，11AB AA C C ⊥面，AB AC ∴⊥，1AC AA ⊥又，11AC AA B B ∴⊥面，1AC A P ∴⊥．（2）以AB 为x 轴，AC 为y 轴，1AA 为z 轴，建立空间直角坐标系A xyz -， 设1BP z =，2CQ z =，则6,0,)P z ，2(0,23,)Q z ，1(0,0,3)A ，123623()2z z AM ++=，1(6,0,,3)A P z =-，12(0,23,3)AQ z =-，1AM A P ⊥，1AM AQ ⊥，⎪⎪⎩⎪⎪⎨⎧=-+++=-+++∴03)3)(3(31203)3)(3(36221121z z z z z z ，得⎩⎨⎧==1221z z 或⎩⎨⎧-==1121z z （舍），∴面1A PQ 的法向量为633(,,2)AM =， 又面11BB C C 的一个法向量是)0,321,61(，∴面1A PQ 与面11BB C C 夹角θ的余弦值2263cos 61211499612θ==+++． 8．如图，直三棱柱111A B C ABC -中，12C C CB CA ===，AC CB ⊥．D E 、分别为棱111C C B C 、的中点．（1）求点E 到平面ADB 的距离；（2）求二面角1E A D B --的平面角的余弦值；（3）在线段AC 上是否存在一点F ，使得EF ⊥平面1A DB ？若存在，确定其位置；若不存在，说明理由．【答案】（1）62（2）66；（3）存在，F 即为AC 中点． 【解析】（1）如图所示，以CB 为x 轴，CA 为y 轴，1CC 为z 轴建立空间直角坐标系， 由12C C CB CA ===，可得(0,0,0)C ，(0,2,0)A ，(2,0,0)B ，(0,0,1)D ，(1,0,2)E ．则(2,2,0)AB =-，(0,2,1)AD =-，(1,0,1)DE =，设平面ADB 的法向量为(),,1x y =n ，得1220221012x x y y y ⎧=⎪-=⎧⎪⇒⎨⎨-+=⎩⎪=⎪⎩，即11,,122⎛⎫=⎪⎝⎭n ，则取法向量为()1,1,2=n ， 则点E 到平面ADB 的距离6DE d ⋅==n n．（2）1(0,2,2)A ，(1,0,2)E ，(0,0,1)D 可得1(1,2,0)A E =-，1(0,2,1)A D =--， 设平面1A ED 的法向量为()1120,,112102x x y x y y y =-⎧-=⎧⎪=⇒⇒⎨⎨--==-⎩⎪⎩n ，故可令()12,1,2=-n ，()10,2,2A ，()0,0,1D ，()2,0,0B ， 可得1(0,2,1)A D =--，1(2,2,2)A B =--， 设平面1A BD 的法向量为()212102,,1222012x y x y x y y ⎧=⎪--=⎧⎪=⇒⇒⎨⎨--=⎩⎪=-⎪⎩n ，故可令()21,1,2=-n ，∴1212126cos ,6⋅〈〉==-n n n n n n ，即求二面角1E A D B -- （3）假设存在点F ，坐标为(0,,0)y ，则(1,,2)EF y =--，EF ⊥平面1A DB ，得2EF ∥n ，即112112y y -==⇒=--， ∴()0,1,0F ，F 即为AC 中点．。

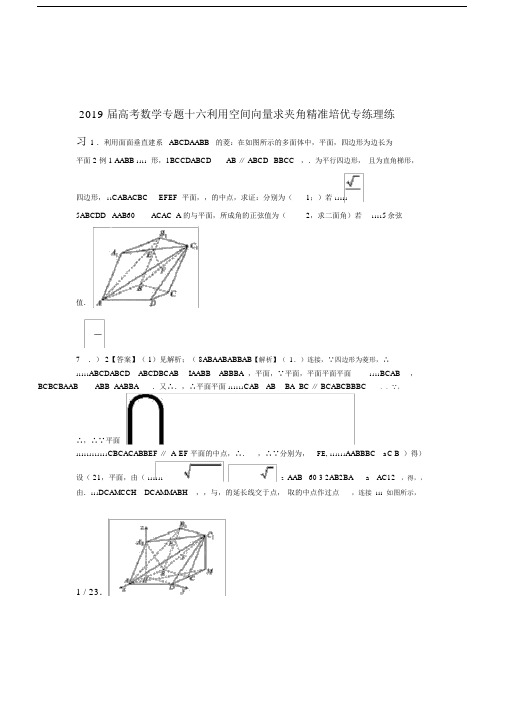
2019 届高考数学专题十六利用空间向量求夹角精准培优专练理练习1 ．利用面面垂直建系 ABCDAABB 的菱：在如图所示的多面体中，平面，四边形为边长为平面 2 例 1 AABB 1111形，1BCCDABCD AB ∥ ABCD BBCC，．为平行四边形，且为直角梯形，四边形， 11CABACBC EFEF 平面，，的中点，求证：分别为（1；）若111115ABCDD AAB60 ACAC A 的与平面，所成角的正弦值为（2，求二面角）若11115余弦值．7．） 2【答案】（ 1）见解析；（ 8ABAABABBAB【解析】（1．）连接，∵四边形为菱形，∴11111ABCDABCD ABCDBCAB IAABB ABBBA ，平面，∵平面，平面平面平面1111BCAB，BCBCBAAB ABB AABBA．又∴．，∴平面平面111111CAB AB BA BC ∥ BCABCBBBC．．∵，∴，∴∵平面111111111111CBCACABBEF∥ A EF 平面的中点，∴．，∴∵分别为，FE, 111111AABBBC aC B ）得）设（ 21，平面，由（1111112AAB 60 3 2AB2BA a AC12，得，，由．111DCAMCCH DCAMMABH，，与，的延长线交于点，取的中点作过点，连接111如图所示，1 / 23．AB ABA60 A △ H AAB，又为等边三角形，∴，∴111AB ABCDABCDAABBABB AABBA AH，，平面平面又平面平面，平面1111111ABCD AH故平面．1BB∥CCBBAA ∥ BCCBCC∵平面，∴为平行四边形，∴．1111111∥CD∥ABCDBBAA．平面又∵，∴11M∥CAABBDCCCICD∵平面，∴平面．1111 BC BCMMBC DCCAABB，∴．由（1），得，∴平面平面1111ABCDABCDACM CAMC ，∴所成角．，∴平面是与平面∵CDCI BC 111ABCDABCD ∥∥ BCBCAB ∥∥ ABABBC ，∵，∵平面，∴平面，11111111BCB ABI ，11111∥ABCDCBA ．∴平面平面111 MC5313M AH C ，∴．，解得 3 a AMsin C1115AC 2a 121ABCDABDE在梯形中，易证， uuuvvvuuuuuuzyHA轴的正方向建立空间直角坐标系．轴，，分别以，轴，的正方向为 HDHAx 1,0,0BA11,0,0 3,00,0,3 2,0,3B CD3,00,A1,，，，则，，，11vuuuvuuuvuuuCC BB33,31,0,C 2,BB，及，，得由1111vuuuvuuuvuuu3 1,0, AD 1,3,0AA AC 3,3,3 ∴，，．11vuuu0 3x 3y 3z0 mAC111 1 ADCzm,x,y 得的一个法向量为，由，设平面vuuu 11110 x 3y0 m AD 111y 3,1,2 m ，得令1 vuuu0 3z3 x 3y0AC n 222 1 z ,x,ynCAA得设平面的一个法向量为，由，vuuu 112220 x3z0 AAn 2212 / 23．1 3,2,n．∴， co,7D A ACACDA．是钝角，∴二面角的余弦值是又∵二面角111182．线段上的动点问题AYABCD30ABD △ AB BD2 翻折到中，，2 例，：如图，在将，沿 3 AD BD △ A 的位置，ABCBDA．使平面平面BCDAD）求证：平面；（1vvuuuuuuu60M CBD ACCAAM M 的大小为，上有一点）若在线段，且二面角满足 2（求的值．13 ．）【答案】（ 1）见解析；（ 222221BD △ ABD ．∴ 1【解析】（，）中，由余弦定理，可得AB ADBD DBCADB90 90ABDFF．作于点，，∴∴BCAABC DFABBDA ABD．∵平面，∴，平面平面平面平面IBCA BC CB ADFBC，∴∵平面．CBCBBDDBA又∵．平面，∴，DI DFBD DACB AD ADB 又∵，∴平面．BCDAD BD AD 又．，∴，平面BBDICB vuuu DDADBDADA轴正方向建立如）由（（21）知，，方向为两两垂直，以为原点，以x 图所示空间直角坐标系，xyzD3 / 23．zyBM,0,1,0x,30,0,3,1,0C A ，，则．设，3 x vvuuuuuuu C yAAM3 M 3,,3 则由，3z 3c,m ,abMDB设平面，的一个法向量为vuuu0b0DB m 则由， vuuuu03 ca b 3 30 m DM vuuuCBD,0,1 c a 1 m3 DA0,0,取，的一个法向量可取．平面vuuu 3131 1DA, m cos ．∴222 2 2 13 1 3 0,1 ．∵，∴ 23 ．翻折类问题 PBCCD △ ABCDPAD △ P 沿 1 中，，为，在边长为 2 的正方形中点，分别将例 3：如图 OAB COPEPAPBD 为中，，如图， 2 所在直线折叠，使点与点．在三棱锥重合于点PB 中点． ABPO ）求证：；（ 1POABP 所成角的正弦值；（ 2）求直线与平面EAO P ）求二面角 3 （的大小．4 / 23．15 ）） 2．；（3）见解析；（【答案】（ 153BCPCCD ABCDADPPD 【解析】（）在正方形，，中，中点， 1 为 OBPOP OABPO OA ．中，，∴在三棱锥OAB PO ∵，∴．平面OOAI OBABPO OAB AB．，∴平面∵AOOFBMABFM）取中点中点．，连接，取，连接（2OGOAB作．过点的平行线OG OFPOPO OABPO．∵，∴，平面OG ABOFOA OBOF ABF，．∴为∵．的中点，∴如图所示，建立空间直角坐标系．xyzO31,0,M0,0,1P，．，，3,01, 1,3,0BA22 OABMOABO BA M ．为∵，的中点，∴5 / 23．OABPO POAPOA PO OAB．∵平面平面平面，∴平面，OABOAB OA BM平面平面，，∵平面 IPOA vuuu 33POA,0 BM , BM∴．平面．∵22 vuuPOA3,1BP 1, 的法向量．．∴平面，31,0 m vuuBPm vuu15 POABP BPsin cosm, 所成角为．设直线，则与平面vuu5BPm15POABP所成角的正弦值为∴直线．与平面 5uvuuvuu1131313,0 1,OA, E ,,,OE ）知（， 3，）由（2．222222vuu0n OA 0 yx 3 OAE，设平面的法向量为即，则有 nvuuu 0 nOE0 z x 3y 12 nm3 n1,2 3, 令，则，．即．∴． 3 x 32z cosm, n 1 y2 4m n2 E AO P 为锐角，∴它的大小为由题知二面角． 3对点增分集训一、单选题ACBBCABC ABED 的中中，的直三棱柱．如图，在所有棱长均为，，分别为1a111111CEAD）点，则异面直线，所成角的余弦值为（6 / 23．4113 ． DCA． B ．．2552C【答案】 vuvuuuuuvuuuOACzyOEOCOB，的中点为，以，，轴建立坐标系，，【解析】设xaaa3 ,00,,0AC0,Da,0, ，则，，，aE0,0, 2222 vuuuuuuvaaa3 a, 0, CE ADa,, ，则，2222aaa3 a0a12222 CE AD ，则设．成的角为与C，故选cos5222aaa322a a4444ABC BCAAABC AD ，点中，底面是边长为2．在三棱柱 1 的正三角形，侧棱底面1111BB在棱上，1sinCAACAD1BD，若与平面）的值是（，则所成的角为且1163102 ． D A ． B ．． C 4242D【答案】13,1D,．【解析】如图，建立空间直角坐标系，易求点227 / 23．3vuuu662CAAC n ,ADcos ．故，∴平面的一个法向量是，则sin1,0,0 n11442 ．选 D 2 OCD2AB为底面圆周上的一点，，．如图，圆锥的底面直径，高3BC120 AOD AD与）所成的角为（，则空间中两条直线9075 60 30．B．A．D C．B【答案】 zOCOOEOByEAB轴，建立空间直为【解析】取中点轴，，以为原点，轴，为为x 角坐标系，如图所示，120 AOD 2OC DAB 2 ∵圆锥的底面直径为底面圆周上的一点，，，，高13,0,D ，∴可得，，， 0,1,0A0, B1,020,0,C228 / 23．vuuu vuuu,0AD ,，则，2BC 0, 1,22 vvuuuuuu3BCAD 12 BC cos AD ，∴与设空间两条直线所成的角为，vuuuuuuv233 BC AD 60 BC 60AD与．所成的角为∴，即直线，故选B ABCDABCDP 5PD PA ，平面 4．已知四棱锥是边长为 2 的正方形，的底面PCOPCOABCD BMMADPAD所成角的的中点，则直线的中点，平面与平面，是是）正弦值是（85558285 ．． A ． CBD． 855585D【答案】，，，，【解析】由题可知1,2,0 P1,2,00,0,2OC0,0,0Bvuvuuuuu则，， ,2,0OC OP 0,0,2 1vuuu31 PC1,1, M ,1,1BM M是的中点，∴，∵22 PCOPCOBM 与平面设平面，的法向量所成角为，直线z,y,n xvuuu 0 2zn OP ，可取则2,1,0 n vuuu 02y nOC x vuuunBM vuuu 8584 n sincos BM ，．，故选Dvuuu 8517nBM 5 49 / 23．G90 BAC 2C AC AAAB ABC ABE 分别，．如图，在直三棱柱5，点中，与1111EFGD ACCCBADFABDF长和是，则线段和分别是的中点，点上的动点．若与111）度的最小值为（325 2255 ．． B ．．D CA555A【答案】建立如图所示的空间直角坐标系，【解析】，，，则，， )(x0,2,1),0,G(1,0,2)0F(E)(0,)y,0DA(0,0,0vuuuuvuu，则， 1 EF x,GD , 1y, 2 2,vuvuuuuuEF GD02 2x y GD EF ，∴由于，∴，22y x 44222222 y )5(4y2xDF y y2 y y 5 8 故， 5510 / 23．24 5 yDF A 长度取得最小值，且最小值为∴当．时，线段．故选55vuuu CB 、 A 、，平分别在空间直角坐标系的三条坐标轴上，6．如图，点 xyzO 0,0,2 OC cosC AB OABC ，设二面角，则（的大小为面的法向量为） 2,1,2n2425 C ． BA．．D．3333 C【答案】 vuuu ABO的一个法向量为：由题意可知，平面，【解析】0,0,2OC vuuu2n4OC C由空间向量的结论可得：．．故选 cos vuuu 且，7．如图所示，五面体平面中，正，的边长为时，平设，若与平面，则当所成的角为，33 2n OCAE ∥ ABCABCCDABCDE△ AE，11AECD ．2ππkCE, ABE 取最大值46 ABCBDE面与平面）所成角的正切值为（0) k(kAE232 C ． B A ． 1 ． D ． 2C【答案】11 / 23．【解析】如图所示，建立如图所示的空间直角坐标系，xyz Ok130,0,D,0B,，，，，则k0,1,AE0,1,0222vuuu3333,0 M ，， ,CM0ABEMAB的一个法向量为取的中点，则平面，，则4444 vuuvuuuu 3CMCE 由题意， sin vuuvuuuu 2 CMCE k1 2ππ 2312 k , 2，解得，，∴ 又由的最大值为，∴ 2k sin46222 2k1 2 2k BDE 的法向量为当时，设平面，zn ,x,yuuuv 20 zn DE y 2 ，则 vuuu 213 0z xy n BE 222 ABC ，由平面取，的法向量为0,0,1m 2 n 3,1, ABCBDE 设平面，和平面所成的角为63 mn 2tan ，∴ sin 则．，故选，∴ C cos 33n mABC △ ABCAABCABC 内的射影为．已知三棱柱8 在底面的侧棱与底面边长都相等， 1111 的中心，ABCAB所成角的正弦值等于（）则与底面12132． DCB． A ．． 3333 B【答案】12 / 23．OAOABCOOAA 分别为为坐标原点，，以在平面内的射影为、【解析】如图，设x 11z 轴建立空间直角坐标系如图．轴、6313ABC △ ,,A,0,0B ，，则，边长为 1 设 1 3223vuuu 6531 ABC0,0,1 n AB,, ∴．又平面．的法向量为1326 vuuu n ABvuuu2 1 ABCAB cos AB,sinn与底面所成角为．，则设 vuuu 3n AB1 2ABCAB ．所成角的正弦值为故直线与底面B．故选 3BCABCD P11 1∥ ABCDABCDAD PB，，底面．如图，四棱锥中，平面9 为直角梯形，3 AD PBAB ABBC BEDEA PEABEE2PA 与平面，，点上，且，则平面在棱的夹角的余弦值为（）6632 C ．． DA． B．3336【答案】BzBCyBPBBA轴，、所在直线为、以【解析】为坐标原点，以、、x建立空间直角坐标系，13 / 23．vuuuvuuu0,2,1P0,0,30,3,0EA3,3,0BD0,0,0，，∴，，，则，3,3,0 0,2,1BDBE vuuu 0 n yBE z 2z,x,n yBED，则设平面的一个法向量为，vuuu BD 3x 3y 0n11,1n ,1,0,0m ABE1z，得，取，平面的法向量为221662BEDABE的夹角的余弦值为．故选与平面∴B．．∴平面cosn,m 6661 2BDABCDBCAABCD所成角的余弦值为（与平面）中，直线10．在正方体1111113232 CD ．A．． B ． 2334C【答案】 zDCyDDDA，，，轴建立如图所示空间直角坐标系：【解析】为分别以，x11,0,1ADC0,0,00,1,1,0,1B1 ，设正方体的棱长为1，可得，，，11ruuururuuuuu，∴，， 1,0,DBC 1 ,0,1 1A,011,BD11vuuu0DA n 0 zx1zxy,,nBDA，设是平面，即的一个法向量，∴vuuu10x y 0BDn1x 1 n 1,1,BDA，∴平面取，得的一个法向量为，1 y z114 / 23．ruuu uuB sicoB,BDBCA ，∴与平面设直线所成角 uu B1 332BDABC 与平面 C∴．，即直线所成角的余11弦值是．故选 cossin 1 33 ABCD2CD BC BD △ AB BD DA ABD2 折起，使 11．已知四边11形沿，，，现将二面角5 CD CA BD,AB与）的大小在所成角的余弦值取值范围是（内，则直线66222522552,0,10 ，0,，．A ． C ．B D．888888 A 【答案】 COAOOBD【解析】取，中点，，连结1 BDCOCO BDAO 3 2BC CDAO2 AB BD DA ．，，∴，∵，且， C BD AOCA ∴是二面角的平面角，ODOOCy 为轴，以轴，为原点，为 xBCDO 的垂线为作平面轴，建立空间直角坐标系，过点z ，，， )(0, 1,0)0,1,0DB()C(1,0,05C A BD, ，则设二面角的平面角为，66 AOCAOBO，则，连，、 sin3,0,cosA3ruuuruu ，，∴ 1,1,0CD sin,1,cos3 BA315 / 23．ruuuuruu CDABco1CD AB设，、，则的夹角为cosuu2CDAB533, , cos∵，∴，66225250, 1 3cos0,cos．故选 A 故，∴．28CCDAABCD ABBPP 所成角的在中，点上运动（包括端点），则 12．正方体与11111）取值范围是（ππππππππ,,,, CA．．．B．D34224366 D【答案】 DCzy 、x、DDDAD轴建立空间直角坐标、以点、为原点，所在直线分别为【解析】1P坐标为，点，系，设正方体棱长为1xx, x,1vuuuvuu，则，,0,11BCx BP x 1, x,1 vuuuuuvBC、，的夹角为设BP 1uuvuuuvBP BC11 1，则cos vuuuuuv22BC BP222xx 1 2112x333π 13x．∴当取最大值，时，cos236π 1 x 1 时，，当取最小值．cos32ππ,ADADBC ∥ BP ．故选 D 与∵．所成角的取值范围是，∴11163二、填空题AC32AC 2CCABC ABCAB BC的中，是．如图，在直三棱柱13 ，中， m1111CBCM 所成角的余弦值为 ________ ．与点，则异面直线1116 / 23．14【答案】28AC2 BCCC BABC ACAB32AC M 的中，在直三棱柱中，，是【解析】1111 ACBM 1 4 3BM．点，∴，ACyMMBMMA为的垂线为轴，轴，过轴，以为原点，作为zx 建立空间直角坐标系，，，，，则 0,0,0M0,1,2B2 C3,0,0C3,0,11vuuuuvuuu，∴，3,1,2 CB23,0, MC 11vuuuuuuuvMC CB14111cosMCBC．所成角为，则设异面直线与vuuuvuuuu 11287 8MCCB1114MCBC与所成角的余弦值为．∴异面直线1128ABCD BAD 60 P ABCD PD，且平面的底面是菱形，，14．已知四棱锥2PF:FC 1:PCEFEADFABPD与平面是棱上，若，点的中点，，则直线在棱ABCD．所成角的正弦值为 __________354 【答案】 35ABCDD，，设菱形的边长为【解析】以点建立如图所示的空间直角坐标系2xyzD17 / 23．u443,0,F0,0,0D,,EF ,E ,0则，，，∴，3336222ABCD0,0,1 n 的一个法向量为平面，4vuuu3543，则n, cosEF35222437623354ABCDEF所成角的正弦值为即直线与平面．35 bab ba 上，，上，向量，向量．设15，在是直线，，是平面，在baa110) b (3,4, ，，则，．所成二面角中较小的一个的余弦值为________ ,1 a,11 113【答案】 15 0) (3,4,b，【解析】由题意，∵，,11,1 a11ba 304 3 11 bcosa,∴，1115 ba5 311 ba ba 在上，，，向量上，向量在∵ba1133，故答案为所成二面角中较小的一个余弦值为．∴，1515ABCDABCDP ABCD2PA AB，，中，底面平面16．在四棱锥为平行四边形，PBCxPA BAD120 PD3AD所成角的取值范与平面，则当，变化时，直线， x ．围是 __________0, 【答案】 618 / 23．3330,2,0B,0,0D, C,2 ，【解析】，如图建立空间直角坐标系，得，2222x0,0,P ，vuuuvuu 33PBCz,m, yx,0 , BC ，，，设平面的法向量x0,2,PB22uuuv0 BC m32 m1,3, ，得，∴vuu x 0PB mvuuuvuuu 2333cosPD, m PD , , x ，又，∴2212 2x3 4 2 x231 ，∴2sin3 36122 244x2x3 4 2x2x10, sin0,∴，则62三、解答题P ABCDABCDAC BDBC CD ， 17．如图所示：四棱锥为四边形，，，底面PCA 30 PAC PC 43AC2PBD PBPD ，，，平面平面，，19 / 23．ABCD PA ；平面（ 1）求证： PC BC120 ABABCD BAD M ，使得直线）若四边形（2，中，是否在上存在一点 PBDBM 与平面PM573 的值，若不存在，请说明理由．所成的角的正弦值为，若存在，求38MCPM ）存在，2（ 1）见解析；（．【答案】 1 MCPO ）设，连接 1【解析】（ OACIBD O BDBC CD ，ACQBD ，为中点 BDPO ，又 PD QPB POPBD PAC PBD 平面平面，平面平面IPACBDPA PACPAC PA BD 平面平面，而222PCA △ cos30PC ACAC PAPC 2 中，由余弦定理得，在32222PC ACPA，而4 3 PA 1612 24 22AC PA ABCD PA PA BD ．平面O BDAC yAPABABA轴建立空间直角坐标系：轴，）过（ 2 作垂线记为轴，为为zx20 / 23．33 ,0 ,D ，，，，0,0,20,0,0PA3,3,03,0,0BC22 vuuuvuuuvuuuuuuv vuu PM33 MC PM 2PD ,, vuuu ，设， 2 PB 3,0,22MC vuuu 232 333,,BM M,, ，1 1 11 11 PBD 设平面，法向量为zy,x,nvuu0z 3 2 0PB n∴，，取33,2,2n vuuu y330nPD2z 0 x2 2 PBDBM所成角为设与平面，32363 2 vuuu 1 1 1573 BMsin cosn ， 382 4 9 3 192 1PM 1 1解，．MCABC3 A BCBBABC ，的正三角形，中，底面18．如图，在斜三棱柱是边长为21111 CBB60 10 AB ．， 1121 / 23．ABCBBCC ；）求证：平面平面（ 111C ABB ）求二面角的正弦值．（ 21 744 ）见解析；（2．）【答案】（ 137OABCOOB ，连接，【解析】（ 1）取，的中点 1 BC ABCOA3OA，，且是边长为 2 的正三角形，∴∵底面2221OB 60 3 CBBBB7 cos60 3 2 OB1 1 3 ，，，∵，∴111222 AB OA10 OB OB AB7 10 ，∴，∴，又∵1111ABC OAOAB OBCCOA OBOBIBC ，又∵，∴平面∴平面，，又∵ 1111 ABCBBCC 平面∴平面． 112 ）如图所示，（OHOCOAOy轴建立空间直角坐标系，其中为以点为坐标原点，为为轴，轴，zx2BH，313,0,B1,0,0B 1,0,0C ，，则，，3,0A0,122vuuuuuuvuuuv331 , 3,AB ，∴，，3,0AB 1,3,0 1,AC12222 / 23．ABB 的法向量，为平面设 z,, nyx 11111vuuu 0 3y x 110AB n 11 y ，即则，令，得； 3,1,1 n vuuu 331 110 AB n yx 3 z0 11 1112 2vuuu 0 n AC 2 CAB ，即设的法向量，则为平面 zx,y, nvuuu 122220AB n 12 03y x 22 ，313 3y z0x 222 2 21 131nn 53213,1,n 1 y，；∴令，得ncosn,2221337n n 37 21 595474 1 CABB．的正弦值为∴二面角1373723 / 23．。

培优点十六 利用空间向量求夹角1．利用面面垂直建系例1：在如图所示的多面体中，平面11ABB A ⊥平面ABCD ，四边形11ABB A 为边长为2的菱形，ABCD 为直角梯形，四边形11BCC B 为平行四边形，且AB CD ∥，AB BC ⊥，1CD =．（1）若E ，F 分别为11A C ，1BC 的中点，求证：EF ⊥平面11AB C ； （2）若160A AB ∠=︒，1AC 与平面ABCD 所成角的正弦值为55，求二面角11A AC D --的余弦值．【答案】（1）见解析；（2）78-．【解析】（1）连接1A B ，∵四边形11ABB A 为菱形，∴11A B AB ⊥． ∵平面11ABB A ⊥平面ABCD ，平面11ABB BA 平面ABCD AB =，BC ⊂平面ABCD ，AB BC ⊥，∴BC ⊥平面11ABB A ．又1A B ⊂平面11ABB A ，∴1A B BC ⊥． ∵11BC B C ∥，∴111A B B C ⊥．∵1111B C AB B =，∴1A B ⊥平面11AB C ．∵,E F 分别为11A C ，1BC 的中点，∴1EF A B ∥，∴EF ⊥平面11AB C ． （2）设11B C a =，由（1）得11B C ⊥平面11ABB A ， 由160A AB ∠=︒，2BA =，得123AB =，2112AC a =+．过点1C 作1C M DC ⊥，与DC 的延长线交于点M ，取AB 的中点H ，连接1A H ，AM ， 如图所示，又160A AB ∠=︒，∴1ABA △为等边三角形，∴1A H AB ⊥， 又平面11ABB A ⊥平面ABCD ，平面11ABB A 平面ABCD AB =，1A H ⊂平面11ABB A ，故1A H ⊥平面ABCD ．∵11BCC B 为平行四边形，∴11CC BB ∥，∴1CC ∥平面11AA BB ．又∵CD AB ∥，∴CD ∥平面11AA BB ． ∵1CC CD C =，∴平面11AA BB ∥平面1DC M ．由（1），得BC ⊥平面11AA BB ，∴BC ⊥平面1DC M ，∴1BC C M ⊥． ∵BCDC C =，∴1C M ⊥平面ABCD ，∴1C AM ∠是1AC 与平面ABCD 所成角．∵11A B AB ∥，11C B CB ∥，∴11A B ∥平面ABCD ，11B C ∥平面ABCD ，∵11111A B C B B =，∴平面ABCD ∥平面111A B C ． ∴113A H C M ==，112135sin 512MC C AM AC a∠===+，解得3a =．在梯形ABCD 中，易证DE AB ⊥，分别以HA ，HD ，1HA 的正方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系． 则()1,0,0A ，()0,3,0D ，()10,0,3A ，()12,0,3B -，()1,0,0B -，()1,3,0C -， 由()11,0,3BB =-，及11BB CC =，得()12,3,3C -， ∴()13,3,3AC =-，()1,3,0AD =-，()11,0,3AA =-．设平面1ADC 的一个法向量为()111,,x y z =m ，由100AC AD ⎧⎪⎨⎪⎩⋅=⋅=m m 得111113330 30x y z x y -++=-=⎧⎪⎨⎪⎩+， 令11y =，得()3,1,2=m设平面11AA C 的一个法向量为()222,,x y z =n ，由1100AC AA ⎧⋅=⋅=⎪⎨⎪⎩n n 得222223330 30x y z x z -++=-=⎧⎪⎨⎪⎩+， 令21z =，得()3,2,1=n ．∴32277cos ,831434188⋅++====++⨯++⨯m n m n m n ， 又∵二面角11A AC D --是钝角，∴二面角11A AC D --的余弦值是78-．2．线段上的动点问题 例2：如图，在ABCD 中，30A ∠=︒，3AD =，2AB =，沿BD 将ABD △翻折到A BD'△的位置，使平面A BC '⊥平面A BD '．（1）求证：A D '⊥平面BCD ；（2）若在线段A C '上有一点M 满足A M A C λ=''，且二面角M BD C --的大小为60︒， 求λ的值．【答案】（1）见解析；（231-． 【解析】（1）ABD △中，由余弦定理，可得1BD =．∴222BD AD AB +=， ∴90ADB ∠=︒，∴90DBC ∠=︒．作DF A B ⊥'于点F ，∵平面A BC '⊥平面A BD '，平面A BC '平面A BD A B '='，∴DF ⊥平面A BC '． ∵CB ⊂平面A BC '，∴DF BC ⊥．又∵CB BD ⊥，BD DF D =，∴CB ⊥平面A DB '． 又∵A D '⊂平面A DB '，∴CB A D ⊥'．又A D BD '⊥，BD CB B =，∴A D '⊥平面BCD ．（2）由（1）知DA ，DB ，DA '两两垂直，以D 为原点，以DA 方向为x 轴正方向建立如图所示空间直角坐标系D xyz -，则()0,1,0B ，()3,1,0C -，()0,0,3A '．设(),,M x y z ，则由3 33x A M A C y z λλλλ⎧=''-⎪=⇒=⎨⎪-=-⎩()3,,33M λλλ⇒--， 设平面MDB 的一个法向量为(),,a b c =m ， 则由0 0DB DM ⎧⎪⎨⎪⎩⋅=⋅=m m ()0 3330b a bc λλλ=⎧⎪⇒⎨-++-=⎪⎩，取()11,0,a c λλλλ=-⇒=⇒=-m ．平面CBD 的一个法向量可取()0,0,3DA '=，∴()2213cos ,231DA λλλ=⇒⋅+-'m 11322λ-±=⇒=． ∵[]0,1λ∈，∴312λ-=． 3．翻折类问题例3：如图1，在边长为2的正方形ABCD 中，P 为CD 中点，分别将PAD △，PBC △沿PA ，PB 所在直线折叠，使点C 与点D 重合于点O ，如图2．在三棱锥P OAB -中，E 为PB 中点．（1）求证：PO AB ⊥；（2）求直线BP 与平面POA 所成角的正弦值； （3）求二面角P AO E --的大小． 【答案】（1）见解析；（215；（3）3π． 【解析】（1）在正方形ABCD 中，P 为CD 中点，PD AD ⊥，PC BC ⊥， ∴在三棱锥P OAB -中，PO OA ⊥，PO OB ⊥． ∵OA OB O =，∴PO ⊥平面OAB ． ∵AB ⊂平面OAB ，∴PO AB ⊥．（2）取AB 中点F ，连接OF ，取AO 中点M ，连接BM ． 过点O 作AB 的平行线OG ．∵PO ⊥平面OAB ，∴PO OF ⊥，PO OG ⊥．∵OA OB =，F 为AB 的中点，∴OF AB ⊥．∴OF OG ⊥． 如图所示，建立空间直角坐标系O xyz -．()3,0A ，()3,0B -，()0,0,1P ，132M ⎛⎫⎪ ⎪⎝⎭．∵BO BA =，M 为OA 的中点，∴BM OA ⊥．∵PO ⊥平面OAB ，PO ⊂平面POA ，∴平面POA ⊥平面OAB ． ∵平面POA 平面OAB OA =，BM ⊂平面OAB ， ∴BM ⊥平面POA ．∵33,,022BM ⎛⎫=- ⎪ ⎪⎝⎭． ∴平面POA 的法向量)31,0=-，m ．()1,3,1BP =-．设直线BP 与平面POA 所成角为α，则15sin cos ,5BP BP BPα⋅===m m m ． ∴直线BP 与平面POA 15． （3）由（2）知131,,222E ⎛⎫- ⎪ ⎪⎝⎭，131,,222OE ⎛⎫=- ⎪ ⎪⎝⎭，()1,3,0OA =． 设平面OAE 的法向量为n ，则有0 0OA OE ⋅⎧⎪=⎪⎩=⎨⋅n n 即3030x y x y z ⎧⎪⎨=-++=⎪⎩+，令1y =-，则3x =，23z =．即()3,1,23=-n ．∴21cos ,242⋅===⋅⨯m n m n m n ． 由题知二面角P AO E --为锐角，∴它的大小为3π．一、单选题1．如图，在所有棱长均为a 的直三棱柱111ABC A B C -中，D ，E 分别为1BB ，11A C 的中点，则异面直线AD ，CE 所成角的余弦值为（ ）A ．12B 3C ．15D ．45【答案】C【解析】设AC 的中点O ，以OB ，OC ，OE 为x ，y ，z 轴建立坐标系， 则0,,02a A ⎛⎫ ⎪⎝⎭，3,0,2a D ⎫⎪⎪⎝⎭，0,,02a C ⎛⎫ ⎪⎝⎭，()0,0,E a ， 则3,,22a a AD ⎛⎫= ⎪ ⎪⎝⎭，0,,2a CE a ⎛⎫=- ⎪⎝⎭， 设AD 与CE 成的角为θ，则222223012222cos 534444a a aaa a a a a θ-⨯+⨯==++⋅+，故选C ． 2．在三棱柱111ABC A B C -中，底面是边长为1的正三角形，侧棱1AA ⊥底面ABC ，点D 在棱1BB 上，且1BD =，若AD 与平面11AA C C 所成的角为α，则sin α的值是（ ） A 3B ．22C 10D 6【答案】D【解析】如图，建立空间直角坐标系，易求点31,12D ⎫⎪⎪⎝⎭． 平面11AA C C 的一个法向量是()1,0,0=n ，∴362cos ,2AD ==n ，则6sin α．故选对点增分集训D ．3．如图，圆锥的底面直径2AB =，高2OC ，D 为底面圆周上的一点，120AOD ∠=︒，则空间中两条直线AD 与BC 所成的角为（ ） A ．30︒ B ．60︒ C ．75︒ D ．90︒【答案】B【解析】取AB 中点E ，以O 为原点，OE 为x 轴，OB 为y 轴，OC 为z 轴，建立空间直角坐标系， 如图所示，∵圆锥的底面直径2AB =，高2OC ，D 为底面圆周上的一点，120AOD ∠=︒， ∴可得()0,1,0A -，()0,1,0B ，(2C ，31,02D ⎫⎪⎪⎝⎭，则33,02AD ⎛⎫= ⎪ ⎪⎝⎭，(0,2BC =-，设空间两条直线AD 与BC 所成的角为θ，∴312cos 233AD BCAD BCθ⋅===⨯⋅， ∴60θ=︒，即直线AD 与BC 所成的角为60︒，故选B ．4．已知四棱锥P ABCD -的底面ABCD 是边长为2的正方形，5PA PD ==，平面ABCD ⊥平面PAD ，M 是PC 的中点，O 是AD 的中点，则直线BM 与平面PCO 所成角的正弦值是（ ） A 5B 25C 85D 885【答案】D【解析】由题可知()0,0,0O ，()0,0,2P ，()1,2,0B ，()1,2,0C -， 则()0,0,2OP =，()1,2,0OC =-，∵M 是PC 的中点，∴1,1,12M ⎛⎫- ⎪⎝⎭，3,1,12BM ⎛⎫=-- ⎪⎝⎭设平面PCO 的法向量(),,x y z =n ，直线BM 与平面PCO 所成角为θ，则20 20OP z OC x y ⋅==⋅=-⎧⎪⎨⎪=⎩+n n 可取()2,1,0=n ，885sin cos 1754BM BM BM θ⋅====⋅⋅，n n n，故选D ． 5．如图，在直三棱柱111ABC A B C -中，90BAC ∠=︒，12AB AC AA ===，点G 与E 分别是11A B 和1CC 的中点，点D 与F 分别是AC 和AB 上的动点．若GD EF ⊥，则线段DF 长度的最小值为（ ） A 255B 355C 5D ．2【答案】A【解析】建立如图所示的空间直角坐标系，则()0,0,0A ，()0,2,1E ，()1,0,2G ，0(),0,F x ，0(0,),D y ， 则()1,,2GD y =--，(),2,1EF x =--，由于GD EF ⊥，∴220GD EF x y =--+=⋅，∴22x y =-， 故()22222244225845()55DF x y y y y y y =+=-+=-+-+，∴当45y =时，线段DF 255．故选A ． 6．如图，点A B C 、、分别在空间直角坐标系O xyz -的三条坐标轴上，()0,0,2OC =，平面ABC 的法向量为()2,1,2=n ，设二面角C AB O --的大小为θ，则cos θ=（ ） A ．43B 5C ．23D ．23-【答案】C【解析】由题意可知，平面ABO 的一个法向量为：()0,0,2OC =， 由空间向量的结论可得：42cos 233OC OC θ⋅===⋅⋅n n．故选C ． 7．如图所示，五面体ABCDE 中，正ABC △的边长为1，AE ⊥平面ABC ，CD AE ∥，且12CD AE =．设CE 与平面ABE 所成的角为α，(0)AE k k =>，若ππ,64α⎡⎤∈⎢⎥⎣⎦，则当k 取最大值时，平面BDE 与平面ABC 所成角的正切值为（ ）A ．22B ．1C 2D 3【答案】C【解析】如图所示，建立如图所示的空间直角坐标系O xyz -， 则()0,1,0A ，0,0,2k D ⎛⎫ ⎪⎝⎭，()0,1,E k ，31,02B ⎫⎪⎪⎝⎭， 取AB 的中点M ，则3304M ⎫⎪⎪⎝⎭，，，则平面ABE 的一个法向量为33,04CM ⎛⎫= ⎪ ⎪⎝⎭， 由题意23sin 21CE CM CE CMkα⋅==⋅+又由ππ,64α⎡⎤∈⎢⎥⎣⎦，∴2132sin 2221kα≤=≤+22k ≤k 2 当2k =BDE 的法向量为(),,x y z =n ， 则20 31202DE y BE x y z ⎧⎪⎪⎨⎪⎪⋅==⋅=++=⎩n n ， 取(3,2=--n ，由平面ABC 的法向量为()0,0,1=m ， 设平面BDE 和平面ABC 所成的角为θ， 则3cos θ⋅==⋅n m n m ，∴6sin θ=，∴tan 2θC ． 8．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 内的射影为ABC △的中心，则1AB 与底面ABC 所成角的正弦值等于（ ）A ．13B ．23C ．33 D ．23【答案】B【解析】如图，设1A 在平面ABC 内的射影为O ，以O 为坐标原点，OA 、1OA 分别为x 轴、z 轴建立空间直角坐标系如图．设ABC △边长为1，则3,0,03A ⎛⎫ ⎪ ⎪⎝⎭，13162B ⎛ ⎝⎭， ∴15316,,623AB ⎛⎫=- ⎪ ⎪⎝⎭．又平面ABC 的法向量为()0,0,1=n ． 设1AB 与底面ABC 所成角为α，则1112sin cos ,3AB AB AB α⋅===⋅n n n． 故直线1AB 与底面ABC 所成角的正弦值为23．故选B ． 9．如图，四棱锥P ABCD -中，PB ⊥平面ABCD ，底面ABCD 为直角梯形，AD BC ∥，AB BC ⊥，3AB AD PB ===，点E 在棱PA 上，且2PE EA =，则平面ABE 与平面BED 的夹角的余弦值为（ ） A ．23B ．66C ．33D ．63【答案】B【解析】以B 为坐标原点，以BC 、BA 、BP 所在直线为x 、y 、z 轴， 建立空间直角坐标系，则()0,0,0B ，()0,3,0A ，()0,0,3P ，()3,3,0D ，()0,2,1E ，∴()0,2,1BE =，()3,3,0BD =设平面BED 的一个法向量为(),,x y z =n ，则20330BE y z BD x y ⎧⎪⎨⎪⋅=+=⋅=+=⎩n n ， 取1z =，得11,,122⎛⎫=- ⎪⎝⎭n ，平面ABE 的法向量为()1,0,0=m ，∴162cos ,6612==⨯n m ．∴平面ABE 与平面BED 的夹角的余弦值为66．故选B ．10．在正方体1111ABCD A B C D -中，直线1BC 与平面1A BD 所成角的余弦值为（ ） A ．24B ．23C ．33D ．32【答案】C【解析】分别以DA ，DC ，1DD 为x ，y ，z 轴建立如图所示空间直角坐标系： 设正方体的棱长为1，可得()0,0,0D ，()1,1,0B ，()10,1,1C ，()11,0,1A ， ∴()11,0,1BC =-，()11,0,1A D =--，()1,1,0BD =--，设(),,x y z =n 是平面1A BD 的一个法向量，∴100A D BD ⎧⎪⎨⎪⎩⋅=⋅=n n ，即0 0x z x y =+=⎧⎨⎩+，取1x =，得1y z ==-，∴平面1A BD 的一个法向量为()1,1,1=--n ， 设直线1BC 与平面1A BD 所成角为θ，∴11126sin cos ,323BC BC BC θ⋅-=〈〉===⨯⋅n n n； ∴23cos 1sin 3θθ=-=，即直线1BC 与平面1A BD 所成角的余弦值是33．故选C ． 11．已知四边形ABCD ，2AB BD DA ===，2BC CD ==ABD △沿BD 折起，使二面角A BD C --的大小在5,66π⎡π⎤⎢⎥⎣⎦内，则直线AB 与CD 所成角的余弦值取值范围是（ ） A ．52⎡⎢⎣⎦B ．2⎡⎢⎣⎦C ．25201⎡⎡⎫⎪⎢⎢⎪⎣⎦⎣⎭，， D ．252⎣⎦【答案】A【解析】取BD 中点O ，连结AO ，CO ，∵2AB BD DA ===．2BC CD ==CO BD ⊥，AO BD ⊥，且1CO =，3AO =， ∴AOC ∠是二面角A BD C --的平面角， 以O 为原点，OC 为x 轴，OD 为y 轴，过点O 作平面BCD 的垂线为z 轴，建立空间直角坐标系， ()0,1,0B -，()1,0,0C ，()0,1,0D ，设二面角A BD C --的平面角为θ，则5,66θπ⎡⎤∈⎢⎥⎣⎦π，连AO 、BO ，则AOC θ∠=，)33sin A θθ，∴()3cos 3sin BA θθ=，()1,1,0CD =-，设AB 、CD 的夹角为α，则13cos cos 22AB CD AB CDθα⋅-==⋅，∵5,66θπ⎡⎤∈⎢⎥⎣⎦π，∴33cos ,θ⎡⎤∈-⎢⎥⎣⎦， 故513cos 0,2θ⎡⎤-∈⎢⎥⎣⎦，∴52cos 0,8α⎡⎤∈⎢⎥⎣⎦．故选A ．12．正方体1111ABCD A B C D -中，点P 在1A C 上运动（包括端点），则BP 与所成角的取值范围是（ ）A ．ππ,43⎡⎤⎢⎥⎣⎦B ．ππ,42⎡⎤⎢⎥⎣⎦C ．ππ,62⎡⎤⎢⎥⎣⎦D ．ππ,63⎡⎤⎢⎥⎣⎦【答案】D【解析】以点D 为原点，DA 、DC 、1DD 所在直线分别为x y z 、、轴建立空间直角坐标系，设正方体棱长为1，点P 坐标为(),1,x x x -， 则()1,,BP x x x =--，()11,0,1BC =-， 设BP 、1BC 的夹角为α， 则()12221cos 122123233BP BC BP BC x x x α⋅===⋅-+⨯⎛⎫-+⋅ ⎪⎝⎭∴当13x =时，cos α3，π6α=．当1x =时，cos α取最小值12，π3α=．∵11BC AD ∥，∴BP 与1AD 所成角的取值范围是ππ,63⎡⎤⎢⎥⎣⎦．故选D ．二、填空题13．如图，在直三棱柱111ABC A B C -中，12AB BC CC ===，23AC =m 是AC 的中点，则异面直线1CB 与1C M 所成角的余弦值为________． 14【解析】在直三棱柱111ABC A B C -中，12AB BC CC ===，23AC =M 是AC 的中点，∴BM AC ⊥，431BM -=．以M 为原点，MA 为x 轴，MB 为y 轴，过M 作AC 的垂线为z 轴， 建立空间直角坐标系，则()3,0,0C -，()10,1,2B ，()13,0,2C ，()0,0,0M ， ∴()13,1,2CB =，()13,0,2MC =-，设异面直线1CB 与1C M 所成角为θ，则111114cos 87CB CB MC MC θ⋅===⋅⋅． ∴异面直线1CB 与1C M 所成角的余弦值为1428．14．已知四棱锥P ABCD -的底面是菱形，60BAD ∠=︒，PD ⊥平面ABCD ，且PD AB =，点E 是棱AD 的中点，F 在棱PC 上，若:1:2PF FC =，则直线EF 与平面ABCD 所成角的正弦值为__________． 【答案】43535【解析】以D 点建立如图所示的空间直角坐标系D xyz -，设菱形ABCD 的边长为2， 则()0,0,0D ， 31,02E ⎫-⎪⎪⎝⎭，240,,33F ⎛⎫⎪⎝⎭，∴374,,263EF ⎛⎫=- ⎪ ⎪⎝⎭， 平面ABCD 的一个法向量为()0,0,1=n ，则22244353cos ,35374263EF ==⎛⎫⎛⎫⎛⎫-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭n ， 即直线EF 与平面ABCD 所成角的正弦值为43535． 15．设a ，b 是直线，α，β是平面，a α⊥，b β⊥，向量1a 在a 上，向量1b 在b 上，()11,1,1=a ，13,(0)4,=-b ，则α，β所成二面角中较小的一个的余弦值为________．【答案】315【解析】由题意，∵()11,1,1=a ，13,(0)4,=-b ， ∴1111113cos ,35⋅===⋅⨯a b a b a b ∵a α⊥，b β⊥，向量1a 在a 上，向量1b 在b 上， ∴α，β所成二面角中较小的一个余弦值为315，故答案为315． 16．在四棱锥P ABCD -中，底面ABCD 为平行四边形，PA ⊥平面ABCD ，2AB =，3AD =，120BAD ∠=︒，PA x =，则当x 变化时，直线PD 与平面PBC 所成角的取值范围是__________．【答案】0,6⎛⎤⎥⎝⎦π【解析】如图建立空间直角坐标系，得()0,2,0B ，33,22C ⎛⎫ ⎪ ⎪⎝⎭，33,2D ⎛⎫ ⎪ ⎪⎝⎭，()0,0,P x ，设平面PBC 的法向量(),,x y z =m ，33,,022BC ⎛⎫=- ⎪ ⎪⎝⎭，()0,2,PB x =-， ∴00BC PB ⎧⎪⎨⎪⋅=⋅⎩=m m ，得231,3,x ⎛⎫= ⎪ ⎪⎝⎭m ， 又33,,22PD x ⎛⎫=-- ⎪ ⎪⎝⎭，∴2223cos ,1243PD x x-=+⋅+m ，∴2222231sin 23361242443x x xx θ-==⋅+++⋅+，∴1sin 0,2θ⎛⎤∈ ⎥⎝⎦，则0,6θ⎛π⎤∈ ⎥⎝⎦三、解答题17．如图所示：四棱锥P ABCD -，底面ABCD 为四边形，AC BD ⊥，BC CD =，PB PD =，平面PAC ⊥平面PBD ，23AC =30PCA ∠=︒，4PC =，（1）求证：PA ⊥平面ABCD ；（2）若四边形ABCD 中，120BAD ∠=︒，AB BC ⊥是否在PC 上存在一点M ，使得直线BM 与平面PBD所成的角的正弦值为357，若存在，求PM MC的值，若不存在，请说明理由． 【答案】（1）见解析；（2）存在，1PMMC=．【解析】（1）设ACBD O =，连接POBC CD AC BD =⊥，，O ∴为BD 中点又PB PD =，PO BD ∴⊥平面PAC ⊥平面PBD ，平面PAC平面PBD PO =BD ∴⊥平面PAC ，而PA ⊂平面PAC PA BD ∴⊥在PCA △中，由余弦定理得2222cos30PA PC AC PC AC =+-⋅︒， 23161224234PA =+-⨯⨯=，而222PA AC PC += PA AC PA BD PA BD AC O ⊥⎫⎪∴⊥⇒⊥⎬⎪=⎭平面ABCD ． （2）过A 作AB 垂线记为y 轴，AB 为x 轴，AP 为z 轴建立空间直角坐标系： ()0,0,0A ，()0,0,2P ，)3,0,0B，33,02D ⎛⎫⎪ ⎪⎝⎭，)3,3,0C()3,0,2PB =-，33,22PD ⎛⎫=-- ⎪ ⎪⎝⎭，设PMPM MC MC λλ=⇒= 332,11M λλλλ⎫⎪⎪++⎝⎭，332,11BM λλλ⎛⎫-= ⎪ ⎪++⎝⎭设平面PBD 法向量为(),,x y z =n ，∴3200 330202z PB yPD z ⎧=⋅=⎪⇒⎨⋅=+-=⎪⎩⎧⎪⎨⎪⎩n n ，取(2,23,3=n ， 设BM 与平面PBD 所成角为ϕ，()22236323111357sin cos 394191BM λλλλϕλλ-+++++=⋅==++⋅+n 解1λ=，1PMMC∴=． 18．如图，在斜三棱柱111ABC A B C -中，底面ABC 是边长为2的正三角形，13BB =，110AB =160CBB ∠=︒．（1）求证：平面ABC ⊥平面11BCC B ； （2）求二面角1B AB C --的正弦值． 【答案】（1）见解析；（2474【解析】（1）取BC 的中点O ，连接OA ，1OB ，∵底面ABC 是边长为2的正三角形，∴OA BC ⊥，且3OA∵13BB =，160CBB ∠=︒，1OB =，∴222113213cos607OB =+-⨯⨯⨯︒=， ∴17OB =110AB =2221110OA OB AB +==， ∴1OA OB ⊥，又∵1OB BC O =，∴OA ⊥平面11BCC B ，又∵OA ⊂平面ABC ，∴平面ABC ⊥平面11BCC B ． （2）如图所示，以点O 为坐标原点，OC 为x 轴，OA 为y 轴，OH 为z 轴建立空间直角坐标系，其中2BH =， 则()3,0A ，()1,0,0B -，()1,0,0C ，11332B ⎛ ⎝⎭，∴1133,3,2AB ⎛=- ⎝⎭，()1,3,0AB =--，()1,3,0AC =-， 设()1111,,x y z =n 为平面1ABB 的法向量，则1110 0AB AB ⎧⎪⎨⋅⎪=⋅=⎩n n ，即1111130133302x x ⎧⎪⎨-=-+=⎪⎩-，令11y =，得()13,1,1=-n ；设()2222,,x y z =n 为平面1AB C 的法向量，则2210 0AC AB ⎧⎪⎩⋅=⎨⎪⋅=n n ，即2222230133302x x y ⎧⎪⎨+=⎪⎩=， 令21y =，得213,1,3⎫=⎪⎭n ；∴12121213153cos 373759,-++⋅===-⋅⨯n n n n n n∴二面角1B AB C --5474137-．。

教学内容利用向量方法求空间角教学目标1.掌握各种空间角的定义，弄清它们各自的取值范围.2.掌握异面直线所成的角，二面角的平面角，直线与平面所成的角的联系和区别，体会求空间角中的转化思想．重点1.掌握各种空间角的定义，弄清它们各自的取值范围.2.掌握异面直线所成的角，二面角的平面角，直线与平面所成的角的联系和区别，体会求空间角中的转化思想．难点1.掌握各种空间角的定义，弄清它们各自的取值范围.2.掌握异面直线所成的角，二面角的平面角，直线与平面所成的角的联系和区别，体会求空间角中的转化思想．教学准备教学过程自主梳理1．两条异面直线的夹角①定义：设a，b是两条异面直线，在直线a上任取一点作直线a′∥b，则a′与a的夹角叫做a与b的夹角．②范围：两异面直线夹角θ的取值范围是_____________________．③向量求法：设直线a，b的方向向量为a，b，其夹角为φ，则有cos θ＝________＝_______________.2．直线与平面的夹角①定义：直线和平面的夹角，是指直线与它在这个平面内的射影的夹角．②范围：直线和平面夹角θ的取值范围是________________________．③向量求法：设直线l的方向向量为a，平面的法向量为u，直线与平面所成的角为θ，a与u的夹角为φ，则有sin θ＝|cos φ|或cos θ＝sin φ.3．二面角(1)二面角的取值范围是____________．(2)二面角的向量求法：①若AB、CD分别是二面角α—l—β的两个面内与棱l垂直的异面直线，则二面角的大小就是向量AB→与CD→的夹角(如图①)．②设n1，n2分别是二面角α—l—β的两个面α，β的法向量，则向量n1与n2的夹角(或其补角)的大小就是二面角的平面角的大小(如图②③)．自我检测1．已知两平面的法向量分别为m＝(0,1,0)，n＝(0,1,1)，则两平面所成的二面角为________．2．若直线l1，l2的方向向量分别为a＝(2,4，－4)，b＝(－6,9,6)，则l1与l2所成的角等于________．3．若直线l的方向向量与平面α的法向量的夹角等于120°，则直线l与平面α所成的角等于________．4．二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB.已知AB＝4，AC＝6，BD＝8，CD＝217，则该二面角的大小为_______________________________________．5．(2010·铁岭一模)已知直线AB、CD是异面直线，AC⊥CD，BD⊥CD，且AB＝2，CD＝1，则异面直线AB与CD所成的角的大小为________．教学效果分析教学过程探究点一利用向量法求异面直线所成的角例1已知直三棱柱ABC—A1B1C1，∠ACB＝90°，CA＝CB＝CC1，D为B1C1的中点，求异面直线BD和A1C所成角的余弦值．变式迁移1如图所示，在棱长为a的正方体ABCD—A1B1C1D1中，求异面直线BA1和AC所成的角．探究点二利用向量法求直线与平面所成的角例2如图，已知平面ABCD⊥平面DCEF，M，N分别为AB，DF的中点，求直线MN与平面DCEF所成的角的正弦值．变式迁移2如图所示，在几何体ABCDE中，△ABC是等腰直角三角形，∠ABC＝90°，BE和CD都垂直于平面ABC，且BE＝AB＝2，CD＝1，点F是AE的中点．求AB与平面BDF所成的角的正弦值．教学效果分析教学过程探究点三利用向量法求二面角例3如图，ABCD是直角梯形，∠BAD＝90°，SA⊥平面ABCD，SA＝BC＝BA＝1，AD＝12，求面SCD与面SBA所成角的余弦值大小．变式迁移3如图，在三棱锥S—ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC＝90°，O为BC中点．(1)证明：SO⊥平面ABC；(2)求二面角A—SC—B的余弦值．探究点四综合应用例4如图所示，在三棱锥A—BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD＝3，BD＝CD＝1，另一个侧面ABC是正三角形．(1)求证：AD⊥BC；(2)求二面角B－AC－D的余弦值；(3)在线段AC上是否存在一点E，使ED与面BCD成30°角？若存在，确定点E的位置；若不存在，说明理由．教学效果分析教学过程变式迁移4 (2011·山东，19)在如图所示的几何体中，四边形ABCD为平行四边形，∠ACB＝90°，EA⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC，AB＝2EF.(1)若M是线段AD的中点，求证：GM∥平面ABFE；(2)若AC＝BC＝2AE，求二面角A－BF－C的大小．1．求两异面直线a、b的所成的角θ，需求出它们的方向向量a，b的夹角，则cos θ＝|cos〈a，b〉|.2．求直线l与平面α所成的角θ.可先求出平面α的法向量n与直线l的方向向量a的夹角．则sin θ＝|cos〈n，a〉|.3．求二面角α—l—β的大小θ，可先求出两个平面的法向量n1，n2所成的角．则θ＝〈n1，n2〉或π－〈n1，n2〉．)一、填空题(每小题6分，共48分)1．在正方体ABCD—A1B1C1D1中，M是AB的中点，则sin〈DB1→，CM→〉的值等于________．2．已知长方体ABCD－A1B1C1D1中，AB＝BC＝1，AA1＝2，E是侧棱BB1的中点，则直线AE与平面A1ED1所成的角的大小为________．3．如图，在正四面体ABCD中，E、F分别是BC和AD的中点，则AE与CF所成的角的余弦值为________．教学效果分析教学过程4．(2011·南通模拟) 如图所示，在长方体ABCD—A1B1C1D1中，已知B1C，C1D与上底面A1B1C1D1所成的角分别为60°和45°，则异面直线B1C和C1D所成的余弦值为________．5．P是二面角α—AB—β棱上的一点，分别在α、β平面上引射线PM、PN，如果∠BPM＝∠BPN＝45°，∠MPN＝60°，那么二面角α—AB—β的大小为________．6．(2011·无锡模拟)已知正四棱锥P—ABCD的棱长都相等，侧棱PB、PD的中点分别为M、N，则截面AMN与底面ABCD所成的二面角的余弦值是________．7．如图，P A⊥平面ABC，∠ACB＝90°且P A＝AC＝BC＝a，则异面直线PB与AC所成角的正切值等于________．8．如图，已知正三棱柱ABC—A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD与平面B1DC所成的角的正弦值为________．二、解答题(共42分)9．(14分) 如图所示，AF、DE分别是⊙O、⊙O1的直径，AD与两圆所在的平面均垂直，AD＝8.BC是⊙O的直径，AB＝AC＝6，OE∥AD.(1)求二面角B－AD－F的大小；(2)求直线BD与EF所成的角的余弦值．10．(14分)(2011·大纲全国，19)如图，四棱锥S－ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB＝BC＝2，CD＝SD＝1.(1)证明：SD⊥平面SAB；(2)求AB与平面SBC所成角的正弦值．教学效果分析教学过程11．(14分)(2011·湖北，18)如图，已知正三棱柱ABC－A1B1C1各棱长都是4，E是BC的中点，动点F在侧棱CC1上，且不与点C重合．(1)当CF＝1时，求证：EF⊥A1C；(2)设二面角C－AF－E的大小为θ，求tan θ的最小值．自主梳理1．②⎝⎛⎦⎤0，π2③|cos φ|⎪⎪⎪⎪a·b|a|·|b| 2.②⎣⎡⎦⎤0，π2 3.(1)[0，π]教学效果分析自我检测 1．45°或135° 2.90° 3.30° 4.60° 5.60° 课堂活动区例1 解题导引 (1)求异面直线所成的角，用向量法比较简单，若用基向量法求解，则必须选好空间的一组基向量，若用坐标求解，则一定要将每个点的坐标写正确．(2)用异面直线方向向量求两异面直线夹角时，应注意异面直线所成的角的范围是⎝⎛⎦⎤0，π2 解如图所示，以C 为原点，直线CA 、CB 、CC 1分别为x 轴、y 轴、z 轴建立空间直角坐标系．设CA ＝CB ＝CC 1＝2，则A 1(2,0,2)，C (0,0,0)，B (0,2,0)，D (0,1,2)， ∴BD →＝(0，－1,2)，A 1C →＝(－2,0，－2)，∴cos 〈BD →，A 1C →〉＝BD →·A 1C →|BD →||A 1C →|＝－105.∴异面直线BD 与A 1C 所成角的余弦值为105.变式迁移1 解 ∵BA 1→＝BA →＋BB 1→，AC →＝AB →＋BC →， ∴BA 1→·AC →＝(BA →＋BB 1→)·(AB →＋BC →) ＝BA →·AB →＋BA →·BC →＋BB 1→·AB →＋BB 1→·BC →. ∵AB ⊥BC ，BB 1⊥AB ，BB 1⊥BC ， ∴BA →·BC →＝0，BB 1→·AB →＝0， BB 1→·BC →＝0，BA →·AB →＝－a 2， ∴BA 1→·AC →＝－a 2. 又BA 1→·AC →＝|BA 1→|·|AC →|·cos 〈BA 1→，AC →〉，∴cos 〈BA 1→，AC →〉＝－a 22a ×2a ＝－12.∴〈BA 1→，AC →〉＝120°.∴异面直线BA 1与AC 所成的角为60°.例2 解题导引 在用向量法求直线OP 与α所成的角(O ∈α)时，一般有两种途径：一是直接求〈OP →，OP ′→〉，其中OP ′为斜线OP 在平面α内的射影；二是通过求〈n ，OP →〉进而转化求解，其中n 为平面α的法向量．解设正方形ABCD ，DCEF 的边长为2，以D 为坐标原点，分别以射线DC ，DF ，DA 为x ，y ，z 轴正半轴建立空间直角坐标系如图．则M (1,0,2)，N (0,1,0)，可得MN →＝(－1,1，－2)．又DA →＝(0,0,2)为平面DCEF 的法向量，可得cos 〈MN →，DA →〉＝MN →·DA →|MN →||DA →|＝－63.所以MN 与平面DCEF 所成的角的正弦值为|cos 〈MN →，DA →〉|＝63.变式迁移2 解 以点B 为原点，BA 、BC 、BE 所在的直线分别为x ，y ，z 轴，建立如图所示的空间直角坐标系，则B (0,0,0)，A (2,0,0)，C (0,2,0)，D (0,2,1)，E (0,0,2)，F (1,0,1)． ∴BD →＝(0,2,1)，DF →＝(1，－2,0)． 设平面BDF 的一个法向量为 n ＝(2，a ，b )，∵n ⊥DF →，n ⊥BD →， ∴⎩⎪⎨⎪⎧n ·DF →＝0，n ·BD →＝0.即⎩⎪⎨⎪⎧(2，a ，b )·(1，－2，0)＝0，(2，a ，b )·(0，2，1)＝0. 解得a ＝1，b ＝－2.∴n ＝(2,1，－2)． 设AB 与平面BDF 所成的角为θ，则法向量n 与BA →的夹角为π2－θ，∴cos ⎝⎛⎭⎫π2－θ＝BA →·n |BA →||n |＝(2，0，0)·(2，1，－2)2×3＝23， 即sin θ＝23，故AB 与平面BDF 所成的角的正弦值为23.例3 解题导引 图中面SCD 与面SBA 所成的二面角没有明显的公共棱，考虑到易于建系，从而借助平面的法向量来求解．解建系如图，则A (0,0,0)， D ⎝⎛⎭⎫12，0，0，C (1,1,0)， B (0，1,0)，S (0,0,1)， ∴AS →＝(0,0,1)，SC →＝(1,1，－1)，SD →＝⎝⎛⎭⎫12，0，－1，AB →＝(0,1,0)，AD →＝⎝⎛⎭⎫12，0，0. ∴AD →·AS →＝0，AD →·AB →＝0. ∴AD →是面SAB 的法向量，设平面SCD 的法向量为n ＝(x ，y ，z )，则有n ·SC →＝0且n ·SD →＝0.即⎩⎪⎨⎪⎧x ＋y －z ＝0，12x －z ＝0.令z ＝1，则x ＝2，y ＝－1.∴n ＝(2，－1,1)．∴cos 〈n ，AD →〉＝n ·AD →|n ||AD →|＝2×126×12＝63.故面SCD 与面SBA 所成的二面角的余弦值为63. 变式迁移3 (1)证明 由题设AB ＝AC ＝SB ＝SC ＝SA . 连结OA ，△ABC 为等腰直角三角形，所以OA ＝OB ＝OC ＝22SA ， 且AO ⊥BC .又△SBC 为等腰三角形，故SO ⊥BC ，且SO ＝22SA .从而OA 2＋SO 2＝SA 2，所以△SOA 为直角三角形，SO ⊥AO . 又AO ∩BC ＝O ，所以SO ⊥平面ABC . (2)解以O 为坐标原点，射线OB 、OA 、OS 分别为x 轴、y 轴、z 轴的正半轴，建立如图的空间直角坐标系O －xyz ，如图．设B (1,0,0)，则C (－1,0,0)， A (0,1,0)，S (0,0,1)．SC 的中点M ⎝⎛⎭⎫－12，0，12， MO →＝⎝⎛⎭⎫12，0，－12，MA →＝⎝⎛⎭⎫12，1，－12， SC →＝(－1,0，－1)， ∴MO →·SC →＝0，MA →·SC →＝0.故MO ⊥SC ，MA ⊥SC ，〈MO →，MA →〉等于二面角A —SC —B 的平面角．cos 〈MO →，MA →〉＝MO →·MA →|MO →||MA →|＝33，所以二面角A —SC —B 的余弦值为33.例4 解题导引 立体几何中开放性问题的解决方式往往是通过假设，借助空间向量建立方程，进行求解．(1)证明作AH ⊥面BCD 于H ，连结BH 、CH 、DH ，则四边形BHCD 是正方形，且AH ＝1，将其补形为如图所示正方体．以D 为原点，建立如图所示空间直角坐标系．则B (1,0,0)，C (0,1,0)，A (1,1,1)． BC →＝(－1,1,0)，DA →＝(1,1,1)， ∴BC →·DA →＝0，则BC ⊥AD .(2)解 设平面ABC 的法向量为n 1＝(x ，y ，z )，则由n 1⊥BC →知：n 1·BC →＝－x ＋y ＝0，同理由n 1⊥AC →知：n 1·AC →＝－x －z ＝0， 可取n 1＝(1,1，－1)，同理，可求得平面ACD 的一个法向量为n 2＝(1,0，－1)． 由图可以看出，二面角B －AC －D 即为〈n 1，n 2〉，∴cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝1＋0＋13×2＝63.即二面角B －AC －D 的余弦值为63. (3)解 设E (x ，y ，z )是线段AC 上一点， 则x ＝z >0，y ＝1，平面BCD 的一个法向量为n ＝(0,0,1)，DE →＝(x,1，x )，要使ED 与平面BCD 成30°角，由图可知DE →与n 的夹角为60°，所以cos 〈DE →，n 〉＝DE →·n |DE →||n |＝x 1＋2x 2 ＝cos 60°＝12.则2x ＝1＋2x 2，解得x ＝22，则CE ＝2x ＝1.故线段AC 上存在E 点，且CE ＝1时，ED 与面BCD 成30°. 变式迁移4(1)证明 方法一 因为EF ∥AB ，FG ∥BC ，EG ∥AC ，∠ACB ＝90°， 所以∠EGF ＝90°， △ABC ∽△EFG . 由于AB ＝2EF ， 因此BC ＝2FG . 连结AF ，由于FG ∥BC ，FG ＝12BC ，在▱ABCD 中，M 是线段AD 的中点，则AM ∥BC ，且AM ＝12BC ，因此FG ∥AM 且FG ＝AM ，所以四边形AFGM 为平行四边形， 因此GM ∥F A .又F A ⊂平面ABFE ，GM ⊄平面ABFE ，方法二 因为EF ∥AB ，FG ∥BC ，EG ∥AC ，∠ACB ＝90°， 所以∠EGF ＝90°， △ABC ∽△EFG . 由于AB ＝2EF ， 所以BC ＝2FG .取BC 的中点N ，连结GN ，因此四边形BNGF 为平行四边形， 所以GN ∥FB .在▱ABCD 中，M 是线段AD 的中点，连结MN ， 则MN ∥AB .因为MN ∩GN ＝N ， 所以平面GMN ∥平面ABFE .又GM ⊂平面GMN ，所以GM ∥平面ABFE .(2)解 方法一 因为∠ACB ＝90°，所以∠CAD ＝90°. 又EA ⊥平面ABCD ，所以AC ，AD ，AE 两两垂直．分别以AC ，AD ，AE 所在直线为x 轴，y 轴和z 轴，建立如图所示的空间直角坐标系，不妨设AC ＝BC ＝2AE ＝2，则由题意得A (0,0,0)，B (2，－2,0)，C (2,0,0)，E (0,0,1)，所以AB →＝(2，－2,0)，BC →＝(0,2,0)．又EF ＝12AB ，所以F (1，－1,1)，BF →＝(－1,1,1)．设平面BFC 的法向量为m ＝(x 1，y 1，z 1)，则m ·BC →＝0，m ·BF →＝0，所以⎩⎪⎨⎪⎧y 1＝0，x 1＝z 1，取z 1＝1，得x 1＝1，所以m ＝(1,0,1)．设平面向量ABF 的法向量为n ＝(x 2，y 2，z 2)，则n ·AB →＝0，n ·BF →＝0，所以⎩⎪⎨⎪⎧x 2＝y 2，z 2＝0，取y 2＝1，得x 2＝1.则n ＝(1,1,0)．所以cos 〈m ，n 〉＝m ·n |m |·|n |＝12.因此二面角A －BF －C 的大小为60°.方法二 由题意知，平面ABFE ⊥平面ABCD . 取AB 的中点H ，连结CH . 因为AC ＝BC ， 所以CH ⊥AB ，过H 向BF 引垂线交BF 于R ，连结CR ，则CR ⊥BF ， 所以∠HRC 为二面角A －BF －C 的平面角． 由题意，不妨设AC ＝BC ＝2AE ＝2，在直角梯形ABFE 中，连结FH ，则FH ⊥AB . 又AB ＝22，所以HF ＝AE ＝1，BH ＝2，因此在Rt △BHF 中，HR ＝63.由于CH ＝12AB ＝2，所以在Rt △CHR 中，tan ∠HRC ＝263＝ 3.因此二面角A －BF －C 的大小为60°. 课后练习区 1.21015 2．90°解析 ∵E 是BB 1的中点且AA 1＝2，AB ＝BC ＝1， ∴∠AEA 1＝90°，又在长方体ABCD －A 1B 1C 1D 1中， A 1D 1⊥平面ABB 1A 1，∴A 1D 1⊥AE ，∴AE ⊥平面A 1ED 1. ∴AE 与面A 1ED 1所成的角为90°. 3.23解析 设四面体的棱长为a ， AB →＝p ，AC →＝q ，AD →＝r ，则AE →＝12(p ＋q )，CF →＝12(r －2q )．∴AE →·CF →＝－12a 2.又|AE →|＝|CF →|＝32a ，∴cos 〈AE →，CF →〉＝AE →，CF →|AE →|·|CF →|＝－23.即AE 和CF 所成角的余弦值为23.4.64 5．90° 解析不妨设PM ＝a ，PN ＝b ，作ME ⊥AB 于E ，NF ⊥AB 于F ， 如图：∵∠EPM ＝∠FPN ＝45°，∴PE ＝22a ，PF ＝22b ，∴EM →·FN →＝(PM →－PE →)·(PN →－PF →) ＝PM →·PN →－PM →·PF →－PE →·PN →＋PE →·PF →＝ab cos 60°－a ×22b cos 45°－22ab cos 45°＋22a ×22b＝ab 2－ab 2－ab 2＋ab2＝0， ∴EM →⊥FN →，∴二面角α—AB —β的大小为90°. 6.255解析 如图建立空间直角坐标系，设正四棱锥的棱长为2，则PB ＝2，OB ＝1，OP ＝1. ∴B (1,0,0)，D (－1,0,0)， A (0,1,0)，P (0,0,1)， M ⎝⎛⎭⎫12，0，12， N ⎝⎛⎭⎫－12，0，12， AM →＝⎝⎛⎭⎫12，－1，12， AN →＝⎝⎛⎭⎫－12，－1，12， 设平面AMN 的法向量为n 1＝(x ，y ，z )，由⎩⎨⎧n ·AM →＝12x －y ＋12z ＝0，n ·AN →＝－12x －y ＋12z ＝0，解得x ＝0，z ＝2y ，不妨令z ＝2，则y ＝1.∴n 1＝(0,1,2)，平面ABCD 的法向量n 2＝(0,0,1)，则cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝25＝255.7. 2解析 PB →＝P A →＋AB →，故PB →·AC →＝(P A →＋AB →)·AC →＝P A →·AC →＋AB →·AC →＝0＋a ×2a ×cos 45°＝a 2.又|PB →|＝3a ，|AC →|＝a .∴cos 〈PB →，AC →〉＝33，sin 〈PB →，AC →〉＝63，∴tan 〈PB →，AC →〉＝ 2. 8.45解析 不妨设正三棱柱ABC —A 1B 1C 1的棱长为2，建立如图所示的空间直角坐标系，则C (0,0,0)，A (3，－1,0)，B 1(3，1,2)，D ⎝⎛⎭⎫32，－12，2.则CD →＝⎝⎛⎭⎫32，－12，2，CB 1→＝(3，1,2)，设平面B 1DC 的法向量为 n ＝(x ，y,1)，由⎩⎪⎨⎪⎧n ·CD →＝0，n ·CB 1→＝0，解得n ＝(－3，1,1)．又∵DA →＝⎝⎛⎭⎫32，－12，－2，∴sin θ＝|cos 〈DA →，n 〉|＝45.9．解 (1)∵AD 与两圆所在的平面均垂直， ∴AD ⊥AB ，AD ⊥AF ，故∠BAF 是二面角B —AD —F 的平面角．(2分) 依题意可知，ABFC 是正方形，∴∠BAF ＝45°. 即二面角B —AD —F 的大小为45°.(5分)(2)以O 为原点，CB 、AF 、OE 所在直线为坐标轴，建立空间直角坐标系(如图所示)，则O (0,0,0)，A (0，－3 2，0)，B (3 2，0,0)，D (0，－3 2，8)，E (0,0,8)，F (0,3 2，0)，(8分)∴BD →＝(－3 2，－3 2，8)， EF →＝(0,3 2，－8)．cos 〈BD →，EF →〉＝BD →·EF →|BD →||EF →|＝0－18－64100×82＝－8210.(12分)设异面直线BD 与EF 所成角为α，则cos α＝|cos 〈BD →，EF →〉|＝8210.即直线BD 与EF 所成的角的余弦值为8210.(14分) 10.方法一 (1)证明 取AB 中点E ，连结DE ，则四边形BCDE 为矩形，DE ＝CB ＝2，连结SE ，则SE ⊥AB ，SE ＝ 3.又SD ＝1，故ED 2＝SE 2＋SD 2，所以∠DSE 为直角，即SD ⊥SE .(4分) 由AB ⊥DE ，AB ⊥SE ，DE ∩SE ＝E ， 得AB ⊥平面SDE ， 所以AB ⊥SD .由SD 与两条相交直线AB 、SE 都垂直，所以SD ⊥平面SAB .(7分)(2)解 由AB ⊥平面SDE 知，平面ABCD ⊥平面SDE .(10分)作SF ⊥DE ，垂足为F ，则SF ⊥平面ABCD ，SF ＝SD ·SE DE ＝32.作FG ⊥BC ，垂足为G ，则FG ＝DC ＝1. 连结SG ，又BC ⊥FG ，BC ⊥SF ，SF ∩FG ＝F ， 故BC ⊥平面SFG ，平面SBC ⊥平面SFG . 作FH ⊥SG ，H 为垂足，则FH ⊥平面SBC .FH ＝SF ·FG SG ＝37，则F 到平面SBC 的距离为217.由于ED ∥BC ，所以ED ∥平面SBC ，E 到平面SBC 的距离d 为217.(12分)设AB 与平面SBC 所成的角为α，则sin α＝d EB ＝217，即AB 与平面SBC 所成的角的正弦值为217.(14分)方法二 以C 为坐标原点，射线CD 为x 轴正半轴，建立如图所示的空间直角坐标系C －xyz .设D (1,0,0)，则A (2,2,0)、B (0,2,0)．(2分) 又设S (x ，y ，z )，则x >0，y >0，z >0.(1)证明 AS →＝(x －2，y －2，z )，BS →＝(x ，y －2，z )， DS →＝(x －1，y ，z )， 由|AS →|＝|BS →|得(x －2)2＋(y －2)2＋z 2＝x 2＋(y －2)2＋z 2， 故x ＝1. 由|DS →|＝1得y 2＋z 2＝1.①又由|BS →|＝2得x 2＋(y －2)2＋z 2＝4， 即y 2＋z 2－4y ＋1＝0.②联立①②得⎩⎨⎧y ＝12，z ＝32.(4分)于是S (1，12，32)，AS →＝(－1，－32，32)，BS →＝(1，－32，32)，DS →＝(0，12，32)．因为DS →·AS →＝0，DS →·BS →＝0， 故DS ⊥AS ，DS ⊥BS .又AS ∩BS ＝S ，所以SD ⊥平面SAB .(7分) (2)解 设平面SBC 的法向量a ＝(m ，n ，p )，则a ⊥BS →，a ⊥CB →，a ·BS →＝0，a ·CB →＝0.又BS →＝(1，－32，32)，CB →＝(0,2,0)，故⎩⎪⎨⎪⎧m －32n ＋32p ＝0，2n ＝0.取p ＝2得a ＝(－3，0,2)．(10分) 又AB →＝(－2,0,0)，cos 〈AB →，a 〉＝|AB →·a ||AB →||a |＝217，所以AB 与平面SBC 所成角的正弦值为217.(14分) 11．(1)证明 建立如图所示的空间直角坐标系，则由已知可得A (0,0,0)，B (23，2,0)，C (0,4,0)，A 1(0,0,4)，E (3，3,0)，F (0,4,1)．(2分)于是CA 1→＝(0，－4,4)， EF →＝(－3，1,1)． 则CA 1→·EF →＝(0，－4,4)·(－3，1,1)＝0－4＋4＝0， 故EF ⊥A 1C .(8分)(2)解 设CF ＝λ(0<λ≤4)，平面AEF 的一个法向量为m ＝(x ，y ，z )， 则由(1)得F (0,4，λ)．(8分) AE →＝(3，3,0)，AF →＝(0,4，λ)，于是由m ⊥AE →，m ⊥AF →可得⎩⎪⎨⎪⎧m ·AE →＝0，m ·AF →＝0，即⎩⎨⎧3x ＋3y ＝0，4y ＋λz ＝0.取m ＝(3λ，－λ，4)．又由直三棱柱的性质可取侧面AC 1的一个法向量为n ＝(1,0,0)，于是由θ的锐角可得cos θ＝|m ·n ||m |·|n |＝3λ2λ2＋4，sin θ＝λ2＋162λ2＋4，所以tan θ＝λ2＋163λ＝13＋163λ2.(10分) 由0<λ≤4，得1λ≥14，即tan θ≥13＋13＝63. 故当λ＝4，即点F 与点C 1重合时，tan θ取得最小值63.(14分)。

专题一：利用空间向量求夹角专题正阳一高二年级数学组一、求异面直线所成的角分别在直线n m ,上取两个定向量,,b a则异面直线n m ,所成的角β等于向量ba ,所成的角或其补角θ，则||c o s c o s ||||ab a b βθ⋅==⋅特殊情形：0a ba b ⊥⇔=, 即异面直线a 垂直于b 。

评注：应用空间向量法解此类题避开了作平移及复杂的逻辑推理，只须求出异面直线所在的向量坐标，应用向量内积即可求夹角，然后利用公式求解异面直线所成的角。

【例1】如图，正方体ABCD —A 1B 1C 1D 1中，求异面直线AC 与BC 1的夹角二、求直线与平面所成的角特殊情形：当(0)a n R λλλ=∈≠ 且，则直线a 与平面α垂直。

一般情形：在直线L 上取定AB （或与直线Ｌ共线的a ），求平面α的法向量n （如图所示），再求c o s ||||A B nA B n θ⋅=⋅ 则 s i n c o s βθ==1||c o s ||||A B n A B n θ⋅=⋅注：,A B n θ〈〉= ，1,B A n θ〈〉= 且 1180θθ+=评注：求线面角关键在于：找到平面的一个法向量，法向量与直线所在的向量夹角的互余的角，即为所求的角。

（如何求平面的一个法向量）:例2: 如图，在正方体ABCD-A 1B !C 1D 1中G 、E 、F 分别 为AA 1、AB 、BC 的中点，求平面GEF 的法向量。

解：以D 为原点建立右手空间直角坐标系，则E(1，21,0) 、F(21，1,0) 、 G(1,0，21)由此得:)21,21,0(-=)021,21(-=FE设平面的法向量为),,(z y x n = 由n ⊥GE 及n ⊥FE 可得⎪⎪⎩⎪⎪⎨⎧=-=∙=-=∙021*******y x FE n z y ⎩⎨⎧==⇒yz y x 令y=1取平面的一个法向量为)1,1,1(=评析 因为平面的法向量有无数个，方向可上可下，模可大可小，我们只要求出平面的某一个法向量（教简单的）即可。

利用空间向量求夹角1．利用面面垂直建系例1：在如图所示的多面体中，平面11ABB A ⊥平面ABCD ，四边形11ABB A 为边长为2的菱形，ABCD 为直角梯形，四边形11BCC B 为平行四边形，且AB CD ∥，AB BC ⊥，1CD =．（1）若E ，F 分别为11AC ，1BC 的中点，求证：EF ⊥平面11AB C ； （2）若160A AB ∠=︒，1AC 与平面ABCD 所成角的正弦值为，求二面角11A AC D --的余弦值．【答案】（1）见解析；（2 【解析】（1）连接1A B ，∵四边形11ABB A 为菱形，∴11A B AB ⊥．∵平面11ABB A ⊥平面ABCD ，平面11ABB BA I 平面ABCD AB =，BC ⊂平面ABCD ，AB BC ⊥，∴BC ⊥平面11ABB A ．又1A B ⊂平面11ABB A ，∴1A B BC ⊥． ∵11BC B C ∥，∴111A B B C ⊥．∵1111B C AB B =，∴1A B ⊥平面11AB C ．∵,E F 分别为11AC ，1BC 的中点，∴1EF A B ∥，∴EF ⊥平面11AB C ． （2）设11B C a =，由（1）得11B C ⊥平面11ABB A ，由160A AB ∠=︒，2BA =，得过点1C 作1C M DC ⊥，与DC 的延长线交于点M ，取AB 的中点H ，连接1A H ，AM ，如图所示，又160A AB ∠=︒，∴1ABA △为等边三角形，∴1A H AB ⊥， 又平面11ABB A ⊥平面ABCD ，平面11ABB A 平面ABCD AB =，1A H ⊂平面11ABB A ，故1A H ⊥平面ABCD ．∵11BCC B 为平行四边形，∴11CC BB ∥，∴1CC ∥平面11AA BB ． 又∵CD AB ∥，∴CD ∥平面11AA BB ．∵1CC CD C =I ，∴平面11AA BB ∥平面1DC M ．由（1），得BC ⊥平面11AA BB ，∴BC ⊥平面1DC M ，∴1BC C M ⊥．∵BC DC C =I ，∴1C M ⊥平面ABCD ，∴1C AM ∠是1AC 与平面ABCD 所成角． ∵11A B AB ∥，11C B CB ∥，∴11A B ∥平面ABCD ，11B C ∥平面ABCD ，∵11111A B C B B =I ， ∴平面ABCD ∥平面111A B C ．在梯形ABCD 中，易证DE AB ⊥，分别以HA uu u v ，HD uuu v ，1HA uuuv 的正方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系．则()1,0,0A ，，()1,0,0B -，，及11BB CC =u u u v u u u v ，得设平面1ADC 的一个法向量为()111,,x y z =m ，由10AC AD ⎧⎪⎨⎪⎩⋅=⋅=uuu vuuu vm m 得令11y =，得()3,1,2=m设平面11AA C 的一个法向量为()222,,x y z =n ，由1100AC AA ⎧⋅=⋅=⎪⎨⎪⎩uuuvuuu vn n 得 令21z =，得又∵二面角11A AC D --是钝角，∴二面角11A AC D --的余弦值是2．线段上的动点问题例2：如图，在ABCD Y 中，30A ∠=︒，，2AB =，沿BD 将ABD △翻折到A BD '△的位置，使平面A BC '⊥平面A BD '． （1）求证：A D '⊥平面BCD ；（2）若在线段A C '上有一点M 满足A M A C λ=''uuuu v uuu v，且二面角M BD C --的大小为60︒， 求λ的值．【答案】（1）见解析；（2． 【解析】（1）ABD △中，由余弦定理，可得1BD =．∴222BD AD AB +=，∴90ADB ∠=︒，∴90DBC ∠=︒．作D F AB⊥'于点F ， ∵平面A BC '⊥平面A BD '，平面A BC 'I 平面ABDAB '='，∴DF ⊥平面A BC '． ∵CB ⊂平面A BC '，∴DF BC ⊥．又∵CB BD ⊥，BD DF D =I ，∴CB ⊥平面A DB '． 又∵A D '⊂平面A DB '，∴CB A D ⊥'．又ADBD '⊥，BD CB B =I ，∴A D '⊥平面BCD ． （2）由（1）知DA ，DB ，DA '两两垂直，以D 为原点，以DA uu u v方向为x 轴正方向建立如图所示空间直角坐标系D xyz -，则()0,1,0B ，．设(),,M x y z ，设平面MDB 的一个法向量为(),,a b c =m ，取()11,0,a c λλλλ=-⇒=⇒=-m ．平面CBD 的一个法向量可取∵[]0,1λ∈，∴3．翻折类问题例3：如图1，在边长为2的正方形ABCD 中，P 为CD 中点，分别将PAD △，PBC △沿PA ，PB 所在直线折叠，使点C 与点D 重合于点O ，如图2．在三棱锥P OAB -中，E 为PB 中点． （1）求证：PO AB ⊥；（2）求直线BP 与平面POA 所成角的正弦值； （3）求二面角P AO E --的大小．【答案】（1）见解析；（2；（3 【解析】（1）在正方形ABCD 中，P 为CD 中点，PD AD ⊥，PC BC ⊥， ∴在三棱锥P OAB -中，PO OA ⊥，PO OB ⊥．∵OA OB O =I ，∴PO ⊥平面OAB ． ∵AB ⊂平面OAB ，∴PO AB ⊥．（2）取AB 中点F ，连接OF ，取AO 中点M ，连接BM ． 过点O 作AB 的平行线OG ．∵PO ⊥平面OAB ，∴PO OF ⊥，PO OG ⊥．∵OA OB =，F 为AB 的中点，∴OF AB ⊥．∴OF OG ⊥． 如图所示，建立空间直角坐标系O xyz -．()A ，()B -，()0,0,1P ，12M ⎛⎫⎪ ⎪⎝⎭．∵BO BA =，M 为OA 的中点，∴BM OA ⊥．∵PO ⊥平面OAB ，PO ⊂平面POA ，∴平面POA ⊥平面OAB ．∵平面POA I 平面OAB OA =，BM ⊂平面OAB ，∴BM ⊥平面POA∴平面POA的法向量)1,0=-m设直线BP 与平面POA 所成角为α∴直线BP 与平面POA．（3）由（2设平面OAE 的法向量为n ，则有0 0OA OE ⋅⎧⎪=⎪⎩=⎨⋅uu vuu u v n n 即 令1y =-，则由题知二面角P AO E --一、单选题1．如图，在所有棱长均为a 的直三棱柱111ABC A B C -中，D ，E 分别为1BB ，11AC 的中点，则异面直线AD ，CE 所成角的余弦值为（ ）对点增分集训A ．12BC ．15D ．45【答案】C【解析】设AC 的中点O ，以OB uu u v ，OC uuu v ，OE uu u v为x ，y ，z 轴建立坐标系， 则0,,02a A ⎛⎫ ⎪⎝⎭，,0,2a D ⎫⎪⎪⎝⎭，0,,02a C ⎛⎫⎪⎝⎭，()0,0,E a ，则,,22a a AD ⎫=⎪⎪⎝⎭uuu v ，0,,2a CE a ⎛⎫=- ⎪⎝⎭uu u v ，设AD 与CE 成的角为θ，则01cos 5a a aaθ-⨯+⨯==，故选C ． 2．在三棱柱111ABC A B C -中，底面是边长为1的正三角形，侧棱1AA ⊥底面ABC ，点D 在棱1BB 上，且1BD =，若AD 与平面11AA C C 所成的角为α，则sin α的值是（ ） ABCD【答案】D【解析】如图，建立空间直角坐标系，易求点1,12D ⎫⎪⎪⎝⎭．平面11AA C C 的一个法向量是()1,0,0=n，∴cos ,AD ===uuu v nsin α=．故选D ．3．如图，圆锥的底面直径2AB =，高OC =D 为底面圆周上的一点，120AOD ∠=︒，则空间中两条直线AD 与BC 所成的角为（ ）A ．30︒B ．60︒C ．75︒D ．90︒【答案】B【解析】取AB 中点E ，以O 为原点，OE 为x 轴，OB 为y 轴，OC 为z 轴，建立空间直角坐标系， 如图所示，∵圆锥的底面直径2AB =，高OC =D 为底面圆周上的一点，120AOD ∠=︒，∴可得()0,1,0A -，()0,1,0B，(C，1,02D ⎫⎪⎪⎝⎭，则3,,02AD ⎫=⎪⎪⎝⎭uuu v，(0,BC =-uu u v，设空间两条直线AD 与BC 所成的角为θ，∴31cos 2AD BC AD BCθ⋅===⋅u uuu v uu u u v v u uu u v ， ∴60θ=︒，即直线AD 与BC 所成的角为60︒，故选B ．4．已知四棱锥P ABCD -的底面ABCD 是边长为2的正方形，PA PD ==，平面ABCD ⊥平面PAD ，M 是PC 的中点，O 是AD 的中点，则直线BM 与平面PCO 所成角的正弦值是（ ）ABCD【答案】D【解析】由题可知()0,0,0O ，()0,0,2P ，()1,2,0B ，()1,2,0C -，则()0,0,2OP =u u u v ，()1,2,0OC =-u u u v，∵M 是PC 的中点，∴1,1,12M ⎛⎫- ⎪⎝⎭，3,1,12BM ⎛⎫=-- ⎪⎝⎭uuu v设平面PCO 的法向量(),,x y z =n ，直线BM 与平面PCO 所成角为θ， 则20 20OP z OC x y ⋅==⋅=-⎧⎪⎨⎪=⎩+uu u vuuu v n n 可取()2,1,0=n，sin cos BM BM BM θ⋅===⋅uuu vuuu v uuu v ，n n n，故选D ．5．如图，在直三棱柱111ABC A B C -中，90BAC ∠=︒，12AB AC AA ===，点G 与E 分别是11A B 和1CC 的中点，点D 与F 分别是AC 和AB 上的动点．若GD EF ⊥，则线段DF 长度的最小值为（ ）A B C D ．【答案】A【解析】建立如图所示的空间直角坐标系，则()0,0,0A ，()0,2,1E ，()1,0,2G ，0(),0,F x ，0(0,),D y ，则()1,,2GD y =--u u u v ，(),2,1EF x =--u u u v，由于GD EF ⊥，∴220GD EF x y =--+=⋅u u u v u u u v，∴22x y =-，故DF ===∴当45y =时，线段DF ．故选A ． 6．如图，点A B C 、、分别在空间直角坐标系O xyz -的三条坐标轴上，()0,0,2OC =u u u v，平面ABC 的法向量为()2,1,2=n ，设二面角C AB O --的大小为θ，则cos θ=（ ）A ．43BC ．23D ．23-【答案】C【解析】由题意可知，平面ABO 的一个法向量为：()0,0,2OC =u u u v，由空间向量的结论可得：42cos 233OC OC θ⋅===⋅⋅u u u v u u u vn n ．故选C ． 7．如图所示，五面体ABCDE 中，正ABC △的边长为1，AE ⊥平面ABC ，CD AE ∥，且12CD AE =． 设CE 与平面ABE 所成的角为α，(0)AE k k =>，若ππ,64α⎡⎤∈⎢⎥⎣⎦，则当k 取最大值时，平面BDE 与平面ABC 所成角的正切值为（ ）AB ．1 CD【答案】C【解析】如图所示，建立如图所示的空间直角坐标系O xyz -，则()0,1,0A ，0,0,2k D ⎛⎫ ⎪⎝⎭，()0,1,E k，1,02B ⎫⎪⎪⎝⎭， 取AB 的中点M ，则304M ⎫⎪⎪⎝⎭，，，则平面ABE的一个法向量为3,04CM ⎫=⎪⎪⎝⎭uuu v ，由题意sin CE CM CE CM α⋅==⋅uu u v u uu u u v v uu v uu 又由ππ,64α⎡⎤∈⎢⎥⎣⎦，∴1sin 2α≤=k ≤≤k当k =BDE 的法向量为(),,x y z =n ，则0 102DE y BE y ⎧⎪⎪⎨⎪⎪⋅==⋅++=⎩uuu v uu u v n n ，取(=-n ，由平面ABC 的法向量为()0,0,1=m ， 设平面BDE 和平面ABC 所成的角为θ，则cos θ⋅==⋅n m n m，∴sin θ=，∴tan θ=C ． 8．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 内的射影为ABC △的中心，则1AB 与底面ABC 所成角的正弦值等于（ ）ABCD【答案】B【解析】如图，设1A 在平面ABC 内的射影为O ，以O 为坐标原点，OA 、1OA 分别为x 轴、z 轴建立空间直角坐标系如图．设ABC △边长为1112B ⎛ ⎝⎭，ABC 的法向量为()0,0,1=n ． 设1AB 与底面ABC 所成角为α故直线1AB 与底面ABCB ． 9．如图，四棱锥P ABCD -中，PB ⊥平面ABCD ，底面ABCD 为直角梯形，AD BC ∥，AB BC ⊥，3AB AD PB ===，点E 在棱PA 上，且2PE EA =，则平面ABE 与平面BED 的夹角的余弦值为（ ）ABCD【答案】B【解析】以B 为坐标原点，以BC 、BA 、BP 所在直线为x 、y 、z 轴， 建立空间直角坐标系，则()0,0,0B ，()0,3,0A ，()0,0,3P ，()3,3,0D ，()0,2,1E ，∴()0,2,1BE =u u u v ，()3,3,0BD =u u u v设平面BED 的一个法向量为(),,x y z =n ，则20330BE y z BD x y ⎧⎪⎨⎪⋅=+=⋅=+=⎩uu u v uu u vn n ， 取1z =ABE 的法向量为()1,0,0=m ，ABE 与平面BEDB ．10．在正方体1111ABCD A B C D -中，直线1BC 与平面1A BD 所成角的余弦值为（ ） ABCD【答案】C【解析】分别以DA ，DC ，1DD 为x ，y ，z 轴建立如图所示空间直角坐标系：设正方体的棱长为1，可得()0,0,0D ，()1,1,0B ，()10,1,1C ，()11,0,1A ，∴()11,0,1BC =-u u u r ，()11,0,1A D =--u u u r ，()1,1,0BD =--u u u r ， 设(),,x y z =n 是平面1A BD 的一个法向量，∴10A D BD ⎧⎪⎨⎪⎩⋅=⋅=uuu vuu u vn n ，即0 0x z x y =+=⎧⎨⎩+， 取1x =，得1y z ==-，∴平面1A BD 的一个法向量为()1,1,1=--n ，设直线1BC 与平面1A BD 所成角为θ，∴ ，即直线1BC 与平面1A BD 所成角的余弦值是C ． 11．已知四边形ABCD ，2AB BD DA ===，BC CD =ABD △沿BD 折起，使二面角A BD C --的大小在5,66π⎡π⎤⎢⎥⎣⎦内，则直线AB 与CD 所成角的余弦值取值范围是（ ）A．⎡⎢⎣⎦B．⎡⎢⎣⎦C．5201⎡⎡⎫⎪⎢⎢⎪⎣⎦⎣⎭， D ．⎣⎦【答案】A【解析】取BD 中点O，连结AO ，CO ，∵2AB BD DA ===．BCCD =CO BD ⊥，AO BD ⊥，且1CO =，AO = ∴AOC ∠是二面角A BD C --的平面角， 以O 为原点，OC 为x 轴，OD 为y 轴，过点O 作平面BCD 的垂线为z 轴，建立空间直角坐标系，()0,1,0B -，()1,0,0C ，()0,1,0D ，设二面角A BD C --的平面角为θ，则5,66θπ⎡⎤∈⎢⎥⎣⎦π，连AO 、BO ，则AOC θ∠=，)A θθ，∴)BA θθ=uu r ，()1,1,0CD =-u u u r，设AB 、CD 的夹角为α，则cos AB CD AB CDα⋅==⋅uu u r uu u r uu u r uu u r ， ∵5,66θπ⎡⎤∈⎢⎥⎣⎦π，∴cosθ⎡∈⎢⎣⎦， 故510,2θ⎡⎤∈⎢⎥⎣⎦，∴cos α⎡∈⎢⎣⎦．故选A ．12．正方体1111ABCD A B C D -中，点P 在1A C 上运动（包括端点），则BP 与所成角的取值范围是（ ）A ．ππ,43⎡⎤⎢⎥⎣⎦B ．ππ,42⎡⎤⎢⎥⎣⎦C ．ππ,62⎡⎤⎢⎥⎣⎦D ．ππ,63⎡⎤⎢⎥⎣⎦【答案】D【解析】以点D 为原点，DA 、DC 、1DD 所在直线分别为x y z 、、轴建立空间直角坐标系，设正方体棱长为1，点P 坐标为(),1,x x x -，则()1,,BP x x x =--u u v ，()11,0,1BC =-u u u v，设BP uuv 、1BC uuu v的夹角为α，则11cos BP BC BP BC α⋅==⋅uu v uu uu u v v uuu v∴当13x =时，cos α，π6α=．当1x =时，cos α取最小值12，π3α=．∵11BC AD ∥，∴BP 与1AD 所成角的取值范围是ππ,63⎡⎤⎢⎥⎣⎦．故选D ．二、填空题13．如图，在直三棱柱111ABC A B C -中，12AB BC CC ===，AC =m 是AC的中点，则异面直线1CB 与1C M所成角的余弦值为________．【解析】在直三棱柱111ABC A B C -中，12AB BC CC ===，AC =M 是AC 的中点，∴BM AC ⊥，1BM =．以M 为原点，MA 为x 轴，MB 为y 轴，过M 作AC 的垂线为z 轴， 建立空间直角坐标系，则()C ，()10,1,2B，()12C ，()0,0,0M ，∴)1CB =uuu v，()12MC =uuuu v，设异面直线1CB 与1C M 所成角为θ，则1111cos CB CB MC MC θ⋅===⋅uuu v uuu v uuuu v uuuu v ． ∴异面直线1CB 与1C M． 14．已知四棱锥P ABCD -的底面是菱形，60BAD ∠=︒，PD ⊥平面ABCD ，且PD AB =，点E 是棱AD 的中点，F 在棱PC 上，若:1:2PF FC =，则直线EF 与平面ABCD 所成角的正弦值为__________．【解析】以D 点建立如图所示的空间直角坐标系D xyz -，设菱形ABCD 的边长为2，则()0,0,0D ，1,02E ⎫-⎪⎪⎝⎭，240,,33F ⎛⎫⎪⎝⎭平面ABCD 的一个法向量为()0,0,1=n ，即直线EF 与平面ABCD 所成角的正弦值为15．设a ，b 是直线，α，β是平面，a α⊥，b β⊥，向量1a 在a 上，向量1b 在b 上，()11,1,1=a ，13,(0)4,=-b ，则α，β所成二面角中较小的一个的余弦值为________．【解析】由题意，∵()11,1,1=a ，13,(0)4,=-b ，∴111111cos ,⋅==⋅a b a b a b ， ∵a α⊥，b β⊥，向量1a 在a 上，向量1b 在b 上， ∴α，β16．在四棱锥P ABCD -中，底面ABCD 为平行四边形，PA ⊥平面ABCD ，2AB =，120BAD ∠=︒，PA x =，则当x 变化时，直线PD 与平面PBC 所成角的取值范围是__________．【解析】如图建立空间直角坐标系，得()0,2,0B，3,22C ⎛⎫-⎪ ⎪⎝⎭，3,2D ⎛⎫⎪ ⎪⎝⎭，()0,0,P x ，设平面PBC 的法向量(),,x y z =m ，()0,2,PB x =-u u v， ∴0BC PB ⎧⎪⎨⎪⋅=⋅⎩=uu u vuu v m m ，得三、解答题17．如图所示：四棱锥P ABCD -，底面ABCD 为四边形，AC BD ⊥，BC CD =，PB PD =，平面PAC ⊥平面PBD，AC =30PCA ∠=︒，4PC =，（1）求证：PA ⊥平面ABCD ；（2）若四边形ABCD 中，120BAD ∠=︒，AB BC ⊥是否在PC 上存在一点M ，使得直线BM 与平面PBDPM MC的值，若不存在，请说明理由． 【答案】（1）见解析；（2）存在，1PMMC=．【解析】（1）设AC BD O =I ，连接PO BC CD AC BD =⊥Q ，，O ∴为BD 中点又PB PD =Q ，PO BD ∴⊥平面PAC ⊥平面PBD ，平面PAC I 平面PBD PO =BD ∴⊥平面PAC ，而PA ⊂平面PAC PA BD ∴⊥在PCA △中，由余弦定理得2222cos30PA PC AC PC AC =+-⋅︒，21612244PA =+-⨯⨯=，而222PA AC PC += PA AC PA BD PA BD AC O ⊥⎫⎪∴⊥⇒⊥⎬⎪=⎭平面ABCD ． （2）过A 作AB 垂线记为y 轴，AB 为x 轴，AP 为z 轴建立空间直角坐标系：()0,0,0A ，()0,0,2P，)B，3,02D ⎛⎫⎪ ⎪⎝⎭，)C)2PB =-uu v，3,22PD ⎛⎫=- ⎪ ⎪⎝⎭uu u v ，设PM PM MC MC λλ=⇒=uuu vuuu v uuu v uuu v32,11M λλλ⎫⎪⎪++⎝⎭，32,11BM λλλ⎫=⎪⎪++⎝⎭uuu v 设平面PBD 法向量为(),,x y z =n ，∴200 30202z PB yPD x z =⋅=⇒⎨⋅=+-=⎪⎩⎧⎪⎨⎪⎩uu v uu u v n n，取(2,=n ，设BM 与平面PBD 所成角为ϕ，sin cos BM ϕ=⋅==uuu v n 解1λ=，1PM MC∴=． 18．如图，在斜三棱柱111ABC A B C -中，底面ABC 是边长为2的正三角形，13BB =，1AB160CBB ∠=︒．（1）求证：平面ABC ⊥平面11BCC B ；（2）求二面角1B AB C --的正弦值．【答案】（1）见解析；（2 【解析】（1）取BC 的中点O ，连接OA ，1OB ，∵底面ABC 是边长为2的正三角形，∴OA BC ⊥，且OA∵13BB =，160CBB ∠=︒，1OB =，∴222113213cos607OB =+-⨯⨯⨯︒=， ∴1OB 1AB =2221110OA OB AB +==，∴1OA OB ⊥，又∵1OB BC O =I ，∴OA ⊥平面11BCC B ，又∵OA ⊂平面ABC ， ∴平面ABC ⊥平面11BCC B ．（2）如图所示，以点O 为坐标原点，OC 为x 轴，OA 为y 轴，OH 为z 轴建立空间直角坐标系，其中2BH =，则()A ，()1,0,0B -，()1,0,0C，112B ⎛ ⎝⎭，∴11,2AB ⎛= ⎝⎭uuu v，()1,AB =-uu u v，()1,AC =uuu v ， 设()1111,,x y z =n 为平面1ABB 的法向量，则1110 0AB AB ⎧⎪⎨⋅⎪=⋅=⎩uu u v uuu v n n，即111110 102x x z ⎧⎪⎨-==⎪⎩，令11y =，得()1=n ； 设()2222,,x y z =n 为平面1AB C 的法向量，则2210 0AC AB ⎧⎪⎩⋅=⎨⎪⋅=uuu u v uu v n n，即222220 102x x z ⎧⎪⎨+=⎪⎩=， 令21y =，得213⎫=⎪⎭n；∴121212131cos ,-++⋅===⋅n n n n n n ∴二面角1B AB C --=．。