6 AVO技术
- 格式:doc
- 大小:2.03 MB
- 文档页数:14

AVO分析技术在塔中碳酸盐岩油气检测中的应用鲜强;蔡志东;王祖君;王熊飞;梁国平;吕海清;张磊;靳懿鑫【摘要】The Ordovician strata of west Tazhong area is the weathering karst reservoir connected with unconformity.When reservoirs are filled by brine, oil and shale, the seismic responses of the reservoirs are the "bead-like" reflections, but the AVO responses are different.We analyze seismic, logging and geological data.AVO analysis technique is used to predict the fluids property in this paper.AVO analyzing technology mainly includes two aspects, the forward modeling and inversion modeling.The forward modeling can be used to recognize the AVO response of different fillings property and determine the type of AVO abnormal.Then we can predict different fillings by means of AVO attributes inversion (such as P, G attributes).Ultimately, we can achieve the goal of lower the exploration risk.%塔中西部奥陶系为不整合面相关的岩溶风化壳型油气藏,储层被不同的流体及泥质充填后,储层的地震响应都为"串珠状"反射,储层的AVO响应是不同的.在对地震、测井及地质资料分析的基础上,利用AVO分析技术对其流体属性进行预测.AVO分析技术主要包括正演及反演两个方面,通过正演可以认识到储层充填不同流体的AVO响应,从而确定AVO异常的类型,然后AVO属性反演(P,G等属性)预测不同的流体,最终达到降低勘探风险的目的.【期刊名称】《物探化探计算技术》【年(卷),期】2017(039)002【总页数】6页(P260-265)【关键词】AVO;碳酸盐岩;油气检测;AVO调谐效应【作者】鲜强;蔡志东;王祖君;王熊飞;梁国平;吕海清;张磊;靳懿鑫【作者单位】中国石油东方地球物理公司研究院库尔勒分院,库尔勒 841000;中国石油东方地球物理公司新兴物探开发处,涿州 072750;中国石油东方地球物理公司研究院库尔勒分院,库尔勒 841000;中国石油东方地球物理公司研究院库尔勒分院,库尔勒 841000;中国石油东方地球物理公司研究院库尔勒分院,库尔勒 841000;中国石油东方地球物理公司研究院库尔勒分院,库尔勒 841000;中国石油东方地球物理公司研究院库尔勒分院,库尔勒 841000;中国石油东方地球物理公司新兴物探开发处,涿州 072750【正文语种】中文【中图分类】P631.4AVO译为振幅随偏移距的变化,是继“亮点”技术后又一项烃类检测技术。



AVO正演模型研究分析AVO技术(Amplitude versus offset)即利用地震反射波振幅与炮检距的关系是最近几十年来发展起来的一项新的寻找油气的地震勘探方法,在世界范围内具有广泛的应用。
AVO正演模型研究是AVO技术的重要组成部分,具有重要的作用。
和其他的地震模型方法一样,AVO正演模型的研究有利于设计以AVO研究为目的野外观测系统,选择正确的采集参数;有利于根据正演模型合成的实际地区目的层AVO响应的曲线类型,进行分析,得到目的层含油气的可行性判断;同时在利用AVO技术反演提取地层参数时也要用到AVO正演模型技术。
众所周知模型参数的选择和计算参数的方法是AVO模型分析成败的关键。
本文从经典的Zoeppritz方程出发,首先介绍了以该方程为理论基础所建立的AVO技术的发展和现状,有利于研究AVO技术的发展走向和应用实践。
在理论方面,通过对Zoeppritz方程的推导,揭示出平面波在入射水平面时的情况,重点分析了在地震勘探中使用较为广泛的纵波波源的Zoeppritz方程,在理论模型的基础上,研究分析了纵波入射时的反射系数与入射角的关系,从而实质性的得到了AVO技术的原理。
经典的Zoeppritz方程能够完全的反映出界面两侧的各种转换波的能量分布情况,但是其方程本身过于复杂,同时在地震勘探中以纵波波源为主,为了减少计算量和不必要的参数对正演模拟的影响,本文在前人的基础上,对比分析了几种Zoeppritz方程的近似方程,通过正演模型对各个方程的解进行了拟合。
结果发现,由于各个方程在化简时的侧重不同,所以在不同模型参数条件下的拟合程度也存在差异。
不同的近似方程有着不同的适用范围,同时在模型参数改变时方程的拟合度也会发生改变。
这就说明在进行AVO正演模拟时,对于方程和参数的选择是至关重要的,也是AVO正演模拟的基础和关键。
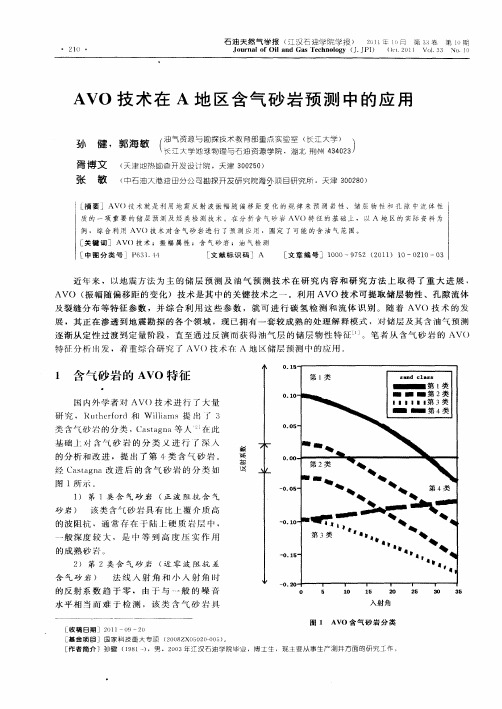
对于模型参数的选择,本文对AVO正演的岩石物理基础进行论述,重点对比了三种含气砂岩的AVO特征,将AVO正演的理论研究与实际工作进行了结合。

反演技术前言一. 反演的概念、目的二. 反演的发展历史及趋势三. 反演的基本方法四. 地震反演难题的解决方案五. 反演的实质六. 反演的基本流程七. AVO反演处理简介前言地震、测井、钻井是石油工作者认识地下地质构造、地层、岩性、物性、含油气性的最重要的信息来源。
虽然测井、钻井仅能提供井孔附近的有关信息,尤其是有关岩性、物性、含油气性的信息,但是这些信息往往具有很高的分辨率,可信度、准确性,能确切地指出含油气层的位置,定量化分析与储层、油藏有关的参数。
然而一个油气田勘探、开发方案的设计、实施、调整仅靠测井、钻井资料是远远不够的,必须与地震资料相结合进行综合分析才能取得良好效果。
地震资料的分辨率虽然远远不及测井、钻井,但是随着地震勘探技术的发展,从光电记录、模拟记录到数字记录,从二维到三维,地震资料的信噪比、分辨率、成像的准确性都获得了极大的提高,由于地震资料包含大量地下地质信息,覆盖面积广,具有三维特性,所以这项技术的使用越来越受到石油工作者的重视,如何利用地震资料研究地下地质构造、地层?如何进行储层预测、油藏描述?如何进行油藏、含油气层的预测?这些问题促使地球物理学家、地质学家开发应用了一系列地震资料特殊处理技术,如地震资料反演技术、地震属性分析技术、AVO 分析技术,这些技术充分利用测井、钻井、地震的长处,使人们对地下储层、油藏的研究从点到面、从二维到三维、从三维可视化研究到油藏动态监测、从定性研究到定量化研究,大大提高了钻探成功率,有效地指导了油田开发,为提高油田最终采收率起到了积极的作用,因此地震技术被列为二十一世纪石油工业发展的首要技术,相信地震资料特殊处理技术(地震资料反演技术、地震属性分析技术、AVO分析技术)也必将在我国油田勘探、开发中起到越来越重要的作用。
一. 反演的概念、目的地震资料反演技术就是充分利用测井、钻井、地质资料提供的丰富的构造、层位、岩性等信息,从常规的地震剖面推导出地下地层的波阻抗、密度、速度、孔隙度、渗透率、沙泥岩百分比、压力等信息。
6 A VO 技术AVO 技术是利用反射系数随入射角变化的原理,在叠前道集上分析振幅随偏移距变化的规律,估求岩石的弹性参数、研究岩性、检测油气的重要技术。
AVO 是振幅随偏移距变化(Amplitude Variation with Offset)的英文缩写或振幅与随偏移距关系(Amplitude Versus Offset) 的英文缩写,AVA 是振幅随入射角变化(Amplitude Variation with Incident Angle)的英文缩写。
在地震勘探中,共中心点道集记录的偏移距可以等价地用入射角表示,故AVO 与AVA 等价。
该技术自20世纪80年代提出以来,在油气勘探中不断发展,并得到迅速推广和广泛应用。
尤其是在天然气勘探中指导寻找天然气藏发挥了重要作用,对提高天然气勘探成功率受到了很好的效果。
从近几年的技术发展情况看,P 波方位AVO 已作为一种预测油气藏各向异性的有效方法而受到青睐。
6.1 A VO 技术的理论基础根据地震波动力学中反射和透射的相关理论,反射系数(或振幅)随入射角的变化与分界面两侧介质的地质参数有关。
这一事实包含两层意思:一是不同的岩性参数组合,反射系数(或振幅)随入射角变化的特性不同,称为AVO 正演方法;二是反射系数(或振幅)随入射角变化本身隐含了岩性参数的信息,利用AVO 关系可以反演岩石的密度、纵波速度和横波速度,称为AVO 反演方法。
6.1.1 Zoeppritz 方程AVO 技术的理论基础就是Zoeppritz 方程及其简化的思路。
设有两层水平各向同性介质,当地震纵波非垂直入射(即非零偏移距)时,在弹性分界面上会产生反射纵波、反射横波、透射纵波和透射横波,见图6—1。
各种波型之间的运动学关系服从斯奈尔定理22221111sin sin sin sin S P S P V V V V ϕθϕθ=== (6-1)图6—1 入射波、反射波和透射波的关系式中 1θ、1ϕ——纵波、横波的反射角;2θ、2ϕ——纵波、横波的透射角;1P V 、2P V ——反射界面上下介质的纵波速度;1S V 、2S V ——反射界面上下介质的横波速度。
在这种情况下,反射系数的变化与偏移距的变化(或者说与入射角的变化)有关,计算反射系数需要解一个四阶线性矩阵,即Zoeppritz 方程(6-2)式中 PP R 、PS R ——纵波、横波的反射系数;PP T 、PS T ——纵波、横波的透射系数;1ρ、2ρ——反射界面上下介质的密度。
(6-2)式揭示了反射系数(影响反射波振幅的主要因素)与入射角及界面两侧介质的物理性质之间的关系。
当入射角为零(即零偏移距)时,按照斯奈尔定理 02121====ϕϕϑθ, 解Zoeppritz 方程得⎪⎪⎪⎩⎪⎪⎪⎨⎧==+=-=+-=11211221111221122PS PS P P PP PP P P P P PP T R P V V V R T V V V V R ρρρρρρρρ (6-3) 用Zoeppritz 方程计算出的反射系数,与实际观测反射波振幅是有差别的,主要原因是:(1) Zoeppritz 方程描述的是平面波,实际观测的是球面波;(2) Zoeppritz 方程给出的是波沿传播方向的反射系数,这与观测所得反射系数不同;(3) Zoeppritz 方程给出的是两个半无限空间界面的反射(非层状介质),不存在各个界面反射子波的相互干涉;(4) 在Zoeppritz 方程中,振幅是在不考虑诸如透射损失、衰减、球面发散、检波器的方向特性等影响因素下的反射系数的测量值。
由此可见,基于Zoeppritz 方程所求的反射系数的解,不可能作为精确的地震响应,只能是一种近似。
Zoeppritz 方程可以预测任意岩性组合时振幅的变化,但对AVO 分析来说,只对以下三种情况感兴趣:(1) 若波阻抗和S P V V /(或σ)值通过界面时同时减小,或者是同时增大(相同方向变化),则反射系数随入射角增加而增加,见图6—2(a);(2) 若波阻抗和S P V V /(或σ)值通过界面时,一个减小,而另一个增大(不同方向变化),则反射系数随入射角增加而减小,见图6—2(b);(3) 若泊松比σ通过界面时保持不变,则反射系数变化很小,可近似认为几乎保持不变,见图6—2(c)。
图6—2 AVO 响应(纵坐标为反射系数,横坐标为入射角)6.1.2 Zoeppritz 方程的近似方程求解Zoeppritz 方程是非常复杂的,并且难以给出清楚的物理概念。
因此,人们提出了不同形式的近似方程,使其更加容易理解,有较明显的物理意义。
这些近似方程也就成为当前AVO 分析的基础表达式。
1.Aki 和Rechards(1980)的近似方程在大多数情况下,认为相邻两层介质的弹性参数变化较小,即P P V V /∆、S S V V /∆、ρρ/∆和其它值相比为小值,所以可略去它们的高次项,纵波的反射系数近似为S S P S P P P S P V V V V V V V V R ∆-∆+∆⎪⎪⎭⎫ ⎝⎛-≈θθρρθθ2222222sin 42sec sin 4121)( (6-4) 其中P V 、S V 和ρ分别为反射界面两侧介质纵波速度、横波速度和密度的平均值,即221P P P V V V += 221S S S V V V += 221ρρρ+=P V ∆、S V ∆和ρ∆分别为反射界面两侧介质纵波速度、横波速度和密度的差值,即12P P P V V V -=∆12S S S V V V -=∆12ρρρ-=∆θ为纵波入射角与纵波透射角的平均值,即221θθθ+=(6-4)式说明纵波反射系数)(θP R 除了与纵波速度、密度有关外,还与入射角、透射角和横波速度(泊松比σ)有关。
因此,在叠前CDP 道集中,非零炮检距地震道的反射系数(或反射振幅)就包含了横波的信息,故AVO 属性中包含了横波与泊松比的信息。
使用AVO 特征相当于纵、横波联合解释有助于提高油气检测的准确性。
由于θθ221sec tg +=,(6-4)式经整理后变为θρρρρθ22222sin 242121)(⎪⎪⎭⎫ ⎝⎛∆-∆-∆+⎪⎪⎭⎫ ⎝⎛∆+∆≈P S S S P S P P P P P V V V V V V V V V V R )s i n (2122θθ-∆+tg V V PP (6-5) 当上式用2/=S P V V 代入后得到θρρρρθ2sin 22121)(⎪⎪⎭⎫ ⎝⎛∆-∆-∆+⎪⎪⎭⎫ ⎝⎛∆+∆≈S S P P P P P V V V V V V R )sin (2122θθ-∆+tg V V P P (6-6)(6-6)式第一项中不包含横波,即0=θ。
令112211221212121221)0(P P P P P P P P P P P V V V V V V V V V V R P ρρρρρρρρρρ+-≈+-++-=⎪⎪⎭⎫ ⎝⎛∆+∆== (6-7) 这就是垂直入射时的纵波反射系数。
当入射角稍大(0°<≤θ30°)时,应加上第二项,因为此时第三项的-θ2tg 083.0sin 2≤θ,而P P V V /∆又较小,所以可略去。
只有当入射角较大(>θ30°)时, 此时-θ2tg θ2sin 增加较快,不能忽视,必须加上第三项。
因此,当入射角小于30°时,(6-6)式可简化为θρρρρθ2sin 22121)(⎪⎪⎭⎫ ⎝⎛∆-∆-∆+⎪⎪⎭⎫ ⎝⎛∆+∆≈S S P P P P P V V V V V V R (6-8) 令⎪⎪⎭⎫ ⎝⎛∆-∆-∆=ρρS S P P V V V V G 221 (6-9) 此时(6-6)式可写成)(θP R θ2sin G P +≈ (6-10)上式为θ2sin 的线性方程,其中P 是由零炮检距截距构成的地震道,即P 波叠加的地震道,它代表对反射界面两侧的波阻抗变化的响应;由斜率G 构成的地震道称为梯度叠加道,它代表对反射界面两侧的横波速度、纵波速度和密度变化的响应,也是振幅随入射角(或炮检距)的变化率。
2.Shuey(1985)的近似方程现在AVO 分析中常用的是Shuey(1985)的简化方程)sin (2sin ])1([)(2222000θθθσσθ-∆+-∆++≈tg V V R A R R P P P (6-11) 其中 ⎪⎪⎭⎫ ⎝⎛∆+∆=ρρP P V V R 210 σσ-++-=1)21)(1(0B B A ⎪⎪⎭⎫ ⎝⎛∆+∆⎪⎪⎭⎫ ⎝⎛∆=ρρP P P P V V V V B σ和σ∆分别为反射界面两侧介质泊松比的平均值与差值,即221σσσ+=, 12σσσ-=∆(6-11)式和(6-6)式基本相同,表明纵波反射系数由三个近似独立的项组成:(1)法线入射项,同波阻抗差成正比;(2)适中角入射项(0°<≤θ30°),同泊松比差成正比,这个范围是研究振幅随炮检距变化的主要区域;(3)广角入射项(>θ30°),同速度差成正比。
当≤θ30°时,083.0sin 22≤-θθtg ,广角入射项可以忽略,(6-11)式简化为θσσθ22000sin ])1([)(-∆++≈R A R R P θ2sin G P +≈ (6-12) 式中,0R P =为垂直入射时的纵波反射系数;200)1/(σσ-∆+=R A G 为与岩石纵、横波速度和密度有关的项。
(6-12)式表明,弹性界面上产生的反射纵波振幅)(θP R 与θ2sin 成线性关系。
在CDP 道集上,对每个样点,作振幅与θ2sin 的线性拟合,可获得截距P 和斜率(梯度)G ,见图6—3。
由直线截距构成的P 剖面表示法线入射的零炮检距剖面,由梯度或斜率构成的G 剖面的物理意义不直观。
根据泊松比与岩石物性参数的关系推导出泊松比σ和纵横速度比SP V V /之间的关系σσ21)1(2--=SP V V 即 2)/(22)/(22--=S P S P V V V V σ (6-13) 图6—4给出它们之间的关系,当S P V V /较小时,微小的变化也会引起σ值有较大的变化。
当2/=S P V V 时,3/1=σ,10-=A ,把它们代入200)1/(σσ-∆+=R A G ,得到σ∆+-=49P G (6-14) 12)(94σσσ-=∆=+G P (6-15) G 的表达式说明,在界面两侧介质波阻抗不变条件下,泊松比差σ∆对反射振幅随入射角的变化影响很大,σ∆越大振幅随入射角的变化也越大。
图6—3 截距P 和斜率G 的关系 图6—4 泊松比σ与S P V V /之间的关系当地层中含气时,明显地降低了岩石的纵波速度,而横波速度则相对保持不变,即其泊松比明显下降,从而导致界面两侧介质的泊松比差相应增加。