自振周期与特征周期

振型分解反响谱法振型分解反响谱法是用来计算多自由度体系地震作用的一种方法。

该法是利用单自由度体系的加速度设计反响谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原那么对各阶振型的地震作用效应进展组合，从而得到多自由度体系的地震作用效应。

振型分解反响谱法一般可考虑为计算两种类型的地震作用：不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。

适用条件〔1〕高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比拟均匀的结构，以与近似于单质点体系的结构，可采用底部剪力法计算。

〔此为底部剪力法的适用围〕〔2〕除上述结构以外的建筑结构，宜采用“振型分解反响谱法〞。

〔3〕特别不规那么的建筑、甲类建筑和规规定的高层建筑，应采用时程分析法进展补充计算。

刚重比刚重比是指结构的侧向刚度和重力荷载设计值之比，是影响重力二阶效应的主要参数刚重比=Di*Hi/GiDi-第i楼层的弹性等效刚度，可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系；周期比的调整将导致结构侧移刚度的变化，从而影响到刚重比。

因此调整周期比时应注意，当某主轴方向的刚重比小于或接近规限值时，应采用加强刚度的方法；当某主轴方向刚重比大于规限值较多时，可采用削弱刚度的方法。

同样，对刚重比的调整也可能影响周期比。

特别是当结构的周期比接近规限值时，应采用加强结构外围刚度的方法重力二阶效应的影响较大，应该予以考虑。

规下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大，防止结构的失稳截面面积。

长细比长细比=计算长度/回转半径。

所以很显然，减小计算长度或者加大回转半径即可。

这里需要注意的是，计算长度并非实际长度，而是实际长度乘以长度系数，长度系数那么与柱子两端的约束刚度有关。

说白了就是要看与柱相连的梁或者根底是否给力，如果这些构件的刚度越高，那么长度系数就越小，柱子的计算长度也就越短。

（二）计算题工程结构抗震计算1．已知一个水塔，可简化为单自由度体系。

10000m kg =，1kN cm k =，该结构位于Ⅱ类场地第二组，基本烈度为7度（地震加速度为0.10g ），阻尼比0.03ξ=，求该结构在多遇地震下的水平地震作用。

解：（1）计算结构的自振周期22 1.99T s === （2）计算地震影响系数查表2得，0.4g T s =，查表3得，max 0.08α=。

由于0.030.05ξ=≠应考虑阻尼比对地震影响系数形状的调整。

20.050.050.0311 1.160.08 1.60.08 1.60.03ξηξ--=+=+=++⨯0.050.050.030.90.90.940.360.360.03ξγξ--=+=+=++⨯由上图2可知，()0.94max 0.40.08 1.160.02051.99g T T γαα⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭（3）计算水平地震作用0.020*******.812011N F G α==⨯⨯=2．计算仅有两个自由度体系的自由振动频率。

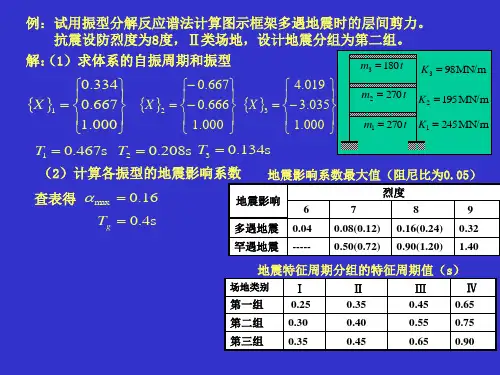
假设[]11122122k k K kk ⎡⎤=⎢⎥⎣⎦ []1200m M m ⎡⎤=⎢⎥⎣⎦解：根据多自由度体系的动力特征方程[][]20K M ω-=，有[][]111212221222000k k m K M kk m ωω⎡⎤⎡⎤-=-=⎢⎥⎢⎥⎣⎦⎣⎦整理得()()4212112221112212210m m k m k m k k k k ωω-++-=解方程得2112211212k k m m ω⎛⎫=+⎪⎝⎭2112221212k k m m ω⎛⎫=++ ⎪⎝⎭3．图示钢筋混凝土框架结构的基本周期10.467T s =，抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第二组（0.40g T s =）。

通过计算已经求得相应于结构基本自振周期的水平地震影响系数值10.139α=，试用底部剪力法计算多遇地震时的层间剪力。

振型分解反应谱法振型分解反应谱法就是用来计算多自由度体系地震作用得一种方法、该法就是利用单自由度体系得加速度设计反应谱与振型分解得原理,求解各阶振型对应得等效地震作用,然后按照一定得组合原则对各阶振型得地震作用效应进行组合,从而得到多自由度体系得地震作用效应。

振型分解反应谱法一般可考虑为计算两种类型得地震作用:不考虑扭转影响得水平地震作用与考虑平扭藕联效应得地震作用。

适用条件(1)高度不超过４0米,以剪切变形为主且质量与刚度沿高度分布比较均匀得结构,以及近似于单质点体系得结构,可采用底部剪力法计算、(此为底部剪力法得适用范围)(2) 除上述结构以外得建筑结构,宜采用“振型分解反应谱法”。

(3) 特别不规则得建筑、甲类建筑与规范规定得高层建筑,应采用时程分析法进行补充计算。

刚重比刚重比就是指结构得侧向刚度与重力荷载设计值之比,就是影响重力二阶效应得主要参数刚重比=Di*Hｉ/GiDi—第i楼层得弹性等效刚度,可取该层剪力与层间位移得比值Hi－第i楼层层高Ｇi-第i楼层重力荷载设计值刚重比与结构得侧移刚度成正比关系;周期比得调整将导致结构侧移刚度得变化,从而影响到刚重比。

因此调整周期比时应注意,当某主轴方向得刚重比小于或接近规范限值时,应采用加强刚度得方法;当某主轴方向刚重比大于规范限值较多时,可采用削弱刚度得方法、同样,对刚重比得调整也可能影响周期比。

特别就是当结构得周期比接近规范限值时,应采用加强结构外围刚度得方法规范上限主要用于确定重力荷载在水平作用位移效应引起得二阶效应就是否可以忽略不计。

见高规5.４。

1与5、4.２及相应得条文说明。

刚重比不满足规范上限要求,说明重力二阶效应得影响较大,应该予以考虑。

规范下限主要就是控制重力荷载在水平作用位移效应引起得二阶效应不致过大,避免结构得失稳倒塌。

见高规５、4.4及相应得条文说明。

刚重比不满足规范下限要求,说明结构得刚度相对于重力荷载过小。

但刚重比过分大,则说明结构得经济技术指标较差,宜适当减少墙、柱等竖向构件得截面面积。

一般来说，隔墙等附属构件仅以荷载的形式反映到结构模型中。

当没有考虑附属构件对结构刚度的影响时，结构的地震作用往往会被低估。

根据《高规》JGJ3-2002第3.3.16条、第3.3.17条的规定，计算结构自振周期时应考虑非承重墙体的刚度影响予以折减，并使用折减后的自振周期计算各振型的地震影响系数。

《高规》第3.3.17条规定，当非承重墙体为填充砖墙时，高层建筑结构的计算自振周期折减系数可按下列规定取值。

周期折减系数在荷载＞荷载控制/地震作用中输入。

多层结构未强调周期折减，这是有一定道理的，因新规范的特征周期TG增长了，按结构自震周期的经验公式：1框架结构可取TI= 0.10X层数；2框架-剪力墙结构可取TI= 0.08X层数；3剪力墙结构可取TI= 0.04X层数；这样，多层结构结构周期不折减地震剪力已经很大了，由其III，IV类土，五层以下房屋更为突出，如再折减，震剪力可超过AMAX，这显然是不合理的。

周期是否折减，要分析而定：一看周期长短，长--折,短--不折或少折，当自震周期和特征周期很接近，折减就不合理了。

二看剪重比，根据大小折或不折。

至于高层建筑结构：高规:3.1.17 条规定得很清楚:当非承重墙体为填充砖墙时，高层建筑结构的计算自振周期折减系数®T可按下列规定取值：1框架结构可取0.6〜0.7;2框架-剪力墙结构可取0.7〜0.8;3 剪力墙结构可取0.9〜1.0。

对于其他结构体系或采用其他非承重墙体时，可根据工程情况确定周期折减系数由于计算模型的简化和非结构因素的作用，导致多层钢筋混凝土框架结构在弹性阶段的计算自振周期（下简称“计算周期”）比真实自振周期（下简称“自振周期”）偏长。

因此，无论是采用理论公式计算还是经验公式计算; 无论是简化手算还是采用计算机程序计算，结构的计算周期值都应根据具体情况采用自振周期折减系数（下简称“折减系数”）加以修正，经修正后的计算周期即为设计采用的实际周期（下简称设计周期”），设计周期=计算周期浙减系数。

建筑场地类别对抗震设计影响的探讨摘要：建筑抗震场地类别的评价划分是岩土工程勘察工作的重要内容，由场地岩土层的等效剪切波速和覆盖层厚度综合确定，关系着场地设计特征周期、地震影响系数和地震作用力，对抗震设防起着决定性作用，当场地平整导致场地覆盖层厚度及性质发生改变时，建筑结构抗震设计工作中应对场地类别进行修正后采用。

关键词：场地类别；覆盖层；设防；修正1、前言建筑抗震设计理论及规范中，用建筑场地类别指标确定设计特征周期，并根据设计特征周期和结构自振周期对应关系，计算得出地震影响系数和地震作用力。

在工程建设过程中，现状工程场坪并非建成后的场坪，往往需要对拟建工程场地进行平整，包括开挖山丘或填埋沟壑，以达到设计所需的场坪条件。

由于场坪的平整或对地基土的技术处理，场地的覆盖层厚度或性质发生了变化，抗震建筑场地类别也发生了变化，设计特征周期、地震影响系数及地震作用力均随之改变。

2、建筑场地类别的确定建筑抗震场地类别通常采用场地覆盖层厚度和土层的等效剪切波速值综合评定划分。

覆盖层作为评价场地类别的因素之一，一般指覆盖在基岩之上各种成因的松散堆积、沉积物，如砂卵砾石层、黏性土层、人工填筑土体等，可采用剪切波速法实测其厚度及深度。

场地内土层的等效剪切波速是指剪切波在有限土层范围内竖向传播的等效速度，有限土层深度一般为覆盖层深度且不大于20m。

在建筑抗震设计中，将场地类别分为I、II、III、IV共4大类，其中I类分为I0、I1两个亚类。

一般地，场地类别等级越高，表明场地覆盖层厚度越大，土层的等效剪切波速值越小，场地的整体土质越软弱，地基条件越差。

当拟建场地为山丘或沟谷地，因建筑需要对场坪进行平整，平整之后场地的覆盖层厚度将发生变化，由此将引起场地类别的改变。

为更深入研究，本文以两个特殊的地段作案例分析探讨。

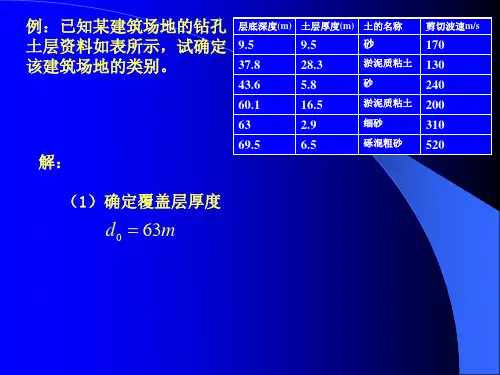
某工程建筑地段一，自上而下分布有①～⑦层土岩层，土层的总体趋势为上软下硬，下部为硬质岩石，各层厚度和剪切波速详见表1；而某工程地段二地层岩性与地段一类似，区别于土层顺序倒置，总体趋势为上硬下软，下部为硬质岩石，各层厚度和剪切波速详见表3。

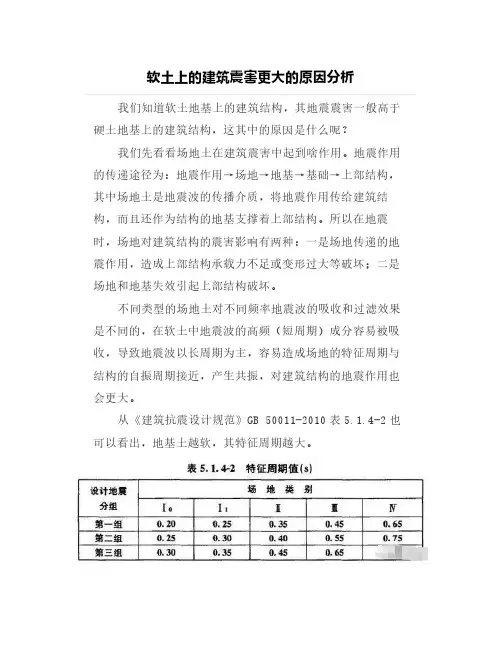
软土上的建筑震害更大的原因分析我们知道软土地基上的建筑结构，其地震震害一般高于硬土地基上的建筑结构，这其中的原因是什么呢？
我们先看看场地土在建筑震害中起到啥作用。

地震作用的传递途径为：地震作用→场地→地基→基础→上部结构，其中场地土是地震波的传播介质，将地震作用传给建筑结构，而且还作为结构的地基支撑着上部结构。

所以在地震时，场地对建筑结构的震害影响有两种：一是场地传递的地震作用，造成上部结构承载力不足或变形过大等破坏；二是场地和地基失效引起上部结构破坏。

不同类型的场地土对不同频率地震波的吸收和过滤效果是不同的，在软土中地震波的高频（短周期）成分容易被吸收，导致地震波以长周期为主，容易造成场地的特征周期与结构的自振周期接近，产生共振，对建筑结构的地震作用也会更大。

从《建筑抗震设计规范》GB50011-2010表5.1.4-2也可以看出，地基土越软，其特征周期越大。

而且，软土越厚的地方，地震波的振幅被放大的越大，会进一步加大地震作用。

另一方面，相对于硬土地基，软土地基更容易发生沉陷、塌方、失稳以及开裂等等破坏，也就会直接导致上部建筑结构的破坏。

综上，地震时，相对于硬土，软土地基上的建筑破坏往往更严重。

《建筑抗震设计规范》GB50011-2010第12.1.3条也规定：建筑结构采用隔震设计时，建筑场地宜为Ⅰ、Ⅱ、Ⅲ类，也就是说硬土场地较适合于隔震房屋。

因为隔震设计的目的之一就是延长整个结构体系的自振周期，减少输入上部结构的水平地震作用，软弱场地滤掉了地震波的中高频分量，延长结构的周期有可能增大而不是减小其地震反应。

1.卓越周期的定义地震发生时，由震源发出的地震波传至地表岩土体，迫使其振动，由于表层岩土体对不同周期的地震波有选择放大作用，某种岩土体总是以某种周期的波选择放大得尤为明显而突出，使地震记录图上的这种波记录得多而好。

这种周期即为该岩土体的特征周期，也叫做卓越周期。

由多层土组成的厚度很大的沉积层，当深部传来的剪切波通过它向地面传播时就会发生多次反射，由于波的叠加而增强，使长周期的波尤为卓越。

卓越周期的实质是波的共振，即当地震波的振动周期与地表岩土体的自振周期相同时，由于共振作用而使地表振动加强。

巨厚冲积层上低加速度的远震，可以使自振周期较长的高层建筑物遭受破坏的主要原因就是共振。

2. 几种周期及相关概念自振周期T：结构按某一振型完成一次自由振动所需的时间，是结构本身的动力特性，与结构的高度H、宽度B有关。

基本周期T1:是指结构按基本振型完成一次自由振动所需的时间。

基本振型：单质点体系在谐波的作用下的振型称为基本振型：任一地震波都可以分解为若干谐波的叠加，多质点体系按振型分解法计算地震作用时，可以简化为具有基本振型的等效单质点体系进行分析。

而对建筑结构而言，有时又称为主振型，一般是指每个主轴方向以平动为主的第一振型。

高阶振型：相对于低阶振型而言。

一般来说，低阶振型对结构振动的影响要大于高阶振型的影响。

对一般较规则的建筑物，选择的振型个数可以取其地震作用计算时的质点数（大多数情况下为楼层数），若质点数较多时，根据计算结果可以只取前几个振型（即低阶振型）进行叠加。

特征周期Tg：即建筑场地自身的周期，是建筑物场地的地震动参数，在地震影响系数曲线中，水平段与下降段交点的横坐标，反映了地震震级，震源机制（包括震源深度）、震中距等地震本身方面的影响，同时也反映了场地的特性；如软弱土层的厚度，类型等场地类别等。

在抗震设计规范中，设计特征周期Tg与场地类别有关：场地类别越高（场地越软），Tg越大；地震震级越大、震中距离越远，Tg越大。

浅探高层建筑的结构设计要点摘要：随着科技的进步与发展，高层建筑已逐步成为城市发展的标志，为了保证人民的生命财产安全，这就对工程师提出了更高的要求。

本文对高层建筑体系的特点进行了分析，并结合高层建筑结构设计的特点，进而阐述了高层建筑结构设计的相应措施及细部设计。

关键词：高层建筑结构设计要点分析前言随着社会经济的发展，高层建筑已经逐渐进入到了人民的生活当中，并在全国各地大量兴建了许多的高层建筑特别是高层的商住楼的数量，从其建筑结构上看大多采用钢筋混凝土的框架剪力墙结构，现在提倡的是“节约型”社会，建筑节能已成为全社会的共识，因此。

在设计上优化建筑结构，降低建筑的成本受到业界的关注和重视。

但如何实现优化高层建筑的结构设计．成为广大设计师不断研究探讨的课题。

1.高层建筑的受力性能分析针对一个建筑物的最初的方案设计，建筑师要考虑更多的是它的空间组成特点，而不是详细地确定它的具体结构。

建筑物底面对建筑物空间形式的竖向稳定和水平方向的稳定都是非常重要的，由于建筑物是由一些大而重的构件所组成，因此结构必须能将它本身的重量传至地面，结构的荷载总是向下作用于地面的，而建筑设计的一个基本要求就是要搞清楚所选择的体系中向下的作用力与地基土的承载力之间的关系，所以，在建筑设计的方案阶段，就必须对主要的承重柱和承重墙的数量和分布作出总体设想。

一般而言，低层、多层和高层建筑，竖向和水平向结构体系的设计基本原理都是相同的，但是，随着高度的不断增加，竖向结构体系成为设计的控制因素，其原因有两个：①较大的垂直荷载要求有较大的柱、墙或者井筒；②侧向力所产生的倾覆力矩和剪切变形要大得多。

与竖向荷载相比，侧向荷载对建筑物的效应不是线性增加的，而随建筑高度的增高迅速增大。

高层建筑结构的受力特点与简单的竖向悬臂构件的受力特点是相似的。

在所有条件相同时，在风荷载作用下，建筑物基底的倾覆力矩近似与建筑物高度的平方成正比，而其顶部的侧向位移与高度的四次方成正比，地震的作用效应更加明显。

振型分解反应谱法振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。

该法是利用单自由度体系的加速度设计反应谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原则对各阶振型的地震作用效应进行组合，从而得到多自由度体系的地震作用效应。

振型分解反应谱法一般可考虑为计算两种类型的地震作用：不考虑扭转影响的水平地震作用和考虑平扭藕联效应的地震作用。

适用条件（1）高度不超过40米，以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法计算。

（此为底部剪力法的适用范围）（2）除上述结构以外的建筑结构，宜采用“振型分解反应谱法”（3）特别不规则的建筑、甲类建筑和规范规定的高层建筑，应采用时程分析法进行补充计算。

刚重比刚憧比是指结构的侧向刚度和重力荷载设计值之比，是影响重力二阶效应的主要参数刚重比二Di*Hi/GiDi-第i楼层的弹性等效刚度，可取该层剪力与层间位移的比值Hi-第i楼层层高Gi-第i楼层重力荷载设计值刚重比与结构的侧移刚度成正比关系；周期比的调整将导致结构侧移刚度的变化，从而影响到刚重比。

因此调整周期比时应注意，当某主轴方向的刚重比小于或接近规范限值时，应采用加强刚度的方法；当某主轴方向刚重比大于规范限值较多时，可采用削弱刚度的方法。

同样，对刚重比的调整也可能影响周期比。

特别是当结构的周期比接近规范限值时，应采用加强结构外围刚度的方法规范上限主要用于确定重力荷载在水平作用位移效应引起的二阶效应是否可以忽略不计。

见高规541和542及相应的条文说明。

刚重比不满足规范上限要求，说明重力二阶效应的影响较大，应该予以考虑。

规范下限主要是控制重力荷载在水平作用位移效应引起的二阶效应不致过大，避免结构的失稳倒塌。

见高规544及相应的条文说明。

刚重比不满足规范下限要求，说明结构的刚度相对于重力荷载过小。

但刚重比过分大，则说明结构的经济技术指标较差，宜适当减少墙、柱等竖向构件的截面面积。

[转载]上海的场地特征周期
原⽂地址：上海的场地特征周期作者：朱来新
5.1.4 建筑结构的地震影响系数应根据烈度、场地类别、设计地震分组和结构⾃振周期以及阻尼⽐确定。

其⽔平地震影响系数最⼤值应按表5.1.4-1采⽤；特征周期应根据场地类别和设计地震分组按表5.1.4-2采⽤，计算罕遇地震作⽤时，特征周期应增加0.05s。

注：周期⼤于6.Os的建筑结构所采⽤的地震影响系数应专门研究。

表5.1.4-1⽔平地震影响系数最⼤值
地震影响6度7度8度9度
多遇地震0.040.08（0.12）0.16(0.24)0.32
罕遇地震0.280.50（0.72）0.90(1.20) 1.40
注：括号中数僮分别⽤于设计基本地震加速度为0. 15g和0.30g的地区。

表5.1- 4-2特征周期值(s)
设计地震分
组
场地类别
Ⅰ0Ⅰ1ⅡⅢⅣ
第⼀组0.200.250.350.450.65
第⼆组0.250.300.400.550.75
第三组0.300.350.450.650.90
上海地区的绝⼤部分区域是软⼟覆盖曾特别厚，越300M，其场地的地运动卓越周期为2~2.4s，与国标规定的4类场地的特征周期有较⼤差距，为使上海抗震具有⼀定的可靠度，同时根据⼟层地震反应分析，再考虑上海的经济实⼒和特⼤城市地位，专家就把上海的特征周期定为0.9s 。

3.5.3 结构自振周期的近似计算通过结构的频率方程求自振周期比较复杂，这里介绍几种近似计算方法。

动能为势能为由能量守恒，有例.已知：解:3.6 竖向地震作用《规范》规定：设防烈度为8度和9度区的大跨度屋盖结构、长悬臂结构、烟囱及类似高耸结构和9度区的高层建筑，应考虑竖向地震作用。

效应：使建筑物上下颠簸F F3.7 结构平扭耦合地震反应与双向水平地震影响 规范规定：对于质量及刚度明显不均匀、不对称的结构，应考虑水平地震作m用的扭转影响。

刚心)(tug质心分析过程：[受弯钢筋凝土构件的滞回曲线滞回模型：描述结构或构件滞回关系的数学模型。

双线性模型双线性模型一般适用于钢结构梁、柱、节点域构件。

钢筋混凝土梁、柱、墙等一般采用退化三线性模型。

退化三线性模型结构非弹性地震反应分析的简化方法适用范围：不超过12层且层刚度无突变的钢筋混凝土框架结构和填充墙钢筋混凝土框架结构；不超过20层且层刚度无突变的钢框架结构和支撑钢框架结构；式中：N N a h +−5.0)(/---系数，混凝土强度等级不超过C50时，取1.0，C80时为0.94，by二、结构薄弱层位置判别结构薄弱层：塑性变形集中的楼层，即ζy 最小或相对较小的楼层对于ζy 沿高度分布均匀的框架结构，底层作为薄弱层。

3.9 结构抗震验算3.9.1 结构抗震计算方法原则(1 ) 一般情况下，应允许在建筑结构的两个主轴方向分别计算水平地震作用，并进行抗震验算各方向的水平地震作用应由该方向抗侧力构件承担。

(2 )有斜交抗侧力构件的结构，当相交角度大于15°时，应分别计算各抗侧力构件方向的水平地震作用。

(3) 质量和刚度分布明显不对称的结构，应计入双向水平地震作用下的扭转影响，其他情况，应允许采用调整地震作用效应的方法计入扭转影响。

(4) 不同方向的抗侧力结构的共同构件（如框架角柱），应考虑双向水平地震作用的影响。

(5)8、9度时的大跨度和长悬臂结构及9度时的高层建筑，应计算竖向地震作用。

有关振型的几个概念振型参与系数：每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量（或者说该模态质量）之比，即为该振型的振型参与系数。

一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。

自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。

振型越高，周期越短，地震力越大，但由于我们地震反应是各振型的迭代，高振型的振型参与系数小。

特别是对规则的建筑物，由于高振型的参与系数小，一般忽略高振型的影响。

振型的有效质量：这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的，不适用于一般结构。

）。

某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方。

一个振型有三个方向的有效质量，而且所有振型平动方向的有效质量之和等于各个质点的的质量之和，转动方向的有效质量之和等于各个质点的转动惯量之和。

有效质量系数：如果计算时只取了几个振型，那么这几个振型的有效质量之和与总质量之比即为有效质量系数。

这个概念是由WILSON E.L. 教授提出的，用于判断参与振型数足够与否，并将其用于ETABS程序。

振型参与质量：某一振型的主质量（或者说该模态质量）乘以该振型的振型参与系数的平方，即为该振型的振型参与质量。

振型参与质量系数：由于有效质量系数只实用于刚性楼板假设，现在不少结构因其复杂性需要考虑楼板的弹性变形，因此需要一种更为一般的方法，不但能够适用于刚性楼板，也应该能够适用于弹性楼板。

出于这个目的，我们从结构变形能的角度对此问题进行了研究，提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数，规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。

一、地震反应谱的概念在给定的地震输入下，不同固有周期的地层或结构物将有不同的振动位移反应，这种反应的时程曲线是由多种频率成分组成的振动曲线叫地震反应谱，取对应于不同固有周期的位移时程曲线的最大值作为纵坐标，取所对应的固有的周期为横坐标，由此绘成曲线，供抗震设计中选用在设计周期下的相应振动幅值。

二、地震反应谱在结构地震反应分析理论发展中的作用1940年，美国比奥特（M.A.Biot）教授通过对强地震动记录的研究，首先提出反应谱这一概念，为抗震设计理论进人一个新的发展阶段奠定了基础，20世纪504代初，美网豪斯纳（G.W.Housener）等人发展了这一理论，并在美国加州抗震设计规范中首先采用反复谱概念作为抗震设计理论，以取代静力法。

这一理论至今仍然是我国和世界上许多国家工程结构设计规范中地震作用计算的理论基础。

反应谱理论考虑了结构的动力特性与地震动特性之间的动力关系，并保持了原有的静力理论的简单形式。

按照反应谱理论，单自由度弹性体系的结构物所受的最大地震基底剪力或地震作用为F=FEk=k⋅ββ⋅G式中G——结构的重力荷载代表值k——地震系数β——动力系数，与结构自振周期和阻尼比有关因而上式表明：结构地震作用的大小不仅与地震强度有关，还与结构的动力特性有关。

这也是地震作用区别于一般作用（荷载）的主要特征。

随着震害经验的积累和研究的不断深人，人们逐步认识到建筑场地（包括表层土的动力特性和覆盖层厚度）、震级和震中距对反应谱的影响。

考虑到这些因素，一般抗震规范中都规定了不同的反应谱形状。

利用振型分解原理，可有效地将上述概念用于多质点体系的抗震计算，这就是抗震设计规范中给出的振型分解反应谱法。

它以结构自由振动的N个振型为厂义坐标，将多质点体系的振动分解成n个独立的等效单质点体系的振动，然后利用反应谱概念求出各个（或前几个）振型的地震作用，并按一定的法则进行组合，即可求出结构总的地震作用。

三、从地震动响应推导出地震反应谱曲线对于单自由度弹性体系，通常把惯性力看作一种反映地震对结构体系影响的等效作用，即把动态作用转化为静态作用，并用其最大值来对结构进行抗震验算。

.ICSCSEE 中国电机工程学会标准T/CSEE XXXX—YYYY变电站电气设备抗震设计规范Code for seismic design of substation electrical equipmen（征求意见稿）XXXX - XX - XX发布XXXX - XX - XX实施目次前言 (II)1 总则 (1)2 规范性引用文件 (1)3 术语和符号 (1)4 电气设备的抗震设计 (4)4.1 基本原则 (4)4.2 地震作用 (4)4.3 抗震设计与计算 (7)4.4 悬吊设备 (10)4.5 抗震试验 (11)5 设备耦联连接的抗震设计 (11)5.1 说明 (11)5.2 软导线连接的电气设备抗震设计 (11)5.3 软导线连接的电气设备净距校核 (13)5.4 硬导线连接的电气设备抗震设计 (14)6 设备安装及减隔震设计 (14)6.1 基本规定 (14)6.2 设备基础连接设计 (14)6.3 电气设备安装设计 (14)6.4 电气设备隔震与消能减震设计 (15)图4.2.1.1 地震影响系数曲线 (5)图4.4.1 悬吊设备组成部分 (10)图5.2.3 软导线的推荐形状 (13)表4.2.1-1 水平地震影响系数最大值 (5)表4.2.1-2 特征周期表 (6)表4.2.1-3 地震影响系数最大值场地调整系数 (7)表5.2.4 单分裂及双分裂软导线的等效端子力 (13)前言本标准按照《中国电机工程学会团体标准管理办法（暂行）》的要求，依据GB/T 1.1—2009《标准化工作导则第1部分：标准的结构和编写》的规则起草。

本标准制定的主要技术内容包括：——规定了适用范围（见第1章）；——明确了本标准适用的术语和定义（见第3章）；——对变电站单体设备的抗震设计提出建议（见第4章）；——对变电站设备耦联连接的抗震设计提出建议（见第5章）；——对设备安装及减隔震设计提出建议（见第6章）。

满足规范剪重比要求的高层结构基本自振周期研究∗王福明;沈蒲生【摘要】介绍了美国等国规范有关剪重比的规定，以及我国《建筑抗震设计规范》(GB 50011—2010)和《高层建筑混凝土结构技术规程》(JGJ 3-2010)中最小剪重比提出的背景，对高层结构满足现行规范剪重比要求的结构自振周期进行了分析。

根据现行抗震规范的要求将地震影响系数曲线分为两种情况，又将每种情况下的地震影响系数曲线分为5段，分析了每段的结构自振周期与楼层最小地震剪力系数值之间的关系，最后对结果进行合并，得到了满足规范要求的楼层最小地震剪力系数值的结构基本周期，根据结构的基本自振周期便可以判断该结构的剪重比是否能够满足规范剪重比的要求。

通过工程实例对分析结果进行了验证。

%The requirements of shear-weight ratio in the codes of United States and some other countries were in-troduced.The regulations and related contents regarding the minimum story shear for the seismic design of buildings issued in Chinese Code for Seismic Design of Buildings (GB 50011 -2010)and Technical Specification for Concrete Structures of Tall Buildings (JGJ 3-2010)were briefly described.A comparison between Chinese code and other seismic design codes was made.The basic structural period oftall structures satisfying shear-gravity ratio of the code wasintroduced.Based on the requirement for seismic shear-gravity ratio,the curves of seismic influence coefficient can be divided into two situations.In either situation,the curves of seismic influence coefficient can be divided into five sections.In each section,the relationship between structural period and the minimum seismic shear gravity ratio was introduced.Thecalculation results of the basic structural period satisfying the base shear factor issued in the code were obtained.It can be easy to determine the basic structural period satisfying the base shear factor issued in the codeby using this table.The analysis result was checked with some engineering examples.【期刊名称】《湖南大学学报（自然科学版）》【年(卷),期】2015(000)009【总页数】6页(P8-13)【关键词】剪重比;高层建筑;楼层最小地震剪力系数值;地震影响系数最大值;结构基本自振周期【作者】王福明;沈蒲生【作者单位】湖南大学土木工程学院，湖南长沙 410082;湖南大学土木工程学院，湖南长沙 410082【正文语种】中文【中图分类】TU318;P315.9由于地震影响系数在长周期段下降较快，对于基本周期大于3.5 s的结构，由此计算所得的水平地震作用下的结构效应可能太小.而对于长周期结构，地震动态作用中的地面运动速度和位移可能对结构的破坏具有更大影响，出于结构安全的考虑，我国《建筑抗震设计规范》(GB 50011—2010)[1]和《高层建筑混凝土结构技术规程》(JGJ 3—2010)[2]提出了对结构总水平地震剪力系数及各楼层水平地震剪力系数(又称为剪重比)最小值的要求，规定了不同烈度下的最小楼层地震剪力系数，当不满足时，需改变结构布置或调整结构总剪力和各楼层的水平地震剪力使之满足要求.《建筑抗震设计规范》和《高层建筑混凝土结构技术规程》引入楼层最小剪力系数λmin来保证长周期结构在地震作用下的安全是合适的.各国规范关于最小剪力系数也有相应的规定.中国与美国等国的规范都对最小地震剪力系数进行了相关的规定.1.1 美国等国规范中最小剪力系数相关规定一般来说，房屋结构底部的剪重比较小，上层的剪重比较大.因此，美国、欧洲、新西兰等的设计规范中都对底部总剪力进行了控制.美国规范UBC[3]规定设计基底总水平剪力的下限计算公式为:Vmin=0.11CaIW.式中:Ca为地震影响系数；I为结构的重要性系数；W为结构的总重力荷载代表值. ASCE 7—05[4]对结构任意方向上的基底总剪力设计值规定为：V=CsW.该规范同时给出了Cs的下限值为：Cs=0.044SDSI≥0.01.式中:Cs为基底剪力系数；SDS为5%阻尼比对应的设计反应谱周期0.2 s对应的谱加速度.IBC[5] 对最小基底总剪力的下限取值与ASCE 7-05相同.欧洲规范EN 1998-1[6] 规定基底总剪力为：Fb=Sd(T1)·m·λ.式中：λ为修正系数；Sd为设计反应谱，定义如下.当0≤T≤TB时，；当TB<T≤TC时，；当TC<T≤TD时，；当TD<T时，式中: ag为欧洲抗震规范A类场地上475年重现期水准的地面峰值加速度；S为场地系数；TB为反应谱水平段对应周期的下限值；TC为反应谱水平段对应周期的上限值；TD为速度控制段与位移控制段的分界点对应的周期；q为结构性能系数；β为设计反应谱放大系数的下限值.新西兰规范NZS 1170.5:2004[7]对设计反应谱规定为:C(T)=Ch(T)·Z·R·N(T,D).同时规定：Cmin(T)=0.010 5.式中:Z为区域地震危险系数；R为50 a超越概率10%时的地震反应修正系数；Ch(T)为反应谱系数.1.2 中国规范中最小剪力系数相关规定《建筑抗震设计规范》GB 50011—2010和《高层建筑混凝土结构技术规程》JGJ 3-2010中对楼层最小地震剪力系数值的规定是根据抗震验算时，当结构扭转效应明显或基本周期小于3.5 s时，地震剪力系数λ应不小于0.2αmax；当结构基本周期大于5.0 s时，λ应不小于0.15αmax；基本周期介于3.5～5 s之间的结构，楼层最小地震剪力系数值λmin(表1)按插入法取值.但是《建筑抗震设计规范》和《高层建筑混凝土结构技术规程》在剪重比取值的规定上存在以下主要问题[8-12]：1)中国规范所规定的楼层最小地震剪力系数与场地类别无关,有悖于软土场地上结构地震反应大于硬土场地上地震反应的一般规律.2)同一栋建筑，建造在设防烈度低的地区时，剪重比有可能不能满足规范要求.但是建造在设防烈度高的地区时，剪重比却有可能满足规范要求.规范有关剪重比的规定还有待完善.本文研究我国规范规定的剪重比与结构基本周期之间的关系，从而通过建筑结构的自振周期就可以判断该结构的剪重比是否满足规范最小地震剪力系数的要求.1.3 中国规范与美国等国规范中最小剪力系数相关规定的对比中国规范和美国等国规范都对最小地震剪力系数的取值进行了规定，但是中国规范与美国等国的规范在具体的规定方面又有差别：1)美国等国的规范对最小剪力系数是针对基底总剪力进行规定的，我国规范则是对层剪力进行规定的.2)美国规范规定在按底部剪力法对结构进行计算设计时，其基底设计总剪力不能小于CsW，按振型分解法对结构进行设计计算时，其基底设计总剪力不能小于0.85CsW；我国规范无此明确规定.3)美国等国规范规定的最小剪力系数大于等于0.01,我国规范规定的最小剪力系数λmin可小于0.01.现行《建筑抗震设计规范》(GB 50011—2010)和《高层建筑混凝土结构技术规程》(JGJ 3-2010)中对地震影响系数α的规定见图1[1-2].图1中，衰减指数按式(11)确定：式中:ζ为阻尼比.直线下降段的下降斜率调整系数按式(12)确定：阻尼调整系数按式(13)确定：由图1, 式(11), 式(12)和式(13)得到的地震影响系数α仅与特征周期Tg, 结构自振周期T, 地震影响系数最大值αmax和阻尼比ζ相关.其中地震影响系数最大值αmax取值见表2，特征周期Tg取值见表3[1-2]．如果将结构的基本周期远大于5 s定义为6 s以上，参照表2可将地震影响系数下降段曲线分段，分段情况分为2种：第1种情况：3.5 s≤5Tg.此时，地震影响系数下降段曲线可分为T≤3.5 s，3.5s<T≤5Tg，5Tg<T≤5 s，5 s<T≤6 s和T>6 s 5段,如图2所示.第2种情况：5Tg<3.5 s.此时，地震影响系数下降段曲线可分为T≤5Tg，5Tg<T≤3.5 s，3.5 s<T≤5 s，5 s<T≤6 s和T>6 s 5段，如图3所示.注：括号内数值分别用于设计基本地震加速度为0.15 g和0.30 g的地区.3.1 地震影响系数下降段曲线为第一种情况的推算按多遇地震进行计算，地震影响系数下降段曲线为第一种情况时，因为3.5 s≤5Tg，即Tg≥0.7 s，依据表2，与第Ⅳ类场地土的第二组和第三组设计地震分组情况对应，Tg分别为0.75和0.90.第1段(T≤3.5 s)：从图2中可知，0<T≤Tg时，α≥0.45αmax>λmin，所以α>λmin恒成立；Tg<T≤3.5 s时，第2段(3.5 s<T≤5Tg)：要使α≥λmin，所以要求第3段(5Tg<T≤5 s)：要使α≥λmin，所以要求第4段(5 s<T≤6 s)：要使α≥λmin，所以要求第5段(T>6 s)：文献[9]提出当结构的基本周期远大于5 s时，可以将结构的楼层最小地震剪力系数值减少15%，即为0.85×0.15αmax=0.127 5αmax.该段楼层最小地震剪力系数值取85%折减系数，即λmin=0.127 5αmax.该段地震影响系数曲线方程与5Tg到6 s段的地震影响曲线方程一样，则要使α≥λmin，要求对式(18)，因为当地震影响系数下降段曲线为第一种分段情况时(如图2所示)，Tg≥0.7 s，对应于表3中的第Ⅳ类场地土的第二组和第三组设计地震分组情况，Tg分别为0.75和0.9．此时，按照规范要求对高层钢结构、高层混合结构和高层混凝土结构的阻尼比ζ应分别取为0.02，0.04和0.05.对式(14)～式(18)的计算结果进行合并汇总，得地震影响系数下降段曲线第一种分段情况下满足规范剪重比要求的结构基本周期.3.2 地震影响系数下降段曲线为第二种情况的推算按多遇地震进行计算，地震影响系数下降段曲线第二种分段情况中每段的计算公式：第1段(T≤5Tg)：(Tg/T)γη2αmax≥0.2αmax．第2段(5Tg<T≤3.5 s)：第3段(3.5 s<T≤5 s):第4段(5 s<T≤6 s):第5段(T>6 s):对式(19)～式(23)的计算结果进行合并汇总，得地震影响系数下降段曲线第二种分段情况下满足规范剪重比要求的结构基本周期.3.3 对两种情况换算结果进行合并对3.1节与3.2节的计算结果进行合并汇总可得满足规范要求的楼层最小地震剪力系数值时结构基本周期的取值，见表4～表6.它们分别代表高层钢结构、高层混合结构和高层混凝土结构满足规范最小地震剪力系数要求时的结构基本周期.本文搜集选取了一些有代表性的高层建筑的相关信息，见表7，对表4～表6进行验证．验证了当结构的周期在表4～表6内所示的区间时,该结构的剪重比能满足规范对剪重比的限值要求，证明了本文推导公式的正确性.基于《建筑抗震设计规范》(GB 50011—2010)与《高层建筑混凝土结构技术规程》(JGJ 3-2010)对结构的最小地震剪力系数值的要求，对符合现行抗震规范地震剪力系数要求的高层结构基本周期进行分析，得到以下结论：1)由于我国规范人为规定的最小剪重比与结构的自振周期有关，因此，根据结构的自振周期值便可以初步判断结构的剪重比是否满足规范的要求.2)当高层建筑结构的剪重比能满足规范的最小剪重比要求时，结构的基本自振周期均满足表4～表6的要求；若结构的自振周期不在表4～表6所示的区间中，则该结构的剪重比一定不满足我国规范对剪重比的要求.3) 由表4～表6可见，在满足规范剪重比要求的结构自振周期最大值的区间内，有可能出现不满足规范剪重比要求的自振周期区段.†通讯联系人，E-mail:*********************【相关文献】[1] GB 50011—2010 建筑抗震设计规范[S].北京：中国建筑工业出版社，2010:33-39.GB 50011—2010 Code for seismic design of buildings[S]. Beijing: China Architecture & Building Press, 2010:33-39.(In Chinese)[2] JGJ 3—2010 高层建筑混凝土结构技术规程[S].北京：中国建筑工业出版社，2010:36-41.JGJ 3-2010 Technical specification for concrete structures of tall building[S]. Beijing: China Architecture & Building Press, 2010:36-41.(In Chinese)[3] UBC. Uniform building code：Volume 2[S].Whittier，California: International Conference of Building Officials，1997:14-24．[4] ASCE 7—05 Minimum design loads for buildings and other structures[S].Reston，Virginia: American Society of Civil Engineers，2005:129．[5] IBC. International building code[S]. Falls Church，Virginia: International Code Council，2006: 302-307．[6] EN 1998-1 Design of structures for earthquake resistance: part 1: general rules seismic actions and rules for buildings [S].London: BSI,2004:56-57．[7] NZS 1170.5:2004 Structural design actions: part 5: earthquake actions [S]. Wellington, New Zealand: Standards New Zealand, 2004:10-21．[8] 廖耘,容柏生,李盛勇. 剪重比的本质关系推导及其对长周期超高层建筑的影响[J]. 建筑结构, 2013,43(5): 1-4.LIAO Yun, RONG Bai-sheng, LI Sheng-yong. Derivation of shear-gravity ratio and its effect on long-period super high-rise buildings[J]. Building Structure, 2013, 43(5): 1-4.(In Chinese)[9] 汪大绥,周建龙,姜文伟, 等. 超高层结构地震剪力系数限值研究[J]. 建筑结构, 2012, 42(5): 24-27. WANG Da-sui, ZHOU Jian-long, JIANG Wen-wei, et al. Research on seismic shear gravity ratio limit for super high-rise buildings higher than 500 m[J]. Building Structure, 2012,42(5): 24-27. (In Chinese)[10]方小丹,魏琏.关于建筑结构抗震设计若干问题的讨论[J]. 建筑结构学报, 2011, 32(12): 46-51. FANG Xiao-dan,WEI Lian. Discuss on issues of seismic design of building structures[J]. Journal of Building Structures, 2011, 32(12): 46-51.(In Chinese)[11]方小丹,魏琏,周靖.长周期结构地震反应的特点与反应谱[J]. 建筑结构学报, 2014, 35(3): 16-23. FANG Xiao-dan, WEI Lian, ZHOU Jing. Characteristics of earthquake response for long-period structures and response spectrum[J]. Journal of Building Structures, 2014, 35(3): 16-23.(In Chinese)[12]王国弢,胡克旭,周礼奎.位移谱阻尼调整系数模型研究[J].湖南大学学报：自然科学版,2014,41(11):48-57.WANG Guo-tao, HU Ke-xu, ZHOU Li-kui. Study on damping scaling factor model for displacement response spectra [J]. Journal of Hunan University：Natural Sciences, 2014, 41(11):48-57.(In Chinese)。