结构基本自振周期计算

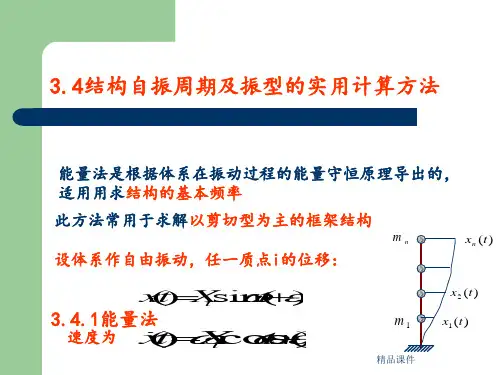
结构基本周期
结构基本周期、结构⾃振周期与设计特征周期、场地卓越周期之间的区别和联系。

⾃振周期是结构按某⼀振型完成⼀次⾃由振动所需的时
计特征周期是在抗震设计⽤的地震影响系数曲线中，反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值；场地卓越周期是根据覆盖层厚度H和⼟层剪切波速VS按公式T0=4H/VS计算的周期，表⽰场地⼟最主要的振动特性。

结构在地震作⽤下的反应与建筑物的动⼒特性密切相关，建筑物的⾃振周期是主要的动⼒特征，与结
周期相等或接近时，建筑物的震害较为严重。

基本周期应该取决于建筑物的结构形式，各种结构形式都是定数。

结构⾃振周期是结构在⽔平作⽤下的震动周期，是变数。

结构在地震作⽤下的反应与建筑物的动⼒特性密切相关，建筑物的⾃振周期是主要的动⼒特征，与结构的质量和刚度相关。

经验表明，当建筑物的⾃振周期与场地的卓越周期相等或接近时，建筑物的震害较为严重。

结构的基本周期可采⽤结构⼒学⽅法计算，对于⽐较规则的结构，也可以采⽤近似⽅法计算：
框架结构 T=（）N
框剪结构、框筒结构 T=（）N
剪⼒墙结构、筒中筒结构 T=（）N
其中N为结构层数。

也可采⽤结构分析得到的结构第1平动周期。

框架-剪力墙结构自振周期及振型计算1. 基本原理（1）连续化方法（2）梁弯曲自由振动动力方程 （3）自由振动位移方程 2. 计算参数（1）刚度参数 框架刚度：C F 剪力墙刚度：EI 刚接连梁刚度：μ （2）质量参数单位高度质量m ，单位高度重量W=mg 3. 计算公式（1）框剪结构刚度特征值EIC HF μλ+= （2）自振周期gEIWH T i i 2ϕ= i ϕ由图表、根据λ及所要计算的振型查得（3）振型参数ϕπλλ221=，212ϕλπλ=或122ϕλπλ=22221λλλ=-()()0sin sh cos ch 2212221212142412221=-+++λλλλλλλλλλλλ一式代入二式，有：221212λϕλπλ=⎪⎪⎭⎫ ⎝⎛-，()022212221=⎪⎪⎭⎫ ⎝⎛--ϕπλλλ 24224221242224⎪⎪⎭⎫⎝⎛+±=⎪⎪⎭⎫ ⎝⎛+±=ϕπλλϕπλλλ 根据物理意义，有：24221242⎪⎪⎭⎫⎝⎛++=ϕπλλλ，2421242⎪⎪⎭⎫⎝⎛++=ϕπλλλ 汇总为：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎭⎫⎝⎛++=⎪⎪⎭⎫ ⎝⎛++=242224212422242ϕπλλϕπλϕπλλλ （4）振型公式()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+-+-=x H x H x H x H Y x Y 221122221121221210sin sh cos ch sh sin cos ch λλλλλλλλλλλλλλλ4. 补充说明（1）应计算3个、最多也只能计算三个振型。

（2）计算梁的刚度时，应计及现浇钢筋混凝土楼板作为梁的翼缘对梁截面刚度的增大效应，其中边梁截面惯性矩增大1.5倍，中梁刚度增大2.0倍。

（3）计算框架-剪力墙结构的自振周期时，应考虑框架填充墙对整体结构刚度的贡献，做法是对计算周期进行折减，折减系数为0.7-0.8。

5．结构刚度 5.1 框架刚度（1）框架梁刚度按矩形截面计算：3121bh I b =按T 型截面修正：3121bh I b β=，对于现浇钢筋混凝土框架边梁，.51=β，现浇钢筋混凝土框架中梁，.02=β（2）框架柱刚度 惯性矩；3c 121bh I =（此处h 为柱截面高度） 梁柱刚度比：cb i i i ∑=柱抗侧刚度修正系数：底层i i ++=2.50α，中间层ii+=2α 柱抗侧刚度D 值：212h i D cα=（此处h 为层高） 柱抗推刚度：Dh C =c （此处h 为层高） （3）框架抗推刚度∑∑===D h C C nm C F 1（此处h 为层高）5.2 剪力墙刚度 5.2.1 整体剪力墙 www d A H I I I 291μ+=5.2.2 开洞剪力墙（1）开洞墙连梁折算惯性矩bb bb A a I I I 271~μ+=，剪应力分布不均匀系数2.1=μ，a 为连梁净跨 （2）连梁刚度特征值32~aI c D b=，c 为连梁轴跨（3）墙肢刚度 墙肢惯性矩： 3121ww h b I =（按矩形截面计算，或按T 型等组合截面计算等）（4）剪切参数 墙肢剪切参数：∑∑∑∑==AHI AG H IE 22238.2μμγ（5）整体影响系数不考虑轴向变形影响的整体参数∑∑=+==ki ik i iD I h H 1112216α（此处k 为洞口总数）考虑轴向变形影响的整体系数T212αα=，轴向变形影响系数T 与洞口数量有关，近似值为墙肢数量3-4时，T=0.80，墙肢数量5-7时，T=0.85，墙肢数量大于8时，T=0.90。

结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系。

自振周期是结构按某一振型完成一次自由振动所需的时
计特征周期是在抗震设计用的地震影响系数曲线中，反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值；场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期，表示场地土最主要的振动特性。

结构在地震作用下的反应与建筑物的动力特性密切相关，建筑物的自振周期是主要的动力特征，与结
周期相等或接近时，建筑物的震害较为严重。

基本周期应该取决于建筑物的结构形式，各种结构形式都是定数。

结构自振周期是结构在水平作用下的震动周期，是变数。

结构在地震作用下的反应与建筑物的动力特性密切相关，建筑物的自振周期是主要的动力特征，与结构的质量和刚度相关。

经验表明，当建筑物的自振周期与场地的卓越周期相等或接近时，建筑物的震害较为严重。

结构的基本周期可采用结构力学方法计算，对于比较规则的结构，也可以采用近似方法计算：
框架结构 T=（）N
框剪结构、框筒结构 T=（）N
剪力墙结构、筒中筒结构 T=（）N
其中N为结构层数。

也可采用结构分析得到的结构第1平动周期。

3.5.3 结构自振周期的近似计算通过结构的频率方程求自振周期比较复杂，这里介绍几种近似计算方法。

动能为势能为由能量守恒，有例.已知：解:3.6 竖向地震作用《规范》规定：设防烈度为8度和9度区的大跨度屋盖结构、长悬臂结构、烟囱及类似高耸结构和9度区的高层建筑，应考虑竖向地震作用。

效应：使建筑物上下颠簸F F3.7 结构平扭耦合地震反应与双向水平地震影响 规范规定：对于质量及刚度明显不均匀、不对称的结构，应考虑水平地震作m用的扭转影响。

刚心)(tug质心分析过程：[受弯钢筋凝土构件的滞回曲线滞回模型：描述结构或构件滞回关系的数学模型。

双线性模型双线性模型一般适用于钢结构梁、柱、节点域构件。

钢筋混凝土梁、柱、墙等一般采用退化三线性模型。

退化三线性模型结构非弹性地震反应分析的简化方法适用范围：不超过12层且层刚度无突变的钢筋混凝土框架结构和填充墙钢筋混凝土框架结构；不超过20层且层刚度无突变的钢框架结构和支撑钢框架结构；式中：N N a h +−5.0)(/---系数，混凝土强度等级不超过C50时，取1.0，C80时为0.94，by二、结构薄弱层位置判别结构薄弱层：塑性变形集中的楼层，即ζy 最小或相对较小的楼层对于ζy 沿高度分布均匀的框架结构，底层作为薄弱层。

3.9 结构抗震验算3.9.1 结构抗震计算方法原则(1 ) 一般情况下，应允许在建筑结构的两个主轴方向分别计算水平地震作用，并进行抗震验算各方向的水平地震作用应由该方向抗侧力构件承担。

(2 )有斜交抗侧力构件的结构，当相交角度大于15°时，应分别计算各抗侧力构件方向的水平地震作用。

(3) 质量和刚度分布明显不对称的结构，应计入双向水平地震作用下的扭转影响，其他情况，应允许采用调整地震作用效应的方法计入扭转影响。

(4) 不同方向的抗侧力结构的共同构件（如框架角柱），应考虑双向水平地震作用的影响。

(5)8、9度时的大跨度和长悬臂结构及9度时的高层建筑，应计算竖向地震作用。

结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系。

结构基本周期:是指结构按基本振型完成一次自由振动所需的时间。

自振周期T：结构按某一振型完成一次自由振动所需的时间，是结构本身的动力特性，仅与结构的质量m、刚度系数k有关。

设计特征周期:是在抗震设计用的地震影响系数曲线中，反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值；场地卓越周期:是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期，表示场地土最主要的振动特性。

卓越周期按地震记录统计得到，地基土随软硬程度的不同有不同的卓越周期，可划分为四级：一级——稳定基岩，卓越周期是0.1-0.2s，平均为0.15s。

二级——一般土层，卓越周期为0.21-0.4s，平均为0.27s。

三级为松软土层，卓越周期在二级和四级之间。

四级——为异常松软的土层，卓越周期为0.3-0.7s，平均为0.5s.特征周期Tg：即建筑场地自身的周期，是建筑物场地的地震动参数，在地震影响系数曲线中，水平段与下降段交点的横坐标，反映了地震震级，震源机制（包括震源深度）、震中距等地震本身方面的影响，同时也反映了场地的特性；如软弱土层的厚度，类型等场地类别等。

在抗震设计规范中，设计特征周期Tg与场地类别有关：场地类别越高（场地越软），Tg越大；地震震级越大、震中距离越远，Tg越大。

Tg越大，地震影响系数α的平台越宽，对于高层建筑或大跨度结构，基本周期较大，计算的地震作用越大。

剪切波速是指震动横波在土内的传播速度，单位是m/s。

可通过人为激震的方法产生震动波，在相隔一定距离处记录振动信号到达时间，以确定横波在土内的传播速度。

测试方法一般有单孔法、跨孔法等。

剪切波速是抗震区确定场地土类别的主要依据。

地震时，从震源发出的地震波在土层中传播时，经过不同性质地质界面的多次反射，将出现不同周期的地震波。

若某一周期的地震波与地基土层固有周期相近，由于共振的作用，这种地震波的振幅将得到放大，此周期称为卓越周期。

自振周期与自振频率由可知其右边是一个周期函数，其周期为（4-16）T表示振动一次所需要的时间。

验证如下：（这里）由此可见，位移确实满足周期运动的下列条件：这表明，在自由振动过程中，质点每隔一段时间T又重复原来的运动情况。

因此，T称为结构的自振周期。

（4-17）f为每秒振动的次数。

单位为1/秒，称为H Z（赫兹）。

一般建筑工程用钢为7～8次/秒，钢筋混凝土为4次/秒，属低频；一般机器为高频。

（4-18）上式表示2π个单位时间（秒）内振动的次数，单位为弧度/秒。

定义：ω是体系固有的非常重要的动力特性。

在强迫振动中，当体系的自振频率ω与干扰力的频率θ很接近时（0.75≤θ/ω≤1.25区段），将会产生共振。

为避免共振，就必须使ω和θ远离。

1、T和ω只与结构的质量m和刚度k11有关，而与干扰力的大小无关。

干扰力的大小只能影响振幅a的大小。

2、质量越大，则ω越小、T越大；刚度越大，则ω越大、T越小。

要改变T、ω，只有从改变结构的质量或刚度（改变截面、改变结构形式）着手。

3、结构的T、ω是结构动力性能的很重要的数量标志。

两个外表相似的结构如果T（ω）相差很大，则动力性能相差很大；反之，两个外表看来并不相同的结构，如果其T （ω）相近，则在动荷载作用下其动力性能基本一致。

地震中常发现这样的现象。

所以T和ω的计算十分重要。

1、自振周期（4-19）2、自振频率（4-20）3、工程频率上式中，表示在质量上沿振动方向施加W的荷载时，沿质量振动方向所产生的静位移。

1. 结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系：自振周期是结构按某一振型完成一次自由振动所需的时间；基本周期是指结构按基本振型完成一次自由振动所需的时间；设计特征周期是在抗震设计用的地震影响系数曲线中，反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值；场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期，表示场地土最主要的振动特性。

结构在地震作用下的反应与建筑物的动力特性密切相关，建筑物的自振周期是主要的动力特征，与结构的质量和刚度相关。

经验表明，当建筑物的自振周期与场地的卓越周期相等或接近时，建筑物的震害较为严重。

2.经验公式一般情况下，高层钢筋混凝土结构的基本自振周期T1为T1=(0.05~1.10)n（4.3－27）其中：钢筋混凝土框架结构：T1=(0.06~0.09)n（4.3－28）框架-剪力墙结构：T1=(0.06~0.08)n（4.3－29）高层钢结构的基本自振周期T1为T1=(0.10~0.15)n（4.3－30）式中:n——建筑层数。

结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系：结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系：自振周期是结构按某一振型完成一次自由振动所需的时间；基本周期是指结构按基本振型完成一次自由振动所需的时间；设计特征周期是在抗震设计用的地震影响系数曲线中，反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值；场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期，表示场地土最主要的振动特性。

结构在地震作用下的反应与建筑物的动力特性密切相关，建筑物的自振周期是主要的动力特征，与结构的质量和刚度相关。

经验表明，当建筑物的自振周期与场地的卓越周期相等或接近时，建筑物的震害较为严重。

用顶点位移法求自振周期：T=1.7*周期折减系数*（层间侧移开方）折减系数：框架结构取0.6~0.7框剪结构取0.7~0.8抗剪墙取1.0按照行业标准《工程抗震术语标准》（JGJ/97）的有关条文，自振周期：结构按某一振型完成一次自由振动所需的时间。

1、《高层规程》3.2.6规定-----结构基本自振周期大致为：框架结构T1=(0.08~0.10)n, 框—剪和框—筒结构T1=(0.06~0.08)n 剪力墙和筒中筒结构T1=(0.05~0.06)n2、周期比即结构扭转为主的第一自振周期（也称第一扭振周期）Tt 与平动为主的第一自振周期（也称第一侧振周期）T1的比值。

周期比主要控制结构扭转效应，减小扭转对结构产生的不利影响，使结构的抗扭刚度不能太弱。

因为当两者接近时,由于振动藕连的影响,结构的扭转效应将明显增大。

2.2 相关规范条文的控制：[高规]4.3.5条规定，结构扭转为主的第一自振周期Tt与平动为主的第一自振周期T1之比（即周期比），A级高度高层建筑不应大于0.9；B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。

[高规]5.1.13条规定，高层建筑结构计算振型数不应小于9,抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不小于15,对于多塔楼结构的振型数不应小于塔楼数的9倍,且计算振型数应使振型参与质量不小于总质量的90%。

2.3 电算结果的判别与调整要点: (1).计算结果详周期、地震力与振型输出文件。

因SATWE电算结果中并未直接给出周期比,故对于通常的规则单塔楼结构，需人工按如下步骤验算周期比: a）根据各振型的两个平动系数和一个扭转系数(三者之和等于1)判别各振型分别是扭转为主的振型（也称扭振振型）还是平动为主的振型（也称侧振振型）。

一般情况下，当扭转系数大于0.5时,可认为该振型是扭振振型,反之应为侧振振型。

当然，对某些极为复杂的结构还应结合主振型信息来进行判断；b）周期最长的扭振振型对应的就是第一扭振周期Tt，周期最长的侧振振型对应的就是第一侧振周期T1；c）计算Tt / T1，看是否超过0.9(0.85)。

对于多塔结构周期比，不能直接按上面的方法验算，这时应该将多塔结构分成多个单塔，按多个结构分别计算、分别验算(注意不是在同一结构中定义多塔，而是按塔分成多个结构)。

地震作用下框架结构的内力和侧移计算4.1横向自振周期的计算横向自振周期的计算采用瑞利（Rayleigh ）法。

瑞利法也称为能量法。

这个方法是根据体系在震动过程中能量守恒定 律导出的。

自振周期T 1（s ）可按下式计算： 21112ni ii Tni i i G u T G u ψ===∑∑注：u i 为第i 层的侧移；T ψ0.5；u i 按照下式计算： δi = ∑G i /∑D i u i =∑δk注：∑D i 为第i 层的层间侧移刚度； δi 为第i 层的层间相对位移。

δk 为第k 层的层间侧移。

基本周期T 1就算表层次 G i （kN ） ∑G i （kN ） ∑D i （kN/m ） δi (m) u i （m ） G i u i (kN ·m)2i i G u ( kN ·m 2)4 8549.73 8549.73 375964 0.0227 0.1794 194.4279 275.0652 3 9593.83 18143.56 669856 0.0271 0.1566 491.4321 445.0913 2 9347.36 27490.92 669856 0.0410 0.1295 1128.229 461.3148 19827.22 37318.14 4218240.08850.0885 3301.48292.2850 统计∑11239.121473.756321112ni ii Tn i ii G uT G uψ===∑∑=2×0.5×=0.362（s ）4.2水平地震作用及楼层地震剪力的计算本结构高度不超过40m，质量和刚度沿高度分布比较均匀，变形以剪切型为主，故可用底部剪力法计算水平地震作用，即：4.2.1结构等效总重力荷载代表值GeqG eq=0.85∑G i=0.85×37318.14=31720.419(kN)4.2.2计算水平地震影响系数а1查表得II类场地，设计地震分组第三组地震特征周期值T g=0.45s。

混凝土梁的自由振动周期计算方法一、前言混凝土梁是建筑结构中常见的一种构件，其自由振动周期的计算对于结构设计和分析具有重要的意义。

本文将介绍混凝土梁自由振动周期的计算方法，包括基本理论、计算公式和实际应用。

二、基本理论混凝土梁的自由振动周期是指在一定的约束条件下，梁在不受外力作用时自然振动一次所需的时间。

计算自由振动周期需要用到梁的弹性模量、截面惯性矩、截面面积、长度等参数，其中最重要的是弹性模量和截面惯性矩。

弹性模量是材料的一种力学性质，反映了材料抵抗形变的能力。

混凝土的弹性模量一般根据混凝土试件的压缩强度来确定，可以根据国家标准《混凝土结构设计规范》中的公式计算得出。

截面惯性矩是描述梁截面抗弯刚度的参数，其大小与梁的截面形状有关。

常见的梁截面形状有矩形、圆形、T形、I形等，对于不同形状的截面，截面惯性矩的计算方法也不同。

三、计算公式1. 矩形截面当混凝土梁的截面为矩形时，其截面惯性矩可以根据以下公式计算：$$I=\frac{1}{12}bh^3$$其中，$b$为矩形截面的宽度，$h$为矩形截面的高度。

梁的自由振动周期可以根据以下公式计算：$$T=2\pi\sqrt{\frac{I}{Ebh^3}}$$其中，$E$为混凝土的弹性模量，$I$为截面惯性矩，$b$为矩形截面的宽度，$h$为矩形截面的高度。

2. 圆形截面当混凝土梁的截面为圆形时，其截面惯性矩可以根据以下公式计算：$$I=\frac{\pi}{4}d^4$$其中，$d$为圆形截面的直径。

梁的自由振动周期可以根据以下公式计算：$$T=2\pi\sqrt{\frac{I}{E\pi d^4}}$$其中，$E$为混凝土的弹性模量，$I$为截面惯性矩，$d$为圆形截面的直径。

3. T形截面当混凝土梁的截面为T形时，其截面惯性矩可以根据以下公式计算：$$I=\frac{1}{12}b_1h_1^3+\frac{1}{12}(b_2-b_1)(h_2^3-h_1^3)$$其中，$b_1$为T形截面的上翼缘宽度，$b_2$为T形截面的下翼缘宽度，$h_1$为T形截面的上翼缘高度，$h_2$为T形截面的下翼缘高度。

附录F 结构基本自振周期的经验公式F.1 高耸结构F.1.1 一般高耸结构的基本自振周期，钢结构可取下式计算的较大值，钢筋混凝土结构可取下式计算的较小值：H T )013.0～007.0(1= (F.1.1)式中：H ——结构的高度(m)。

F.1.2 烟囱和塔架等具体结构的基本自振周期可按下列规定采用：1，烟囱的基本自振周期可按下列规定计算：1)高度不超过60m 的砖烟囱的基本自振周期按下式计算：dH T 2211022.023.0-⨯+= (F.1.2-1) 2)高度不超过150m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211010.041.0-⨯+= (F.1.2-2) 3)高度超过150m ，但低于210m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211008.053.0-⨯+= (F.1.2-3) 式中：H ——烟囱高度(m)；d ——烟囱1/2高度处的外径(m)。

2，石油化工塔架（图F.1.2）的基本自振周期可按下列规定计算：图F.1.2 设备塔架的基础形式(a)圆柱基础塔；(b)圆筒基础塔；(c)方形（板式）框架基础塔；(d)环形框架基础塔1)圆柱（筒）基础塔(塔壁厚不大于30mm)的基本自振周期按下列公式计算： 当H 2/D 0＜700时2311085.035.0D H T -⨯+= (F.1.2-4)当H 2/D 0≥700时2311099.025.0D H T -⨯+= (F.1.2-5) 式中：H ——从基础底板或柱基顶面至设备塔顶面的总高度(m)；D 0——设备塔的外径(m)；对变直径塔，可按各段高度为权，取外径的加权平均值。

2)框架基础塔(塔壁厚不大于30mm)的基本自振周期按下式计算：2311040.056.0D H T -⨯+= (F.1.2-6) 3)塔壁厚大于30mm 的各类设备塔架的基本自振周期应按有关理论公式计算。

4)当若干塔由平台连成一排时，垂直于排列方向的各塔基本自振周期T 1可采用主塔（即周期最长的塔）的基本自振周期值；平行于排列方向的各塔基本自振周期T 1可采用主塔基本自振周期乘以折减系数0.9。