体能测试时间安排数学模型解答
- 格式:doc
- 大小:93.00 KB
- 文档页数:40

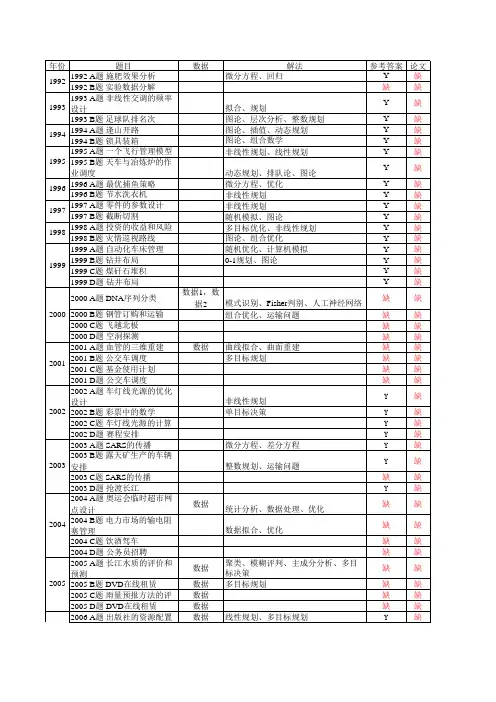

历届数学建模题目浏览:1992--20091992年 (A) 施肥效果分析问题(北京理工大学:叶其孝)(B) 实验数据分解问题(华东理工大学:俞文此; 复旦大学:谭永基)1993年 (A) 非线性交调的频率设计问题(北京大学:谢衷洁)(B) 足球排名次问题(清华大学:蔡大用)1994年 (A) 逢山开路问题(西安电子科技大学:何大可)(B) 锁具装箱问题(复旦大学:谭永基,华东理工大学:俞文此)1995年 (A) 飞行管理问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 天车与冶炼炉的作业调度问题(浙江大学:刘祥官,李吉鸾)1996年 (A) 最优捕鱼策略问题(北京师范大学:刘来福)(B) 节水洗衣机问题(重庆大学:付鹂)1997年 (A) 零件参数设计问题(清华大学:姜启源)(B) 截断切割问题(复旦大学:谭永基,华东理工大学:俞文此)1998年 (A) 投资的收益和风险问题(浙江大学:陈淑平)(B) 灾情巡视路线问题(上海海运学院:丁颂康)1999年 (A) 自动化车床管理问题(北京大学:孙山泽)(B) 钻井布局问题(郑州大学:林诒勋)1999年(C) 煤矸石堆积问题(太原理工大学:贾晓峰)(D) 钻井布局问题(郑州大学:林诒勋)2000年 (A) DNA序列分类问题(北京工业大学:孟大志)(B) 钢管订购和运输问题(武汉大学:费甫生)(C) 飞越北极问题(复旦大学:谭永基)(D) 空洞探测问题(东北电力学院:关信)2001年 (A) 血管的三维重建问题(浙江大学:汪国昭)(B) 公交车调度问题(清华大学:谭泽光)(C) 基金使用计划问题(东南大学:陈恩水)(D) 公交车调度问题(清华大学:谭泽光)2002年 (A) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 彩票中的数学问题(解放军信息工程大学:韩中庚)(C) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(D) 赛程安排问题(清华大学:姜启源)2003年 (A) SARS的传播问题(组委会)(B) 露天矿生产的车辆安排问题(吉林大学:方沛辰)(C) SARS的传播问题(组委会)(D) 抢渡长江问题(华中农业大学:殷建肃)2004年 (A) 奥运会临时超市网点设计问题(北京工业大学:孟大志)(B) 电力市场的输电阻塞管理问题(浙江大学:刘康生)(C) 酒后开车问题(清华大学:姜启源)(D) 招聘公务员问题(解放军信息工程大学:韩中庚)2005年 (A) 长江水质的评价和预测问题(解放军信息工程大学:韩中庚)(B) DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦大学:谭永基)(D) DVD在线租赁问题(清华大学:谢金星等)2006年 (A) 出版社的资源配置问题(北京工业大学:孟大志)(B) 艾滋病疗法的评价及疗效的预测问题(天津大学:边馥萍)(C) 易拉罐的优化设计问题(北京理工大学:叶其孝)(D) 煤矿瓦斯和煤尘的监测与控制问题(解放军信息工程大学:韩中庚)2007年 (A) 中国人口增长预测(B) 乘公交,看奥运(C) 手机“套餐”优惠几何(D) 体能测试时间安排2008年(A)数码相机定位,(B)高等教育学费标准探讨,(C)地面搜索,(D)NBA赛程的分析与评价2009年(A)制动器试验台的控制方法分析(B)眼科病床的合理安排(C)卫星和飞船的跟踪测控(D)会议筹备历年全国数学建模试题及解法归纳赛题解法93A非线性交调的频率设计拟合、规划93B足球队排名图论、层次分析、整数规划94A逢山开路图论、插值、动态规划94B锁具装箱问题图论、组合数学95A飞行管理问题非线性规划、线性规划95B天车与冶炼炉的作业调度动态规划、排队论、图论96A最优捕鱼策略微分方程、优化96B节水洗衣机非线性规划97A零件的参数设计非线性规划97B截断切割的最优排列随机模拟、图论98A一类投资组合问题多目标优化、非线性规划98B灾情巡视的最佳路线图论、组合优化99A自动化车床管理随机优化、计算机模拟99B钻井布局 0-1规划、图论00A DNA序列分类模式识别、Fisher判别、人工神经网络00B钢管订购和运输组合优化、运输问题01A血管三维重建曲线拟合、曲面重建赛题解法01B 公交车调度问题多目标规划02A车灯线光源的优化非线性规划02B彩票问题单目标决策03A SARS的传播微分方程、差分方程03B 露天矿生产的车辆安排整数规划、运输问题04A奥运会临时超市网点设计统计分析、数据处理、优化04B电力市场的输电阻塞管理数据拟合、优化05A长江水质的评价和预测预测评价、数据处理05B DVD在线租赁随机规划、整数规划06A出版社书号问题整数规划、数据处理、优化06B Hiv病毒问题线性规划、回归分析07A 人口问题微分方程、数据处理、优化07B 公交车问题多目标规划、动态规划、图论、0-1规划08A 照相机问题非线性方程组、优化08B 大学学费问题数据收集和处理、统计分析、回归分析赛题发展的特点:1. 对选手的计算机能力提出了更高的要求:赛题的解决依赖计算机,题目的数据较多,手工计算不能完成,如03B,某些问题需要使用计算机软件,01A。

集体活动的时间规划作者:彭雪峰陈杨林来源:《中小企业管理与科技·下旬刊》2016年第12期摘要:本文针对具体的学校学生体能测试时间安排问题展开了深入研究。
对于学生等待时间的理解为,学生在测试场地的时间与各项测试的总时间之差。
为了满足该校的要求和条件,分析了将所有学生分批次进行测试的原因,而每批次的最佳学生数为40人,次佳学生数为50人,而40人和50人的可选组合人数为80、90、100和120,并通过建模得到了学生班级的28个测试批次,同进同出进行测试。
如果28个测试批次的学生采用紧凑式进出场地,即前后两批次的学生测试时间可以重叠。
我们将模型优化后可得到最优测试时间安排:整个测试时间段为3段,学生总等待时间约减半。
按照上述模型和算法,我们得到五个测试项目重组为三个项目进行轮转为最佳,因而提出了如下调整建议:需引进立定跳远、肺活量测试仪器各1台,一个班的学生需要分组,每组30人,这样测试场所的人员容量只需30人。
关键词:线性规划;可选组合数;轮转法;数学模型;MATLAB中图分类号: G523 文献标识码: A 文章编号: 1673-1069(2016)36-82-21 问题描述与分析首先,由于考虑到测试场所最多可容纳150个学生,同一班的所有学生在同一时间内完成所有项目的测试所用时间最少的情况下,我们先将150个学生看成一个班级不考虑学生的学号,利用数学软件(lingo)求出最短时间和满足最短时间的条件。
如果将150个人分为了两个班级,通过计算最短时间可知,后者比前者多了5秒钟的录入学号时间。
依此做法,每增加一个班级就会多出5秒钟的录入学号时间。
即,多n个班级就会有n个录入学号时间。
在对问题的模型建立过程中,我们对附表中的班级采取合并的方法,即将一个班或几个班看成一个整体,又考虑到学生的学号不同,我们对模型进行了修改,采取轮转法求最短时间。
我们还计算了耗时多的向耗时少的方向轮转与耗时少的向耗时多的方向轮转的区别。

2007高教社杯全国大学生数学建模竞赛题目(请先阅读“对论文格式的统一要求”)D题:体能测试时间安排某校按照教学计划安排各班学生进行体能测试,以了解学生的身体状况。
测试包括身高与体重、立定跳远、肺活量、握力和台阶试验共5个项目,均由电子仪器自动测量、记录并保存信息。
该校引进身高与体重测量仪器3台,立定跳远、肺活量测量仪器各1台,握力和台阶试验测量仪器各2台。
身高与体重、立定跳远、肺活量、握力4个项目每台仪器每个学生的平均测试(包括学生的转换)时间分别为10秒、20秒、20秒、15秒,台阶试验每台仪器一次测试5个学生,需要3分30秒。
每个学生测试每个项目前要录入个人信息,即学号,平均需时5秒。
仪器在每个学生测量完毕后学号将自动后移一位,于是如果前后测试的学生学号相连,就可以省去录入时间,而同一班学生的学号是相连的。
学校安排每天的测试时间为8:00-12:10与13:30-16:45两个时间段。
5项测试都在最多容纳150个学生的小型场所进行,测试项目没有固定的先后顺序。
参加体能测试的各班人数见附表。
学校要求同一班的所有学生在同一时间段内完成所有项目的测试,并且在整个测试所需时间段数最少的条件下,尽量节省学生的等待时间。
请你用数学符号和语言表述各班测试时间安排问题,给出该数学问题的算法,尽量用清晰、直观的图表形式为学校工作人员及各班学生表示出测试时间的安排计划,并且说明该计划怎样满足学校的上述要求和条件。
最后,请对学校以后的体能测试就以下方面提出建议,并说明理由:如引进各项测量仪器的数量;测试场所的人员容量;一个班的学生是否需要分成几个组进行测试等。
附表参加体能测试的各班人数这道题是北京某医科大学一个学生根据本校实际情况提出的,据说这个自已并没有答案,后经过全国组委会老师修改才变成这样。
并请有关人员做了计算解答。
全国组委会所给的参考答案并不是最好的。
一. 问题的分析题目的要求是给全校56个班(每个班的的学生数已知)的学生安排一次体能测试,每个人要进行5项体能测试,使等待时间最少。

体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答【摘要】本文对体能测试时间安排问题进行简化,建立数学模型。
我们针对学生该怎样分组、怎样合理安排班级测试次序等问题进行了分析讨论。
并用线性规划模型对测试时间安排进行了优化,最后得到一个合理的体能测试时间表。
建立模型的主要目的是使测试总时间最短,次要目的是在满足整个测试所用时间段最少的条件下,尽量节省学生的等待时间。
我们通过分析,最终确定以20人为一组,对问题进行了研究。
对此我们建立了两个模型,逐次解决了每个时间段测试的最多组数、各个时间段内班级的分配情况和如何合理安排各班级具体的测试时间等问题。
在不考虑班级排序时间的情况下,得出了能够独立完成所有项目的测试周期,建立了一个在极值条件下的数学模型,并计算求出了最优解,即在8:00-12:10和13:30-16:45这两个时间段内所能测试的最多组数,分别为34组和26组。
通过对第一个模型进行分析,得出要完成所有测试,需要四个时间段。
但是学生的等待时间可以进一步优化,于是建立了第二个模型,求解各个时间段内班级的分配问题。
然后,编写C语言程序求得了一个以班级为单位、具体的测试时间表,从而满足整个测试所用时间段数最少,且能节省学生等待时间。
【关键词】【关键词】线性规划;测试周期模型优化顺序线性规划;测试周期模型优化顺序一、问题重述某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握力和台阶试验。



体能测试时间安排方案模型组员:齐建英董亮佚毛洁晶杨欢米红玉赵红蔡春彦孙鑫李鹏摘要为了了解学生的身体状况,学校要对各班同学进行体能测试。
测试包括身高与体重、立定跳远、肺活量、握力和台阶试验共5个项目。
由于测试器材与场地的限制,需要设计一个合理的体能测试方案使消耗的时间段最短,等待时间尽量少。
若要使体能测试消耗时间最短,需要充分利用耗时最长的测试项目(台阶测试)。
因此,本文建立了单元循环与接龙的模型,通过比较两种模型的总消耗时间段数及等待时间,得出两种模型的消耗的时间段数相同均为4段,但接龙方法的等待时间要短,因此选择接龙的测试方法。
又考虑到班级总人数是否为20的倍数,班与班之间的人数是否能组合成20的倍数进行分班,得到令接龙法最有利发挥的班级排列顺序,从而得到最佳方案。
关键词单元循环接龙方法最少时间段数最短等待时间一、问题重述1.1问题背景某校按照教学计划安排各班学生进行体能测试,以了解学生的身体状况。
测试包括身高与体重、立定跳远、肺活量、握力和台阶试验共5个项目,均由电子仪器自动测量、记录并保存信息。
学校已有的各项目的仪器数和测试所需时间如表1所示。
表1 测试仪器数量及所用时间信息项目身高与体重立定跳远肺活量握力台阶测试仪器数量(台) 3 1 1 2 2测试时间(秒)10 20 20 15 210 注:测试时间即每台仪器每个学生的平均测试时间,其中每台台阶测试仪器可同时测试。
在每个班测试时录入个人信息所需时间为5秒,学校安排每天上午测试时间为8:00-12:10(共15000秒),下午测试时间为13:30-16:45(共11700秒)。
测试场所的容量为150个学生,测试项目没有固定的先后顺序,参加体能测试的各班人数见附表2。
表2 体能测试的各班人数班号1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 人数41 45 44 44 26 44 42 20 20 38 37 25 45 45 45 班号16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 人数44 20 30 39 35 38 38 28 25 30 36 20 24 32 33 班号31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 人数41 33 51 39 20 20 44 37 38 39 42 40 37 50 50 班号46 47 48 49 50 51 52 53 54 55 56人数42 43 41 42 45 42 19 39 75 17 171.2需要解决的问题学校要求同一班的所有学生在同一时间段内完成所有项目的测试,并且在整个测试所需时间段数最少的条件下,尽量节省学生的等待时间。
数学建模2007d题体能测试以下是2007年数学建模竞赛D题“体能测试”的参考解答,供您参考:一、问题重述某中学为了检测本校学生体能状况,组织了一次耐力跑测试。
测试中,学生需要完成3000米跑,并记录完成时间。
为了确保公平,测试采用了标准田径跑道,学生从同一起点出发,跑相同的距离。
我们需要设计一个模型来评价学生的体能状况。
该模型应考虑学生的完成时间、性别和体重等因素。
二、模型建立1. 建立评价函数:根据问题的要求,我们需要建立一个评价函数来评价学生的体能状况。
考虑到完成时间、性别和体重等因素,我们可以将完成时间作为主要评价指标,同时考虑体重对耐力的影响。
因此,我们可以将完成时间与体重的乘积作为评价函数的输入,即:体能评价 = 完成时间× 体重。
2. 标准化处理:为了消除不同指标量纲的影响,我们将完成时间和体重进行标准化处理。
标准化公式为:Z = (X - μ) / σ,其中Z为标准化值,X为原始值,μ为均值,σ为标准差。
通过标准化处理,我们将完成时间和体重都转换为均值为0、标准差为1的变量。
3. 综合评价:将标准化后的完成时间和体重相乘,得到体能评价的综合得分。
根据得分情况,我们可以将学生体能划分为不同的等级,如优秀、良好、一般等。
三、模型应用1. 数据收集:收集所有参与耐力跑测试的学生的完成时间和体重数据。
2. 数据预处理:对数据进行清洗和整理,确保数据准确无误。
3. 模型计算:根据上述建立的模型,计算每个学生的体能评价得分。
4. 结果分析:根据得分情况,对每个学生的体能状况进行分析和评价。
同时,也可以对不同年级、班级或性别的学生体能状况进行比较和分析。
5. 反馈与改进:根据分析结果,为学生提供针对性的体能训练建议,并不断优化和改进模型,以更准确地反映学生的体能状况。
竞赛题汇集:中国大学生建模竞赛题目汇集1992年(A) 施肥效果分析问题(北京理工大学:叶其孝)(B) 实验数据分解问题(华东理工大学:俞文此; 复旦大学:谭永基)1993年(A) 非线性交调的频率设计问题(北京大学:谢衷洁)(B) 足球排名次问题(清华大学:蔡大用)1994年(A) 逢山开路问题(西安电子科技大学:何大可)(B) 锁具装箱问题(复旦大学:谭永基,华东理工大学:俞文此)1995年(A) 飞行管理问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 天车与冶炼炉的作业调度问题(浙江大学:刘祥官,李吉鸾)1996年(A) 最优捕鱼策略问题(北京师范大学:刘来福)(B) 节水洗衣机问题(重庆大学:付鹂)1997年(A) 零件参数设计问题(清华大学:姜启源)(B) 截断切割问题(复旦大学:谭永基,华东理工大学:俞文此)1998年(A) 投资的收益和风险问题(浙江大学:陈淑平)(B) 灾情巡视路线问题(上海海运学院:丁颂康)1999年(A) 自动化车床管理问题(北京大学:孙山泽)(B) 钻井布局问题(郑州大学:林诒勋)(C) 煤矸石堆积问题(太原理工大学:贾晓峰)(D) 钻井布局问题(郑州大学:林诒勋)2000年(A) DNA序列分类问题(北京工业大学:孟大志)(B) 钢管订购和运输问题(武汉大学:费甫生)(C) 飞越北极问题(复旦大学:谭永基)(D) 空洞探测问题(东北电力学院:关信)2001年(A) 血管的三维重建问题(浙江大学:汪国昭)(B) 公交车调度问题(清华大学:谭泽光)(C) 基金使用计划问题(东南大学:陈恩水)(D) 公交车调度问题(清华大学:谭泽光)2002年(A) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 彩票中的数学问题(解放军信息工程大学:韩中庚)(C) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(D) 赛程安排问题(清华大学:姜启源)2003年(A) SARS的传播问题(组委会)(B) 露天矿生产的车辆安排问题(吉林大学:方沛辰)(C) SARS的传播问题(组委会)(D) 抢渡长江问题(华中农业大学:殷建肃)2004年(A) 奥运会临时超市网点设计问题(北京工业大学:孟大志)(B) 电力市场的输电阻塞管理问题(浙江大学:刘康生)(C) 酒后开车问题(清华大学:姜启源)(D) 招聘公务员问题(解放军信息工程大学:韩中庚)2005年(A) 长江水质的评价和预测问题(解放军信息工程大学:韩中庚)(B) DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦大学:谭永基)(D) DVD在线租赁问题(清华大学:谢金星等)2006年(A) 出版社的资源配置问题(北京工业大学:孟大志)(B) 艾滋病疗法的评价及疗效的预测问题(天津大学:边馥萍)(C) 易拉罐的优化设计问题(北京理工大学:叶其孝)(D) 煤矿瓦斯和煤尘的监测与控制问题(解放军信息工程大学:韩中庚)2007年(A) 中国人口增长预测(B) 乘公交,看奥运(C) 手机“套餐”优惠几何(D) 体能测试时间安排注:C、D题是大专组赛题。
数学建模及全国历年竞赛题目(2010-09-28 21:58:01)分类:专业教学标签:数学建模应用数学模型教育一、数学建模的内涵(一)数学建模的概念数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化建立能近似刻画并"解决"实际问题的一种强有力的数学手段。
使用数学语言描述的事物就称为数学模型,这个建立数学模型的全过程就称为数学建模。
(二)应用数学模型应用数学去解决各类实际问题,把错综复杂的实际问题简化、抽象为合理的数学结构。
通过调查、收集数据资料,观察和研究实际对象的固有特征和内在规律,抓住问题的主要矛盾,建立起反映实际问题的数量关系,然后利用数学的理论和方法去分析和解决问题。
需要诸如数理统计、最优化、图论、微分方程、计算方法、神经网络、层次分析法、模糊数学,数学软件包如Mathematica,Matlab,Lingo,Spss,Mapple的使用,甚至排版软件等知识的基础。
(三)数学建模的特点数学建模具有难度大、涉及面广、形式灵活,对教师和学生要求高等特点;数学建模的教学本身是一个不断探索、不断创新、不断完善和提高的过程。
(四)数学建模的指导思想数学建模的指导思想就是:以实验室为基础、以学生为中心、以问题为主线、以培养能力为目标来组织教学工作。
(五)数学建模的意义数学建模是联系数学与实际问题的桥梁,是数学在各个领械广泛应用的媒介,是数学科学技术转化的主要途径。
通过教学使学生了解利用数学理论和方法去分析和解决问题的全过程,提高他们分析问题和解决问题的能力;提高他们学习数学的兴趣和应用数学的意识与能力,使他们在以后的工作中能经常性地想到用数学去解决问题,提高他们尽量利用计算机软件及当代高新科技成果的意识,能将数学、计算机有机地结合起来去解决实际问题。
1.培养创新意识和创造能力;2.训练快速获取信息和资料的能力;3.锻炼快速了解和掌握新知识的技能;4.培养团队合作意识和团队合作精神;5.增强写作技能和排版技术;6.训练人的逻辑思维和开放性思考方式。
关于体能测试的时间安排问题沈剑摘要:某校按照教学计划安排各班学生进行体能测试,测试包括身高与体重、立定跳远、肺活量、握力和台阶,学校要求整个测试所需时间段最少的条件下,尽量节省学生的等待时间,该如何安排班级测试?以每个时间段测试的人最多为目标,用时间的限制为约束,建立0-1整数规划模型,在lingo中求解得到各个时间段测试的班级,计算各班测试时间。
这5项测试的仪器测试时间不同,总体上讲台阶、立定跳远和肺活量时间较长,学校可以考虑引进这几项仪器,测完的同学就可以离开测试场所,人员容量就不用再扩大,在模型中为节省时间把班级分组。
关键词:组合方式;0-1规划;lingo某校按照教学计划安排各班学生进行体能测试,以了解学生的身体状况。
包括身高与体重、立定跳远、肺活量、握力和台阶试验5个项目,均由电子仪器动测量、阶试验测量仪器各2台。
其中,身高与体重、立定跳远、肺活量、握力4个项目每台仪器每个学生的平均测试(包括学生的转换)时间分别为10秒、20秒、20秒、15秒,台阶试验每台仪器一次测试5个学生,需要3分30秒。
每个学生测试每个项目前要录入个人信息,即学号,平均需时5秒。
仪器在每个学生测量完毕后学号将自动后移一位,于是如果前后测试的学生学号相连,就可以省去录入时间,而同一班学生的学号是相连的。
学校安排每天的测试时间为8:00-12:10与13:30-16:45两个时间段。
5项测试都在最多容纳150个学生的小型场所进行,测试项目没有固定的先后顺序。
同时学校要求同一班的所有学生在同一时间段内完成所有项目的测试,并且在整个测试所需时间段数最少的条件下,尽量节省学生的等待时间。
一、问题的分析经过初步分析,用0-1整数规划可以优化此问题。
考虑到学校的要求:同一班级的所有同学在同一时间段内完成所有项目的测试,并且在整个测试所需时间段数最少的条下,尽量节省学生的等待时间。
考虑以下几方面:(1)为节省等待时间我们按班级一一测试,在测试过程中把班级人数分组,测试完的同学可以走,5人一组,但要求每组的学生的学号相连减少录入时间。
体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答【摘要】本文对体能测试时间安排问题进行简化,建立数学模型。
我们针对学生该怎样分组、怎样合理安排班级测试次序等问题进行了分析讨论。
并用线性规划模型对测试时间安排进行了优化,最后得到一个合理的体能测试时间表。
建立模型的主要目的是使测试总时间最短,次要目的是在满足整个测试所用时间段最少的条件下,尽量节省学生的等待时间。
我们通过分析,最终确定以20人为一组,对问题进行了研究。
对此我们建立了两个模型,逐次解决了每个时间段测试的最多组数、各个时间段内班级的分配情况和如何合理安排各班级具体的测试时间等问题。
在不考虑班级排序时间的情况下,得出了能够独立完成所有项目的测试周期,建立了一个在极值条件下的数学模型,并计算求出了最优解,即在8:00-12:10和13:30-16:45这两个时间段内所能测试的最多组数,分别为34组和26组。
通过对第一个模型进行分析,得出要完成所有测试,需要四个时间段。
但是学生的等待时间可以进一步优化,于是建立了第二个模型,求解各个时间段内班级的分配问题。
然后,编写C语言程序求得了一个以班级为单位、具体的测试时间表,从而满足整个测试所用时间段数最少,且能节省学生等待时间。
【关键词】【关键词】线性规划;测试周期模型优化顺序线性规划;测试周期模型优化顺序一、问题重述某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握某校安排学生进行体能测试,的内容有:身高与重、立定跳远肺活量握力和台阶试验。
学校分别引进了力和台阶试验。
学校分别引进了 3台、 1台、 1台、 2台、 2台。
前面台。
前面台。
前面 4个项目每台仪器每个学生的平均测试时间分别为: 10 秒、 20 秒、 20 秒、 15 秒,台阶试验每仪器一次秒,台阶试验每仪器一次测试 5个学生(可以少于 5个学生),需要个学生),需要 3分 30 秒。
仪器名称身高与体重立定跳远肺活量握力台阶试验仪器数量31122每人平均测试时间 (s)1020201521每个学生测试项目前要录入人信息,平均耗时每个学生测试项目前要录入人信息,平均耗时 5秒,在同一班级的学生号秒,在同一班级的学生号相连,则可以省去录入时间。
每天的测试段为 8:00 —12 :10 和 13 :30 —16 :45 。
学生在最多容纳 150 人的场所进行,测试项目没有先后次序。
要求在整个中用时人的场所进行,测试项目没有先后次序。
要求在整个中用时人的场所进行,测试项目没有先后次序。
要求在整个中用时间段最少并且在此条件下尽量节省学生的等待时。
同一班级所有间段最少并且在此条件下尽量节省学生的等待时。
同一班级所有内完成所有测试项目。
然后对以的体能在关仪器引进、场地容量和具内完成所有测试项目。
然后对以的体能在关仪器引进、场地容量和具内完成所有测试项目。
然后对以的体能在关仪器引进、场地容量和具方面的问题向学校提供有益合理建议。
(方面的问题向学校提供有益合理建议。
(如附录表 1)二、问题分析问题分析本题要解决的主问是使整个测试所需时间最少。
而定这一关键点有两本题要解决的主问是使整个测试所需时间最少。
而定这一关键点有两个,一是测试仪器的充分利用二合理安排班级次序尽量使每时间段内人个,一是测试仪器的充分利用二合理安排班级次序尽量使每时间段内人个,一是测试仪器的充分利用二合理安排班级次序尽量使每时间段内人个,一是测试仪器的充分利用二合理安排班级次序尽量使每时间段内人数最多。
对于测试仪器的充分利用问题,由于各个项目仪器每次测试人数分别为1 人(身高与体重),1 人(立定跳远),1 人(肺活量),1 人(握力),5 人(台阶试验),而台阶试验测试仪有两台,所以我们不妨设20 人为一小组对每组的测试时间进行研究。
在考虑所有录入时间时,每组独立完成每个测试项目的时间分别为153200+ 秒(身高与体重测量仪3 台),210 秒(立定跳远测量仪1 台,肺活量测量仪1 台),155 秒(握力测量仪2 台),215 秒(台阶试验测量仪2 台),可以看出做台阶测试试验所用的时间是最长的,而一个时间段时间一定,若使测试人数达到最大,台阶测试仪必须充分利用。
因此在第一组完成测试所需时间为690 秒。
在前一组测试完成台阶实验和立定跳远、肺活量测量后下一组则可继续测量,因此在一个时间段内可测量的最多组数设为1 C ,有430 690 15000 1 ⨯C + ≤ 可求出组数。
由于每个组做身高与体重测试需要105 秒,做握力测试需要155 秒,显然在430 秒这一周期内,用三台身高与体重测量仪和两台握力测量仪就可满足要求。
同时在前一组完成台阶实验和立定跳远、肺活量测量后下一组人进场,依次类推在一个循环中,使用该安排场地人数最多为120 人小于场地限制的150计要求,则整个体能测试的流程如图一。
图1 体能测试流程安排图三、模型的基本假设1、假设测试过程中同学交换场地时间不计入测试耗时。
2、假设测试过程同学的体能消耗不影响测试。
3、假设测试过程中每台机器运作正常,不受外界影响。
4、假设负责测试的老师准时到岗,每个班级在安排测试的时间前都能保证到达测试地点。
5、假设学生在测试完所有项目测试后能迅速离开,并不再占用场所空间。
6、假设台阶试验测试仪在测试人数不足5 人时也可进行测试。
7、假设体能测试时按照图1 所示体能测试流程图进行。
四、符号说明i ……班级号i X ……第i 班的人数1 C ……上午最大测量组数2 C ……下午最大测量组数max1 Z ……上午测量最大总人数max 2 Z ……下午测量最大总人数五、模型的建立与求解5.1 模型分析通过问题分析,建立的测试过程可以看出,在第一小组同学进行测试的时候后边机器有空闲,但是综合考虑其总体测试进程可以将进行测试的第一小组测试的同学所用的时间忽略,当测试第二小组以及后面的小组时,测试进入正常的运行,每个小组的10为同学进行台阶测试的时间为:210 + 5 = 215秒(学号相连、包括信息录入时间),同时其余的10 为同学再分为每5 人一小组分别进行立定跳远、肺活量测试,在他们小组完成后互换测试项目则整个测试时间为:(20⨯5 + 5)⨯2 = 210秒(学号相连、包括信息录入时间),与台阶测试的时间存在5 秒的差值,但同学等待的时间在这三项测试短。
在握力测试中,两台握力测试机同时进行即排在第一位的两个同学是需要20 秒的测试时间(信息录入时间5 秒),紧跟他们后面的9 位同学则均是只用15 秒,则整个批次中所用时间为:5+10⨯15 =155秒。
显然整个测试过程是没有等待时间的,假如不让机器闲置,在第一小组做完台阶测试、肺活量测量和立定跳远后,第二小组就可以进场测试,依次类推完成一个小组的测试时间为430 秒,即为测试的最小周期。
每个时间段首次测量小组所需时间为:430 +155+105 = 690秒。
5.2 模型建立根据所求得的测试周期长我们可得出学校上午、下午所测组数的最大值,从而得出所测人数的最大值。
上午所测组数的最大值为:430 690 15000 1 ⨯C + ≤下午所测组数的最大值为:430 690 11700 2 ⨯C + ≤将一个完整的时间段看作一个整体,完整时间段内所测最多人数作为目标函数即:上午:∑==nii Z X1max 1s.t max1 1 Z ≤ 20⨯C下午:∑==niZ X1max 2 1s.t max 2 2 Z ≤ 20⨯C5.3 模型的求解通过模型可以求出上午的测试组数为33 1 C = ,最大人数为660 人;下午的测试组数为25 2 C ,最大人数为500 人。
其中组数计算结果只取整数部分,全局时间差为580秒。
针对每组测试同学为20 人,则用Visual Studio2010 编程把所有班级分为3 个大组,A 组为20 的倍数,B 组为5 的倍数,C 组为剩余的班级。
经计算可得 A组总人数为: 160 人, B组总人数为 :545 人, C组人数为 1331 人。
观察可知, B组去掉一个 25 人的班级( 12 号班级)与 A组刚好构成 680 人作为第一天上午测试。
对于上午测试。
对于 C组班级,我们再次分为组班级,我们再次分为 8类以 1,2,3,4,6,7,8,9为尾。
则有:为尾。
则有:以 1为尾:(为尾:( 1,41 ),( 31 ,41 )( 33 ,51 )(4 8,41)以 2为尾:(为尾:( 7,42 )( 29 ,32 )(41,42)(46,42)(49,42)(51,42)以 3为尾:(为尾:( 30 ,33 )( 32 ,33 )(47,43) 以 4为尾:(为尾:( 3,44 )( 4,44 ,)( 6,44 )( 16 ,44 )( 28 ,24 )( 37 ,44 )以 6为尾:(为尾:( 5,26 )( 26 ,36 )以 7为尾:(为尾:( 11 ,37 )(38,37)(43,37)(55,17)(56,17)以 8为尾:(为尾:( 10 ,38 )( 21 ,38 )( 22 ,38 )( 23 ,28 )(39,38)以 9为尾:(为尾:( 19 ,39 )( 34 ,39 )(40,39)(52 ,19)(53,39)以 1,9为尾可以组合成 4组,总人数为组,总人数为 320 人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余52 , 19 );以);以);以 2,8为尾可以组合成 5组,总人数为组,总人数为 390 人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余29 , 32 );以);以);以 3,7,为尾可以组合成,为尾可以组合成 3组,总人数为组,总人数为 220 人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余人(优先取班级最多数),剩余55 , 17 )( 56 ,17 );以 4,6为尾可以组合成 2组,总人数为组,总人数为 140 人(优先取班级最多数),人(优先取班级最多数),人(优先取班级最多数),剩余( 6,44 )( 16 ,44 )( 28 ,24 )( 37 ,44 )。