体能测试时间安排 MCM.doc

体能测试时间安排摘要：本问题属于优化问题，要求我们从学校管理人员出发，在整个测试所需时间段数最少的条件下，尽量节省学生的等待时间为目标，制定5个体能测试项目的最优测试安排和班级的最优测试时刻表。

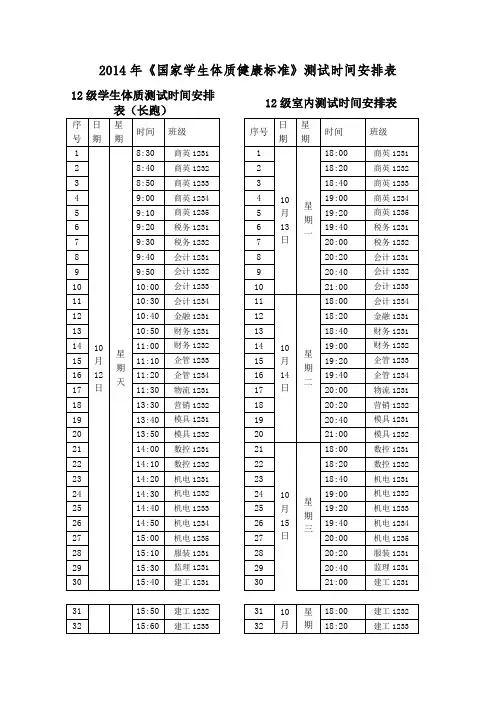
首先，根据模糊数学理论与同一时间内五项测试所能够测试人数比相结合，确定了20人一组的测试方案，具体安排见表1。

五项测试中台阶试验测试的平均速度最慢，为保证时间段尽可能的少，应该使台阶试验仪器在每个时间段内连续工作而不间歇，确定了在三天上午的三个时间段内完成所有测试的可行性。

最终排出了在同一班级学生同时进测试室，并且学生等待时间尽可能少的条件下的各班级测试时间安排表（见表3）。

此外，建立了学生测试平均等待时间=nT ini ∑=1=()nt T Tni i i∑=--1121的数学模型。

从而近似得出学生测试平均等待时间为306秒。

随后，从各项测试仪器的数量、同一班级学生人数分组情况以及测试室人员容量三个方面对已建模型进行综合分析，给出了满足学校要求的、更加科学合理的改进方案。

关键词：模糊数学 优化 综合分析 平均等待时间一、问题重述某校按照教学计划安排各班学生进行体能测试，以了解学生的身体状况。

测试包括身高与体重、立定跳远、肺活量、握力和台阶测试共5个项目，均由电子仪器自动测量、记录并保存信息。

该校引进身高与体重测量仪器3台，立定跳远、肺活量测量仪器各1台，握力和台阶试验测量仪器各2台。

身高与体重、立定跳远、肺活量、握力4个项目每台仪器每个学生的平均测试（包括学生的转换）时间分别为10秒、20秒、20秒、15秒，台阶试验每台仪器一次测试5个学生，需要3分30秒。

每个学生测试每个项目前要录入个人信息，即学号，平均需时5秒。

仪器在每个学生测量完毕后学号将自动后移一位，于是如果前后测试的学生学号相连，就可以省去录入时间，而同一班学生的学号是相连的。

学校安排每天的测试时间为8:00-12:10与13：30-16:45两个时间段。

学校体能测试策划书3篇篇一《学校体能测试策划书》一、策划背景为了贯彻落实国家教育部关于加强学生体质健康的要求，促进学生积极参加体育锻炼，提高身体素质，我校决定组织开展体能测试工作。

本次测试旨在全面了解学生的体能状况，为学校体育教学和学生体育锻炼提供科学依据。

二、测试对象全体学生三、测试项目1. 男生：1000 米跑、引体向上、立定跳远2. 女生：800 米跑、仰卧起坐、立定跳远四、测试时间和地点1. 时间：[具体日期]2. 地点：学校操场五、测试安排1. 测试前，体育老师将向学生详细讲解测试项目的规则和要求，确保学生了解测试流程。

2. 各班按照规定时间在操场指定区域集合，由体育老师带领进行热身运动。

3. 测试过程中，将安排专人负责记录测试成绩，确保测试结果的准确性。

4. 测试结束后，将及时公布测试结果，并对优秀学生进行表彰和奖励。

六、注意事项2. 测试时，学生应严格按照测试规则进行操作，确保测试结果的真实性和公正性。

3. 如有特殊情况无法参加测试，需提前向体育老师请假。

4. 测试过程中，学生应注意安全，避免因剧烈运动导致身体不适。

七、保障措施1. 学校将提供充足的测试设备和场地，确保测试工作的顺利进行。

2. 安排专业的体育老师担任测试工作人员，确保测试过程的安全和规范。

3. 学校将对测试结果进行科学分析，为体育教学和学生体育锻炼提供有针对性的指导。

八、其他事项1. 本策划书最终解释权归学校所有。

2. 如遇特殊情况，测试时间和地点将另行通知。

希望全体学生积极参与体能测试，努力提高自己的身体素质，为今后的学习和生活打下坚实的基础。

[学校名称][策划日期]篇二《学校体能测试策划书》一、策划背景二、测试对象全体在校学生三、测试项目1. 男生项目：1000 米跑、引体向上、立定跳远2. 女生项目：800 米跑、仰卧起坐、立定跳远四、测试时间和地点1. 时间：[具体测试时间]2. 地点：学校操场五、测试规则和方法1. 参照《国家学生体质健康标准》（2014 年修订）的相关要求进行测试。

体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答体能测试时间安排数学模型解答【摘要】本文对体能测试时间安排问题进行简化，建立数学模型。

我们针对学生该怎样分组、怎样合理安排班级测试次序等问题进行了分析讨论。

并用线性规划模型对测试时间安排进行了优化，最后得到一个合理的体能测试时间表。

建立模型的主要目的是使测试总时间最短，次要目的是在满足整个测试所用时间段最少的条件下，尽量节省学生的等待时间。

我们通过分析，最终确定以20人为一组，对问题进行了研究。

对此我们建立了两个模型，逐次解决了每个时间段测试的最多组数、各个时间段内班级的分配情况和如何合理安排各班级具体的测试时间等问题。

在不考虑班级排序时间的情况下，得出了能够独立完成所有项目的测试周期，建立了一个在极值条件下的数学模型，并计算求出了最优解，即在8:00-12:10和13:30-16:45这两个时间段内所能测试的最多组数，分别为34组和26组。

通过对第一个模型进行分析，得出要完成所有测试，需要四个时间段。

但是学生的等待时间可以进一步优化，于是建立了第二个模型，求解各个时间段内班级的分配问题。

然后，编写C语言程序求得了一个以班级为单位、具体的测试时间表，从而满足整个测试所用时间段数最少，且能节省学生等待时间。

【关键词】【关键词】线性规划；测试周期模型优化顺序线性规划；测试周期模型优化顺序一、问题重述某校安排学生进行体能测试，的内容有：身高与重、立定跳远肺活量握某校安排学生进行体能测试，的内容有：身高与重、立定跳远肺活量握某校安排学生进行体能测试，的内容有：身高与重、立定跳远肺活量握某校安排学生进行体能测试，的内容有：身高与重、立定跳远肺活量握某校安排学生进行体能测试，的内容有：身高与重、立定跳远肺活量握某校安排学生进行体能测试，的内容有：身高与重、立定跳远肺活量握力和台阶试验。

体能测试时间安排[摘要]利用动态规划方法建立了该校体能测试时间安排的数学模型。

首先，对该校的学生和班级以及进行体能测试的机器状况和场地作了详尽、细致、深入的分析，只要合理的安排测试流程，那么当所有的学生测完台阶项目时，其它的四个项目都已完成。

为了保证整个测试时间段最少，在安排测试流程时主要考虑台阶机器不停的工作所用时间与所用录入时间最少即可。

在此前提下，再考虑尽量让学生的等待时间最短，所以在具体的安排流程时按班级人数分两种情况来讨论，分别给出不同的流程图。

同时，笔者对学校以后的体能测试所涉及到的机器数、测试场所的人员容量、班级的分组情况也提出了一些建议。

[关键词]流程图时间段等待时间时间安排一、问题提出为了解学生的身体状况,某校按照教学计划安排各班学生进行体能测试。

测试包括身高与体重、立定跳远、肺活量、握力和台阶试验共5个项目，均由电子仪器自动测量、记录并保存消息。

该校引进身高与体重测量仪器3台，立定跳远、肺活量测量仪器各一台，握力和台阶试验测量仪器各2台。

身高与体重、立定跳远、肺活量、握力4个项目每台仪器每个学生的平均测试（包括学生的转换）时间分别为10秒、20秒、20秒、15秒，台阶试验每台仪器一次测试5个学生，需要3分30秒。

每个学生测试每个项目前要录入个人信息，即学号，平均需时5秒。

仪器在每个学生测量完毕后学号将自动后移一位，于是如果前后测试的学生学号相连，就可以省去录入时间，而同一班学生的学号是相连的。

学校安排每天的测试时间为8：00~12：10与13：30~16：45两个时间段。

5项测试都在最多容纳150个学生的小型场所进行，测试项目没有固定的先后顺序。

参加体能测试的各班人数见附表。

学校要求同一班的所有学生在同一时间段内完成所有项目的测试，并且在整个测试所需时间段数最少的条件下，尽量节省学生的等待时间。

请用数学符号和语言表述各班测试时间安排问题，给出该数学问题的算法，尽量用清晰、直观的图表形式为学校工作人员及各班学生表示出测试时间的安排计划，并且说明该计划怎样满足学校的上述要求和条件。

体能测试时间安排摘要为了了解学生的身体情况，某校按照教学计划安排要对学生进行身高和体重，立定跳远，肺活量以及握力和台阶试验这5方面的测试。

这5个项目所匹配的仪器台数和测试的时间不同。

学校要求每班每个学生在同一时间段内完成所有项目的测试，并在5个测试所用的时间段数最少的条件下，尽量节省学生的等待时间。

本文先根据学校的实际情况，应用学校现有的仪器设备、场地容纳人员数量、在规定测试的时间，利用队列原理对学生由小到大分成4组，并使他们的总等待时间最短，我们在此基础上建立数学模型：minQ=S/T*2。

并利用Mathematica、Word和Excel等软件对有关数据进行了分析计算，得出一种比较合理的方法，使得学生等待时间最短。

在上面模型的基础上，我们提出三种方案，回答了题目中的问题二。

方案一虽然运行速度比较快，但需要引进各项仪器22台，且场所需要扩容，所以该方案不可行；方案二在一上午可以完成学生测试，需要引进仪器13台，在条件允许的情况下我们认为方案二也可行；方案三在一天的时间可以完成全校学生的测试且引进器材比较少，共4台，通过以上比较我们认为方案三最合理。

关键词效率分组队列原理等待时间一、问题的提出体能测试主要是测量身体的四大基本素质：力量、耐力、速度、柔韧性。

通过这些测试，才可以了解自身的基本体质状况，以便提高身体素质。

现有某校按照教学计划安排各班学生进行体能测试，以了解学生的身体状况。

测试包括身高与体重、立定跳远、肺活量、握力和台阶试验5个项目，均由电子仪器自动测量、记录并保存信息。

该校引进身高与体重测量仪器3台，立定跳远、肺活量测量仪器各1台，握力和台阶试验测量仪器各2台。

身高与体重、立定跳远、肺活量、握力4个项目每台仪器每个学生的平均测试（包括学生的转换）时间为10秒、20秒、20秒、15秒，台阶试验每台仪器一次测试5个学生，需要210秒。

每个学生测试每个项目前要登记学号，平均需时5秒。

仪器在每个学生测量完毕后学号将自动后移一位，于是如果前后测试的学生学号相连，就可以省去录入时间，而同一班学生的学号是相连的。

体能测试最优时间安排的数学模型数学与信息科学系摘要:运用集装箱装备的思路,借助Matlab6.5程序,较方便快捷地得到各班级在时间安排上的最佳组合,确定了一个最优的时间安排表;并运用流水线设计原理进一步优化模型,使得模型的实用性得到推广.由此,对2007“高教社杯”全国大学生数学建模竞赛D题的各问题给出了完整的解答.关键词:排序优化;集装箱;流水线原理一．问题的描述某校安排56个班的学生进行体能测试,参加体能测试的各班人数见表1.测试包括身高与体重、立定跳远、肺活量、握力和台阶试验共5个项目,均由电子仪器自动测量、记录并保存信息.该校身高与体重测量仪器3台,立定跳远、肺活量测量仪器各1台,握力和台阶试验测量仪器各2台.前4个项目每台仪器每个学生的平均测试(包括学生的转换)时间分别为10、20、20、15s,台阶试验每台仪器一次测试5个学生,需要3.5min.5项测试都在最多容纳150个学生的小型场所进行,测试项目没有固定的先后顺序.请你用数学符号和语言表述各班测试时间安排问题,给出该数学问题的算法,尽量用清晰、直观的图表形式为学校工作人员及各班学生表示出测试时间的安排计划.并对学校以后的体能测试就引进各项测量仪器的数量、测试场所的人员容量等方面提出建议,详细要求参照2007“高教社杯”全国大学生数学建模竞赛中的D题[1].二．模型假设和符号2.1 模型的假设(1) 同一班学生的学号相连,按学号顺序测试每人可节省5s录入时间,故设一个班集体测试,且每班同学都按照其学号相连的顺序进行测试;(2) 忽略班与班之间进场交替的时间;(3) 假设每个班进入场所后全部测试完毕方退出,且忽略测试项目间的转换时间;(4) 假设体能测试中没有发生突发情况(如:某同学反复重测一个项目,工作人员的仪器突发暂时性的停止运作等),且测试中所有项目均连贯进行,无人员闲置,空等的现象发生.2.2 变量及符号(表2)表2 变量及符号三．问题分析(1) 模型Ⅰ集装箱装配集装箱使用的特点之一,必须将货车完全装满,不容许欠装,由于在装车时,一辆车既可以装一种箱型又可以多种箱型混装[2].所以联想到与本问题有相似之处,可将班级测试完成的时间看作箱子,而规定的时间段看作货车.于是此问题就成了箱子装进货车的问题.(2) 模型Ⅱ流水线工序安排模型流水线的基本原理是把一个重复的过程分解为若干个子过程,前一个子过程为下一个子过程创造执行条件,每一个过程可以与其他子过程同时进行.流水线各段执行时间最长的那段为整个流水线的瓶颈,一般地,将其执行时间称为流水线的周期[3].考虑到与本问题有相似之处,于是将体能测试看成一条完整的流水作业,生产人员看作是体能测试中的工作人员,测试人员看作是生产零件,所以此问题就成了零件加工的问题.测试项目的相关数据见表3.表3 测试项目数据根据表3,测试中平均每人消耗在台阶测试项目的时间最多,因此可以假设,某班同学全部完成台阶测试时,已经测完了其他项目,这样在模型的合理假设下就可以把一个班所花费的最长时间计算出,10/T n t i ⨯= （1） ()()x T T x n t i /10/+⨯-=()的个位数为n x （2） 其中n 表示每个班级人数;当n 为10的倍数时用式(1),当n 出现个位数时用式(2).此式可求出每班完成所有项目所用的最少时间.四．模型的建立(1) 模型Ⅰ集装箱装配 将班级测试所耗时间看作是集装箱,而将规定的时间段看作货车.由于台阶设备有2台,可同时测试10人,所以为了能够充分地利用台阶测试的资源去节省不必要的时间消耗,将班级进行凑整组合(计算机编程语言代码见附录所示).经过计算机的合理筛选,定了初步的分配方案.为达到最优化设计目标函数,即t n T G i i ∑-=1min 1 （3） t n T G i i ∑-=2min 2 （4） 函数(3)表示装入尽可能多的组合班级让其在第一个时间段剩余时间最少;函数(4)表示装入尽可能多的组合班级让其在第二个时间段剩余时间最少.(2) 模型Ⅱ流水线设计方式 由于“流水线设计式”体能测试的基本原则是测试效率高,这包括了减少工作人员的使用,减少生产时间,平衡测试各环节,减少测试人员回流等内容.①求流水线的最佳编制效率E()[].,3,2,1%,100/max =⨯∙=k n T E N k （5） 一般流水线的编制效率要求在85%以上,所以在求解过程中要尽可能让其效率达到最大.②求解各工序的最优分配让测试过程保持平衡,并且耗时最少,使录入时间和测试时间以及中间项目转换时间的总和最少,可以得出流水线作业的最优化目标函数G.,2,1,max =⨯+⨯=∑k G N w T w k s m m （6） 权数的确定可以根据不同实际情况进行合理调配,一般可设为1.五．问题求解（1）模型Ⅰ集装箱装配求解为使G 1 (即规定时间段剩余时间)达到最小值,进行班级最优组合安排,计算机处理流程图见图1所示.按照计算机处理模式(详见附录部分),可以得到表4.图1 集装箱装配解题流程图(2) 模型Ⅱ流水线设计方式求解观察函数(3)可知,当T 为定值,N k n max ∙的值达到最大时,E 的值能达到最大(即效率最大);为使函数(4)中G 1达到最大,由于∑T m 的确值无法准确算出,但在实际生活中,对于有些量可根据经验和要求将其定量化,所以只要同时满足上面2个函数式的最值条件,就能算出在非理想化的生活实际中消耗的最长时间.但现设定各项目之间的距离可以适当的安排,因此∑Tm 能近似的看作为0.所以最后耗时t i 会无限逼近21s ,这样模型Ⅱ的最优解划归为模型1,即可以用和模型Ⅰ中相同的计算求解方法和计算机处理模式进行最优筛选,此处不再赘述.体能测试最优时间安排的数学模型表4六．模型的评价与推广模型符合现代效率经济的相关理论,利用矩阵列表,运用计算机筛选从而大大简化计算过程.从两个模型的实际运用效果上看,上述模型还可以运用于其他领域.如模型Ⅰ可广泛运用于生活中的日常调度,装配问题等,而模型Ⅱ可以广泛运用于企业生产流水线,运输线路以及一些传送运输系统的生活实际问题中.考虑到经费和场地问题,测试仪器不可能无限的增多,所以在尽可能少仪器的情况下达到各测试点基本相同是最理想的,经过计算分析得出,学校应该具备的仪器为身高体重仪器2台,立定跳远、肺活量仪器各4台,握力3台,台阶试验仪器8台.鉴于学校原来所具有的仪器量,因此建议学校在原来的基础上,引进仪器设备为立定跳远、肺活量仪器各3台,握力1台,台阶试验仪器6台.参考文献:[1]中国大学生数学建模网，/mcm07/problems2007c.asp[2] 党业,王业祥,沈海燕.编制集箱中转装配计划的数学模型的研究[J].铁路计算机应用,1995,4(2):8-11.[3] 陈晓鹏,张祖芳,李克兢.服装生产流水线设计和工序分配的优化目标[J].东华大学学报:社会科学版,2005,5(5):56-59.附录:所使用的Visual Basic的程序代码Private Sub Command1_Click()Dim a(1 To 56) As Integer, b(1 To 56) As Integer, c(3 To 15)Open “各班级的人数.txt” For Input As #1Open “已经安排好的班级.txt” For Output As #2For x = 1 To 56Input #1, a(x)For d = 1 To 7If a(x) = d * 10 ThenPrint #2, x & “班”, a(x)a(x) = 0End IfNext dNext xFor y = 1 To 55For z = y + 1 To 56For w = 3 To 15If a(y) <> 0 ThenIf a(y) + a(z) = w * 10 ThenPrint #2, y & “班” & “和” & z & “班”, 10 * wa(y) = 0a(z) = 0End IfEnd IfNext wNext zNext yFor i = 1 To 54For j = i + 1 To 55For k = j + 1 To 56For v = 5 To 15If a(i) <> 0 ThenIf a(i) + a(j) + a(k) = v * 10 ThenPrint #2, i & “班” & “和”& j & “班” & “和” & k & “班”, 10 * v a(i) = 0a(j) = 0a(k) = 0End IfEnd IfNext vNext kNext jNext iFor o = 1 To 56If a(o) <> 0 ThenPrint #2, o & "班", a(o) End IfNext oClose #1, 2End Sub。

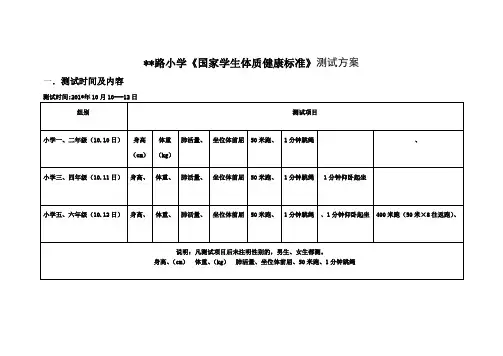
关于体能测试的时间安排问题沈剑摘要：某校按照教学计划安排各班学生进行体能测试，测试包括身高与体重、立定跳远、肺活量、握力和台阶，学校要求整个测试所需时间段最少的条件下，尽量节省学生的等待时间，该如何安排班级测试？以每个时间段测试的人最多为目标，用时间的限制为约束，建立0-1整数规划模型，在lingo中求解得到各个时间段测试的班级，计算各班测试时间。

这5项测试的仪器测试时间不同，总体上讲台阶、立定跳远和肺活量时间较长，学校可以考虑引进这几项仪器，测完的同学就可以离开测试场所，人员容量就不用再扩大，在模型中为节省时间把班级分组。

关键词：组合方式；0-1规划；lingo某校按照教学计划安排各班学生进行体能测试，以了解学生的身体状况。

包括身高与体重、立定跳远、肺活量、握力和台阶试验5个项目，均由电子仪器动测量、阶试验测量仪器各2台。

其中，身高与体重、立定跳远、肺活量、握力4个项目每台仪器每个学生的平均测试（包括学生的转换）时间分别为10秒、20秒、20秒、15秒，台阶试验每台仪器一次测试5个学生，需要3分30秒。

每个学生测试每个项目前要录入个人信息，即学号，平均需时5秒。

仪器在每个学生测量完毕后学号将自动后移一位，于是如果前后测试的学生学号相连，就可以省去录入时间，而同一班学生的学号是相连的。

学校安排每天的测试时间为8：00－12：10与13：30－16：45两个时间段。

5项测试都在最多容纳150个学生的小型场所进行，测试项目没有固定的先后顺序。

同时学校要求同一班的所有学生在同一时间段内完成所有项目的测试，并且在整个测试所需时间段数最少的条件下，尽量节省学生的等待时间。

一、问题的分析经过初步分析，用0-1整数规划可以优化此问题。

考虑到学校的要求：同一班级的所有同学在同一时间段内完成所有项目的测试，并且在整个测试所需时间段数最少的条下，尽量节省学生的等待时间。

考虑以下几方面：(1)为节省等待时间我们按班级一一测试，在测试过程中把班级人数分组，测试完的同学可以走，5人一组，但要求每组的学生的学号相连减少录入时间。

体能测量时间安排模型一．摘要本文讨论了在学生服从按排的条件下，如何安排班级体能测量的分配方案。

问题一：先对所给条件和数据进行分析，发现台阶测量所用的时间最长，需等待的时间最长，所以以台阶测量仪器的测量人数和时间为基准。

因为每次测量台阶的人数最多为10人，每台只能同时测量5人，为了省去学号录入时间我将5名学号相连的同学分为一组。

用一个表进行排列，找出每轮测量的人数，每轮测量所用最少时间，同学等待测量时间最短以及他们之间的关系。

第1列表示时间，起始时间为0秒，间隔时间为5秒，因为5秒和每台测量仪器的测量时间有关系，第2列到第10列分别是测量仪器（A1，A2，A3，B，C，D1，D2，E1，E2），先将第两组同学安排到E1和E2进行测试，考虑到测试E1和E2的时间太长，所以我只安排两组同学去进行其它项的测量，从仪器最少所需时间最长的仪器开始安排，让这两个组分别去B，C，D1，D2，A1，A2，A3进行测量，等测量台阶的两组同学测量完毕后，这两个组在去测量台阶，测量台阶的两组在去测量其余四项。

具体排列见表1。

这样排列每轮能测量20名同学，用时430秒。

这样的方法最适合20人的班级，考虑到班级人数的不同，我们对班级用C程序进行了分类和优化组合，让班级等待时间和整体测量间最小。

所有班级分为三类，每类班级都按照表1的方法进行轮转测量，再根据每类班级的特点列出公式计算出每个班级的测量安排时间。

问题二：在问题一的结果上进行数据分析得出建议。

学校应该充分利用场地容量大的条件，在引进一定的数量的测量仪器，使每轮测试的学生人数达到最大，最好一次能进行1到3个班级的测量，这样可以有效的缩减班级学生测试的等待时间和整体测试时间。

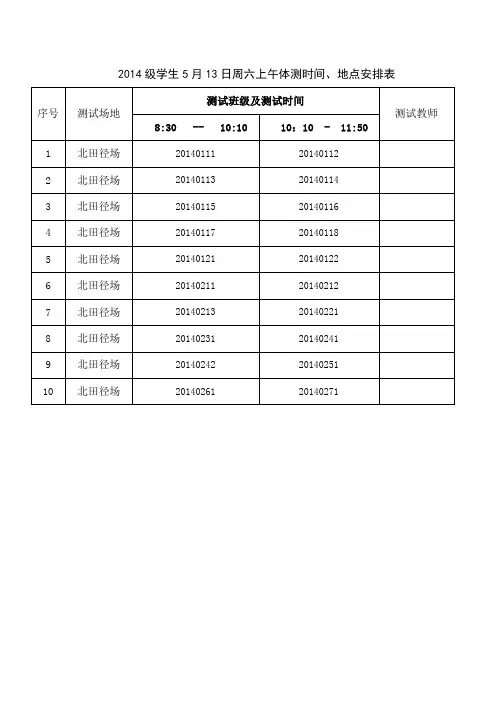
二．问题重述某校按照教学计划安排各班学生进行体能测量，以了解学生的身体状况。

测量包括身高与体重、立定跳远、肺活量、握力和台阶试验共5个项目，均由电子仪器自动测量、记录并保存信息。

该校引进身高与体重测量仪器3台，立定跳远、肺活量测量仪器各1台，握力和台阶试验测量仪器各2台。