高斯投影及换带计算
- 格式:ppt
- 大小:1.83 MB
- 文档页数:50

高斯投影带号计算公式一、引言高斯投影带号是一种用于地图投影的方法,它将地球表面的经纬度坐标转换为平面坐标,以便更方便地绘制地图和进行测量。
高斯投影带号计算公式是用来计算特定经纬度点所在的高斯投影带号的数学公式。
本文将详细介绍高斯投影带号计算公式及其应用。
二、高斯投影带号的定义高斯投影带号是根据地球表面的经线和纬线将地球划分为一系列带状区域的方法。
每个带状区域都有一个唯一的带号,用来表示该区域的位置。
在高斯投影带号系统中,每个带号由一个字母和一个数字组成,字母表示带的纬度范围,数字表示带的经度范围。
三、高斯投影带号计算公式高斯投影带号计算公式可以根据给定的经纬度坐标来计算该点所在的高斯投影带号。
公式如下:带号 = (经度 + 180) / 6 + 1其中,经度是待转换的经度坐标,范围为-180到180度。
带号的取值范围为1到60,表示地球表面的60个高斯投影带。
四、高斯投影带号的应用高斯投影带号广泛应用于地图制作、测量和导航等领域。
通过将地球表面的经纬度坐标转换为高斯投影带号,可以方便地绘制各种比例尺的地图,便于人们进行地理位置的确定和测量。
同时,高斯投影带号还可以用于导航系统中,帮助人们快速准确地定位目标位置。
五、高斯投影带号计算公式的示例为了更好地理解高斯投影带号计算公式的应用,下面举一个例子。
假设某地的经度为120度,根据高斯投影带号计算公式,可以计算出该地点所在的带号为:带号 = (120 + 180) / 6 + 1 = 51因此,该地点所在的高斯投影带号为51。
通过这个带号,可以在地图上快速找到该地点的位置。
六、总结高斯投影带号计算公式是一种将地球表面的经纬度坐标转换为高斯投影带号的数学公式。
它为地图制作、测量和导航等领域提供了便利,使得人们可以更方便地确定地理位置和进行测量。
通过理解和应用高斯投影带号计算公式,可以更好地利用地图和导航系统,提高工作效率和准确性。
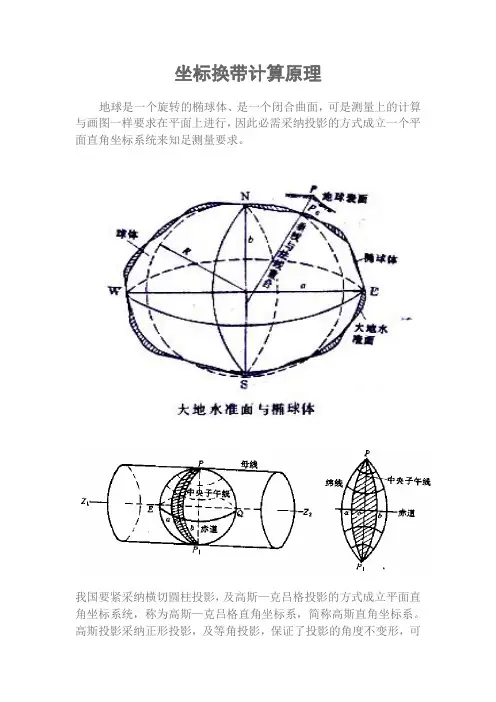
坐标换带计算原理地球是一个旋转的椭球体、是一个闭合曲面,可是测量上的计算与画图一样要求在平面上进行,因此必需采纳投影的方式成立一个平面直角坐标系统来知足测量要求。
我国要紧采纳横切圆柱投影,及高斯—克吕格投影的方式成立平面直角坐标系统,称为高斯—克吕格直角坐标系,简称高斯直角坐标系。
高斯投影采纳正形投影,及等角投影,保证了投影的角度不变形,可是其长度变形较为严峻。
高斯投影平面上的中央子午线投影为直线且长度不变,其余的子午线均为凹向中央子午线的曲线,其长度大于投影前的长度,离中央子午线越远长度变形越大。
为了限制高斯投影的长度变形,必需依据中央子午线进行分带,把投影范围限制在中央子午线东、西双侧必然的狭长带内别离进行。
但这又使得统一的坐标系分割成各带的独立坐标系。
于是,因分带的结果产生了新的矛盾,即在生产建设中提出了各相邻带的相互联系的问题。
那个问题是通过一个带的平面坐标换算到相邻带的平面坐标,简称为“邻带换算”的方式来解决的。
具体来讲,在以下情形下需要进行坐标邻带换算:(1)如图1所示,A、B、一、二、3、4、C、D为位于两个相邻带边缘地域并跨越两个投影带(东、西带)的操纵网。
假设起算点A、B和C、D的起始坐标是按两带别离给出的话,那么为了能在同一带内进行平差计算,必需把西带的A、B点起始坐标换算到东带,或把东带的C、D点的起始坐标换算到西带。
图1(2)在分界子午线周围地域测图时,往往需要用到另一带的三角点作为操纵,因此必需将这些点的坐标换算到同一带中;为了实现两邻带地形图的拼接和利用,位于45′(或′)重叠的三角点需具有相邻带的坐标值,如图2所示。
图2(3)当大比例尺(1:1000或更大)测图时,专门是在工程测量中,要求采纳3°带、°带或任意带,而国家操纵点通常只有6°带坐标,这时就产生了6°带同3°带(或°带、任意带)之间的彼此坐标换算问题。


高斯投影分带计算题摘要:1.高斯投影分带计算题的概述2.高斯投影分带的原理3.高斯投影分带计算的方法4.高斯投影分带计算的实例5.总结正文:一、高斯投影分带计算题的概述高斯投影分带计算题是地理信息科学中的一种计算题,主要涉及到高斯克吕格投影的分带计算。
高斯克吕格投影,又称高斯投影,是一种将地球表面的地理坐标(经度和纬度)转换为平面直角坐标的投影方法。
这种投影方法被广泛应用于我国的地图制图、工程测量、导航定位等领域。
二、高斯投影分带的原理高斯投影分带是为了减少投影误差而进行的一种分带计算。
由于地球是一个椭球体,而投影平面是一个平面,因此在进行投影时,会产生一定的投影误差。
高斯投影分带就是将地球表面按照一定的经度间隔划分为多个投影带,每个投影带内的投影误差相对较小。
三、高斯投影分带计算的方法高斯投影分带计算的方法主要包括以下步骤:1.确定投影带的数量:根据需要绘制的地区范围和精度要求,确定投影带的数量。
一般来说,投影带的数量越多,投影误差越小,但计算过程也越复杂。
2.计算每个投影带的经度范围:根据投影带的数量和地球表面的经度范围,计算每个投影带的经度范围。
3.计算每个投影带的横纵坐标转换公式:根据每个投影带的经度范围,使用高斯克吕格投影的公式,计算每个投影带的横纵坐标转换公式。
四、高斯投影分带计算的实例以我国为例,我国常用的高斯投影分带计算方法为6 度分带。
即按照每6 度经度间隔划分为一个投影带,我国共划分为18 个投影带。
每个投影带的横纵坐标转换公式都不同,需要根据具体的经度范围进行计算。
五、总结高斯投影分带计算题是地理信息科学中的一种重要计算题,涉及到高斯克吕格投影的分带计算。

高斯投影3度带计算公式
高斯投影是一种常用的地图投影方法,广泛应用于地理信息系统和地图制作中。
其中,高斯投影3度带是指将地球划分为每3度经度为一个投影带,每个投影带都有其特定的计算公式。
以下是高斯投影3度带的计算公式。
1.计算中央子午线经度
中央子午线经度可以通过经度除以3再取整得到。
例如,经度120度所在的投影带的中央子午线经度为39度。
2.计算投影坐标系原点
投影坐标系原点的纬度可以通过将纬度分为北纬和南纬两个区间,再通过选择不同的公式计算得到。
北纬区间为0度到84度,南纬区间为0度到80度。
公式如下:
在北纬区间内,原点纬度等于3度带数乘以3度再减去1.5度;
在南纬区间内,原点纬度等于80度减去3度带数乘以3度再减去1.5度。
3.计算投影系数
投影系数是指将经纬度转换为XY平面坐标的转换参数。
根据不同的投影带和纬度区间,投影系数有不同的计算公式。
可以使用以下公式计算投影系数:
投影系数等于扁率乘以半长轴,再乘以纬度差值,再除以360。
4.计算辅助角度
辅助角度可以通过以下公式计算得到:
辅助角度等于经度差值乘以60等于输入经度减去中央子午线经度。
5.计算投影坐标
投影坐标由X和Y两个部分组成,可以通过以下公式计算得到:
X等于投影系数乘以辅助角度的正弦值;
Y等于投影系数乘以辅助角度的余弦值。
这就是高斯投影3度带的计算公式。
通过这些公式,可以将经纬度坐标转换为平面坐标,实现地图投影和测量分析等功能。
高斯投影3度带的计算公式是地图制作和测绘工作中的重要工具,具有广泛的应用前景。


辽宁工程技术大学大地测量基础综合训练二教学单位测绘与地理科学学院专业测绘工程名称 80椭球高斯投影坐标换带计算编程班级测绘14-1学号学生姓名指导教师王佩贤目录一、高斯投影坐标换带的原理 (3)二、高斯投影坐标换带的目的 (6)三、坐标换带的意义 (8)四、程序设计基础 (8)五、程序界面及源码 (11)六、程序验证 (15)七、软件评价 (15)八、软件使用说明 (16)一、高斯投影坐标换带的原理1.1高斯投影基本概念想象有一个椭圆柱面横套在地球椭球体外面,并与某一条子午线(此子午线称为中央子午线或轴子午线)相切,椭圆柱的中心轴通过椭球体中心,然后用一定投影方法,将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上,再将此柱面展开即成为投影面。
特点:(1)正形投影(角度不变,a=b:长度比与方向无关);(2)中央子午线投影为纵坐标轴;(3)中央子午线投影后长度不变。
1.2高斯投影邻带换算1.定义:将一个带的高斯平面坐标换算为另一带的高斯平面坐标称为高斯坐标的邻带换算2.内容: 1 )不同六度带和不同三度带之间的化算2 )三度带和六度带之间的化算3.方法: 1 )直接法: 利用相邻两带坐标之间关系式进行坐标互换2 )间接法:通过大地坐标进行高斯正反算互相换算目前广泛采用间接换带计算法,因此下面就此方法作介绍。
如将第一带(东带或西带)的平面坐标换算为第二带(西带或东带)的平面坐标,方法是先根据第一带的平面坐标x,y和中央子午线的经度L。
按高斯投影坐标反算公式求得大地坐标B,L然后根据B,L和第二带的中央子午线经度按高斯投影坐标正算公式求得在第二带中的平面坐标。
由于在换带计算中,把椭球面上的大地坐标作为过渡坐标,因而称为间接换带法。
这种方法理论上是严密的,精度高,而且通用性强,他适用于6°带与6°带,3°带与3°带,6°带与3°带之间的坐标换带。




高斯投影正反算与换带计算True BASIC程序欧龙;陈性义;欧阳平【摘要】实际测量工作中,经常需要进行高斯投影正、反算与换带计算,如果用手工完成,则计算量庞大,且容易出错.为此,利用True BASIC编写了计算程序,只需输入高斯平面坐标,就能在克拉索夫斯基和IUGG-1975参考椭球面上进行高斯投影正、反算和换带计算,还可将计算成果导入CASS中展点,或上传到全站仪内存中使用.【期刊名称】《铁道勘察》【年(卷),期】2006(032)005【总页数】4页(P12-15)【关键词】高斯投影;正反算;换带计算;True BASIC【作者】欧龙;陈性义;欧阳平【作者单位】中国地质大学,湖北武汉,430074;中国地质大学,湖北武汉,430074;中国地质大学,湖北武汉,430074【正文语种】中文【中图分类】U21 数学模型1.1 参考椭球面的高斯投影参考椭球面的高斯投影是指将地表的观测元素先投影到参考椭球面上(称为高斯归化[1]),再投影到高斯平面上(称为高斯投影改化[1]),这样就可以在高斯平面直角坐标系中进行测量平差计算。
在控制测量学中,由控制点的大地经纬度(L,B)计算其高斯平面坐标(x,y),称为高斯投影正算;由高斯平面坐标(x,y)计算其大地经纬度(L,B),称为高斯投影反算;由一个投影带的高斯平面坐标(x1,y1)计算其在另一个投影带的高斯平面坐标(x2,y2),称为高斯投影换带计算。
1.2 参考椭球面的高斯投影正算公式设投影带的主子午线经度为L0,地表P点的经纬度为(L,B),其高斯平面坐标为(x,y),子午线收敛角为γ,经度差为l=L-L0,则有高斯投影正算公式[2](1)γ0为以度为单位的子午线收敛角。
式中它们均与高程修正值ΔH无关。
X为子午圈弧长,计算公式为(2)式中,B0是以度为单位的纬度值,5个系数的计算公式为1.3 参考椭球面的高斯投影反算公式高斯投影反算就是已知地面点P的高斯坐标x,y,求其大地坐标L,B。
坐标换带计算原理地球是一个旋转的椭球体、是一个闭合曲面,但是测量上的计算与绘图一般要求在平面上进行,所以必须采用投影的方法建立一个平面直角坐标系统来满足测量要求。
我国主要采用横切圆柱投影,及高斯—克吕格投影的方法建立平面直角坐标系统,称为高斯—克吕格直角坐标系,简称高斯直角坐标系。
高斯投影采用正形投影,及等角投影,保证了投影的角度不变形,但是其长度变形较为严重。
高斯投影平面上的中央子午线投影为直线且长度不变,其余的子午线均为凹向中央子午线的曲线,其长度大于投影前的长度,离中央子午线越远长度变形越大。
为了限制高斯投影的长度变形,必须依据中央子午线进行分带,把投影范围限制在中央子午线东、西两侧一定的狭长带内分别进行。
但这又使得统一的坐标系分割成各带的独立坐标系。
于是,因分带的结果产生了新的矛盾,即在生产建设中提出了各相邻带的互相联系的问题。
这个问题是通过一个带的平面坐标换算到相邻带的平面坐标,简称为“邻带换算”的方法来解决的。
具体来说,在以下情况下需要进行坐标邻带换算:(1)如图1所示,A、B、1、2、3、4、C、D为位于两个相邻带边缘地区并跨越两个投影带(东、西带)的控制网。
假如起算点A、B以及C、D的起始坐标是按两带分别给出的话,那么为了能在同一带内进行平差计算,必须把西带的A、B点起始坐标换算到东带,或者把东带的C、D点的起始坐标换算到西带。
图1(2)在分界子午线附近地区测图时,往往需要用到另一带的三角点作为控制,因此必须将这些点的坐标换算到同一带中;为了实现两邻带地形图的拼接和使用,位于45′(或37.5′)重叠的三角点需具有相邻带的坐标值,如图2所示。
图2(3)当大比例尺(1:1000或更大)测图时,特别是在工程测量中,要求采用3°带、1.5°带或者任意带,而国家控制点通常只有6°带坐标,这时就产生了6°带同3°带(或1.5°带、任意带)之间的相互坐标换算问题。