换带计算专题
- 格式:pdf
- 大小:588.05 KB
- 文档页数:27

3度带与6度带理解要点1.我国采用6度分带和3度分带:1∶万及1∶5万的地形图采用6度分带投影,即经差为6度,从零度子午线开始,自西向东每个经差6度为一投影带,全球共分60个带,用1,2,3,4,5,……表示.即东经0~6度为第一带,其中央经线的经度为东经3度,东经6~12度为第二带,其中央经线的经度为9度。
1∶1万的地形图采用3度分带,从东经度的经线开始,每隔3度为一带,用1,2,3,……表示,全球共划分120个投影带,即东经~度为第1带,其中央经线的经度为东经3度,东经~度为第2带,其中央经线的经度为东经6度.我省位于东经113度-东经120度之间,跨第38、39、40共计3个带,其中东经度以西为第38带,其中央经线为东经114度;东经~度为39带,其中央经线为东经117度;东经度以东到山海关为40带,其中央经线为东经120度。
地形图上公里网横坐标前2位就是带号,例如:1∶5万地形图上的横坐标为,其中20即为带号,345486为横坐标值。
2.当地中央经线经度的计算六度带中央经线经度的计算:当地中央经线经度=6°×当地带号-3°,例如:地形图上的横坐标为20345,其所处的六度带的中央经线经度为:6°×20-3°=117°(适用于1∶2.5万和1∶5万地形图)。
三度带中央经线经度的计算:中央经线经度=3°×当地带号(适用于1∶1万地形图)。
3、如何计算当地的中央子午线当地中央子午线决定于当地的直角坐标系统,首先确定您的直角坐标系统是3度带还是6度带投影公式推算:6度带中央子午线计算公式:当地经度/6=N;中央子午线L=6 * N (带号)当没有除尽,N有余数时,中央子午线L=6*N - 33度带中央子午线计算公式:当地经度/3=N;中央子午线L=3 X N我国的经度范围西起73°东至135°,可分成六度带十一个(13号带—23号带),各带中央经线依次为(75°、81°、……123°、129°、135°);三度带二十二个(24号带—45号带)。



设计说明书设计题目: 高斯投影换带计算姓名:指导教师:专业:测绘工程2013 年 7月 2 日成绩评分表1 设计内容1.1设计意义高斯投影虽然保证了角度投影前后没有变形,但其长度变形仍然存在,并且距离中央子午线愈远,长度变形愈大。
为了限制高斯投影的长度变形,将椭球面按一定经度的子午线划分成不同的投影带,把投影范围限制在中央子午线东西两侧一定的狭长地带内分别进行投影。
由于中央子午线的经度不同,使得椭球面上统一的大地坐标系,分割成为各带独立的平面坐标系。
为了得到统一的坐标系,必须进行换带计算。
在实际测量工作中,我们常常遇到坐标不统一的情况,为了计算简便,把不同形式的坐标转换成我们所需的坐标,为我们的工程服务,经常需要进行高斯投影正算、反算、坐标换带和子午线收敛角的计算工作。
为此,我们编写了这一程序设计,希望能使以后的转换工作更加简便。
本软件主要应用相关的转换公式,采用C#编程可随时随地实现任何参考椭球体下高斯坐标转换与大地坐标之间的正反算和换带计算,达到高斯平面坐标转换的目的。
本文所编程序的特点是,操作简单.输出简捷、结果完整,不需要另加辅助内容。
本设计主要是利用C#作为前端开发工具进行应用程序开发。
1.2基础理论正算是指:由大地坐标(L,B)求得高斯平面坐标(x,y)的过程。
反算是指:由高斯平面坐标(x,y)求得大地坐标(L,B)的过程。
正算:高斯投影必须满足的三个条件:(1),中央子午线投影后为直线。
(2),中央子午线投影后长度不变。
(3),投影具有正性性质,即正性投影条件。
由第一个条件可知,中央子午线东西两侧的投影必然对称于中央子午线。
设在托球面上有P1 ,P2,且对称于中央子午线。
其大地坐标为(l,B),(-l,B)则投影后的平面坐标一定为P1·(x,y),P2·(x,-y).由第二个条件可知,位于中央子午线上的点,投影后的纵坐标x应该等于投影前从赤道量至该点的子午弧长。

坐标的换带计算为了限制高斯投影长度变形,将椭球面按一定经度的子午线划分成不同的投影带;或者为了抵偿长度变形,选择某一经度的子午线作为测区的中央子午线。
由于中央子午线的经度不同,使得椭球面上统一的大地坐标系,变成了各自独立的平面直角坐标系,就需要将一个投影带的平面直角坐标系,换算成另外一个投影带的平面直角坐标,称为坐标换带。
2.2.3. 1坐标换带的方法坐标换带有直接换带计算法和间接换带计算法两种。
目前采用间接换带计算法,因此下面仅就此方法作一介绍。
如将第一带(东带或西带)的平面坐标换算为第二带(西带或东带)的平面坐标,方法是先根据第一带的平面坐标x,y和中央子午线的经度L。
按高斯投影坐标反算公式求得大地坐标B,L然后根据B,L和第二带的中央子午线经度按高斯投影坐标正算公式求得在第二带中的平面坐标,。
由于在换带计算中,把椭球面上的大地坐标作为过渡坐标,因而称为间接换带法。
这种方法理论上是严密的,精度高,而且通用性强,他适用于6°带与6°带,3°带与3°带,6°带与3°带之间的坐标换带。
虽然这种方法计算量较大,但可用电子计算机计算来克服,故已成为坐标换带中最基本的方法。
2.2.3. 2坐标换带的实际应用在生产实践中通常有以下两种情况需要换带计算⑴控制网中的已知点位于相邻的两个投影带中。
如图5(图5:坐标换带示意图)中的附合导线,A,B,C,D为已知高级点。
A,B 两点位于西带内,具有西带的高斯平面直角坐标值;C,D两点位于东带内,具有东带的高斯平面直角坐标值。
在坐标平差计算时,就必须将它们的坐标系统统一起来,或是将A,B点的西带坐标值换算至东带,或是将C,D点的东带坐标值换算至西带。
⑵国家控制点的坐标通常是6°带的坐标,而在工程测量中往往需要采用带或1.5°带,这就产生了6°带与带或 1.5°带之间的坐标换算问题。


坐标换带计算南方测绘石家庄导航产品部蔡高峰按照一定的经差将地球椭球面划分成若干投影带,这是高斯投影中限制长度变形中最有效的方法。
在分带时既要控制长度变形使其不大于测图误差,又要使带数不致过多以减少换带计算工作,根据此原则将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带进行投影。
通常按经差6度或3度,分为六度带或三度带。
六度带是自0度子午线起每隔经差6度自西向东分带,带号依次编为第1、2 (60)带。
三度带是在六度带的基础上分成的,它的中央子午线与六度带的中央子午线和分带子午线重合,即自1.5度子午线起每隔经差3度自西向东分带,带号依次编为三度带第1、2…120带。
六度带可用于中小比例尺(如1:250000)测图,三度带可用于大比例尺(如1:10000)测图,城建坐标多采用的是三度带的高斯投影。
高斯——克吕格投影是按分带方法各自进行投影,故各带坐标成独立系统。
以中央经线投影为纵轴(x),赤道投影为横轴(y),两轴交点即为各带的坐标原点。
纵坐标以赤道为零起算,赤道以北为正,以南为负。
我国位于北半球,纵坐标均为正值。
横坐标如以中央经线为零起算,中央经线以东为正,以西为负,横坐标出现负值,使用不便,故规定将坐标纵轴西移500公里当作起始轴,凡是带内的横坐标值均加500公里。
由于高斯——克吕格投影的每一个投影带的坐标都是对本带坐标原点的相对值,所以各带的坐标完全相同,为了区别某一坐标系统属于哪一带,在横轴坐标前加上带号,如(4231898m,21655933m),其中21即为带号。
6度带中央子午线计算公式:中央子午线L=6 ×N-3 。
N=当地经度/6,N值不进行四舍五入,只取整数部分,(N+1)即为6度带的带号。
3度带中央子午线计算公式:中央子午线L=3 ×N 。
N=当地经度/3,N值进行四舍五入后即为3度带的带号。
由于城建坐标多采用3度带的高斯投影,有时知道的控制点坐标是6度带的坐标,这时就需要将其转换为3度带的坐标。


高斯正反算及坐标换带高斯正反算是指在平面直角坐标系中,将椭球面上的点坐标转换为大地坐标系中的经纬度,或者将地球上的经纬度转换为平面直角坐标系中的点坐标的过程。
一种常用的方法是高斯投影法。
高斯投影法是根据转换点处的经纬度和椭球参数来推算出该点的高斯坐标(x,y),或者反过来,根据高斯坐标(x,y)和椭球参数来推算出该点的经纬度。
高斯正算的基本步骤如下:1.输入要转换的点的经纬度和所在的带号,以及该带所采用的椭球参数;2.利用所在带的中央子午线的经度,与待转换点的经度进行比较,求出两者之间的经差Δλ;3.根据公式计算出所在带的缩比因子、子午线弧长、子午线曲率半径、椭球面上的子午线曲率半径、蒙卡托投影系数、坐标系数、角度系数,以及待转换点的子午线弧长;4.根据公式计算出该点的高斯坐标(x,y)。
高斯反算的基本步骤如下:1.输入要转换的点的高斯坐标(x,y)和所在的带号,以及该带所采用的椭球参数;2.根据公式计算出该点的反高斯子午线弧长和反高斯纬度;3.利用所在带的中央子午线的经度,以及待转换点的反高斯子午线弧长和反高斯纬度,求出该点的经度和纬度。
坐标换带是指将一个点的坐标从一个投影带转换到另一个投影带的过程,可以通过中央子午线的经度进行换带。
换带时需要考虑两个投影带的缩比因子、子午线弧长、子午线曲率半径、椭球面上的子午线曲率半径等参数的差异。
具体步骤如下:1.将原始坐标从原始带转换到以0度经线为中央子午线的坐标系,即不考虑换带问题时的坐标;2.根据原始坐标所在的带和目标坐标所在的带,计算两者子午线的经差Δλ;3.根据两个投影带的椭球参数和所在位置的中央子午线经度,计算出两个投影带的缩比因子、子午线弧长、子午线曲率半径及椭球面上的子午线曲率半径;4.利用计算出的参数,将原始坐标从以0度经线为中央子午线的坐标系转换为目标坐标系中的坐标。

测绘坐标3度带与6度带换带计算测绘坐标系统是用于描述地球表面上点的位置的一种方法。
在测绘坐标系统中,有两种常用的带号方式,即3度带和6度带。
3度带和6度带都是基于经度线划分的。
地球被划分为360个经度线,每个经度线之间相隔1度。
在3度带系统中,每个带的宽度是3度,而在6度带系统中,每个带的宽度是6度。
这两种系统在测绘和导航中常常被使用。
在进行3度带和6度带的换带计算时,需要考虑到点的经度和纬度。
以下是一种常用的方法:1.确定原始坐标点的带号:首先,需要根据原始坐标点的经度确定其所在的带号。
在3度带系统中,带号的计算方式为经度除以3,并向下取整。
在6度带系统中,带号的计算方式为经度除以6,并向下取整。
2.确定原始带号的中央经线:在确定原始带号后,需要计算原始带号所对应的中央经线的经度。
在3度带系统中,中央经线的经度为带号乘以3加上1.5、在6度带系统中,中央经线的经度为带号乘以6加上33.计算原始坐标点在原始带号中的相对位置:根据原始坐标点的经度,减去原始带号的中央经线的经度,就可以得到原始坐标点在原始带号中的相对位置。
这个相对位置可以表示为一个0到1之间的比例。
4.计算换带后的新带号:在计算得到原始带号的相对位置后,可以根据这个比例来计算新带号。
在3度带系统中,新带号的计算方式为原始带号加上1,再加上相对位置的值的整数部分。
在6度带系统中,新带号的计算方式为原始带号加上2,再加上相对位置的值的整数部分。
5.计算换带后的新中央经线:根据新带号计算得到新中央经线的经度。
在3度带系统中,新中央经线的经度为新带号乘以3加上1.5、在6度带系统中,新中央经线的经度为新带号乘以6加上36.计算换带后的新坐标点:最后,根据新中央经线的经度和原始坐标点的纬度,得到换带后的新坐标点。
需要注意的是,在进行换带计算时,应根据具体的需求选择使用3度带还是6度带。
由于6度带系统的带宽度较大,所以在换带计算时可能会存在一定的误差。
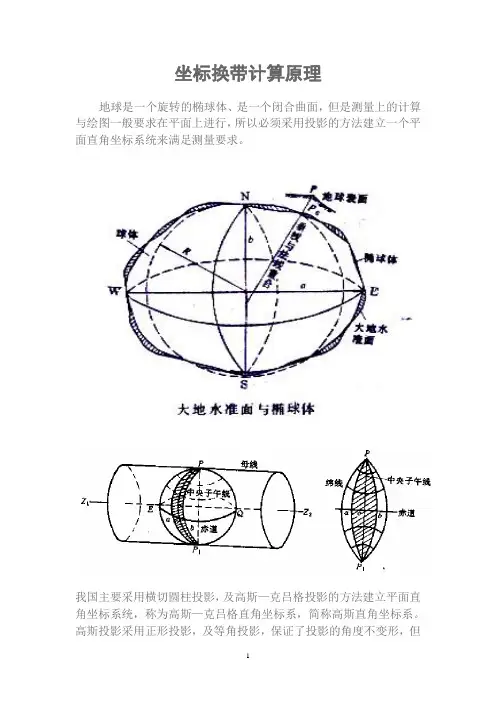
坐标换带计算原理地球是一个旋转的椭球体、是一个闭合曲面,但是测量上的计算与绘图一般要求在平面上进行,所以必须采用投影的方法建立一个平面直角坐标系统来满足测量要求。
我国主要采用横切圆柱投影,及高斯—克吕格投影的方法建立平面直角坐标系统,称为高斯—克吕格直角坐标系,简称高斯直角坐标系。
高斯投影采用正形投影,及等角投影,保证了投影的角度不变形,但是其长度变形较为严重。
高斯投影平面上的中央子午线投影为直线且长度不变,其余的子午线均为凹向中央子午线的曲线,其长度大于投影前的长度,离中央子午线越远长度变形越大。
为了限制高斯投影的长度变形,必须依据中央子午线进行分带,把投影范围限制在中央子午线东、西两侧一定的狭长带内分别进行。
但这又使得统一的坐标系分割成各带的独立坐标系。
于是,因分带的结果产生了新的矛盾,即在生产建设中提出了各相邻带的互相联系的问题。
这个问题是通过一个带的平面坐标换算到相邻带的平面坐标,简称为“邻带换算”的方法来解决的。
具体来说,在以下情况下需要进行坐标邻带换算:(1)如图1所示,A、B、1、2、3、4、C、D为位于两个相邻带边缘地区并跨越两个投影带(东、西带)的控制网。
假如起算点A、B以及C、D的起始坐标是按两带分别给出的话,那么为了能在同一带内进行平差计算,必须把西带的A、B点起始坐标换算到东带,或者把东带的C、D点的起始坐标换算到西带。
图1(2)在分界子午线附近地区测图时,往往需要用到另一带的三角点作为控制,因此必须将这些点的坐标换算到同一带中;为了实现两邻带地形图的拼接和使用,位于45′(或37.5′)重叠的三角点需具有相邻带的坐标值,如图2所示。
图2(3)当大比例尺(1:1000或更大)测图时,特别是在工程测量中,要求采用3°带、1.5°带或者任意带,而国家控制点通常只有6°带坐标,这时就产生了6°带同3°带(或1.5°带、任意带)之间的相互坐标换算问题。
铁路勘测中坐标换带计算方法作者:董立刚来源:《科技创新导报》 2012年第4期董立刚(铁道第三勘察设计院集团有限公司天津 300251)摘要:在铁路勘测作业中,需要通过投影得到便于工程施工的平面坐标,在相邻施工坐标系接边处的点通常需要提供两套网格坐标,因此就带来了坐标换带计算问题。
本文详细介绍了一种简单而实用的坐标换带计算方法,并通过数据实验证明该方法的正确性,对铁路勘测作业中的换带计算有较高的参考价值。
关键词:坐标换带计算椭球膨胀法高斯投影中图分类号:U442.4 文献标识码:A 文章编号:1674-098X(2012)02(a)-0078-02引言铁路特别是高速铁路的发展正逐步改变着人们的生活节奏和方式。
在铁路勘测作业中,需要通过投影得到便于工程施工的平面坐标。
在国家高斯坐标系中,其投影面为参考椭球面;而在施工坐标系中,投影面通常为测区平均高程面,从而导致了投影变形,即实际地面的长度与坐标反算出来的距离不相等。
为了消除该投影变形,减小高斯投影变形和高程归化改正带来的影响,在铁路勘测作业中,需要将一条线路特别是东西走向的线路分为若干个施工坐标系,每个施工坐标系选取特定的中央子午线和投影面高程。
为了保证贯通精度,在相邻施工坐标系接边处的点通常需要提供两套网格坐标,因此就带来了坐标换带计算问题。
当前,国内外许多学者提出了若干解决方法,但由于所用模型、基准等不同,导致转换出的坐标也不尽相同,不利于工程实际应用。
2 实验数据分析实验选取某高速铁路精密工程控制网的若干点,将其在同椭球下从122°换带计算为123°,并将结果与商用软件进行比对,选取其中距离较远的三个点成果列入表1.由实验结果可以看出,本文所用模型与商用软件的结果基本一致。
由于所用模型有差异,因此东坐标转换后略有不同,且离中央子午线越远差别越大,而北坐标不受影响,但总体上看,可认为其成果一致。
将上述三个点进行换代计算后再换算回原来的坐标,将其比对并将成果列入表2。
采用CASIO fx-4500p计算器进行换带计算
杨其全
【期刊名称】《《阳煤科技》》
【年(卷),期】1996(000)004
【摘要】坐标换带计算是我们日常测量工作中经常遇到的问题,该项工作通常都是用微机或用计算器配合《高斯克吕格换带计算表》进行计算,本文介绍一种采用CASIO fx-4500p型计算器进行坐标换带的简易方法。
fx-4500p计算器是日本CASIO公司生产的系列产品之一,具有能同时显示方程式及计算结果的2行式显示屏幕;
【总页数】3页(P29-31)
【作者】杨其全
【作者单位】阳泉矿务局地测处
【正文语种】中文
【中图分类】P226.3
【相关文献】
1.利用CASIO fx-4500P计算器进行林业抽样调查的计算方法 [J], 李云梅
2.巧用CASIOfx-4800P计算器进行坐标换带计算 [J], 许锡文;张囡;许恩庆
3.CASIO fx-4500P计算器计算不规则图形面积的程序设计与应用 [J], 桂军耀;袁自立;郭海涛
4.fx-4500p计算器坐标换带直接算法 [J], 吴少波
5.CASIO fx-4500P计算器小班片蚀模数计算程序 [J], 李波
因版权原因,仅展示原文概要,查看原文内容请购买。
2.2.3坐标的换带计算为了限制高斯投影长度变形,将椭球面按一定经度的子午线划分成不同的投影带;或者为了抵偿长度变形,选择某一经度的子午线作为测区的中央子午线。
由于中央子午线的经度不同,使得椭球面上统一的大地坐标系,变成了各自独立的平面直角坐标系,就需要将一个投影带的平面直角坐标系,换算成另外一个投影带的平面直角坐标,称为坐标换带。
2.2.3. 1坐标换带的方法坐标换带有直接换带计算法和间接换带计算法两种。
目前采用间接换带计算法,因此下面仅就此方法作一介绍。
如将第一带(东带或西带)的平面坐标换算为第二带(西带或东带)的平面坐标,方法是先根据第一带的平面坐标x,y和中央子午线的经度L。
按高斯投影坐标反算公式求得大地坐标B,L然后根据B,L和第二带的中央子午线经度按高斯投影坐标正算公式求得在第二带中的平面坐标,。
由于在换带计算中,把椭球面上的大地坐标作为过渡坐标,因而称为间接换带法。
这种方法理论上是严密的,精度高,而且通用性强,他适用于6°带与6°带,3°带与3°带,6°带与3°带之间的坐标换带。
虽然这种方法计算量较大,但可用电子计算机计算来克服,故已成为坐标换带中最基本的方法。
2.2.3. 2坐标换带的实际应用在生产实践中通常有以下两种情况需要换带计算⑴控制网中的已知点位于相邻的两个投影带中。
如图5(图5:坐标换带示意图)中的附合导线,A,B,C,D为已知高级点。
A,B 两点位于西带内,具有西带的高斯平面直角坐标值;C,D两点位于东带内,具有东带的高斯平面直角坐标值。
在坐标平差计算时,就必须将它们的坐标系统统一起来,或是将A,B点的西带坐标值换算至东带,或是将C,D点的东带坐标值换算至西带。
⑵国家控制点的坐标通常是6°带的坐标,而在工程测量中往往需要采用带或1.5°带,这就产生了6°带与带或 1.5°带之间的坐标换算问题。
我们知道,带的中央子午线中,有半数与6°带的中央子午线重合。
所以,由6°带到3°带的换算区分为2种情况:① 3°带与6°带的中央子午线重合如图所示,3°带第(图6:坐标换带示意图)41带与6°第21带的中央子午线重合。
既然中央子午线一致,坐标系统也就一致。
所以,图中P1点在6°带第21带的坐标,也就是该点在3°带第41带的坐标。
在这种情况下,6°带与3°带之间,不存在换带计算问题。
② 3°带中央子午线与6°带分带子午线不重合如图所示,若已知P2点在6°带第21带的坐标,求它在3°带第42带的坐标。
由于这2个投影带的中央子午线不同,坐标系统不一致,必须进行换带计算。
不过P2点在6°带第21带的坐标与它在3°第41带的坐标相同,所以6°带到3°带坐标换算,也可看作是3°带到3°带的邻带坐标换算。
换带计算目前广泛采用高斯投影坐标正反算方法,他适用于任何情况下的换带计算工作。
这种方法的程序是:首先将某投影带的已知平面坐标(x1,y1 ),按高斯投影坐标反算公式求得其大地坐标(B,L);然后根据纬度B和对于所选定的中央子午线的经差,按高斯投影坐标正算公式求其在选定的投影带的平面坐标(x2,y2)。
例如,某点A在新54坐标系6°带的平面坐标为x1=3589644.287y1=20679136.439求A点在3°带的平面直角坐标(x2,y2).首先确定A点所在投影带中央子午线经度。
由横坐标的规定值可以直接判定,A点位于6°带第20带,其中央子午线经度L。
=117°,横坐标的自然值为y1=679136.493-500000=+179136.439m;该坐标等同于3°带第39带的平面坐标。
其次将已知的6°带坐标反算为大地坐标。
为此,可直接应用坐标反算公式进行计算,其结果为B=32°2457.6522"L=118°5415.2206"由大地经度L可判断,A点位于3°第40带,中央子午线为L。
=120°。
最后根据高斯投影坐标正算公式,由已知的纬度B和经度计算A点在3°带第40带的平面直角坐标,得x2=3588576.591y2=40396922.874其中横坐标y2为规定值。
2.2.3. 3相邻带坐标换算存在的问题及解决方案在具有不同抵偿高程面的两个相邻投影带之间进行坐标换带计算时,由于具有不同的抵偿高程面而使一个带中的坐标换至相邻带时使长度变形超线,在线路工程测量中就需要进行精度预算,从而在进行坐标换带计算时使长度变形控制在允许的范围内。
其基本方法如下:根据高斯投影长度综合变形公式将长度综合变形容许值1:40000代入上式即可得到下列方程对于已知高程面的测区,利用该式可以计算出相对变形不超过1:40000的投影带内y坐标的取值范围,根据y坐标的取值范围使在布设控制导线边时,使跨带边的长度变形在y坐标的取值范围之内,这样就可以进行换带计算而不使综合长度变形超线。
其具体解决方案如下:⑴国家统一带相邻带的坐标换算方法:在线路工程中,如果由于线路过长而需要进行相邻带的坐标换算,这是就需要对控制点进行精度预算,从而使换带计算顺利进行。
其主要方法如图:根据高斯投影长度综合变形公式将长度综合变形容许(图7:坐标换带示意图)值1:40000代入上式即可得到下列方程对于已知高程面的测区,利用该式可以计算出相对变形不超过1:40000的投影带内y坐标的取值范围,根据y坐标的取值范围使在布设控制导线边时使P点处于41带的扩展区域内,该扩展区内所有的点都满足精度要求。
这样P点在两个投影带中都满足精度要求同时又利于换带计算。
利用这种方法就可以很方便的进行相邻带的坐标换算。
⑵带相邻带的换带计算当国家统一带不能满足精度要求时,即如上图P点在相交处不能达到精度要求时就必须考虑其他方法来解决此问题。
由于投影带划分的目的是限制高斯投影长度变形,所以可以通过细分投影带的方法来限制高斯投影长度变形。
其方法是:如图P点,当该点在带第42带换算至第41带时不能满足精度要求时,就可以通过在原带的基础上细划分为带从而减少高斯投影长度变形,这样相邻带之间在满足精度要求的基础上就有(图8:坐标换带示意图)一部分扩展区域,在这部分扩展区域内所有的点在相邻带都满足精度要求,这样就可以用如上1分析的方法进行相邻带之间的坐标换算。
3 独立坐标系统的建立在工程建设地区(如公路、铁路、管线)布设测量控制网时,其成果不仅要满足1:500比例尺测图需要,而且还应满足一般工程放样的需要。
在线路测量中,总是要将测得的数据经计算再放到实地而施工放样时要求控制网由坐标反算的长度与实测的长度尽可能相符,但国家坐标系的成果很难满足这样的要求,这是因为国家坐标系每个投影带(高斯投影)都是按一定的间隔(6°或3°)划分,由西向东有规律地分布.由于每项工程的建设地区不同,且国家坐标系统的高程归化面是参考椭球面,各地区的地面位置与参考椭球面都有一定的距离,这两项将产生高斯投影变形改正和高程归化改正,经过这两项改正后的长度不可能与实测的长度相等。
建立独立坐标系的主要目的就是为了减小高程归化与投影变形产生的影响,因此必须将它们控制在一个微小的范围内,使计算出来的长度在实际利用时(如工程放样)不需要做任何改算。
本章就如何建立独立坐标系统而使其长度变形控制在允许范围内作详细讨论。
3.1.1测量投影面与投影带的选择3.1.1. 1 有关投影变形的基本概念平面控制测量投影面和投影带的选择,主要是解决长度变形问题。
这种投影变形主要由以下两方面因素引起:⑴实量边长归算到参考椭球体面上的变形影响(3-1)其推导过程为:(图9:实量边长归算到参考椭球体面示意图)由图知由上式可得从而可得式中,为归算边高出参考椭球面的平均高程;S为归算边的长度;为实量边长在参考椭球面上的长度R为归算边方向参考椭球法截弧的曲率半径。
归算边的相对变形为:(3-2)由公式可以看出:值与成正比,随增大而增大。
⑵将参考椭球面上边长归算到高斯投影面上的变形影响(3-3)式中,,即为投影归算边长即,为归算边两端点横坐标平均值,为参考椭球面平均曲率半径。
投影边的相对变形为:(3-4)由公式可以看出:的值总为正,即椭球面上长度归算至高斯面上,总是增大的,值与成正比而增大,离中央子午线愈远变形愈大。
3.1.1. 2 有关工程测量平面控制网的精度要求的概念为便于施工放样的顺利进行,要求由控制点坐标直接反算的边长与实地量得的边长,在长度上应该相等,即由上述两项归算投影改正而带来的变形或改正数,不得大于施工放样的精度要求。
一般地,施工放样的方格网和建筑轴线的测量精度为1/5000~1/20000。
因此,由归算引起的控制网长度变形应小于施工放样允许误差的1/2,即相对误差为1/10000~1/40000,也就是说,每公里的长度改正数,不应该大于10~2. 5cm。
3.1.1. 3工程测量投影面和投影带选择的基本出发点⑴ 在满足精度要求的前提下,为使测量结果一测多用,应采用国家统一带高斯平面直角坐标系,将观测结果归算至参考椭球面上。
即工程测量控制网应同国家测量系统相联系;⑵当边长的两次归算投影改正不能满足上述要求时,为保证测量结果的直接利用和计算的方便,可采用任意带的独立高斯平面直角坐标系,归算测量结果的参考面可自己选定。
为此可用以下手段实现:① 通过改变从而选择合适的高程参考面,将抵偿分带投影变形(称为抵偿投影面的高斯正形投影);② 改变从而对中央子午线作适当移动,以抵偿由高程面的边长归算到参考椭球面上的投影变形(称为任意带高斯正形投影);③ 通过既改变(选择高程参考面),又改变(移动中央子午线),来抵偿两项归算改正变形(称为具有高程抵偿面的任意带高斯正形投影)。
3.1.2 投影改正值的变化规律一般情况下,将投影改正作为常数看待,不考虑测区内不同位置投影改正值的变化问题。
然而在实际情况中,即使在地形比较平坦的地区或较小范围的测区,其影响也是不容忽视的。
设测区中任一点 k 与测区中心在东西方向(y轴)上的距离为y,与测区平均高程的高差为h 。
k点的两项投影改正与测区中心过平均高程面的改正是不一样的。
3.1.2. 1观测值化至参考椭球面投影改正值的变化k 点的大地水准面投影改正为:上式中等号右边的第二项即为椭球面投影改正的变化量,令由上式可知,高差h与投影改正的变化量成正比,随着h的增大而增大。