福建省春季高考高职单招数学模拟试题(十二)及答案word.doc

2022年福建省南平市普通高校高职单招数学摸底卷(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.下列函数是奇函数的是A.y=x+3B.C.D.2.为了了解全校240名学生的身高情况，从中抽取240名学生进行测量，下列说法正确的是（）A.总体是240B.个体是每-个学生C.样本是40名学生D.样本容量是403.下列函数中，既是偶函数又在区间（0,+∞)上单调递减的是（）A.y=1/xB.y=e xC.y=-x2+1D.y=lgx4.A.B.C.5.若lgx＜1，则x的取值范围是（）A.x＞0B.x＜10C.x＞10D.0＜x＜106.函数y=lg(x+1)的定义域是（）A.(-∞，-1)B.(-∞,1)C.(-l,+∞)D.(1,+∞)7.(1 -x)4的展开式中，x2的系数是( )A.6B.-6C.4D.-48.已知等差数列中{a n}中，a3=4，a11=16,则a7=( )A.18B.8C.10D.129.“没有公共点”是“两条直线异面”的( )A.充分而不必要条件B.充分必要条件C.必要而不充分条件D.既不充分也不必要条件10.已知sin(5π/2+α)=1/5，那么cosα=()A.-2/5B.-1/5C.1/5D.2/511.A.(1,2）B.(-1,2)C.(-1,-2)D.(1,-2)12.拋掷两枚骰子，两次点数之和等于5的概率是（）A.B.C.D.13.直线以互相平行的一个充分条件为（）A.以都平行于同一个平面B.与同一平面所成角相等C.平行于所在平面D.都垂直于同一平面14.为A.23B.24C.25D.2615.命题“若f(x)是奇函数，则f(-x)是奇函数”的否命题是（）A.f(x)是偶函数，则f(-x)是偶函数B.若f(x)不是奇函数，则f(-x)不是奇函数C.若f(-x)是奇函数，则f(x)是奇函数D.若f(-x)不是奇函数，则f(x)不是奇函数16.A.B.C.D.17.cos240°=()A.1/2B.-1/2C./2D.-/218.下列各组数中，表示同一函数的是（）A.B.C.D.19.由数字0，1，2，3，4，5组成没有重复数字的六位数，其中个位数小于十位数的共有（）A.210B.360C.464D.60020.下列句子不是命题的是A.5+1-3=4B.正数都大于0C.x>5D.二、填空题(20题)21.长方体中，具有公共顶点A的三个面的对角线长分别是2，4，6，那么这个长方体的对角线的长是_____.22.己知0<a<b<1，则0.2a 0.2b。

2024年高职单招数学仿真试卷一、选择题（每题3分，共30分）1. 若集合A = {1, 2, 3}，B = {2, 3, 4}，则A ∩ B =（）A. {1}B. {2, 3}C. {1, 2, 3, 4}D. ∅答案：B。

解析：A ∩ B是指由既属于A又属于B的所有元素组成的集合，所以A ∩ B = {2, 3}。

2. 函数y = sin(x + π/2)的图象是由函数y = sinx的图象（）A. 向左平移π/2个单位得到B. 向右平移π/2个单位得到C. 向上平移π/2个单位得到D. 向下平移π/2个单位得到答案：A。

解析：对于函数y = f(x + a)，当a>0时，图象向左平移a个单位，这里y = sin(x + π/2)，是y = sinx向左平移π/2个单位得到的。

3. 已知向量a=(1,2)，b=(3, - 4)，则a·b =（）A. - 5B. - 2C. 2D. 5答案：A。

解析：向量a=(x1,y1)，b=(x2,y2)，则a·b=x1x2 + y1y2，所以a·b= 1×3+2×(-4)=3 - 8=-5。

4. 在等差数列{an}中，a1 = 1，公差d = 2，则a5 =（）A. 7B. 9C. 11D. 13答案：B。

解析：等差数列通项公式an=a1+(n - 1)d，所以a5 = 1+(5 - 1)×2 = 1+8 = 9。

5. 圆x²+y²=4的圆心坐标和半径分别是（）A. (0,0)，2B. (0,0)，4C. (2,0)，2D. (-2,0)，2答案：A。

解析：圆的标准方程为(x - a)²+(y - b)²=r²，其圆心坐标为(a,b)，半径为r，对于x²+y²=4，即(x - 0)²+(y - 0)²=2²，圆心坐标为(0,0)，半径为2。

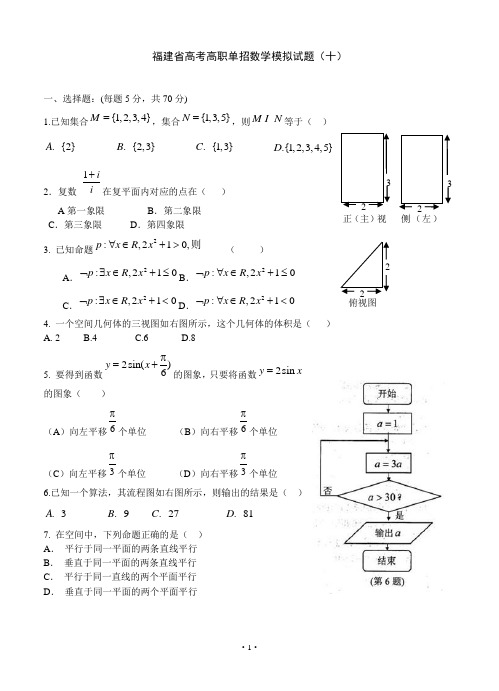
福建省高考高职单招数学模拟试题（十）一、选择题：(每题5分，共70分)1.已知集合{1,2,3,4}M =，集合{1,3,5}N =，则M N 等于（ ）.{2}A .{2,3}B .{1,3}C .{1,2,3,4,5}D2．复数 1ii +在复平面内对应的点在（ ）A 第一象限B ．第二象限C ．第三象限D ．第四象限3. 已知命题2:,210,p x R x ∀∈+>则 （ ） A ．2:,210p x R x ⌝∃∈+≤B ．2:,210p x R x ⌝∀∈+≤C ．2:,210p x R x ⌝∃∈+<D ．2:,210p x R x ⌝∀∈+< 4. 一个空间几何体的三视图如右图所示，这个几何体的体积是（ ） A. 2 B.4 C.6 D.85. 要得到函数2sin()6y x π=+的图象，只要将函数2sin y x =的图象（ ）（A ）向左平移6π个单位 （B ）向右平移6π个单位 （C ）向左平移3π个单位 （D ）向右平移3π个单位6.已知一个算法，其流程图如右图所示，则输出的结果是（ ）.3A .9B .27C .81D7. 在空间中，下列命题正确的是（ ） A ． 平行于同一平面的两条直线平行 B ． 垂直于同一平面的两条直线平行 C ． 平行于同一直线的两个平面平行 D ． 垂直于同一平面的两个平面平行正（主）视侧（左）俯视图8.若AD 为ABC ∆的中线，现有质地均匀的粒子散落在ABC ∆内，则粒子在ABD ∆内的概率等于（ ）4.5A 3.4B 1.2C 2.3D9. 计算sin 240︒的值为（）.A 1.2B - 1.2CD⒑"tan 1"α=是""4πα=的 （ ）A.必要而不充分条件B.充分而不必要条件C.充要条件D.既不充分也不必要条件 11. 下列函数中，在),0(+∞上是减函数的是（ ）.Ax y 1=.B 12+=x y .C xy 2= .D x y 3l o g =⒓已知直线的点斜式方程是21)y x -=-，那么此直线的倾斜角为（ ）.6A π.3B π2.3C π 5.6D π13.已知实数x 、y 满足04x y x y ⎧⎪⎨⎪+⎩≥≥0≥4，则z x y =+的最小值等于（ ）.0A .1B .4C .5D14、设椭圆的两焦点为F1、F2，过F2作椭圆长轴的垂线交椭圆于点P ，若△F1PF2为等腰直角三角形，则椭圆的离心率为（ ） A 、22B 、212-C 、22-D 、12-二、 填空题：本大题共4个小题，每小题5分，共20分。

2022年福建省福州市普通高校高职单招数学测试题(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.若集合M={3,1,a-1}，N = {-2,a2}，N为M的真子集，则a的值是( )A.-1B.1C.0D.2.袋中有大小相同的三个白球和两个黑球，从中任取两个球，两球同色的概率为（）A.1/5B.2/5C.3/5D.4/53.函数A.1B.2C.3D.44.下列句子不是命题的是A.B.C.D.5.正方形ABCD的边长为12，PA丄平面ABCD，PA=12，则点P到对角线BD的距离为（）A.12B.12C.6D.66.A.11B.99C.120D.1217.A.B.{-1}C.{0}D.{1}8.若将函数：y=2sin(2x+π/6)的图象向右平移1/4个周期后，所得图象对应的函数为（）A.y=2sin(2x+π/4)B.y=2sin(2x+π/3)C.3;=2sin(2x-π/4)D.3；=2sin(2x-π/3)9.A.(5, 10)B.(-5, -10)C.(10, 5)D.(-10, -5)10.若x2-ax+b＜0的解集为（1，2)，则a+b=( )A.5B.-5C.1D.-111.函数y=log2x的图象大致是（）A.B.C.D.12.A.B.C.D.13.命题“若f(x)是奇函数，则f(-x)是奇函数”的否命题是（）A.f(x)是偶函数，则f(-x)是偶函数B.若f(x)不是奇函数，则f(-x)不是奇函数C.若f(-x)是奇函数，则f(x)是奇函数D.若f(-x)不是奇函数，则f(x)不是奇函数14.已知函数f(x)=x2-x+1，则f(1)的值等于（）A.-3B.-1C.1D.215.袋中装有4个大小形状相同的球，其中黑球2个，白球2个，从袋中随机抽取2个球，至少有一个白球的概率为（）A.B.C.D.16.若102x=25，则10-x等于（）A.B.C.D.17.一条线段AB是它在平面a上的射景的倍，则B与平面a所成角为（）A.30°B.45°C.60°D.不能确定18.A ≠ф是A∩B=ф的( )A.充分条件B.必要条件C.充要条件D.无法确定19.椭圆x2/16+y2/9的焦点坐标为（)A.(,0)(-,0)B.(4,0)(-4,0)C.(3,0)(-3,0)D.(7,0)(-7,0)20.贿圆x2/7+y2/3=1的焦距为（）A.4B.2C.2D.2二、填空题(20题)21.从含有质地均匀且大小相同的2个红球、N个白球的口袋中取出一球，若取到红球的概率为2/5，则取得白球的概率等于______.22.23.24.25.长方体中，具有公共顶点A的三个面的对角线长分别是2，4，6，那么这个长方体的对角线的长是_____.26.已知_____.27.数列{a n}满足a n+1=1/1-a n，a2=2，则a1=_____.28.设AB是异面直线a，b的公垂线段，已知AB=2，a与b所成角为30°，在a上取线段AP=4，则点P到直线b的距离为_____.29.不等式(x-4)(x + 5)>0的解集是。

福建省春季高考高职单招数学模拟试题（三）班级： 姓名： 座号：一. 填空题（本大题满分36分）1. 函数2log (2)y x =+的定义域是2. 方程28x =的解是3. 抛物线28y x =的准线方程是 4. 函数2sin y x =的最小正周期是 5. 已知向量(1 )a k = ，，(9 6)b k =- ，。

若//a b ，则实数 k = 6. 函数4sin 3cos y x x =+的最大值是7. 复数23i +（i 是虚数单位）的模是 8. 在ABC ∆中，角 A B C 、、所对边长分别为 a b c 、、，若5 8 60a b B === ，，，则b= 9.在如图所示的正方体1111ABCD A B C D -中，异面直线1A B 与1B C 所成角的大小为10. 从4名男同学和6名女同学中随机选取3人参加某社团活动，选出的3人中男女同学都有的概率为 。

11. 若等差数列的前6项和为23，前9项和为57，则数列的前n 项和n =S 12. 36的所有正约数之和可按如下方法得到：因为2236=23⨯，所以36的所有正约数之和为22222222(133)(22323)(22323)(122)133)91++++⨯+⨯++⨯+⨯=++++=（参照上述方法，可求得2000的所有正约数之和为二．选择题（本大题满分36分） 13.展开式为ad-bc 的行列式是（ ）（A ）a bd c (B)acb d(C)a d bc(D)b a dc14.设-1()f x为函数()f x = ）(A) 1(2)2f-= (B) 1(2)4f -=(C) 1(4)2f-= (D) 1(4)4f -=15.直线2310x y -+=的一个方向向量是（ ） (A) (2 3)-， (B) (2 3)， (C) (3 2)-， (D) (3 2)，16函数12()f x x -=的大致图像是（ ）17.如果0a b <<，那么下列不等式成立的是（ ） (A)11a b < (B) 2ab b < (C) 2ab a -<- (D) 11a b-<- 18.若复数12 z z 、满足21z z =，则12 z z 、在复数平面上对应的点12 Z Z 、（ ） (A) 关于x 轴对称 (B)关于y 轴对称 (C) 关于原点对称 (D)关于直线y x =对称19. 10(1)x +的二项展开式中的一项是（ ）（A ）45x （B ）290x （C ） 3120x （D ）4252x 20.既是偶函数又在区间(0 )π，上单调递减的函数是（ ）（A ）sin y x = （B ）cos y x = （C ）sin 2y x = （D ）cos 2y x = 21．若两个球的表面积之比为1:4，则这两个球的体积之比为（ ） （A ）1:2 （B ）1:4 （C ）1:8 （D ）1:16 22.设全集U R =，下列集合运算结果为R 的是（ ）D 1 C 1 B 1A 1D CA B（A ）N C Z U （B ）N C Z U （C ）}{φU C （D ）{0}U C23.已知 a b c R ∈、、，“240b ac -<”是“函数2()f x ax bx c =++的图像恒在x 轴上方”的（ ） （A ）充分非必要条件 （B ）必要非充分条件 （C ）充要条件 （D ）既非充分又非必要条件24.已知 A B 、为平面内两定点，过该平面内动点M 作直线AB 的垂线，垂足为N .若2MN AN NB λ=⋅，其中λ为常数，则动点M 的轨迹不可能是（ ）（A ）圆 （B ） 椭圆 （C ） 抛物线 （D ）双曲线三、解答题（本大题满分78分）本大题共有7题，解答下列各题必须写出必要的步骤。

2011年福建省高职单招《数学》试题2012年福建省高职单招《数学》试题一、单项选择题（本大题共10小题，每小题3分，共30分。

在每小题的四个备选答案中，选出一个正确答案，并将正确答案的字母标号填涂在答题卡的相应位置上）1.已知集合{}a A 21，=，若A ∈2，则a 的值为A.1B.2C.4D.62.集合{}11|<<-x x 用区间表示为A.(]1,1-B.[)1,1-C.()1,1-D.[]1,1-3.下列函数是偶函数的是A.x y 1= B.2x y = C.3x y = D.x y =4.函数x y sin =的最大值是A.1-B.0C.1D.25.已知三个数x ,4,2成等比数列，则x 等于A.8B.10C.12D.166.已知两点()()3,30,2B A 、，则直线AB 的斜率为 A.32 B.23 C.2 D.37.投掷一颗正方体骰子，设骰子的构造是均匀的，则掷得1点的概率为 A.61 B.41 C.21 D.1 8.不等式()()021<-+x x 的解集是A.{}1|-<x xB.{}2|>x xC.{}21|-><x x x 或D.{}21|<<-x x9.等差数列 ,9,7,5,3,1的一个通项公式是A.n a n 2=B.12-=n a nC.22-=n a nD.32-=n a n10.若三个平面两两相交，那么它们最多能有几条交线？A.1B.2C.3D.4二、填空题（本大题共12小题，每小题2分，共24分。

把答案填在答题卡的相应位置上）1.已知集合{}1,0=M ，{}2,1=N ，则N M 等于2.已知22>a ，则a 的取值范围是3.函数4-=x y 的定义域为4.等比数列{}n a 的通项公式为n n a 5=，则2a 等于5.不等式2<x 的解集为6.已知直线32::21+==x y l kx y l ，，若21//l l ，则k 等于7.已知圆的方程为()()13222=-+-y x ，则圆心坐标为 8.若指数函数xa y =的图像经过点()3,1，则a 等于 9.1log 2等于10.已知()()2,64,3B A ，-，则的坐标为11.已知2sin a A =，a A =cos ，则A tan 等于 12.如图，棱长为1的正方体的对角线C A '长为三、解答题（本大题共7小题，共46分。

福建省春季高考高职2017-2018学年单招数学模拟试题班级： 姓名： 座号： 成绩： 一、选择题：本大题共14个小题，每小题5分，共70分。

在每小题给出的四个选项中，只有一项符合题目要求，请将答案填写在答题卡上。

1.已知集合{1,2,3,4}M =，集合{1,3,5}N =，则MN 等于（ ）.{2}A .{2,3}B .{1,3}C .{1,2,3,4D 2．复数1ii+在复平面内对应的点在（ ） A 第一象限 B ．第二象限 C ．第三象限 D3. 已知2:,210,p x R x ∀∈+>则 （ ） A ．2:,210p x R x ⌝∃∈+≤ B ．2:,210p x R x ⌝∀∈+≤C ．2:,210p x R x ⌝∃∈+<D ．2:,210p x R x ⌝∀∈+<4. 一个空间几何体的三视图如右图所示，这个几何体的体积是（ ）A. 2B.4C.6D.85. 要得到函数2sin()6y x π=+的图象，只要将函数2sin y x =的图象（ ）（A ）向左平移6π个单位 （B ）向右平移6π个单位（C ）向左平移3π个单位 （D ）向右平移3π个单位6.已知一个算法，其流程图如右图所示，则输出的结果是（ ）.3A .9B .27C .81D 7. 在空间中，下列正确的是（ ）A ． 平行于同一平面的两条直线平行B ． 垂直于同一平面的两条直线平行C ． 平行于同一直线的两个平面平行D ． 垂直于同一平面的两个平面平行8.若AD 为ABC ∆的中线，现有质地均匀的粒子散落在ABC ∆内，则粒子在ABD ∆内的概率等于（ ）4.5A 3.4B 1.2C 2.3D 9. 计算sin 240︒的值为（ ）.A 1.2B - 1.2C D⒑"tan 1"α=是""4πα=的 （ ）（A ）必要而不充分条件 （B ）充分而不必要条件 （C ）充要条件 （D ）既不充正（主）视侧（左）俯视图分也不必要条件11. 下列函数中，在),0(+∞上是减函数的是（ ）.A xy 1=.B 12+=x y .C x y 2= .D x y 3l o g =⒓已知直线的点斜式方程是21)y x -=-，那么此直线的倾斜角为（ ）.6A π.3B π2.3C π 5.6D π13.已知实数x 、y 满足04x y x y ⎧⎪⎨⎪+⎩≥≥0≥4，则z x y =+的最小值等于（ ）.0A .1B .4C .5D14、设椭圆的两焦点为F 1、F 2，过F 2作椭圆长轴的垂线交椭圆于点P ，若△F 1PF 2为等腰直角三角形，则椭圆的离心率为（ ）A 、22 B 、212- C 、22- D 、12-厦门市海沧中学高职高考 数学模拟试卷答题卡一、 请将选择题答案填入：题号1 2 3 4 5 6 7 8 9 10 11 12 13 14 答案非选择题（共80分）二、 填空题：本大题共4个小题，每小题5分，共20分。

FC B AED 某某省高考高职单招数学模拟试题一、选择题：(每题5分，共70分)1．已知集合{1,0,1}A =-，则（ ）A ．1i A +∈B ．21i A +∈C ．31i A +∈D ．41i A +∈2．已知命题P ：“2,230x R x x ∀∈++≥”，则命题P 的否定为（ ） A.2,230x R x x ∀∈++< B. 2,230x R x x ∃∈++≥ C.2,230x R x x ∃∈++< D.2,230x R x x ∃∈++≤ 3．已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是（ ）A ．,,αγβγαβ⊥⊥若则‖B ．,,m n m n αα⊥⊥若则‖C ．,,m n m n αα若则‖‖‖D ．,,m m αβαβ若则‖‖‖4．已知()f x 是定义在R 上的奇函数，当0x ≥时()3xf x m =+（m 为常数），则函数()f x 的大致图象为（ ）5．已知倾斜角为α的直线l 与直线220x y -+=平行，则tan 2α的值为( )A.45B. 34C. 43D.23 6．已知双曲线2221x y a -=的一个焦点为(2,0)，则它的离心率为( )A. 33B. 63C.32 D.27．如图，已知ABCDEF 是边长为1的正六边形，则()BA BC AF ⋅+的值为（ ）A.1-3 D.0第7题图侧视图俯视图主视图222160/3120/3100/360/340/380/320/3频率/组距pm2.5()0.1050.1000.0950.0900.0850.0800.0750.0700.0658．某几何体的三视图及尺寸如图示，则该几何体的表面积为（）A.3πB. 4πC. 6πD.10π9．已知向量(,1),(2,)a x zb y z=-=+，且a b⊥，若变量x,y满足约束条件1325xy xx y≥-⎧⎪≥⎨⎪+≤⎩，则z的最大值为 ( )A.1B.2C.3D.410.若复数2(1)(1)z x x i=-+-为纯虚数，则实数x的值为( )A.1- B.0C.1D.1-或111. 函数)1ln()(2+=xxf的图象大致是 ( )A．B．C．D．12. 已知2()22xf x x=-，则在下列区间中，()0f x=有实数解的是（）A. （－3，－2）B. （－1，0）C. （2，3）D. （4，5）13. 已知11tan,tan()43ααβ=-=则tanβ=( )A.711 B.117-C.113-D.11314. 我国潜艇外出执行任务，在向正东方向航行，测得某国的雷达站在潜艇的东偏北30方向的100海里处，已知该国的雷达扫描半径为70海里，若我国潜艇不改变航向，则行驶多少路程后会暴露目标？（）A、50海里B、)225(310-海里 C、620海里 D、350海里二.填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．15．函数1()lg(1)f xx=-的定义域16．近年来，随着以煤炭为主的能源消耗大幅攀升、机动车保有量急剧增加，我国许多大城市灰霾现象频发，造成灰霾天气的“元凶”之一是空气中的pm2.5（直径小第8题图第12题图24小时平均浓于等于2.5微米的颗粒物）.右图是某市某月（按30天计）根据对“pm2.5” 24小时平均浓度值测试的结果画成的频率分布直方图，若规定空气中“pm2.5”24小时平均浓度值不超过0.075毫克/立方米为达标，那么该市当月有 天“pm2.5”含量不达标． 17．在△ABC 中，已知60,4,5,A b c ===则sin B = . 18. 某程序框图如下图所示，该程序运行后输出的S 的值为 ． 三．解答题：本大题共6小题，满分60分． 19．（本小题满分8分）已知数列{}n a 是公比1q >的等比数列，且1240a a +=， 12256,a a =又2log n nb a =．求数列{nb }的通项公式；20．（本小题满分8分）已知函数()sin()cos ,()f x x x x R π=--∈．(1) 求函数()f x 的最小正周期；(2) 求函数()f x 的最大值和最小值；(3) 若1(),(0,)42f παα=∈，求sin cos αα+的值．21. （本小题满分10分）某产品按行业生产标准分成8个等级，等级系数ξ依次为1,2,,8…，其中5ξ≥为标准A ，3ξ≥为标准B ，产品的等级系数越大表明产品的质量越好，已知某厂执行标准B 生产该产品，且该厂的产品都符合相应的执行标准．从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下： 3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 38 3 4 3 4 4 7 5 6 7该行业规定产品的等级系数7ξ≥的为一等品，等级系数57ξ≤<的为二等品，等级系数35ξ≤<的为三等品．（1）试分别估计该厂生产的产品的一等品率、二等品率和三等品率；（2）从样本的一等品中随机抽取2件，求所抽得2件产品等级系数都是8的概率．结束开始FEDP22. （本小题满分10分）如图①边长为1的正方形ABCD 中，点E 、F 分别为AB 、BC 的中点，将△BEF 剪去，将△AED 、△DCF 分别沿DE 、DF 折起，使A 、C 两点重合于点P 得一三棱锥如图②示. （1）求证：PD EF ⊥；（2）求三棱锥P DEF -的体积；①②23．（本小题满分12分）已知直线:l y x m =+，m R ∈． （1）若以点()2,1M -为圆心的圆与直线l 相切与点P ，且点P 在x 轴上，求该圆的方程；（2）若直线l 关于x 轴对称的直线l '与抛物线21:C x ym =相切，求直线l 的方程和抛物线C的方程． 24．（本小题满分12分）已知函数32()2f x x ax x =--+.(a R ∈). （1）当1=a 时，求函数)(x f 的极值； （2）若对x R ∀∈，有4'()||3f x x ≥-成立，某某数a 的取值X 围．某某省高考高职单招数学模拟试题（十一）参考答案及评分说明第22题图一．选择题：B C B B C A D B C A ABCB 19 ∴11211842n n n n a a q --+==⨯=---------------------------------6分∴2log n n b a ==212log 221n n +=+-------------------------------------------8分20．解：（1）∵()sin cos ),4f x x x x x Rπ=--∈------------------------------2分∴函数()f x 的最小正周期2T π=--------------------------------------3分（2）函数()f x．----------------------------------5分（3）由1()4f α=得1sin cos 4αα-=∴21(sin cos )16αα-=， 1151sin 2,sin 21616αα-==∴21531(sin cos )1sin 211616ααα+=+=+=∵(0,)2πα∈，∴sin cos 0αα+>∴sin cos αα+=．21．解：（1）由样本数据知，30件产品中等级系数7ξ≥有6件，即一等品有6件，二等品有9件，三等品有15件-----------------------------------------------------------3分∴样本中一等品的频率为60.230=，故估计该厂生产的产品的一等品率为0.2；-------4分二等品的频率为90.330=，故估计该厂生产的产品的二等品率为0.3；---------------5分三等品的频率为150.530=，故估计该厂生产的产品的三等品的频率为0.5．-----------6分（2）样本中一等品有6件，其中等级系数为7的有3件，等级系数为8的也有3件，--7分记等级系数为7的3件产品分别为1C 、2C 、3C ，等级系数为8的3件产品分别为1P 、2P 、3P .则从样本的一等品中随机抽取2件的所有可能为：121323(,),(,),(,),C C C C C C 12(,),P P 1323(,),(,)P P P P ,11121321(,),(,),(,),(,),C P C P C P C P 2223(,),(,)C P C P ,3132(,),(,),C P C P 33(,)C P .共15种，-------------------------------10分记从“一等品中随机抽取2件，2件等级系数都是8”为事件A ， 则A 包含的基本事件有12(,),P P 1323(,),(,)P P P P 共3种，-------------------------11分故所求的概率31()155P A ==.-------------------------------------------------12分23．解（1）∴所求的圆的方程为()222(1)2x y -++=．分】（2）解法1．将直线方程y x m =+中的y 换成y -，可得直线l '的方程为y x m =--．--------------------------------------------7分由21,.x y m y x m ⎧=⎪⎨⎪=--⎩得20mx x m ++=，(0)m ≠-----------------------------------9分2Δ14m =-，--------------------------------------------------------------10分∵直线l '与抛物线21:C x ym =相切∴0∆=，解得12m =±．----------------------------------------------------12分当12m =时，直线l 的方程为12y x =+，抛物线C 的方程为22x y =， 13分 当12m =-时，直线l 的方程为12y x =-，抛物线C 的方程为22x y =-． 14分24．解：（1）当1=a 时，32()2f x x x x =--+ 2'()321f x x x =--=(1)(31)x x -+，------------------------------------------2分令'()0f x =，解得121,13x x =-=.当'()0f x >时，得1x >或13x <-； 当'()0f x <时，得113x -<<.当x 变化时，'()f x ，()f x 的变化情况如下表：-------------------------------------------------------------------------------4分∴当13x =-时，函数()f x 有极大值，15()=()2,327f x f -=极大-----------------------5分当1x =时函数()f x 有极小值，()(1)1f x f ==极小---------------------------------6分（2）∵2'()321f x x ax =--，∴对x R ∀∈，4'()||3f x x ≥-成立，即24321||3x ax x --≥-对x R ∀∈成立，--------------------------------------7分①当0x >时，有213(21)03x a x -++≥，即12133a x x +≤+，对(0,)x ∀∈+∞恒成立 ∵1323x x +≥=，当且仅当13x =时等号成立， ∴212a +≤12a ⇒≤------------------------------------------------------11分②当0x <时，有213(12)03x a x +-+≥，即1123||3||a x x -≤+，对(,0)x ∀∈-∞恒成立，∵13||23||x x +≥=，当且仅当13x =-时等号成立， ∴11222a a -≤⇒≥-----------------------------------------------------13分③当0x =时，a R ∈综上得实数a 的取值X 围为11[,]22-.-------------------------------------------14分。