最新上海市松江区六年级数学下册6.11一次方程组的应用(1)沪教版五四制优选教学课件
- 格式:ppt
- 大小:194.00 KB
- 文档页数:7


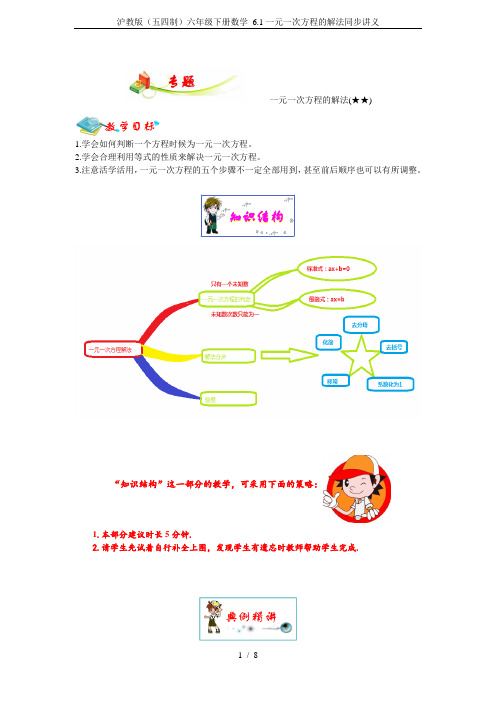
--------一元一次方程的解法(★★)1.学会如何判断一个方程时候为一元一次方程。
2.学会合理利用等式的性质来解决一元一次方程。
3.注意活学活用,一元一次方程的五个步骤不一定全部用到,甚至前后顺序也可以有所调整。
知识结构1.本部分建议时长5分钟.2.请学生先试着自行补全上图,发现学生有遗忘时教师帮助学生完成.“知识结构”这一部分的教学,可采用下面的策略:1.本部分建议时长20分钟.2.进行例题讲解时,教师宜先请学生试着自行解答.若学生能正确解答,则不必做过多的讲解;若学生不能正确解答,教师应对相关概念、公式进行进一步辨析后再讲解例题.3.在每一道例题之后设置了变式训练题,应在例题讲解后鼓励学生独立完成,以判断学生是否真正掌握了相关考点和题型.4.教师应正确处理好例题与变式训练题之间的关系,宜采用讲练结合的方式,切不可将所有例题都讲完后再让学生做变式训练题.下列格式中哪些是一元一次方程?为什么? (★) (1)3463-=-x x (2)0=-xy x (3))1(3x x -- (4)021=+y y(5)16122+=-x x (6)2)532(12522=+---+y y y y答案:(1)是,符合一元一次方程定义 (2)不是,以为它含有两个未知数 (3)不是,因为它不是等式 (4)不是,因为分母含有未知数(5)不是,因为未知数的次数不是一次(6)是,因为去括号后二次项抵消,变为235=-y判断一个等式是否是一元一次方程,必须根据定义中的两个要素进行检查。
注意:有的方程需化简,不能只看表面。
“典例精讲”这一部分的教学,可采用下面的策略:我来试一试!下列方程是否为一元一次方程?为什么?(★)(1),103=x (2),35745=-y x (3),0142=-x (4)1)2(34=+-z z 解答方法:严格遵循定义:①含有一个未知数的等式; ②未知数的次数只能是1 答案:(1)是,符合定义(2)不是,其中含有两个未知数 (3)不是,未知数的次数为2 (4)是,符合定义例题1解下列方程:(★★)(1)84)2(58)2(3--+=++x x x(2)432163-=-+y y (3)2503.002.003.05.09.04.0-=+-+x x x (4)261514131-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-x 解答方法:(1)原方程化为)2(4)2(58)2(3+-+=++x x x 化简,得8)2(2-=+x 系数化为1,得42-=+x移项、化简,得6-=x 所以原方程的解为6-=x(2)去分母,得)32(312)3(2-=-+y y 去括号,得961262-=-+y y 移项,得6962+-=-y y化简,得34-=-y 系数化为1,得43=y 所以原方程的解为43=y (3)根据分数的基本性质,原方程化为25323594-=+-+x x x 去分母,得)5(15)23(10)94(6-=+-+x x x 去括号,得751520305424-=--+x x x移项,得2475154--=-x x 化简,得9911-=-x 系数化为1,得9=x 所以原方程的解为9=x (4)两边同乘以3得6615141-=-⎪⎭⎫⎝⎛-x 即015141=⎪⎭⎫⎝⎛-x 从而0151=-x 移项,得151=x系数化为1,得5=x 所以原方程的解为5=x答案:(1)6-=x (2)43=y (3)9=x (4)5=x我来试一试!解下列方程:(★★) (1) 0.50.70.30.110.30.2x x -+-= (2) 3211212223423x x ⎡⎤⎛⎫-+-= ⎪⎢⎥⎝⎭⎣⎦(3) )1(3202216--=+⎪⎭⎫ ⎝⎛+x x (4) 22126++=x x答案:(1)23=x (2)56-=x (3)2=x (4)3-=x例题2当m 为何值时,方程(1) 3445-=+x x 和方程(2) )2(3)1(2--=-+m m x 有相同的解。


数学六年级(下) 第六章 一次方程(组)和一次不等式(组)6.11一次方程组的应用(1)一、填空题1. 一个三位数,个位数字为a ,十位数字为b ,个位数字为c ,则这个三位数可表示为 。
2. 两个数的和是17,差为-9,这两个数分别是 。
3. 鸡兔同笼,同有头40个,脚96只,则笼中鸡有 只,兔有 只。
4、两数之差为9,又知此两数各扩大3倍后的和为51,则这样的两个数分别为________.5、武炜购买8分与10分邮票共16枚,花了一元四角六分,购买8分和10分的邮票的枚数分别为_________.6、在1996年全国足球甲级A 组的前11轮(场)比赛中,大连万达队保持连续不败,共积23分,按比赛规则,胜一场得3分,平一场得1分,那么该队共胜了________场.7、某车间有28名工人,生产一种螺栓和螺母,每人每天平均能生产螺栓12只或螺母18只,要求一个螺栓配两个螺母,应分配______人生产螺栓,____人生产螺母,才能使螺栓与螺母恰好配套. 8、已知甲、乙两人从相距18千米的两地同时出发,相向而行,154小时相遇.如果甲比乙先走32小时,那么在乙出发后23小时两人相遇.设甲、乙两人速度分别为每小时x 千米和y 千米,则x =________,y =________.9、一个两位数,十位上的数字与个位上的数字之和为9,如果把个位上的数字与十位上的数字对调,则所得的新的两位数比原来的两位数大9。
设个位上的数字为x ,十位上的数字为y ,根据题意列方程组是 .10、某彩电原价1998元,若价格上涨x%,那么彩电的新价格是________元,若价格下降y%,那么彩电的新价格是____________元.11、一个两位数,若个位上数字为x,十位上的数字比个位数字的3倍多1,则这个两位数为____________。
12. 汽车从A 地到B 地,如果每小时行驶50千米就要迟到半小时,如果每小时行驶60千米就要提前半小时到达,则A 、B 相距 千米。