初中数学几何图形十大解法

初中几何最值问题常用解法初中几何最值问题一直是学生们的难点，但通过一些常用的解法，我们可以轻松解决这些问题。

以下将介绍9种常用的解法，帮助您更好地理解和学习。

一、轴对称法轴对称法是一种常用的解决最值问题的方法。

通过将图形进行轴对称变换，可以将问题转化为相对简单的问题，从而找到最值。

二、垂线段法垂线段法是指在几何图形中，利用垂线段的性质来求取最值。

例如，在矩形中，要使矩形的周长最小，可以将矩形的一条边固定，然后通过调整其他边的长度，使得矩形的周长最小。

三、两点之间线段最短两点之间线段最短是几何学中的基本原理。

在解决最值问题时，我们可以利用这个原理，找到两个点之间的最短距离。

四、利用三角形三边关系三角形三边关系是指在一个三角形中，任意两边之和大于第三边，任意两边之差小于第三边。

利用这个关系，可以解决一些与三角形相关的最值问题。

五、利用余弦定理求最值余弦定理是三角学中的基本定理，它可以用来解决一些与角度和边长相关的问题。

通过余弦定理，我们可以找到一个角的最大或最小余弦值，从而求得最值。

六、利用基本不等式求最值基本不等式是指在一个数列中，平均值总是小于等于几何平均值。

利用这个不等式，可以解决一些与数列相关的最值问题。

七、代数运算求最值代数运算是一种基本的数学运算方法，它可以用来解决一些与代数式相关的最值问题。

例如，通过求导数或微分的方法，可以找到一个函数的最大或最小值。

八、代数方程求最值代数方程是一种基本的数学方程形式，它可以用来解决一些与代数方程相关的最值问题。

例如，通过解二次方程或不等式的方法，可以找到一个表达式的最大或最小值。

九、几何变换求最值几何变换是指在几何图形中，通过平移、旋转、对称等方式改变图形的形状和大小。

利用几何变换的方法，可以解决一些与图形变换相关的最值问题。

例如，在矩形中，要使矩形的面积最大。

初中数学作为学生学习的基础课程之一，其中的几何模型在数学解题中占据着重要的地位。

掌握几何模型的解题技巧不仅可以帮助学生更好地理解数学知识，还可以提高他们的解题效率。

本文将介绍初中数学几何模型的60种解题技巧，希望能为学生们的学习提供帮助。

1. 角度概念的运用：在几何模型的解题过程中，学生可以通过具体的角度概念来解答问题，例如利用垂直角、平行线、内角和为180度等概念来解题。

2. 图形相似的判断：判断两个图形是否相似是解题的基础，学生可以利用边长比例、角度比例等方法来确定图形的相似性。

3. 平行线相关性质的应用：平行线的性质在几何模型的解题中经常会出现，学生可以通过平行线与角度的关系来解答问题。

4. 圆的相关性质的利用：圆的性质在几何模型中也是常见的，学生需要掌握圆的直径、半径、圆心角等概念，以便解题。

5. 三角形的分类和性质的运用：学生需要掌握等边三角形、等腰三角形、直角三角形等不同类型三角形的性质，并根据题目的要求来进行合理的运用。

6. 应用解题：在学习几何模型的解题过程中，学生需要结合实际的应用场景，将抽象的几何原理与具体的问题相结合来解答问题。

7. 连线问题的求解：对于一些多边形的连线问题，学生可以通过几何模型的知识来进行合理的求解。

8. 几何图形的对称性：对称图形在几何模型中也是常见的，学生可以通过对称性来解答与对称图形相关的问题。

9. 正多边形的性质：正多边形的性质是几何模型解题中的重要内容，学生需要掌握正多边形的内角和为180度、外角的性质等知识。

10. 形状的变换：在几何模型的解题中，学生需要掌握形状的平移、旋转、翻转等变换操作，以便解答形状变换后的问题。

11. 圆的面积和周长的求解：学生需要掌握圆的面积和周长的相关公式，并结合题目要求来进行求解。

12. 三角形的面积和周长的求解：学生需要掌握不同类型三角形的面积和周长的求解方法，并灵活运用到不同的题目中。

13. 平行四边形的面积和周长的求解：平行四边形的面积和周长的求解也是初中数学几何模型解题的重要内容，学生需要掌握相关公式及其应用。

初中数学立体几何题解题方法归纳立体几何是数学中的一个重要分支，它研究的是空间中的点、线、面以及它们之间的关系。

在初中数学中，立体几何是一个重要的内容，学生需要掌握解决立体几何题的方法。

本文将对初中数学中常见的立体几何题解题方法进行归纳总结，以帮助学生更好地理解和掌握这一知识点。

一、平面图形的展开与还原平面图形的展开与还原是解决立体几何题的基本方法之一。

具体来说，当给出一个立体图形的展开图形时，我们可以通过将展开图形还原成立体图形来解决问题。

例如，当给出一个长方体的展开图形时，我们可以根据展开图形的边长以及折叠方式来还原出长方体的形状。

同样的方法也适用于其他立体图形，如正方体、棱柱等。

二、计算表面积和体积计算表面积和体积是解决立体几何题的主要手段之一。

对于给定的立体图形，我们可以通过计算其表面积和体积来得到一些相关信息，如图形的特征、大小等。

对于常见的立体图形，计算表面积和体积的公式是已知的。

例如，长方体的表面积等于底面积的2倍加上底面周长乘以高，体积等于底面积乘以高。

而对于其他立体图形，我们可以根据其特点来推导出相应的计算公式。

三、利用空间几何关系在解决立体几何题的过程中，我们常常利用空间几何关系来推导解答。

根据空间几何关系，我们可以通过观察两个图形之间的位置关系、角度关系等，来推导出一些结论。

举个例子，当给定一个立方体的棱长时，通过观察可知，立方体的对角线可以分成两段等长的线段。

这样，我们就可以利用这个关系来推导出立方体的对角线的长度。

四、利用相似性质在解决立体几何题时，我们还可以利用相似性质来推导解答。

具体而言，当给定两个图形，如果它们的形状相似，那么它们的一些性质也会相似。

例如，当给定两个相似棱锥时，它们的相似性质可以帮助我们计算它们的体积比。

进一步，我们可以利用这个体积比来解决其他与这两个棱锥相关的问题。

五、切割与拼接切割与拼接是一种常用的解决立体几何题的方法。

当遇到复杂的图形时，我们可以通过切割和拼接来简化问题，从而更容易解决。

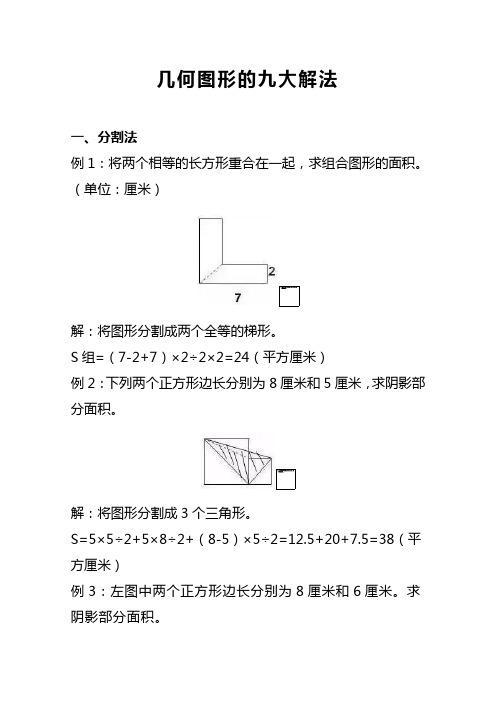
几何图形的九大解法一、分割法例1：将两个相等的长方形重合在一起，求组合图形的面积。

（单位：厘米）解：将图形分割成两个全等的梯形。

S组=（7-2+7）×2÷2×2=24（平方厘米）例2：下列两个正方形边长分别为8厘米和5厘米，求阴影部分面积。

解：将图形分割成3个三角形。

S=5×5÷2+5×8÷2+（8-5）×5÷2=12.5+20+7.5=38（平方厘米）例3：左图中两个正方形边长分别为8厘米和6厘米。

求阴影部分面积。

解：将阴影部分分割成两个三角形。

S阴=8×（8+6）÷2+8×6÷2=56+24=80（平方厘米）二、添辅助线例1：已知正方形边长4厘米，A、B、C、D是正方形边上的中点，P是任意一点。

求阴影部分面积。

解：从P点向4个定点添辅助线，由此看出，阴影部分面积和空白部分面积相等。

S阴=4×4÷2=8（平方厘米）例2：将下图平行四边形分成三角形和梯形两部分，它们面积相差40平方厘米，平行四边形底20.4厘米，高8厘米。

梯形下底是多少厘米？解：因为添一条辅助线平行于三角形一条边，发现40平方厘米是一个平行四边形。

所以梯形下底：40÷8=5（厘米）例3：平行四边形的面积是48平方厘米，BC分别是这个平行四边形相邻两条边的中点，连接A、B、C得到4个三角形。

求阴影部分的面积。

解：如果连接平行四边形各条边上的中点，可以看出空白部分占了整个平行四边形的八分之五，阴影部分占了八分之三。

S阴=48÷8×3=18（平方厘米）三、倍比法例1：已知OC=2AO,SABO=2㎡，求梯形ABCD的面积。

解：因为OC=2AO，所以SBOC=2×2=4（㎡）SDOC=4×2=8（㎡）SABCD=2+4×2+8=18（㎡）例2：已知S阴=8.75㎡，求下图梯形的面积。

几何图形的十大解法（30例）一、分割法例：将两个相等的长方形重合在一起，求组合图形的面积。

（单位：厘米）2 解：将图形分割成两个全等的梯形。

7S组=（7-2+7）×2÷2×2=24（平方厘米）例：下列两个正方形边长分别为8厘米和5厘米，求阴影部分面积。

解：将图形分割成3个三角形。

S=5×5÷2+5×8÷2+（8-5）×5÷2=12.5+20+7.5=38（平方厘米）例：左图中两个正方形的边长分别为8厘米和6厘米。

求阴影部分面积。

解：将阴影部分分割成两个三角形。

S阴=8×（8+6）÷2+8×6÷2=56+24=80（平方厘米）二、添辅助线例：已知正方形边长4厘米，A、B、C、D是正方形边上的中点，P 是任意一点。

求阴影部分面积。

C 解：从P点向4个定点添辅助线，由此看出，阴影部分面积和空白部分面积相等。

P S阴=4×4÷2=8（平方厘米）D BA例：将下图平行四边形分成三角形和梯形两部分，它们面积相差40平方厘米，平行四边形底20.4厘米，高8厘米。

梯形下底是多少厘米？解：因为添一条辅助线平行于三角形一条边，发现40平方厘米是一个平行四边形。

所以梯形下底：40÷8=5（厘米）例：平行四边形的面积是48平方厘米，BC分别是A 这个平行四边形相邻两条边的中点，连接A、B B、C得到4个三角形。

求阴影部分的面积。

C 解：如图连接平行四边形各条边上的中点，可以看出空白部分占了整个平行四边形的八分之五，阴影部分占了八分之三。

S阴=48÷8×3=18（平方厘米）三、倍比法例： A B 已知：OC=2AO，S ABO=2㎡，求梯形ABCD O 的面积。

解：因为OC=2AO，所以SBOC=2×2=4(㎡)D C S DOC=4×2=8(㎡)S ABCD=2+4×2+8=18(㎡)例：7.5 已知：S阴=8.75㎡，求下图梯形的面积。

2添加辅助线法▌例1：已知正方形边长4厘米，A、B、C、D是正方形边上的中点，P是任意一点。

求阴影部分面积。

解：从P点向4个定点添辅助线，由此看出，阴影部分面积和空白部分面积相等。

S阴=4×4÷2=8（平方厘米）▌例2：将下图平行四边形分成三角形和梯形两部分，它们面积相差40平方厘米，平行四边形底20.4厘米，高8厘米。

梯形下底是多少厘米？解：因为添一条辅助线平行于三角形一条边，发现40平方厘米是一个平行四边形。

所以梯形下底：40÷8=5（厘米）▌例3：平行四边形的面积是48平方厘米，BC分别是这个平行四边形相邻两条边的中点，连接A、B、C得到4个三角形。

求阴影部分的面积。

解：如果连接平行四边形各条边上的中点，可以看出空白部分占了整个平行四边形的八分之五，阴影部分占了八分之三。

S阴=48÷8×3=18（平方厘米）3倍比法▌例1：已知S阴=8.75㎡，求下图梯形的面积。

解：因为7.5÷2.5=3（倍）所以S空=3S阴S=8.75×（3+1）=35（㎡）▌例2：下图AB是AD的3倍，AC是AE的5倍，那么三角形ABC的面积是三角形ADE的多少倍？解：设三角形ADE面积为1个单位。

则SABE=1×3=3 SABC=3×5=15所以三角形ABC的面积是三角形ADE的15倍。

4割补平移▌例1：已知S阴=20㎡，EF为中位线求梯形ABCD的面积。

解：沿着中位线分割平移，将原图转化成一个平行四边形。

从图中看出，阴影部分面积是平行四边形面积一半的一半。

SABCD=20×2×2=80（㎡）▌例2：求下图面积（单位厘米）。

解1：S组=S平行四边形=10×（5+5）=100（平方厘米）解2：S组=S平行四边形=S长方形=5×（10+10）=100（平方厘米）▌例3：把一个长方形的长和宽分别增加2厘米，面积增加24平方厘米。

初中数学几何12个解题模型初中数学几何是一门非常重要的学科，对于提高学生的数学思维能力和解决实际问题的能力具有重要的意义。

在初中数学几何中，我们可以用一些解题模型来帮助我们更好地解决问题。

下面，我们将介绍12个初中数学几何的解题模型。

一、直角三角形的性质。

直角三角形是数学几何中经常使用的一个基本图形，掌握直角三角形的性质对于解决许多几何问题非常有帮助。

二、相似三角形的性质。

相似三角形也是数学几何中应用广泛的一个基本图形，掌握相似三角形的性质可以帮助我们解决许多相似三角形问题。

三、勾股定理。

勾股定理是直角三角形中一个非常重要的定理，它可以用来求解许多三角形的边长和面积。

四、正弦定理。

正弦定理是三角形中另一个非常重要的定理，用来解决三角形中的边和角的关系。

五、余弦定理。

余弦定理也是三角形中一个重要的定理，适合于求解三角形中的边和角的关系。

六、面积公式的运用。

了解各种基本几何图形的面积公式可以方便我们计算这些图形的面积。

七、平移、旋转和翻转。

平移、旋转和翻转是几何中常见的变换方式，可以用来解决各种几何问题。

八、梯形的性质。

梯形是常见的几何图形之一，掌握梯形的性质对于解决许多梯形问题非常有帮助。

九、四边形的性质。

四边形也是常见的几何图形之一，了解各种四边形的性质可以帮助我们更好地解决四边形问题。

十、圆的性质。

圆是几何中重要的一个基本图形，了解圆的性质可以帮助我们更好地解决圆的各种问题。

十一、相交线和平行线的性质。

相交线和平行线是几何中重要的一个概念，掌握这些线的性质可以帮助我们更好地解决几何问题。

十二、三角形的三线定理。

三角形的三线定理是三角形中常用的定理之一，可以用来解决三角形的各种问题。

这些解题模型是初中数学几何中非常重要的一部分，我们在学习数学几何时，需要不断地练习，不断地巩固这些知识点，才能更好地应对各种几何问题。

几何60种解题技巧一、三角形相关1. 找全等三角形- 看边边边（SSS）：如果三个边都对应相等，那就直接喊“全等啦”，就像三条腿一样长的凳子肯定是一样的嘛。

- 边角边（SAS）：两边和它们的夹角相等，这就好比两个人胳膊一样长，夹着的角度也一样，那他们的姿势就一样，三角形也就全等啦。

- 角边角（ASA）和角角边（AAS）：有两个角相等，再加上一条边，这就像两个人长得有点像（角相等），再有个部位一样（边相等），那就是全等的。

2. 三角形内角和- 三角形内角和是180度这个得牢记。

如果给了两个角，求第三个角，直接用180度减去那两个角就行，就像从一个大蛋糕（180度）里切走两块（已知的两个角），剩下的就是第三个角啦。

3. 等腰三角形- 等腰三角形两腰相等，底角也相等。

如果知道是等腰三角形，又给了一个角，要分清楚这个角是顶角还是底角哦。

如果是底角，那另一个底角也一样；如果是顶角，就用180度减去顶角再除以2就得到底角啦，就像平分两个一样的东西。

4. 等边三角形- 等边三角形三边相等，三个角都是60度。

看到等边三角形就像看到三个一模一样的小士兵，啥都一样。

二、四边形相关1. 平行四边形- 平行四边形对边平行且相等。

如果要证明是平行四边形，可以找对边平行或者对边相等。

就像两列火车轨道，平行而且长度一样。

- 平行四边形对角线互相平分。

如果给了平行四边形的对角线相关的条件，就可以利用这个性质，就像把一个平行四边形从中间切开，两边分得的线段是一样长的。

2. 矩形- 矩形是特殊的平行四边形，四个角都是直角。

如果知道是矩形，就可以用直角这个性质，比如在计算边长或者角度关系的时候。

3. 菱形- 菱形的四条边相等，对角线互相垂直平分。

看到菱形就想到四条边像四个等长的小棍，对角线像交叉的十字剑，还互相垂直平分呢。

4. 正方形- 正方形是最特殊的四边形，既是矩形又是菱形，四条边相等，四个角都是直角，对角线互相垂直平分且相等。