初中数学几何常见基本图形归纳总结大全

数学几何图形初中知识点总结数学几何是初中数学中的重要分支，涉及到平面几何和立体几何两个方面。

通过学习几何，学生可以培养逻辑思维能力和空间想象能力，并且为高中阶段的学习打下坚实的基础。

下面我将从初中数学几何的基本概念、图形的性质和常见的几何推理等方面，对几个重要的知识点进行总结。

一、图形的基本概念在几何学中，图形是指由点和线组成的可见形状。

初中数学中常见的图形包括：点、线段、直线、射线、角、多边形等。

1. 点：没有大小和形状，用大写字母表示，如A、B、C。

2. 线段：由两个点A和B确定，有起点和终点，并且有固定的长度。

用线段AB表示。

3. 直线：无限延伸的线段，没有起点和终点。

用小写字母表示，如l、m、n。

4. 射线：由一个起点和一个方向确定的直线。

用起点和任一点的字母表示，如射线AB。

5. 角：由两条射线共同起点构成的图形。

常用度（°）表示，如∠ABC。

6. 多边形：由若干条线段组成的封闭图形。

常见的多边形有三角形、四边形、五边形等。

二、图形的性质和关系了解图形的性质和关系对于几何学的学习非常重要，它们帮助我们判定图形的种类，以及解决各种几何问题。

1. 三角形的性质：（1）三角形的内角和为180°。

（2）等边三角形的三条边都相等，内角都是60°。

（3）等腰三角形的两条边相等，两个底角也相等。

（4）直角三角形的一个角是90°。

2. 四边形的性质：（1）矩形的对角线相等，且相交于中点。

（2）平行四边形的对边分别平行且相等。

（3）菱形的对角线互相垂直，且互相平分。

（4）正方形是矩形和菱形的特例，四条边相等且四个角都是90°。

3. 圆的性质：（1）圆是由平面上与一个点距离相等的所有点组成的图形。

（2）圆心到圆上任意一点的距离称为半径。

（3）圆上任意两点之间的距离称为弧，弧上的距离等于半径的长度。

（4）直径是通过圆心的两个点，并且等于半径的两倍。

三、常见的几何推理通过推理，可以从已知条件中得出推论，解决各种几何问题。

初三上数学几何知识点归纳总结在初三数学学科中，几何是一个非常重要且需要重点掌握的部分。

几何不仅涉及到图形的性质和构造，还涉及到空间的理解和分析等。

为了帮助同学们更好地掌握初三上数学中的几何知识，下面对初三上数学几何知识点进行归纳和总结。

一、平面几何基本概念1. 点：几何中最基本的图形元素，没有大小和形状。

2. 线段：由两个端点确定的线段，具有长度和方向。

3. 直线：由无数个点组成的连续直的线，延伸无限远，没有端点。

4. 射线：一个端点开始，延伸无限远的线。

5. 角：由两条射线共享一个端点形成的图形。

6. 三角形：由三条线段组成的图形。

7. 四边形：由四条线段组成的图形。

二、三角形的性质和分类1. 三角形的内角和等于180度。

2. 三角形根据边的关系可以分为等边三角形、等腰三角形和一般三角形。

3. 根据角的关系可以分为直角三角形、锐角三角形和钝角三角形。

4. 根据边长的关系可以分为斜边三角形、等腰锐角三角形等。

三、圆相关的知识点1. 圆的定义：平面上到一个点的距离相等的点的集合。

2. 圆的性质：圆的直径是圆上任意两点之间的最大距离，圆的半径是圆心到圆上的任意一点的距离。

3. 圆周率的计算：π是一个无理数，通常取3.14作为近似值来计算。

四、平行线与相交线1. 平行线的定义：在同一个平面内，不相交且两两平行的线。

2. 平行线的判定：平行线的判定条件包括同位角相等、内错角相等、同旁内角或同旁外角互补等。

3. 相交线的性质：相交线的同位角相等、内错角互补、邻补角相等等。

五、相似三角形1. 相似三角形的定义：两个三角形对应角相等并且对应边成比例，则称这两个三角形相似。

2. 相似三角形的性质：相似三角形的对应角相等、对应边成比例。

六、三角形的面积计算1. 面积计算公式：- 直角三角形的面积 = 底边长 ×高 ÷ 2- 一般三角形的面积 = 1/2 ×底边长 ×高- 等边三角形的面积 = 边长平方 ×根号3 ÷ 4- 任意三角形的面积 = 1/2 ×两条边的乘积 ×正弦夹角的正弦七、几何的证明方法1. 直接证明法：通过已知条件和几何定理，直接推导出结论。

初中数学图形知识点整理数学是一门既抽象又实用的学科，而图形知识点则是数学中的重要组成部分。

在初中数学教学中，图形知识点的学习和掌握至关重要。

下面，我将为大家整理初中数学图形知识点，希望对大家的学习有所帮助。

一、平面图形1. 点：点在平面上没有大小，表示为大写字母。

2. 直线：连续的一组点，没有宽度和厚度，用大写字母表示或用直线符号表示。

3. 射线：起点固定，延伸方向无限远的直线段。

4. 线段：起点和终点固定的直线段。

5. 角：由两条有共同端点的线段组成，用大写字母表示或用角符号表示。

6. 三角形：由三条线段组成的图形，分为等边三角形、等腰三角形和普通三角形。

7. 四边形：由四条线段组成的图形，分为矩形、正方形、菱形、平行四边形和梯形等。

8. 多边形：由多条线段组成的图形，分为五边形、六边形、七边形等。

二、立体图形1. 空间几何体：立方体、正方体、长方体、棱柱、棱锥、棱台等。

2. 球体：表面上的所有点到球心的距离都相等，如地球。

3. 圆柱体：底面为圆的几何体，如铅笔。

4. 圆台体：底面为圆的柱体，如喇叭。

5. 锥体：底面为多边形，侧面在同一个顶点相交于一个点，如蜡烛。

6. 配几体：由正方形和等边三角形组成的立体图形，如魔方。

三、图形的计算1. 周长：封闭曲线的长度，计算方法为各边长之和。

2. 面积：封闭图形所围成的平面的大小，计算方法根据不同图形而定。

- 圆形的面积计算公式为πr²，其中r为圆的半径。

- 矩形的面积计算公式为长×宽。

- 三角形的面积计算公式为底边长×高÷2。

3. 体积：立体图形所占的空间大小，计算方法根据不同图形而定。

- 立方体、正方体、长方体的体积计算公式为长×宽×高。

- 球体的体积计算公式为4/3πr³，其中r为球的半径。

- 圆柱体的体积计算公式为底面积×高，底面积为πr²。

- 圆台体的体积计算公式为（上底面积 + 下底面积 + 平行面积）×高 ÷ 3。

初中几何图形知识点归纳第一篇：初中几何图形知识点归纳初中几何图形知识点归纳1.三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2.三角形的分类3.三角形的三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边。

4.高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高。

5.中线：在三角形中，连接一个顶点和它的对边中点的线段叫做三角形的中线。

6.角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。

7.高线、中线、角平分线的意义和做法8.三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫三角形的稳定性。

9.三角形内角和定理：三角形三个内角的和等于180°推论1 直角三角形的两个锐角互余推论2 三角形的一个外角等于和它不相邻的两个内角和推论3 三角形的一个外角大于任何一个和它不相邻的内角；三角形的内角和是外角和的一半10.三角形的外角：三角形的一条边与另一条边延长线的夹角，叫做三角形的外角。

11.三角形外角的性质（1）顶点是三角形的一个顶点，一边是三角形的一边，另一边是三角形的一边的延长线；（2）三角形的一个外角等于与它不相邻的两个内角和；（3）三角形的一个外角大于与它不相邻的任一内角；（4）三角形的外角和是360°。

四边形（含多边形）知识点、概念总结一、平行四边形的定义、性质及判定1.两组对边平行的四边形是平行四边形。

2.性质：（1）平行四边形的对边相等且平行（2）平行四边形的对角相等，邻角互补（3）平行四边形的对角线互相平分3.判定：（1）两组对边分别平行的四边形是平行四边形（2）两组对边分别相等的四边形是平行四边形（3）一组对边平行且相等的四边形是平行四边形（4）两组对角分别相等的四边形是平行四边形（5）对角线互相平分的四边形是平行四边形4.对称性：平行四边形是中心对称图形二、矩形的定义、性质及判定1.定义：有一个角是直角的平行四边形叫做矩形2.性质：矩形的四个角都是直角，矩形的对角线相等3.判定：（1）有一个角是直角的平行四边形叫做矩形（2）有三个角是直角的四边形是矩形（3）两条对角线相等的平行四边形是矩形4.对称性：矩形是轴对称图形也是中心对称图形。

初中几何知识点总结归纳几何学是数学的一个重要分支，研究平面图形、空间图形以及它们的性质、关系和变换等。

在初中阶段，学生将会学习到许多几何概念和知识，下面是对一些常见的初中几何知识点进行了总结归纳。

一、基本概念1.点：几何中的最基本单位，没有大小，用大写字母表示。

2.线段：由两个端点确定的线段，可以用一条直线表示。

3.直线：无限延长又无限窄的线段，用小写字母表示。

4.射线：由一个端点和延伸出的一段部分组成的线段。

5.角度：由两条不同的线段（称为边）组成的形状，有角心和两个端点。

用大小写字母表示，如∠ABC。

6.平行线：在同一平面上，永远不会相交的线段。

7.垂直线：两条直线相交时，形成的四个角度中有两个角度互为补角，被称为垂直线。

8.对称：一个图形相对于条线或中心点形成的镜像图形。

9.相似：两个图形的对应角相等，对应边成比例。

10.全等：两个图形的对应边和对应角都相等。

二、图形的性质1.三角形：由三条线段组成的图形，其中最常见的三种三角形是等边三角形、等腰三角形和直角三角形。

2.正方形：具有四条边相等且四个角都为直角的四边形。

3.长方形：具有相对边相等且四个角都为直角的四边形。

4.平行四边形：具有两对平行边的四边形。

5.梯形：具有一对平行边的四边形。

6.圆：平面上所有离圆心的距离都相等的点的集合。

7.弧：圆上两个点间的部分称为弧，圆上一个点所对应的弧称为圆心角。

8.弦：圆上连接两个点的线段。

9.切线：与圆只有一个公共点的直线。

三、图形的计算1.周长：图形的边长总和，矩形、正方形和长方形的周长可以通过边长相加得到。

2.面积：图形所占的二维空间大小，矩形、正方形和长方形的面积可以通过底边乘以高得到。

3.体积：三维图形所占的空间大小。

4.高度：从底边到顶点的垂直距离。

5.半径：从圆心到圆上特定点的距离。

6.直径：穿过圆心的线段的长度，是半径的两倍。

四、相关定理和公式1.垂直角定理：如果两条直线相交，形成的四个角中，两个互为补角。

几何图形数学知识点总结一、点、线、面和体在几何图形中，最基本的概念是点、线、面和体。

点是几何图形的最小单元，它没有长度、宽度或高度，只有位置。

线是由无数点连接而成的集合，它有长度但没有宽度。

面是由线相交的区域，它有长度和宽度但没有厚度。

体是由面相交而成的区域，它有长度、宽度和高度。

二、圆圆是一个非常重要的几何图形，它有很多独特的性质。

圆是一个闭合的曲线，它的每一点到圆心的距离都相等。

圆的直径是通过圆心，并且两端在圆上的线段，它的长度是圆的直径。

圆的半径是从圆心到圆上的任意一点的距离，它的长度是圆的半径。

圆的周长是圆上一周的长度，它等于圆的直径乘以π。

圆的面积是圆内部的区域，它等于π乘以半径的平方。

三、三角形三角形是一个三边的多边形，它也有很多独特的性质。

三角形的三个顶点分别是三角形的顶点，三边的长度分别是三角形的边长。

三角形的周长是三边的长度之和，它等于三角形的周长。

三角形的面积是三角形的内部区域，它等于底边乘以高的一半。

三角形的角是三边的交点，它有三个角度，分别是三角形的内角。

三角形的角和等于180度，这是三角形的一个重要性质。

四、四边形四边形是一个四边的多边形，它也有很多独特的性质。

四边形的对角线是四边形的两个对边的交点，它把四边形分成两个三角形。

四边形的周长是四边的长度之和，它等于四边形的周长。

四边形的面积是四边形的内部区域，它等于对角线的乘积乘以正弦角的一半。

四边形的角是四边的交点，它有四个角度，分别是四边形的内角。

四边形的角和等于360度，这是四边形的一个重要性质。

五、多边形多边形是一个多边形，它也有很多独特的性质。

多边形的边是多边形的各边的长度之和，它等于多边形的周长。

多边形的面积是多边形的内部区域，它等于多边形的面积。

多边形的角是多边形的交点，它有多个角度，分别是多边形的内角。

多边形的角和等于180度，这是多边形的一个重要性质。

六、平行四边形平行四边形是一个有两对相对边平行的四边形。

图形与变换1、图形的轴对称轴对称：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴。

轴对称图形：①角的平分线上的点到这个角的两边的距离相等。

②线段垂直平分线上的点到这条线段两个端点的距离相等。

③等腰三角形的“三线合一”。

轴对称的性质：对应点所连的线段被对称轴垂直平分，对应线段/对应角相等。

2、图形的平移和旋转平移：①在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做平移。

②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等。

旋转：①在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动叫做旋转。

②经过旋转，图形商店每一个点都绕旋转中心沿相同方向转动了相同的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等。

3、图形的相似比：①A/B=C/D，那么AD=BC，反之亦然。

②A/B=C/D，那么A 土B/B=C土D/D。

③A/B=C/D=。

=M/N，那么A+C+…+M/B+D+…N=A/B。

黄金分割：点C把线段AB分成两条线段AC与BC，如果AC/AB=BC/AC，那么称线段AB被点C黄金分割，点C叫做线段AB的黄金分割点，AC与AB的比叫做黄金比(根号5-1/2)。

相似：①各角对应相等，各边对应成比例的两个多边形叫做相似多边形。

②相似多边形对应边的比叫做相似比。

相似三角形：①三角对应相等，三边对应成比例的两个三角形叫做相似三角形。

②条件：AAA、SSS、SAS。

相似多边形的性质：①相似三角形对应高，对应角平分线，对应中线的比都等于相似比。

②相似多边形的周长比等于相似比，面积比等于相似比的平方。

图形的放大与缩小：①如果两个图形不仅是相似图形，而且每组对应点所在的直线都经过同一个点，那么这样的两个图形叫做位似图形，这个点叫做位似中心，这时的相似比又称为位似比。

②位似图形上任意一对对应点到位似中心的距离之比等于位似比。

初中几何基本图形归纳(基本图形+常考图形)初中几何常见基本图形1.基本图形及结论A、B、C、D分别为四边形的顶点，AC=BD，AD=BC，∠AOC=∠BOD，∠AOD=∠BOC。

2.直角三角形在直角三角形ABC中，∠C=90°，OA为斜边的中线，OD⊥XXX。

3.等腰三角形在等腰三角形ABC中，AB=AC，AD为角A的平分线，BD=CD。

4.三角形的面积公式在三角形ABC中，AB2=BD×BC，AC2=CD×BC。

5.三角形内角和公式在三角形ABC中，∠A+∠B+∠C=180°。

6.平行四边形在平行四边形ABCD中，∠A+∠B=∠C+∠D，AC平分∠BAD。

7.直角三角形的斜边中线在直角三角形ABC中，BD为斜边AC的中线，∠B=∠D。

8.直角三角形的高线在直角三角形ABC中，PA⊥AB，PB⊥AC，PC⊥BC，且PA=PB+PC，∠P=∠A/2.9.直角三角形的内心在直角三角形ABC中，∠P=∠A/2，PD为角A的平分线，AD=BD=AC=DC。

10.直角三角形的外心在直角三角形ABC中，∠P=90°-∠A/2，以AB的中点O为圆心，AB为半径作圆，交AC于点P，则P为三角形ABC的外心。

11.等腰三角形的中线在等腰三角形ABC中，AB=CB，BD为角B的平分线，且BC∥AD。

12.等边三角形在等边三角形ABC中，AB=AC=BC。

13.等角三角形在等角三角形ABC中，∠A=∠B=∠C。

14.三角形的相似在三角形ABC和DEF中，如果∠A=∠D，∠B=∠E，∠C=∠F，则称三角形ABC与DEF相似。

15.圆的基本性质在圆O中，AB为直径，则∠C=90°，且AC=BC=OD。

16.圆的切线在圆O中，以点A为圆心，AB为半径作圆，则CD为圆O的切线。

17.圆的割线在圆O中，以点A为圆心，AC为半径作圆，则BD为圆O的割线。

18.圆的弦在圆O中，AB为圆O的弦，R为圆O的半径，则弦长公式为AB2=BD×BC，且弦AB平分∠AOB。

初中数学几何图形知识点掌握归纳初一上册数学几何图形初步知识点归纳1.几何图形：点、线、面、体这些可帮助人们有效的刻画错综复杂的世界，它们都称为几何图形。

从实物中抽象出的各种图形统称为几何图形。

有些几何图形的各部分不在同一平面内，叫做立体图形。

有些几何图形的各部分都在同一平面内，叫做平面图形。

虽然立体图形与平面图形是两类不同的几何图形，但它们是互相联系的。

2.几何图形的分类：几何图形一般分为立体图形和平面图形。

3.直线：几何学基本概念，是点在空间内沿相同或相反方向运动的轨迹。

从平面解析几何的角度来看，平面上的直线就是由平面直角坐标系中的一个二元一次方程所表示的图形。

求两条直线的.交点，只需把这两个二元一次方程联立求解，当这个联立方程组无解时，二直线平行;有无穷多解时，二直线重合;只有一解时，二直线相交于一点。

常用直线与X轴正向的夹角(叫直线的倾斜角)或该角的正切(称直线的斜率)来表示平面上直线(对于X轴)的倾斜程度。

4.射线：在欧几里德几何学中，直线上的一点和它一旁的部分所组成的图形称为射线或半直线。

5.线段：指一个或一个以上不同线素组成一段连续的或不连续的图线，如实线的线段或由“长划、短间隔、点、短间隔、点、短间隔”组成的双点长划线的线段。

线段有如下性质：两点之间线段最短。

6. 两点间的距离：连接两点间线段的长度叫做这两点间的距离。

7. 端点：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。

线段用表示它两个端点的字母或一个小写字母表示，有时这些字母也表示线段长度，记作线段AB或线段BA，线段a。

其中AB表示直线上的任意两点。

8.直线、射线、线段区别：直线没有距离。

射线也没有距离。

因为直线没有端点，射线只有一个端点，可以无限延长。

9.角：具有公共端点的两条不重合的射线组成的图形叫做角。

这个公共端点叫做角的顶点，这两条射线叫做角的两条边。

一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角。

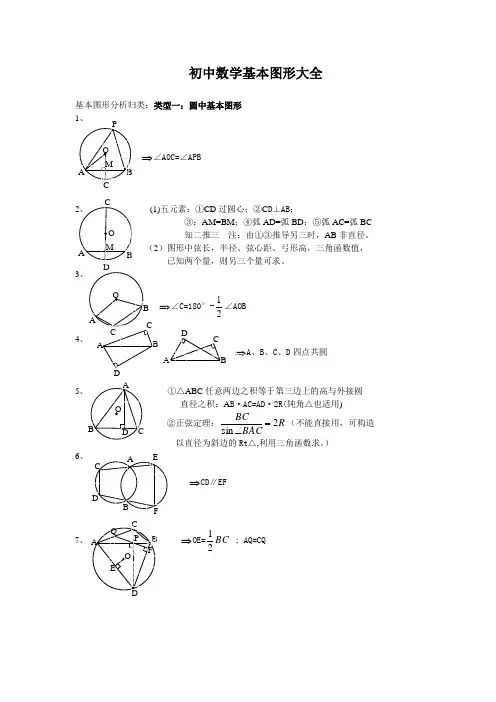
初中数学基本图形大全基本图形分析归类：类型一：圆中基本图形D⊥AB；弧BD；⑤弧AC=弧BCAB非直径。

、C、D四点共圆·2R(钝角△也适用)=（不能直接用，可构造R2）8、（弧AC=弧EC ） ⇒AM=CM=FM ;AC=EC;AE CD 21=; ABAD AE AM AC ⋅=⋅=2;BF OM 21=9∽CDE, △ABD ∽△AEC ∽BED,·AC=AD ·AE,AE ·DE=BE ·CEBAD ∠cos 2 关注∠BAC 为特殊角时图形的 10 AC 、AB 的对称点在⊙O 上，11DC 切⊙O 于C 点 知二推一12 ,BO ⊥DE , ∠DEF=90°-21∠A 13 14CE 切⊙O 于点E,知二推一15⇒C △PDE=PA+PB ∠DOE=)180(21P ∠-16 ①EA 切⊙O 于点A AE ∥CF ③AP=EP 知二推一17、 △ABD 、△ACE 为等边△⇒ BE=CD,BE 、CD 相交所成锐角为60° 18、正方形ABDE 、正方形ACFG ⇒EC=BG ,BG ⊥CE注：条件可为等腰Rt △19、①AD 平分∠CAB, ②DE ∥AC,③AE=DE 知二推一20、 △ABC 为等腰Rt △，AE 平分∠CAB ，BD ⊥AD⇒AE=2BD21、⇒C △ADE=AB+ACA B C DEA B C D E F G A B CD E A B C D E A B C D E M22、 △ACD 、△BCE 为等边△，A 、C 、B 三点共线⇒ △ACE ≌△DCB , △ACM ≌△DCN , △MCE ≌△NCB AE=BD,AM=DN,EM=BN,CM=CN,AE 、BD 相交所成锐角为60° AO=DO+CO,BO=EO+CO,OM+ON=OC,OC 平分∠AOB 注：△BCE 旋转时，结论有变化。