当前位置：文档之家 › 线性系统的时域分析法PPT课件

线性系统的时域分析法PPT课件

  • 格式：ppt
  • 大小：895.00 KB
  • 文档页数：76

下载文档原格式

  / 76

合集下载

线性系统的时域 分析法

线性系统的时域 分析法
▪ 如果m < n，即开环零点数小于开环极点数，除有m条根轨迹 终止于开环零点外，还有n-m条根轨迹终止于无穷远点。
证明：对负反馈控制，根据特征方程1+G(s)H(s)=0
m
Kr (s zi )
G(s)H (s)
i 1 n
1
(s pj)
j 1
n
m
(s p j ) Kr (s zi ) 0
4.1.1 根轨迹的定义
所谓根轨迹就是当开环系统的某个参数从0→+∞变化时，闭环系
统特征根（闭环极点）在s复平面上移动所形成的轨迹。
例4-1 控制系统结构如图所示，其开环传递函数为
试绘出当Kr 从0→+∞变化时的根轨迹。
G(s)H (s)
Kr
(s 1)(s 2)
R(s)
-
Kr
C(s)
(s 1)(s 2)
▪ 1948年，伊万斯（Evans）根据反馈控制系统中开、闭环传递 函数之间的关系，首先提出了一种根据开环传递函数的零、极 点分布，用图解方法来确定闭环传递函数极点随参数变化的运 动轨迹，这种方法被称为根轨迹法。
▪ 轨迹法是一种图解的方法，具有直观、形象的特点，且可以避 免繁琐的计算，故在控制工程领域中获得了广泛地应用。
jω
Kr=4.25
2
Kr=0.25 Kr=0
-2
Kr=1.25 Kr=0 -1
Kr=1.25
1
0
σ
-1
Kr=4.25
-2
4.1.2 根轨迹与系统性能
1. 稳定性
当Kr 从0→+∞变化时，显然，由上图可知，闭环系统的根轨迹均在s平 面的左半平面，故系统对所有大于0的Kr 值都是稳定的。如果系统根 轨迹越过了虚轴而进入右半s平面，则在相应Kr 值下系统是不稳定的， 其中根轨迹与虚轴交点处的Kr 值，一般称为临界根增益。

数字信号处理线性系统的时域分析法

数字信号处理线性系统的时域分析法
(1)稳定必要条件
a0>0
ai(i=0,1,2,…n)>0
(2)劳思稳定判据 1)劳思表
cij=
i---列；j---行
ci+1.j-2 c1.j-2 ci+1.j-1 c1.j-1
c1.j-1
稳定充分必要条件 C1,j >0 (j=0,1…n+1)
Sn
a0
a2
a4
a6
…
Sn-1
a1
a3
a5
a7
…
Sn-2
0
s0
-4
-7
-4
-4
0
-4
0 (dF(s)/d(s)=0 系数)
由于劳思表第一列数值有一次符号变化,故系统不稳定,且 有一个正实部根.其特征根是±2, ±j,(-1±j√3)/2
辅助方程:F(s)=s4-3s2-4=(s2-4)(s2+1)=0
3)劳思稳定判据的应用 例:设比例-积分(PI)控制系统如图所示.其中,K1为与积分器
r k 1
Ck Bkkk k 1 k2
e k k t
sin(
k
1 k2 )t
t0
特征根实部
0
lim
k(t)
t
c或振荡
全负
稳定
1个为正
不稳定
1个为零其余为负 临界稳定
r(t)
0
t
j
s
× ××
×× × 0
× ××
特征根全部位于左半S平面
c(t)
0
t
c(t)
0
t
c(t)
0
t
稳定判据
设: D(s) a0sn a1sn1 an1s an 0

线性系统的时域分析法二阶系统

线性系统的时域分析法二阶系统
实验法具有直观性和可验证性的优点，适用于各种类型的二阶系统。但是，实验法需要实际设备和实 验条件，成本较高。
04
二阶系统的稳定性分析稳定性定义平衡状态
线性系统在平衡状态下的输出称为平衡状态输出。
稳定性
如果一个系统的平衡状态输出对于所有初始条件和输入都是稳定的，则称该系统是稳定 的。
稳定性判据
劳斯-赫尔维茨判据
数值法
数值法是通过数值计算来求解二阶系 统的方法。它通过将时间轴离散化， 将微分方程转化为差分方程，然后使 用迭代或直接计算的方法求解。
数值法具有简单易行和适用性广的优 点，适用于各种类型的二阶系统。但 是，对于某些特殊类型的系统，数值 法可能存在精度和稳定性问题。
实验法
实验法是通过实际实验来测试二阶系统的方法。它通过在系统中输入激励信号，然后测量系统的输出 响应，从而得到系统的性能参数。
线性系统的时域分析 法二阶系统
目录
CONTENTS
• 线性系统的时域分析法概述 • 二阶系统的基本概念 • 二阶系统的时域分析方法 • 二阶系统的稳定性分析 • 二阶系统的性能指标分析 • 二阶系统的应用实例
01
线性系统的时域分
析法概述
定义与特点
定义
时域分析法是一种通过在时间域 内对系统进行直接分析的方法， 用于研究系统的动态性能和响应 特性。
通过计算系统特征方程的根来判断系统 的稳定性。如果所有根都位于复平面的 左半部分，则系统稳定；如果有根位于 右半部分，则系统不稳定。
VS
Nyquist稳定判据
通过绘制系统的开环传递函数的Nyquist 曲线，判断曲线是否不穿越复平面的右半 部分，从而判断系统的稳定性。
稳定性分析方法
直接法

第三章 线性系统时域分析法 第2讲

第三章 线性系统时域分析法 第2讲
1
[
e
( 2 1 )n t

e
( 2 1 )n t
2 1
]
1时，二阶系统的单位阶跃响应含有两个衰减指 从上式看出，
数项。当阻尼比
远大于1时，闭环极点 s ( 2 1) 1 n
n 3 n 2 1 n
一定时，随n 的增大，系统的响应速度变快。
4、无阻尼情况 0
0 时 ，特征根为一对纯共轭虚数，将欠阻尼二阶系统的单 位阶跃响应中的 用零代替，可得到无阻尼二阶系统的单位阶
跃响应为：
C(t ) 1 sin(nt 900 ) 1 cos(nt )
同时反映响应速度和阻尼程度的综合性指标。
% 评价系统的阻尼程度。
1.等价关系——线性定常系统的重要特性: 系统对输入信号导数的响应，就等于系统对该输入信号响 应的导数; 系统对输入信号积分的响应，就等于系统对该输入信号响 应的积分; 注意:积分常数由零初始条件确定。该结论可推广至高阶系统。 2.动态特性: 由时间常数T决定。T响应速度，即响应时间，反之亦 然 3.跟踪能力: 阶跃输入无稳态误差，能跟踪阶跃信号，跟踪速度取决于T; 斜坡输入有位置误差，且稳态误差等于时间常数T; 加速度输入稳态误差无穷大，一阶系统不能跟踪加速度信号。 4. 一阶系统只有一个特征参数T，即时间常数。在一定的输入 信号作用下，其时间响应c(t)由其时间常数惟一确定。
越大，超调量越小，响应速度越慢；决定了系统振荡特性
2) 0 1时，系统输出有超调，且
n 越大，响应速度越快。
3) 1时，系统输出无超调，系统的响应速度随
的
增大而变慢，随 n 的增大而变快。
二阶系统极点分布同单位阶跃响应之间的对应关系

第三章 线性系统的时域分析法(第三四五讲)

第三章 线性系统的时域分析法(第三四五讲)
若变号系统不稳定!
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为：
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e

1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0＜ξ＜1 s1, 2 n jjn 1 2 ξ＝0 0＜ξ＜1
0
h( t ) 1 ξ＝0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示，试在同一平面画出3个系统闭环 极点的相对位置，并说明理由。

第3章 线性系统的时域分析第九节_3

第3章 线性系统的时域分析第九节_3

（3）根轨迹起始于开环极点，终止于开环零点
说明 当根轨迹增益K1从0变化到∞时，在s平面就会画 出一条一条的根轨迹，每条根轨迹都有起点和终 点，对应于K1 =0的s点叫根轨迹的起点，对应于 K1 →∞的s点叫根轨迹的终点。 由幅值条件
可见 当s=pj时， K1 =0 ；根轨迹起始于开环极点； 当s=zi时， K1 →∞ ；终止于开环零点； 当|s|→∞且n≥m时， K1 →∞。如果开环零点个 数m少于开环极点个数n，则有(n-m)条根轨迹终 止于无穷远处。
（5）两条根轨迹的交点方程为
其中sd为交点。
说明： 交点sd是指两支根轨迹会合后分离的点， 该点为闭环特征方程的重根
假设闭环特征方程有2个重根，则可将其 改写为
例3-6 单位负反馈系统开环传递函数为
试画出系统实轴上的根轨迹并求出系统根轨迹 的交点。
解： 由规则1），系统有3条根轨迹； 由规则3），3条根轨迹的起点为
（4）实轴上的根轨迹 实轴上的某一区域，若其右边开环实数零、 极点个数之和为奇数，则该区域必是根轨迹。 （如红线所示）
红色部分 为根轨迹
说明：以实轴上的s0点为例，根据相角条 件，分三个方面说明这个法则。
G ( s ) H ( s )
m n
(s z ) (s p )
解 系统有3条根轨迹分支，且3条根轨迹都趋 于无穷远处。 实轴上的根轨迹： ,2 1,0 渐近线：
根轨迹的交点满足以下方程
交点必须在根轨迹上，所以交点取
根轨迹与虚轴的交点及临界增益。
令s=iω
令实部及虚部分别为0
解得
第一组解为根迹的起点,第二组得根迹和虚轴的 交点 ,临界根轨迹增益为6
K s ( s 1)( s 2） K 1 s ( s 1)( s 2）

线性系统的时域分析法

线性系统的时域分析法

三、动态性Leabharlann 和稳态性能动态性能：通常在阶跃函数作用下，测定或计算系统的动
态性能。一般认为阶跃输入对系统来说是最严峻的工作状态。
描述稳定的系统在阶跃函数作用下，动态过程随时间的
变化状况的指标称为动态性能指标。通常包括：
延迟时间 td ：指响应曲线第一次到达稳态值一半所需的时间。
上升时间 tr ：指响应第一次 h(t) % 误差带
洛比特法则
lim lim
(s pi )N (s)
(s pi )N (s) N (s) N ( pi )
s pi
D(s)
s pi
D(s)
D( pi )
f (t) L1
F (s)
L1
n i1
Ai s pi
n i 1
Aie pi t
② 具有多重极点的有理函数的反变换
F (s)
误差平方积分(ISE，Integral of Square Error)
ISE e2 (t)dt 0
( e(t)是输入输出之间存在的误差)
时间乘误差平方积分(ITSE，Integral of Timed Square Error)
ITSE te2 (t)dt 0
误差绝对值积分(IAE，Integral of Absoluted Error)
(s a
j)F (s) sa j
N (s) D(s)
sa j
k1
e j
思考：为何 k1，k2 必为共轭复数？
f
(t)
L1 F (s)
L1
s
A1 p1
k1 sa
j
k2 sa
j
A1e p1t
k1e(a j)t

自动控制原理-第3章-时域分析法

自动控制原理-第3章-时域分析法
系统响应达到峰值所需要的时间。
调节时间
系统响应从峰值回到稳态值所需的时间。
振荡频率
系统阻尼振荡的频率，反映系统的动态性能。
系统的阶跃响应与脉冲响应
阶跃响应
系统对阶跃输入信号的响应，反映系 统的动态性能和稳态性能。
脉冲响应
系统对脉冲输入信号的响应，用于衡 量系统的冲激响应能力和动态性能。
03
一阶系统时域分析
01
单位阶跃响应是指系统在单位阶跃函数作为输入时的
输出响应。
计算方法
02 通过将单位阶跃函数作为输入，代入一阶系统的传递
函数中，求出系统的输出。
特点
03
一阶系统的单位阶跃响应是等值振荡的，其最大值为1，
达到最大值的时间为T，且在时间T后逐渐趋于0。
一阶系统的单位脉冲响应
定义
单位脉冲响应是指系统在单 位脉冲函数作为输入时的输
无法揭示系统结构特性
时域分析法主要关注系统的动态行为和响应，难以揭示系统的结构特 性和稳定性。
对初值条件敏感
时域分析法的结果对系统的初值条件较为敏感，初值条件的微小变化 可能导致计算结果的较大偏差。
感谢您的观看
THANKS
计算简便
时域分析法通常采用数值积分方法进 行计算，计算过程相对简单，易于实 现。
时域分析法的缺点
数值稳定性问题
对于某些系统，时域分析法可能存在数值稳定性问题，例如数值积分 方法的误差累积可能导致计算结果失真。
计算量大
对于高阶系统和复杂系统，时域分析法需要进行大量的数值积分计算， 计算量较大，效率较低。
自动控制原理-第3章-时域 分析法
目录
• 时域分析法概述 • 时域分析的基本概念 • 一阶系统时域分析 • 二阶系统时域分析 • 高阶系统时域分析 • 时域分析法的优缺点

2-连续时间线性定常系统时域分析

2-连续时间线性定常系统时域分析

- f (t) g(t) g(t) f (t) （可交换性） - f (t) {g(t) h(t)} { f (t) g(t)} h(t) （可结合性）
- { f (t) g(t)} h(t) f (t) h(t) g(t) h(t) （线性）
- 定义：
f (t) 1
• 对任意两个信号 f1(t) 、f2(t) ，两者的卷积运 算定义为：
• 性质
f1(t) f2 (t) @ f1( ) f2 (t )d
– 代数性质 – 拓扑性质
设 f (t)、g(t)、h(t) L1()
定义：L1()，是绝对可积函数的集合。
27
卷积的性质：
• 代数性质（课后可自行推导）
y(t) 零输入响应yzi (t) 零状态响应yzs (t)
| n
齐次解 Aieit
1 4 4 2i 41 43 自由响应
特1 4解2 B43t 带入 y(0+ ) y(0 )＝0 强迫响应
yzi (t) Azikekt，Azik由Y 0 =Y 0 代入求得；
k
yzs (t) 齐次解 Azskekt 特解B t ，
@H ( p)v(t)
N( p)
n
v(t)
( p i)
i 1
N ( p)[ent L e1t v(t)]
()
其中，
互异；
i
n
yzs (t) 齐次解项 Aieit 特解项 B t i 1
结论：系统响应 y t = yzi t + yzs t
21
• 4. 系统响应 = 自由响应 + 强迫响应
k
Ait
k i
e1t
i1
特解：将v t 代入右端，选取特解形式，求待定系数，

自动控制原理-第3章

自动控制原理-第3章

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4＜ζ＜0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法

线性系统的时域分析法

线性系统的时域分析法

第三章 线性系统的时域分析法●时域分析法在经典控制理论中的地位和作用时域分析法是三大分析方法之一，在时域中研究问题，重点讨论过渡过程的响应形式。

时域分析法的特点：1).直观、精确。

2).比较烦琐。

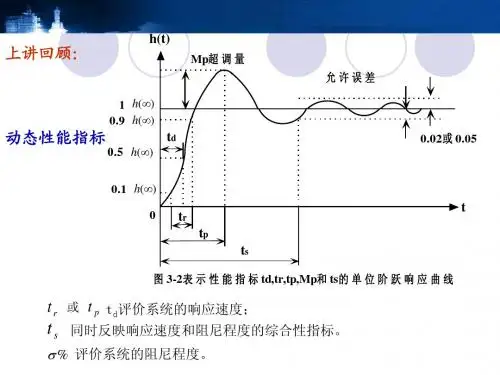
§3.1 系统时间响应的性能指标1. 典型输入2. 性能指标∙稳→基本要求 ∙准→稳态要求↓ss e ：∙快→过渡过程要求⎪⎩⎪⎨⎧↓↓⨯∞∞-=s p t h h t h %)()()(%σ§3.2 一阶系统的时域分析设系统结构图如右所示 开环传递函数sK s G =)(闭环传递函数)1(11111)(T Ts T s T Ks K s K s Ks -=+=+=+=+=Φλ:)(1)(时t t r =Ts sTs s T s R s s C 111)1(1)()()(+-=+=Φ=1)(,0)0( 1)(1=∞=-=∴-c c e t c tTTc eT t c tT 1)0( 1)(1='='-依)(t h 特点及s t 定义有：95.01)(1=-=-st T s e t h05.095.011=-=-st T e305.0ln 1-==-s t TT t s 3=∴一阶系统特征根1s T=-分布与时域响应的关系：21110 ()().(). ()s C s s R s h t t s s s∙==Φ===时 11 () ()1()ata s a C s h t e s s a ss a∙===-+=-+--时例1 已知系统结构图如右 其中：12.010)(+=s s G加上H K K ,0环节，使s t 减小为原来的0.1倍，且总放大倍数不变，求H K K ,0解：依题意，要使闭环系统02.00.21.0*=⨯=s t ，且闭环增益=10。

11012.0)101(10 1012.01012.010112.010.)(1)(.(s)0000+++=++=+++=+=Φs K K K K s K s K s K s G K s G K HH HH H令 101011002.01012.00⎪⎪⎩⎪⎪⎨⎧=+==+=H H K K K K T 联立解出⎩⎨⎧==109.00K K H 例2 已知某单位反馈系统的单位阶跃响应为atet h --=1)(求(1).闭环传递函数)(s Φ；(2).单位脉冲响应；(3).开环传递函数。

信号与系统概论PPT第二章线性时不变系统的时域分析2

信号与系统概论PPT第二章线性时不变系统的时域分析2
卷积重要性质： 1) 信号与延迟冲激信号的卷积等于延迟信号
f t* t t0 f t t0
2) 信号与阶跃信号的卷积等于信号积分
f t*ut t0 f t* 1t t0 f t* t t0 1 f 1 t t0
第三节 卷积与卷积和、解卷积
卷积重要性质： 3) 信号与冲激偶的卷积等于信号微分
t
2
t
2
*
r
t
2
r
t
2
r t r t r t r t
r t 2r t r t
f(t)
f(t)
1
1
=
0 t 22
(a)
0 t 22
(b)
f΄(t)
f (-1)(t)
1
2 0 2
τ
t
0
22
=
t
(c)
(d)
f(t)f(t) τ
-τ 0 τ t 22
m
f1 m f2 n m mMaxn,0
第三节 卷积与卷积和、解卷积
重要结论：信号与冲激信号（脉冲信号） 的卷积（卷积和），其结果就是对该信号 进行移位，位移量取决于冲激（脉冲）信 号出现的位置。该结论也可视作信号通过 移位系统得到的零状态响应。
f
t*δt
t0
f
t
δ
t0 d
f
t
注意此处的 处理方式
ut 1 t1e d ut 1 t1e d
0
0
1
1
e t 1
u t Hale Waihona Puke 1 et1u t 1
例2-8：计算 cost* t 1 t 1
解：
M
M
f t* wi t ti wi f t ti

机械工程操纵基础课件第三章线性系统的时域分析第2讲

机械工程操纵基础课件第三章线性系统的时域分析第2讲

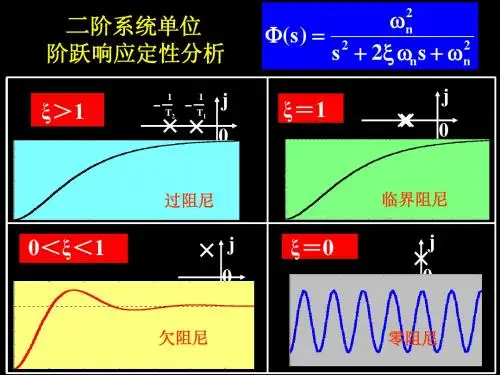
机械工程操纵基础课件第三章_线性系统的时域分析(第2讲)二阶系统的标准形式，相应的方块图如图3-8所示（3-18）－自然频率（或无阻尼振荡频率）－阻尼比（相对阻尼系数）二阶系统的动态特性，能够用和加以描述,二阶系统的特点方程：（3-19）（3-20）33>.3.2 二阶系统的单位阶跃响应Unit-Step Response of Second-Order Systems阻尼比是实际阻尼系数F与临界阻尼系数的比值－临界阻尼系数，时，阻尼系数机械工程二．二阶系统的单位阶跃响应假设系统的输入信号为单位阶跃函数，即那么二阶系统的阶跃路应函数的Laplace变换式为：机械工程其响应函数讨论如下：（1）当，系统为欠阻尼系统时，由式（3.4.8）有或式（3.4.10）中的第二项是瞬态项，是减幅正弦振荡函数，它的振幅随时刻t的增加而减小。

（3.4.10）机械工程（2）当，系统为无阻尼系统时，由式(3.4.9)可知（3）当，系统为临界阻尼系统时，由式（3.4.8），有其响应的转变速度为：由此式可知：当t=0时，时，时，，这说明过渡进程在开始时刻和最终时刻的转变速度为零，过渡进程是单调上升的。

(3.4.12)机械工程（4）当，系统为过阻尼系统时，由式（3.4.8）有式中，(3.4.13)机械工程计算说明，当时，在式（3.4.13）的两个衰减的指数项中，的衰减比的要快得多，因此，过渡进程的转变以项其要紧作用。

从S平面看，愈靠近虚轴的根，衰减越慢，对过渡进程阻碍愈大，起主导作用。

机械工程机械工程二阶系统的单位阶跃响应函数过渡进程特性：为衰减振荡，随着阻尼的减小，振荡越发强烈；ξ=0：等幅振荡；ξ=1和ξ&gt;1时：单调上升。

过渡进程的持续时刻：无振荡单调上升的曲线：ξ=1时的时刻t最短；在欠阻尼系统中，当ξ=0.4-0.8时，时刻比ξ=1时的更短，而且振荡不太严峻。

设计：二阶系统一样工作在ξ=0.4-0.8的欠阻尼状态。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
T——时间常数（达 到63Leabharlann 2％的时间）T越大，上升越慢
减小T，可以提高快 速性
-
14
3. 性能指标：
①、t=3T时， h(t)=0.95 t=4T时, h(t)=0.98
∴调节时间 ts=3T(对应5%误差带) 或 ts=4T(对应2%误差带)
∴ T越小, ts越小,快速性越好
②、ess=1-h(∞)=0 无稳态误差
1. 二阶系统的数学模型
定义
C R((ss))sS22n n2sn2
是标准形式， 其中 ωn——无阻尼振荡频率 ζ——阻尼比 [zi:ta]
-
18
标准形式的二阶系统结构图：
R(s)
n2 S 2 2 nS
C(s)
-
19
LR
Ur
Uc
C
Uc(s)
1
Ur(s) LCS 2 RCS 1
1
S2
LC
R L
Asinω0t
t
试验信号的选择原则 1. 反映系统工作的大部分实际情况 2. 应使形式尽量简单，便于分析 3. 选择使系统工作在最不利的情况下的输入信号。 4. （对系统动态特性 最不利的是阶跃信号）
-
6
2、典型时间响应（输出）
定义： 在零初始条件下（典型的初始条件），在典型信号作用下 的输出。
(1)、单位阶跃响应
加载
-
4
(2) 单位斜坡函数：
t1(t )
0 t<0
t 1（t）=
t t>=0
t L[t1(t)]=1/s2
(3) 单位脉冲信号：
1 h
h
∞ t=0 δ (t) =
0 t≠0 L[δ (t)]=1
t
h→0
-
5
(4) 正弦信号 A sinω0t L[A sin ω0t]=A ω0/(s2+ ω02)
* 实用意义：将脉冲信号输入系统，测得的响应就是系统 的动态特性（数学模型）
或：将单位阶跃响应输入系统，测得的响应求导就是系统 的动态特性（数学模型）
-
8
3、响应的性能指标 以最恶劣的，严格的情况——跟踪阶跃输入的能力
为例，来讨论控制性能的好坏（从响应来看） 稳、准、快三个要求具体用那个参数恒量 ？
③、Mp%=0,无超调
-
15
例: 结构图如下:
是一阶系统,
对快速性的要求是,
-
在0.1秒之内进入 5%
误差带(即 ts=0.1 ) 看是否满足要求?如不能,
一个怎样调整 反馈系数 H
解:
100
①
(s) G 1 GH
S 0.1*100
1
S
100
10
S 10 0.1S 1
-
100/S 0.1
T=0.1 ts=0.3秒不能满足
-
7
(3)、单位脉冲响应： 定义：在单位脉冲信号作用下的响应,用g (t)表示
C(s)= Φ(s) *R(s)
R(s)=1
∴ C脉冲(s)= Φ(s)=SC阶跃(S)
c(t)=g(t) =L-1[Φ(s)]， dh(t) g (t ) dt
* g(t)有着特殊的意义： 单位脉冲响应的拉氏变换＝传递函数
S
1 LC
标准化
2 n
1 LC
,
R R L 2Ln 2 C
-
20
2. 二阶系统的单位阶跃响应
C(s) sR(s)
h(t)
tr tp
ts
-
t
9
参数：
上升时间tr — 第一次到达h(∞)的时间
峰值时间tp— 超过稳态到达第一个峰值的时间
调节时间ts— 进入 5% h(∞)不再超出的最小时间 （或 3％的误差带）
超调量Mp％ — Mp%h(pht)(-h)()*100%
稳态误差ess — 阶跃响应稳态值与给定值之差 ess =1-h(∞)
*规定一些特殊的试验输入信号，称为 典型信号
*规定所有的初始状态是零状态，称为
典型初始状态
-
3
1.典型试验信号 有四种（阶跃函数，斜坡函数，脉冲函
数，三角函数） (1) 单位阶跃信号 1（t）
1 t>=0 1(t ) 1（t）＝
0 t<0
t
L[1(t)]=1/s
相应实际情况：电源突然接通， 负荷突然加载，指令突然
称为一阶系统
方块图：
或
R(S)
C(S)
× 1/Ts
—
R(S)
C(S)
1/(Ts+1)
-
12
2.一阶系统的单位阶跃响应：
C(s)(s)R(s) 1 1 T s1 s
h(t)
c(t)
L1
S
1 (Ts
1)
L1
1 s
T Ts 1
1
1
eT
t
-
13
h(t)
1 63.2%
T
t
一阶系统阶跃响应
响应是指数曲线， 没有振荡，
定义：在单位阶跃信号作用下的响应,用h(t)表示 已知： C(s)= Φ(s) R(s) ，
R(s)=1/s ∴c(t)= h(t)=L-1[Φ(s)/s]
(2)、单位斜坡响应
定义：在单位斜坡信号作用下的响应,用c(t)表示
C(s)= Φ(s) *R(s) R(s)=1/s2 ∴c(t)= L-1 [Φ(s)/s2]
-
10
分析：
① tp(峰值时间)表示初始段的快速性， ts(调节时间)表示总的过渡过程持续时间。
∴ts （调节时间）恒量—快 （小，快）
② Mp％（超调量）恒量—稳 （小，稳）
③ ess（稳态误差）恒量—准 （小，准）
BACK
-
11
§3-2 一阶系统的时域分析
1. 一阶系统的数学模型
定义： (S) C(S) 1 R(S) TS1
第三章 线性系统的时域分析法
❖ §3-1 系统时间响应和性能指标 ❖ §3-2 一阶系统的时域分析 ❖ §3-3 二阶系统的时域分析 ❖ §3-4 高阶系统的时域分析 ❖ §3-5 线性系统的稳定性分析 ❖ §3-6 线性系统的稳态误差计算
-
1
应用动态数学模型（微分方程、传递函数、方框图）， 可对系统的控制性能（稳、准、快）进行分析。时域分 析法是其中的一种方法（还有根轨迹法、频率法）。
*前提：分析控制系统的第一步工作，是推导系统的数 学模型，获取模型后才能采用各种分析方法。
※什么是时域法？
根据系统的微分方程（或数学模型），解出系 统的响应（可应用拉氏变换），然后从响应表达式和曲 线中分析稳、准、快的指标。
-
2
§3-1 系统时间响应和性能指标
系统的时间响应不仅仅取决于本身结构、参数（R、 C的大小），也与输入、初始状态有关。 为能够比较系统与系统之间的好坏，预先
16
② 设反馈系数为H
100
1
∵
(s)10H S01S1100H 00
H S 1
S
10H0
Tts 0.1 1 3 3 10H 0
∴改为H=0.3
*至于放大系数变为1/H=10/3,相当于串联一个K=10/3的放 大器，与时间常数无关。
-
BACK
17
§3-3 二阶系统的时域分析
电动机，机械动力，小功率系统均为二阶系统