2017中考复习《图形的初步认识与三角形》单元测试(四)含答案

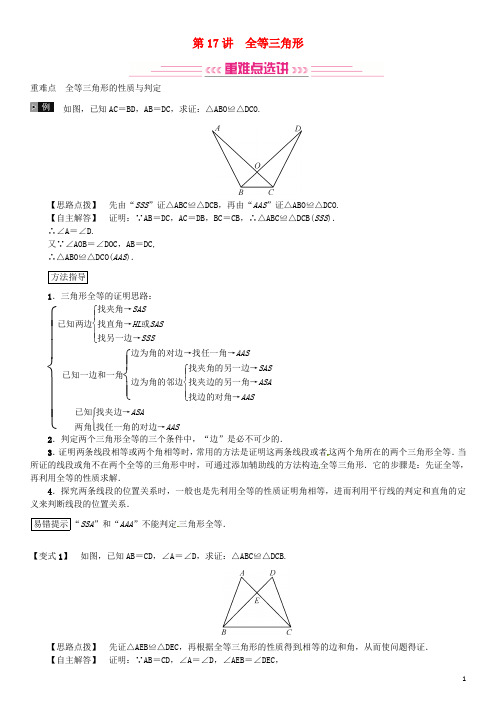
第17讲 全等三角形重难点 全等三角形的性质与判定如图，已知AC ＝BD ，AB ＝DC ，求证：△ABO≌△DCO.【思路点拨】 先由“SSS ”证△ABC≌△DCB，再由“AAS ”证△ABO≌△DCO. 【自主解答】 证明：∵AB＝DC ，AC ＝DB ，BC ＝CB ，∴△ABC≌△DCB(SSS )． ∴∠A＝∠D.又∵∠AO B ＝∠DOC，AB ＝DC, ∴△ABO≌△DCO(AAS )． 方法指导1．三角形全等的证明思路：⎩⎪⎪⎨⎪⎪⎧已知两边⎩⎪⎨⎪⎧找夹角→SAS找直角→HL 或SAS找另一边→SSS已知一边和一角⎩⎪⎨⎪⎧边为角的对边→找任一角→AAS 边为角的邻边⎩⎪⎨⎪⎧找夹角的另一边→SAS 找夹边的另一角→ASA找边的对角→AAS已知两角⎩⎪⎨⎪⎧找夹边→ASA找任一角的对边→AAS2．判定两个三角形全等的三个条件中，“边”是必不可少的．3．证明两条线段相等或两个角相等时，常用的方法是证明这两条线段或者这两个角所在的两个三角形全等．当所证的线段或角不在两个全等的三角形中时，可通过添加辅助线的方法构造全等三角形．它的步骤是：先证全等，再利用全等的性质求解．4．探究两条线段的位置关系时，一般也是先利用全等的性质证明角相等，进而利用平行线的判定和直角的定义来判断线段的位置关系．易错提示“SSA ”和“AAA ”不能判定三角形全等．【变式1】 如图，已知AB ＝CD ，∠A＝∠D，求证：△ABC≌△DCB.【思路点拨】 先证△AEB≌△DEC，再根据全等三角形的性质得到相等的边和角，从而使问题得证． 【自主解答】 证明：∵AB＝CD ，∠A＝∠D，∠AEB＝∠DEC，∴△AEB≌△DEC(AAS )． ∴BE＝CE ，∠ABE＝∠DCE.∴∠EBC＝∠ECB.∴∠ABC＝∠DCB. 又∵BC＝CB ，∴△ABC≌△DCB(ASA )．【变式2】 如图，已知点D 在AB 上，点E 在AC 上，BE 和CD 相交于点O ，OB ＝OC ，∠ABE＝∠ACD.求证：△ABE≌△ACD.【思路点拨】 已知△ABE 和△ACD 的两组对应角相等，则只需找到一组对应边相等即可． 【自主解答】 证明：∵OB＝OC ， ∴∠OBC＝∠OCB. 又∵∠ABE＝∠ACD， ∴∠ABC＝∠ACB. ∴AB＝AC.在△ABE 和△ACD 中， ⎩⎪⎨⎪⎧∠A＝∠A，AB ＝AC ，∠ABE＝∠ACD， ∴△ABE≌△ACD(ASA )．【变式3】 如图，已知AC ，BD 相交于点O ，∠DBA＝∠CAB，∠1＝∠2，求证：∠CDA＝∠DCB.【思路点拨】 要证∠CDA＝∠DCB，观察发现∠CDA 与∠CAB 分别在△ADC 与△BCD 中，故只需证明△ADC≌△BCD，由全等三角形的性质即可使问题得证．【自主解答】 证明：∵∠DBA＝∠CAB，∠1＝∠2，AB ＝BA ， ∴△DAB≌△CBA(AAS )． ∴AC＝BD ，AD ＝BC. 又∵CD＝DC ，∴△ADC≌△BCD(SSS )． ∴∠CDA＝∠DCB.考点1 全等三角形的概念及性质1．(2016·厦门)如图，点E ，F 在线段BC 上，△ABF 与△DCE 全等，点A 与点D ，点B 与点C 是对应点，AF 与DE 相交于点M ，则∠DCE＝(A )A ．∠B B ．∠AC ．∠EMFD ．∠AFB2．(2016·成都)如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝120°．考点2 全等三角形的判定3．(2018·成都)如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB 的是(C )A ．∠A＝∠DB ．∠ACB＝∠DBC C ．AC ＝DBD ．AB ＝DC4．(2018·黔东南)在下列各图中，a ，b ，c 为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC 全等的是(B )A ．甲和乙B ．乙和丙C ．甲和丙D ．只有丙5．(2018·临沂)如图，∠ACB＝90°，AC ＝BC ，AD⊥CE，BE⊥CE，垂足分别是D ，E ，AD ＝3，BE ＝1.则DE 的长是(B )A .32B ．2C ．2 2D .106．如图，在等边△ABC 中，M ，N 分别在BC ，AC 上移动，且BM ＝CN ，AM 与BN 相交于点Q ，则∠BAM＋∠ABN 的度数是(A )A ．60°B ．55°C ．45°D ．不能确定7．(2018·南京)如图，AB⊥CD，且AB ＝CD.E ，F 是AD 上两点，CE⊥AD，BF⊥AD.若CE ＝a ，BF ＝b ，EF ＝c ，则AD 的长为(D )A ．a ＋cB ．b ＋cC ．a －b ＋cD ．a ＋b －c8．(2018·衢州)如图，在△ABC 和△DEF 中，点B ，F ，C ，E 在同一直线上，BF ＝CE ，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是答案不唯一，如：AB ＝DE 或∠A＝∠D 或∠ACB＝∠DFE(或AC∥DF)．(只需写一个，不添加辅助线)9．(2018·荆州)已知：∠AOB ，求作：∠AOB 的平分线．作法：①以点O 为圆心，适当长为半径画弧，分别交OA ，OB 于点M ，N ；②分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧在∠AOB 内部相交于点C ；③画射线OC.射线OC 即为所求．上述作图用到了全等三角形的判定方法，这个方法是SSS ．10．(2018·娄底)如图，在△ABC 中，AB ＝AC ，AD⊥BC 于点D ，DE⊥AB 于点E ，BF⊥AC 于点F ，DE ＝3 cm ，则BF ＝6__cm ．11．(2018·南充)如图，已知AB ＝AD ，AC ＝AE ，∠BAE＝∠DAC.求证：∠C＝∠E.证明：∵∠BAE＝∠DAC，∴∠BAE－∠CAE＝∠DAC－∠CAE. ∴∠BAC＝∠DAE. 在△AB C 和△ADE 中， ⎩⎪⎨⎪⎧AB ＝AD ，∠BAC＝∠DAE，AC ＝AE ，∴△ABC≌△ADE(SAS )． ∴∠C＝∠E.12．(2018·桂林)如图，点A ，D ，C ，F 在同一条直线上，AD ＝CF ，AB ＝DE ，BC ＝EF.(1)求证：△ABC ≌△DEF；(2)若∠A＝55°，∠B＝88°，求∠F 的度数．解：(1)证明：∵AD＝CF ， ∴AC＝DF.在△ABC 和△DEF 中， ⎩⎪⎨⎪⎧AB ＝DE ，BC ＝EF ，AC ＝DF ，∴△ABC≌△DEF(SSS )．(2)∵△ABC≌△DEF，∴∠F＝∠ACB . ∵∠A＝55°，∠B＝88°，∴∠ACB＝180°－(∠A＋∠B)＝37°. ∴∠F＝∠ACB＝37°.13．(2018·泰州)如图，∠A＝∠D＝90°，AC ＝DB ，AC ，DB 相交于点O ，求证：OB ＝OC.证明：在Rt △ABC 和Rt △DCB 中，⎩⎪⎨⎪⎧AC ＝DB ，BC ＝CB ，∴Rt △ABC≌Rt △DCB(HL )． ∴∠ACB＝∠DBC. ∴OB＝OC.14．(2018·怀化T 19，10分)如图，点A ，F ，E ，C 在同一直线上，AB∥CD，AB ＝CD ，∠B＝∠D.(1)求证：△ABE≌△CDF；(2)若点E ，G 分别为线段FC ，FD 的中点，连接EG ，且EG ＝5，求AB 的长．解：(1)证明：∵AB∥DC， ∴∠A＝∠C.2分在△ABE 和△CDF 中， ⎩⎪⎨⎪⎧∠A＝∠C，AB ＝CD ，∠B＝∠D，∴△ABE≌△CDF(ASA ).4分(2)∵点E ，G 分别为线段FC ，FD 的中点， ∴EG＝12CD.6分∵EG＝5， ∴CD＝10.8分 ∵△ABE≌△CDF， ∴AB＝CD ＝10.10分15．(2017·哈尔滨)已知△ACB 和△DCE 都是等腰直角三角形，∠ACB＝∠DCE＝90°，连接AE ，BD 相交于点O.AE 与DC 相交于点M ，BD 与AC 相交于点N.(1)如图1，求证：AE ＝BD ；(2)如图2，若AC ＝DC ，在不添加任何辅助线的情况下，请直接写出图2中四对全等的直角三角形．图1 图2解：(1)证明：∵△ACB 和△DCE 都是等腰直角三角形，∠ACB＝∠DCE＝90°， ∴AC ＝BC ，DC ＝EC.∴∠ACB＋∠ACD＝∠DCE＋∠ACD，即∠BCD＝∠ACE. 在△ACE 和△BCD 中， ⎩⎪⎨⎪⎧AC ＝BC ，∠ACE＝∠BCD，CE ＝CD ，∴△ACE≌△BCD(SAS )． ∴AE＝BD.(2)答案不唯一，如：△ACB ≌△DCE，△EMC≌△BNC，△AON≌△DOM，△AOB≌△DOE.16．(2017·滨州)如图，点P 为定角∠AOB 的平分线上的一个定点，且∠MPN 与∠AOB 互补．若∠MPN 在绕点P 旋转的过程中，其两边分别与OA ，OB 相交于M ，N 两点，则以下结论：①PM＝PN 恒成立；②OM＋ON 的值不变；③四边形PMON 的面积不变；④MN 的长不变．其中正确的个数为(B )A ．4B ．3C ．2D ．117．(2018·青岛)如图，正方形ABCD 的边长为5，点E ，F 分别在AD ，CD 上，AE ＝DF ＝2，BE 与AF 相交于点G ，点H 为BF 的中点，连接GH ，则GH 218．(2018·滨州)在△ABC 中，∠A＝90°，AB ＝AC ，点D 为BC 的中点．(1)如图1，若点E ，F 分别为AB ，AC 上的点，且DE⊥DF，求证：BE ＝AF ；(2)若点E ，F 分别为AB ，CA 延长线上的点，且DE⊥DF，那么BE ＝AF 吗？请利用图2说明理由．图1 图2解：(1)证明：连接AD. ∵∠A＝90°，AB ＝AC ，∴△ABC 为等腰直角三角形，∠EBD＝45°. ∵点D 为BC 的中点， ∴AD＝12BC ＝BD ，∠FAD＝45°.∵∠BDE＋∠EDA＝90°，∠EDA＋∠ADF＝90°， ∴∠BDE＝∠ADF.在△BDE 和△ADF 中，⎩⎪⎨⎪⎧∠EBD＝∠FAD，BD ＝AD ，∠BDE＝∠ADF，∴△BDE≌△ADF(ASA )．∴BE＝AF.(2)BE ＝AF.理由如下：连接AD.由(1)知，∠ABD＝∠BAD＝45°， ∴∠EBD＝∠FAD＝135°.∵∠EDB＋∠BDF＝90°，∠BDF＋∠FDA＝90°，∴∠EDB＝∠FDA. 在△EDB 和△FDA 中，⎩⎪⎨⎪⎧∠EBD＝∠FAD，BD ＝AD ，∠EDB＝∠FDA，∴△EDB≌△FDA(ASA )．∴BE＝AF.。

第16讲等腰三角形与直角三角形1．下列四组线段中，可以构成直角三角形的是( B )A．4，5，6 B．1.5，2，2.5C．2，3，4 D．1，2，32．(2016·广安岳池县一诊)在△ABC中，其两个内角如下，则能判定△ABC为等腰三角形的是( C )A．∠A＝40°，∠B＝50° B．∠A＝40°，∠B＝60°C．∠A＝20°，∠B＝80° D．∠A＝40°，∠B＝80°3．(2015·北京)如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AM的长为1.2 km，则M，C两点间的距离为( D )A．0.5 km B．0.6 kmC．0.9 km D．1.2 km4．(2016·河南)如图，在△ABC中，∠ACB＝90°，AC＝8，AB＝10，DE垂直平分AC交AB于点E，则DE的长为( D ) A．6 B．5 C．4 D．35．(2016·邵阳)如图所示，点D是△ABC的边AC上一点(不含端点)，AD＝BD，则下列结论正确的是( A ) A．AC＞BC B．AC＝BCC．∠A＞∠ABC D．∠A＝∠ABC6．(2016·荆州)如图，在Rt△ABC中，∠C＝90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E，若BC＝3，则DE的长为( A )A．1 B．2 C．3 D．47．(2016·滨州)如图，△ABC中，D为AB上一点，E为BC上一点，且AC＝C D＝BD＝BE，∠A＝50°，则∠CDE的度数为( D )A．50° B．51° C．51.5° D．52.5°8．(2016·烟台)如图，O为数轴原点，A，B两点分别对应－3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M9．(2016·龙岩)如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE＝1，∠E＝30°，则BC ＝2．10．(2016·西宁)如图，OP平分∠AOB，∠AOP＝15°，PC∥OA，PD⊥OA于点D，PC＝4，则PD＝2．11．(2016·宁夏)在等边△ABC中，点D，E分别在边BC，AC上，若CD＝2，过点D作DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，求EF的长．解：∵△ABC是等边三角形，∴∠B＝∠ACB＝60°.∵DE∥AB，∴∠EDC＝∠B＝60°.∴△EDC是等边三角形．∴DE＝DC＝2.∵EF⊥DE，∴∠F＝30°.∠在Rt△DEF中，∵∠DEC＝90°，DE＝2，∠F＝30°，∴DF＝2DE＝4.∴EF＝DF2－DE2＝42－22＝2 3.12．(2016·雅安)如图所示，底边BC为23，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为( A )A．2＋2 3 B．2＋ 3 C．4 D．3 313．(2016·达州)如图，在△ABC中，BF平分∠ABC，AF⊥BF于点F，D为AB的中点，连接DF延长交AC于点E.若AB ＝10，BC ＝16，则线段EF 的长为( B )A ．2B ．3C ．4D ．514．(2015·泸州)在平面直角坐标系中，点A(2，2)，B(32，32)，动点C 在x 轴上，若以A ，B ，C 三点为顶点的三角形是等腰三角形，则点C 的个数为( B )A ．2B ．3C ．4D ．515．(2016·广安)在数学活动课上，老师要求学生在5×5的正方形ABCD 网格中(小正方形的边长为1)画直角三角形，要求三个顶点都在格点上，而且三边与AB 或AD 都不平行．画四种图形，并直接写出其周长(所画图象相似的只算一种)．解：如图1，三角形的周长为25＋10； 如图2，三角形的周长为42＋25； 如图3，三角形的周长为52＋34； 如图4，三角形的周长为32＋10.16．(2016·淄博)如图，已知△ABC，AD 平分∠BAC 交BC 于点D ，BC 的中点为M ，ME ∥AD ，交BA 的延长线于点E ，交AC 于点F.(1)求证：AE ＝AF ； (2)求证：BE ＝12(AB ＋AC)．证明：(1)∵DA 平分∠BAC ， ∴∠BAD ＝∠CAD. ∵AD ∥EM ，∴∠BAD ＝∠A EF ，∠CAD ＝∠AFE. ∴∠AEF ＝∠AFE. ∴AE ＝AF.(2)过点C 作CG∥EM，交BA 的延长线于点G. ∵EF ∥CG ，∴∠G ＝∠AEF，∠ACG ＝∠AFE. ∵∠AEF ＝∠AFE， ∴∠G ＝∠ACG. ∴AG ＝AC.∵BM ＝CM ，EM ∥CG ， ∴BE ＝EG.∴BE ＝12BG ＝12(BA ＋AG)＝12(AB ＋AC)．17．(2016·鄂州)如图，AB＝6，O是AB的中点，直线l经过点O，∠1＝120°，P是直线l上一点．当△APB为直角三角形时，AP。

安徽省2017年中考数学总复习第一轮中考考点系统复习第四单元图形的初步认识与三角形第16讲全等三角形试题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（安徽省2017年中考数学总复习第一轮中考考点系统复习第四单元图形的初步认识与三角形第16讲全等三角形试题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为安徽省2017年中考数学总复习第一轮中考考点系统复习第四单元图形的初步认识与三角形第16讲全等三角形试题的全部内容。

第16讲全等三角形1．(2016·厦门）如图,点E，F在线段BC上，△ABF与△DCE全等，点A与点D,点B与点C 是对应顶点，AF与DE交于点M，则∠DCE＝（ A )A．∠B B．∠A C．∠EMF D．∠AFB2．(2016·永州）如图,点D，E分别在线段AB，AC上，CD与BE相交于点O，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD( D )A．∠B＝∠C B．AD＝AE C．BD＝CE D．BE＝CD3．如图，用尺规作∠AOB的平分线的方法如下:以点O为圆心,任意长为半径画弧交OA，OB于C,D两点，再分别以点C，D为圆心,大于12CD的长为半径画弧,两弧交于点P，作射线OP。

由作法得△OCP≌△ODP的根据是（ D )A．SAS B．ASA C．AAS D．SSS4．(2016·怀化)如图，OP为∠AOB的平分线，PC⊥OA，PD⊥OB，垂足分别是点C，D,则下列结论错误的是（ B ）A。

PC＝PD B．∠CPO＝∠DOP C．∠CPO＝∠DPO D．OC＝OD5．如图，∠B＝∠D＝90°，BC＝CD，∠1＝40°，则∠2＝( B ）A．40° B．50° C．60° D．75°6．(2014·长沙）如图，点B，E,C，F在一条直线上,AB∥DE，AB＝DE,BE＝CF，AC＝6,则DF ＝6．7．(2016·济宁)如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E,AD与CE交于点H，请你添加一个适当条件答案不唯一,如:A H＝BC或AE＝CE或EH＝EB等_，使△AEH≌△CEB.8．(2016·泉州)如图,△ABC,△CDE均为等腰直角三角形,∠ACB＝∠DCE＝90°，点E在AB上．求证：△CDA≌△CEB.证明：∵△ABC、△CDE均为等腰直角三角形，∠ACB＝∠DCE＝90°，∴CE＝CD，BC＝AC.∴∠ACB－∠ACE＝∠DCE－∠ACE，即∠ECB＝∠DCA.在△CEB和△CDA中，错误!∴△CDA≌△CEB（SAS)．9．如图，已知∠ABO＝∠DCO，OB＝OC，求证：△ABC≌△DCB。

第四章图形的初步认识与三角形、四边形第一节线段、角、相交线和平行线1．(2017常德中考)若一个角为75°，则它的余角的度数为( D)A．285°B．105°C．75°D．15°2．(2017自贡中考)如图，a∥b，点B在直线a上，且AB⊥BC，∠1＝35°，那么∠2＝( C)A．45°B．50°C．55°D．60°(第2题图)(第3题图)3．(2017百色中考)如图，直线a，b被直线c所截，下列条件能使a∥b的是( B)A．∠1＝∠6 B．∠2＝∠6C．∠1＝∠3 D．∠5＝∠74．(东营中考)如图，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于( C)A．30°B．35°C．40°D．50°(第4题图)(第5题图)5．(襄阳中考)如图，AD是∠EAC的平分线，AD∥BC，∠B＝30°，则∠C的度数为( C)A．50°B．40°C．30°D．20°6．(2017福州中考)下列图形中，由∠1＝∠2能得到AB∥CD的是( B),A),B),C),D)7．(湘西中考)如图，直线CD∥EF，直线AB与CD，EF分别相交于点M，N，若∠1＝30°，则∠2＝__30°__．8．(2017荆州中考)一把直尺和一块三角板ABC(含30°，60°角)摆放位置如图所示，直尺一边与三角板的两直角边分别交于点D，点E，另一边与三角板的两直角边分别交于点F，点A，且∠CDE＝40°，那么∠BAF的大小为( D)A．40°B．45°C．50°D．10°(第8题图)(第9题图)9．(2017宁波中考)已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置(∠ABC＝30°)，其中A，B两点分别落在直线m，n上，若∠1＝20°，则∠2的度数为( D)A．20°B．30°C．45°D．50°10．(枣庄中考)如图，∠AOB的一边OA为平面镜，∠AOB＝37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是( B)A．75°36′B．75°12′C．74°36′D．74°12′(第10题图)(第11题图)11．(昆明中考)如图，AB∥CE，BF交CE于点D，DE＝DF，∠F＝20°，则∠B的度数为__40°__．12．(宜宾中考)如图，直线a∥b，∠1＝45°，∠2＝30°，则∠P＝__75°__．(第12题图)(第13题图)13．(2017德州中考)如图，利用直尺和三角板过已知直线l外一点P作直线l平行线的方法，其理由是__同位角相等，两直线平行__．。

图形初步与三角形(时间:120分钟满分:150分)一、选择题(本大题共10小题,每小题4分,共40分)1.已知线段AB=16 cm,O是线段AB上一点,M是AO的中点,N是BO的中点,则MN=()A.10 cmB.6 cmC.8 cmD.9 cm解析:∵M是AO的中点,N是BO的中点,∴MN=MO+ON=AO+OB=AB=8 cm.答案:C2.已知∠1=1°30',∠2=1°18',则∠1与∠2的数量关系为()A.∠1=∠2B.∠1-∠2=12'C.∠1-∠2=22'D.∠2-∠1=12'解析:∠1-∠2=1°30'-1°18'=12'.答案:B3.如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为()A.26°B.36°C.46°D.56°解析:∵∠1=∠2+∠4,∠1=124°,∠2=88°,∴∠4=36°.∵l1∥l2,∴∠3=∠4=36°.故选B.答案:B4.现有3 cm,4 cm,7 cm,9 cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数有()解析:四条木棒的所有组合:3,4,7;3,4,9;3,7,9;4,7,9,只有3,7,9和4,7,9能组成三角形.故选B. 答案:B5.等腰三角形的底边长为6,底边上的中线长为4,它的腰长为()答案:A6.如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2,CD=,点P在四边形ABCD的边上.若点P到BD的距离为,则点P的个数为()解析:过点A作AE⊥BD于点E,过点C作CF⊥BD于点F,∵∠BAD=∠ADC=90°,AB=AD=2,CD=,∴∠ABD=∠ADB=45°.∴∠CD F=90°-∠ADB=45°.∵sin ∠ABD=,∴AE=AB·sin ∠ABD=2·sin 45°=2=2>,∴在AB和AD边上符合P到BD的距离为的点有2个.答案:A7.如图为八个全等的正六边形紧密排列在同一平面上的情形.根据图中标示的各点位置,判断△ACD 与下列哪一个三角形全等?()A.△ACFB.△AEDC.△ABCD.△BCF解析:∵根据图形可知AD=AD,AE=AC,DE=DC,∴△ACD≌△AED.答案:B8.如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1 200 m,从飞机上看地平面指挥台B的仰角α=30°,则飞机A与指挥台B的距离为()A.1 200 mB.1 200 mC.1 200 mD.2 400 m解析:∵∠ABC=∠α=30°,∴AB==2 400(m).答案:D9.如图,若正方形网格中每个小方格的边长为1,则△ABC是()解析:根据勾股定理计算出BC2,AB2,AC2,再根据勾股定理逆定理可得△ABC是直角三角形.答案:A10.如图,点A,C都在直线l上,AE⊥AB且AE=AB,BC⊥CD且BC=CD,三点E,B,D到直线l的距离分别是6,3,4,计算图中由线段AB,BC,CD,DE,EA所围成的图形的面积是()解析:如图,过点E,B,D分别作EF⊥l,BG⊥l,DH⊥l,点F,G,H分别为垂足.易得△EFA≌△AGB,△BGC≌△CHD,从而AF=BG,AG=EF;GC=DH,CH=BG.故FH=FA+AG+GC+CH=3+6+4+3=16,则所求面积为(6+4)×16-3×4-6×3=50.答案:A二、填空题(本大题共4小题,每小题5分,共20分)11.如图,AC与BD相交于点O,且AB=CD,请添加一个条件,使得△ABO≌△CDO.解析:由题意可知∠AOB=∠COD,AB=CD,∵AB是∠AOB的对边,CD是∠COD的对边,∴只能添加角相等,故可添加∠A=∠C或∠B=∠D或AB∥CD.答案:∠A=∠C (或AB∥CD 或∠B=∠D)12.如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,CD=2,则点D到AB的距离是.解析:由角平分线的性质,得点D到AB的距离等于CD,也是2.答案:213.如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为.解析:如图,分三种情况讨论:(1)(2)(3)图(1)中,∠APB=90°,∵AO=BO,∠APB=90°,∴PO=AO=BO=2,又∠AOC=60°,∴△APO是等边三角形,∴AP=2.图(2)中,∠APB=90°,∵AO=BO,∠APB=90°,∴PO=AO=BO=2,又∠AOC=60°,∴∠BAP=30°,在Rt△ABP中,AP=cos 30°×4=2.图(3)中,∠ABP=90°,∵BO=AO=2 ,∠BOP=∠AOC=60°,∴PB=2.∴AP==2.答案:2,2或214.已知△ABC是直角边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是.解析:反复运用勾股定理,得AC=,AD=()2,AE=()3,…,所以第n个等腰直角三角形的斜边长是()n.答案:()n三、(本大题共2小题,每小题8分,共16分)15.如图,锐角三角形ABC中,直线l为BC的中垂线,直线m为∠∠A=60°,∠ACP=24°,求∠ABP的度数. 解:∵直线m为∠ABC的角平分线,∴∠ABP=∠CBP.∵直线l为BC的中垂线,∴BP=CP,∴∠CBP=∠BCP,∴∠ABP=∠CBP=∠BCP,在△ABC中,3∠ABP+∠A+∠ACP=180°,即3∠ABP+60°+24°=180°,解得∠ABP=32°.16.如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.(1)求证:BE=AD.(2)求证:AC是线段ED的垂直平分线.(3)△DBC是等腰三角形吗?并说明理由.(1)证明:∵∠ABC=90°,BD⊥EC,∴∠1与∠3互余,∠2与∠3互余.∴∠1=∠2.∵∠ABC=∠DAB=90°,AB=BC,∴△BAD≌△CBE(ASA).∴AD=BE.(2)证明:∵E是AB中点,∴EB=EA.由(1)AD=BE得AE=AD.∵AD∥BC,∴∠7=∠ACB=45°.∵∠6=45°,∴∠6=∠7.由等腰三角形的性质,得EM=MD,AM⊥DE.∴AC是线段ED的垂直平分线.(3)解:△DBC是等腰三角形(CD=BD).理由:由(2),得CD=CE.由(1),得CE=BD.∴CD=BD.∴△DBC是等腰三角形.四、(本大题共2小题,每小题8分,共16分)17.如图,已知∠DAB+∠D=180°,AC平分∠A,且∠CAD=25°,∠B=95°.(1)求∠DCA的度数;(2)求∠ACE的度数.解:(1)∵∠DAB+∠D=180°,∴AB∥CD.∵∠CAD=∠CAB=25°,∴∠DCA=∠CA B=25°.(2)∵∠CAD=∠CAB=25°,∠B=95°,∠ACE是△ABC的外角,∴∠ACE=∠B+∠CAB=95°+25°=120°.18.如图,四边形ABCD是平行四边形,△AB'C和△ABC关于AC所在的直线对称,AD和B'C相交于点O,连接BB'.(1)请直接写出图中所有的等腰三角形(不添加字母);(2)求证:△AB'O≌△CDO.(1)解:△ABB',△AOC和△BB'C;(2)证明:在▱ABCD中,AB=DC,∠ABC=∠D,由轴对称知AB'=AB,∠ABC=∠AB'C,∴AB'=CD,∠AB'O=∠D.在△AB'O和△CDO中,∴△AB'O≌△CDO.五、(本大题共2小题,每小题10分,共20分)19.2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20 km.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A,B,AB相距2 m,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据≈1.41,≈1.73)解:过点C作CD⊥AB,设CD=x m,∵∠ABE=45°,∴∠CBD=45°,∴DB=CD=x m,∵∠CAD=30°,∴AD=CD=x m.∵AB相距2米,∴x-x=2,解得x=.答:生命所在点C与探测面的距离是 m.20.如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=,BE=2.(1)求CD的长;(2)求四边形ABCD的面积.解:(1)如图,过点D作DH⊥AC,∵∠CED=45°,DH⊥EC,DE=,∴EH=DH,∵EH2+DH2=ED2,∴EH2=1,∴EH=DH=1.又∵∠DCE=30°,∴DC=2.(2)由(1)知HC=,∵∠AEB=45°,∠BAC=90°,BE=2,∴AB=AE=2,∴AC=2+1+=3+,∴×2×(3+)+×1×(3+)=.六、(本题满分12分)21.如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.(1)求证:AD=AE;(2)连接BC,DE,试判断BC与DE的位置关系,并说明理由.证明:(1)在△ACD与△ABE中,∵∠A=∠A,∠ADC=∠AEB=90°,A B=AC,∴△ACD≌△ABE.∴AD=AE.(2)互相平行.在△ADE与△ABC中,∵AD=AE,AB=AC,∴∠ADE=∠AED,∠ABC=∠ACB,且∠ADE==∠ABC.∴DE∥BC.七、(本题满分12分)22.如图,在△ABC中,AD是∠BAC的角平分线,且∠B=∠ADB,过点C作CM垂直于AD的延长线,垂足为M.(1)若∠DCM=α,试用α表示∠BAD;(2)求证:AB+AC=2AM.解:(1)∵CM⊥AM,∠DCM=α,∴∠CDM=∠ADB=∠B=90°-α,∴∠BAD=180°-2∠ABD=180°-2(90°-α)=2α.(2)证明:如图,延长AM到F使MF=AM,连接CF,则有AC=CF.∵AD平分∠CAB,∴∠CAF=∠BAF=∠F.∴CF∥AB.∴∠FCD=∠ABD=∠ADB=∠CDF.∴CF=DF.∵AD+DF=2MA,∴AB+AC=2MA.八、(本题满分14分)23.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC 的中线,AF⊥△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=2时,a= ,b=;如图2,当∠ABE=30°,c=4时,a=,b=;图1图2图3归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,利用图3证明你发现的关系式;拓展应用(3)如图4,在▱ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2,AB=3,求AF的长.图4解:(1)如图1,连接EF,则EF是△ABC的中位线,∴EF=AB=.∵∠ABE=45°,AF⊥BE,∴△ABP是等腰直角三角形.∵EF∥AB ,∴△EFP也是等腰直角三角形.∴AP=BP=2 ,EP=FP=1.∴AE=BF=.∴a=b=2.图1图2图3图4 如图2,连接EF,则EF是△ABC的中位线.∵∠ABE=30°,AF⊥BE,AB=4,∴AP=2,BP=2.∵EF AB,∴PE=,PF=1.∴AE=,BF=.∴a=2 ,b=2.(2)a2+b2=5c2.如图3,连接EF,设AP=m ,BP=n,则c2=AB2=m2+n2,∵EF AB,∴PE=BP=n,PF=AP=m.∴AE2=m2+n2,BF2=n2+m2.∴b2=AC2=4AE2=4m2+n2,a2=BC2=4BF2=4n2+m2.∴a2+b2=5(m2+n2)=5c2.(3)如图4,延长EG,BC交于点Q,延长QD,BA交于点P,延长QE,BE分别交PB,PQ于点M,N,连接EF.∵四边形ABCD是平行四边形,∴AD BC,AB CD.∵E,G分别是AD,CD的中点,∴△EDG≌△QCG≌△EAM,∴CQ=DE=,DG=AM=1.5,∴BM=4.5.∵,∴.∴BP=9.∴M是BP的中点.∵AD FQ,∴四边形ADQF是平行四边形.∴AF∥PQ.∵E,F分别是AD,BC的中点,∴AE BF. ∴四边形ABFE是平行四边形,∴OA=OF.由AF∥PQ得:,,∴.∴PN=QN.∴N是PQ的中点.∴△BQP是“中垂三角形”,∴PQ2=5BQ2-BP2=5×(3)2-92=144,∴PQ=12.∴AF=PQ=4.。

单元测试(四) 图形的初步认识与三角形(时间：45分钟满分：100分)一、选择题(每小题4分，共32分)1．若∠α＝32°，则∠α的补角为( C )A．58° B．68° C．148° D．168°2．(2016·长沙)下列各图中，∠1与∠2互为余角的是( B )3．(2016·毕节)到三角形三个顶点的距离都相等的点是这个三角形的( D )A．三条高的交点B．三条角平分线的交点C．三条中线的交点D．三条边的垂直平分线的交点4．如图，字母B所代表的正方形的面积是( B )A．12 B．144 C．13 D．1945．(2016·河北)如图，△ABC中，∠A＝78°，AB＝4，AC＝6.将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是( C )6．如图，△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是( D )A．1对 B．2对 C．3对 D．4对7．将两个含30°和45°的直角三角板如图放置，则∠α的度数是( B )A．10° B．15° C．20° D．25°8．(2016·武汉)平面直角坐标系中，已知A(2，2)、B(4，0)．若在坐标轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是( A )A．5 B．6 C．7 D．8二、填空题(每小题4分，共24分)9．如图，在△ABC 中，∠ACB ＝90°，CD ∥AB ，∠ACD ＝40°，则∠B 的度数为50°．10．如图所示，小明同学利用一个锐角是30°的三角板测量一棵树的高度，测量时如图所示放置三角板，已知他与树之间的水平距离BE 为5 m ，小明的眼睛距地面的距离AB 为1.5 m ，那么这棵树高是4.39m(可用计算器，精确到0.01)．11．若a 、b 、c 为三角形的三边，且a ，b 满足a 2－9＋(b －2)2＝0，则第三边c 的取值范围是1<c<5． 12．(2016·南京)如图，AB 、CD 相交于点O ，OC ＝2，OD ＝3，AC ∥BD ，EF 是△ODB 的中位线，且EF ＝2，则AC 的长为83．13．如图，在△ABC 中，BF 平分∠ABC，AF ⊥BF 于点F ，D 为AB 的中点，连接DF 延长交AC 于点E.若AB ＝10，BC ＝16，则线段EF 的长为3．14．(2016·临沂)一般地，当α、β为任意角时，sin (α＋β)与sin (α－β)的值可以用下面的公式求得：sin(α＋β)＝s in α·cos β＋cos α·sin β；sin (α－β)＝sin α·cos β－cos α·sin β.例如sin90°＝sin(60°＋30°)＝sin60°·cos30°＋cos60°·sin30°＝32×32＋12×12＝1.类似地，可以求得4三、解答题(共44分)15．(10分)已知：如图，△ABC 中，AD ＝DB ，∠1＝∠2.求证：△ABC∽△EAD.证明：∵AD ＝DB ， ∴∠B ＝∠BAD.∵∠BDA ＝∠1＋∠C＝∠2＋∠ADE，∠1＝∠2， ∴∠C ＝∠ADE. ∴△ABC ∽△EAD.16．(10分)如图，在△ABC 中，AB ＝AC.(1)作∠BAC 的平分线，交BC 于点D(尺规作图，保留痕迹)；(2)在AD 的延长线上任取一点E ，连接BE 、CE.求证：△BDE≌△CDE.解：(1)如图．(2)证明：∵AB＝AC ，AD 平分∠BAC， ∴BD ＝CD ，AD ⊥BC. ∴∠BDE ＝∠CDE＝90°. 在△BDE 和△CDE 中， ⎩⎪⎨⎪⎧BD ＝CD ，∠BDE ＝∠CDE，DE ＝DE ，∴△BDE ≌△CDE.17．(12分)如图，以△ABC 的三边为边分别作等边△ACD、△ABE、△BCF，则下列结论：①△EBF ≌△DFC ；②四边形AEFD 为平行四边形；③当AB ＝AC ，∠BAC ＝120°时，四边形AEFD 是正方形．其中正确的结论是哪几个？并说明理由．解：正确的结论有：①②.理由：①∵△BCF 和△ACD 为等边三角形， ∴∠FCB ＝60°，∠DCA ＝60°. ∴∠FCB －∠FCA＝∠DCA－∠FCA， 即∠ACB＝∠DCF. 在△ABC 和△DFC 中， ⎩⎪⎨⎪⎧BC ＝FC ，∠ACB ＝∠DCF，AC ＝DC ，∴△ABC ≌△DFC(SAS)．∴AB ＝DF.同理可证：AC ＝EF. 又∵AB＝AE ＝BE ，AD ＝DC ＝AC ， ∴BE ＝FD ＝AE ，EF ＝DC ＝AD. 可知在△EBF 和△DFC 中，⎩⎪⎨⎪⎧BE ＝FD ，BF ＝FC ，EF ＝DC ，∴△EBF ≌△DFC(SSS)．②由EF ＝AD ，AE ＝DF 可知四边形AEFD 为平行四边形．18．(12分)如图所示，港口B 位于港口O 正西方向120 km 处，小岛C 位于港口O 北偏西60°的方向．一艘游船从港口O 出发，沿OA 方向(北偏西30°)以v km/h 的速度驶离港口O.同时一艘快艇从港口B 出发，沿北偏东30°的方向以60 km/h 的速度驶向小岛C ，在小岛C 用1 h 加装补给物资后，立即按照原来的速度给游船送去．(1)快艇从港口B 到小岛C 需要多长时间？(2)若快艇从小岛C 到与游船相遇恰好用时1 h ，求v 的值及相遇处与港口O 的距离．解：(1)∵∠BOC＝30°，∠CBO ＝60°， ∴∠BCO ＝90°.∴BC ＝OB·cos60°＝120×12＝60(km)．∴快艇从港口B 到小岛C 需要的时间为6060＝1(小时)．答：快艇从港口B 到小岛C 需要1小时． (2)作CD⊥OA，设相交处为点E ，连接CE.∴OC ＝OB·cos30°＝60 3 km ，CD ＝12OC ＝30 3 km ，OD ＝OC·cos30°＝90 km.∴DE ＝90－3v(km)． ∵CE ＝60 km ，∴CD 2＋DE 2＝CE 2，即(303)2＋(90－3v)2＝602. 解得v ＝20或v ＝40.当v ＝20 km/h 时，OE ＝3×20＝60(km)； 当v ＝40 km/h 时，OE ＝3×40＝120(km)．答：v 的值为20 km/h 或40 km/h ，相遇处与港口O 的距离分别为60 km 或120 km.。

1 第四章 图形的初步认识与三角形自我测试 一、选择题 1．(2016·南平)如图，直线a∥b，直线c与a，b分别交于A，B两点，若∠1＝46°，则∠2＝( B ) A．44° B．46° C．134° D．54°

,第1题图) ,第2题图)

2．(2016·东营)如图，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于( C ) A．30° B．35° C．40° D．50° 3．(2016·长沙)若一个三角形的两边长分别为3和7，则第三边长可能是( A ) A．6 B．3 C．2 D．11 4．(2016·莆田)如图，OP是∠AOB的平分线，点C，D分别在角的两边OA，OB上，添加下列条件，不能判定△POC≌△POD的选项是( D ) A．PC⊥OA，PD⊥OB B．OC＝OD C．∠OPC＝∠OPD D．PC＝PD

,第4题图) ,第5题图)

5．(2016·雅安)如图所示，底边BC为23，顶角A为120°的等腰△ABC中，DE垂直平分AB于点D，则△ACE的周长为( A ) A．2＋23 B．2＋3 C．4 D．33 二、填空题 6．(2016·茂名)已知∠A＝100°，那么∠A补角为__80__度． 7．如图，∠1，∠2是△ABC的外角，已知∠1＋∠2＝260°，求∠A的度数是__80°__．

,第7题图) ,第8题图) 8.(2016·南京)如图，AB，CD相交于点O，OC＝2，OD＝3，AC∥BD，EF是△ODB的中

位线，且EF＝2，则AC的长为__83__．

9．(2016·自贡)如图，在边长相同的小正方形网格中，点A，B，C，D都在这些小正方 2

形的顶点上，AB，CD相交于点P，则APBP的值＝__3__，tan∠APD的值＝__2__． 10．(2016·宿迁)如图，在矩形ABCD中，AD＝4，点P是直线AD上一动点，若满足△PBC是等腰三角形的点P有且只有3个，则AB的长为__23或4__.

亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光……学 习 资 料 专 题第17讲 全等三角形重难点 全等三角形的性质与判定如图，已知AC ＝BD ，AB ＝DC ，求证：△ABO≌△DCO.【思路点拨】 先由“SSS ”证△ABC≌△DCB，再由“AAS ”证△ABO≌△DCO. 【自主解答】 证明：∵AB＝DC ，AC ＝DB ，BC ＝CB ，∴△ABC≌△DCB(SSS )． ∴∠A＝∠D.又∵∠AOB＝∠DOC，AB ＝DC, ∴△ABO≌△DCO(AAS )． 方法指导1．三角形全等的证明思路：⎩⎪⎪⎨⎪⎪⎧已知两边⎩⎪⎨⎪⎧找夹角→SAS找直角→HL 或SAS找另一边→SSS已知一边和一角⎩⎪⎨⎪⎧边为角的对边→找任一角→AAS 边为角的邻边⎩⎪⎨⎪⎧找夹角的另一边→SAS 找夹边的另一角→ASA找边的对角→AAS已知两角⎩⎪⎨⎪⎧找夹边→ASA找任一角的对边→AAS2．判定两个三角形全等的三个条件中，“边”是必不可少的．3．证明两条线段相等或两个角相等时，常用的方法是证明这两条线段或者这两个角所在的两个三角形全等．当所证的线段或角不在两个全等的三角形中时，可通过添加辅助线的方法构造全等三角形．它的步骤是：先证全等，再利用全等的性质求解．4．探究两条线段的位置关系时，一般也是先利用全等的性质证明角相等，进而利用平行线的判定和直角的定义来判断线段的位置关系．易错提示“SSA ”和“AAA ”不能判定三角形全等．【变式1】 如图，已知AB ＝CD ，∠A＝∠D，求证：△ABC≌△DCB.【思路点拨】 先证△AEB≌△DE C ，再根据全等三角形的性质得到相等的边和角，从而使问题得证． 【自主解答】 证明：∵AB＝CD ，∠A＝∠D，∠AEB＝∠DEC， ∴△AEB≌△DEC(AAS )． ∴BE＝CE ，∠ABE＝∠DCE.∴∠EBC＝∠ECB.∴∠ABC＝∠DCB. 又∵BC＝CB ，∴△ABC≌△DCB(ASA )．【变式2】 如图，已知点D 在AB 上，点E 在AC 上，BE 和CD 相交于点O ，OB ＝OC ，∠ABE＝∠ACD.求证：△ABE≌△ACD.【思路点拨】 已知△ABE 和△ACD 的两组对应角相等，则只需找到一组对应边相等即可． 【自主解答】 证明：∵OB＝OC ， ∴∠OBC＝∠OCB. 又∵∠ABE＝∠ACD， ∴∠ABC＝∠ACB. ∴AB＝AC.在△ABE 和△ACD 中， ⎩⎪⎨⎪⎧∠A＝∠A，AB ＝AC ，∠ABE＝∠ACD， ∴△ABE≌△ACD(ASA )．【变式3】 如图，已知AC ，BD 相交于点O ，∠DBA＝∠CAB，∠1＝∠2，求证：∠CDA＝∠DCB.【思路点拨】 要证∠CDA＝∠DCB，观察发现∠CDA 与∠CAB 分别在△ADC 与△BCD 中，故只需证明△ADC≌△BCD，由全等三角形的性质即可使问题得证．【自主解答】 证明：∵∠DBA＝∠CAB，∠1＝∠2，AB ＝BA ， ∴△DAB≌△CBA(AAS )． ∴AC＝BD ，AD ＝BC. 又∵CD＝DC ，∴△ADC≌△BCD(SSS )． ∴∠CDA＝∠DCB.考点1 全等三角形的概念及性质1．(2016·厦门)如图，点E ，F 在线段BC 上，△ABF 与△DCE 全等，点A 与点D ，点B 与点C 是对应点，AF 与DE 相交于点M ，则∠DCE＝(A )A ．∠B B ．∠AC ．∠EMFD ．∠AFB2．(2016·成都)如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝120°．考点2 全等三角形的判定3．(2018·成都)如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB 的是(C )A ．∠A＝∠DB ．∠ACB＝∠DBC C ．AC ＝DBD ．AB ＝DC4．(2018·黔东南)在下列各图中，a ，b ，c 为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC 全等的是(B )A ．甲和乙B ．乙和丙C ．甲和丙D ．只有丙5．(2018·临沂)如图，∠ACB＝90°，AC ＝BC ，AD⊥CE，BE⊥CE，垂足分别是D ，E ，AD ＝3，BE ＝1.则DE 的长是(B )A .32B ．2C ．2 2D .106．如图，在等边△ABC 中，M ，N 分别在BC ，AC 上移动，且BM ＝CN ，AM 与BN 相交于点Q ，则∠BAM＋∠ABN 的度数是(A )A ．60°B ．55°C ．45°D ．不能确定7．(2018·南京)如图，AB⊥CD，且AB ＝CD.E ，F 是AD 上两点，CE⊥AD，BF⊥AD.若CE ＝a ，BF ＝b ，EF ＝c ，则AD 的长为(D )A ．a ＋cB ．b ＋cC ．a －b ＋cD ．a ＋b －c8．(2018·衢州)如图，在△ABC 和△DEF 中，点B ，F ，C ，E 在同一直线上，BF ＝CE ，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是答案不唯一，如：AB ＝DE 或∠A＝∠D 或∠ACB＝∠DFE(或AC∥DF)．(只需写一个，不添加辅助线)9．(2018·荆州)已知：∠AOB ，求作：∠AOB 的平分线．作法：①以点O 为圆心，适当长为半径画弧，分别交OA ，OB 于点M ，N ；②分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧在∠AOB 内部相交于点C ；③画射线OC.射线OC 即为所求．上述作图用到了全等三角形的判定方法，这个方法是SSS ．10．(2018·娄底)如图，在△ABC 中，AB ＝AC ，AD⊥BC 于点D ，DE⊥AB 于点E ，BF⊥AC 于点F ，DE ＝3 cm ，则BF ＝6__cm ．11．(2018·南充)如图，已知AB ＝AD ，AC ＝AE ，∠BAE＝∠DAC.求证：∠C＝∠E.证明：∵∠BAE＝∠DAC，∴∠BAE－∠CAE＝∠DAC－∠CAE. ∴∠BAC＝∠DAE. 在△ABC 和△ADE 中， ⎩⎪⎨⎪⎧AB ＝AD ，∠BAC＝∠DAE，AC ＝AE ，∴△ABC≌△ADE(SAS )． ∴∠C＝∠E.12．(2018·桂林)如图，点A ，D ，C ，F 在同一条直线上，AD ＝CF ，AB ＝DE ，BC ＝EF.(1)求证：△ABC ≌△DEF；(2)若∠A＝55°，∠B＝88°，求∠F 的度数．解：(1)证明：∵AD＝CF ， ∴AC＝DF.在△ABC 和△DEF 中， ⎩⎪⎨⎪⎧AB ＝DE ，BC ＝EF ，AC ＝DF ，∴△ABC≌△DEF(SSS )．(2)∵△ABC≌△DEF，∴∠F＝∠ACB . ∵∠A＝55°，∠B＝88°，∴∠ACB＝180°－(∠A＋∠B)＝37°. ∴∠F＝∠ACB＝37°.13．(2018·泰州)如图，∠A＝∠D＝90°，AC ＝DB ，AC ，DB 相交于点O ，求证：OB ＝OC.证明：在Rt △ABC 和Rt △DCB 中，⎩⎪⎨⎪⎧AC ＝DB ，BC ＝CB ，∴Rt △ABC≌Rt △DCB(HL )． ∴∠ACB＝∠DBC. ∴OB＝OC.14．(2018·怀化T 19，10分)如图，点A ，F ，E ，C 在同一直线上，AB∥CD，AB ＝CD ，∠B＝∠D.(1)求证：△ABE≌△CDF；(2)若点E ，G 分别为线段FC ，FD 的中点，连接EG ，且EG ＝5，求AB 的长．解：(1)证明：∵AB∥DC， ∴∠A＝∠C .2分在△ABE 和△CDF 中， ⎩⎪⎨⎪⎧∠A＝∠C，AB ＝CD ，∠B＝∠D，∴△ABE≌△CDF(ASA ).4分(2)∵点E ，G 分别为线段FC ，FD 的中点， ∴EG＝12CD.6分∵EG＝5， ∴CD＝10.8分 ∵△ABE≌△CDF， ∴AB＝CD ＝10.10分15．(2017·哈尔滨)已知△ACB 和△DCE 都是等腰直角三角形，∠ACB＝∠DCE＝90°，连接AE ，BD 相交于点O.AE 与DC 相交于点M ，BD 与AC 相交于点N.(1)如图1，求证：AE ＝BD ；(2)如图2，若AC ＝DC ，在不添加任何辅助线的情况下，请直接写出图2中四对全等的直角三角形．图1 图2解：(1)证明：∵△ACB 和△DCE 都是等腰直角三角形，∠ACB＝∠DCE＝90°，∴AC ＝BC ，DC ＝EC.∴∠ACB＋∠ACD＝∠DCE＋∠ACD，即∠BCD＝∠ACE. 在△ACE 和△BCD 中， ⎩⎪⎨⎪⎧AC ＝BC ，∠ACE＝∠BCD，CE ＝CD ，∴△ACE≌△B CD(SAS )． ∴AE＝BD.(2)答案不唯一，如：△ACB ≌△DCE，△EMC≌△BNC，△AON≌△DOM，△AOB≌△DOE.16．(2017·滨州)如图，点P 为定角∠AOB 的平分线上的一个定点，且∠MPN 与∠AOB 互补．若∠MPN 在绕点P 旋转的过程中，其两边分别与OA ，OB 相交于M ，N 两点，则以下结论：①PM＝PN 恒成立；②OM＋ON 的值不变；③四边形PMON 的面积不变；④MN 的长不变．其中正确的个数为(B )A ．4B ．3C ．2D ．117．(2018·青岛)如图，正方形ABCD 的边长为5，点E ，F 分别在AD ，CD 上，AE ＝DF ＝2，BE 与AF 相交于点G ，点H 为BF 的中点，连接GH ，则GH 218．(2018·滨州)在△ABC 中，∠A＝90°，AB ＝AC ，点D 为BC 的中点．(1)如图1，若点E ，F 分别为AB ，AC 上的点，且DE⊥DF，求证：BE ＝AF ；(2)若点E ，F 分别为AB ，CA 延长线上的点，且DE⊥DF，那么BE ＝AF 吗？请利用图2说明理由．图1 图2解：(1)证明：连接AD. ∵∠A＝90°，AB ＝AC ，∴△ABC 为等腰直角三角形，∠EBD＝45°. ∵点D 为BC 的中点，∴AD＝12BC ＝BD ，∠FAD＝45°.∵∠BDE＋∠EDA＝90°，∠EDA＋∠ADF＝90°， ∴∠BDE＝∠ADF.在△BDE 和△ADF 中，⎩⎪⎨⎪⎧∠EBD＝∠FAD，BD ＝AD ，∠BDE＝∠ADF，∴△BDE≌△ADF(ASA )．∴BE＝AF.(2)BE ＝AF.理由如下： 连接AD.由(1)知，∠ABD＝∠BAD＝45°， ∴∠EBD＝∠FAD＝135°.∵∠EDB＋∠BDF＝90°，∠BDF＋∠FDA＝90°，∴∠EDB＝∠FDA. 在△EDB 和△FDA 中，⎩⎪⎨⎪⎧∠EBD＝∠FAD，BD ＝AD ，∠EDB＝∠FDA，∴△EDB≌△FDA(ASA )．∴BE＝AF.。