2009年秋学期高三9月月考数学试卷(理科)

衡水中学2009届高三下学期第一次调研考试理科数学试题河北衡水中学2008-2009学年度高三第二学期第一次调研考试高三年级数学试卷（理科）第Ⅰ卷（选择题共60分）一、 选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上） 1. 在等差数列{}na 中，的值为，则119158131203a a a a a-=++（ ）A 6B 12C 24D 48U是实数集R ，{}⎭⎬⎫⎩⎨⎧≥-==112,42x x N xx M 则图中阴影部分表示的集合是（ ）{}21≤≤x x C ， {}2 x x D3.（理）设复数()()721111z i iiz +-+-+=则展开式的第五项是（ ）A-21 B 35 C -21i D-35i()()()()00,0012,0lg x x f x x x x f x 则若 ⎪⎩⎪⎨⎧≥-=的取值范围是（ ）()()+∞-∞-,11, A B ()()+∞-∞-,01,C ()()1,00,1 -D ()()+∞-,00,1()()2111=-=→x x f iml x x f x 处连续，且在，则()1f 等于（ ）A -1B 0C 1D 2 （ ）7.(理)为迎接2008年北京奥运会，某校举行奥运知识竞赛，有6支代表参赛，每队2名同学，若12名参赛同学中有4人获奖，且这4人来自3个不同代表队，则不同获奖情况种数有（ ）A 412C B1312121236C C C C C C12121336C C C CD221312121236A C C C C C8.已知随即变量ε服从二项分布，且44.1,4.2==E εεD 则二项分布的参数n 、p 的值为（ ）A n=4.p=0.6B n=6. p=0.4 C9.PAB ∆所在平面a 和四边形ABCD 所在平面β垂直，A D ⊥a BC ⊥β, AD=4 BC=8 AB=6 ∠APD=∠CPB,则点P 在平面a 内轨迹为（ ） A 圆的一部分 B 椭圆的一部分 C 双曲线的一部分D 抛物线的一部分10．()x f 是偶函数，且()x f 在[)∞+.0上是增函数，如果()()⎥⎦⎤⎢⎣⎡∈-≤+1..2121x x f ax f 在上恒成立，则实数a 的取值范围是（ ）A []0.2-B []0.5-C []1.`5-D []1.2-12222=+by a x 的左、右焦点分别为F 1.F 2，且cFF 221=，点A 在椭圆上，,,0221211c AF AF F F AF =⋅=⋅则椭圆的离心率e =（ ）33.A 215,-B C213- D 222，侧棱长为2，它的所有顶点在一个球面上，则次球的表面积等于（ ）A π16B π332C π316D π27332二、填空题（每小题5分，共20分 ，请把答案写在答案纸的相应位置上） 13.yx z y y x y x xy 420005+=⎪⎩⎪⎨⎧≤≤-≥++则满足已知的最小值是1B 1C 1,.则二面角A 1-BC-A 的平面角的正切值为()()()()00.0.0121222c c F c F a y ax C 和的两个焦点是：设椭圆-=+，且椭圆C 与222:c y x Q =+圆有公共点（Ⅰ）求a 的取值范围；（Ⅱ）若椭圆上的点到焦点的最短距离为23-，求椭圆C 的方程及圆Q 的方程。

2009年惠州市高三年级理科数学命题考卷(32)一、选择题（本大题共10小题，每小题5分，共50分）1. 设集合A={x|0≤x≤2}，集合B={x|x²3x+2=0}，则A∩B的结果是（）A. {1, 2}B. {1}C. {2}D. ∅2. 若复数z满足|z1|=|z+i|，则z在复平面内对应的点位于（）A. 第一象限B. 第二象限C. 直线y=x上D. 直线y=x上3. 函数f(x)=x²2x+3的对称轴是（）A. x=1B. x=1C. x=2D. x=24. 已知数列{an}是等差数列，a1=1，a3=3，则a5的值为（）A. 5B. 6C. 7D. 85. 若向量a=(2, 3)，向量b=(1, 2)，则2a3b的模长为（）A. 5B. 10C. 15D. 206. 已知函数f(x)=|x1|，则f(x)在区间（0, 2）上的最小值为（）A. 0B. 1C. 2D. 37. 设等比数列{an}的公比为q，若a1+a3=6，a2+a4=18，则q的值为（）A. 2B. 3C. 4D. 58. 若直线y=kx+b与圆(x1)²+(y2)²=4相切，则k的取值范围是（）A. [3, 3]B. (3, 3)C. [2, 2]D. (2, 2)9. 已知函数f(x)=ln(x+1)，则f'(x)在区间（0, 1）上的符号为（）A. 正B. 负C. 零D. 无法确定10. 设三角形ABC的三边长分别为a、b、c，若a²+b²=3c²，则三角形ABC的形状为（）A. 锐角三角形B. 钝角三角形C. 直角三角形D. 等边三角形二、填空题（本大题共5小题，每小题5分，共25分）11. 已知数列{an}是等差数列，a1=1，a3=3，则an=______。

12. 若函数f(x)=x²2x+3，则f(x)的最小值为______。

09届高三数学第一学期月考一试卷（时量：120分钟）一、选择题：本大题共8小题，每小题5分,共40分．在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知函数()f x =M ，()ln(1)g x x =+的定义域为N ，则M N =（ ）A 、{|11}x x -<<B 、{|1}x x <C 、{|1}x x >-D 、∅2、命题“若2≥x ，则0322<-+x x ”的否．命题和命题的否定．．分别是（ ） A 、若2≤x ，则0322<-+x x ；若2≥x ，则0322≥-+x x B 、若2<x ，则0322≥-+x x ；若2≥x ，则0322≥-+x x C 、若2≥x ，则0322<-+x x ；若2<x ，则0322<-+x x D 、若2<x ，则0322≥-+x x ；若2>x ，则0322≥-+x x 3、满足2104x x ->-的x 范围是（ ） A 、(21)-， B 、(2)+∞，C 、(21)(2)-+∞，， D 、(2)(1)-∞-+∞，，4、设a b ，为两条直线，αβ，为两个平面，下列四个命题中，正确的命题是（ ） A 、若a b ，与α所成的角相等，则a b ∥ B 、若a b αβ，∥∥，αβ∥，则a b ∥ C 、若a b a b αβ⊂⊂，，∥，则αβ∥ D 、若a b αβ⊥⊥，，αβ⊥，则a b ⊥5、把函数e xy =的图像按向量(23)=，a 平移，得到()y f x =的图像，则()f x =（ ） A 、3e2x -+ B 、3e2x +-C 、2e3x +- D 、2e3x -+6．若不等式组502x y y a x -+0⎧⎪⎨⎪⎩≥，≥，≤≤表示的平面区域是一个三角形，则a 的取值范围是（ ）A 、[)7,5B 、()[)+∞∞-,75,C 、()5,∞-D 、[)+∞,77、设R b a ∈,，若集合{}⎭⎬⎫⎩⎨⎧⊆+b a b a b a ,,0,,1，则a b -等于（ ）A 、1B 、-1C 、2D 、-28、若数列{}n a 满足212n na p a +=（p 为正常数，n *∈N ），则称{}n a 为“等方比数列”．甲：数列{}n a 是等方比数列；乙：数列{}n a 是等比数列，则（ ）A 、甲是乙的充分条件但不是必要条件；B 、甲是乙的必要条件但不是充分条件；C 、甲是乙的充要条件；D 、甲既不是乙的充分条件也不是乙的必要条件。

2009—2010学年度高三年级第二次月考数学试卷（考试时间：2009年11月26日,满分150分）班级__________姓名__________分数__________一、 选择题：（本大题共8个小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

将正确答案填写在答题卡上。

） 答题卡题号 1． 2． 3． 4． 5． 6． 7． 8．答案⒈复数的共轭复数是 534+iA ．B ．C ．D ． 34-i 3545+i 34+i 3545-i ⒉（理）已知函数，则集合中含 ()()y f x a x b =≤≤{}{}(,)(),(,)0x y y f x a x b x y x =≤≤= 有元素的个数为A ．0B ．1或0C ．1 D ．1或2 （文）已知垂直时k 值为(1,2),(3,2),3a b ka b a b ==-+- 与 A ．17 B ．18 C ．19 D ．20⒊(理)函数的图象的一条对称轴方程是 252sin(π+=x y A ． B ． C ． D ． 4π-=x 2π-=x 8π=x 45π=x (文) 满足的函数是'()()f x f x =　A ． B ． C ． D ． ()1f x x =-()f x x =()0f x =()1f x =⒋命题“”的否定为2,240x R x x ∀∈-+≤A. B.042,2≥+-∈∀x x R x 042,2>+-∈∃x x R x C. D.042,2≤+-∉∀x x R x 042,2>+-∉∃x x R x ⒌已知数列的首项，则下列结论正确的是{}n a *111,3()n n a a S n N +==∈A ．数列是等比数列 B ．数列是等比数列23,,,,n a a a {}n a C ．数列是等差数列 D ．数列是等差数列23,,,,n a a a {}n a⒍（理）设函数在定义域内可导，的图象如图1所示，则导函数可 ()f x ()y f x ='()y f x = 能为（文）下列函数中，周期为1的奇函数是A ．B ． C． D ． x yπ2sin 21-=32(sin ππ+=x y tan 2y x π=x x y ππcos sin =⒎(理)设实数满足 ，则的取值范围是 ,x y 2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩22x y u xy +=A ． B ． C ． D ． 5[2,]2510[,2310[2,31[,4]4(文)不等式组所表示的平面区域的面积等于03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩A. B. C. D. 32234334⒏如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横纵坐标分别对应数列的前12项，如下表所示：{}*()n a n N ∈ 1a 2a 3a 4a 5a 6a 7a 8a 9a 10a 11a12a 1x 1y 2x 2y 3x 3y 4x 4y 5x 5y 6x6y 按如此规律下去，则200920102011a a a ++=A ．1003 B ．1005 C ．1006 D ．2011二、填空题：（本大题共6个小题，每小题5分，共30分。

江苏省无锡市2009—2010学年度普通高中高三质量调研数 学 试 题注：本文仅供学习交流讨论。

请勿用于商业用途，本人不付任何法律责任。

考生注意：1．本试卷共4页，包括填空题（第1题—第14题）、解答题（第15题—第20题）两部分。

本试卷满分160分，考试时间120分钟。

2．答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色字迹的签字笔填写在试卷的指定位置。

3．作答各题时，必须用书写黑色字迹的0.5毫米签字笔写在试卷的制定位置，在其它位置作答一律无效。

4．如有作图需要，可用2B 铅笔作答，并请加黑加粗，描写清楚。

参考公式： 柱体体积公式：V Sh =柱体；锥体体积公式：13V Sh =锥体，其中S 为底面面积，h 为柱体、锥体的高。

一、填空题：本大题共14小题，每小题5分，共70分。

请把答案填写在答题卡相应位置上。

1．已知向量m =（1，1）与向量n=（x ，22x -）垂直，则x = 。

2．若将复数212ii+-表示为(,,a bi a b R +∈i 是虚数单位)的形式，则a b += 。

3．若“21x >”是“x a <”的必要不充分条件，则a 的最大值为 。

4．已知集合11{|()}24xA x =>，2{|log (1)2}B x x =-<。

则A B = 。

5．今年9月10日，某报社做了一次关于“尊师重教”的社会调查，在A 、B 、C 、D 四个单位回收的问卷数一次成等差数列，因报道需要，从回收的问卷中按单位分层抽取容量为300的样本，其中在B 单位抽的60份，则在D 单位抽取的问卷是 份。

6．直线4y x b =+是曲线41y x =-的一条切线，则实数b 的值为 。

7．已知双曲线的中心在原点，对称轴为坐标轴，且经过点（2，0），则双曲线的焦点坐标为 。

8．在可行域内任取一点，规则如流程图所示，则能输出数对（x ，y ）的概率是 。

9．集合{1,2,3,4,5}A =，{0,1,2,3,4}B =，点P的坐标为（m ，n ），m A ∈，n B ∈，则点P 在直线5x y +=下方的概率为 。

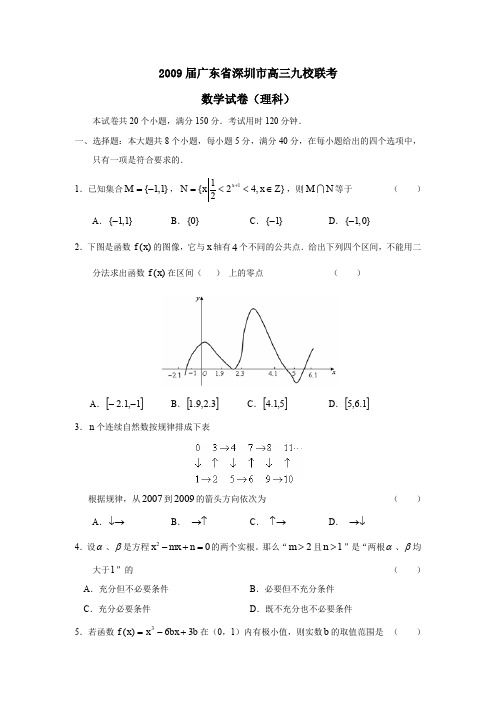
2009届广东省深圳市高三九校联考数学试卷（理科）本试卷共20个小题，满分150分．考试用时120分钟．一、选择题：本大题共8个小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合要求的． 1．已知集合{1,1}M =-，11{24,}2x N xx Z +=<<∈，则M N 等于（ ）A ．{1,1}-B ．{0}C ．{1}-D ．{1,0}-2．下图是函数()f x 的图像，它与x 轴有4个不同的公共点．给出下列四个区间，不能用二分法求出函数()f x 在区间（ ） 上的零点（ ）A ．[]1,1.2--B ．[]3.2,9.1C ．[]5,1.4D ．[]1.6,5 3．n 个连续自然数按规律排成下表根据规律，从2007到2009的箭头方向依次为（ ）A ．↓→B ． →↑C ． ↑→D ． →↓4．设α、β是方程20-+=x mx n 的两个实根。

那么“2>m 且1>n ”是“两根α、β均大于1”的（ ）A ．充分但不必要条件B ．必要但不充分条件C ．充分必要条件D ．既不充分也不必要条件5．若函数b bx x x f 36)(3+-=在（0，1）内有极小值，则实数b 的取值范围是 （ ）A ．（0，1）B ．（－∞，1）C ．（0，+∞）D ．（0，21）6．在∆ABC 中，角A 、B 、C 的对边分别为,,,,1,3a b c A a b π===则c = （ ）A ．1B ．2C 1D ．37．式1019113sin)tan()3423πππ---的值是（ ）A ．1B ．1-C 1D ．1-8．已知定义域为R 的函数()f x 在(8)+∞，上为减函数，且函数(8)y f x =+为偶函数，则（ ）A ．(6)(7)f f >B ．(6)(9)f f >C ．(7)(9)f f >D ．(7)(10)f f >二、填空题：本大题共6个小题，每小题5分，满分30分． 9．曲线cos ([,])22y x x ππ=∈-与x 轴所围成的封闭图形的面积是 ．10．把函数()2cos(2)6π=--f x x 的图像向左平移6π个单位，再把所得图像上每一点的纵坐标不变，横坐标变为原来的12，那么所得到的图像的函数解析式是 ．11． 已知等差数列{}n a 中，25a = ，411a =，则前10项和=10S ． 12．不等式143x x +-->的解集为 ．13．已知[0,]π∈x ．若向量(2cos 1,2cos 22)=++a x x 和向量(cos ,1)=-b x 垂直，则x的值为 ．14．已知)(x f 是定义域为R 的奇函数)(x f ，若当(0,)∈+∞x 时，()lg =f x x ，则满足()0>f x 的x 的取值范围是 ．三、解答题:本大题共6个小题,满分80分．解答须写出文字说明、证明过程和演算步骤． 15．（本小题满分12分）已知实数0a >且1a ≠，函数()log a f x x =在区间[,2]a a 上的最大值比与最小值大12，求实数a 的值． 16．（本小题满分12分）已知数列{}n a 满足121+=-n n a a ，13=a ． （Ⅰ）求证：数列{1}-n a 是等比数列；（Ⅱ）求数列{}n a 的通项公式和前n 项和n S ． 17．（本小题满分14分）在∆ABC 中，已知31tan ,21tan ==B A ，该三角形的最长边为1．（Ⅰ）求角C ；（Ⅱ）求∆ABC 的面积S ．18．（本小题满分14分）若函数2()sin sin cos (0)f x ax ax ax a =->的图象与直线y m =（m 为实常数）相切，并且从左到右切点的横坐标依次成公差为2π的等差数列． （Ⅰ）求m 和a 的值；（Ⅱ）若点00(,)A x y 是()y f x =图象的对称中心，且]2,0[0π∈x ，求点A 的坐标；（Ⅲ）写出函数()y f x =-的所有单调递增区间；19．（本小题满分14分）2008年北京奥运会中国跳水梦之队取得了辉煌的成绩。

安徽省怀远三中2009届高三第四次月考数学（理科）试题一、选择题：本大题共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1．若A = {2，3，4}，B = {x | x = n ·m ，m ，n ∈A ，m ≠n }，则集合B 的元素个数为（ ）A ．2B ．3C ．4D ．52．已知向量a = (1– sin θ，1)，b = (12，1+sin θ)，且a ∥b ，则锐角θ等于（ ）A ．30°B ．45°C ．60°D ．75°3．命题“对任意的3210x x x ∈-+R ，≤”的否定是A ． 不存在3210x x x ∈-+R ，≤B ． 存在3210x x x ∈-+R ，≤C ． 存在3210x x x ∈-+>R ， D ． 对任意的3210x x x ∈-+>R ， 4．在△ABC 中，“cos A = 2sin B sin C ”是“△ABC 为钝角三角形”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 5．函数],0[cos sin 3π∈-=x x x y 在上的最小值为（ ）A ．－1B ．－2C ．0D ．3-6．设S n 是公差不为0的等差数列{a n }的前n 项和，且S 1,S 2,S 4成等比数列，则21aa 等于A ．1B ．2C ．3D ．47．已知等差数列{a n }中，前n 项和为S n ，若1193,6S a a 则=+等于 （ ）A ．12B ．33C ．66D ．118．在R 上定义一种运算⊗：x ⊗y = x (1– y )．若不等式(x – a )⊗( x + a )＜1对任意实数x 成立，则（ ） A ．–1322a << B ．0＜a ＜2 C ．–1＜a ＜1D ．3122a -<<9． 某人要将3本不同的书放入书柜的4个方格里，且同一方格放入的书不超过2本，则不同的放书方法种数有（ ）A 、64种B 、60种C 、48种D 、32种10．已知函数y = 2sin(x ωθ+) (0＜θ＜π)为偶函数，其图象与直线y = 2某两个交点的横坐标分别为x 1、x 2，若|x 2 – x 1|的最小值为π，则该函数的一个递增区间可以是（ ） A ．(,)24ππ-- B ．(,)44ππ-C ．(0,)2πD ．3(,)44ππ11、为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin 2y x =的图象A ．向左平移5π12个长度单位B ．向右平移5π12个长度单位C ．向左平移5π6个长度单位 D ．向右平移5π6个长度单位 12、已知函数x x f x2log )31()(-=，0a b c <<<，0)()()(<c f b f a f ，实数d 是函数()f x 的一个零点．给出下列四个判断：①a d <；②b d >；③c d <；④c d >． 其中可能成立的个数为A ．1B ．2C ．3D ．4第II 卷二、填空题：本大题共4小题，每小题5分，共25分，把答案填在题中横线上.13．计算复数= ． 14．已知函数()()5sin 2f x x ω=+满足条件)()3(x f x f -=+，则正数ω= 。