当前位置：文档之家 › 第二章平面汇交力系的合成平衡

第二章平面汇交力系的合成平衡

  • 格式：ppt
  • 大小：595.50 KB
  • 文档页数：32

下载文档原格式

  / 32

合集下载

第2章平面汇交力系与第3章平面力偶系

第2章平面汇交力系与第3章平面力偶系


F
x
0
F
y
0
FA F sin 45 sin( 180 90 1 ) 10 FA F 7.9 N 4
FA
F
1
FN B FA
FNB
2-10
解2: 解析法 研究AB杆，画受力图
F F
X
0 FA cos 1 F cos 0 0 FA sin 1 FN B F sin 0
d
d
m1 F1d1;
m2 F2 d 2
又m1 P 1d
m2 P2d
' RA P P 1 2 ' RB P 1 P 2
合力矩 M RA d ( P1 P2' )d P1d P2' d m1 m2
2-23
m 即合力偶矩等于各个力偶矩的代数和。 2. 平衡： m m 0
方向：以逆时针为正，顺时针为负。
若用矢量表示： m BA F
2-18
注：力偶无合力，即不能与某力作等效变换，其是一个 基本的力素。 证明： FR=F-F'=0
由合力距定理，可知
M
C
0, F 'CB F CA 0 CB F 1 CA F '
FR
若CB CB d成立, 必有CB
A
1
Y
O
10 FA F 7.9 N 4
F
C
45°
B
FA
FNB
2-11
§2-3 力矩、力偶的概念及其性质
力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向 一、力对点的矩
工程力学_单辉祖主编第2章汇交力系

工程力学_单辉祖主编第2章汇交力系




F1

y
合力投影定理
代数和
合力在某一轴上的投影，等于各分力在同一轴上投影的
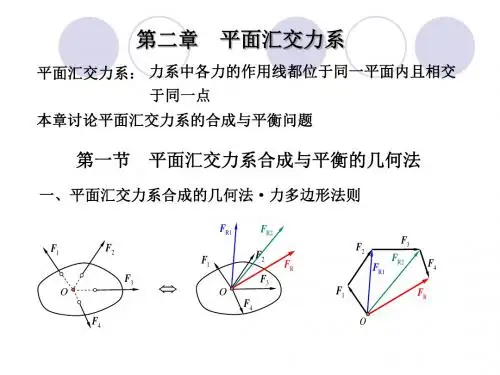
§ 2-1 汇交力系的合成
合力的大小为
2 2 2 FR FRx FRy FRz

Fx 2 Fy 2 Fz 2
cos( FR FR Fy cos( FR , j ) FR cos( F , k ) Fz R FR Fx , i)
F Fx2 Fy2 Fz2
Fy F
z


F

F2 y
F3 = Fz k
F = Fxi+ Fyj +Fzk 合力大小 合力方向余弦
F cos( F , i ) x F
cos( F , j )
cos( F , k )
Fz F
§ 2-1 汇交力系的合成
5. 汇交力系合成的解析法 平面汇交力系F1、F2、F 3汇交于A点, 求合力 y
3. 力在直角坐标轴上的投影
z
Fxy=F cos Fx = Fxy cos = F cos cos Fy = Fxy sin = F cos sin Fz = F sin
x Fx Fz F

Fy Fxy
y
§ 2-1 汇交力系的合成
4. 力的解析表示式 F = F1+ F2+ F3 若用 i、j、k 分别表示x、 y、z 轴的单位矢量，则 F1 = Fx i F2 = Fy j F3 F1 x
求FCD , FA?
②画出受力图
③列平衡方程
F F
x
FA cos FCD cos45 0 0 0 P FA sin FCD sin 45 0 y
02平面汇交力系

02平面汇交力系

与各处摩擦，试求水平压榨力的大小。
y
F
B
FBA
x
FBC
F
B
A


C D
解： 1）首先选取销钉B 为研究对象， 画受力图 建立坐标轴，列平衡方程
Fix 0, Fiy 0,
FBA cos FBC cos 0 FBA sin FBC sin F 0
解得
F
FBC FBA 2sin
30
x
F3
45
F4
2 F4x F4 cos 45 4 2 2.83 kN
2 F4 y F4 sin 45 4 2 2.83 kN
二、平面汇交力系合成的解析法
1. 合力投影定理 力系的合力在任一坐标轴上的投影等于其各分力在同一轴上投 影的代数和，即
FRx Fix
F1
F2
FR
O
F3

O
F2
F3
FR1 FR2
F4
F1
FR
F4
O
任一平面汇交力系均可合成为一个作用线通过汇交点的合力。 合力的大小和方向由各分力矢依次首尾相连构成的开口多边形 的封闭边矢量确定。
对应的矢量关系式为
FR F1 F2
Fn Fi
二、平面汇交力系的平衡条件 平面汇交力系平衡的充要条件为其合力为零。
FRx 129.3 N
FRy 112.3 N
2）确定合力的大小和方向
FR FR2x FR2y 129.32 112.32 N 171.3 N
cos FRx 129.3 0.755
FR 171.3
cos FRy 112.3 0.656
《建筑力学》2.1平面汇交力系的合成与平衡

《建筑力学》2.1平面汇交力系的合成与平衡


（2）建立平衡方程求解未知力FNAC、FNBC
FX FY
0 0
FNACcos60 FNBC 0 FNAC sin 60 W 0
（3）把W=10kN代入解得
FNAC=11.55kN（拉力）
FNBC=5.77kN（压力）
作业
《学习指导与练习》P25—28 填空1、2、3 单选1、2 判断4、5 计算3
平面汇交力系的平衡条件是： 该力系的合力 FR 为零。
（四）平面汇交力系的平衡 ——几何法
平面汇交力系平衡的充要条件是：力多边形自行封闭，
即
FR =0
或
F1+F2+F3+F4=0
F4
F1
O
F2
F3F1 baFra bibliotekF4F2
c
F3
d
（四）平面汇交力系的平衡 ——解析法
由几何法知：平面汇交力系平衡的必要和充分条件
是该力系的合力为零，即 F 0
而
F2 xi
F2 yi
0
则 Fxi 0 ， Fyi 0
即平面汇交力系平衡的解析条件是：力系中各力在两个坐标轴
上的投影之代数和均等于零。
FX FY
0 0
练一练
求图示三角支架中杆AC和杆BC所受的力（已知重物D 重W=10 kN）。
解：（1）取铰C为研究对象，其受力图如下
练一练
例2：已知FT1= FT2=10kN，FT=14kN，如下图所示，试计 算FT1、FT2、FT在X、Y轴上的投影。
（1）F1在x、y轴上的投影 Fx1=F1=10kN Fy1=0 （2）F2在x、y轴上的投影 Fx2=0 Fy2=-F2=-20kN
(1) FT1x=-F T1cos45°=-7.07kN FT1y=-F T1sin45°=-7.07kN
第二章 平面汇交力系

第二章 平面汇交力系


FB
h
FA FB FA F P
解得
R−h θ = arccos = 30o R
另由图中
FB sin θ = F FA + FB cos θ = P
FA =11.3 kN , FB=10kN
§2-3 平面汇交力系合成的几何条件 （3） 欲将碾子拉过障碍物，求水平拉力F
FB
碾子拉过障碍物时，FA=0 用几何法
第二章 平面汇交力系
§2-3 平面汇交力系平衡的几何条件
§2-3 平面汇交力系合成的几何条件
一、平面汇交力系的平衡条件
平面汇交力系平衡的必要和充分条件是：物体在平 面汇交力系作用下，合力等于零.即力多边形自行封闭 . （各力首尾连接）. r Fi = 0 用矢量表示 物体上受有4个力
∑
§2-3 平面汇交力系合成的几何条件 例2-1 钢梁重量P=6kN，θ=30°,试求平衡时钢丝绳 的约束反力. 解： （1）选钢梁为研究对象
第二章 平面汇交力系
§2-1 工程中的平面汇交力系问题
§2-1 工程中的平面汇交力系问题 汇交力系 作用在物体上各力的作用线相交于一点时，则称这些 力组成的力系为汇交力系 汇交力系. 汇交力系 各力的作用线都在同一平面内，且汇交于一点时，则 称为平面汇交力系 平面汇交力系. 平面汇交力系 工程实例
FR = FRx2 + FRy2
方向
y
FRx
r r cos FR , i =
∑ Fix ( ) F R r r ∑ Fiy cos ( FR , j ) =
FR
FRy
F3 y
F2 y
A
FR
D F3
C
F2
F1 y
F1 B
第二章、平面汇交力系

第二章、平面汇交力系


第二章 平面汇交力系§2-1平面汇交力系的合成与平衡— 几何法
理 力系合成—几何法
论
力
学
F1
F2
F3
A
c F3
d
F2
FR1 FR2
F4 e
b
F4
F1
FR
a
F2
F4
FR F1
F3
结论: 平面汇交力系可以合成为一个合力，合力作用线通过 汇交点，合力的大小和方向可由力多边形的封闭边矢量 确定，即等于各分力的矢量和。
论
将上述合力投影与分力投影的关系
力 推广到n个力组成的平面汇交力系中，则得
学
FRx = F1x+ F2x+ F3x……+ Fnx= ∑Fx
第二章 平面汇交力系§2-1平面汇交力系的合成与平衡— 几何法
理 力系合成—几何法
论
力
学
F1
F2
F3
A
c F3
d
F2
FR1 FR2
F4 e
b
F4
F1
FR
a
F2
F4
FR F1
F3
若各力合成的次序不同，则得到的力矢图的形状显然各不 相同，但是所得合力矢FR则完全相同，由此可知，合力矢FR与 各分力矢的作图次序无关。
理 力在坐标轴的投影
投影与力的大小及方向有关。
论
力
设力F与坐标轴正向间的夹角分别为α及β，
学
则分力的大小为：
Fx F cos
y
Fy

F
c
os

F
即力在某轴上的投影等于力的大小 Fy

x
乘以力与该轴的正向间夹角的余弦。
2汇交力系、力偶系平衡

2汇交力系、力偶系平衡

摇杆 FA
A

例2-6
30 ;

解：取轮，由力偶只能由力偶平衡的性质，画受力图。
M1
O
M1
FO

销子
M 0
解得
M1 FA r sin 0 M1 2 FO FA 8 kN 0 r sin 0.5 sin 30
例2-6
解得 FO FA 8kN
FA
A
力的投影
y
F
投影
x
投影
Fy Fy Fx Fx
y F
分力
F1
Fy Fx
y
F
分力
Fy
x
Fx
x
2）合矢量投影定理
合矢量在轴上的投影等于
y F1
各分矢量在同一轴上投影的代数和。
y
F2 j O
Fn i F3 x Fy j O
b
FR

Fx Fxi
x
i
Fy Fyi
Fx
合力大小 FR Fx 2 Fy 2 ( Fxi )2 ( Fyi )2 Fx Fy 合力方向 cos FR , i） （ cos FR , j） （ FR FR
F'= F''=F
B F''
d
F A B
d
B
d
F
A
F B A
M
F'
M
A
附加力偶矩：M=MB(F)=±Fd
2. 平面任意力系向作用面内一点简化 主矢和主矩 各力向矩心平移
矩心 Fn
F1 O
平面汇交力系 平面力偶系
Fn F1 Fi
Fi
第2章-力的投影与平面汇交力

第2章-力的投影与平面汇交力


F2x F2 cos 30 150N 0.866 = 129.9N
F2y F2 sin 30 150N0.5 = 75N
F3x F3 cos 90 0
F3y F3 sin 90 200N1.0 = 200N F4x F4 cos 60 200N 0.5 = 100N
FHale Waihona Puke y F4 sin 60 200N0.866 = 173.2N
一、力在坐标轴上的投影
•
力F在平面直角坐标轴上的
投影定义为：过力F两端向坐标 轴引垂线得垂足a,b 和a/,b/。线段
a称b和为a力/bF/冠在以x轴相上应的的投正影号和或力负F号在，ya′bFY′
y
A
(起点）
α
FX
FY
F
B（终点）
轴上的投影，用Fx,Fy表示。投影 o
的符号规定为：由起点a到终点b 连线（或a/由b/到）的指向与坐标
投影练习
【例2-1】 试分别求出图2-2中各力在x轴和y轴上投影。已知
F1 100N
F2 150N F3 F4 200N ，各力方向如图所示。
【解】可得出各力在x，y轴上的投影为
，
F1x F1 cos 45 100N 0.707 = 70.7N
，
F1y F1 sin 45 100N0.707 = 70.7N
a a2
F
y
α
b2
Fx
x
a1
α、β为力与x轴和y轴所
Fy
夹的锐角，
若已知力F在x、y轴上的投影
b
X、Y，那么力的大小及方向
就可以求得
x
b1
投影：
分力大小：
X=Fcosα Y=-Fsinα
静力学第二章平面汇交力系与力偶系

静力学第二章平面汇交力系与力偶系


请思考：力矩和力偶矩的异同？
力偶矩:度量力偶对物体转动效应 的量。记作：M（F, F′）或M
A
F C d F′
M Fd
力偶矩正负号规定:
逆时针转动为正，反之为负
B
力偶矩正负号意义：表示力偶转向
请思考：平面（内）力偶等效的条件？
力偶矩大小相等、转动方向相同
平面力偶的性质
性质1 : 力偶无合力,即FR=0
第二章 平面汇交力系与平面力偶系
本章重点：
1、平面汇交力系(几何法、解析法）
2、力偶的概念
3、平面力偶系
§2-1 平面汇交力系
汇交力系：所有力的作用线
汇交于一点的力系。
共点力系：所有力的作用点为同一点的力系。
平面汇交力系合成—几何法
力多边形
平面汇交力系平衡—几何法
平衡几何条件：汇交力系的力多边形自行封闭。
平面力偶系的简化结果： Mo
平面力偶系的平衡条件：Mo = 0
平衡方程：
M
0
例5 图中M, r 均为已知, 且 l=2r, 各杆自重不计。
求:C 处的约束力。
解：取 BDC 为研究对象
作出受力图 由力偶理论，知 FB = FC M 0
2 2 FB r FB 2r M 0 2 2 注意：计算(FB，FC )的力偶矩
性质2 : 力偶作用效应只与力偶矩有关 性质3 : 力偶只能与力偶矩相等的另一力偶等效 性质4 : 力偶对其作用面上任一点的矩等于力偶矩
F
F´
F
F´
F
F´ F/2
（d）
F´/ 2
只要保持力偶矩不变，力偶必等效
F
F´
M
M
M
第二章 平面汇交力系-2010

第二章 平面汇交力系-2010


第三章 平面一般力系 §3－2 力矩及其计算
二、合力矩定理： 合力对点O的矩，等于各分力对点O 合力对点O的矩，等于各分力对点O的矩的代数和。
mO(R )=mO(F1)+mO(F2)+…+mO(Fn)=∑mO(Fi) )+…
第三章 平面一般力系 §3－2 力矩及其计算
三、力矩的计算 力矩可用定义式计算，也可用合力矩定理计算力矩。 方法是先把力分解成两个合适的分量，分别求分量 对某点矩，按3 对某点矩，按3-2求合力的矩。
二、力偶矩
力偶矩是两个力对某一点的转动效应的衡量： m=±Fd 力偶的单位与力矩相同
三、力偶的性质 力偶无合力：是一个基本的力学量， 力偶无合力：是一个基本的力学量，不能与一个力平 衡，力偶只能与力偶平衡。 力偶只能与力偶平衡。 力偶可以在其作用平面内任意移动而不改变它对刚体 的作用。因这个移动不改变其力偶矩。 的作用。因这个移动不改变其力偶矩。 只要保持力偶矩不变， 只要保持力偶矩不变，可以同时改变力偶中的力的大 小和力偶臂的长短，而不改变它对刚体的作用效果。 小和力偶臂的长短，而不改变它对刚体的作用效果。 平面力偶系的合成
x y O
Fx- FBsin30º=0
即：
Fy+ FBcos30º-2F=0 -Fa-2Fa+ 3aFBcos30º=0
求得：FB =2.3KN Fx = 1.15KN Fy =2KN
例2.固定端约束 2.固定端约束
例3 如下图所示 三个半径为a的光滑圆 三个半径为 的光滑圆 柱体放在宽为4.4a的槽 柱体放在宽为 的槽 中，已经圆柱体的重量 均为G。 均为 。 求： （1）上面的圆柱体对下面 ） 的圆柱体的压力 （2）下面的圆柱体对侧面 ） 和底面的压力。 和底面的压力。
建筑力学2平面力系

建筑力学2平面力系


12
2.2 力对点之矩与平面力偶 2.2.1 力对点之矩—简称为：力矩 在力的作用下，物体将发生移动和转动。力 的转动效应用力矩来衡量，即力矩是衡量力转 动效应的物理量。 讨论力的转动效 应时，主要关心 力矩的大小与转 动方向。
13
1.定义 力臂—某定点O到力F的作用线的垂直距离。
矩心—该点O称为矩心。 力对点之矩—力使物体绕某点转动效应的度量。其 数值等于力的大小F与力臂d的乘积。其方向，规 定：力使物体绕矩心逆时钟方向转动时力矩为正， 反之为负。记为 MO(F)=±Fd
F F

y
0
FAC FAC
3
解得
x
4 2 32 63.2kN 4
FT 2
2 12 2 2 FT 2
FT 1 0
0
FAB FAC FAB
1 12 2 2
解得
4 2 32 41.6kN
0
力FAC 是负值，表示该力的假 设方向与实际方向相反 ， 因此杆AC是受压班。
力的等效平移的几个性质：
1、当力平移时，力的大小、方向都不改变，但附 加力偶的矩的大小与正负一般要随指定O点的 位置的不同而不同。
2、力平移的过程是可逆的，即作用在同一平面内
的一个力和一个力偶，总可以归纳为一个和原
力大小相等的平行力。
3、力平移定理是把刚体上平面任意力系分解为一 个平面共点力系和一个平面力偶系的依据。
9
【例2-5】重W=20kN的重物被绞车匀速吊起，绞车 的绳子绕过光滑的定滑轮A,，滑轮由不计重量的 杆AB、AC支撑，A、B、C三点均为光滑铰链， 可忽略滑轮A的尺寸。求杆AB、AC所受的力。
B
4 A FBA B A FAB FAC F’AB y A x F’AC FT2 FT1

02平面汇交力系

∑Fx=0 F+FAcos<CAD=0 ∑Fy=0 FD+FAsin<CAD =0 (3)联解方程得： FBC=5000N, FA=5000N
§2-2
平面汇交力系合成与平衡 的解析法（坐标法）
一.力在坐标轴上的投影与力沿轴的分解 1、力在坐标轴上的投影 力在 x 轴上的投影： 力在 y 轴上的投影：
F1
O Fn R
合力R为力多边形的封闭边
若将合成过程中出现的各个“过程合力”略 去，则F1、F2、……Fn与它们的合力R就构成一 个力多边形。这种合成方法称为力多边形规则。
四、平面汇交力系平衡的几何条件
平衡几何条件： 即：力多边形自行封闭
例如：一平面汇交力系，作其力多边形
由图可知，该力多边形封闭，所以该平面汇交力系为平衡力系。
前章回顾
1、力、刚体、平衡、约束等概念 2、力学公理 3、约束及约束力
人体关 节.mpg
4、受力分析及受力图
力系分类
平面 力系分类 空面
任意 共线力系、平面力偶系 平面汇交力系：各力的作用线都在同一平 面内且 汇交于一点的力系。 研究方法：几何法，解析法。 汇交
平行
§2-1
平面汇交力系合成与平衡的
R
X Y
2
2
0
所以，平面汇交力系的平衡方程为 ：
X 0 Y 0
[例2-7] 已知如图P、Q， 求平衡时 面的反力ND=？ 解：研究球受力如图，
选投影轴列方程为
=？ 地
X 0
T2cos T 0 1
①
②
Y 0
由①得
T2 sin Q N D 0
第二章 平面汇交力系
第二章 平面汇交力系

理论力学第二章


解：AB、BC杆为二力杆，
取滑轮B（或点B），画受力图。 用解析法，建图示坐标系
Fix 0
FBA F1 cos 60 F2 cos 30 0

F1 F2 P
解得： FBA
7.321kN

Fiy 0 FBC F1 cos 30 F2 cos 60 0
2 2
（1）
二.平面汇交力系合成的解析法
FR Fi
(a) (b) (c)
Fi Fxii Fyi j FR FR x i FR y j
将（b）代入（a）式，并注意i 和 j为常矢量，则有
FR ( Fxi )i ( Fyi ) j
（今后为了便于书写，将下标“i”省略。） 比较(c)、(d)等式两边，可得
FCA AC 1 P AB
解得 图2-2
FC B BC 1 P AB 2
FCA 10kN, FCB 5 kN
也可给P一定比例，量出FCA和FCB的大小，如取比例尺为1cm=5kN，作 出封闭的力三角形后，由比例尺量得
FCA 10kN, FCB 5 kN
例2-2 已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm的障碍物。
转动效应--取决于力矩的大小、方向。
一、力对点的矩
B
力矩：力绕某一点转动效应的度量。
F
M O ( F ) F d
+
A
d
-
说明：
① M O ( F )是代数量。
② F↑,d↑转动效应明显。 ③ M O ( F )是影响转动的独立因素。
M O ( F )=0。 当F=0或d=0时，
④单位Nm或kNm ⑤ M O ( F ) =2⊿AOB=Fd ,2倍⊿形面积。

理论力学第二章


T
T1
T2
二、平面汇交力系合成的几何法
设有一个平面汇交力系 F1、F2、F3、F4作用于汇交点，如图2-1a
所示。我们可以依次地应用力三角形法则来求该平面汇交力系的
合力。即先将力 F1与 F2合成为一个力 FR1，再将力FR1与F3 合成 为一个力 FR2，最后将力FR2 与F4合成，即得该平面汇交力系的合 力 FR ，且合力的作用线通过汇交点，如图2-1b所示。
第二章 平面汇交力系和平面力偶系
2.1 平面汇交力系合成与平衡的几何法 2.2 平面汇交力系合成与平衡的解析法 2.3 平面力对点之矩的概念与计算 2.4 平面力偶
武汉大学出版社
1
§2-1 平面汇交力系合成与平衡的几何法
一.平面汇交力系的概念
平面汇交力系：各力在同一平面内，作用线交于一
点的力系。
例：起重机的挂钩。
例2-3
已知：图示平面共点力系； 求：此力系的合力.
解：用解析法
FRx
F ix

F1
cos 30

F2
cos 60

F3
cos 45

F4
cos 45
129.3N
FRy
F iy

F1
sin
30

F2
sin
60

F3
sin
45

F4
sin
45
112.3N
FR
FCA AC 1 P AB
FCB BC 1 P AB 2
图2-2
解得
FCA 10 kN, FCB 5 kN
也可给P一定比例，量出FCA和FCB的大小，如取比例尺为1cm=5kN，作

第二章 平面力系


F1 + F2 + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ Fn
Rx = ∑ X k
k =1 n
n
R y = ∑ Yk
k =1
— 合力投影定理
则：
2 R = Rx2 + R y
Ry Rx cos(R , i ) = ,cos(R , j ) = R R
4、平面汇交力系的平衡方程 RX= ∑X=0 RY =∑Y =0 ∑X=0 ∑Y =0 解析条件的应用 平面汇交力系的平衡方程
X 2 = − F2 cos θ 2 Y2 = − F2 sin θ 2
cos(F , i ) =
(2) 平面汇交力系合成的解析法 求合力 R（R=Rxi+Ryj )可先求Rx，Ry。 已知： R = 则 ：
⎛ n ⎞ ⎛ n ⎞ Rx ⋅ i + R y ⋅ j = ⎜ ∑ X k ⎟ ⋅ i + ⎜ ∑ Yk ⎟ ⋅ j ⎝ k =1 ⎠ ⎝ k =1 ⎠
第二章 平面力系
平面力系：各力作用线位于同一平面。 平面汇交力系 平面力偶系 平面平行力系 平面任意力系
§2-1、平面汇交力系
平面汇交力系：各力作用线位于同一平面且汇交于一点。
问题举例：
FAy
Q
FA
O B
Q
A
FAx
FC
C
1、平面汇交力系合成的几何法
R123
F2
F3
R12 F2
R
F3
A3
A2 A1
r
h
A
2、合力矩定理与力矩的解析表达式 合力矩定理：平面汇交力系的合力对平面内任一点的矩 等于力系中各分力对同一点 的矩的代数和。 即 ： 若F1+F2+……+Fn=R，则： MO（R）=

考研复习—工程力学——第2章 平面力系

解：M= m1+ m2+ m3+m4 =4×(－15 N·m)= －60 N·m
负号表示合力偶为顺时针转向。
图2-10
第2章
2.3 平面任意力系的简化
2.3.1 力的平移定理
平移定理：作用在刚体上的力，可以平移至刚体内任一指定点，若不改变该力对于 刚体的作用则必须附加一力偶，其力偶矩等于原力对新作用点的矩。
Fx 0
RAx R By P 0
RAx P RBx 20 kN 10 kN 10 kN
M A (F) 0 RBy a P a F 2a 0
RBy 2F P 20 kN 20 kN 0
（2）画ACD杆及CEB杆受力图,如图(b)、图(c)所示。
(3)研究CEB杆，如图（c）所示，则有
例2-16：图所示梯子，AB一端靠在铅垂的墙壁上，另一端搁置 在水平地面上。假设梯子与墙壁间为光滑约束，而梯子与地面之间存 在摩擦。已知：摩擦因数为 ，梯子长度AB=L,梯子重力为W。求：（ 1）若梯子在倾角 的位置保持平衡，求梯子与地面之间的摩擦力 和其 余约束力；（2）为使梯子不致滑倒，求倾角α的取值范围。
2 3 Fp
Fs1
Fs 2
1 3
Fp
(拉)
2 3
Fp (压)
（3）考察节点B的平衡： Fs3 0
第2章
2.7 考虑摩擦时的平衡问题
2.7.1 工程中的摩擦问题
1、摩擦平衡问题： 工程中有一类问题摩擦力不能忽略。例如车辆的制动、螺旋连接与锁 紧装置、楔紧装置、缆索滑动和传动系统等。这类平衡问题统称为摩擦平衡问题。
Fd fFN
第2章
2.7 考虑摩擦时的平衡问题
2.7.3 摩擦角与自锁现象
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平面汇交力系的合成与平衡
y
一、力在坐标轴上的投影：
Fx＝ F cos Fy＝ F sin
b´ F a´
B
y


F Fx
b x
O
a
结论：力在某轴上的投影，等于力的大小乘以力与投 影轴正向间夹角的余弦。
反之，当投影Fx 、Fy 已知时，则可求出 力 F 的大小和方向： Fy 2 2 t an F Fx Fy Fx
• 投影的正负号规定如下： • 从投影的起点a到终点b的指向与坐标轴的正向 一致时，该投影取正号；与坐标轴的正向相反 时取负号。 • 如下图 (a)中，F在x，y轴上的投影均为正， (b) 中，F在x，y轴上的投影均为负。
y b'
Fy
y B β A x a Fx (a) b O b'
Fy
B β A x a Fx (b) b
F
α
F
α
a' O
a'
• 结论： • （1）当力与坐标轴垂直时，力在该轴上的投影为零； • （2）当力与坐标轴平行时，其投影的绝对值与该力的大 小相等 • （3）当力平行移动后，在坐标轴上的投影不变。
• 力的投影计算举例 • 例1：试求图中各力在 x、y轴上的投影。已知 F1= 100 N， F2= 150 N， F3= F4= 200 N。 • 解：Fx1= F1cos 45°= 100 ×0.707 = 70.7 N • Fy1= F1sin 45°= 100 ×0.707 = 70.7 N • Fx2= -F2cos 30°= -150 ×0.866 = -129.9 NFy2= F2sin 30°= 150 ×0.5 = 75 N • Fx3= F3cos 60°= 200 ×0.5 = 100 N • Fy3= -F3sin 60°= -200 ×0.866 • = -173.2 N • Fx4= F4cos 90°=0 • Fy4= -F4sin 90°= -200 ×1= -200 N
根据合力投影定理得
FR y Fy1 Fy 2 Fy3 Fy
合力的大小
FR
2 2 FRx FRy
Fx
2
Fy
2
合力R 的方向
t an
FRY FRX

FY FX
例题3
• 用解析法求图示平面汇交力系的合 解： 力
FR
0 0 Fx1 F1 cos30 Fx2 F2 cos60 ; 0 0 F F sin 30 F F sin 60 y 1 1 y 2 2 0 0 F F cos 45 F F cos 45 x3 x4 3 4 ; 0 0 F F sin 45 F F sin 45 3 4 y3 y4
F
x
0
F
y
0
例4 图示三角支架，求两杆所受的力。
解：取B节点为研究对象，画受力图
由 ∑Y = 0 ，建立平衡方程：
NBC sin300 P 0
解得： N BC 2P 60KN 负号表示假设的指向与真实指向相反。 由 ∑X = 0 ，建立平衡方程： NBA NBC
NBC cos300 NBA 0 3 解得： N BA N BC (60) 0.866 52 KN 2
FRx Fx 129.3N FRy Fy 112.3N
2 2 FR FRx FRy 171.3N
arctg F
FRy
Rx
arctg
112.3 0 40.975 129.3
三、平面汇交力系平衡的充要解析条件：
力系中所有各力在任意坐标轴上投影的代数 和分别等于零。 平面汇交力系的平衡方程:
二、合力投影定理： 合力在某一坐标轴上的投影，等于各分力在 同一轴上的投影的代数和。 证明： 以三个力组成的共点力系为例。设有三个共点力 F1、F2、F3 如图。 F
1
B
F1 A F2
A
F2
C R
D F3 x
(b)
F3
(a)
各力在x 轴上投影：

FX 1 ab
FX 2 bc FX 3 dc
F1
A R
B
F2 C
合力 R 在x 轴上投影：
D
a
F3 x
FRx ad ab bc dc FR x FX1 FX 2 FX 3
b d c (b)
推广到任意多个力F1、F2、 Fn 组成的空间共 点力系，可得：
FRx Fx1 Fx 2 Fx3 Fxn Fx
相反。即杆AB 实际上受拉力。
投影法的符号法则： 当由平衡方程求得某一未知力的值为负时，表 示原先假定的该力指向和实际指向相反。
解析法求解平面汇交力系平衡问题的 一般步骤:
1.选分离体，画受力图。分离体选取应最好含题设 的已知条件。 2.建立坐标系。 3.将各力向各个坐标轴投影，并应用平衡方程
•力矩与平面力偶系
• [例2]试分别求出下图中各力在x轴和y轴上的投影。 已知F1=100N，F2=150N，F3=F4=200N，各力 的方向如图所示。
• • • • • • • • • •
解：由公式可得各力 在x，y轴上的投影为： FY1=F1sin45°=100N×0.707=70.7N FX1=-F1cos45°=-100N×0.707=-70.7N FX2=-F2cos30°=-150N×0.866=-129.9N FY2=-F2sin30°=-150N×0.5=-75N FY3=-F3sin90°=-200N×1=-200N FX3=F3cos90°=200N×0=0 FY4=-F4sin60°=-200N×0.866=-173.2N FX4=F4cos60°=200N×0.5=100N
P
例 5
图(a)所示体系，物块重 P = 20 kN ，不计滑轮
的自重和半径，试求杆AB 和BC 所受的力。
解：1.
取滑轮B 的轴销作为研究对象，画出其受力图。
2、列出平衡方程：
由 ∑Y = 0 ，建立平衡方程：
解得：
由 ∑X = 0 ，建立平衡方程：
解得： 反力NBA 为负值，说明该力实际指向与图上假定指向