北理工理论力学讲义第03章
- 格式:pdf
- 大小:1.29 MB
- 文档页数:34
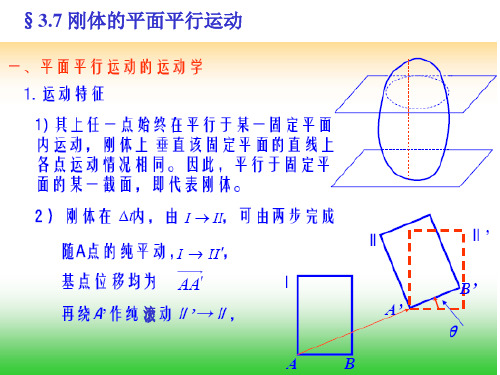

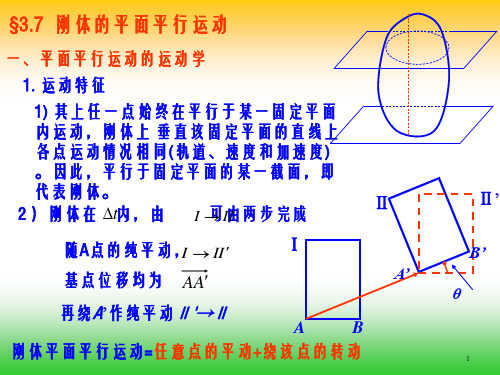

内部资料翻版必究1.2,1.3,1.4,1.5,1.62.4,2.9,2.10,2.12,2.16,2.18,2.23,2.24,2.29,2.30,2.32,2.333.6,3.7,3.8,3.16,3.17,3.18,3.19,3.20,3.21,3.305.2,5.3,5.4,5.6,6.2,6.3,6.4,6.5,6.6,7.7,7.8,7.9,7.10,7.12,7.14,7.15,7.20,7.26,7.2719.5,19.10,19.12,19.13,19.15,19.16,19.18,19.19;20.5,20.10,20.12,20.13,20.14,20.1521.1,21.2,21.4,21.9,21.11,21.12,21.13,21.14理论力学静力学 刚体在力系作用下平衡规律 运动学 运动特性之间的几何关系动力学 物体变化规律与其所受力之间的关系理论力学上半部分重点 运动学点的运动学:直角坐标法 弧坐标法刚体运动学:平动 定轴转动 一般平面运动运动学——刚体一般平面运动平面图形上任意两点的速度关系B A BA v v v =+平面图形上任意两点的加速度关系nB A BA BAτ=++a a a a平面图形上点的速度分析方法 1. 基点法B A BA v v v =+2. 速度投影定理[][]A B AB AB v v = 不能求出刚体的角速度!3. 速度瞬心法BA AB ω=⋅v BA AB ω=⋅vM MP v v =确定速度瞬心 P 点位置的方法1.已知平面图形上A,B 两点的速度方向 a.两点速度不相平行b.两点速度平行,AB 连线不垂直于速度2.已知平面图形上A,B 两点的速度方向,且AB 连线垂直于两点上的速度方向 a.两点速度大小不相同 b.两点速度大小相同3.平面图形沿某固定曲线作纯滚动运动学——点的合成运动基本概念绝对运动、牵连运动;动点、动系 点的速度合成定理 牵连运动为平动时的加速度合成定理(1) 动点的选择----两部件之间的接触点(明确指明是哪个部件上的哪个点) ----圆轮的圆心 ----相交点(2) 动系的选择a.动点对动系一定要有相对运动(故动系不能固结于动点所在的刚体上)b.相对运动的轨迹要清楚2. 分析动点的绝对运动轨迹、相对运动轨迹及动系相对于定系的牵连运动状态3. 对动点写出速度合成关系 分析各速度矢量的方向、大小,求解矢量方程 选取合适的动点,动系v(a) (b) (c)MP MPω=⋅v v v v a e r=+a e r =+a a a re a v v v +=(d) (e)FDEC A BO 1O 2θω(f)OOv O 1CBA60︒(g)BωOCϕDEF O1A(h)静力学基本概念力偶、约束和约束反力、受力分析;力系平衡与等效的基本性质,二力体(杆)力系的简化主矢、主矩,平面平行力系的简化分布载荷力系的平衡平衡的充分必要条件平面任意力系平衡方程的形式(3 个独立方程)()0ixiyA iFFM⎧=⎪=⎨⎪=⎩∑∑∑F(x , y 互不平行) (x 不垂直于AB)(A、B、C 三点不共线)物系平衡()0iA A iM M⎧'==⎪⎨==⎪⎩∑∑F FF()0()0ixA iB iFMM⎧=⎪⎪=⎨⎪=⎪⎩∑∑∑FF()0()0()0A iB iC iMMM⎧=⎪⎪=⎨⎪=⎪⎩∑∑∑FFF(a )aF(b )q 2q(c )特殊的空间力系及独立平衡方程个数(1) 空间汇交力系 3个独立方程 (3) 空间力偶系 3个独立方程 (3) 空间平行力系 3个独立方程 平面任意力系的独立平衡方程为3个 一矩式 二矩式 三矩式对于单个刚体,在平面力系作用下的平衡问题,只能写出3个独立的平衡方程,求解3个未知量;当未知量超过3个时,问题无法求解。


习 题3-1 台阶形鼓轮装在水平轴上,小头重量为2Q ,大头重量为1Q ,半径分别为2r 和1r ,分别挂一重物,物体A 重为2P ,物体重B 为1P ,且12P P >。
如3-1题图所示,求鼓轮的角加速度。
解:本题有明显的转轴o ,因而可以用角动量定理求解。
系统只有一个转轴,求运动而不求内力,所以取质心为研究对象。
因重力12,P P对轴o 的力矩不为零,可得:01122()L PQ PQ k =-质心系的动量距为:21202OQ OP OP k J J J J =+++2212121212211()22Q Q p p r r v v r k g g g gωωω=+++ 另外还有运动学补充方程:1122v r v r ωω==所以22220112211221(22)2J Q r Q r Pr P r k gω=+++应用角动量定理由 0i d J L dt =∑得 222211*********(22)2d Q r Q r Pr P r Pr g dtω+++=+11Pr 又 d dt ωε= 则有 11222222112211222()22Pr P r g Q r Q r Pr P r ε-=⋅+++答案:()12112222221122122d d 22Pr -P r g t Q r +Q r +Pr +P r ω=。
3-2 如图所示,两根等长等重的均匀细杆AC 和BC ,在C 点用光滑铰链连接,铅直放在光滑水平面上,设两杆由初速度为零开始运动。
试求C 点着地时的速度。
解: 系统在水平方向上受力为零,角动量守恒有2211222h mv m ω+⨯2(I )=2g其中 002/2vv l l ω==0v 为C 点着地时A 点速度002c v v v ===答案:c v =3-3 半径为a ,质量为M 的薄圆片,绕垂直于圆片并通过圆心的竖直轴以匀角速度ω转动,求绕此轴的角动量。
3-2题图3-1题图解 由题意作图 如图所示由某一质点组对某个固定轴的动量矩1ni i i i J r m v==⨯∑20adm rd dr rdr d πρθρθ==⎰⎰其中2Ma ρπ=故 223001()2a J r dmv d r dr Ma πθρωω=⨯==⎰⎰⎰⎰答案:212J Ma ω=3-4 一半径为r ,重量为P 的水平台,以初角速度0ω绕一通过中心o 的铅直轴旋转;一重量为Q 的人A 沿半径B o 行走,在开始时,A 在平台中心。