对偶线性规划理论及其在经济中的应用开题报告
- 格式:docx
- 大小:112.88 KB
- 文档页数:10
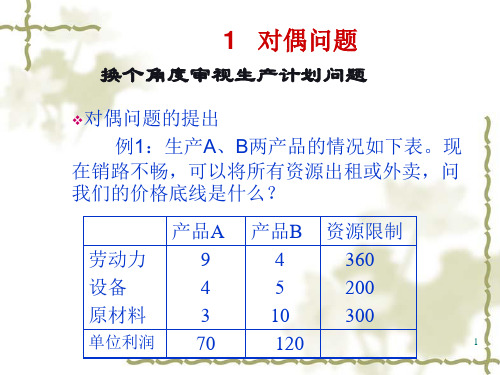

第三章 线性规划的对偶理论内涵一致但从相反角度提出的一对问题互为对偶(Dual )问题。
例如,我们可以问当四边形的周长一定时,什么形状的面积最大?答案当然是正方形;我们也可以这样来问,四边形的面积一定时,什么形状的周长最短?答案同样是正方形。
对偶现象相当普遍,它广泛地存在于数学、物理学、经济学等诸多领域。
每一个线性规划问题都有和它相伴随的另一个问题,一个问题称为原问题,则另一个则称为其对偶问题。
原问题与对偶问题有着非常密切的关系,以至于可以根据一个问题的最优解,得出另一个问题最优解的全部信息。
然而,对偶性质远不仅是一种奇妙的对应关系,它在理论和实践上都有着广泛的应用。
§1对偶问题的提出对偶理论是以对偶问题为基础的,研究对偶理论,首先必须讨论对偶问题的提出。
对偶问题可以从经济学和数学两个角度来提出,本教材仅限于从经济学角度提出对偶问题。
[例3-1] 构造例2-1的对偶问题我们已构造了例2-1追求最大利润的数学模型(见第6页),现在让我们从另外一个侧面来反映一下该问题。
倘若工厂有意放弃甲、乙两种产品的生产,而将其所拥有的资源转让出去;假设有一厂商要购买该工厂的三种资源,那么对三种资源的报价问题将成为关注的焦点。
设1y 、2y 和3y 分别代表厂商对A 、B 、C 三种资源的报价,那么站在厂商的立场上,该问题的数学模型又将是什么样子的呢?首先分析一下厂商购买所付出的代价32112168y y y w ++=。
自然,作为买方厂商当然是希望价格压得越低越好,因此厂商追求的应是付出代价的最小值,即:32112168min y y y w ++=然而,价格能否无限地压低呢?答案当然是否定的,因为最低报价必须以卖方能够接受为前提,否则报价再低也是没有意义的。
落实到这一问题上就是必须保证企业让出资源的收益不低于自己生产创造的利润,即:1y + 42y ≥ 221y +43y ≥ 31y ,2y ,3y ≥ 0至此我们得到了一个完整的线性规划模型:32112168min y y y w ++=1y + 42y ≥ 221y +43y ≥ 31y ,2y ,3y ≥ 0将站在厂商的立场上建立起来的数学模型同站在工厂立场上所建立的数学模型加以对比,可以发现它们的参数是一一对应的。

线性规划对偶理论前言线性规划(linear programming, LP)是一种求解线性模型的算法,该算法可以在目标函数下寻找最佳的解决方案。
通常情况下,线性规划可以被看作是一种最优化问题,其目的是在满足一组约束条件的前提下,找到可以最大化或最小化目标函数的变量值。
而对偶理论是线性规划问题中的重要概念之一,在很多情况下,使用对偶理论能够有效地求解出更优的解答。
线性规划与对偶理论在介绍线性规划对偶理论之前,我们先来简单了解一下线性规划的概念。
线性规划可以被定义为一组决策变量的线性函数,该函数的取值范围应在满足一组线性方程(或不等式)约束条件的前提下,使得目标函数达到最小(或最大)值。
换句话说,线性规划要求我们在可接受的条件下,寻找到最优的决策变量值。
围绕这种思想,我们可以进一步探讨线性规划的对偶问题。
在实践中,我们常常会面对一些较复杂的线性规划问题,此时我们可以使用对偶理论对其进行简化处理。
形式化地说,对于一个线性规划问题,我们可以构建一个对应的对偶问题,二者之间的关系可以被描述为一种对称的互补关系。
具体而言,在每个线性规划问题中,我们可以根据不同的约束条件求出一个对应的乘法因子,这个乘法因子可以在构建对偶问题时被使用。
通过这种方式,我们总是可以在对偶问题中找到一组最优解,而这组最优解实际上是原始问题的一个下界。
同时,我们可以利用对偶问题的最优解来求解原始问题的最优解,这种方法被称为对偶算法。
相比于原始的线性规划问题,对偶问题有着更为简洁的约束条件和更为易于求解的优化问题,因此其求解效率较高。
对偶问题的分析与求解在实际求解中,我们通常需要对给定的线性规划问题进行对偶化处理,并使用一系列的对偶算法来求解对偶问题。
下面,我们将会举两个例子来说明对偶问题的分析与求解。
例1:最小费用最大流问题最小费用最大流问题是一种最优化问题,其目的是在给定图中求出最大流量下的最小费用。
在具体求解中,我们可以通过建立一个对应的线性规划问题,并将其对偶化得到一个更加简洁的对偶问题。

线性规划的若干算法研究的开题报告一、研究背景随着社会经济的不断发展和科技的不断进步,各行各业对于效率的要求越来越高,然而这些要求又可能相互冲突。
如何合理地规划和利用有限的资源,使得目标最大化或者最小化,就成为了一个重要的问题,例如在生产计划、物流运输、金融投资等方面都需要进行规划和优化。
其中一种被广泛采用的方法便是线性规划,即以线性模型描述问题,并且在一定的约束条件下,利用线性规划算法求解最优解。
线性规划被广泛应用于工业生产、管理决策、金融投资等领域,其高效且可靠的特点受到了广泛的认可。
目前,线性规划的解法主要有单纯形法、内点法和基于神经网络的方法。
单纯形法是最早也是最广泛应用得到的线性规划算法之一,但是它在求解大规模问题时效率较低,甚至可能出现“画大饼”现象。
内点法则相对而言,可以在多项式时间复杂度下求解海量数据的线性规划问题,并且具有较好的收敛性能,成为了目前研究竞争力最强的线性规划算法之一。
近年来,基于神经网络的方法也逐渐受到人们的关注,其以模拟人脑神经系统的思维模式来解决线性规划问题,不仅可以提高求解速度,而且具有良好的适应性和泛化能力。
二、研究内容及目标本文将围绕线性规划算法进行研究,主要包括以下几个方面:(1)宏观了解线性规划算法的相关基本概念和演化历程;(2)深入分析线性规划算法的数学原理和基本步骤,并对各种算法作比较和总结;(3)针对线性规划算法的优化问题,探讨内点法以及基于神经网络的方法;(4)通过实验验证研究结果,比较不同算法在不同情况下的性能表现,为实际应用提供具有参考价值的数据支持。
研究的目标是深入掌握线性规划算法的数学理论和实现方法,对不同算法进行比较和优化,以提高算法效率和求解准确率,同时使得实际应用中能够更加方便和快捷地进行优化问题的求解。
三、研究方法和步骤本文主要采用文献综述和实验研究相结合的研究方法。
(1)文献综述:对线性规划的相关概念和算法进行详细阐述,包括单纯形法、内点法和基于神经网络的方法,总结出各自的优劣性及在实际综合中的适用情况。


毕业论文开题报告
信息与计算科学
对偶线性规划理论及其在经济中的应用
一、选题的背景、意义
[1]
21世纪中国进入到了一个新的时代,随着经济的快速发展和社会的进步,整个社会运
行的各个方面——无论是在政治、经济、文化、科技、军事、外交方面,还是在环境、生态、
资源问题方面,都将着眼于解决能否实现的问题扩充到更加重视解决如何优化实现的问题,
从解决局部的简单问题扩充到解决系统的复杂问题,从静态地解决问题到动态地解决问题,
从解决涉及单一领域的独立发展问题扩充到解决涉及多个领域的协同发展的问题,从通过直
接办法解决问题扩充到通过间接的办法解决问题等,都迫切需要线性规划理论及其应用。
随着计算机技术的发展和普及,线性规划的应用越来越广泛。它已成为人们合理利用
有限资源制定最佳决策的有利工具。
二、研究的基本内容与拟解决的主要问题
2.1 对偶线性规划理论概述
2.1.1 对偶线性规划理论的发展历程及现状[2] [3]
线性规划理论产生于20世纪30年代。1939年,苏联数学家康托罗维奇在《生产
组织与计划中的数学方法》一书中,最早提出和研究了线性规划问题。 1947年,美
国数学家丹齐克提出线性规划的一般数学模型和求解线性规划问题的通用方法─单
纯形法,为这门学科奠定了基础。1947年,美国数学家诺伊曼提出对偶理论,开创了
线性规划的许多新的研究领域,扩大了它的应用范围和解题能力。 1951年,美国经
济学家库普曼斯把线性规划应用到经济领域;1960年,康托罗维奇再次发表《最佳资
源利用的经济计算》,创立了享誉全球的线性规划要点,对资源最优分配理论做出了
贡献。为此,库普曼斯与康托罗维奇一起获1975年诺贝尔经济学奖。1984年,美国
贝尔电话实验室的印度数学家卡马卡提出求解线性规划问题的投影尺度法,这是一个
有实用意义的新的多项式时间算法。这个算法引起了人们对内点算法的关注,此后相
继出现看多种更为简单实用的内点算法。随着计算机技术的发展和普及,线性规划的
应用越来越广泛。它已成为人们合理利用有限资源制定最佳决策的有利工具。
由于对偶规划问题的全面性,考虑的多面性,现在的很多经济问题都通过对偶规划问题
来解决。从而衍生出的影子价格也是现今各大企业在资产经营策略中一个非常重要的交易工
具。它的应用已经遍及各大企业的经营策略中。
2.1.2 对偶问题的基本性质[4] [5]
给定一个线性规划问题
1122111211121222221212min..,,,0nn
n
n
mm
mmmn
n
cxcxcxaaaxbaaaxbstxbaaaxxx
L
L
L
MM
MMOM
L
L
使用向量与矩阵表示形式为
minmax()..()..00TTTTcxwb
PstAxbDstwAcxw
1.对称性
对偶问题的对偶是原问题。
2.弱对偶性
设x和w分别是问题()P和()D的可行解,则
TT
cxwb
3.无界性
问题()P和()D同时有最优解的充分必要条件是它们同时有可行解。而且,若其中有一
个问题无界,则另一个问题无解。
4.强对偶性
设*x和*w分别为()P和()D的可行解,则它们分别为()P和()D的最优解当且仅当
**()TT
cxwb
5.互补松弛性
设*x和*w分别为原问题()P和对偶问题()D的可行解,则它们分别为()P和()D的最
优解当且仅当
**
1**1()0,1,2,,()0,1,2,,niijjijmjijijibaxwimcawxjn
L
L
使用矩阵形式,可得*x和*w的互补松弛性条件:
****()()0,()0TT
wAxbcwAx
6.唯一性
问题()P有非退化的最优基可行解,那么,其对偶规划()D有唯一的最优解。
7.对偶变量的经济解释
假定所讨论的是下面的线性规划问题
max()..0Tcx
PstAxbx
其中 b——某工厂所拥有的m种资源的总量;
ij
a
——生产每件第i种产品需消耗第i种资源的量。
该问题的实际背景是在资源有限的条件下安排生产,以使效益最大。
2.2 线性规划的对偶原理及其应用
2.2.1 对偶理论[6]
以如下一对问题来表示线性规划问题的对偶:
:min:max....00PcxDwbstAxbstwAcxw
这里P表示原问题,D表示其对偶问题.
注意到两个问题间的变换特点,这里w为对偶问题的变量向量,每一个原问题的约束
条件,对应一个对偶变量(m个);每一个原问题变量对应一个对偶问题约束条件(n个).
原问题为求最大值,则对偶问题为求最小值.原问题与对偶问题中,其目标函数系数与右端
常数互换;约束条件系数矩阵互为转置;约束条件符号则按一定规则转换为此首先说明原问
题()P及对偶问题()D称为对偶的对称形式,它们是互相逆转的,现证明如下.
由于上式的对偶问题本身仍旧是一线性规划问题,应用转置矩阵概念,可把它写成如
下形式:
min()..()()0TTTTTTbwstAwcw
以Tx表示这个问题的对偶变量,则它的对偶问题为
max()..()()0TTTTTTxcstxAbx
而这个问题即为该问题的左边问题,即原始的原问题.因此得出如下结论:对偶问题的对偶
是原问题.
2.2.2对偶性的其他问题[7]
对偶定理有多种解释,是由许多学者提出并以不同形式发表的,其中包括Fourier
(1826),Gordan(1873),Minkowski(1896),Farkas(1901).
定理6.16给出的是线性方程组的对偶定理.它的另一种形式是:线性方程组Axb有解
当且仅当对任意满足0yA的行向量有0yb成立.这是Fredholm(1903)提出的.
下面的系统有且只有一个是可行的:
();()0,0.aAxbbyAyb
我们将给出线性不等式系统的对偶定理.首先我们给出由原问题导出对偶问题的方法.主要思
想是利用原问题的线性约束找到它的最优值的一个下界,即我们线性地合并给定的约束来得
到这个下界.对偶问题转化为:最大化此下界.
2.2.3 对偶规划问题的三种解法介绍[8]
例2.1 利用对偶转换规则,将下列线性规划模型转换为其对偶规划模型。
某原问题的数学模型如下:
12345123451234512345min23523234233,,,,0zxxxxxxxxxxxxxxxxxxxx
求解上式的对偶规划问题有三种方法。
第一种是先把上式转换为对偶模型,并让w对应z,让y对应x,使用普通的单纯形
法线性规划程序求解出对偶规划的结果。使用这种方法求解对偶规划问题,需要手工完成一
次由原问题向对偶问题转换的过程,当问题规模较小时,使用这种方法不会出现多大的问题,
但是当问题规模较大时,问题就来了,一是转换过程非常繁琐,工作量大;二是特别容易出
错,效率很低。
第二种方法是利用计算机程序,直接读取原问题解算过程中自动生成的数据文件,自动
地转换原问题为对偶问题,并直接求解,给出对偶规划的结果来。
第三种解法则是利用原问题的求解数据直接获得对偶问题的最优解。
2.2.4最优对偶变量(影子价格)的经济解释[9] [10]
我们之所以对线性规划的对偶问题感兴趣,是由于对偶问题的最优解相对于原始线性规