线性规划的对偶理论 ppt
- 格式：ppt
- 大小：1.79 MB
- 文档页数：40
下载文档原格式
合集下载
第二章 线性规划的对偶理论
max 3 2 A= 2 1 0 3 c=
对偶问题： Min f = 65 y1 + 40 y2 + 75 y3
s.t. 3y1 + 2 y2
y1, y2 , y3
min
≥1500
≥ 0
2y1 + y2 + 3y3 ≥2500
b=
65 40 75
A=
3 2
2 1
0 3
b=
1500 2500
1500 2500
例：
Min z= 5x1+ 25x2 7x1+ 75x2 ≤98 s.t. 5x1 + 6x2 = 78 24x1+ 12x2≥54 x1≥0 、x2 ≤ 0
怎么样， 没问题吧！
Max w= 98y1+ 78y2 + 54y3 7y1+ 5y2 + 24y3 ≤ 5 s.t. 75y1+ 6y2 + 12y3 ≥25 y1 ≤ 0 、y2无限制、 y3≥0
二、对偶规划问题的求解
1、利用原问题的最优单纯形表
3x1 x2 3x3 ≤100 x1, x2 , x3 ≥0 解: 对偶问题为
min w 100y1 100y2
max z 4 x1 3x2 7 x3 s.t. x1 2 x2 2 x3≤100
s.t.
2 y1 y2 ≥3 2 y1 3 y2≥7
原问题检验数与对偶问题的解的总结
•在主对偶定理的证明中我们有：对偶(min型)变量的最 优解等于原问题松弛变量的机会成本，或者说原问题松 弛变量检验数的绝对值 •容易证明，对偶问题最优解的剩余变量解值等于原问 题对应变量的检验数的绝对值 •由于原问题和对偶问题是相互对偶的，因此对偶问题 的检验数与原问题的解也有类似上述关系。 •更一般地讲，不管原问题是否标准，在最优解的单纯 型表中，都有原问题虚变量(松弛或剩余) 的检验数对应 其对偶问题实变量 (对偶变量)的最优解，原问题实变量 (决策变量) 的检验数对应其对偶问题虚变量 (松弛或剩 余变量)的最优解。因此，原问题或对偶问题只需求解 其中之一就可以了。
对偶问题： Min f = 65 y1 + 40 y2 + 75 y3
s.t. 3y1 + 2 y2
y1, y2 , y3
min
≥1500
≥ 0
2y1 + y2 + 3y3 ≥2500
b=
65 40 75
A=
3 2
2 1
0 3
b=
1500 2500
1500 2500
例：
Min z= 5x1+ 25x2 7x1+ 75x2 ≤98 s.t. 5x1 + 6x2 = 78 24x1+ 12x2≥54 x1≥0 、x2 ≤ 0
怎么样， 没问题吧！
Max w= 98y1+ 78y2 + 54y3 7y1+ 5y2 + 24y3 ≤ 5 s.t. 75y1+ 6y2 + 12y3 ≥25 y1 ≤ 0 、y2无限制、 y3≥0
二、对偶规划问题的求解
1、利用原问题的最优单纯形表
3x1 x2 3x3 ≤100 x1, x2 , x3 ≥0 解: 对偶问题为
min w 100y1 100y2
max z 4 x1 3x2 7 x3 s.t. x1 2 x2 2 x3≤100
s.t.
2 y1 y2 ≥3 2 y1 3 y2≥7
原问题检验数与对偶问题的解的总结
•在主对偶定理的证明中我们有：对偶(min型)变量的最 优解等于原问题松弛变量的机会成本，或者说原问题松 弛变量检验数的绝对值 •容易证明，对偶问题最优解的剩余变量解值等于原问 题对应变量的检验数的绝对值 •由于原问题和对偶问题是相互对偶的，因此对偶问题 的检验数与原问题的解也有类似上述关系。 •更一般地讲，不管原问题是否标准，在最优解的单纯 型表中，都有原问题虚变量(松弛或剩余) 的检验数对应 其对偶问题实变量 (对偶变量)的最优解，原问题实变量 (决策变量) 的检验数对应其对偶问题虚变量 (松弛或剩 余变量)的最优解。因此，原问题或对偶问题只需求解 其中之一就可以了。
线性规划的对偶理论(第一部分
对偶问题的约束条件 对应于原问题的目标 函数和约束条件的系 数。
对偶问题的可行解集 是原问题可行解集的 凸包。
原问题与对偶问题关系
弱对偶性
对于任意一对原问题和对偶问题 的可行解，原问题的目标函数值 总是大于或等于对偶问题的目标
函数值。
强对偶性
当原问题和对偶问题都存在可行 解时，它们的最优解对应的目标
强对偶性定理
若原问题和对偶问题都有可行解，则 它们分别存在最优解，且这两个最优 解的目标函数值相等。
在满足某些约束规格（如Slater条件） 的情况下，强对偶性成立。
互补松弛条件
在原问题和对偶问题的最优解中，如果某个约束条件的对偶变量值为正，则该约束 条件必须是紧的（即取等号）。
如果原问题（对偶问题）的某个变量在最优解中取正值，则其对应的对偶问题（原 问题）的约束条件必须是紧的。
标准形式
通常将线性规划问题转化为标准 形式，即求解目标函数的最小值 ，约束条件为一系列线性不等式 。
对偶问题定义与性质
对偶问题定义：对于 给定的线性规划问题， 可以构造一个与之对 应的对偶问题，该问 题的目标函数和约束 条件与原问题密切相 关。
对偶问题性质
对偶问题的目标函数 是原问题约束条件的 线性组合。
解决对偶间隙等关键问题
在实际应用中，由于原问题和对偶问题之间可能存在对偶间隙，导致对偶理论的实用性受到一定的限制。 未来可以研究如何缩小或消除对偶间隙，提高对偶理论的实用性和应用范围。
THANKS
感谢您的观看
简化了复杂问题的求解过程
对偶理论能够将一些复杂的线性规划问题转化为相对简单的对偶问题进行求解，从而降低了问题 的求解难度和计算量。
揭示了原问题和对偶问题之间的内在联系
2.454线性规划的对偶理论
故y=CBB-1 是对偶问题的最优解
由对偶定理可得：
（1）对偶问题最优解的表达式：
Y* =CB B-1 (2) 对于Y* 没必要重新求解，可从原问题的
最终单纯形表中获得。
即：对偶问题的最优解(即实变量的值)是原 问题虚变量（即松弛变量）检验数的负值.
任何一个LP问题总是属于下列三种情况之一
⑴有最优解； ⑵问题无界； ⑶无可行解. 一个原问题和它的对偶问题有四种可能的组合
(5) 主对偶定理(可行解是最优解的性质）
互为对偶的线性规划问题中，若一个有最优解, 则另一个也有最优解,且目标函数值相等.
推论：若原问题和对偶问题两者皆可行,则
两者均有最优解,且此时目标函数值相等.
由于原问题和对偶问题均可行,根据弱对偶性, 可知两者均有界,于是均有最优解.
证：设原问题有最优解， 当XB=B-1b是原问题的最优解时，有
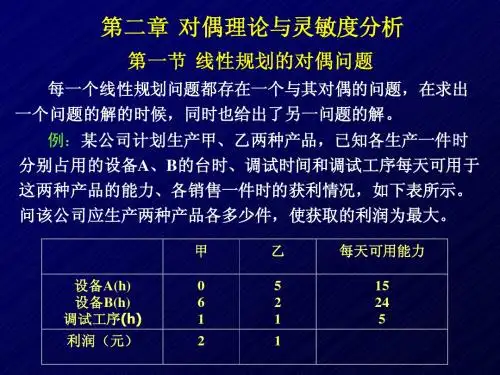
解： 对偶问题是
因为x1≠0, x2≠0, 所以对偶问题的第一，第
二约束的松弛变量为0
即y1 + 2y2 = 3 2y1 +2y2 =4
得解y1 =1 , y2=1 从而对偶的最优解为
Y=(1 ,1), 最优值为 w=26
利偶m用问ax上题述（Z 关或 系原3x，问1 建题4立）x2对的 x3 约程2x束组x1 线的12性解2x方即x2 2程为x组最x3 3，优1则解016方， 即解x得可j 到由 0另一, 一个j 个问1,问题2,题的3 的最最优
2x1 2x2 x3
12 y1
4x1
5x2
x4
16 y2
x5 15 y3
xj 0(j 1,,5)
s.t.
22yy11
4y
2
运筹学课件 第2章：线性规划的对偶理论
min w 16y1 36y2 65y3
90 y1 3 y 2 y1 2 y 2 5 y 3 70 y , y , y 0 1 2 3
原问题 A b C 约束系数矩阵
对偶问题 约束系数矩阵的转臵
约束条件的右端项向量 目标函数中的价格系数向量 目标函数中的价格系数向量 约束条件的右端项向量 Max z=CX Min w=Y’b 目标函数 AX≤b A’Y≥C’ 约束条件 X≥0 Y≥0 决策变量
若原问题为求极小形式的对称形式线性规划问题， 对偶问题应该具有什么形式？
Min w Y 'b A'Y C Y 0
max w Y 'b A'Y C Y 0
min z CX
Max z CX
AX b X 0
AX b X 0
min w 5 y1 4 y2 6 y3 4 y1 3 y2 2 y3 2 y1 2 y2 3 y3 3 3 y1 4 y3 5 2 y 7 y y 1 2 3 1 y1 0, y2 0, y3无约束
对偶问题 约束系数矩阵的转臵
目标函数中的价格系数向量
目标函数 约束条件
变量
Max z=CX m个 ≤ ≥ = n个 ≥0 ≤0 无约束
约束条件的右端项向量 目标函数 Min w=Y’b m个 ≥0 变量 ≤0 无约束 n个 ≥ 约束条件 ≤ =
【例2-3】写出下列线性规划问题的对偶问题
min 2x1 3x2 5x3 x4
1.初始表中单位阵在迭代后单纯形表中对应的位臵就是B-1 2.对于原问题的最优解，各松弛变量检验数的相反数恰好 是其对偶问题的一个可行解，且两者具有相同的目标函数 值。根据下面介绍的对偶问题的基本性质还将看到，若原 问题取得最优解，则对偶问题的解也为最优解。
运筹学胡运权第五版课件-第二章
min Z 3 x1 2 x2 3 x3 4 x4 x1 2 x2 3 x3 4 x4 3 x2 3x3 4 x4 5 s.t. 2 x1 3 x2 7 x3 4 x4 2 x1 0，x2 0, x3、x4无约束 解：对偶问题为： max W 3 y1 5 y2 2 y3
3、矩阵形式： P max z CX AX b s.t. X 0
其中
D min w bT Y AT Y C T s.t. Y 0
a1n a2 n amn
C (c1 , c2 , , cn )
b1 b2 b bm
T T
A Y C C Y A
T T T
CX Y AX Y b b Y
T T T
2、最优性： 若 X* 和 Y* 分别是 P 和 D 的可行解且 CX* = bT Y* ， 则X*，Y*分别是问题 P和D 的最优解。
对偶问题（D）：
max z 2 x1 3 x2 2 x1 2 x2 12 4 x 16 1 s.t. 5 x2 15 x1 , x2 0
min w 12 y1 16 y2 15 y3 2 2 y1 4 y2 s.t. 2 y1 5 y3 3 y , y , y 0 1 2 3
解：第一步 改写为 min 的基本形式
令x1 x1，x2 x2 x2 min z 7 x1 （ 4 x2 x2） 3x3 4 x （ 2 x2 x2） 6 x3 24 1 3x1 （ 6 x2 x2） 4 x3 15 s.t. （ 5 x2 x2） 3x3 30 （ 5 x2 x2） 3x3 30 x1 ，x2，x2，x3 0
第三章线性规划的对偶定理
特点：
1． max min 2．限定向量b 价值向量C
其它形式 的对偶
?
（资源向量）
3．一个约束 一个变量。
4． max z的LP约束“ ” min z 的
LP是“ ”的约束。
5．变量都是非负限制。
二、原问题与对偶问题的数学模型
❖ 1．对称形式的对偶
当原问题对偶问题只含有不等式约束
时，称为对称形式的对偶。
根据对称形式的对偶模型,可直接 写出上述问题的对偶问题:
b max w (Y 1,Y 2 ) -b
(Y
1,Y
2
)
A A
C
Y1 0 ,Y2 0
max w (Y 1 Y 2 ) b
(Y
1
Y
2
)
A
C
Y 1 0, Y 2 0
令 Y Y，1 Y得2对偶问题为：
max w Yb
❖ （3）若原问题可行，但其目标函数值无 界，则对偶问题无可行解。
❖ （4）若对偶问题可行，但其目标函数值 无界，则原问题无可行解。
❖ （5）若原问题有可行解而其对偶问题无 可行解，则原问题目标函数值无界。
❖ （6）对偶问题有可行解而其原问题无可 行解，则对偶问题的目标函数值无界。
CX Yb
原问题
设备A 设备B 调试工序
产品Ⅰ 产品Ⅱ
0
5
6
2
1
1
利润（元） 2
1
D
15时 24时 5时
x 设 Ⅰ产量––––– 1
x Ⅱ产量––––– 2
如何安排生产， 使获利最多？
max z 2 x1 x2
s.t.
5x2 15
6 x1 2 x2 24
第三章-对偶理论及灵敏度分析3课件
二、原问题与对偶问题的数学模型
继续
三、原问题与对偶问题的对应关系
返回
第三章-对偶理论及灵敏度分析3
一、对偶问题的提出
对
偶 问
实例：某家电厂家利用现有资源生产两种
题
产品， 有关数据如下表：
上页 下页 返回
设备A 设备B 调试工序
产品Ⅰ 产品Ⅱ
0
5
6
2
1
1
利润（元） 2
1
D
15时 24时 5时
第三章-对偶理论及灵敏度分析3
第三章 对偶理论及灵敏度分析
3.1.1 线性规划对偶问题 3.1.2 对偶问题的基本性质 3.1.3 影子价格 3.1.4 对偶单纯形法 3.2.1 灵敏度问题及其图解法 3.2.2 灵敏度分析 3.2.3 参数线性规划
第三章-对偶理论及灵敏度分析3
3.1.1 线性规划的对偶问题
一、对偶问题的提出
下页
(Y1,Y2
)
A A
C
返回
Y1 0 ,Y2 0
第三章-对偶理论及灵敏度分析3
对 偶 问
(mY1inwY2 )(YA1YC2 )b
题
Y1 0, Y2 0
令 YY1 ，Y 得2对偶问题为：
上页
下页
maYxA
w C
Yb
返回
Y无约束
证毕。
第三章-对偶理论及灵敏度分析3
三、原问题与对偶问题的对应关系
设备B –––– 元／y时2
问 题
调试工序 –––– 元y／3时
付出的代价最小，
且对方能接受。
上页
下页
出让代价应不低于
返回
用同等数量的资源
收
第二章 线性规划的对偶理论1-对偶问题
矩阵表达形式：
min w Y b AY C Y 0
对偶的经济解释
1、原问题是利润最大化的生产计划问题
总利润（元）
单位产品的利润（元/件）
产品产量（件）
max z c1 x1 c2 x2 cnx n b1 s.t. a11 x1 a12 x2 a1n xn xn 1 xn 2 b2 a21 x1 a22 x2 a2 n xn xn m bm am1 x1 am 2 x2 amn xn x1 x2 xn xn 1 xn 2 xn m ≥ 0 消耗的资源（吨）
第二章 对偶理论与灵敏度分析
第一节 线性规划的对偶问题
每一个线性规划问题都存在一个与其对偶的问题，在求出
一个问题的解的时候，同时也给出了另一问题的解。
例：某公司计划生产甲、乙两种产品，已知各生产一件时 分别占用的设备A、B的台时、调试时间和调试工序每天可用于 这两种产品的能力、各销售一件时的获利情况，如下表所示。 问该公司应生产两种产品各多少件，使获取的利润为最大。
A
b
约束系数矩阵
约束条件右端项向量
约束系数矩阵的转置
目标函数中价格系数向量
C
目标函数
目标函数中价格系数向量
max z
约束条件右端项向量
min w
c
j 1
n
j
xj
b
i 1
m
i
yi
变量 xj (j=1,·,n) · ·
约束条件有n个
xj ≥0
xj ≤0 xj 无约束 约束条件有m个 ≤bi ≥bi =bi
min z 2 x1 3x 2 5 x3 x 4
第2章 线性规划的对偶理论
≤9
y1≤0， y2≥0， y3无约束
2.1 线性规划的对偶模型 Dual model of LP
1.本节以实例引出对偶问题; 2.介绍了如何写规范与非规范问题的对偶问题;
作业：教材P61 T 1、2 下一节：对偶性质
2.2 对偶性质
Dual property
2.2 对偶性质 Dual property
时得到最优解，C CB B 1 A 是 X＝（X B，X N）的检验数 CB CB B 1B 和
CN CB B1N 的合并。
令 Y CB B1 ,由 C CB B 1 A 0与 CB B 1 0 得
YA C Y 0
可见，这是Y是对偶问题的一个可行解。 思考：Y右边的部分是什么？
C X°≤Y°AX≤Y°b
这一性质说明了两个线性规划互为对偶时，求最大值的 线性规划的任意目标值都不会大于求最小值的线性规划 的任一目标值，不能理解为原问题的目标值不超过对偶 问题的目标值。
2.2 对偶性质 Dual property
由这个性质可得到下面几个结论：
（1）（LP）的任一可行解的目标值是（DP）的最优值下界； （DP）的任一可行解的 目标是（LP）的最优值的上界；
【例2.3】 写出下列线性规划的对偶问题
max Z 4x1 3x2
5x1 x2 6 7x1x135x2x2108 x1 0, x2 0
【解】这是一个规范形式的线性规划，它的对偶问题求 最小值，有三个变量且非负，有两个“ ≥”约束，即
min w 6 y1 8 y2 10 y3
5yy1172yy22
y3 3y3
4
3
yi 0,i 1,2,3
2.1 线性规划的对偶模型 Dual model of LP
第四讲 线性规划的对偶理论(Max型)
析：将问题转换成对称形式，再由定理1写出其对偶问题 （1）将约束（2）转换成：
a21x1 a22 x2 a23 x3 b2 a21x1 a22 x2 a23 x3 b2
线性规划的对偶问题的基本定理（3）
（2）将约束（3）转换成：
a31x1 a32 x2 a33 x3 b3
线性规划的对偶问题的基本定理（4） 令各约束对应的对偶变量为 y1,y2,y2,y3 ， 再由定理 1 得其 对偶问题为：
b2 y2 b3 y3 minw b1 y1 b2 y2 a21 y2 a31 y3 c1 a11 y1 a21 y2 a y a y a y a y c 12 1 22 2 22 2 32 3 2 a23 y2 a33 y3 c3 s.t. a13 y1 a23 y2 a y a y a y a y c 3 13 1 23 2 23 2 33 3 0, y2 0, y3 0 y1 0, y2
min bT Y T T T T ( LP) A Y C s.t. T Y 0
线性规划的对偶问题的基本定理（2）
原 问 题
max z c1 x1 c2 x2 c3 x3 （） 1 a11 x1 a12 x2 a13 x3 b1 a21 x1 a22 x2 a23 x3 =b2 2 s.t. a31 x1 a32 x2 a33 x3 b3 3 x 0, x 0, x 自由 2 3 1
1 2
对生产一件产品P2的资源出售的收入应不低于生产一 件产品P2的 因此 2 y 4 y 3
1 3
线性规划的对偶理论(第2部分)
在某些情况下，求解对偶问题可能比直接求解原问题更简单。通过对偶转化，可以将复杂的问题 转化为相对简单的问题进行求解。
灵敏度分析（Sensitivity Analysis）
对偶问题的解可以用于分析原问题参数变化对最优解的影响。通过对偶问题的灵敏度分析，可以 了解原问题解的稳定性以及参数调整对最优解的影响程度。
Part
05
目标规划与多目标决策
目标规划基本概念
目标函数
在目标规划中，目标函数表示决策者希望优化的目标，可以是最 大化或最小化某个或多个变量的函数。
约束条件
约束条件限制了决策变量的取值范围，确保解在实际可行域内。
优先级与权重
不同目标之间可能存在冲突，通过设定优先级和权重可以权衡各 个目标的重要性。
分支定界法的步骤
分支定界法主要包括分支、定界和剪枝三个步骤。首先，将原问题分解为若干个子问题；其次，对每个子问题分别求 解，并更新上下界；最后，通过剪枝策略删除不可能得到最优解的子问题，以减少计算量。
分支定界法的优缺点
分支定界法具有适用范围广、可求得全局最优解等优点；但同时也存在计算量大、求解效率不高等缺点。 因此，在实际应用中需要根据问题的特点和要求选择合适的算法。
多目标决策方法
线性加权法
将多个目标函数线性加权为一个综合目标函数，通过求解该综合目 标函数的最优解来实现多目标决策。
理想点法
先确定每个目标的理想值，然后构造一个评价函数来衡量实际解与 理想解之间的差距，通过最小化该评价函数来求解多目标决策问题。
分层序列法
将多个目标按照重要程度排序，依次求解各层目标的最优解，最终得 到综合考虑所有目标的满意解。
要点三
混合整数规划的应用 案例
混合整数规划在实际应用中有着广泛 的应用，如生产调度中的任务分配问 题、物流运输中的路径优化问题等。 通过运用混合整数规划方法，可以有 效地解决这些问题，提高生产效率和 运输效率。
灵敏度分析（Sensitivity Analysis）
对偶问题的解可以用于分析原问题参数变化对最优解的影响。通过对偶问题的灵敏度分析，可以 了解原问题解的稳定性以及参数调整对最优解的影响程度。
Part
05
目标规划与多目标决策
目标规划基本概念
目标函数
在目标规划中，目标函数表示决策者希望优化的目标，可以是最 大化或最小化某个或多个变量的函数。
约束条件
约束条件限制了决策变量的取值范围，确保解在实际可行域内。
优先级与权重
不同目标之间可能存在冲突，通过设定优先级和权重可以权衡各 个目标的重要性。
分支定界法的步骤
分支定界法主要包括分支、定界和剪枝三个步骤。首先，将原问题分解为若干个子问题；其次，对每个子问题分别求 解，并更新上下界；最后，通过剪枝策略删除不可能得到最优解的子问题，以减少计算量。
分支定界法的优缺点
分支定界法具有适用范围广、可求得全局最优解等优点；但同时也存在计算量大、求解效率不高等缺点。 因此，在实际应用中需要根据问题的特点和要求选择合适的算法。
多目标决策方法
线性加权法
将多个目标函数线性加权为一个综合目标函数，通过求解该综合目 标函数的最优解来实现多目标决策。
理想点法
先确定每个目标的理想值，然后构造一个评价函数来衡量实际解与 理想解之间的差距，通过最小化该评价函数来求解多目标决策问题。
分层序列法
将多个目标按照重要程度排序，依次求解各层目标的最优解，最终得 到综合考虑所有目标的满意解。
要点三
混合整数规划的应用 案例
混合整数规划在实际应用中有着广泛 的应用，如生产调度中的任务分配问 题、物流运输中的路径优化问题等。 通过运用混合整数规划方法，可以有 效地解决这些问题，提高生产效率和 运输效率。
线性规划的对偶理论(NO8)
AX b
(P)
s.t
X
0
minW Yb YA C
(D) s.t Y 0
从上述性质中，可看到原问题与对偶问题的解必然是下列三种情况之一： ①原问题与对偶问题都有最优解，且CX=Yb； ②一个问题具有无界解，则它的对偶问题无可行解； ③两个问题均无可行解。
7
（5）（互补松驰性定理），若X*、Y*分别是原问题和对偶问题的可行
max Z 2x1 x2 x3
2x1 x2 2
s.t.3x1 x2 x3 4
x1
,
x2 ,
x3
0
目标函数 无界
其对偶问题为：
min W 2 y1 4 y2
2 y1 3 y2 2
s.t
.
y1
y2 1 y2 1
y1 , y2 , y3 0
无可行解
6
max Z CX
3
一、对偶问题的基本定理
对偶问题的基本定理
MaxZ=CX
MinW=Yb
AX b
X
0
YA C Y 0
（1）（弱对偶定理）若X(0)是原问题的可行解，Y(0)是对偶
问题的可行解, 则有 证明：
C X(()) Y(0) b
CX (0) YAX(0) Y ( AX (0) ) Yb
（2）（最优性定理），若X(0) 、 Y(0)分别是互为对偶问题 LP和DP的可行解，且C X(0) = Y(0) b，则X(0) 、 Y(0)分别是 它们的最优解
4
（3）（强对偶定理）若互为对偶问题之一有最优解，则另一 问题必有最优解，且它们的目标函数值相等。
证明：设X*是原问题的最优解，对应的最优基是B，引入松弛
变量Xs后化为标准形式
第2章线性规划讲义的对偶问题
称CBB-1为单纯形乘子
19
二、对偶问题的基本性质
1. 对称性
2. 弱对偶性
推论：
(1)原问题任一可行解的目标函数值是其对偶问题目标函数 值的下界；反之对偶问题任一可行解的目标函数值是其 原问题目标函数值的上界。
(2)如原问题有可行解且目标函数值无界，则其对偶问题无 可行解；反之对偶问题有可行解且目标函数值无界，则 其原问题无可行解。
35
三、分析cj的变化 线性规划目标函数中变量系数cj的变化仅仅影响到检验 数，所以将cj的变化直接反映到最终单纯形表中，只可 能出现表2-9中的第一、二两种情况。
例5：在美佳公司例子中， (1) 若家电Ⅰ的利润降至1.5元/件, 而家电Ⅱ的利润增 至2元/件, 美佳公司最优生产计划有何变化? (2) 若家电Ⅰ的利润不变, 而家电Ⅱ的利润在什么范围 内变化时, 该公司的最优生产计划不发生变化。
28
练习： 用对偶单纯形法求解下述LP问题：
min w x1 4x2 3x4 x1 2x2 x3 x4 3
st. 2x1 x2 4x3 x4 2 xi 0(i 1,2,3,4)
29
min z cx
注: 若LP问题的标准形式为:
Ax b
st
.
x
0
其对偶单纯形法的求解步骤确定换入基变量的原则如下:
目标函数求极小值时，约束方程均为≥
2
二、对称形式下对偶问题的一般形式
对称形式的LP问题(LP1)：
M Z c 1 x a 1 c 2 x x 2 c n x n
a 1 x 1 1 a 1 x 2 2 a 1 n x n b 1 a 2 x 1 1 a 2 x 2 2 a 2 n x n b 2
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第3章PPT课件
B1b CB B1b
z
B 1 CBB
1
XB X N1 X N2
(27)
12
.
第1节 单纯形法的矩阵描述
单纯形表中的数据
基变量
非基变量
等式右边
XB 系数矩阵 B 1 B 1
检验数
0
XN
Xs RHS
B1N1
B1
B1b
CN1 CBB1N1 CBB1 CBB1b
13
.
小结
4
.
第1节 单纯形法的矩阵描述
若以Xs为基变量，并标记成XB，可将系数矩阵（A，I） 分为（B，N）两块。B是基变量的系数矩阵，N是非基 变量的系数矩阵。并同时将决策变量也分为两部分：
X
X X
B N
相应地可将目标函数系数C分为两部分：CB和CN，分别 对应于基变量XB和非基变量XN，并且记作
C=（CB, CN）
10
.
第1节 单纯形法的矩阵描述
（2）θ规则表示为：
RHS值
表示选用>0的分量
m i((B B n 1 1 P bj))ii (B1P j)i0 ((B B 11 P bj))ii
换入变量的系数向量
11
.
第1节 单纯形法的矩阵描述
（3）单纯形表与矩阵表示的关系
0 1
B 1 N1
1 0 CN CB B1N1
a1m a2m
am1
am2
amm
16
.
第2节 改进单纯形法
以a11为主元素, 进行变换
主元素
a11 P1 a12
1/ a11
1
a21/
a11
(1)
a1m
运筹学02对偶理论1线性规划的对偶模型,对偶性质幻灯片PPT
min w=36y1+40y2+76y3
表示。企业生产一件产品甲用了四种资源的数量分别是3，5和9 个单位，利润是32, 企业出售这些数量的资源所得的利润不能少 于32，即
3 y 1 5 y 2 9 y 3 3 2
同理，对产品 乙有
4 y 1 4 y 2 8 y 3 3 0
3.1 线性规划的对偶模型 Dual model of LP
m
y
* i
x
S
i
0
i1
பைடு நூலகம்
n
y
S
j
x
* j
0
j1
由于变量都非负，要使求和式等于零，那么必定每一
分量为零，因而有以下关系：
3.2 对偶性质 Dual property
Chapter3 对偶理论 Dual Theory
(1)当yi*>0时，xSi 0 , 反之当 xSi 0 , 时yi*=0；
( 2 ) y S j 0 时 x * j 0 , 反 之 当 x * j 0 时 y S j 0
3.1 线性规划的对偶模型 Dual model of LP
Chapter3 对偶理论 Dual Theory
m ax Z 32 x1 30 x2
3 x1 4 x2 36
5
x1
4 x2
40
9
x1
8 x2
76
x1 , x 2 , x3 0
注：以上两问题是同一组数据参 数，只是位置有所不同，所描述 的问题实际上是从两个不同的角 度去描述。原始线性规划问题考 虑的是充分利用现有资源，以产 品数量和单位产品的利润来决定
7 x
x
1
1
线性规划的对偶理论
0
xB x3 x4
cj - zj
b
8 4 4 2
1 x1 2 0
1 y3 2 0 1
2 x2 2 2
2 y4 0 1 0
0 x3 1 0
0 y1 1 0 0
0 x4 0 1
0 y2 -1 1/2 -1
Θ 8/2=4 4/2=2 Min 4/2=2
2 1
2
x3 x2
cj - z j
/
x1 x2
cj - z j
[例5] 用对偶单纯形法求解下列LP问题 （P64）
min w = 12y1 + 16y2 + 15y3
2y1 + 4 y2 ≥2 2y1 + 5y3 ≥ 3
y1 , y2 , y3 ≥ 0
标准形式为:
max w’ = －12y1 － 16y2 － 15y3＋ 0y4 ＋ 0y5 －2y1 － 4 y2 ＋ y4 =-2 －2y1 － 5y3 ＋ y5 = - 3 y1 , y2 , y3 , y4 , y5 ≥ 0
y1 y2 y3
设备 A B C 单位产品利润
产品 I 2 4 0 2元
产品 II 2 0 5 3元
设备有效台时 12 16 15
问如何安排生产最有利？
Next
生产产品的数学模型
设产品I和产品II的产量分别为x1和x2件, 利润为Z,
y1 y2 y3
Max Z 2 x1 + 4 x1 + 0x1 + x1 , = 2 x1 + 3 x2 2 x2 ≤ 12 0 x2 ≤ 16 5 x2 ≤ 15 x2 ≥ 0
一、对偶问题的概念
内容一致但从相反角度提出的一对问题 称为对偶问题
xB x3 x4
cj - zj
b
8 4 4 2
1 x1 2 0
1 y3 2 0 1
2 x2 2 2
2 y4 0 1 0
0 x3 1 0
0 y1 1 0 0
0 x4 0 1
0 y2 -1 1/2 -1
Θ 8/2=4 4/2=2 Min 4/2=2
2 1
2
x3 x2
cj - z j
/
x1 x2
cj - z j
[例5] 用对偶单纯形法求解下列LP问题 （P64）
min w = 12y1 + 16y2 + 15y3
2y1 + 4 y2 ≥2 2y1 + 5y3 ≥ 3
y1 , y2 , y3 ≥ 0
标准形式为:
max w’ = －12y1 － 16y2 － 15y3＋ 0y4 ＋ 0y5 －2y1 － 4 y2 ＋ y4 =-2 －2y1 － 5y3 ＋ y5 = - 3 y1 , y2 , y3 , y4 , y5 ≥ 0
y1 y2 y3
设备 A B C 单位产品利润
产品 I 2 4 0 2元
产品 II 2 0 5 3元
设备有效台时 12 16 15
问如何安排生产最有利？
Next
生产产品的数学模型
设产品I和产品II的产量分别为x1和x2件, 利润为Z,
y1 y2 y3
Max Z 2 x1 + 4 x1 + 0x1 + x1 , = 2 x1 + 3 x2 2 x2 ≤ 12 0 x2 ≤ 16 5 x2 ≤ 15 x2 ≥ 0
一、对偶问题的概念
内容一致但从相反角度提出的一对问题 称为对偶问题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
aij 0，则确定最小的 bk 0对应变量 xk 为出基变量。
(3) 确定进基变量。 计算
j l min | a kj 0 a kj aik
确定 l 为进基变量x Nhomakorabea(4) 迭代更新单纯形表。 以 kl 为中心元素，参照单纯形法对表 进行迭代计算。 (5) 通过循环迭代找出最优解。
原问题（P） 决策变量 目标函数 约束条件 xi 第i种产品数量
对偶问题（D） yi 第i个约束条件
max z c T X
min w bT y
Ax b x0
A yc y0
T
从表中可以看出对称形式的对偶关系具有如下的对应关系： 目标函数最大 最小；约束条件不大于 不小于
对偶理论
推论3：
线 性 规 划 对 偶 问 题
若规划（P）或（D）有可行解，则（P）或（D）有最优解 的充要条件是规划（D）或（P）有可行解 例 试用对偶理论判断下面线性规划是否有最优解 所以…
显然无可行解
解：此规划存在可行解
x ,0,0 0
其对偶规划为
T
对偶理论
例 用对偶理论判断下面线性规划是否存在最优解
j c j c B P j c j y P j c j y aij
T B 1 T i 1
i
m
某种产品的产值
生产该产品的消耗资源的总和
即隐含成本
因此，当检验数为正时，说明生产有利，可以在计划中安排。
影子价格 线 性 规 划 对 偶 问 题
例：某外贸公司准备购进两种产品A1, A2。购进产品A1 ,每件需 要10元，占用5立方米的空间，待每件A1卖出后，可获纯利润3 元；购进产品A2 ，每件需要15元，占用3立方米的空间，待每件 A2卖出后，可获纯利润4元。公司现有资金1400元，有430立方 米的仓库空间存放产品，根据这些条件，可以建立求最大的线性 规划模型：
约束矩阵：一个为另一个的转置
常数向量b和c互换 目标变量皆为非负 对称形式对偶问题
原问题和对偶问题的关系
非对称形式的对偶问题
线 性 规 划 对 偶 问 题
不具备对称形式的一对线性规划称为非对称形式的对偶问题 转换方式为： 1、将模型统一为规范形式，然后先按对称形式转换 2、对等式约束按（3）或（4）处理 3、若原规划中某个约束为等式，则在对偶规划中与此对应的 变量取值没有非负约束 4、若原规划中的某个变量没有非负限制，则在对偶问题中对 应的那个约束为等式。 教材P56例题
c xb y
T T
证明： 从原规划的约束条件有
Ax b y T Ax y T b bT y
从对偶规划的约束条件有
cT x bT y
AT y c c T y T A cT x y T Ax
对偶理论
定理3.1（弱对偶性）：若 x & y 分别为原规划（P）和
线 性 规 划 对 偶 问 题
线 性 规 划 对 偶 问 题
因此原规划存在最优解
解
此规划存在可行解
其对偶规划为
存在可行解
对偶理论
定理3.2（强对偶性，或称对偶定理）：
线 性 规 划 对 偶 问 题
若原规划（P）有最优解，则对偶规划（D）也有最优解，反 之亦然。且二者最优解的目标函数值相等。 （证明：教材P58-59） 定理3.3（互补松弛性）： 在线性规划问题的最优解中，如果某一约束条件的对偶变量值为非 零，则该约束条件取严格等式；反之，若如果约束条件取严格不等 式，则其对偶变量一定为零。 定理3.4（互补基本解）： 线性规划问题的原问题和对偶问题存在一对互补的基本解，其中原 问题的非基变量（松弛变量）对应对偶问题的基变量，而对偶问题 的非基变量（松弛变量）对应原问题的基变量。
设 y y1
y2 ym
T
为（D）的最优解，则称 yi
为规划（P）的第i个约束对应的影子价格（Shadow Price）
y 换句话说， i 为第第i 种资源（例如设备台时）的一种估价
影子价格
影子价格的经济含义
线 性 规 划 对 偶 问 题
影子价格是对现有资源实现最大效益时的一种估价，由此可以 决定是否将既有资源出租或投资购买新资源。从这种意义上说， 影子价格是一种机会成本。
（2）原规划的目标函数是从资源拥有者的角度得出利润最大 化，而其对偶规划的目标函数是从想获得该资源方的角度得出 成本最小化 （3）两个问题共用一套参数，但组合方式不同
原问题和对偶问题的关系
对偶问题在解释资源的影子价格、扩大单纯形法计算方法以及对问题进 行灵敏度分析等方面有很多应用。
线 性 规 划 对 偶 问 题
a x
j 0 ij
n
j
而当该资源的影子价格 bi yi 0 时，其影子价格为0。
不为0，则说明该种资源已经耗费完毕：yi
0 aij x j bi
j 0
n
影子价格
影子价格的经济含义
线 性 规 划 对 偶 问 题
一般而言，线性规划问题的求解是确定资源的最优分配方案， 而对于对偶问题的求解则是确定资源的恰当估价。 例如，用于 公司内部结算等。 单纯形法中各检验数的经济意义：
a
对偶单纯形法 线 性 规 划 对 偶 问 题
例：用对偶单纯形法求解下面的线性规划
min w 3x1 2 x2
3 x1 x 2 3 4 x 3 x 6 1 2 （s.t.） x1 3 x 2 2 x1 , x 2 0
对偶单纯形法 线 性 规 划 对 偶 问 题
w yi 影子价格是一种边际价格，衡量资源变化对总效益的影响 bi
投资影子价格最高的资源可以让总效益最大。但要注意，影子价格 不是一成不变的，当约束条件、产品利润发生变化时，有可能使影 子价格发生变化。另外，资源增加有个度的问题，这在后面的灵敏 度分析中会讲到。 定理3.3（互补松弛性）表明当某种资源未得到充分利用时，即
z zmax
z zmax
影子价格
考虑如下的互为对偶的线性规划
线 性 规 划 对 偶 问 题
max z c1 x1 c2 x2 cn xn
min w b1 y1 b2 y2 bm ym
c1 c2 cn
a1n xn b1 a11 x1 a12 x2这个价格不是市场价格，而是针对具体企业在 y n a11 y1 a21 y 2 am1 a x a x a x a y a y a b2 21 1 22 2一定时期内存在的一种特殊价格，它蕴含在追 y n 2n n 22 2 m2 12 1 求最大利润的生产计划之中。资源的市场价格 am1 x1 am 2 x2 amn xn bm 随供求关系而变，而他的影子价格则有赖于资 y a1n y1 a2 n y 2 amn n 源的利用情况，随企业生产任务、产品结构等 x1 , x2 ,, xn 0 情况发生变化而改变。 y1 , y 2 ,, y m 0
c xb y
T T
推论1（最优性）：
设 若
对偶规划（D）的可行解，则
x&y
分别为原规划（P）和对偶规划（D）的可行解
c T x b T y 则 x & y 分别为P和D的最优解 显而易见
推论2（无界性）： 如原规划（P）或其对偶规划（D）具有无界解，则对偶规 划（D）或原规划（P）无可行解。 显而易见 注意：改推论不可逆，教材P58
假设公司现有闲余资金585元，准备用于投资，增 加每立方米仓库需0.8元。问这笔资金是用来投资 仓库好呢还是购买产品好？
影子价格
cB xB b 3 x1 4 x2 0 x3 0 x4
线 性 规 划 对 偶 问 题
4
3
x2
x1 cj-zj
60
50
0
1 0
1
0 0
1/9
-1/15 -11/45
-2/9
第二章 线性规划的对偶理论和 灵敏度分析
从经济意义上研究线性规划的对偶问题，通过对对偶问题的研究， 从不同的角度对线性规划问题进行分析，从而利用有限的数据，得 出更广泛的结果，间接地获得更多的有用信息，为企业经营决策提 供更多的科学依据
主要内容
原规划与对偶规划的转换 对偶定理
影子价格的概念和经济学意义
对偶理论
定理3.4（互补基本解）：
线 性 规 划 对 偶 问 题
线性规划问题的原问题和对偶问题存在一对互补的基本解，其中原 问题的非基变量（松弛变量）对应对偶问题的基变量，而对偶问题 的非基变量（松弛变量）对应原问题的基变量。
在单纯形法迭代的每一步： 如果原问题是可行解，而对偶问题非可行解，则 如果对偶问题是可行解，而原问题非可行解，则 如果原问题和对偶问题同为可行解，则为最优解
x1 11 x2 125
将585元投资购买产品后，最大利润增加为：585*11/45=143元
对偶单纯形法
基本思路
线 性 规 划 对 偶 问 题
(1) 从原规划的一个基本解出发（未必为可行解），其对应一 个对偶可行解（检验数非正）。 (2) 检验原规划的基本解是否可行（即是否有负分量），如果有 小于0的分量，则进行迭代，求另一个基本解，此基本解对应 着另一个对偶可行解（检验数非正）。 (3) 如果得到的基本解的分量皆非负，则该解为最优解。 也就是说，对偶单纯形法在迭代过程中始终保持对偶解的可行 性（即检验数非正），使原规划的基本解逐步变为可行，并得 到最优解。
解： (1)引入松弛变量 式两侧同乘-1，得到 化为标准形,并在约束等
为基变量，此式即为典式形式，并且检验数皆非 正，因此可构造初始对偶单纯形表。 初始表中基本解的三个分量小于零，不是可行解，需进行迭代 求解新的基本解。