混合粒子群算法:基于杂交的算法
- 格式:docx
- 大小:13.05 KB
- 文档页数:4

改进粒子群算法的舰载武器目标分配陈曼;周凤星【摘要】针对舰载火力打击中的武器目标分配问题,设计了一种改善的混合粒子群优化算法来求解.对粒子更新速度的最大值进行线性递减,使得前期加强全局寻优能力,后阶段提高收敛能力;采用异步变化的学习因子,以及基于正切函数的惯性权重改进法来解决全局搜索能力与收敛精度之间的矛盾;引进了遗传算法中的杂交算子并采取模拟退火思想更新粒子,避免得到局部最优解.仿真结果显示,设计的算法能有效适宜地求解武器目标分配问题.【期刊名称】《火力与指挥控制》【年(卷),期】2018(043)011【总页数】5页(P72-76)【关键词】粒子群算法;异步;惯性权重改进;杂交;模拟退火【作者】陈曼;周凤星【作者单位】武汉科技大学信息科学与工程学院,武汉430081;武汉科技大学信息科学与工程学院,武汉430081【正文语种】中文【中图分类】TP301.6;TJ810.3+70 引言在舰载武器系统实施火力打击的过程中,当多个目标同时来袭时,就需要快速地作出决策如何进行武器目标分配,武器目标分配是指按照一定的最优分配原则将多种武器分配给多个来袭目标。
近年来,舰艇编队防空领域的武器目标分配问题受到了广泛关注,有关学者提出了许多智能算法进行求解,如遗传算法、蚁群算法、粒子群算法等,极大地提高了武器目标分配问题的效率和可行性[1-5]。
粒子群算法被广泛应用于武器目标分配问题中,如文献[6]将遗传算法中的交叉、变异操作加入到粒子群算法,降低了算法陷入局部收敛的可能,但增加了运行时间;文献[7]提出了一种离散粒子群优化算法,对粒子的速度和位置公式作出了新的定义,但这种方法增加了陷入局部最优的可能。
考虑到基本粒子群算法极可能陷入局部最优解的缺陷,本文提出了一种改善的粒子群算法对舰载武器目标分配问题进行求解,对解即分配结果采取十进制整数编码;对粒子更新的速度最大值进行线性递减,在初始阶段加强算法的全局寻优能力,后阶段提高收敛能力;对粒子位置更新基本公式中的学习因子采用异步变化的方式,并采用一种基于正切函数的惯性权重改进方法,平衡全局和局部寻优能力;最后将杂交操作引入算法,对更新后的粒子采用模拟退火策略进行替换,进一步增加搜索精度,仿真结果表明提出的算法能快速合理地求解武器目标分配问题。

粒子群算法介绍优化问题是工业设计中经常遇到的问题,许多问题最后都可以归结为优化问题. 为了解决各种各样的优化问题,人们提出了许多优化算法,比较著名的有爬山法、遗传算法等.优化问题有两个主要问题:一是要求寻找全局最小点,二是要求有较高的收敛速度. 爬山法精度较高,但是易于陷入局部极小. 遗传算法属于进化算法( Evolutionary Algorithms) 的一种,它通过模仿自然界的选择与遗传的机理来寻找最优解. 遗传算法有三个基本算子:选择、交叉和变异. 但是遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码,另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验.1995 年Eberhart 博士和kennedy 博士提出了一种新的算法;粒子群优化(Partical Swarm Optimization -PSO) 算法 . 这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视,并且在解决实际问题中展示了其优越性.粒子群优化(Partical Swarm Optimization - PSO) 算法是近年来发展起来的一种新的进化算法( Evolu2tionary Algorithm - EA) .PSO 算法属于进化算法的一种,和遗传算法相似,它也是从随机解出发,通过迭代寻找最优解,它也是通过适应度来评价解的品质. 但是它比遗传算法规则更为简单,它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作. 它通过追随当前搜索到的最优值来寻找全局最优 .粒子群算法1. 引言粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation),有Eberhart博士和kennedy博士发明。
源于对鸟群捕食的行为研究PSO同遗传算法类似,是一种基于叠代的优化工具。

2015.3数据通信技术交流Technology Discussion粒子群算法研究进展邢晓溪( 国网北京市电力公司物资分公司北京 100054)摘要:粒子群算法(PSO)是一种仿鸟群食行为的智能化算法,是目前解决组合化的重要工具之一。
为了扩展粒子群算法在工程实际中的应用范围,有助于针对工程应用行算法选择,本文讨论了粒子群算法理论基础,述了该算法的实现步骤与特点,并分析讨论了几种典型粒子群算法的算方法与特点,即交粒子群算法(HPSO)、离散二制粒子群算法(BPSO与DPSO)、同粒子群算法(CPSO)及免疫粒子群算法(IM-PSO)。
最后,根据粒子群算法的研究现状,展望了该算法所面的挑与一步研究方向。
关键词:粒子群算法;交粒子群算法;同粒子群算法;免疫粒子群算法中图分类号:TP18文献标志码:A1引言粒子群算法(PSO)由美国心理学家Kennedy与电气工程师Eberhart[1]首次提出,该算法源于针对鸟群捕食行为的研究,通过模拟鸟群捕食过程中相互协作从而找到最优路径的行为以获取最优解。
目前,该算法已被广泛应用于各个工业领域。
其中,最具备实际应用价值的领域主要包含物资运输的路径选择、多目标问题的优化求解、模式识别、决策与模拟等。
虽然已经有大量文献针对粒子群算法进行了一定的研究,但是,在理论与实践中该算法均尚未成熟,需要进行改进。
PSO算法[2][3]主要解决自身与种群位置最佳的求解问题,具备收敛速度好的优点,但是,容易出现局部收敛的情况从而影响最终求解。
杂交PSO算法(HPSO)[4]结合了进化计算,提高了PSO 算法的收敛速度并在一定程度上保证了全局最优的获得。
离散PSO算法(BPSO与DPSO)[5][6][7]有效解决了针对二进制问题优化求解的困难。
协同PSO 算法(CPSO)[8]将搜索空间进行分割,以达到使每个粒子群具备独立进行粒子更新的能力,降低了对其他粒子群的依赖性。
为了提高粒子群的记忆,避免重复工作,提出了免疫记忆粒子群优化算法[9](IM-PSO),该算法具备较高的收敛速度与精度。

一种新混合粒子群算法及其在阵列天线方向图综合中的应用作者:姚旭曹祥玉陈沫来源:《现代电子技术》2008年第08期摘要:针对传统粒子群算法(PSO)中存在的易陷入局部最优解和后期收敛速度慢的问题,首次提出一种新混合粒子群算法(NHPSO),采用杂交粒子群算法和固定惯性权重策略,并把简化的二次插值法融入杂交粒子群算法中。
实验证明新算法大大提高了收敛速度,改善了解的质量。
对阵列天线特殊主瓣形式的波束赋形和旁瓣电平优化结果取得了非常好的效果,计算机仿真证实该新算法应用于此类问题非常有效。
关键词:粒子群算法;混合粒子群算法;二次插值法;阵列天线;波瓣赋形中图分类号:TN82文献标识码:B文章编号:1004-373X(2008)08-084-YAO Xu,CAO Xiangyu,(Laboratory of Microwave and Antennas Technology,Telecommunication College,Air ForceAbstract:A hybrid Particle Swarm Optimization(PSO) algorithm is proposed with fixed inertia weight in the hybrid particle swarm optimization algorithm,and a simplified quadratic interpolation method is integrated into this algorithm,aiming at overcoming easily trapping in the local extreme points and slow evolving speed of convergence.The experiment shows that this new algorithm improved the global search ability and the quality of optima.The results of both mainlobe shaping and sidelobe levels are very effective.The simulation results prove that the proposed hybrid new algorithm is efficieKeywords:particle swarm optimization algorithm;hybrid particle swarm optimization algorithm;quadratic interpolation method;array antennas;shaped beam在雷达、无线通信等众多领域中,常要求阵列天线具有确定的主瓣宽度、特殊形状的主瓣形状 (如余割波束、余割平方波束、扇形波束等)和低的副瓣电平。

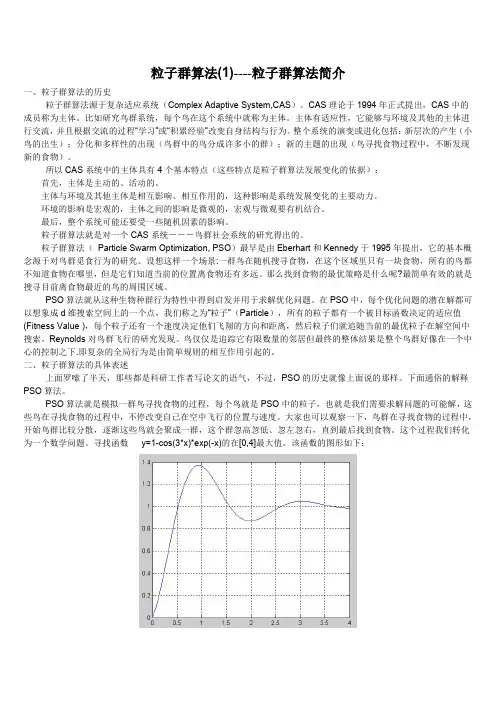
粒子群算法(1)----粒子群算法简介一、粒子群算法的历史粒子群算法源于复杂适应系统(Complex Adaptive System,CAS)。
CAS理论于1994年正式提出,CAS中的成员称为主体。
比如研究鸟群系统,每个鸟在这个系统中就称为主体。
主体有适应性,它能够与环境及其他的主体进行交流,并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。
整个系统的演变或进化包括:新层次的产生(小鸟的出生);分化和多样性的出现(鸟群中的鸟分成许多小的群);新的主题的出现(鸟寻找食物过程中,不断发现新的食物)。
所以CAS系统中的主体具有4个基本特点(这些特点是粒子群算法发展变化的依据):首先,主体是主动的、活动的。
主体与环境及其他主体是相互影响、相互作用的,这种影响是系统发展变化的主要动力。
环境的影响是宏观的,主体之间的影响是微观的,宏观与微观要有机结合。
最后,整个系统可能还要受一些随机因素的影响。
粒子群算法就是对一个CAS系统---鸟群社会系统的研究得出的。
粒子群算法(Particle Swarm Optimization,PSO)最早是由Eberhart和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。
设想这样一个场景:一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有的鸟都不知道食物在哪里,但是它们知道当前的位置离食物还有多远。
那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。
在PSO中,每个优化问题的潜在解都可以想象成d维搜索空间上的一个点,我们称之为“粒子”(Particle),所有的粒子都有一个被目标函数决定的适应值(Fitness Value),每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索。
Reynolds对鸟群飞行的研究发现。


遗传粒子群优化算法混合遗传算法(Genetic Algorithm,GA)和粒子群优化算法(Particle Swarm Optimization,PSO)是两种常见的进化优化算法,它们各自有着优点和不足。
为了充分发挥它们的优势并弥补其不足之处,研究者们对这两种算法进行了混合。
本文将详细介绍遗传粒子群优化算法混合的相关内容。
首先,我们来了解一下遗传算法和粒子群优化算法的原理和特点。
遗传算法是一种模拟生物进化过程的优化算法,其基本思想是通过生物进化中的遗传、变异和选择等算子来最优解。
遗传算法通常由编码、适应度评价、选择、交叉和变异等步骤组成。
编码将待优化问题的解表示为染色体,适应度评价函数用于度量染色体的优劣,选择算子根据适应度选择个体进行繁殖,交叉算子和变异算子模拟生物的遗传和变异操作。
粒子群优化算法是一种模拟鸟群觅食行为的优化算法,其基本思想是通过多个粒子在解空间中的和迭代来找到最优解。
每个粒子都有自己的位置和速度,通过更新速度和位置来不断调整方向和距离。
粒子群优化算法主要包括初始化粒子群、更新速度和位置、更新最优个体和全局最优个体等步骤。
遗传粒子群优化算法混合的基本思想是将粒子群优化算法的能力和遗传算法的全局优化能力结合起来,形成一种新的混合优化算法。
具体来说,在遗传算法的基础上引入粒子群优化算法的思想和操作,使得算法能够更好地在空间中寻找到全局最优解。
将遗传算法和粒子群优化算法进行混合有以下几种常见的方式:1.遗传算法与粒子群优化算法交替使用:先使用遗传算法进行初始化种群和进行交叉变异操作,然后再使用粒子群优化算法进行和更新操作。
通过交替使用这两种算法,可以综合利用它们的优点,提高算法的效率和精度。
2.遗传算子和粒子群优化算法算子的融合:将遗传算法和粒子群优化算法的算子进行融合,形成一种新的算子。
例如,可以将遗传算法的交叉操作与粒子群优化算法的速度更新操作相结合,形成一种新的交叉操作方式;或者将遗传算法的变异操作与粒子群优化算法的位置更新操作相结合,形成一种新的变异操作方式。


以进化算法为代表的仿生随机算法由于具有智能性、通用性和全局搜索能力,以成为求解复杂优化问题的重要工具。
本文对于单目标和多目标优化问题进行了深入的研究,提出了几种求解不同问题的进化算法,本文主要进行了下面几个方面的工作:1.将具有任意个约束条件的单目标优化问题转化为双目标优化问题,其中一个为原目标函数,另一个为违反约束程度最大的约束条件。
采用偏好于第二个目标的粒子比较准则;为了避免算法陷入局部最优,当全局最优解连续几代不发生改变时,采用改进的多父体单形杂交算子对其进行扰动,使得产生的新点更好的继承父代的特性,将扰动后的粒子作为新的寻优方向。
数值实验表明:对于某些特定函数,本算法寻优性能优良。
2.对于较复杂的约束单目标优化问题,提出了模糊粒子群算法。
设计了一个新的扰动算子,使得扰动后的粒子偏向于当前种群中约束违反度小或目标函数值小的粒子。
在此基础上定义了模糊个体极值和模糊全局极值,利用这两个定义改进了粒子群进化方程,利用该方程更新粒子的速度与位置,可以避免早熟收敛问题;定义了不可行度阈值,利用此定义给出了新的粒子比较准则,该准则采用对约束逐个处理的技术,使得一部分性能较优的不可行解微粒得以保留,从而达到使不可行解向可行解进化的目的。
仿真结果表明,对于复杂约束优化问题,算法寻优性能优良,特别是对超高维约束优化问题,该算法获得了更高精度的解。
3.提出了基于粒子群优化的多目标Memetic算法。
将无约束多目标优化问题转化成单目标约束优化问题,其中将解的质量度量看作是约束条件,均匀性度量看作是目标函数。
对转化后的问题提出了基于约束主导原理的比较准则;用基于模拟退火的加权法对非劣解进行局部搜索。
算例测试说明该算法寻优性能优良。
4.提出了解决无约束多目标优化问题的模糊粒子群算法。
设计了新的扰动算子,使得扰动后的粒子偏向于当前种群中序值较小或位于目标空间稀疏区域中的粒子。
在此基础上定义了模糊个体极值和模糊全局极值,利用这两个定义改进了粒子群进化方程;通过改进的进化方程和遗传算法共同作用产生新群体。

1.介绍:粒子群算法(Particle Swarm Optimization, PSO)最早是由Eberhart 和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。
设想这样一个场景:一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有的鸟都不知道食物在哪里,但是它们知道当前的位置离食物还有多远。
那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
经过实践证明:全局版本的粒子群算法收敛速度快,但是容易陷入局部最优。
局部版本的粒子群算法收敛速度慢,但是很难陷入局部最优。
现在的粒子群算法大都在收敛速度与摆脱局部最优这两个方面下功夫。
其实这两个方面是矛盾的。
看如何更好的折中了。
粒子群算法主要分为4个大的分支:(1)标准粒子群算法的变形在这个分支中,主要是对标准粒子群算法的惯性因子、收敛因子(约束因子)、“认知”部分的c1,“社会”部分的c2进行变化与调节,希望获得好的效果。
惯性因子的原始版本是保持不变的,后来有人提出随着算法迭代的进行,惯性因子需要逐渐减小的思想。
算法开始阶段,大的惯性因子可以是算法不容易陷入局部最优,到算法的后期,小的惯性因子可以使收敛速度加快,使收敛更加平稳,不至于出现振荡现象。
经过本人测试,动态的减小惯性因子w,的确可以使算法更加稳定,效果比较好。
但是递减惯性因子采用什么样的方法呢?人们首先想到的是线型递减,这种策略的确很好,但是是不是最优的呢?于是有人对递减的策略作了研究,研究结果指出:线型函数的递减优于凸函数的递减策略,但是凹函数的递减策略又优于线型的递减,经过本人测试,实验结果基本符合这个结论,但是效果不是很明显。
对于收敛因子,经过证明如果收敛因子取0.729,可以确保算法的收敛,但是不能保证算法收敛到全局最优,经过本人测试,取收敛因子为0.729效果较好。
对于社会与认知的系数c2,c1也有人提出:c1先大后小,而c2先小后大的思想,因为在算法运行初期,每个鸟要有大的自己的认知部分而又比较小的社会部分,这个与我们自己一群人找东西的情形比较接近,因为在我们找东西的初期,我们基本依靠自己的知识取寻找,而后来,我们积累的经验越来越丰富,于是大家开始逐渐达成共识(社会知识),这样我们就开始依靠社会知识来寻找东西了。
粒群算法的改进方法一.与其他理论结合的改进1.协同PSO(CPSO)算法原理:提出了协同PSO的基本思想,采用沿不同分量划分子群体的原则,即用N个相互独立的微粒群分别在D维的目标搜索空间中的不同维度方向上进行搜索。
优点:用局部学习策略,比基本PSO算法更容易跳出局部极值,达到较高的收敛精度.缺点:此算法在迭代初期,适应值下降缓慢,且其收敛速度与种群所含微粒数目成反比.2.随机PSO(SPSO)算法原理:其基本思想是利用停止进化的微粒来改善全局搜索能力。
即将式(1)中的当前速度项V过去掉,从而使得速度本身失去记忆性,减弱了全局搜索能力.但这样也使得在进化的每一代均至少有一个微粒出予处于微粒群的历史最好位置而停止进化.然后在搜索空问中重新随机产生新的微粒以代替停止微粒的进一步进化.这样就大大增强了全局搜索麓力.3.有拉伸功能的PSO算法原理:为了有效地求解多模态复杂函数优化问题,Parsopoulos等人将函数“Stretching”技术引入PSO算法,形成了一种高效的全局优化算法一“Stretching PSO”(SPSO)。
它通过消除不理想的局部极小而保留全局最小来避免陷入局部极小.在检测到目标函数的局部极小点后,立即对待优化的目标函数进行拉伸变换.优点:.SPSO具有稳健的收敛性和良好的搜索能力,在很多高维度,多局部极值的函数最小值的求解问题上,搜索成功率显著提高。
缺点:计算耗时相应地也会增加.4.耗散PSO(DPSO)算法原理:谢晓峰等人根据耗散结构的自组织性,提出了一种耗散型PSO 算法.耗散PSO算法构造了一个开放的耗散系统.微粒在开放系统中的“飞行”不只依赖于历史经历,还要受环境的影响.附加噪声从外部环境中,持续为微粒群弓|入负熵,使得系统处于远离平衡态的状态.又由于群体中存在内在的非线性相互作用,从而使群体能够不断进化。
二.与其他算法结合的改进1.混合PSO(HPSO)算法原理:Angeline于1998年提出采用进化计算中的选择操作的改进型PSO模型,成为混合PSO(HPSO)。
粒子群蚁群混合算法
粒子群蚁群混合算法是一种优化算法,将粒子群算法和蚁群算法相结合,利用它们各自的优点进行优化。
该算法通常用于解决复杂的优化问题,如多目标优化、非线性优化等。
在粒子群蚁群混合算法中,粒子群算法模拟了一群鸟或昆虫在搜索环境中的行为,通过粒子的位置和速度来探索解空间。
而蚁群算法则模拟了蚂蚁在寻找食物时的行为,通过蚂蚁遗留的信息素来引导搜索过程。
粒子群蚁群混合算法中,粒子群算法的速度和位置更新公式如下: $$v_i^{t+1} = wv_i^t + c_1r_1(pbest_i - x_i^t) +
c_2r_2(gbest - x_i^t)$$
$$x_i^{t+1} = x_i^t + v_i^{t+1}$$
其中,$v_i^t$表示粒子$i$在$t$时刻的速度,$x_i$表示粒子
$i$在$t$时刻的位置,$pbest_i$表示粒子$i$的个体最优解,$gbest$表示全局最优解,$w$是惯性因子,$c_1$和$c_2$是学习因子,$r_1$和$r_2$是随机数。
蚁群算法则通过信息素的更新和挥发来实现搜索过程,信息素更新公式如下:
$$tau_{ij}^{t+1} = (1-rho)tau_{ij}^t + Deltatau_{ij}^t$$ 其中,$tau_{ij}$表示从节点$i$到节点$j$的信息素浓度,$rho$是信息素挥发系数,$Deltatau_{ij}$是信息素增量。
粒子群蚁群混合算法中,将粒子群算法和蚁群算法的更新公式相
结合,实现了更加高效的搜索过程。
该算法的应用范围广泛,可用于机器学习、神经网络等领域的优化问题。
粒子群算法原理粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,最早由Kennedy和Eberhart于1995年提出。
它是一种模拟鸟群觅食行为的优化算法,通过模拟鸟群中个体之间的信息共享和协作来寻找最优解。
粒子群算法在优化问题中具有较高的效率和鲁棒性,被广泛应用于工程优化、机器学习、神经网络训练等领域。
粒子群算法的原理基于群体智能的思想,通过模拟群体中个体之间的信息交流和协作来寻找最优解。
在粒子群算法中,每个解被称为一个粒子,粒子具有位置和速度两个属性。
在搜索过程中,每个粒子根据自身的经验和群体的经验来调整自己的位置和速度,以寻找最优解。
粒子群算法的基本原理可以概括为以下几个步骤:1. 初始化粒子群,首先随机生成一定数量的粒子,并为每个粒子随机赋予初始位置和速度。
2. 评估粒子适应度,根据问题的优化目标,计算每个粒子的适应度值,即目标函数的取值。
适应度值越高表示粒子的解越优秀。
3. 更新粒子的速度和位置,根据粒子群算法的更新规则,更新每个粒子的速度和位置。
通常情况下,粒子的速度和位置会受到个体最优解和群体最优解的影响。
4. 更新个体最优解和群体最优解,根据每个粒子的适应度值,更新个体最优解和群体最优解。
个体最优解是粒子自身搜索过程中找到的最优解,而群体最优解是所有粒子中适应度值最高的解。
5. 终止条件判断,在满足一定条件下,如达到最大迭代次数或者适应度值满足一定要求时,终止算法并输出最优解。
粒子群算法的优势在于其简单、易于实现、对参数不敏感等特点。
此外,粒子群算法还具有较好的全局搜索能力和收敛速度,能够有效地应用于多种优化问题中。
总之,粒子群算法是一种基于群体智能的优化算法,通过模拟个体之间的信息共享和协作来寻找最优解。
它具有较高的效率和鲁棒性,被广泛应用于工程优化、机器学习、神经网络训练等领域。
希望通过本文的介绍,读者能对粒子群算法有一个更深入的了解,并能够在实际问题中灵活运用。
混合粒子群算法:基于杂交的算法
1. 算法原理
借鉴遗传算法中杂交的概念,在每次迭代中,根据杂交率选取指定数量的粒子放入杂交
池内,池内的粒子随机两两杂交,产生同样数目的子代粒子( child),并用子代粒子代替亲代粒子(pare nt )。
子代位置由父代位置进行交叉得到:
child (x) = p.pare nt|(x) (l-p).pare nt2(x)
或
child (x) =(1_ p).parent((x) p. parent2(x)
其中,P是o到1之间的随机数。
子代的速度由下式计算:
child(v)= pa訥(V)parant2(v)|parant i(v)
| parant/v) + parant2(v)|
或
child(v)=冋眦⑼ parant2(v)|parant2(v)
| para nt i(v) + para nt2(v)|
2. 算法步骤
基于自然选择的粒子群算法的基本步骤如下:
(1)随机初始化种群中各微粒的位置和速度;
(2)评价每个微粒的适应度,将当前各微子的位置和适应值存储在各微子的pbest中,
将所有的pbest中适应最优个体的位置和适应值存储在gbest中;
(3)更新每个微粒的速度和位置;
(4)对每个微粒,将其适应值与其经历过的最好位置作比较,如果较好,则将其作为当
前的最好位置;
(5)比较当前所有pbest和gbest的值,更新gbest ;
(6)根据杂交概率选取指定数量的粒子放入杂交池中,池中的粒子随机两两杂交产生同样数目
的子代粒子,子代的位置和速度计算公式如下:
child (x)二p.parent|(x) (1 _ p).parent2(x)
child (v^ parant1(v)叩呢⑼ |parant1(v)。
保持pbest 和gbest不变;
| paran h(v) + para nt2(v)|
(7)若满足停止条件(通常为预设的运算精度或迭代次数) ,搜索停止,输出结果,否则
返回(3)继续搜索。
3.算法MATLAB实现
在MATLAB中编程实现的基于杂交的粒子群算法优化函数为:BreedPSO。
功能:用基于杂交的粒子群算法求解无约束优化问题。
调用格式:[xm, fv]二PSO( fitness, N,o),c2,w, Pc, Sp, M , D)
其中,fitness :待优化的目标函数;
N :粒子数目;
G:学习因子1 ;
C2:学习因子2;
W :惯性权重;
Pc :杂交概率;
Sp :杂交池的大小比例;
M :最大迭代次数;
D :自变量的个数;
xm:目标函数取最小值时的自变量值;
fv :目标函数的最小值。
基本粒子群算法的MATLAB代码如下:
fun ctio n [xm,fv]=BreedPSO(fitiness,N,c1,c2,w,Pc,Sp,M,D)
% fitn ess :待优化的目标函数;
% N:粒子数目;
% cl:学习因子1;
% c2:学习因子2;
% w:惯性权重;
% Pc杂交概率;
% Sp杂交池的大小比例;
% M:最大迭代次数;
% D:自变量的个数;
% xm:目标函数取最小值时的自变量值;
% fv:目标函数的最小值。
format long; for i=1:N
for j=1:D
x(i,j)=ra nd n;%随机初始化位置
v(i,j)=ra ndn; %随机初始化速度
end
end
for i=1:N p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
pg=x(N,:); %pg 为全局最优
for i=1:(N-1)
if fitness(x(i,:))<fitness(pg)
pg=x(i,:);
end
end
for t=1:M
for i=1:N %速度、位移更新
v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
if fitness(x(i,:))<p(i)
p(i)=fitness(x(i,:));
y(i,:)=x(i,:);
end
if p(i)<fitness(pg)
pg=y(i,:);
end
r1=rand();
if r1<Pc %杂交概率
numPool=round(Sp*N); %杂交池大小
PoolX=x(1:numPool,:); %杂交池中粒子的位置PoolVX=v(1:numPool,:); %
杂交池中粒子的速度for i=1:numPool
seed1=floor(rand()*(numPool-1))+1; seed2=floor(rand()*(numPool-
1))+1; pb=rand();
%子代位置计算childx1(i,:)=pb*PoolX(seed1,:)+(1-
pb)*PoolX(seed2,:);
%子代速度计算
childv1(i,:)=(PoolVX(seed1,:)+PoolVX(seed2,:))*norm(PoolVX(seed1,:))/norm(PoolVX(seed1,:)
+PoolVX(seed2,:));
end
x(1:numPool,:)=childx1; %子代的位置替换父代的位置
v(1:numPool,:)=childv1; %子代的速度替代父代的速度
end end end
xm=pg'; fv=fitness(pg);
例
基于杂交的粒子群算法应用实例。
求下面函数的最小值
取粒子数目为40,学习因子都取2,惯性权重取0.7,杂交概率取0.9,杂交池大小比例 取0.2,迭代步数取10000。
解:
首先建立目标函数文件 fitness.m .
fun cti on F=fit ness(x)
F=0;
for i=1:5
F=F+1/(i+(x(i)-1)A 2);
end
F=1/(0.01+F);
在MATLAB 命令窗口中输入:
>> [xm,fv]=BreedPSO(@fit ness,40,2,2,0.7,0.9,0.2,10000,5)
所得结果为:
xm =
0.999999998142068
1.000000018187727
1.000000018663603
0.999999985688029
1.000000009915268
fv =
0.436046511627907
从结果可以看出,基于杂交的粒子群求得的结果精度是非常高的。
f(x)
0.01+Z 一 i J i +。