空间点阵

的研究更加完美，而且逐渐走出大块晶体的范畴，开始了对微细材料
和无序固体的开发和利用，新发现、新进展接踵而来：
第 22 页
二、固体物理学发展历程
英国曼彻斯特大学科学家安德烈·海姆和康斯坦丁·诺沃
肖洛夫以石墨烯研究获得２０１０年度诺贝尔物理学奖
康斯坦丁·诺沃肖洛夫 1974年8月月出生
安德烈·海姆 1958年10月出生
因其电阻率极低，电子迁移的速度极快，因此被期待可用来发展更薄、导
例如液氦、液晶、熔盐、液态金属、电解液、玻璃、凝胶等。
第 14 页
二、固体物理学发展历程
凝聚态物理学研究对象日益扩展，更为复杂。一方面传统的固体物理 各个分支如金属物理、半导体物理、 磁学、低温物理和电介质物理等的研 究更深入，各分支之间的联系更趋密切； 另一方面许多新的分支不断涌现，如强关联电子体系物理学、无序体
第 23 页
二、固体物理学发展历程
人们常见的石墨是由一层层以蜂窝状有序排列的平面碳原子堆叠而形
成的，石墨的层间作用力较弱，很容易互相剥离，形成薄薄的石墨片。当把 石墨片剥成单层之后，这种只有一个碳原子厚度的单层就是石墨烯。
石墨烯是由碳六元环组成的两维(2D)周期蜂窝状点阵结构, 它可以翘曲成 零维(0D)的富勒烯(fullerene),卷成一维(1D)的碳纳米管(carbon nano-tube,
《固体物理学》教学课件
高
峰
合肥工业大学 电子科学与应用物理学院 2015年09月
第1页
绪论
一、固体物理学主要研究内容 二、固体物理学发展历程--为什么要学习固体物理学 三、固体物理学课程特点 四、固体物理学的研究方法 五、固体物理学参考教材
第2页
一、固体物理学主要研究内容

面心立方格子
（3）布拉菲格子 （4）复式格子 （5）格矢
2、一维布拉菲格子 3、一维复式格子 3、二维情况
4、三维情况：
重复单原是平行六面体，晶格周期性可表为：
(r) (r l1a1 l2a2 l3a3 )
采用原胞基矢 R l1a1 l2a2 l3a3 采用晶胞基矢 R ma nb pc
一、空间点阵
1、晶体的微观结构具周期性，其几何模型即空间点阵。 2、空间点阵：晶体中诸结点的空间排列
3、基元：晶体中一种或几种粒子组成的最小结构单元。 4、晶体结构=点阵+格点（基元）
碳 60 晶 体 的 晶 胞 ， 晶 体 的 基 元 包 含 60 个 碳 原 子
二、晶格的周期性 基矢 1、定义： （1）原胞（固体物理学原胞）：晶体中最小的重复单元 （2）晶胞（结晶学原胞）：同时反映周期性和对称性， 不一定是最小的重复单元。
正 五 边 形 无 法 填 满 整 个 平 面
4、七个晶系 （1）晶系：在晶体学中，有共用特征对称素的一族点群称~ （共同的特征对称素决定着共同的晶胞形状） （2）每个晶系都有确定了标准的晶胞和基矢，晶系的对称性 可以完全由晶胞的对称性来描述。 （3）所有晶体可分为7个晶系：三斜、单斜、正交、四方、 三角、六角和立方（如图）
3、基本对称操作： （1）转动操作（n次旋转对称） 旋转轴：将晶体绕某轴旋转一定角度后，若晶体能完全 复原，该轴称为旋转对称轴。若转动 后能复 原，则定义 n 2 / 为该转轴的次数。 可证明晶体只有1、2、3、4、6次旋转轴 （2）镜面 （3）反演
（4）象转轴：只有 1,2, 3,4,6 五种 但： 1 i, 2 m, 3 3 i, 6 3 m

点阵是一组无限的点，点阵中每个点都具有 完全相同的周围环境。在平移的对称操作下,（连 结点阵中任意两点的矢量,按此矢量平移）,所有 点都能复原,满足以上条件的一组点称为点阵。
(a) (b)
(c) (d) 一维周期排列的结构及其点阵（黑点代表点阵点） (a) Cu ， (b) 石墨 ， (c) Se ， (d) NaC l
晶体结构的基本重复单位是晶胞，整个晶体 就是晶胞在三维空间周期地重复排列堆砌而成 的。只要将一个晶胞的结构剖析透彻，整个晶 体结构也就掌握了。
晶胞有两个要素： ⑴ 晶胞的大小和形状，由晶胞参数
a , b , c , α , β , γ 规定； ⑵晶胞内部各个原子的坐标位置，由原子坐标 参数 (x , y , z )规定。
第2章 晶体结构和空间点阵
➢ 内容
✓ 晶体结构的周期性与空间点阵。 ✓ 晶胞、晶列、晶面和晶面指数。 ✓ 倒易点阵 ✓ 晶体的对称性。 ✓ 7个晶系和14种Bravias空间格子。 ✓ 晶体缺陷
➢ 教学目标
通过本章学习，掌握晶体所具有的周期性结构与它的 点阵表示，倒易点阵，了解晶体对称性与空间群。
材料科学与工程
ห้องสมุดไป่ตู้
▪ 体心点阵，I
除8个顶点外，体 心上还有一个阵点， 因此，每个阵胞含 有两个阵点，000， 1/2 1/2 1/2
• 面心点阵。F
除8个顶点外，每 个面心上有一个 阵点，每个阵胞 上有4个阵点，其 坐标分别为000， 1/2 1/2 0， 1/2 0 1/2， 0 1/2 1/2
2. 2 晶体的周期性，晶胞
晶体结构(晶格） = 点阵 + 结构基元
原胞和晶胞
• 原胞（primitive cell）：最小的重复单元。 • 晶胞（unit cell）：体现所有对称性的最

数据库系统设计基础空间点阵一、数据库系统设计基础1.1 数据库系统的定义与特点数据库系统是指在计算机上建立、存储、管理和利用数据的一种系统。

它具有以下特点：（1）数据共享性强：多个用户可以共同使用同一个数据库，实现数据的共享和交换。

（2）数据冗余度低：通过数据库系统的设计，可以避免数据冗余，从而提高了数据的存储效率。

（3）数据独立性高：通过数据库系统的设计，可以将应用程序与具体的数据存储方式分离开来，从而提高了应用程序的可维护性和可扩展性。

（4）数据安全性高：通过数据库系统提供的安全机制和权限管理，可以保证数据的安全性。

1.2 数据库设计过程数据库设计是指按照一定规则和方法对需要处理的信息进行分析、组织、设计和实现。

其过程包括以下几个步骤：（1）需求分析：根据用户需求确定数据库中需要存储哪些信息以及这些信息之间的关系。

（2）概念设计：根据需求分析结果，建立概念模型，包括实体、属性和关系等。

（3）逻辑设计：根据概念模型建立逻辑模型，包括表结构、字段定义、关系定义等。

（4）物理设计：根据逻辑模型建立物理模型，包括数据库表的存储结构、索引等。

（5）实施和维护：根据物理模型进行数据库的实施和维护，包括数据导入、备份和恢复等。

1.3 数据库范式数据库范式是指在关系数据库中对关系模式的规范化，目的是消除数据冗余、提高数据存储效率和数据查询效率。

常见的数据库范式有以下几种：（1）第一范式（1NF）：要求每个属性都是原子性的，即不可再分解。

（2）第二范式（2NF）：要求每个非主属性都完全依赖于候选键。

（3）第三范式（3NF）：要求每个非主属性都不存在传递依赖关系。

（4）BCNF范式：在满足第三范式的基础上，进一步消除主属性之间存在函数依赖关系。

二、空间点阵2.1 空间点阵的定义空间点阵是指将空间划分为规则的网格单元，在每个网格单元中记录该单元所代表区域内某种特征或属性值。

空间点阵通常用于地图制图、遥感影像处理、空间分析等领域。

晶体结构＝点阵结构＝点阵＋结构基元
结构基元 每个点阵点所代表的具体内容。
2019/6/1
7
第七章 晶体的点阵结构和晶体的性质
(1) 直线点阵
以直线连接各个阵点形成的点阵称为直线点阵。 a
a —直线点阵的单位矢量，因是平移时阵点 复原的最小距离, 故为平移素向量或素单位 。
b
b=2a
含有两个以上阵点的单位为复单位或复向量。
实例 NaCl(100)晶面如何抽象成点阵？
点阵结构
2019/6/1
点阵
20
第七章 晶体的点阵结构和晶体的性质
(3) 空间点阵
向空间三维方向伸展的点阵称为空间点阵。
空间点阵与正当空间格子
2019/6/1
21
第七章 晶体的点阵结构和晶体的性质
划分空间格子的原则 尽可能选具有较规则形状的、体积较小的 平行六面体单位。按此规则划分出的格子称为正 当格子。
点阵结构中存在点阵，点阵的表 示符号用平移群。
2019/6/1
24
第七章 晶体的点阵结构和晶体的性质
三、晶 胞
1 晶胞的定义 晶体结构的基本重复单元称为晶胞。
晶胞与空间点阵的关系
晶体结构 点阵结构 空间点阵 结构基元


晶 胞 空间点阵单位 结构基元
2019/6/1
25
第七章 晶体的点阵结构和晶体的性质
晶体的理想外形具有特定的对称性，这是内 部结构对称性的反映。晶体结构的周期大小和X 射线的波长相当，使它成为天然的三维光栅，能 够对X射线产生衍射。而晶体的X射线衍射，成为 了解晶体内部结构的重要实验方法。
2019/6/1
4
第七章 晶体的点阵结构和晶体的性质

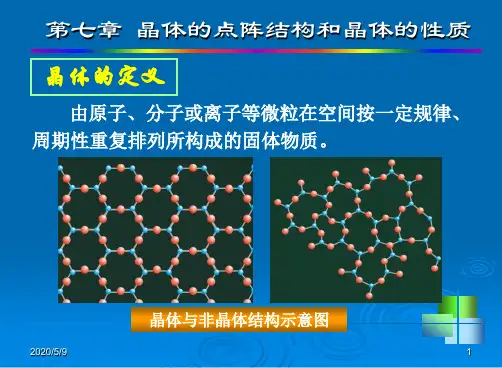
1.阵点：晶体中的质点抽象位规则排列于空间的几何点。

2.空间点阵：阵点在空间呈周期性规则排列，并具有完全相同的周围环境，这种由它们在三维空间规则排列的阵列称为空间点阵。

3.空间格子：用来描述空间点阵的三维几何格架。

4.简单晶胞：只有在平行六面体每个顶角上有一阵点的晶胞。

5.复杂晶胞：除在顶角外，在体心、面心或底心上有阵点。

6等同点：晶体结构中物质环境和几何环境完全相同的点。

7.合金：由两种或两种以上的金属或金属与非金属经熔炼、烧结或其他方法组合而成，并具有金属特性的物质。

8.组元：组成合金的基本的、独立的物质。

9.相：合金中具有同一聚集状态、同一晶体结构和性质并以界面相互隔开的均匀组成部分。

10.单相合金：有一种相组成的合金。

11.多相合金：由几种不同的相组成的合金。

12.固溶体：以某一组元位溶剂，在其晶体点阵中融入其他组元原子（溶质原子）所形成的均匀混合的固态溶体，它保持着溶剂的晶体结构类型。

13.中间相：两组元A 和B 组成合金时，除了形成以A 为基或以B 为基的固溶体外，还可能形成晶体结构与A，B 两组元均不相同的新相。

由于它们在二元相图上的位置总是位于中间，故通常把这些相称为中间相。

14.中间相的分类：正常价化合物、电子化合物、与原子尺寸因素有关的化合物（间隙相和间隙化合物、拓扑密堆相）固溶体根据溶质原子在溶剂点阵中所处位置，分为置换固溶体和间隙固溶体。

按固溶度分类：有限固溶体和无限固溶体。

按各组元原子分布的规律性分类：无序固溶体和有序固溶体。

15.置换固溶体：溶质原子置换了溶剂点阵的部分溶剂原子的固溶体。

16.极限电子浓度：最大溶解度时的电子浓度数值接近位1.4。

17.间隙固溶体：溶质原子分布于溶剂晶格间隙而形成的固溶体。

18间隙相：当非金属X和金属M原子半径的比值r x/r M<0.59时，形成具有简单的晶体结构的相。

19.间隙化合物：当r x/r M>0.59时，形成具有复杂的晶体结构的相。

立方正方斜方cba???90??????cba??????90???cba??????90???菱方六方单斜三斜cba??????90???cba?????90????120?cba?????????90cba??????90???7大晶系包含14种空间点阵布拉布拉菲abravais点阵3
第一章 晶体学基础
1、晶面指数 、
方法和步骤与三指数时相同， 方法和步骤与三指数时相同， 只是要找出晶面 在四个坐标 轴上的截距。 轴上的截距。 例如： 例如： a3 o a1 a2
(1010) (0110) (1100)
(1010)
2、晶向指数： 、晶向指数：
四坐标晶向指数的确定方法有行走法和解析法。 四坐标晶向指数的确定方法有行走法和解析法。由于行走法 确定的晶向指数不是唯一的，所以这里仅介绍解析法 解析法。 确定的晶向指数不是唯一的，所以这里仅介绍解析法。 步骤： 步骤： 1)求出待定晶向在 1,a2,c三个坐标轴下的指数：U, V, W 求出待定晶向在a 三个坐标轴下的指数： 求出待定晶向在 三个坐标轴下的指数 2)按以下公式算出在四坐标轴下的指数：u, v, t, w 按以下公式算出在四坐标轴下的指数： 按以下公式算出在四坐标轴下的指数
多数金属和非金属材料都是晶体。因此， 多数金属和非金属材料都是晶体。因此，首先 要掌握晶体的特征及其描述方法。 要掌握晶体的特征及其描述方法。 晶体——组成晶体的质点在三维空间作周期性地、 组成晶体的质点在三维空间作周期性地、 晶体 组成晶体的质点在三维空间作周期性地 规则地排列。 规则地排列。 晶体的特点： 晶体的特点： 质点排列具有规则性、 质点排列具有规则性、周期性 有固定熔点（结晶温度） 非晶体没有固定的熔点 非晶体没有固定的熔点] 有固定熔点（结晶温度）[非晶体没有固定的熔点 各向异性（包含多种性能） 各向异性（包含多种性能）

晶体与非晶体的区别：
1. 原子规排：晶体中原子（分子或离子）在三维空间呈周 期性重复排列，而非晶体的原子无规则排列的。 2. 固定熔点：晶体具有固定的熔点，非晶体无固定的熔点， 液固转变是在一定温度范围内进行。 3. 各向异性：晶体具有各向异性（anisotropy），非晶体为 各向同性。
二、空间点阵和晶胞

晶 格 常 数 示 意 图
3. 空间点阵类型（晶系）

根据６个参数间相关系可将全部空间点阵归为七大类，十四种（称为 布拉菲点阵）。
1）七大晶系
① ② ③ ④ ⑤ ⑥ ⑦
三斜晶系（Triclinic System） 单斜晶系（Monoclinic System） 正交晶系（斜方晶系，Orthogonal System） 四方晶系（正方晶系，Tetragonal System） 立方晶系（Cubic System） 六方晶系（Hexagonal System） 菱形晶系（Rhombohedral System）


晶体结构的微观特征 晶体可看作某种结构单元（基元）在三维空间作周期 性规则排列 质点或基元(basis)：原子、分子、离子或原子团 (组 成、位形、取向均同)
抽象为 质点 抽象为
阵点
质点的三维空间周期排列
空间点阵
1. 空间点阵

空间格子：把晶体中质点的中心用直线联起来构成的空 间格架即空间格子(Lattice)。 晶体点阵：由这些结点构成的空间总体称为晶体点阵。 晶体结点为物质质点的中心位置。 空间点阵中结点仅有几何意义，并不真正代表任何质点。
⑦菱形晶系（RHOMBOHEDRAL SYSTEM） 特点：对称轴和单胞的一个轴 （设a轴）夹角为某一角度α， 另外两个轴和对称轴夹角亦为 α并且长度相等。这三个轴构 成的六面体就是一个菱形单胞。 菱形晶系点阵常数间的关系为：

1 1 1 ， 2 2 2
Cs+的坐标为 (000)。 )
典型的晶体结构 结构型 单晶胞中 原子在单晶 最近邻 原子个数 胞中的位置 距离 配位数
(Cu) )
fcc
4 2
Cs+ 1 Cl- 1
bcc
11 ( 0) (000) 22 1 1 ( 0 ) (0 1 1) 2 2 22
2a 2 3a 2 3a 2
每个格点包含2个原子，属于复式晶格。 每个格点包含2个原子，属于复式晶格。
1 2 3 4
1 4
1 2
1 4 3 4 1 2
1 2
A类碳原子的 共价键方向
B类碳原子的 共价键方向
金刚石结构每个固体物理学原胞 包含1个格点 基元由两个碳原子组成, 个格点, 包含 个格点,基元由两个碳原子组成, 位于（ ） 位于（000）和 (b)氯化钠结构 b)氯化钠结构
a a1 = − i + j + k 2 a a2 = i − j + k 2 a a3 = i + j − k 2
( ( (
)
) )
平均每个布拉维原胞包含2个格点。 平均每个布拉维原胞包含 个格点。 固体物理学原胞的体积
1 3 = a1 ⋅ a2 ×a3 = a 2
(
)
立方晶系中几种实际晶体结构
§1.3 布喇菲空间点阵 原胞 晶胞 1.3
一. 布喇菲空间点阵
(a)
(b)
(c)
(a)、(b)、(c)为二维晶体结构示意图，它们有何异同 ) ) )为二维晶体结构示意图，它们有何异同?
(a)Leabharlann (b)(c)一个理想的晶体是由完全相同的结构单元在空间周期性重 复排列而成的。 复排列而成的。 所有晶体的结构可以用布喇菲格子 又称晶格）来描述， 布喇菲格子（ 所有晶体的结构可以用布喇菲格子（又称晶格）来描述， 这种晶格的每个格点上附有一群原子， 这种晶格的每个格点上附有一群原子，这样的一个原子群称为 基元，基元在空间周期性重复排列就形成晶体结构。 基元，基元在空间周期性重复排列就形成晶体结构。 晶体结构 晶格+基元= 晶格+基元=晶体结构

1 空间点阵与晶体结构的异同空间点阵晶体结构人为的、抽象的几何图形客观的具有具体的物质内容,其基本的单元是结构单元（原子或离子)组成空间点阵的结点是没有物质内容的几何点结构单元与结点在空间排列的周期是一致的，或者说它们具有同样的T矢量；抽象的空间点阵不能脱离具体的晶体结构而单独存在，所以它不是一个无物质基础的纯粹的几何图形。

这种抽象能更深入地反映事物的本质与规律，因此是一个科学的抽象。

空间点阵只是一个几何图形，它不等于晶体内部具体的格子构造，是从实际晶体内部结构中抽象出来的无限的几何图形。

虽然对于实际晶体来说，不论晶体多小，它们所占的空间总是有限的，但在微观上，可以将晶体想象成等同点在三维空间是无限排列的。

2 在同一行列中结点间距是相等的；在平行的行列上结点间距是相等的；不同的行列，其结点间距一般是不等的（某些方向的行列结点分布较密；另一些方向行列结点的分布较疏。

）3 面网密度：面网上单位面积内结点的数目面网间距：任意2个相邻面网的垂直距离相互平行的面网的面网密度和面网间距相等面网密度大的面网其面网间距也大4 宏观晶体中对称要素的集合，包含了宏观晶体中全部对称要素的总和以及它们相互之间的组合关系（1）对称变换的集合——对称变换群（2）对称要素的集合——对称要素群合称对称群在宏观晶体中所存在的对称要素都必定通过晶体的中心，因此不论对称变换如何，晶体中至少有一个点是不变的，所以将对称型称为点群，该点称为点群中心5 点阵几何元素的表示法☆坐标系的确定任一点阵结点------------坐标原点单位平行六面体的三个互不平行的棱---坐标轴点阵常数a、b、c所代表的三个方向---x、y、z轴坐标单位：a、b、c ☆结点的位置表示法以它们的坐标值来表示的。

6 晶向的表示法晶向—空间点阵中由结点连成的结点线和平行于结点线的方向晶向指数uvw—通过原点作一条直线与晶向平行，将这条直线上任一点的坐标化为没有公约数的整数。

空间点阵与晶体结构的区别与联系示例文章篇一：哎呀！同学们，你们知道吗？空间点阵和晶体结构这两个概念可把我绕晕了好久呢！咱先来说说空间点阵吧。

就好像咱们在操场上排队做体操，每个人都站在规定好的位置上，这些位置就像是空间点阵里的点。

这些点可不是随便乱排的，它们有规律，有秩序，整整齐齐的。

那晶体结构又是什么呢？这就好比是一个用积木搭成的城堡。

每一块积木就像是组成晶体的原子、分子或者离子，它们按照特定的方式组合在一起，形成了美丽又独特的城堡，也就是晶体结构。

你说空间点阵和晶体结构难道没有相似的地方吗？那肯定有呀！它们就像一对双胞胎兄弟，都有着内在的规律和秩序。

空间点阵是晶体结构的基础，没有空间点阵那些有规律的点，哪来晶体结构中原子、分子、离子的有序排列呢？比如说，氯化钠晶体，它的结构不就是钠离子和氯离子按照一定的规律排排站嘛！这和空间点阵不就有着密切的关系吗？再想想看，要是没有空间点阵来指引，晶体结构能那么规整漂亮吗？肯定不能啊！那它们就没有区别啦？当然不是！空间点阵只是抽象的点的排列，可没有实际的物质存在。

而晶体结构呢，那可是实实在在的原子、分子或者离子组合在一起的呀！老师上课讲这些的时候，我就在想，这多像我们班级的座位排列和整个班级的组成呀！座位排列就像是空间点阵，有规矩，而我们每个同学就像是组成班级这个“晶体”的一份子，共同构成了一个独特的集体。

所以说呀，空间点阵和晶体结构既有联系又有区别，它们就像一对相互依存又各自独特的好伙伴，共同构成了奇妙的物质世界。

怎么样，同学们，你们是不是也像我一样搞清楚啦？示例文章篇二：哇塞！今天老师给我们讲了空间点阵和晶体结构，一开始我还一头雾水呢，这俩家伙到底是啥？又有啥区别和联系呀？先来说说空间点阵吧。

就好像我们排队做操一样，每个人都站在规定好的位置上，整整齐齐的。

空间点阵里的那些点，就跟我们做操的位置一样，是有规律地排列着的。

晶体结构呢，就像是一座超级漂亮的城堡。

42
第二章固体结构（2）习题
1. 用文字阐述以下名词及其它们的关联性和异同点。
晶胞参数 点阵参数 晶格参数 a,b,c,,, 结构基元 晶体结构 晶胞 非初级阵胞 复胞 阵点 空间点阵 阵胞 初级阵胞 原胞 单胞 结晶学元胞
十四种布拉菲点阵 七个晶系
格点
晶格
基本单元
简单晶格
43
单位矢量
复式晶格
将周期性重复排列的原子/分子或原子群/分子群称为结构基
元（structural motif）。
结构基元是具有不同种类和几何位置的原子 / 离子的集合，
包含原子或分子的种类和数量及其排列方式，可以是单个原 子/分子，或是在空间以一定方式排列的原子群或分子群。
• 晶体结构可以看作由结构基元在三维空间组成的空间图案， 这些图案按一定的周期平移后可以自身重合。
期重复堆积而成的。
34
固体结构 — 空间点阵
• 晶胞的选择也有多种，通常按照反映晶体结构最高对称性原 则（十四种布拉菲点阵）进行划分 。 • 晶胞参数和其对应的阵胞（单胞）具有相同的点阵参数（a、 b、c和、、），即两者的形状和大小相同。
• 晶胞的结构基元抽象为阵点，就转化为相应的阵胞，在阵胞
31
固体结构 — 空间点阵
aP Triclinic三斜
mP Monoclinic单斜
mC
oP
32
oC oI Orthorhombic正交
oF
固体结构 — 空间点阵
hR Rhombohedral菱方
tP Tetragonal四方
tI
33
hP Hexagonal六方
cP
cI Cubic立方
cF
固体结构 — 空间点阵 晶胞：按照晶体结构的周期性划分的几何单元，构成晶体结构 的基本单元，整个晶体可看作是由晶胞在三维空间按一定的周

在晶体内部结构中 (以及在相应抽象出来的空间点阵 中) 可能存在的对称要素以及相应可以进行的宏观对 称操作主要有以下几类： q 对称中心 q 对称面 q 旋转轴 q 倒转轴 (有时也称为象转轴)
v 对称中心是一个假想的几何 点，其对应的对称操作是对于 这个点的倒反 (反演)。 v 通过对称中心作任意直线， 在此直线上位于对称中心两侧 等距离的两点是性质完全相同 的对应点。 v 在晶体中，如果存在有对称 中心，则对称中心肯定位于晶 体的几何中心。 v在结晶学中，对称中心一般 用符号 “i” 表示。
从等大球体堆积构型中抽象出空间点阵 (四) 体心立方堆积
体心位置和顶点位置是等同位置
小结一下
• 六方最紧密堆积的晶体结构图形与空间点阵图 形是不一样的，而三种立方堆积的晶体结构图 形与空间点阵图形则是一样的 • 六方最紧密堆积结构的基元由两个圆球构成， 是导致晶体结构与空间点阵图形不一样的原因 • 三种立方堆积中的基元均由一个圆球构成，因 此晶体结构图形与空间点阵图形是一样的
在晶体研究中经常遇到两个名词：
q点群：在宏观晶体中存在的所有对称要素都必定 通过晶体的中心，因此不论如何进行对称操作，晶 体中至少有一个点是不变的，因此对称型也称为点 群。(点群有32种) q 空间群：晶体结构中还有一些微观的对称要 素，微观对称要素的核心是平移轴，微观对称要素 的集合构成平移群。晶体结构中存在的一切对称要 素 (包括平移轴在内) 的集合称为空间群。晶体中 可能存在的空间群只有 230 种
v 对称面是一个假想的平面，相应 的对称操作为对此平面的反映。对 称面就像一面镜子，把物体的两个 相同的部分以互成镜像反映的关系 联系起来。 v 垂直于对称面作任意直线，位于 直线两侧等距离的两点是性质完全 相同的对应点 v 晶体中如果存在有对称面，则必 定通过晶体的几何中心并将晶体分 为互成镜像反映的两个相同部分 v在结晶学中，对称面一般用符号 “m” 表示。

常用金属的空间点阵 金属是一种常见的物质，具有特殊的空间点阵结构。下面将以几种常用金属的空间点阵为题，通过人类视角进行创作，使文章富有情感和真实感。

1. 长方体点阵的铁 铁是一种重要的金属材料，它的空间点阵结构呈现出长方体的形状。当我拿起一块铁制品时，能感受到它的坚硬和冷凉。铁的空间点阵结构让它具有良好的延展性和韧性，使其成为制作工具和建筑材料的理想选择。

2. 密排六方点阵的钢 钢是一种强大的金属材料，它的空间点阵结构呈现出密排六方的形状。钢具有优异的强度和耐腐蚀性，因此被广泛应用于建筑、汽车和航空等领域。当我触摸到钢制品时，可以感受到它的坚固和稳定，给人一种安全感。

3. 体心立方点阵的铝 铝是一种轻巧而坚固的金属材料，它的空间点阵结构呈现出体心立方的形状。铝具有良好的导热性和导电性，因此广泛应用于电子产品和航空工业。当我看到铝制品时，可以感受到它的轻盈和亮丽，给人一种现代感。

4. 面心立方点阵的铜 铜是一种具有优异导电和导热性能的金属材料，它的空间点阵结构呈现出面心立方的形状。铜被广泛应用于电线、管道和电路板等领域。当我接触到铜制品时，可以感受到它的柔软和温暖，给人一种亲切感。

5. 钻石立方点阵的金 金是一种珍贵的金属材料，它的空间点阵结构呈现出钻石立方的形状。金具有良好的延展性和韧性，因此被广泛应用于珠宝和装饰品制作。当我抚摸金制品时，可以感受到它的光滑和闪耀，给人一种奢华感。

通过以上对常用金属空间点阵的描写，我们可以感受到金属的不同特性和用途。金属作为一种重要的材料，贯穿于人类的生活和工业各个领域，给我们带来便利和美感。让我们珍惜和善用金属这一宝贵资源，为人类的发展做出更大的贡献。

第17页/共53页
晶向指数的确定
1. 建立坐标系，结点为原点，三 棱为方向，点阵常数为单位 ；
2. 在晶向上任两点的坐标 (x1,y1,z1) (x2,y2,z2)。(若 平移晶向或坐标，让在第一点 在原点则下一步更简单)；
3. 计算x2-x1 ： y2-y1 ： z2z1 ；
4. 化成最小、整数比u：v：w ； 5. 放在方括号[uvw]中，不加逗
七个晶系及有关特征
特征对称元素
晶胞特点
4个按立方体对 角线取向的3重
旋转轴
6重对称轴
4重对称轴
a=b=c α=β=γ=90°
a=b≠c α=β=90°,γ=12
0°
a=b≠c α=β=γ=90°
3重对称轴
a=b=c α=β=γ≠90°
2个互相垂直的 对称面或3个互 相垂直的2重对
称轴
a≠b≠c α=β=γ=90°
a/h、b/k、c/l。
即与原点位置无关；每一指数对应一组平行的晶面。
第23页/共53页
立方晶系几组晶面及其晶面指标。
（100）晶面表示晶面与a轴相截与b轴、c轴平行； （110）晶面表示与a和b轴相截，与c轴平行； （111）晶面则与a、b、c轴相截，截距之比为1:1:1
(100) (110) (111) 在点阵中的取向
表示方法：用{hkl}表示。
例如：立方晶系中{100}晶面族包括六个晶面
（100）、（010）、（001）、（-100）、（0-10）、（00-1）
注意，在其他晶系中，通过数字位置互换而得到的晶面不一定属于同 一晶面族，例如，正方晶系中a=bc，因此，{100}晶面族分为两组， 一个包含（100）（010）（-100）（0-10）晶面；另一个包含（001） （00-1）两个晶面。

晶系
三斜Triclinic a≠b≠c ，α≠β≠γ
布拉菲点阵 晶系
简单三斜
六方 Hexagonal
a1=a2＝a3≠c，α=β＝90º， γ=120º
布拉菲点 阵
简单六方
单斜 Monoclinic a≠b≠c， α=γ=90º≠β
正交 a≠b≠c，α=β=γ＝90º
简单单斜 底心单斜
简单正交 底心正交 体心正交 面心正交
3.晶面指数（Indices of Crystallographic Plane）
求法： 1） 在所求晶面外取晶胞的某一顶点为原点o，三棱边为三坐标轴x，y，z 2） 以棱边长a为单位，量出待定晶面在三个坐标轴上的截距； 3） 取截距之倒数，并化为最小整数h，k，l并加以圆括号（h k l）即是。
求法： 1） 确定坐标系 2） 过坐标原点，作直线与待求晶向平行； 3） 在该直线上任取一点，并确定该点的坐标（x，y，z） 4） 将此值化成最小整数u，v，w并加以方括号[u v w]即是。 （代表一组互相平行，方向一致的晶向）
晶向族<u v w>：具有等同性能的晶向归并而成；
（x1,y1,z1）,(x2,y2,z2)二点连线的晶向指数：[x2-x1,y2-y1,z2-z1] *指数看特征，正负看走向
120°
（h k i l ) [u v t w]
i= -( h+k ) t= -( u+v )
三指数系统 → 四指数系统 three－index system four－index system

（h k l） （h k il） i＝-（h＋k）
[U V W]
[u v t w]
U = u - t, V = v - t, W = w