当前位置：文档之家 › 晶体简介及倒易点阵(优.选)

晶体简介及倒易点阵(优.选)

  • 格式：pdf
  • 大小：1.12 MB
  • 文档页数：46

下载文档原格式

  / 46

合集下载

XRD(2-晶体学基础)(1)

XRD(2-晶体学基础)(1)


1．倒易点阵的定义？ 2．倒易点阵的重要性质？
34
<100>等效晶向
16
（三）晶面和晶面间距 1、晶面
➢ 在布拉菲格子中作一簇平行的平面，这些相互平行、 等间距的平面可以将所有的格点包括无遗。
➢ 这些相互平行的平面称为晶体的晶面 ➢ 同一布拉菲格子中可以存在位相不同的的晶面
17
（hkl）：表示一组相互平行的晶面， 称为晶面指数或米勒指数。
（hkl）是平面在三个坐标轴上截距倒数的互质比。 晶格中一组晶面不仅平行，并且等距；
一组晶面必包含了所有格点而无遗漏。
同一个格子，两组不同的晶面
18
例
以晶胞参数a,b,c为三个对应晶轴的度量单位，晶面ABC在 坐标轴上的截距分别为2、3、6； 其倒数为1/2、 1/3 、 1/6，
h:k:l = 1/2 :1/3 : 1/6
=3:2:1
故: 该晶面的晶面指数 （hkl）为(321)。
带轴。
凡属于[uvw]晶带的晶面，其面指数（hkl）必符合关系：
hu+kv+lw=0
晶带定律
跳过下一页PPT 26
二、倒易点阵（倒点阵）
倒点阵可以直观地解释衍射图的成因， 它是虚拟的、抽象的教学工具。
晶体学中的正点阵（空间点阵），通过某种联系，将其 抽象出另外一套结点的集合，得到倒点阵。
➢ 晶体点阵中的一个晶面（hkl），在倒点阵中将用 一个点Phkl表示。该点与其对应的晶面有倒易关系。
E、当晶面指数中某个位置上的指数为0时， 表示该晶面与对应的晶轴平行。 如（100）(001）。
22
2、晶面间距dhkl
晶面间距是指两个相邻的平行晶面间的垂直距离。 通常用dhkl 或简写为d来表示。
§1.5 倒易点阵

§1.5 倒易点阵


′ ′ ′ ′ ′ ′ = 2 π( l1h1 + l 2 h2 + l 3 h3 )
= 2 πµ
3.
(2π)3 Ω* =
Ω* = b 1 ⋅ b 2 × b 3
3
(
Ω
分别为正、倒格原胞体积) (其中Ω和Ω*分别为正、倒格原胞体积 其中
)
) [( ) ( )]
2π = a2 × a3 ⋅ a3 × a1 × a1 × a2 Ω
′ ′ ′ Rl′ = l1 a1 + l2 a 2 + l3 a 3
′ ′ ′ K h′ = h1 b1 + h2 b2 + h3 b3
上页 下页 返回 结束
第一章 晶体结构
′ ′ ′ ′ ′ ′ Rl′ ⋅ K h′ = (l1 a1 + l2 a 2 + l3 a 3 ) ⋅(h1 b1 + h2 b2 + h3 b3 )
2π a
2π a
上页 下页 返回 结束
第一章 晶体结构 例2：证明体心立方的倒格是面心立方。 证明体心立方的倒格是面心立方。 体心立方的原胞基矢： 解： 体心立方的原胞基矢：
a1 a a
2
3
a = − i + j + k 2 a i − j + k = 2 a i + j − k = 2
( ( (
a a 2 +k 2 a a 2 2
−
a 2 a 2
a2 a2 j+ k = 2 2
上页 下页 返回 结束
第一章 晶体结构
a2 a2 a2 × a3 = j + k 2 2
2π b1 = a2 × a3 = Ω
倒易点阵介绍

倒易点阵介绍


n O
光程差 On Am OA S OA S0 OA ( S S0 )

相应的位向差为
2

2
( S S0 )

OA
其中p、q、r是整数 因为S0是入射线方向单位矢量, S是衍射线方向为单 位矢量，因此S- S0是矢量，则：(S S0 ) * *
2
1/
A
O
S0 /
5 、以S0端点O点为原点，作
倒易空间，某倒易点（代表
某倒易矢量与hkl面网）的 端点如果在反射球面上， 说明该g*=S, 满足Bragg’s Law。某倒易点的端点如果
P
S/
S S0 g
2
不在反射球面上， 说明不
满足Bragg’s Law，可以直
1/
A
O
S0 /
25
概念回顾
以A为圆心，1/λ 为半径所做的球称为反 射球，这是因为只有在这个球面上的倒 易点所对应的晶面才能产生衍射。有时 也称此球为干涉球， Ewald球。 围绕O点转动倒易晶格，使每个倒易点 形成的球称为倒易球 以O为圆心，2/λ 为半径的球称为极限球。

26
大倒易球半径为
g=1/d≤ 2/:
hkl
即 d hkl

2
S/的晶面不Fra bibliotek1/
2 C S0/
g
O
Direction of direct beam
可能发生衍射
Sphere of reflection
极限球
Limiting sphere
关于点阵、倒易点阵及Ewald球的思考
(1) 晶体结构是客观存在，点阵是一个数学抽象。 晶体点阵是将晶体内部结构在三维空间周期平移这 一客观事实的抽象，有严格的物理意义。 (2) 倒易点阵是晶体点阵的倒易，不是客观实在， 没有特定的物理意义，纯粹为数学模型和工具。 (3) Ewald球本身无实在物理意义，仅为数学工具。 但由于倒易点阵和反射球的相互关系非常完善地描 述了X射线和电子在晶体中的衍射，故成为研究晶 体衍射有力手段。
倒易点阵

倒易点阵


倒易点阵的应用—解释X射线及电子衍射
• 劳厄方程
当相邻原子的散射X射线光程差等于 入射X射线波长整数倍时发生衍射。
a(cosα-cosα0) = Hλ
一维原子列的衍射示意图
倒易点阵的应用—解释X射线及电子衍射
• 劳厄方程
设空间点阵的三个平移向量为a ,b和c,入射的X射线与它们的交角分别为α0，β0和γ0。 衍射方向与它们的交角分别为α，β和γ 。根据上述讨论可知，衍射角α，β和γ在x, y, z三个轴上应满足以下条件：
单晶体电子衍射花样标定
• 确定零层倒易截面上各ghkl矢量端点(倒易阵点)的指数，定出零层倒易截面的 法向(即晶带轴[uvw])，并确定样品的点阵类型、物相及位向。 (1)测量靠近中心斑点的几个衍射斑点至中心斑点距离R1、R2、R3、R4…及 R1与R2、R1与R3等衍射斑点之间的夹角。 (2) 计算R12∶R22∶R32∶…=N1∶N2∶N3∶… 其中N = h2 + k2 + l2
故
于是，它们的点乘 根据倒易基矢定义式，显然有
和
都为0。
倒易点阵的应用—解释X射线及电子衍射
• „ 劳厄的一个科学假设
1911年埃瓦尔德在索末菲的指导下在慕尼黑大学从事博士论文研究，劳厄在 与他的讨论中了解到晶格的平移周期与X射线的波长属于同一量级，因此想到 在二维光栅的两个衍射方程组中再加一个类似的方程，就可以描述X射线在三 维晶体中的衍射。 在此假设的指导下，Knipping和Friedrich在1912年4月开始用CuSO4 后来 用闪锌矿（立方ZnS）进行实验，很快就得到X射线衍射的证据。这不但证明 了X射线的波动性，还确定了晶体的三维周期性。
a*、b*、c*
即倒易基矢
倒易点阵

倒易点阵

二维问题一维化处理
材料现代研究方法讲义
正点阵和倒易点阵中基本平移矢量之间的关系 r r r 正点阵基本平移矢量： a , b , c
uur uu uu r r 倒易点阵基本平移矢量： a *, b *, c *
rr r rr r rr r 晶胞体积 V = a b × c = b c × a = c a × b r r r r uur b × c r uur r uu r uu r r b×c a*= = r r r a a* = b b* = c c* =1 V a ⋅b × c r r r r r uu r uu r uur r r uu c × a r c×a a b* = b c* = c a* = 0 b* = =r r r
P=
k
−
h
Q=
l
−
k
0 a/h
u r S hkl
ur ur ur ur uu r P×Q P×Q ∝ r*= ＝ r r r 规一化因子 a ⋅b×c hkl
u b/k r P
r r r r uu r hkl b a c b r * = r r r − × − h l k a ⋅b×c k
衍射矢量方程及厄瓦尔德图解
材料现代研究方法讲义
衍射矢量方程
r r s − s 0 ⊥ ( HKL) 衍射矢量
r r u r s − s 0 = 2 S sin θ = 2sin θ r r 1 s − s0 = λ ⋅ d HKL uuur r r * s − s 0 = λ ⋅ rHKL uu r uur uu r uu r r * = H a * + Kb * + Lc *
材料现代研究方法讲义
厄瓦尔德图解：衍射矢量方程与倒易点阵结合， 厄瓦尔德图解：衍射矢量方程与倒易点阵结合，表示 衍射条件与衍射方向
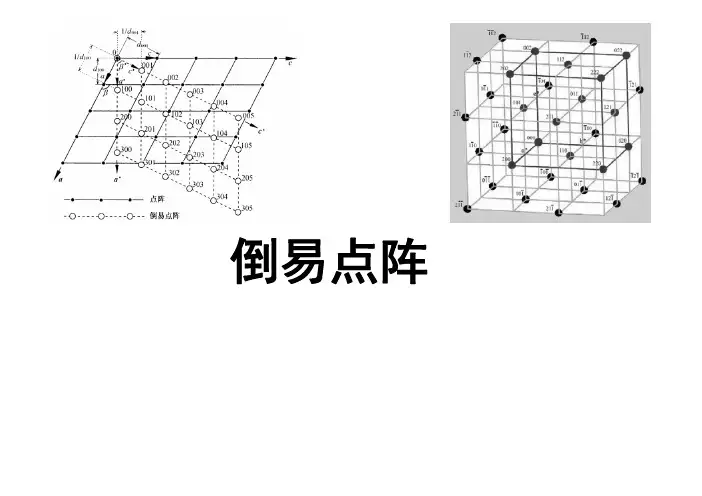
晶体学基础-倒易点阵

晶体学基础-倒易点阵

倒易点阵晶体学中最关心通常是晶体取向，即晶面的法线方向。

倒易点阵是在晶体点阵的基础上按一定对应关系建立起来的空间几何图形（倒易空间），是晶体点阵的另一种表达形式。

将晶体点阵空间称为正空间。

倒易空间中的结点称为倒易点。

部分。

a a * = b把正点阵基矢与倒易点阵基矢的关系代入，得正点阵与倒易点阵的关系•O 点到(hkl)晶面的垂直距离就是晶面间距d hkl 。

倒数关系（大小）●d hkl =h a H H H1=•确定倒易矢量H ，就确定了正点阵晶面。

S hkl P 及Q ⊥•倒易矢量[hkl]的大小（模）就是其正点阵中相邻平行(hkl)晶面间距的倒数。

(倒—Reciprocal)进行矢量相乘并且展开。

a H hkl •在倒易点阵中，从原点指向阵点[坐标hkl ]的倒易矢量H hkl = ha* +kb* +lc*•H hkl 必和正点阵的(hkl )面垂直，•即倒易点阵的阵点方向[hkl ]*和正点阵的(hkl )面垂直：[hkl ]*⊥(hkl )。

CBAx y z(010)(100)(001)a例：由单斜点阵导出其倒易点阵•单斜点阵：b轴垂直于a和c轴。

左图图面为（010）面。

•从作图可以看出，正点阵和其对应的倒易点阵同属一种晶系。

把上面三个式子写成矩阵形式：•同理，可按下式求出与方向指数为[uvw]的方向相垂直的面的面指数(hkl):•例如，对立方系而言，a*●a* = b* ●b* = c*●c *=1/a2;a*●b* = b* ●c* = c*●a *=0;•u:v:w=h:k:l。

所以(hkl)面的法线指数和面指数同名，即为[hkl]。

倒易点阵名词解释

倒易点阵名词解释

倒易点阵名
倒易点阵是由被称为倒易点的点所构成的一种点阵，它也是描述晶体结构的一种几何方法，它和空间点阵具有倒易关系。

倒易点阵中的一倒易点对应着空间点阵中一组晶面间距相等的点格平面。

倒易点阵的概念在晶体结构和固体物理学中都有十分重要的作用。

到目前为止，大多数教程都是在密勒指数或晶面指数无关的情况下来定义倒易点阵概念的。

由于晶面指数的概念出现得很早，有一些老的晶体学和固体物理学教程中甚至没有提到倒易点阵这个概念。

在目前流行的固体物理学教科书中，对倒易点阵均有叙述，而且处处应用。

但是，倒易点阵概念的引入比较生硬，对倒易点阵与晶面指数的关系交待得不够清楚。

倒易点阵——精选推荐

倒易点阵——精选推荐

倒易点阵倒易点阵:晶体点阵结构与其电⼦衍射斑点之间可以通过另外⼀个假想的点阵很好地联系起来，这就是~零层倒易截⾯：电⼦束沿晶带轴的反向⼊射时，通过原点的倒易平⾯只有⼀个，我们把这个⼆维平⾯叫做~消光距离：透射束或衍射束在动⼒学相互作⽤的结果，在晶体深度⽅向上发⽣周期性的振荡，这种振荡的深度周期叫做~明场像：通过衍射成像原理成像时，让透射束通过物镜光阑⽽把衍射束挡掉形成的图像称为明场像。

暗场像：通过衍射成像原理成像时，让衍射束通过物镜光阑⽽把透射束挡掉形成的图像称为暗场像。

衍射衬度：由于样品中不同位向的晶体的衍射条件不同⽽造成的衬度差别叫~质厚衬度：是建⽴在⾮晶体样品中原⼦对⼊射电⼦的散射和透射电⼦显微镜⼩孔径⾓成像基础上的成像原理，是解释⾮晶态样品电⼦显微图像衬度的理论依据。

⼆次电⼦：在⼊射电⼦束作⽤下被轰击出来并离开样品表⾯的样品的核外电⼦叫~吸收电⼦：⼊射电⼦进⼊样品后，经多次⾮弹性散射能量损失殆尽，然后被样品吸收的电⼦。

透射电⼦：如果被分析的样品很薄，那么就会有⼀部分⼊射电⼦穿过薄样品⽽成为透射电⼦。

结构消光：当Fhkl=0时，即使满⾜布拉格定律，也没有衍射束产⽣，因为每个晶胞内原⼦散射波的合成振幅为零。

这叫做~分辨率：是指成像物体（试样）上能分辨出来的两个物点间的最⼩距离。

焦点：⼀束平⾏于主轴的⼊射电⼦束通过电磁透镜时将被聚焦在轴线上⼀点。

焦长：透镜像平⾯允许的轴向偏差.景深：透镜物平⾯允许的轴向偏差.磁转⾓：电⼦束在镜筒中是按螺旋线轨迹前进的，衍射斑点到物镜的⽽⼀次像之间有⼀段距离，电⼦通过这段距离时会转过⼀定的⾓度.电磁透镜：透射电⼦显微镜中⽤磁场来使电⼦波聚焦成像的装置。

透射电⼦显微镜：是以波长极短的电⼦束作为照明源，⽤电磁透镜聚焦成像的⼀种⾼分辨率，⾼放⼤倍数的电⼦光学仪器。

弹性散射：当⼀个电⼦穿透⾮晶体薄样品时，将与样品发⽣相互作⽤，或与原⼦核相互作⽤，或与核外电⼦相互作⽤，由于电⼦的质量⽐原⼦核⼩得多，所以原⼦核⼊射电⼦的散射作⽤，⼀般只引来电⼦改变运动⽅向，⽽能量没有变化，这种散射叫做弹性散射。

倒易点阵 晶体结构

倒易点阵 晶体结构

倒易点阵晶体结构倒易点阵晶体结构倒易点阵晶体结构是一种特殊的晶体结构，它具有许多独特的性质和应用。

本文将介绍倒易点阵晶体结构的基本概念、性质和应用。

一、基本概念倒易点阵是指在晶体中原子或分子排列的方式。

晶体是由周期性排列的原子或分子组成的固体，而倒易点阵则是晶体中原子或分子排列的镜像。

倒易点阵具有高度的对称性和周期性，其结构可以用倒易点群来描述。

二、性质1. 高度的对称性：倒易点阵具有高度的对称性，这是由于晶体中原子或分子的周期性排列所决定的。

倒易点阵的对称性可以通过倒易点群来描述，倒易点群是一组对称操作，包括旋转、镜像和反演等操作。

2. 布拉格定律：倒易点阵的周期性排列使得它们能够散射入射的电磁波。

布拉格定律描述了散射波与倒易点阵的相互作用。

根据布拉格定律，散射波的波矢量与倒易点阵的倒格矢量之间满足关系式：2π/λ = |G|，其中λ是散射波的波长，G是倒格矢量的模长。

3. 能带结构：倒易点阵的周期性排列使得它们具有能带结构。

能带结构是描述固体中电子能量与动量关系的理论。

倒易点阵的能带结构对于材料的电子输运和光学性质具有重要影响。

三、应用倒易点阵晶体结构在许多领域都有重要的应用，以下列举几个典型的应用：1. 光学器件：倒易点阵晶体结构具有特殊的光学性质，可用于制造光学器件。

例如，倒易点阵光纤具有高度的光学导引性能，可用于制造光纤通信设备。

2. 光子晶体：倒易点阵晶体结构可以形成光子禁带，即在某一频率范围内禁止光的传播。

光子晶体具有重要的光学性质，可用于制造光学滤波器、光学调制器等光学器件。

3. 电子器件：倒易点阵晶体结构对于电子输运具有重要的影响，可用于制造电子器件。

例如，倒易点阵晶体管具有优良的电子输运性能，可用于制造高频放大器和微波器件。

4. 气体吸附：倒易点阵晶体结构具有大的表面积和孔隙度，可用于吸附气体。

倒易点阵材料可以用作气体传感器、催化剂和分离膜等。

四、总结倒易点阵晶体结构是一种特殊的晶体结构，具有高度的对称性和周期性。

倒易点阵

倒易点阵

倒易点阵:晶体点阵结构与其电子衍射斑点之间可以通过另外一个假想的点阵很好地联系起来，这就是~零层倒易截面：电子束沿晶带轴的反向入射时，通过原点的倒易平面只有一个，我们把这个二维平面叫做~消光距离：透射束或衍射束在动力学相互作用的结果，在晶体深度方向上发生周期性的振荡，这种振荡的深度周期叫做~明场像：通过衍射成像原理成像时，让透射束通过物镜光阑而把衍射束挡掉形成的图像称为明场像。

暗场像：通过衍射成像原理成像时，让衍射束通过物镜光阑而把透射束挡掉形成的图像称为暗场像。

衍射衬度：由于样品中不同位向的晶体的衍射条件不同而造成的衬度差别叫~质厚衬度：是建立在非晶体样品中原子对入射电子的散射和透射电子显微镜小孔径角成像基础上的成像原理，是解释非晶态样品电子显微图像衬度的理论依据。

二次电子：在入射电子束作用下被轰击出来并离开样品表面的样品的核外电子叫~吸收电子：入射电子进入样品后，经多次非弹性散射能量损失殆尽，然后被样品吸收的电子。

透射电子：如果被分析的样品很薄，那么就会有一部分入射电子穿过薄样品而成为透射电子。

结构消光：当Fhkl=0时，即使满足布拉格定律，也没有衍射束产生，因为每个晶胞内原子散射波的合成振幅为零。

这叫做~分辨率：是指成像物体（试样）上能分辨出来的两个物点间的最小距离。

焦点：一束平行于主轴的入射电子束通过电磁透镜时将被聚焦在轴线上一点。

焦长：透镜像平面允许的轴向偏差.景深：透镜物平面允许的轴向偏差.磁转角：电子束在镜筒中是按螺旋线轨迹前进的，衍射斑点到物镜的而一次像之间有一段距离，电子通过这段距离时会转过一定的角度.电磁透镜：透射电子显微镜中用磁场来使电子波聚焦成像的装置。

透射电子显微镜：是以波长极短的电子束作为照明源，用电磁透镜聚焦成像的一种高分辨率，高放大倍数的电子光学仪器。

弹性散射：当一个电子穿透非晶体薄样品时，将与样品发生相互作用，或与原子核相互作用，或与核外电子相互作用，由于电子的质量比原子核小得多，所以原子核入射电子的散射作用，一般只引来电子改变运动方向，而能量没有变化，这种散射叫做弹性散射。

1-4倒易点阵

1-4倒易点阵

• 用倒易点阵处理衍射问题时，能使几何概念更清楚， 数学推理简化。能够简朴地想象，每一幅单晶旳衍射 把戏就是倒易点阵在该把戏平面上旳投影。
四、倒易点阵
2 怎样拟定倒易点阵
2.1 什么是倒易基矢 我们将正点阵中晶胞中旳a、b、c、、、六个点阵
常数用三个基矢 a、b、c 来替代，那么 a、b、c 就能
四、倒易点阵
4 实际晶体中旳倒易点阵
倒易点阵中出现节点旳条件： 正点阵中相互平行旳（hkl）面旳全体包括（经过）全部旳正点阵节 点。 例如：BCC和FCC旳（002）平行晶面族包括了全部原子
（001）平行晶面族只包括了二分之一原子 所以：在BCC和FCC旳倒易点阵中只出现（0，0，2）节点，而不 出现（0，0，1）节点。
四、倒易点阵
1 什么是倒易点阵
• 为了从几何学上形象旳拟定衍射条件， 人们就找到一个新旳点阵（倒易点阵），使 其与正点阵（实际点阵）相相应。
•
相应旳条件：新点阵中旳每一个结点都 相应着正点阵旳一定晶面，该结点既反O映P 该
晶面旳取向也反映该晶面旳面间距。
•
具体条件：OP 1/d(hkl)
• a. 新点阵中原点O到任意结点P(hkl) （倒易 点）旳矢量 正好沿正点阵中{hkl}面旳法 线方向。
（100）
四、倒易点阵
2.2 怎样拟定倒易基矢 2经过怎正样点拟阵定，倒能易够点得阵到：
d(100) =a
b b
c c
（2）
将（2）式代入（1）式得到：
a*= bc bc abc V
一样：b*
=
c
a V
c*
ab V
V 为正点阵晶胞旳体积。
（100）
四、倒易点阵
2 怎样拟定倒易点阵

倒易点阵介绍综述


(2) 波长连续， 使Ewald球的数 量增加，即球壁 增厚（Laue法）
S / 1/
A
S 0 /
O
Δλ
增大晶体产生衍射几率的方法
（ 3 ） Ewald 球 不 动 ， 增 加随机分 布的晶体 数量 ， 相当于围绕O点转动倒易
S / 1/ hkl
晶格，使每个倒易点均
形成一个 球 （倒易 球 ）。 （粉晶法的基础）

OA pa qb rc
ha k b l c*
现在不明确h、k、l一定是整数。由：
2
( S S0 )
可见，只有当φ =2π n时，才能发生衍射，此时n应 为整数。 由于p、q、r是整数，因此满足衍射条件时h、k、l 一定是整数。于是得到结论：

OA 2 (ha* k b* l c* ) ( pa qb r c) 2 (hp kq lr )
5
倒易点阵的性质
1. 正倒点阵异名基矢点乘为0; a*·b= a*·c=b*·a=b*·c=c*·b=0 同名基矢点乘为1。 a*·a=b*·b=c*·c=1. 2. 在倒易点阵中，由原点O*指向任意坐标为hkl的阵点的矢量 ghkl(倒易矢量)为：ghkl=h a*+k b*+lc* 式中hkl为正点阵中 的晶面指数 3. 倒易矢量的长度等于正点阵中相应晶面间距的倒数，即 ghkl=1/dhkl 4. 对正交点阵，有 a*∥a，b*∥b，c*∥c， a*=1/a，b*=1/b，c*=1/c， 5. 只有在立方点阵中，晶面法线和同指数的晶向是重合（平行） 的。即倒易矢量ghkl是与相应指数的晶向[hkl] 平行的。
O
观地看出那些面网的衍射状
况。

倒易点阵介绍


❖ 晶带定理：因为各倒易矢量都和
其晶带轴r=[uvw]垂直，固有
ghkl•r=0 ，即 hu+kv+lw=0, 这就
7
是晶带定理。
衍射条件
设:入射线波长为λ,入
射线方向为单位矢量S0,
衍射线方向为单位矢量S,
那么在S方向有衍射线的
条件是:在与S方向相垂
1
直的波阵面上,晶体中各
原子散射线的位向相同。
5. 只有在立方点阵中，晶面法线和同指数的晶向是重合（平行） 的。即倒易矢量ghkl是与相应指数的晶向[hkl] 平行的。
5
ghkl=h a*+k b*+lc* 表明：
❖ 1平.倒行易于矢它量的法gh向kl垂N直hkl于正点阵中相应的 [hkl]晶面，或 ❖ 2.倒易点阵中的一个点代表的是正点阵中的一组晶面
a*=b×c/V, b*=c×a /V, c*=a×b/V. 式中，V为正 点阵中单胞的体积： V=a·(b×c) =b·(c×a) =c·(a×b)
表明某一倒易基矢垂直于 正点阵中和自己异名的二基矢 所成平面
4
倒易点阵的性质
1. 正倒点阵异名基矢点乘为0; a*·b= a*·c=b*·a=b*·c=c*·b=0
先计算原点O和任一原子 A的散射线在与S方向的 位向差。
ghkl
m
θ
A
θ
θ
n O
光程差 On Am OA S OA S0
OA (S S0 )
S2 (S-S0) (HKL)
S0
❖ 相应的位向差为 2 2 (S S0 ) OA
OA pa qb rc 其中p、q、r是整数
由于p、q、r是整数，因此满足衍射条件时h、k、l 一定是整数。于是得到结论：

倒易点阵

倒易点阵晶体点阵：－－实空间(用S表示) 由晶体的周期性直接抽象出的点阵(正点 阵)； 倒易点阵：－－倒易空间(用S*表示) 根据空间点阵虚构的一种点阵。

倒易点阵 (reciprocal lattice)倒易空间 倒易晶格c* c b b* a* auu r uur uur uu r r * = ha * + k b * + lc *uur uu uu r r 以 a *, b *, c * 为新的三个基矢，引入另一个点阵，显然该点阵中的点阵的方向uu r uur uu uu r r r * = ha * + kb * + lc *就是晶面 (hkl)的法线方向，该矢量指向的点阵点指数即为hkl。

倒易点阵的一个结点对应空间 点阵的一个晶面。

二维问题一维化处理倒易矢量的性质倒易点阵矢量垂直于正空间点阵平面。

正空间点阵平面间距等于倒易点阵矢量的 倒数。

dhkl=1/r*倒易矢量：由倒易点阵的原点O至任一倒易点 hkl的矢量为r* 。

r* = ha* + kb* + lc*倒易矢量的两个重要性质(1) r*的方向与实际点阵面（hkl）相垂直，或r* 的方向是实际点阵面（hkl）的法线方向。

(2) r*的大小等于实际点阵面（hkl）面间距的倒数， 即:rhkl1 = d hkl倒易基矢的方向:要求倒易基矢垂直于晶面001a* ⊥ (100) b* ⊥ (010) c* ⊥ (001)c*c*c b b*a* a 100010Z立方晶格的倒易变换 （简单点阵）0.25 Å-1 1Å b (220) (010) (110) b* 010 H110C*Y 220 X020120 H220 110 H210 100 a*(100)210c(210) a200000正晶格倒易晶格Z立方晶格的倒易变换 （面心点阵）0.25 Å-1 1Å b (220) (010) (110) b* 020 H220 220 X Y(100)c(210) aC*200 000 a*正晶格倒易晶格。

倒易点阵


正点阵基矢间夹角和倒点阵 基矢间夹角间的关系
• 根据基矢之间的夹角的定义，有 • 把正点阵基矢与倒易点阵基矢的关系代入，得
• 最后得 • 同理得 • 按同样的方法，可用倒易点阵的α*、β*、γ*来表示正点阵的 α、β、γ。
正点阵与倒易点阵的关系
a
Hhkl
垂直关系（方向）
在倒易点阵中，从原点指向阵点[坐标hkl]的 倒易矢量 Hhkl = ha* +kb* +lc* Hhkl必和正点阵的(hkl)面垂直， 即倒易点阵的阵点方向[hkl]*和正点阵的(hkl) 面垂直：[hkl]*⊥(hkl)。
晶体学基础
倒易点阵
Outline
• 倒易点阵的定义
• 倒易点阵的基本性质
• 由正点阵导出倒易点阵 • 倒易矢量在晶体学中几何关系的应用
倒易点阵引入（1）
• 1913-1921年Ewald根据Gibbs倒易空间概念提出了倒易点阵。 • 晶体学中最关心通常是晶体取向，即晶面的法线方向。 • 用3个基失a, b, c表示某晶面的法向矢量Shkl。
• 底心点阵的倒易点阵仍为底心点阵，如果是C面有 心化，倒易点阵单胞的棱长已不是a*, b*, c*，而是 2a*, 2b*, c* 。单胞体积变为正点阵单胞的4倍。
SUMMARY
• 倒易点阵的定义
• 倒易点阵的基本性质（垂直及倒数关系） • 如何由正点阵导出倒易点阵 • 求点阵平面的法线方向指数
倒易点阵定义
点阵参数分别为a, b, c和a*,b*,c* 的两个点阵的基矢存在如下关系：
则，这两个点阵互为倒易。 正点阵晶胞体积为V，则 V = a●b×c 因a ● a*=1，则 a* =(b×c)/V 同理 b* =(c×a)/V; c* =(a×b)/V 同理 a =(b* ×c*)/V*; b =(c* ×a *)/V*; c =(a* ×b)/V* 正点阵晶胞体积与倒易点阵晶胞体积之间也存在倒易关系，即 V● V*≡1

晶体简介及倒易点阵


a×b c = V
(仅当正交晶系)
1 1 1 a = ,b = ,c = a b c
倒易点阵的基本性质
根据定义在倒易点阵中,从 倒易原点到任一倒易点P的 矢量称倒易矢量ghkl g*
hkl
= ha + kb + lc
可以证明:
1. g*矢量的长度等于其
对应晶面间距的倒数 g* hkl = n/dhkl
小结:晶系与点阵常数的关系
晶系 立方晶系 三方晶系 四方晶系 六方晶系 正交晶系 单斜晶系 三斜晶系 边长 a=b=c a=b=c a = b≠c a = b≠c a≠b≠c a≠b≠c a≠b≠c 夹角 α=β=γ= 900 α=β=γ≠900 α=β=γ= 900 α=β= 900, γ= 1200 α=β=γ= 900 α=β= 900, γ≠ 900 α≠β≠γ≠ 900 晶体实例 NaCl Al2O3 SnO2 AgI HgCl2 KClO3 CuSO45H2O
000,1/2 1/2 1/2
◆面心点阵 F
除8个顶点外,每 个面心上有一个 阵点,每个阵胞 上有阵点: 4个 其坐标分别为: 000, 1/2 1/2 0, 1/2 0 1/2, 0 1/2 1/2
空间点阵和晶体结构的关系
空间点阵+结构基元=晶体结构
虽然空间点阵只有14种,但晶体结构的 种类是无限的.
倒易点阵(Reciprocal Lattice )
倒易点阵的定义
定义:将晶体学中的空间点阵(正点阵),通 过某种联系,抽象出另一套结点的组合,称倒 易点阵. 在晶体点阵中的一组晶面(hkl),在倒易空 间中将用一个点Phkl表示,该点与晶面有倒易 关系.
如何确定倒易点阵的阵点

晶体简介及倒易点阵

倒易点阵矢量垂直于正空间点阵平面. 正空间点阵平面间距等于倒易点阵矢量的 倒数. dhkl=1/r* 同样倒易点阵平面间距也等于正空间点阵 矢量的倒数
�
例:立方晶系中的一些重要晶向
[100]: 轴向 [110]: 面对角线 [111]: 体对角线 [112]: 顶点到面心方向 在立方晶系中,如果一 个晶面指数与一个晶 向指数数值相等,符 号相同,则该晶面与 晶向互相垂直[100].
4,平面间距 d(hkl)
平面间距是指平面点阵族(hkl)中两个相邻的平行晶面间 的垂直距离.通常用d(hkl)或简写为d来表示. 点阵中所有的晶面都有自己的面间距,一般的规律是:在 空间点阵中,晶面的晶面指数越小,其晶面间距越大,晶 面的结点密度越大,它的X射线衍射强度越大,它的重要 性越大.晶面间距在X射线分析中是十分重要的.
只含一个阵点的晶胞---简单晶胞(单位晶胞, unit cell) 含有一个以上的晶胞---复杂晶胞
晶轴的选择原则
晶轴的选择不是任意的,应遵守下列原则: 1)应符合晶体所固有的对称性.因此,晶 轴与对称轴或对称面的法线重合,若无对 称轴和对称面,则晶轴可平行晶棱选取. 2)在上述前提下,应尽可能使晶轴垂直或 近于垂直,并使轴长趋于近于相等,即尽 可能趋于α=β=γ=90°,a=b=c.
小结:晶系与点阵常数的关系
晶系 立方晶系 三方晶系 四方晶系 六方晶系 正交晶系 单斜晶系 三斜晶系 边长 a=b=c a=b=c a = b≠c a = b≠c a≠b≠c a≠b≠c a≠b≠c 夹角 α=β=γ= 900 α=β=γ≠900 α=β=γ= 900 α=β= 900, γ= 1200 α=β=γ= 900 α=β= 900, γ≠ 900 α≠β≠γ≠ 900 晶体实例 NaCl Al2O3 SnO2 AgI HgCl2 KClO3 CuSO45H2O
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、图中虚线代表平面点阵(hkl)的法线，在虚线 上等间距排列的点为倒易点阵点nh nk nl； 2、相邻两倒易点阵点间的距离为1/dhkl；
3、晶体中有无数组平面点阵，对每一平面点阵 族都可按上图那样得到一个直线点阵；
4、由于晶体的点阵性质，所有这些直线点阵中 的点形成三维点阵，称为点阵S 的倒易点阵S*。
1.G(hkl)垂直于正点阵中的（hkl）晶面; 2.其长度G(hkl)等于（hkl）晶面之晶面间距d(hkl)
的倒数。
倒易点与正点阵中的（hkl）晶面的
对应关系
• G(hkl)的基本性质确切表达了其与(hkl)的一 一对应关系，即一个G(hkl) 与一组(hkl)对
应；
• G(hkl) 的方向与大小表达了(hkl)在正点阵
• 1. g*矢量的长度等于其
对应晶面间距的倒数
• g* hkl = n/dhkl • 2.其方向与晶面相垂
直 • g* //N(晶面法线)
倒易点阵的基本性质
3 正点阵和倒易点阵的同名基矢的点积 为1，不同名基矢的点积为零，即：
(1) 正点阵晶胞（或原胞）体积V与倒易 点阵晶胞（或原胞）体积V*成倒数关
只含一个阵点的晶胞---简单晶胞（单位晶胞， unit cell） 含有一个以上的晶胞---复杂晶胞
晶轴的选择原则
晶轴的选择不是任意的，应遵守下列原则： 91)应符合晶体所固有的对称性。因此，晶
轴与对称轴或对称面的法线重合，若无对 称轴和对称面，则晶轴可平行晶棱选取。 92)在上述前提下，应尽可能使晶轴垂直或 近于垂直，并使轴长趋于近于相等，即尽 可能趋于α=β=γ=90°，a=b=c。
夹角
α=β=γ= 900 α=β=γ≠900 α=β=γ= 900 α=β= 900, γ= 1200 α=≠γ≠ 900
晶体实例
NaCl
Al2O3 SnO2 AgI HgCl2 KClO3 CuSO4·5H2O
小结：晶系与点阵常数的关系
二、晶面指数和晶向指数
(2) 反之，一个阵点指数为hkl的倒易点对 应正点阵中一组(hkl)，(hkl)方位与晶面
间距由该倒易点相应的H(hkl) 决定。
总结：倒易点阵的性质
• 倒易点阵矢量垂直于正空间点阵平面。 • 正空间点阵平面间距等于倒易点阵矢量的
倒数。 • dhkl=1/r* • 同样倒易点阵平面间距也等于正空间点阵
例：立方晶系中的一些重要晶向
[100]: 轴向 [110]: 面对角线 [111]: 体对角线 [112]: 顶点到面心方向 在立方晶系中，如果一
个晶面指数与一个晶 向指数数值相等，符 号相同，则该晶面与 晶向互相垂直[100]。
4、平面间距 d(hkl)
• 平面间距是指平面点阵族(hkl)中两个相邻的平行晶面间 的垂直距离。通常用d(hkl)或简写为d来表示。
对于立方体
(100) 面等效的晶面数分别为：3个 表示为 {100} (110) 面等效的晶面数分别为：6个 表示为 {110} (111) 面等效的晶面数分别为：4个 表示为 {111}
—— 符号相反的晶面指数只是在区别晶体的外表面时才 有意义, 在晶体内部这些面都是等效的。
(3) 立方体的几个主要晶面及晶面指数
• 显然，h, k, l为互质整数
(2) 晶面指数的确定方法---举例
• 如果在坐标轴上的截距分别为1、2、3，其 倒数为1、1/2、1/3，将三个倒数化为简单 整数为：6、3、2，所以，该晶面的晶面指 数为(632)。
几点注意:
A、当晶面交于晶轴的负端时，对应的指数就 是负的，并将负号标在数字的上面。
• 点阵中所有的晶面都有自己的面间距，一般的规律是:在 空间点阵中，晶面的晶面指数越小，其晶面间距越大，晶 面的结点密度越大，它的X射线衍射强度越大，它的重要 性越大。晶面间距在X射线分析中是十分重要的。
晶面指数与晶面间距和晶面上结点密度的关系（二维）
平面间距d(hkl)的计算
• 不同晶系的平面间距可用不同的公式计算：
—— 这些相互平行的平 面称为晶体的晶面
二、晶面指数和晶向指数
同一个格子，两组不同的晶面族
1、晶面指数的确定方法
(1)、晶体的定向 • 在晶体学中，将坐标系引入晶体图形中的
手续称为晶体的定向。 • 通常根据矢量a, b, c选择晶体的坐标轴x,
y ,z，所选取的三个坐标轴称为晶轴，三 个晶轴上的单位向量a, b, c 称为轴单位。
矢量的倒数
立方晶系
正方晶系
六方晶系
可见，平面间距既与晶胞参数有关，又与晶面指数有关
晶面夹角的计算
• 若已知某晶体上两个晶面(h1k1l1)和(h2k2l2)，可 以求二者之间的夹角ψ(晶面法线的夹角 )。 立方晶系的公式 ：
倒易点阵（Reciprocal Lattice ）
倒易点阵的定义
定义：将晶体学中的空间点阵（正点阵），通 过某种联系，抽象出另一套结点的组合，称倒 易点阵。 在晶体点阵中的一组晶面（hkl），在倒易空 间中将用一个点Phkl表示，该点与晶面有倒易 关系。
• 结点(阵点）的空间位置表示： 用它在三个晶轴上的截距并用a，b，c 来度量。 如000；111； 1/2 1/2 1/2 等。
晶系与布拉菲点阵
◆简单（原始）点阵 P
• 单胞中结点的数目：1 • 简单点阵的阵点坐标为:
000
◆底心点阵 C
除八个顶点上有阵点 外，两个相对的面心上 有阵点，面心上的阵点 为两个相邻的平行六面 体所共有。
空间点阵和晶体结构的关系
空间点阵+结构基元=晶体结构
虽然空间点阵只有14种，但晶体结构的 种类是无限的。
小结：晶系与点阵常数的关系
晶系 立方晶系 三方晶系 四方晶系 六方晶系 正交晶系 单斜晶系 三斜晶系
边长 a=b=c a=b=c a = b≠c a = b≠c a≠b≠c a≠b≠c a≠b≠c
晶系与布拉菲点阵
• 从以上原则来选取晶胞，只需7种晶胞就可 包括所有的晶体，从而所有晶体都分成7种 晶系：
立方晶系(等轴晶系) 正方晶系(四方晶系) 六方晶系 菱方晶系（三方晶系） 斜方晶系 单斜晶系 三斜晶系
晶系与布拉菲点阵
• 布拉菲点阵 如果在空间点阵的单位阵胞中只有一个阵点，或 者包含有两个或两个以上的阵点，而每个阵点的 环境和阵胞中其它阵点的环境都完全相同，则这 种点阵称为布拉菲点阵。
a∗ = b × c V
b∗ = c× a V
c∗ = a×b V
•(仅当正交晶系）
a∗ = 1 ，b∗ = 1 ，c∗ = 1
a
b
c
倒易点阵的基本性质
• 根据定义在倒易点阵中,从 倒易原点到任一倒易点P的
矢量称倒易矢量ghkl
• g* hkl = ha ∗ + kb∗ + lc ∗
• 可以证明:
B、晶面指数中第一、二、三位分别代表与X、 Y、Z轴的关系，它们之间不能随意变换。
C、一个晶面指数实际上是代表某个方向上的 一组面，而不是一个面。
几点注意：
D、对于高对称性的晶体来说，结晶学上等价 的面具有相同的指数，这些结晶学上的等 价面就构成一个晶面族 {hkl}。
E、当晶面指数中某个位置上的指数为0时， 表示该晶面与对应的晶轴平行。如（100） (001）。
中的方位与晶面间距；反之，(hkl)决定了
G(hkl) 的方向与大小; • G(hkl) 的基本性质也建立了作为H(hkl) 终点
的倒易(阵)点与(hkl)的一一对应关系：
倒易点与正点阵中的（hkl）晶面的
对应关系
(1) 正点阵中每一组(hkl)对应着一个倒易 点，该倒易点在倒易点阵中的坐标(可称阵 点指数)即为hkl ；
系。 (2) 正点阵的基矢与倒易点阵的基矢互
为倒易。
倒易矢量、倒易点
• 在倒易点阵中建立坐标系，一般取倒易坐标原点 与正点阵的坐标原点重合。
• 由倒易坐标原点向任意倒易阵点（倒易点）的连
接矢量称为倒易矢量，记为G(hkl)。 • G(hkl)的终点坐标为（h, k, l) • G(hkl) =ha*+kb*+lc* • G(hkl)的基本性质为：
2、晶向指数
• 晶向指数表示某一晶向（线）的方向，一 个晶向的指数就是其方向余弦数。
立方体系中的几个 晶向指数
3、晶向指数的确定方法
• 在一族互相平行的结点直线中引出过坐标原点的 结点直线；
• 在该直线上选距原点最近的结点，量出它的结点 坐标（用a, b, c度量） ；
• 将三个坐标值化为简单整数u, v, w，用方括号括 起，即为该晶向族结点直线的晶向指数。当泛指 某晶向指数时，用[uvw]表示。
正倒易点阵的几何对应关系
晶面与倒易结点（矢量）的关系
定义倒易点阵（见书）
• 定义：倒易点阵的基本矢量垂直于正点阵异 名矢量构成的平面
c∗ ⋅c = a∗ ⋅ a = b∗ ⋅b = 1
a∗ ⋅b = a∗ ⋅c = b∗ ⋅ a = b∗ ⋅c = c∗ ⋅ a = c∗ ⋅b = 0
倒易点阵基矢与正点阵基矢的关系
¾ 它们是法国晶体学家布拉菲总结出来的，故亦称 为布拉菲点阵。
¾ 根据点阵参数的特点和结点的分布，所有晶体空 间点阵的种类有14种。
14种可能的Bravais点阵
晶系与布拉菲点阵
• 根据结点在单胞中的分布，单位点阵有 简单（原始）点阵（P）： 结点均在角顶上 底心点阵（C）： 除角顶外每一对面上各有一个 结点 体心点阵（I）： 除角顶外中央有一个结点 面心点阵（F）： 除角顶外每个面上均还有一个 结点
晶体学知识、倒易点阵
2007.9.18 胡小平
点阵划分为晶格可 以有不同的方法
晶胞的选择方式（原则）