下载文档原格式
对同一量，进行多次计量，然后算出平均值。
对于偏离平均值的正负差值，就是其不确定度。
其差值越大，则计量的不确定度就越大。
在数理统计学上，一般用方差（S）来表示：S^2＝｛(x1－X)^2+(x2-X)^2+(x3-X)^2……＋(xn-X)^2｝/(n-1)。
注：X为平均值，n为测量的次数。
方差越大，其不确定度则越大；方差越小，其不确定度就越小。
交谈中请勿轻信汇款、中奖信息、陌生电话，勿使用外挂软件。
侯 8:07:05评定与表示测量不确定度的步骤可归纳为1） 分析测量不确定度的来源，列出对测量结果影响显著的不确定度分量。
2）评定标注不确定度分量，并给出其数值 ui 和自由度vi 。
3）分析所有不确定度分量的相关性，确定各相关系数ρij 。
4）求测量结果的合成标准不确定度，则将合成标准不确定度uc 及自由度v . 5）若需要给出展伸不确定度，则将合成标准不确定度uc 乘以包含因子k ，得展伸不确定度 U=kuc 。
6）给出不确定度的最后报告，以规定的方式报告被测量的估计值y 及合成标准不确定度uc或展伸不确定度U ，并说明获得它们的细节。
根据以上测量不确定度计算步骤，下面通过实例说明不确定度评定方法的应用。
按照中华人民共和国国家计量技术规范《测量不确定度评定与表示》JJF1059—1999，不确定度的评定方法可归纳为A 、B 两类。
1.1 标准不确定度的A 类评定在重复性或复现性条件下对被测量X 进行了n 次测量，测得n 个结果i x （i = 1，2，… n ），被测量x 真值的最佳估计值是取n 次独立测量值的算术平均值：∑==ni ix n x 11（1-2-1）由于测量误差的存在，每一个独立测量值i x 不一定相同，它与平均值之间存在着残差x x i i -=)(υ表征测量值分散性的量——实验标准偏差为：1)()(21--=∑=n x xx s ni ii（1-2-2）标准差的上述计算与i x 的分布无关。
测量不确定度公式在测量不确定度的计算中，常用的方法是使用标准差或标准偏差的概念。
标准差是指在一组数据中，各个数据与平均值的离差平方和的平均值再开根号，即标准差等于方差的算术平方根。
标准偏差则是标准差的一个良好的估计，使用样本标准差来估计总体标准差。
标准差的计算公式如下：\[ \sigma = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N}(x_i-\bar{x})^2} \]其中，N表示测量数据的数量，\(x_i\)表示第i个测量数据，\(\bar{x}\)表示所有测量数据的平均值。
比如，假设一个物理实验中需要测量一个力的大小，实验者使用了一台力量计来测量。
然而，由于力量计的不准确性，每次测量结果都会有一定的偏差。
为了计算测量不确定度，实验者进行了多次测量，得到了以下结果：\[x_1=5.2N,\:x_2=4.9N,\:x_3=5.1N,\:x_4=4.8N,\:x_5=5.0N\]首先，计算这些测量结果的平均值：\[ \bar{x} = \frac{1}{N} \sum_{i=1}^{N} x_i = \frac{5.2 + 4.9 + 5.1 + 4.8 + 5.0}{5} = 5.0N \]然后，计算每个测量结果与平均值的离差平方和的平均值：\[ \sigma = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N}(x_i-\bar{x})^2} = \sqrt{\frac{(5.2-5.0)^2 + (4.9-5.0)^2 + (5.1-5.0)^2 + (4.8-5.0)^2 + (5.0-5.0)^2}{4}} = 0.141N \]因此，测量不确定度为0.141N。
为了更直观地表示测量结果的可靠性，通常会使用置信区间来表示测量不确定度。
置信区间是指在统计学意义下，在一定置信水平下，测量结果的变动范围。
其中，常用的置信水平有95%和99%。
对于95%的置信水平，通常使用两倍的标准差来表示置信区间。
动量守恒定律实验不确定度计算公式好的，以下是为您生成的文章：咱们在物理的世界里遨游，经常会碰到各种各样神奇的定律和实验，其中动量守恒定律那可是相当重要的一块基石。
而今天咱们要聊的，就是跟动量守恒定律实验紧密相关的不确定度计算公式。
先来说说啥是不确定度。
简单点说，就是咱们在做实验的时候，得到的结果不是百分百准确的，总有那么一些小误差，不确定度就是用来衡量这些误差大小的。
那在动量守恒定律实验里，不确定度计算公式到底是咋来的呢？咱们一步一步来。
比如说，在实验中测量物体的速度、质量这些物理量，可这些测量值都不可能是绝对精确的。
我记得有一次在课堂上给学生们做这个实验，那场面真是热闹非凡。
我们用了一个简单的气垫导轨装置，让两个滑块在上面碰撞。
当时有个小组，测量速度的时候特别认真，眼睛紧紧盯着光电门的示数，手还不停地记录着数据。
可到最后计算的时候，发现结果和理论值相差有点大。
这可把他们急坏了，一个个抓耳挠腮，不知道问题出在哪。
后来经过仔细检查，发现是测量滑块质量的时候，天平没有调零，导致质量数据有偏差。
这就像盖房子地基没打好，上面再怎么努力也白搭。
所以说，测量过程中的每一个小细节都可能影响最终的结果。
而不确定度计算公式，就是要把这些可能的误差都考虑进去。
咱们常见的不确定度计算公式，通常会涉及到测量物理量的标准差、仪器的精度等等。
比如说测量速度的不确定度，可能就和光电门的响应时间、测量次数有关。
就像刚才那个实验，假设我们测量速度的时候，光电门的响应时间有一定的波动，测量了多次的数据分别是 v1、v2、v3……vn，那平均速度就是（v1 + v2 + v3 + …… + vn）/ n 。
而速度的不确定度，就可以通过计算这些数据的标准差来得到。
再来说说质量的不确定度，如果用天平测量，天平本身的精度就会对结果产生影响。
假如天平的最小分度值是 0.1g，那测量出来的质量就可能在 ±0.1g 的范围内有误差。
总之，动量守恒定律实验的不确定度计算公式，就是要把实验中各种可能的误差来源都综合考虑，让我们对实验结果有一个更准确、更可靠的评估。
大学物理实验中测量不确定度的评定方法
在大学物理实验中，测量不确定度是一项重要的任务。
不确定度
的评定方法在测量精度和准确度评估中起着至关重要的作用，以便识
别物理实验数据中的任何可能源导致的误差。
测量不确定度的评定，
可归纳为两个步骤：步骤一，识别影响测量结果的因素；步骤二，应
用不同方法子测量不确定度。
首先，确定可能影响测量结果的因素是评估不确定度的关键。
不
同的物理实验可能存在不同的变量，需要分析和识别的变量可以是无
量纲变量，比如电流、电压、时间间隔以及定量变量，如温度、湿度、压力等。
通过分析实验中所有可能影响结果的变量，可以找出误差的
源头，有助于提高测量精度。
其次，在确定影响测量结果的变量的基础上，可以采用不同的方
法来评估不确定度，并可以尝试多种评估方法，以更准确地衡量不确
定程度。
比如，可以分析设备的精度，采用估算的统计方法，以及采
用假设检验。
这些方法的使用可能会受到实验条件的限制，但是，一
旦选定了合适的方法，就可以得到非常准确的反馈，有助于准确衡量
物理实验中的不确定度。
总之，大学物理实验中测量不确定度的评定方法，主要有：识别
影响结果的变量，以及确定的基础上，选择合适的测量方法衡量不确
定程度。
只有经过科学的分析和准确的测量，才能准确衡量物理实验
数据中的不确定度。
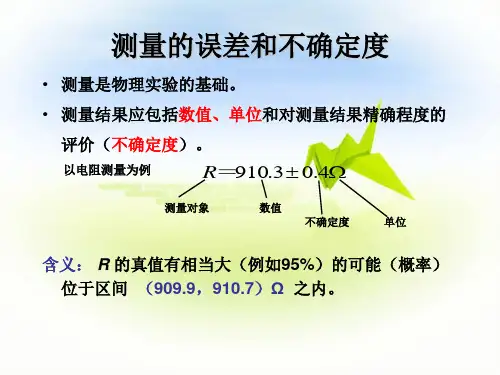
物理实验的不确定度表示和计算方法摘要本文在分析物理实验中引入不确定度必要性的基础上, 介绍了不确定度的有关概念, 提出了不确定度的表示和计算方法。
关键词物理实验; 不确定度; 置信概率0 引言在物理实验中总是通过各种测量方法和测量仪器对各个物理量进行测量, 但如何对测量结果的可靠性进行评价, 一直是测量和数据处理环节的重要问题。
过去的传统方法是用测量误差来评定测量结果的可靠性, 而测量误差定义为测量值与真值之差, 由于真值是永远也测不到的, 所以测量误差也是一个不可知量, 即用测量误差来评定测量结果的可靠性是不科学的。
1980 年国际计量局提出了关于实验不确定度表示的建议书《R ecomm endation INC-1C19980》, 1992 年发表了《测量不确定度表示法指南》, 在世界范围内开展了用不确定度来评价测量结果的推广和使用。
在此基础上, 国际理论与应用物理联合会与国际标准化组织( ISO) 等7 个国际组织联合颁发了《国际通用计量学基本术语》)之后,对物理教学中有关误差分析和数据处理方法提出了新的要求。
在于某一个量值范围内的评定, 它反映了可能存在的误差分布范围, 其大小给出了测量结果可信程度的高低。
不确定度实际上具有非常明确的含义, 它具有确定的量值, 其量纲与被测量的量纲相同, 但通常总是联系于一定的概率。
不确定度一般含有多个分量, 但按其数值的评定方法可归并成两类:A 类分量: 由测量列的统计分析评定的不确定度分量, 即随机误差分量, 用△表示。
B 类分量: 由非统计方法评定的不确定度分量, 即未定系统误差分量, 用△表示。
合成不确定度: 为A 类分量和B 类分量按方差合成原理进行合成, 用u 表示可写为u=∑△+∑△(1)总不确定度 ( 展伸不确定度) : 将合成不确定度u 乘以一个与置信概率有关的包含因子K , 则得总不确定度, 用U 表示, U = K u。
2 不确定度的表示2. 1 平均值是测量值的最佳值一般情况下, 单位误差间隔内出现某误差值的概率密度函数f ( x ) 可表示为f ( x ) = 1 ·e- ∞< X < ∞1991年我国推出了《国家计量技术规范JJ G1027-912no( 2)测量误差及数据处理》,规定测量结果的最终表示形式用总不确定度或用其相对值相对不确度表示。
至此, 推广与使用不确定度表示是物理学研究和教学式中o=∑( X -X )nn→∞n 中的必然趋势, 掌握不确定度的基本概念和简单的称为标准差, 反映一列测量数据的离散程度。
计算方法, 是对理工科物理实验教学的基本要求。
1 不确定度的概念由于lim1 ∑n( X - X) = 0 ( 3)不确定度概念表示被测量的真值以较大概率存固有X = li m 1∑X = X - ( 4) 即在系统误差忽略的情况下, 测量的平均值等 于真值。
但实际测量不可能是无限次, 既使是有限 次的测量, 测量值的平均值最接近真值, 即平均值是测量值的最佳值。
=1ex p - 12. 2 平均偏差和标准偏差2no 2o由于物理量的真值 X 是不可知的, 不能用上 式计算标准误差, 而采用平均值代替真值, 各测量= 0. 683 ( 10)如对 ( 9) 式在区间 〔µ-2o , µ+ 2o 〕积分, 则有值与平均值之差 ( v = X - X - ) 称残差, 用残差计算P =F ( x )的平均偏差是平均误差的最佳描述, 其公式为1- 1 2∑ ( X - X - ) 2no测量列平均偏差 t =n ( n - 1)( 5)= 0. 955( 11)对 ( 9) 式在区间 〔µ- 3o , µ+ 3o 〕积分, 得∑ ( X - X - ) P =F ( x ) 平均值的平均偏差 t=n n - 1( 6)1=ex p- 1 用残差计算的标准偏差是标准误差的最佳描述, 其 2no2o公式为测量列的标准偏差 S =∑∑( X - X - )n - 1(7)( X - X - )= 0. 997 ( 12)( 10) 、( 11) 和 ( 12) 式分别表示, 当一组测量值的 标准偏差为 o 时, 则这一组测量值中任一次测量值 X 的偏差 V 落在 µ±o 的区间的可能性为 68. 3% , 落在 µ±2o 区间的可能性是 95. 5% , 落在 µ±o 区 间的可能性是 99. 7%, 这三个百分数就是我们常用 平均值的标准偏差 S =n ( n -1)(8)=S= \ ( x -的三个置信概率。
究竟是采用平均偏差还是标准偏差来估算误差更为合适, 主要根据国家计量规范的要求和数值计算的方便性, 计算结果在表征测量列离散程度的有效性、精密性等综对于物理实验中的有限次测量, 一般为5—10次, 这时测量结果偏离正态分布, 而服从t 分布。
A类不确定度可由贝塞尔公式求出-合考虑, 结果表明, 用标准偏差估算误差更为合适。
2. 3 A 类不确定度A 类不确定度为随机误差分量, 是由随机变量的概率分布决定。
当随机变量呈离散型时, 其概率分布是多种多样的, 最主要的有二项分布、多项分布、泊松分布、均匀分布、x 分布、F 分布、正态n-1考虑到在一组等精度测量值中, 算术平均值比任何一次测量值的可靠性都高, 为测量值的最佳值, 由误差理论可知, 算术平均值的偏差S与一组测量值的标准偏差S有如下关系:-分布和t 分布, 每种分布都有自己的概率密度函数,彼此相差很大。
但当随机变量呈连续型时, 即测量S=S=n\ ( x -x )n ( n-1)( 13)次数趋于无穷, 则这些分布都趋向于正态分布( 高斯分布) , 所以我们可以认为大量的测量误差接近正态分布。
由于正态分布理论完善, 计算公式简便, 在再考虑到t 分布当n→∞时的极限是正态分布而采取的适当修正, 即6= tS=tS ( 14)n多种分布规律中最具典型性, 是误差理论中运用最多的具体分布规律, 所以我们可以采用正态分布加修正的方法来表示A 类不确定度。
对于正态分布的分布函数F ( x ) 有式中t为置信因子, 与置信概率有关。
为了与世界上大多数工业化国家所广泛采用的约定概率一致, 我国国家计量规范亦取约定概率p=0.95,则可取t/n≈1(见下表),即有F ( x ) =12no d x(9)6= S ( p = 0. 95)式中µ为x 的期待值 ( 实数) , o 为标准差( 大于0 的实数) , x 为随机变量分布区间e如对 ( 9) 式在区 间 〔µ- o , µ+ o 〕积分, 则有表 p = 0. 95 时的因子 ( t / n )P = F ( x )测量次数 n 4 5 6 7 8 9 10 15 20 ∞t / n1. 1. 1. 0. 0. 0. 0. 0. 0. 1.n6≤n ≤10 时,n ≥10 时,近似值1. 1.t n t n nU = d U ,其中 U = S + 6 6x36 长 春 大 学学 报 第 9 卷2. 4 B 类不确定度B 类不确定度为未定系统误差分量, 不能够用佳值—算术平均值y-= f ( x -) 统计方法评定, 一般可根据经验和其它信息进行估 而测量结果的不确定度为 计, 在物理实验中, 只考虑由仪器误差所带来的 B类分量。
如 B 类分量的误差限为 6 , 则 B 类不确定度由下式得出d x当 y = f ( x , x , x ) 时, 测量结果的总不6= K6( 15)C式中 K 为与置信概率有关的置信因子, C 为置信U =6U6x U +6U 6xU + + 6U U系数。
K 在 p = 0. 95 置信概率时, 通常取K = 1. 95≈2其中 U = S + 6, U =S + 6,其结果表达式为对于 C 值的选取, 如仪器误差服从均匀分布,C 值取 3 ; 如仪器误差服从正态分布, C 值取3, 物4 结 论y = -y ±U理 实验教学中仪器误差分布一般不 知道, C 可取3 , 这时6= 26/ 3 ≈6 ( p = 0. 95) 2. 5 总不确定度 ( 展伸不确定度)将 A 类不确定度分量和 B 类不确定分量在高 置信概率 p = 0. 95 条件下进行方和根合成, 即得总 不确定度U =6+ 6= S + 6对于受多个误差来源影响的直接测量量, 其测 量结果的总不确定度, 用下式表示:引入不确定度表示是物理实验教学内容改革的重要方面, 不确定度概念和体系的发展也是计量科学的一个重要进展, 是测量结果评定和表示国际标准化和规范化的重要体现。
不确定度的概念和体系是在现代误差理论发展的基础上建立和完善的。
不确定度和误差是两个不同的概念, 又都是由于测量过程的不完善性引起的。
不确定度是对测量结果可信度的合理的、科学的评定。
习惯上仍用误差来定性地描述理论和概念, 当要评定测量结果的精确度和计量器具的精度时, 就应当采用不确定度来描述。
U=∑S+∑6测量结果的表达式为参考文献1 朱鹤年. 物理实验研究. 北京: 清华大学出版社,1990.X=X-±U3 间接测量结果的不确定度计算方法在间接测量中, 测量量y 是直接测量量x 的函数。
即y = f ( x ) , 首先仍是求出间接测量量y 的最12～432 朱永生. 实验物理中的概率和统计. 北京: 科学出版社,1991. 1093 李惕碚. 实验的数学处理. 北京: 科学出版社, 1980. 39Expression and Calculation of uncertainty in physicalexperimentsZhu L i H an Ye Zhou J ing Zhang Baolin Faculty o f Basic science Studies, Chang chun University, Changchun 130022Abstract T his paper explains the fact that it is necessary to intro duce uncertainty in physical ex periments, presents the rele- vant concepts of uncertaint y, and puts forward the ex pression and calculatio n of uncertaint y.Key words uncertainty; physical experiment; confidence level。
