勾股定理公开课

美丽的勾股树----勾股定理的探索与应用教材分析勾股定理是学生在已经掌握了直角三角形的有关性质的基础上进行学习的，它是直角三角形的一条非常重要的性质，是几何中最重要的定理之一，它揭示了一个三角形三条边之间的数量关系，它可以解决直角三角形中的计算问题，是解直角三角形的主要根据之一，同时在实际生活中具有广泛的用途，“数学源于生活，又用与生活”是这章书所体现的主要思想。

教材在编写时注意培养学生的动手操作能力和分析问题的能力，通过实际操作，使学生获得较为直观的印象；通过联系比较、探索、归纳，帮助学生理解勾股定理，以利于进行正确的应用。

学情分析学生通过对勾股定理的学习，已基本掌握了勾股定理及其逆定理，了解了勾股定理的文化背景，体验了勾股定理的证明过程，为进一步探索应用勾股定理做好了铺垫.教学目标1. 经历对问题情景的观察、分析、一般化等思维活动，提出猜想，体验勾股定理的应用.2. 能运用勾股定理的数学模型解决现实世界的实际问题.3. 通过问题的探索，让学生感受勾股定理在实际生活中的应用.4. 在勾股定理的探索过程中，发展合情推理能力，体现数形结合的思想.5. 体会勾股定理的应用价值，体会数学来源于生活，又应用到生活中去，增强学生应用数学知识解决实际问题的经验和感受，同时在学习的过程中体会获得成功的喜悦，提高了学生学习数学的兴趣和信心.教学重点应用勾股定理解决实际问题.教学难点勾股定理的灵活运用.教学过程一、创设情境，激发兴趣教师创设情境，导入新课.同学们，在我们美丽的地球王国上，原始森林，参天古树给我们以神秘的遐想；绿树成荫，微风习习，给我们以美的享受.你知道吗？在古老的数学王国里，有一种树木，它很奇妙，生长速度大的惊人，它是什么呢？下面让我们带着这个疑问一同到数学王国去欣赏吧！【设计意图】教师利用多媒体播放视频，欣赏美丽的勾股树图片，设置疑问：这些美丽的勾股树是怎样做出来的呢？激发学生对勾股定理的应用的探索兴趣和热情.二、回顾与练习师生活动：教师利用多媒体出示问题，学生思考后回答问题：1. 请说说勾股定理的内容.2. 如图所示，a2+b2=,a=,b= ,c= .3. 边长为6cm的正方形的对角线长 .4. 直角三角形两直角边为3和4，则斜边上的高为 .5. 下列各组数据能否构成直角三角形？(1) 5 7 9(2)√2 √3 √5(3) 12 14 18(4) 3a 4a 5a6. 求下列阴影部分的面积（1）阴影部分是正方形（2）阴影部分是矩形（3）阴影部分是半圆7. 等边三角形ABC的边长为a，求它的面积为多少？师生活动：教师指导学生完成第7题的证明过程.【设计意图】通过对勾股定理的回顾与练习，为向下面的问题探索做好知识准备.三、探索与思考问题1 如图1，分别以Rt∆ABC三边为边向外作三个正方形，其面积分别用S1、S2、S3表示，那么S1、S2、S3之间有什么关系？图 1师生活动：教师利用多媒体出示问题，学生思考后回答问题.问题2 如图2，分别以Rt∆ABC三边为直径向外作三个半圆，其面积分别用S1、S2、S3表示，猜想S1、S2、S3之间有什么关系？请加以说明.图 2师生活动：教师鼓励学生进行大胆猜想，并利用勾股定理来证明.问题3 如图3 ，分别以Rt∆ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，猜想S1、S2、S3之间有什么关系？请加以说明.师生活动：教师鼓励学生进行大胆猜想，并利用勾股定理、回顾与练习7和三角形面积公式等知识加以证明.【设计意图】 1. 问题1由学生独立完成，问题2和3，让学生经历猜想、证明的过程，用类比的方法进行研究.2. 引导学生建立数学模型，提高学生分析问题、解决问题的能力.3. 规范学生的解题步骤.四、应用与巩固1. 如图，这是一棵奇妙的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形M 的边长是9cm ，则正方形A 、B 、C 、D 的面积和是多少？师生活动：学生独立思考，然后口答．2S 1S 3S A B C 图 32. 如图，分别以直角三角形的三边为边长作正方形，然后分别以三个正方形的中心为圆心、正方形边长的一半为半径作圆.试探索三个圆的面积之间的关系.师生活动： 指导学生独立完成并请一名学生板书解答过程．3. 如图，已知直角三角形ABC 的三边分别为6、8、10，分别以它的三边为直径向上作三个半圆，求图中阴影部分的面积.师生活动：指导学生独立完成并请一名学生板书解答过程．【设计意图】 练习对学生来说，达到了进一步巩固所学知识的目的. 问题2和问题3的设计师让学生有更开阔的思维空间，让所学到的知识进一步得到深化.五、欣赏图片，布置作业1. 欣赏美丽的勾股树在琅琊山4A 级国家森林公园里，有许许多多千姿百态的植物.1S 2S 3S CBA可是你是否见过数学王国里的树-----勾股树呢？【设计意图】多媒体出示勾股树图片，让学生在图片欣赏中感受数学美，体会生活中处处有数学，进一步体会数学来源于生活，应用到生活的道理.2. 布置作业必做题：你知道这是如何画出来的吗？仔细看看，你就会发现那一个个细小的部分正是我们学过的勾股图，一个一个连接在一起，构成了多么奇妙美丽的勾股树！动手画画看，相信你也能画出其他形态的勾股树.选做题：如图，分别以Rt∆ABC三边为边向外作三个一般的三角形，其面积分别用S1、S2、S3表示，为使S1、S2、S3仍具有与问题3相同的关系，所作三角形应满足什么条件？【设计意图】必做题是运用所学知识解决实际问题，选做题是在问题3的基础上将题目的条件稍作改动，引发学生对问题的探索兴趣，从而积极主动的去完成探索和思考.。

40
解:过A作铅垂线,过B作水平线
,两线交于点C,则∠C =90。
A
AC=90-40=50(mm), BC=160-40=120(mm).
90 C
∵ ∠C =90。
∴ AB2=AC2+BC2 =在5实02+际1问20题2 中，要会160 =16900(mm2) 根据需要构造直角三
∵AB>0
角形，再通过勾股定
∴a2+b2=c2
5
看
看8
17
谁 算
x
得 由勾股定理得：
快
！
82+x2=172
∴x2=172-82
=225
又∵x>0 ∴x=15
x
16
x 12
20
由勾股定理得：
x2+162=202
∴x2=202-162 =144
又∵x>0 ∴x=12
由勾股定理得：
52+122=x2
∴x2=52+122 =169
∠C=Rt∠,BC=a,AC=b,AB=C (1)已知: a=1, b=2, 求c;
(2)已知: a=15, c=17, 求b;
(3)已知：c=34, a:b=8:15, 求a, b.
变式一：已知Rt△ABC中，∠B=90°，AB=c， BC=a，AC=b．如果 a=1, b=2, 求c;
变式二：已知Rt△ABC中，AB=c，BC=a，
2.7 探索勾股定理(1)
小组合作、看看谁最强
1.作直角三角形,使其两条直角边长分别为 3cm和4cm; 6cm和8cm; 5cm和12cm 2.分别测量这三个直角三角形斜边的长.
3.根据所测得的结果填写下表:

数学勾股定理公开课教案设计一、教学目标：1. 知识与技能：（1）理解勾股定理的定义及证明方法；（2）能够运用勾股定理解决实际问题。

2. 过程与方法：（1）通过观察、分析、归纳，培养学生的逻辑思维能力；（2）学会运用几何画板等工具，进行勾股定理的验证。

3. 情感态度与价值观：（2）感受数学在生活中的应用，提高学生解决实际问题的能力。

二、教学重点与难点：1. 教学重点：（1）勾股定理的定义及应用；（2）勾股定理的证明方法。

2. 教学难点：（1）勾股定理的证明方法；（2）运用勾股定理解决实际问题。

三、教学准备：1. 教师准备：（1）熟练掌握勾股定理的相关知识；（2）准备相关的教学案例和实际问题；（3）制作PPT和教学课件。

2. 学生准备：（1）预习勾股定理的相关知识；（2）准备笔记本和文具。

四、教学过程：1. 导入新课：（1）利用PPT展示勾股定理的的历史背景；（2）引导学生思考勾股定理的实际应用。

2. 自主学习：（1）让学生阅读教材，了解勾股定理的定义；（2）学生展示自主学习成果，教师点评并总结。

3. 课堂讲解：（1）讲解勾股定理的证明方法；（2）通过PPT展示勾股定理的证明过程；（3）引导学生跟随教师一起验证勾股定理。

4. 课堂练习：（1）教师提出实际问题，让学生运用勾股定理解决；（2）学生独立解答，教师点评并讲解答案。

5. 课堂小结：（1）教师引导学生总结本节课的学习内容；（2）学生分享学习收获和感受。

五、课后作业：1. 完成教材上的相关练习题；2. 调查生活中运用勾股定理的实例，下节课分享。

教学反思：本节课结束后，教师应认真反思教学效果，针对学生的掌握情况，调整教学策略，以提高教学效果。

关注学生的学习兴趣和需求，不断改进教学方法，激发学生的学习积极性。

六、教学策略与方法：1. 讲授法：教师通过讲解勾股定理的历史背景、定义、证明及应用，使学生掌握知识要点。

2. 演示法：教师利用几何画板等工具，展示勾股定理的证明过程，帮助学生直观理解。

• 1881 年成为美国第 20 任总统
• 1876 年提出有关证明
想一想
小明妈妈买了一部29英寸（74厘米）旳 电视机.小明量了电视机旳屏幕后，发觉屏幕 只有58厘米长和46厘米宽，他觉得一定是售 货员搞错了.你同意他旳想法吗？你能解释这 是为何吗？
练一练
1. 如图，根据下列数学情境，你能够提出多少个 数学问题？你能处理所提出旳问题吗？
5 .在直角△ ABC中,a=5,c=13,则△ ABC旳面积 S=_____________.
6. 在直角△ ABC中, ∠C=90°,c=20,b=15,则 a=__________.
1. 如图1.1-1,求图中字母M所代表旳正方形旳面积.
图1.1-1
图1.1-2
2. 如图1.1-2,在四边形ABCD中, ∠ BAD=90°,
看一看
C A
B
图1--1

C A
B
图1--2 （图中每个小方格代表一种单位面积）
（1）观察图1-1
正方形A中具
有 9 个小方格，即 A旳面积是 9 个单
位面积；
正方形B中具
有 9 个小方格，即 B旳面积是 9 个单
位面积；
正方形C中具
有 18个小方格，即 C旳面积是 18 个单
位面积。
正方形A，B，C 旳面积之间有什么 关系吗？
幾何原本
• 欧几里得（Euclid of Alexandria; 约 325 B.C. 约 265 B.C.）
• 欧几里旳旳《几何原本》 是用公理措施建立演绎 数学体系旳最早典范
• 《几何原本》第一卷旳 第 47 命題也有对勾股定 理旳证明。
美国总统旳证明
• 加菲（James A. Garfield； 1831 1881）

AC=12， BC=5,
根据勾股定理得：
12
2
AB AC BC 2 2 12 5
2
5
13
答：要用13米长的钢丝绳才能把电线杆固定.
（四）归纳总结
（1）这节课你学到了什么知识？ ①勾股定理：直角三角形两直角边的平方和等于斜边的平方 ②在直角三角形中，任意已知两边，可以用勾股定理求第三边。 （2） 运用“勾股定理”时应注意什么问题？ ①要利用图形找到未知边所在的直角三角形； ②看清未知边是所在直角三角形的哪一边；
2 2 (2) a c b
(3) b c 2 a 2
2
52 122
13
10 8
2
252 7 2
24
6
小试牛刀
2、若一个直角三角形的三边长分别为3，4， x ，求第三边 x 的长度
（1）如图 （2）如图
4
x
3
x
4 3
解：由勾股定理得：
解：由勾股定理得：
A B
C
S正方形c
1 7 7 4 ( 3 4) 2
49 4 6
25（面积单位）
方法二：
分割成四个直角边为 整数格的三角形，再 加上一个小方格。
A
C
S正方形c
1 4 4 3 1 2
B
25（面积单位）
做一做
分别以5cm、12cm为直角三角形的直角边作 出一个直角三角形ABC，测量斜边的长度，然后 验证上述关系对这个直角三角形是否成立。
A
5
13
C
12
B
综上：
A
C a c b
我们得出：SA+SB=SC 即：a2&三角形中，两直角边的平方和等于斜边的平方。

勾股定理证明简述
直角三角形中两直角边a、
b的平方和，等于斜边c的
平方
a
c
a2+b2=c2
b
方法一:
△ABD≌△FBC， 矩形BL=2△ABD， 方形GB=2△FBC。 于是 矩形BL=正方形GB。 同样有 矩形CL=正方形AK。 所以 正方形GB+正方形AK=正方形BE
方法二
如图一：两个正方形边长 分别是a ,b, 它们的面积和 为a2+b2
___________________________________________________________________________ 2．达·芬奇的“蒙娜丽莎”是全人类文 化宝库 中一颗 璀璨的 明珠。 （缩写 句子） ___________________________________________________________________________ 3．我在她面前只停留了短短的几分钟。 她已经 成了我 灵魂的 一部分 。（用 关联词 连成一 句话） ___________________________________________________________________________
1、世上没有绝望的处境，只有对处境 绝望的 人。 2、挑水如同武术，武术如同做人。循序 渐进， 逐步实 现目标 ，才能 避免许 多无谓 的挫折 。 3、别想一下造出大海，必须先由小河川 开始。 4、自信是所有成功人士必备的素质之一 ，要想 成功， 首先必 须建立 起自信 心，而 你若想 在自己 内心建 立信心 ，即应 像洒扫 街道一 般，首 先将相 当于街 道上最 阴湿黑 暗之角 落的自 卑感清 除干净 ，然后 再种植 信心， 并加以 巩固。 信心建 立之后 ，新的 机会才 会随之 而来。 5、一个人在科学探索的道路上，走过弯 路，犯 过错误 ，并不 是坏事 ，更不 是什么 耻辱， 要在实 践中勇 于承认 和改正 错误。 ——爱 因斯坦 6、瓜是长大在营养肥料里的最甜，天才 是长在 恶性土 壤中的 最好。 ——培 根 7、发光并非太阳的专利，你也可以发光 。 8、人们常用“心有余而力不足”来为自 己不愿 努力而 开脱， 其实， 世上无 难事， 只怕有 心人， 积极的 思想几 乎能够 战胜世 间的一 切障碍 。 9、如果你希望成功，当以恒心为良友， 以经验 为参谋 ，以当 心为兄 弟，以 希望为 哨兵。 ——爱 迪生 10、涓滴之水终可磨损大石，不是由于 它力量 大，而 是由于 昼夜不 舍的滴 坠。只 有勤奋 不懈的 努力才 能够获 得那些 技巧， 因此， 我们可 以确切 地说： 说：不 积跬步 ，无以 致千里 。—— 贝多芬 11、一定要做最适合自己的事情，不要 迎合别 人的口 味而去 做一件 不属于 自我的 “难事 ”。一 旦“发 现自我 ”，就 要尽力 而为， 但要全 面了解 自己和 周围的 环境， 知道适 可而止 。 12、要有自信，然后全力以赴--假如具 有这种 观念， 任何事 情十之 八九都 能成功 。—— 威尔逊 13、莫找借口失败，只找理由成功。 14、一个有坚强心志的人，财产可以被 人掠夺 ，勇气 却不会 被人剥 夺的。 ——雨 果 15、积极的人在每一次忧患中都看到一 个机会 ，而消 极的人 则在每 个机会 都看到 某种忧 患。 16、不是境况造就人，而是人造就境况 。 17、在人生的竞赛场上，没有确立明确 目标的 人，是 不容易 得到成 功的。 许多人 并不乏 信心、 能力、 智力， 只是没 有确立 目标或 没有选 准目标 ，所以 没有走 上成功 的途径 。这道 理很简 单，正 如一位 百发百 中的神 射击手 ，如果 他漫无 目标地 乱射， 也不能 在比赛 中获胜 。 18、生活就像海洋，只有意志坚强的人 ，才能 到达彼 岸。— —马克 思 19、别因为落入了一把牛毛就把一锅奶 油泼掉 ，别因 为犯了 一点错 误就把 一生的 事业扔 掉。— —蒙古 20、许多人之所以在生活中一事无成， 最根本 原因在 于他们 不知道 自己到 底要做 什么。 在生活 和工作 中，明 确自己 的目标 和方向 是非常 必要的 。只有 在知道 你的目 标是什 么、你 到底想 做什么 之后， 你才能 够达到 自己的 目的， 你的梦 想才会 变成现 实。 21、怠惰是贫穷的制造厂。 22、先知三日，富贵十年。 23、自信是向成功迈出的第一步。—— 爱因斯 坦 24、一个人除非自己有信心，否则不能 带给别 人信心 ；已经 信服的 人，方 能使人 信服。 ——麦 修·阿诺 德 25、凡是挣扎过来的人都是真金不怕火 炼的； 任何幻 灭都不 能动摇 他们的 信仰： 因为他 们一开 始就知 道信仰 之路和 幸福之 路全然 不同， 而他们 是不能 选选择 的，只 有往这 条路走 ，别的 都是死 路。这 样的自 信不是 一朝一 夕所能 养成的 。你绝 不能以 此期待 那些十 五岁左 右的孩 子。在 得到这 个信念 之之前 ，先得 受尽悲 痛，流 尽眼泪 。可是 这样是 好的， 应该要 这样… …—— 罗曼·罗 兰 26、一个人在科学探索的道路上，走过 弯路， 犯过错 误，并 不是坏 事，更 不是什 么耻辱 ，要在 实践中 勇于承 认和改 正错误 。—— 爱因斯 坦88我 们的理 想应该 是高尚 的。我 们不能 登上顶 峰，但 可以爬 上半山 腰，这 总比待 在平地 上要好 得多。 如果我 们的内 心为爱 的光辉 所照亮 ，我们 面前前 又有理 想，那 么就不 会有战 胜不了 的困难 。—— 普列姆 昌德 27、旁观者的姓名永远爬不到比赛的计 分板上 。

北师大版八年级数学（上）第一章：§勾股定理景德镇十六中：汤瑛一、教学背景勾股定理是人类数学最伟大的发现之一，也是几何学中几个最重要、最基本的定理之一。

它揭示了直角三角形三边之间的数量关系，既是直角三角形性质的拓展，又是后续学习解直角三角形的基础，它紧密联系了数学中最基本的两个量—数与形，能够把形（直角三角形中一个角是直角）转化成数量关系（三边之间满足的关系），既是数形结合的典范，又体现了转化和方程思想。

勾股定理导致了无理数的发现以及第一次数学危机，有人把它提为人类科学史上的十大发现之一，天文学家开普勒亦把它称为几何定理中的"黄金"。

二、教学目标1、知识目标：1经历探索发现并验证勾股定理的过程，进一步发展学生的推理能力；2）理解并掌握勾股定理，会初步运用勾股定理解决一些简单的数学问题和实际问题．2、能力目标：1让学生经历“探索—发现—猜想—验证—应用—检测—拓展”的学习过程，并体会“特殊—一般—特殊”的数学思想方法；2通过定理的证明过程体会数学的数形结合思想。

3、情感目标：1在探索勾股定理的过程中，让学生体验解决问题方法的多样性，培养学生的合作交流意识和探索精神．通过获得成功的经验和克服困难的经历，增进数学学习的信心2使学生在定理探索的过程中，感受数学之美，探究之趣3通过了解我国古代辉煌的数学成就，体会勾股定理的文化价值，激发学生的爱国热情，激励学生发奋学习教学重点：经历探索和验证勾股定理的过程，会利用两边求三角形的另一边长。

教学难点：运用欧氏几何的基本定理进行证明及拼图法验证勾股定理。

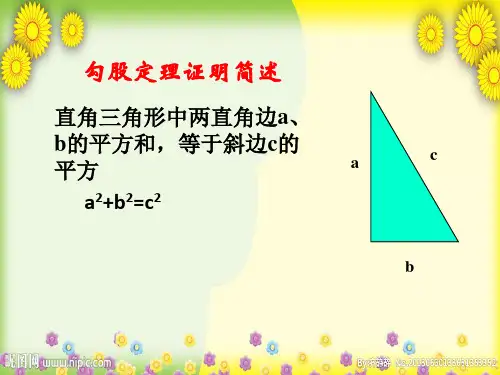
三、教学过程一情景导入（1）如图，强大的台风使得一根旗杆在离地面9米处折断倒下，旗杆顶部落在离旗杆底部12米处旗杆折断之前有多高（2）邮票欣赏：猜想直角三角形三边的平方关系二做一做1如图，直角三角形三边的平方分别是多少，它们满足前面所猜想的数量关系吗你是如何计算的与同伴交流2如图，对下图中的直角三角形，是否还满足这样的关系你又如何计算的呢三勾股定理勾股定理：如果直角三角形两直角边分别为a、b，斜边为c，那么a2b2=c2即直角三角形两直角边的平方和等于斜边的平方我国古代把直角三角形中较短直角边称为勾，较长的直角边称为股，斜边称为弦四定理证明用四张全等的直角三角形通过拼摆，得到一大正方形与一个小正方形你能用两种方法表示大正方形的面积吗大正方形面积表示为：①______②______对比两种表示方法你得到勾股定理了吗五定理应用1、比比谁算的快2如图，强大的台风使得一根旗杆在离地面9米处折断倒下，旗杆顶部落在离旗杆底部12米处旗杆折断之前有多高3小明的妈妈买了一部29英寸74厘米的电视机小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了你同意他的想法吗你能解释这是为什么吗（六）小结：通过这节课我们学会了什么（七）课后作业：习题。

14.1.3ห้องสมุดไป่ตู้反证法
14.1.3 反证法
探究新知
活动1 知识准备 命题“过直线外一点有且只有一条直线与已知直线平行” 的条件是_____直__线__及__直__线__外__一__点_________， 结论是_过__这__个__点__只__有___一__条__直__线__与_．已知直线平行
14.1.3 反证法
有读有思
我们可以安静一点吗？（节选）
• 德国摄影记者在东京旅行，拍下一辑东京地铁挤拥的照 片。许多日本人默默承受挤拥，不论西装笔挺，脸孔压在车 厢门的玻璃上，鼻扁嘴凸，面容扭曲，就是一副死忍，绝不 吭声半句。这个照片系列，成为日本国民性格的代表作。 • 日本人乘搭公共交通工具，不论地铁还是飞机，其恬静 是一大景观。手机不会响，为他人着想，固不必说，车厢里 鲜有交谈，即使有，声音也自觉低下来，令西方记者称奇。 • 日本火车与瑞士和欧洲各国的火车类似，就是乘客自觉 恬静，读书看报，或者上网工作。这方面，难怪日本早身在 西方文明国家之列，公共交通，首重一个“公”字，国民无 公德，国家再强，GDP再高，没有人心中真正看得起你。
14.1.3 反证法
重难互动探究
探究问题 用反证法进行证明 例 1 用反证法证明：等腰三角形的底角是锐角． 证明：假设等腰三角形的底角不是锐角，则大于或等于 90 °. 根据等腰三角形的两个底角相等，可知两个底角的和大于 或等于 180°， 则该三角形的三个内角的和一定大于 180°，这与三角形的 内角和定理相矛盾，故假设不成立． 所以等腰三角形的底角是锐角．
14.1.3 反证法
[归纳总结] 原则上来说，当直接证明问题有困难时考 虑采用反证法．一般地，当求证的结论出现“最(至) 多”“最(至)少”“不(相等、平行、垂直、相交)”，就需要 运用反证法．其次，证明一个数是无理数通常也采用反证法．