贵州省桐梓县第五中学2014届九年级数学上学期第二次月考试题

学校： 姓名： 考场： 考号：2014—2015石桥镇中九年级数学第二次月考试卷一、选择题:本大题共有10个小题，每小题3分，共30分．1.有12只外观完全相同的杯子,其中一等品7只,二等品3只,三等品2只,则从中任取1只,是二等品的概率等于( )A.112B.16C.14D.7122. 已知圆锥的底面半径为3，母线长为4，则它的侧面积是（ ） A. π24 B. π12 C.π6 D. 123. 如果△ABC ∽△A ′B ′C ′，相似比为k (k ≠1)，则k 的值是（ ） A 、∠A ：∠A ′ B 、A ′B ′：AB C 、∠B ：∠B D 、BC ：B ′C ′4. 某种商品零售价经过两次降价后，每件的价格由原来的800元降为现在的578元，则平均每次降价的百分率为（）A ．10%B ．12%C ．15%D ．17%5. 已知点A(－3，y 1)，B(－2，y 2)，C(3，y 3)都在反比例函数y ＝4x 的图象上，则()．A ．y 1＜y 2＜y 3B ．y 3＜y 2＜y 1C ．y 3＜y 1＜y 2 D．y 2＜y 1＜y 3 6.如图，O ⊙是ABC △的外接圆，已知50ABO ∠=°，则ACB ∠的大小为（）A ．40°B ．30°C ．45°D ．50°7.关于x 的一元二次方程2210kx x +-=有两个不相等的实数根，则k 的取值范围是（ ）A.1k >-B.1k ≥-C.1k ≥-且0k ≠D.1k >-且0k ≠8. 如图，若000a b c <><，，，则抛物线2y ax bx c =++的图象大致为（）9.如图，点M 在BC 上，点N 在AM 上，CM=CN ，CM BMAN AM =，下列结论正确的是（ ）A ．∆ABM ∽∆ACB B ．∆ANC ∽∆AMBC ．∆ANC ∽∆ACMD ． ∆CMN ∽∆BCA10.设a 、b 、c 、d 都是整数，且a<2b,b<3c,c<4d,d<20,则a 的最大值是（） A.480 B.479 C.448 D.447 二、填空题：本大题共有7小题，每小题3分，共21分．11．将一个正六边形绕着其中心，至少旋转度可以和原来的图形重合。

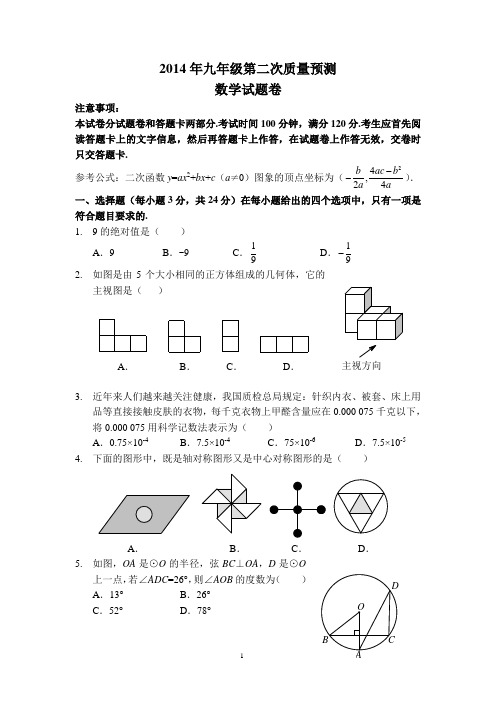
主视方向2014年九年级第二次质量预测数学试题卷注意事项：本试卷分试题卷和答题卡两部分.考试时间100分钟，满分120分.考生应首先阅读答题卡上的文字信息，然后再答题卡上作答，在试题卷上作答无效，交卷时只交答题卡.参考公式：二次函数y =ax 2+bx +c （a ≠0）图象的顶点坐标为（24,24b ac b a a--）．一、选择题（每小题3分，共24分）在每小题给出的四个选项中，只有一项是符合题目要求的.1. 9的绝对值是（ ）A ．9B ．-9C ．19D ．19-2. 如图是由5个大小相同的正方体组成的几何体，它的主视图是（ ）A ．B ．C ．D ．3. 近年来人们越来越关注健康，我国质检总局规定：针织内衣、被套、床上用品等直接接触皮肤的衣物，每千克衣物上甲醛含量应在0.000 075千克以下，将0.000 075用科学记数法表示为（ ） A ．0.75×10-4B ．7.5×10-4C ．75×10-6D ．7.5×10-54. 下面的图形中，既是轴对称图形又是中心对称图形的是（ ）A ．B ．C ．D ．5. 如图，OA 是⊙O 的半径，弦BC ⊥OA ，D 是⊙O上一点，若∠ADC =26°，则∠AOB 的度数为（ ） A ．13° B ．26°C ．52°D ．78°6. 在一次体育达标测试中，九年级（3）班15名男同学的引体向上成绩如下表所示：A ．12，13B ．12，12C ．11，12D ．3，47. 小明用一张半径为24cm 的扇形纸板做一个如图所示的圆锥形小丑帽子的侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm ，那么这张扇形纸板的面积是（ ） A ．120πcm 2B ．240πcm 2C ．260πcm 2D ．480πcm 2C'PEDCBA第7题图 第8题图8. 如图，矩形ABCD 中，AB =3，BC =5，点P 是BC 边上的一个动点（点P 不与点B ，C 重合），现将△PCD 沿直线PD 折叠，使点C 落在点C ′处，作 ∠BPC ′的角平分线交AB 于点E ，设BP =x ，BE =y ，则下列图象中，能表示y 与x 函数关系的图象大致是（ ）A ． 二、填空题（每小题3分，共21分） 9. 计算：2(1) =___________．10. 如图，一把矩形直尺沿直线断开并错位，点E ，D ，B ，F 在同一条直线上，若∠ADE =128°，则∠DBC 的度数为___________．FED C BA11. 一位园艺设计师计划在一块形状为直角三角形且有一个内角为60°的绿化区域上种植四种不同的花卉，要求种植的四种花卉分别组成面积相等、形状完全相同的几何图形图案．某同学为此提供了如图所示的4种设计方案，其中可以满足园艺设计师要求的有___________种．12. 农历5月5日是中华民族的传统节日端午节，有吃粽子的习俗．端午节早上，妈妈给小华准备了4个粽子：1个肉馅，1个豆沙馅，2个红枣馅．4个粽子除内部馅料不同外其他一切均相同，小华喜欢吃红枣馅的粽子，小华吃了一个粽子刚好是红枣馅的概率是___________．13. 若一次函数(2)(2)y a x a =-++不经过第三象限，则a 的取值范围为_______． 14. 如图，在平面直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行，点(2)P a a ，是反比例函数2y x=的图象与正方形的一个交点，则图中阴影部分的面积是___________．864第15题图15. 在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为4，6，8，则原直角三角形纸片的斜边长是___________． 三、解答题（本大题共8个小题，共75分）16. （本题8分）有三个代数式：①a 2-2ab +b 2，②2a -2b ，③a 2-b 2，其中a ≠b ；（1）请你从①②③三个代数式中任意选取两个代数式，分别作为分子和分母构造成一个分式；（2）请把你所构造的分式进行化简；（3）若a ，b 为满足不等式0<x <3的整数解，且a >b ，请求出化简后的分式的值．17. （本题9分）郑州地铁1号线在2013年12月28日通车之前，为了解市民对地铁票的定价意向，市物价局向社会公开征集定价意见．某学校课外小组也开展了“你认为郑州地铁起步价定为多少合适？”的问卷调查，征求市民的意见，并将某社区市民的问卷调查结果整理后制成了如下统计图：票价10%15%5元4元3元2元根据统计图解答：（1）同学们一共随机调查了________人； （2）请你把条形统计图补充完整；（3）假定该社区有1万人，请估计该社区支持“起步价为3元”的市民大约有多少人？18. （本题9分）已知命题：“如图，点A ，D ，B ，E 在同一条直线上，且AD =BE ，AC ∥DF ，则△ABC ≌△DEF ．”这个命题是真命题还是假命题？如果是真命题，请给出证明；如果是假命题，请添加一个适当的条件，使它成为真命题，并加以证明．FEC19. （本题9分）“城市发展，交通先行”，我市启动了缓堵保畅的高架桥快速通道建设工程，建成后将大大提升道路的通行能力．研究表明，某种情况下，高架桥上的车流速度V （单位：千米/时）是车流密度x （单位：辆/千米）的函数，且当028≤x <时，V =80；当28188≤x <时，V 是x 的一次函数．函数关系如图所示．（1）求当28188≤x <时，V 关于x 的函数表达式；（2）请你直接写出车流量P 和车流密度x 之间的函数表达式；当x 为多少时，车流量P （单位：辆/时）达到最大，最大值是多少？（注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量=车流速度×车流密度）（辆/千米）20. （本题9分）在某飞机场东西方向的地面l 上有一长为1km 的飞机跑道MN（如图），在跑道MN 的正西端14.5千米处有一观察站A .某时刻测得一架匀速直线降落的飞机位于点A 的北偏西30°，且与点A 相距15千米的B 处；经过1分钟，又测得该飞机位于点A 的北偏东60°，且与点A 相距千米的C 处．（1）该飞机航行的速度是多少千米/小时？（结果保留根号）（2）如果该飞机不改变航向继续航行，那么飞机能否降落在跑道MN 之间？请说明理由．北东21. （本题10分）某学校开展“我的中国梦”演讲比赛，学校准备购买10支某种品牌的水笔，每支水笔配x （x ≥2）支笔芯，作为比赛获得一等奖学生的奖品．A ，B 两家文具店都有这种品牌的水笔和笔芯出售，且每支水笔的标价均为30元，每支笔芯的标价为3元．目前两家文具店同时在做促销活动：A 文具店：所有商品均打九折（按标价的90%）销售；B 文具店：买一支水笔送2支笔芯．设在A 文具店购买水笔和笔芯的费用为y A （元），在B 文具店购买水笔和笔芯的费用为y B （元）.请解答下列问题： （1）分别写出与y A ，y B 与x 之间的函数表达式；（2）若该校只在一家文具店购买奖品，你认为在哪家文具店购买更优惠？ （3）若每支水笔配15支笔芯，请你帮助学校设计出最省钱的购买方案．22. （本题10分）如图1，点P ，Q 分别是边长为4cm 的等边△ABC 边AB ，BC上的动点，点P 从顶点A ，点Q 从顶点B 同时出发，且它们的速度都为1cm/s. （1）连接AQ ，CP 交于点M ，在点P ，Q 运动的过程中，∠CMQ 的大小变化吗？若变化，则说明理由，若不变，请直接写出它的度数；（2）点P ，Q 在运动过程中，设运动时间为t ，当t 为何值时，△PBQ 为直角三角形？（3）如图2，若点P ，Q 在运动到终点后继续在射线AB ，BC 上运动，直线AQ ，CP 交点为M ，则∠CMQ 的大小变化吗？若变化，则说明理由；若不变，请求出它的度数。

遵义市九年级上学期数学第二次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题；共16分)1. （2分）(2017·揭西模拟) 若二次函数y=x2﹣2x+c的图象与x轴没有交点，则c的值可能是（）A . ﹣3B . ﹣2C . 0D . 22. （2分）(2017·锡山模拟) 现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为x小明掷B立方体朝上的数字为y来确定点P（x，y），那么它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为（）A .B .C .D .3. （2分） (2017九上·深圳期中) 下列命题正确的是（）A . 方程x2-4x+2=0无实数根；B . 两条对角线互相垂直且相等的四边形是正方形C . 甲、乙、丙三人站成一排合影留念，则甲、乙二人相邻的概率是D . 若是反比例函数，则k的值为2或-1。

4. （2分）改革开放40年以来，城乡居民生活水平持续快速提升。

居民教育、文化和娱乐消费支出持续增长。

下图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图。

说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如2018年第二季度与2017年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如2018年第二季度与2018年第一季度相比较。

根据上述信息，下列结论中错误的是（）A . 2017年第二季度环比有所提高B . 2017年第四季度环比有所降低C . 2018年第一季度同比有所提高D . 2018年第四季度同比有所提高5. （2分）在1，2，3，－4这四个数中，任选两个数的积作为k的值，使反比例函数的图象在第二、四象限的概率是（）A .B .C .D .6. （2分） (2019九上·灌云月考) 关于抛物线，以下说法正确的是（）A . 开口向下B . 对称轴是x= —3C . 顶点坐标是（0，0）D . 当x＞—3时，y随x增大而减小7. （2分）(2019·南通) 如图是王阿姨晚饭后步行的路程s(单位：m)与时间t(单位：min)的函数图象，其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是（）A . 25min~50min，王阿姨步行的路程为800mB . 线段CD的函数解析式为C . 5min~20min，王阿姨步行速度由慢到快D . 曲线段AB的函数解析式为8. （2分） (2019九上·灌云月考) 抛物线y＝ax2+bx+c（a≠0，a、b、c为常数）上部分点的横坐标x，纵坐标y的对应值如下表：x……﹣3﹣2﹣1012……y……44m0……则下列结论中：①抛物线的对称轴为直线x＝﹣1；②m＝；③当﹣4＜x＜2时，y＜0；④方程ax2+bx+c﹣4＝0的两根分别是x1＝﹣2，x2＝0，其中正确的个数有（）A . 1个B . 2个C . 3个D . 4个二、填空题 (共8题；共8分)9. （1分） (2019九下·崇川月考) 反比例函数y＝的图象满足：在所在象限内，y随x的增大而减小，则n的取值范围是________.10. （1分）已知，可以取，，，中任意一个值，则直线的图象经过第四象限的概率是________.11. （1分）(2017·南山模拟) 小明用S2= [（x1﹣3）2+（x2﹣3）2+…+（x10﹣3）3]计算一组数据的方差，那么x1+x2+x3+…+x10=________．12. （1分） (2019九上·灌云月考) 如图，墙上有一个同心圆纸板，大圆的半径为40cm，小圆的半径为30cm，若向这个纸板投掷飞镖（每次飞镖均落在纸板上），则飞镖落在阴影区域的概率为________.13. （1分） (2019九上·灌云月考) 将抛物线先向右平移1个单位长度，再向上平移2个单位长度，得到的抛物线的解析式是________.14. （1分） (2019九上·灌云月考) 二次函数y1＝ax2+bx+c与一次函数y2＝mx+n的图象如图所示，则满足ax2+bx+c≥mx+n的x的取值范围是________．15. （1分） (2019九上·灌云月考) 如图，经过抛物线y＝x2+x﹣2与坐标轴交点的圆与抛物线另交于点D，与y轴另交于点E，则∠BED＝________．16. （1分） (2019九上·灌云月考) 二次函数y＝2x2的图象如图所示，坐标原点O，点B1 ， B2 ， B3在y轴的正半轴上，点A1 ， A2 ， A3在二次函数y＝2x2位于第一象限的图象上，若△A1OB1 ，△A2B1B2 ，△A3B2B3都为等腰直角三角形，且点A1 ， A2 ， A3均为直角顶点，则点A3的坐标是________．三、解答题 (共10题；共75分)17. （10分） (2018九上·丹江口期末) 已知二次函数y＝x2﹣2x+k﹣1的图象与x轴交于不同的两点A(x1 ，0)，B(x2 ， 0).（1）求k的取值范围；（2）若AB＝2，求k的值.18. （6分）(2020·牡丹江) 在一条公路上依次有A，B，C三地，甲车从A地出发，驶向C地，同时乙车从C地出发驶向B地，到达B地停留0.5小时后，按原路原速返回C地，两车匀速行驶，甲车比乙车晚1.5小时到达C地．两车距各自出发地的路程y（千米）与时间x（小时）之间的函数关系如图所示．请结合图象信息解答下列问题：（1）甲车行驶速度是________千米1时，B，C两地的路程为________千米；（2）求乙车从B地返回C地的过程中，y（千米）与x（小时）之间的函数关系式（不需要写出自变量x的取值范围）；（3）出发多少小时，行驶中的两车之间的路程是15千米？请你直接写出答案．19. （7分） (2019九上·宁波期末) 在三个完全相同的小球上分别写上-2，-1，2三个数字，然后装入一个不透明的布袋内搅匀，从布袋中取出一个球，记下小球上的数字为，放回袋中再搅匀，然后再从袋中取出一个小球，记下小球上的数字为，组成一对数 .（1）请用列表或画树状图的方法，表示出数对的所有可能的结果；（2）求直线不经过第一象限的概率.20. （10分）(2018·吉林模拟) 已知反比例函数与一次函数y=x+2的图象交于点A（﹣3，m）．（1）求反比例函数的解析式；（2）如果点M的横、纵坐标都是不大于3的正整数，求点M在反比例函数图象上的概率．21. （11分）(2017·海陵模拟) 有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B 布袋中有三个完全相同的小球，分别标有数字﹣1，﹣2和﹣3．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y）．（1）用列表或画树状图的方法写出点Q的所有可能坐标；（2）求点Q落在直线y=﹣x﹣1上的概率．22. （2分）在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2，；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．（1）用树状图或列表法列举点M所有可能的坐标；（2）求点M（x，y）在函数y=﹣x+1的图象上的概率；（3）在平面直角坐标系xOy中，⊙O的半径是2，求过点M（x，y）能作⊙O的切线的概率．23. （10分）(2017·响水模拟) 在甲、乙两个不透明的布袋里，都装有3个大小、材质完全相同的小球，其中甲袋中的小球上分别标有数字0，1，2；乙袋中的小球上分别标有数字﹣1，﹣2，0．现从甲袋中任意摸出一个小球，记其标有的数字为x，再从乙袋中任意摸出一个小球，记其标有的数字为y，以此确定点M的坐标（x，y）．（1）请你用画树状图或列表的方法，写出点M所有可能的坐标；（2）求点M（x，y）在函数y=﹣的图象上的概率．24. （2分） (2019九上·杭州月考) 在一个不透明的盒子里，装有四个分别标有数字1，2，3，4的小球，它们的形状、大小、质地等完全相同.小米先从盒子中随机取出一个小球，记下数字为x，且不放回盒子，再由小华随机取出一个小球，记下数字为y.（1）用列表法或画树状图表示出（x，y）的所有可能出现的结果；（2）求小米、小华各取一次小球所确定的点（x，y）落在反比例函数y= 的图象上的概率.25. （2分）(2018·高台模拟) 在甲、乙两个不透明的布袋里，都装有3个大小、材质完全相同的小球，其中甲袋中的小球上分别标有数字0，1，2；乙袋中的小球上分别标有数字﹣1，﹣2，0．现从甲袋中任意摸出一个小球，记其标有的数字为x，再从乙袋中任意摸出一个小球，记其标有的数字为y，以此确定点M的坐标（x，y）．（1）请你用画树状图或列表的方法，写出点M所有可能的坐标；（2）求点M（x，y）在函数y=﹣的图象上的概率．26. （15分） (2019九上·灌云月考) 如图，已知抛物线经过两点A（﹣3，0），B（0，3），且其对称轴为直线x＝﹣1．（1）求此抛物线的解析式．（2）若点Q是对称轴上一动点，当OQ+BQ最小时，求点Q的坐标．（3）若点P是抛物线上点A与点B之间的动点（不包括点A，点B），求△PAB面积的最大值，并求出此时点P的坐标．参考答案一、单选题 (共8题；共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共8题；共8分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共10题；共75分)17-1、17-2、18-1、18-2、18-3、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、22-3、23-1、23-2、24-1、24-2、25-1、25-2、26-1、26-2、26-3、。

2024年中考第二次模拟考试（贵州卷）数学·全解全析第Ⅰ卷一、选择题（本大题共12个小题，每小题3分，共36分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）1．下列各数中，是负整数的是（）A．+2B．﹣1C．﹣1.5D．解：+2是正整数；﹣1是负整数；﹣1.5是负分数；是正分数；故选：B．2．据统计，2023年山西中考报名人数约为35万，数据35万用科学记数法可表示为（）A．3.5×105B．0.35×106C．3.5×104D．0.35×105解：35万＝350000＝3.5×105．故选：A．3．下列几何体中，同一个几何体的主视图与左视图不同的是（）A．圆柱B．正方体C．圆锥D．球解：圆柱体的主视图是长方体．左视图是圆形．故选：A．4．如图是一款手推车的平面示意图，其中AB∥CD，∠1＝24°，∠2＝76°，则∠3的度数为（）A．104°B．128°C．138°D．156°解：如图：∵AB∥CD，∠1＝24°，∴∠A＝∠1＝24°，∵∠2＝76°，∠2+∠4＝180°，∴∠4＝180°﹣∠2＝180°﹣76°＝104°，∴∠3＝∠4+∠A＝104°+24°＝128°．故选：B．5．周末，青华到公园游玩，参加套环游戏，共进行四局，套中的次数分别为1，2，3，4，若将这组数每一个加1，则对这一组新数据描述正确的是（）A．平均值不变B．方差不变C．中位数不变D．众数不变解：将一组数据中的每个数都加1，那么所得的新数据的众数、中位数、平均数都增加1，方差不变．故选：B．6．任意掷一枚骰子，下列情况出现的可能性比较大的是（）A．面朝上的点数是3B．面朝上的点数是奇数C．面朝上的点数小于2D．面朝上的点数不小于3解：A．面朝上的点数是3的概率为；B．面朝上的点数是奇数的概率为＝；C．面朝上的点数小于2的概率为；D．面朝上的点数不小于3的概率为＝；∴概率最大的是面朝上的点数不小于3，故选：D．7．如图，在△ABC中，点D是AC的中点，分别以点A，C为圆心，大于AC的长为半径作弧，两弧交于F，直线FD交BC于点E，连接AE，若AD＝2，△ABE的周长为12，则△ABC的周长为（）A．13B．14C．15D．16解：∵点D是AC的中点，∴AC＝2AD＝4，由题意得：ED是AC的垂直平分线，∴EA＝EC，∵△ABE的周长为12，∴AB+BE+AE＝12，∴AB+BE+EC＝12，∴AB+BC＝12，∴△ABC的周长＝AB+BC+AC＝12+4＝16，故选：D．8．近年来，由于新能源汽车的崛起，燃油汽车的销量出现了不同程度的下滑，经销商纷纷开展降价促销活动．某款燃油汽车今年10月份售价为23万元，12月份售价为19.68万元，设该款汽车这两月售价的月平均降价率是x，则所列方程正确的是（）A．23（1﹣x）2＝19.68B．19.68（1+x）2＝23C．19.68（1﹣x）2＝23D．23（1﹣2x）＝19.68解：根据题意得：23（1﹣x）2＝19.68．故选：A．9．如图，在矩形ABCD中，对角线AC，BD交于点O，过点O作EF⊥AC交AD于点E，交BC于点F．已知AB＝4，△AOE的面积为5，则DE的长为（）A．2B．C．D．3解：如图，连接CE，由题意可得，OE为对角线AC的垂直平分线，∴AE＝CE，S△AOE＝S△COE＝5，∴S△ACE＝2S△COE＝10．∴AE•CD＝10，∵CD＝4，∴AE＝EC＝5，在Rt△CDE中，由勾股定理得：DE＝＝3．故选：D．10．一次函数y＝﹣2x﹣1的图象不经过的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限解：一次函数y＝﹣2x﹣1中，∵﹣2＜0，﹣1＜0，∴函数图象经过第二、三、四象限，不经过第一象限．故选：A．11．如图，▱ABCD中，∠A＝50°，AD＝6，O为BC的中点以O为圆心，OB为半径画弧交AD于点E．若E为AD的中点，则图中阴影部分的面积为（）A ．B ．C ．D ．5π解：如图，连接BE 、OE 、OD ，∵四边形ABCD 是平行四边形，∴AD ＝BC ＝6，AD ∥BC ，∵O 、E 分别是AD 、BC 的中点，∴AE ＝DE ＝OB ＝OC ＝3，∴四边形ABOE 、四边形OBED 是平行四边形，∴∠BOE ＝∠A ＝50°，BE ∥OD ，∴S △BDE ＝S △BOE ，∴S 阴影＝S 扇形OBE ＝＝．故选：A ．12．如图，抛物线y ＝ax 2+bx+c （a≠0）与x 轴交于点，与y 轴的交点B 在（0，0）和（0，﹣1）之间（不包括这两点），对称轴为直线x ＝．则下列结论：①x ＞3时，y ＜0；②4a+b ＜0；③﹣＜a＜0；④2a ＜c ．其中正确的个数是（）解：由题知，因为抛物线的对称轴为直线x＝，且与x轴的一个交点坐标为（，0），所以抛物线与x轴的另一个交点坐标为（，0），所以当x＞时，y＜0，则当x＞3时，y＜0．故①正确．因为抛物线的对称轴是直线x＝，所以，则3a+b＝0，又因为a＜0，所以4a+b＜0．故②正确．将（，0）代入函数解析式得，又因为b＝﹣3a，则c＝．而抛物线与y轴的交点B在（0，0）和（0，﹣1）之间（不包括这两点），所以﹣1＜c＜0，则﹣1＜＜0，得．故③正确．因为，a＜0，所以．又因为c＝，所以2a＜c．故④正确．故选：D．第Ⅱ卷二、填空题（本大题共4个小题，每小题4分，共16分）13．若代数式有意义，则实数x的取值范围是x≠﹣2．解：∵x+2≠0，∴x≠﹣2，故答案为：x≠﹣2．14．一个密闭不透明的口袋中有质地均匀、大小相同的白球若干个，在不允许将球倒出来的情况下，为估计白球的个数，小华往口袋中放入10个红球（红球与白球除颜色不同外，其它都一样），将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有63次摸到红球．估计这个口袋中白球的个数约为6个．解：设袋子中白球有x个，根据题意，得：＝，解得x≈6，经检验x＝6是分式方程的解，所以袋子中白球的个数约为6个，故答案为：6．15．已知a是方程x2+3x﹣1＝0的一个实数根，则2a2+6a+2021的值为2023．解：∵a是方程x2+3x﹣1＝0的一个实数根，∴a2+3a﹣1＝0，即a2+3a＝1，∴2a2+6a+2021＝2（a2+3a）+2021＝2×1+2021＝2023．故答案为：2023．16．如图，点A、B、E在同一条直线上，正方形ABCD的边长为3，正方形BEFG的边长为4，H为线段DF的中点，则BH的长为．解：如图所示，连接BD、BF，∵四边形ABCD和四边形BEFG都是正方形，且边长分别为3、4，∴AD＝AB＝3，BE＝EF＝4，∠A＝∠E＝90°，∠ABD＝∠CBD＝∠EBF＝∠FBG＝45°，∴，，∴在Rt△DBF中，，∵H为线段DF的中点，∴，故答案为：．三、解答题（本大题共9个小题，共98分．解答应写出文字说明，证明过程或演算步骤）17．（1）计算：（m+n）2﹣m（m+2n）．解：原式＝m2+2mn+n2﹣（m2+2mn）＝m2+2mn+n2﹣m2﹣2mn＝n2．（2）解不等式组．解：，解①得：x≥﹣1，解②得：x＞﹣4，∴原不等式组的解集为：x≥﹣1．18．为了让同学们了解自己的体育水平，初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试（得分均为整数），成绩满分为10分，1班的体育委员根据这次测试成绩，制作了统计图和分析表如下：初二1班体育模拟测试成绩分析表：平均分方差中位数众数男生7.9 1.9987女生7.92 1.993688根据以上信息，解答下列问题：（1）这个班共有男生20人，共有女生25人．（2）你认为在这次体育测试中，1班的男生队、女生队哪个表现更突出一些？并说明理由．（至少从两个不同的角度说明推断的合理性）（3）若1班恰有3名女生和1名男生在体育测试中表现优异，预计从这4名学生中随机选取2名学生参加区运动会，请用列表法或画树状图法求选出的2名学生恰好为一名男生、一名女生的概率．解：（1）由条形统计图可知，男生有1+2+6+3+5+3＝20（人），∴女生有45﹣20＝25（人）；故答案为：20，25；（2）我认为女生队表现更突出，理由如下：女生队的平均数较高，表示女生队测试成绩较好；女生队的众数较高，女生队的众数为8，中位数也为8，而男生队众数为7低于中位数8，表示女生队的测试成绩高分较多；（3）根据题意画树状图如下：共有12种等可能的结果，恰好为一名男生、一名女生的有6种，∴恰好为一名男生、一名女生的概率是＝．19．如图，在△ABC 中，AB ＝AC ，点D 在AC 边上，以CB ，CD 为边作▱DCBE ，DE 交AB 于点F ．（1）若∠A ＝50°，求∠E 的度数．（2）若AD ＝3CD ，BC ＝6，求EF ．解：（1）在△ABC 中，∵∠A ＝50°，AB ＝AC ，∴∠C ＝∠ABC ＝（180°﹣50°）÷2＝65°，∵四边形BCDE 是平行四边形，∴∠E ＝∠C ＝65°；（2）∵AD ＝3CD ，∴＝．∵四边形DCBE 是平行四边形，∴DE ∥BC ，DE ＝BC ＝6．∴＝＝．∴DF＝BC．∵BC＝6，∴DF＝．∴EF＝ED﹣DF＝6﹣＝．20．乐乐超市准备购进甲、乙两种商品进行销售，已知，每个甲商品的进价比每个乙商品的进价少2元，且用80元购进甲商品的数量与用100元购进乙商品的数量相同．（1）求每个甲、乙两种商品的进价分别是多少元？（2）若该商场购进甲商品的数量比乙商品的数量的3倍还少5个，甲、乙两种商品的售价分别是装12元/个和15元/个，且将购进的甲、乙两种商品全部售出后，可使总利润不少于456元，那么商场至少购进乙商品多少个？解：（1）设每件乙种商品的进价为x元，则每件甲种商品的进价为（x﹣2）元，根据题意，得＝，解得：x＝10，经检验，x＝10是原方程的根，每件甲种商品的进价为：10﹣2＝8．答：每件甲种商品的进价为8元，每件乙种商品件的进价为10元．（2）设购进乙种商品y个，则购进甲种商品（3y﹣5）个，根据题意得：（12﹣8）（3y﹣5）+（15﹣10）y≥456，解得：y≥28．∴该商场至少购进乙种商品28个．21．如图，一次函数y＝﹣x+3的图象与反比例函数y＝（k≠0）在第一象限的图象交于A（1，a）和B 两点，与x轴交于点C．（1）求反比例函数的解析式；（2）若点P在x轴上，且△APC的面积为6，求点P的坐标．解：（1）把点A（1，a）代入y＝﹣x+3，得a＝2，∴A（1，2）把A（1，2）代入反比例函数y＝（k≠0），∴k＝1×2＝2；∴反比例函数的表达式为y＝；（2）在直线y＝﹣x+3中，令y＝0，则x＝3，∴C（3，0），设P（m，0），∴PC＝|m﹣3|，∵△APC的面积为6，∴|m﹣3|×2＝6，∴|m﹣3|＝6，∴m＝﹣3或m＝9，∴P（﹣3，0）或（9，0）．22．图1是东缉虎营路口临时设置的一个太阳能移动交通信号灯，图2是信号灯的几何图形，信号灯由太阳能板、支架、指示灯、灯杆、底座构成，该信号灯是轴对称图形．太阳能板MN＝PQ＝102cm，且D，E是靠近N，Q的三等分点，支架AD＝AE＝80cm．经过调研发现，当太阳能板MN与支架AD所成的∠MDA＝104°，且支架AD与灯杆AC所成的∠DAC＝135°时，太阳能板接收的光能最充足，信号灯的续航时间最长，求此时两个太阳能板之间MP的长度．（结果精确到1cm）（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60，≈1.414）解：过点D作BA的垂线，交BA延长线于点F，过点M作DF的垂线，交DF与点G，连接MP交BA 延长线于点H，∴∠DFA＝90°，∠MGD＝90°．且由题意可知，四边形MGFH是矩形，∴MH＝GF，∵∠DAC＝135°，∴∠DAF＝45°，在Rt△DFA中，∠DAF＝45°，，又∵DA＝80cm，∴．∵MN＝102cm，且D是靠近N的三等分点，∴．∵∠MDA＝104°，∴∠MDG＝∠MDA﹣∠DAF＝104°﹣45°＝59°．在Rt△DMG中，∠DMG＝90°﹣∠MDG＝90°﹣59°＝31°，，∴DG＝DM⋅sin31°＝68×0.52≈35.36，∴GF＝DF﹣DG＝56.56﹣35.36＝21.20≈21（cm），∵该信号灯几何图形是轴对称图形，∴MP＝2MH＝2GF＝2×21＝42（cm），答：MP的长度为42cm．23．如图，AB为⊙O的直径，C、D为圆上两点，∠ABD＝2∠BAC．（1）尺规作图：作CE⊥BD于E（保留作图痕迹，不用写作图步骤）；（2）求证：CE是⊙O的切线；（3）若BE＝1，BD＝7，求CE的长度．（1）解：①以C为圆心，以任意长为半径画弧，但要和DB有两个交点M、N．②分别以M、N为圆心，以大于MN的一半的长为半径画弧，交于点P．③作射线CP，交DB于E．则CE即为所求．如图：（2）证明：连OC．∵OA＝OC，∴∠OAC＝∠OCA，∴∠BOC＝2∠BAC，∵∠ABD＝2∠BAC，∴∠ABD＝∠BOC，∴OC∥DB，∴∠OCA＝∠DEC＝90°，∴CE是⊙O的切线．（3）作直径CQ，连QB．∵QC为直径，∴∠Q+∠QCB＝90°，∵∠BCE+∠QCB＝90°，∴∠Q＝∠BCE，∵∠Q＝∠CDE，∴∠CDE＝∠BCE．∵∠BEC＝∠CED＝90°，∴△ECB～△EDC，∴＝，∴＝，∴EC＝2．24．已知抛物线y＝ax2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴的负半轴交于点C，且OB ＝OC，连接BC．（1）求抛物线的解析式．（2）P是抛物线上位于BC下方的一动点，且点P的横坐标为t．①求△AOP的最大面积．②是否存在一点P，使若存在，求出t的值；若不存在，请说明理由．解：（1）∵点B（3，0），OB＝OC，且点C在y轴负半轴，∴点C（0，﹣3）．设抛物线的解析式为y＝ax2+bx﹣3．将点A（﹣1，0），B（3，0）代入y＝ax2+bx﹣3，得，解得，∴抛物线的解析式为y＝x2﹣2x﹣3；（2）①∵P是抛物线上位于BC下方的一动点，且点P的横坐标为t．∴P（t，t2﹣2t﹣3），∵S△AOP＝AO•|t2﹣2t﹣3|＝（﹣t2+2t+3）＝﹣（t﹣1）2+2，∴当t＝1时△AOP的最大面积为2．②∵S＝S△ABC＝S△ABC+S△BCP，四边形ACPB∴S△BCP＝S△ABC＝××4×3＝3，过点P作PQ⊥x轴，交BC于Q，∵P（t，t2﹣2t﹣3），∴Q（t，t﹣3），∴PQ＝t﹣3﹣t2+2t+3＝﹣t2+3t，∴S△BCP＝×3（﹣t2+3t）＝3，解得t＝1或2，∴存在，t的值为1或2．25．（1）探究规律：如图1，点P为平行四边形ABCD内一点，△PAB、△PCD的面积分别记为S1、S2，平行四边形ABCD 的面积记为S，试探究S1+S2与S之间的关系．（2）解决问题：如图2矩形ABCD中，AB＝4，BC＝7，点E、F、G、H分别在AB、BC、CD、DA上，且AE＝CG＝3，AH＝CF＝2．点P为矩形内一点，四边形AEPH、四边形CGPF的面积分别记为S1、S2，求S1+S2．解：（1），理由如下，如图所示，过P点作EF∥AB，作PG⊥BA延长线于点G，延长GP交CD于点H，∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD∴EF∥CD∥AB，GH⊥BG，GH⊥CD，∴S1＝AB•PG，S2＝CD•PH，S▱ABFE＝AB•PG，S▱FECD＝CD•PH，∴，．∵S＝S▱ABCD＝AB⋅GH＝S▱ABFE+S▱EFCD，∵S▱ABFE+S▱EFCD＝S，∴．（2）如图所示，连接EF、FG、GH、HE得四边形EFGH，∵四边形ABCD是矩形，∴∠A＝∠B＝∠C＝∠D＝90°，AB＝CD＝4，AD＝BC＝7，∵AE＝CG＝3，∠A＝∠C，AH＝CF＝2，∴△AEH≌△CGF（SAS），∴EH＝GF，且S△AEH＝S△CGF＝AH•AE＝×2×3＝3，同理可得，△BFE≌△DHG（SAS），HG＝EF，BE＝AB﹣AE＝4﹣3＝1，BF＝BC﹣CF＝7﹣2＝5，S△BFE＝S△DHG＝BE•BF＝×1×5＝，∴四边形EFGH为平行四边形，S▱EFGH＝S矩形ABCD﹣S△AEH﹣S△BEF﹣S△CFG﹣S△DGH，∴，由（1）可得，∴S1+S2＝S△AEH+S△CFG+S△EHP+S△FGP＝3+3+8.5＝14.5．。

贵州省贵阳市2024-2025学年九年级上学期12月月考数学试题一、单选题1．在3，1，0，1-四个数中最小的一个数是（）A ．3B ．1C ．0D ．1-2．下列几何图形既是中心对称图形又是轴对称图形的是（）A ．B ．C ．D ．3．已知2x =是一元二次方程280ax -=的解，则a 的值是（）A ．2B ．1C ．1-D ．2-4．如图，ABC V 是等腰直角三角形，a b ∥．若1125∠=︒，则2∠的度数是（）A ．30︒B ．35︒C ．40︒D ．45︒5．下列计算正确的是（）A ．22a a -=B ．824a a a ÷=C ．()236a a =D ．3412a a a ⋅=6．《九章算术》中有这样一道题，大意是：假设有5头牛、2只羊，值10两金；2头牛、5只羊，值8两金．问1头牛、1只羊各值多少金？设1头牛、1只羊分别值x ，y 金，则列方程组正确的是（）A ．510,58.x y x y +=⎧⎨+=⎩B ．5210,258.x y x y +=⎧⎨+=⎩C ．58,510.x y x y +=⎧⎨+=⎩D ．528,2510.x y x y +=⎧⎨+=⎩7．如图，O 是PAB 的外接圆，OC AB ⊥，连接OB ．若50BOC ∠=︒，则APB ∠的度数是（）A ．45︒B ．50︒C ．55︒D ．60︒8．在一列数1，8，x ，4，9，4，11中，众数是4，平均数是7，中位数是8，则数x 是（）A ．3B ．6C ．9D ．129．如图，四边形ABCD 为菱形，对角线AC ，BD 交于点O ，DE AB ⊥，垂足为E ．若5AB =，6BD =，则DE 的长是（）A ．125B ．185C ．245D ．48510．某函数自变量x 与函数值y 的对应关系如下表，则该函数的表达式可以是（）x…3-2-1-01…y…3-3533-…A ．y x=B ．615y x =+C ．223y x =+D ．2243y x x =--+11．如图，正方形ABCD 中，AC 为对角线，E ，F 分别为AB ，CD 上的点，将BCE 与DAF △分别沿CE ，AF 折叠，使B ，D 分别落在对角线AC 上的B '，D '处．若2AB =，则B D ''的长是（）A ．4-B ．4C ．2D ．112．在平面直角坐标系中，函数2y ax bx c =++（0a ≠）的图象与坐标轴交于A ，B ，C 三点，则下列说法正确的是（）（1）240b ac -<；（2）若ABC V 是周长为0c >，则函数图象经过点()1,2-；（3）若a ，c 的值不变，则ABC V 的面积随b 的增大而减小；（4）若ABC V 是直角三角形，则20ax bx c ++=的判别式4∆≥．A ．（1）（3）B ．（2）（3）C ．（2）（4）D ．（3）（4）二、填空题13x 的取值范围是．14．将三个小球分别标上C ，O ，H 三种化学元素符号（除标记符号外，其余均相同），放入一个不透明的袋中，探匀后从中任意摸出2个小球，能够组成CO （一氧化碳）的概率是．15．已知12,x x 是方程2310x x +-=的两个根，则211252x x x ++的值是．16．如图，AC 是矩形ABCD 的对角线，DE AC ⊥，垂足为E ，点M ，N 分别在线段AC ，BC 上，:2AM CN =MNE 是以ME 为腰的等腰三角形，10AB =，30CAD ∠=︒，则AM 的长是．三、解答题17．（11122-⎛⎫⎪⎝⎭；（2）下面是用配方法解一元二次方程2450x x --=的过程：解：移项，得245x x -=，……第一步配方，得2441x x -+=，……第二步即()221x -=．开方，得21x -=±，……第三步解得13x =，21x =．……第四步以上过程从第______步开始出错．请用适当的方法解该方程．18．请从①221x x x -+，②221x xx +-，③1x x +中选取两个式子相乘并化简，再从1-，1，2中选择合适的数代入求值．19．某校为落实“双减”政策，利用课后服务时间开展社团活动，社团分为美术、体育、劳技、音乐、科技共五大类，每个学生只能选报一个社团、为了解学生参与社团的情况，学校随机抽取了部分学生进行调查，根据调查结果绘制成如下统计图，解答下列问题．(1)学校随机抽取了______名学生进行调查，补全条形统计图：(2)该校1800名学生中参加科技社团的学生大约有多少人？(3)该校从美术社团中挑选了男、女生各两名，再从这四名学生中随机抽取两人参加绘画比赛，请用树状图或列表的方法求恰好抽到男、女生各一名的概率．20．如图，二次函数2y ax bx c =++的图象与x 轴交于A ，B 两点，与y 轴交于点C ，点B 的横坐标为4，当32x =时，y 有最大值254：(1)求二次函数的表达式；(2)点P 在对称轴上，当PA PC +的值最小时，求点P 的坐标．21．如图，AB 为O 的直径，D 为O 上一点，过点D 的直线与AB 的延长线交于点C ，点E 在直线CD 上，连接AD ，AE ．有下列条件：①AE CD ⊥；②AD 平分CAE ∠；③CD 为O 的切线，(1)请从以上①②③中选取两个作为条件，证明另外一个成立．(2)当6AB =，30C ∠=︒时，求图中阴影部分的面积．22．某商品每件的成本为100元，销售价（元/件）与时间（天）之间的函数关系如下图所示，商家预测未来30天的日销售量（件）与时间（天）满足函数表达式2140y x =-+．(1)求销售价（元/件）与时间（天）之间的函数表达式，写出自变量的取值范围；(2)在未来30天中哪天销售利润最大？求出该天销售利润．23．如图，在平面直角坐标系中，AOB V 为等腰直角三角形，90B Ð=°，点A 的坐标为()2,0，将AOB V 绕点O 逆时针旋转90°得到A OB ''△（A 的对应点为A '，B 的对应点为B '）．(1)写出图中一个度数为45°的角：________；(2)在平面直角坐标系中画出A OB ''△，点B '的坐标是________；(3)以()2,0M -为圆心的圆与A OB ''△三边中的一边所在直线相切，求⊙M 的半径．24．如图，在正方形ABCD 中，点Q 在射线DC 上（不与C ，D 重合），点P 为直线BC 上一点，DAQ PAQ ∠=∠．(1)如图①，若30DAQ ∠=︒，3AB =，DQ 的长是________，AP 的长是________；(2)如图②，当Q 在线段DC 上时，猜想AP ，BP ，DQ 之间的数量关系并证明；(3)当Q 在线段DC 的延长线上时，第()2问中的结论是否成立？若成立，说明理由；若不成立，请探究AP ，BP ，DQ 之间的数量关系．25．初中阶段学习函数的方法：通过“列表、描点、连线”的方法画函数图象，根据图象研究性质，用性质解决问题。

62014中考数学模拟考试数学试卷1．﹣3的相反数为（ ▲ ）A 、3B 、13C 、﹣3D 、13-2．已知地球上海洋面积约为316 000 000km 2，316 000 000这个数用科学记数法可表示为( ▲ )A ．3.16×109B ．3.16×108C ．3.16×107D ．3.16×1063．如图所示的是零件三通的立体图，则这个几何体的俯视图是（ ▲ ）A B C D4．已知反比例函数1y x-=，下列结论中正确的是（ ▲ ）A.图象经过点（1，1）B.图象在第一、三象限C.当1>x 时，10y -<<D.当0<x 时，y 随着x 的增大而减小5．如图，在Rt △ABC 中，90C ∠=︒，4AC =，3BC =，则tan A 的值为（ ▲ ） A ．34 B ．43 C ．35 D ．456．已知圆锥的母线长为5，底面半径为3，则圆锥的表面积为（ ▲ ） A ．15π B ．24π C ．30π D ．39π7．已知⊙O 1和⊙O 2的半径分别为2cm 和5cm ，两圆的圆心距是3cm ，则两圆的位置关系是（ ▲ ）A ．内含B ．外切C ．内切D ．相交8．某班体育委员调查了本班46名同学一周的平均每天体育活动时间，并制作了如图所示的频数分布直方图，从直方图中可以看出，该班同学这一周的平均每天体育活动时间的中位数和众数依次是（ ▲ ）A ．40分，40分B ．50分，40分C ．50分，50分 D ．40分，50分（第5题图）(第8题图)主视方向（第3题图）D (第9题图)(第10题图)E PABCF(第16题图）9．如图，AC 是菱形ABCD 的对角线，AE EF FC ==，则:BMNABCD S S 菱形 =（ ▲ ）A ．34 B ．37 C ．38 D ．31010．如图，在Rt △ABC 中，90A ∠=︒，P 为边BC 上一动点，PE ⊥AB 于E ，PF ⊥AC 于F ，动点P 从点B 出发，沿着BC 匀速向终点C 运动，则线段EF 的值大小变化情况是（ ▲ ） A. 一直增大 B.一直减小 C. 先减小后增大 D.先增大后减少 11．计算：23()a ▲ ．12．如图，已知//,,35AB CD BC ABE C BEC ∠∠=︒∠平分，则的度数是 ▲ ． 13．某校艺术节演出中，5位评委给某个节目打分如下：9分，9.2分，8.9分，8.8分，9.1分，则该节目的平均得分是 ▲ 分．14．阳阳从家到学校的路程为2400米，他早晨8点离开家，要在8点30分到8点40分之间到学校，如果用x 表示他的速度（单位：米/分），则x 的取值范围为 ▲ ． 15．如图，在平面直角坐标系xoy 中，直线AB 过点A （－4，0），B （0，4），⊙O 的半径O 为坐标原点），点P 在直线AB 上，过点P 作⊙O 的一条切线PQ ，Q 为切点，则切线长PQ 的 最小值为 ▲ ．16．如图，已知直线y ＝2x ＋6交y 轴于点A ，点B 是这条直线上的一点，并且位于第一象限，点P 是直线x=8上的一动点，若△APB 是等腰直角三角形，则点B 的坐标为17．（本题10分）（1）计算：101()(2013)3π-+-+（2）解方程：xx x -=+--2312318．（本题6分）（1）在图①中确定格点D ，并画出一个以A ，B ，C ，D 为顶点的四边形，使其为轴对称图形；（2）在图②中确定格点E ，并画出一个以A ，B ，C ，E 为顶点的四边形，使其为中心对称图形．（第12题图）AD(第15题图)19．（本题8分）如图，在□ABCD 中，分别延长BA ，DC 到点E ，使得AE=AB ，CH=CD ，连接EH ，分别交AD ，BC 于点F ,G 。

2014-2015年张武帮中学九年级上第二次月考数学试卷及答案一、精心选一选，相信你一定能选对！（每小题3分，共30分）1．下列关于一元二次方程122=-x x 的各项系数说法正确的是( ) A. 二次项系数为：0 B. 一次项系数为：2 C. 常数项为：1 D. 以上说法都不对 2．在反比例函数xm1y -=的图象的每一条曲线上，y 都随x 的增大而增大，则m 的值可以是 （ ）.A.2B.1C.0D. －13．用配方法解方程2420x x -+=，下列配方正确的是（ ） A ． 2(2)2x -=B ．2(2)2x +=C ．2(2)2x -=-D ．2(2)6x -=4．若△ABC ∽△A ＇B ＇C ＇，则相似比k 等于（ ） A ．A ＇B ＇:AB B ．∠A: ∠A ＇C ．S △ABC ：S △A`B`C`D ．△ABC 周长：△A ＇B ＇C ＇周长5．如图5，已知菱形ABCD 的边长为2，∠DAB =60°，则对角线BD 的长是 （ ）A ．1B ．2 D ．6．如图6，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E 、B 、D 、F ，AC ＝ 4，CE ＝ 6，BD ＝ 3，则BF 等于（ ） A ． 7 B ． 7.5 C ． 8 D ． 8.57．观察下列表格，一元二次方程21.1x x -=的一个近似解是（ ）8．已知x=2是一元二次方程x 2﹣2mx+4=0的一个解，则m 的值为（ ）A ．2B ．0C ．0或2D ．0或﹣29．下列各组图形中相似的图形是（ ） A 、对应边成比例的多边形 B 、四个角都对应相等的两个梯形 C 、有一个角相等的两个菱形 D 、各边对应成比例的两个平行四边形10. 如图，A （1x ，1y ）、B （2x ，2y ）、C （3x ，3y ）是函数1y x=的图象在第一象限分支上的三个点，且1x ＜2x ＜3x ，过A 、B 、C 三点分别作坐标轴的垂线，得矩形ADOH 、BEON 、CFOP ，它们的面积分别为S 1、S 2、S 3，则下列结论中正确的是（ ） A ．S 1<S 2<S 3 B ．S 3 <S 2< S 1 C ．S 2< S 3< S 1 D ．S 1=S 2=S 3图5 图6 图10二、细心填一填，相信你填得又快又准！（每小题4分，共24分） 11．若关于x 的一元二次方程2210kx x --=有两个不相等的实数根， 则实数k 的取值范围是 ．12．下列函数中是反比例函数的有 _________ （填序号）. ①3x y ＝－； ②x y 2＝－； ③xy 23－＝； ④21＝xy ； ⑤1－＝x y ；⑥2＝x y ； ⑦x k y ＝（k 为常数，0≠k ）13．抽屉里有２只黑色和１只白色的袜子，它们混在一起，随意抽出两只刚好配成一双的概率是________.14．已知P 是线段AB 的黄金分割点，且AB ＝10cm ，则AP 长为_____________. 15．如图15， C 为线段AB 上的一点，△ACM、△CBN 都是等边三角形， 若 AC ＝3，BC ＝2，则△MCD 与△BND 的面积比为______.16．在平面坐标系中，正方形ABCD 的位置如图16所示，点A 的坐标为（1，0）， 点D 的坐标为（0，2），延长CB 交x 轴于点A1，作正方形A1B1C1C ，延长C1B1交x 轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第2014个正方形的面积为____.图15 图162014～2015学年度张武帮中学九年级上第二次月考数学答题卷一、选择题（每小题3分，共30分） 二、填空题（每小题4分，共24分）11．_______ ；12. ________ ；13. _______、______ 14．________； 15. _________ ；16. __________ . 三、解答题（一）（每小题6分，共18分）17．解方程：x 2－4x －12=018．画出下面实物的三视图：19．如图，ABC △中，DE BC ∥，2AD =，3AE =，4BD =，求AC 的长。