基于TMS320F206 DSP 的冗余度TT-VGT 机器人的运动学求解
- 格式:pdf
- 大小:161.95 KB
- 文档页数:5
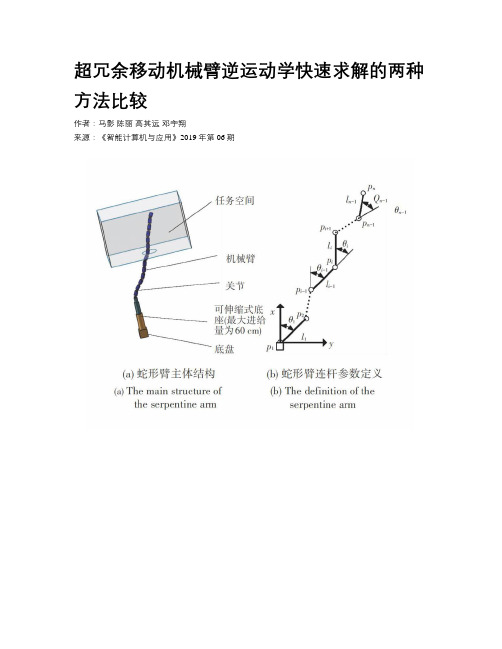
超冗余移动机械臂逆运动学快速求解的两种方法比较作者:马影陈丽高其远邓宇翔来源:《智能计算机与应用》2019年第06期摘要:超冗余移动机械臂的逆运动学求解一直是机器人领域研究的热点,特别是逆运动学求解过程中导致的计算量大、机械臂的位形偏移量大及能耗大等问题还未得到有效解决。
因此本文给出基于几何方法的超冗余机械臂逆运动学快速求解算法,并分析了两种关节位置更新策略的能耗。
第一种关节位置更新策略为“关节落在连线上”,即更新后的关节位置落在该关节的目标点和与其相连的前一个关节的连线上;第二种关节位置更新策略为“关节落在轴线上”,即更新后的关节位置落在前一时刻的该关节和与其相连的前一个关节的轴线上。
从运动过程中关节跟踪角度变化范围多少出发,比较超冗余移动机械臂在这2种关节更新策略下运动特点。
实验结果显示,方法1具有关节移动范围小,移动距离短的特点。
方法2具有各个关节都有相似的运动轨迹,机械臂的末端跟随效果好的特点。
关键词:超冗余移动机械臂;逆运动学;几何解析法;关节更新策略0引言超冗余移动机械臂是由杆件、关节、末端执行器组成的互相连接互相依赖的运动机构。
相对于固定机械臂而言,超冗余移动机械臂具有作业范围大、灵活性高和广阔的应用前景。
因此移动机械臂广泛应用在搬运、焊接、灾后救援、探测、等恶劣环境中。
但是对于冗余型移动机械臂而言,逆运动学求解计算量大且不唯一、机械臂运动位形偏移量大、逆解求解速度缓慢等是需要攻克的难题。
近年来,求解机械臂逆解的方法主要有数值迭代法、智能算法。
目前,也相继涌现出一系列的研究成果。
朱经纬等人提出了一种自适应粒子群算法求解机械臂逆运动学,以正向运动学方程为基础,将冗余机械臂逆运动学解问题转化为等效最小值问题。
张熙峰等人提出了基于遗传算法的机械臂逆运动学求解,将种群定义为机械臂的关节角轨迹层面。
利用连续性函数来实现算法的初始化算子、交叉算子和变异算子。
张云峰等人提出了基于改进QPSO-NN(粒子群优化)的冗余机械臂逆运动学算法,以冗余机械臂末端位姿为输入,利用神经网络算法求得其逆解。

运动学逆解公式
运动学逆解是指已知机器人末端执行器的位置、姿态和运动学参数,求解机器人各关节的角度。
运动学逆解公式的具体形式取决于机器人的类型和结构,以下是几种常见机器人的运动学逆解公式:
1. 二自由度平面机械臂的运动学逆解公式:
θ1 = atan2(y, x) - acos((l1^2 + l2^2 - r^2)/(2*l1*l2))
θ2 = -acos((x^2 + y^2 - l1^2 - l2^2)/(2*l1*l2))
其中,θ1和θ2分别为机械臂两个关节的角度,x和y为末端执行器的位置坐标,l1和l2为机械臂两个关节的长度,r为末端执行器到机械臂起点的距离。
2. 三自由度空间机械臂的运动学逆解公式:
θ1 = atan2(y, x)
θ3 = acos((x^2 + y^2 + z^2 - l1^2 - l2^2 - l3^2)/(2*l2*l3))
k1 = l2 + l3*cos(θ3)
k2 = l3*sin(θ3)
θ2 = atan2(z, sqrt(x^2 + y^2)) - atan2(k2, k1)
其中,θ1、θ2和θ3分别为机械臂三个关节的角度,x、y和z为末端执行器的位置坐标,l1、l2和l3为机械臂三个关节的长度。
3. 六自由度工业机器人的运动学逆解公式:
由于六自由度工业机器人的运动学逆解公式比较复杂,这里不再给出具体公式。
通常采用数值计算方法求解,如牛顿-拉夫逊法、雅可比逆法等。
需要注意的是,运动学逆解公式只能求解机器人的正解,即机器人末端执行器的位置、姿态和运动学参数必须是合法的。
如果末端执行器的位置、姿态和运动学参数不合法,就无法求解出机器人各关节的角度。

一种冗余机械臂的简化运动学求解方法
高春艳;唐家豪;吕晓玲;张明路
【期刊名称】《机械科学与技术》
【年(卷),期】2022(41)8
【摘要】七自由度机械臂从结构上冗余一个自由度,是为躲避障碍物和奇异点而设置。
但因其冗余自由度导致运动学求解难度增加,计算耗时长,直接影响后续运动及
控制效率。
本文基于一款轻型仿人七自由度机械臂,提出了一种求逆解的简化方法,
基于机械臂的自运动特性,将几何方法与解析方法结合,此方法在传统的利用罗德里
格斯变换的方法基础上简化了求解臂型角为零时求解θ_(1)、θ_(2)、θ_(3)的过程,有效的对此机械臂进行运动学求解。
并通过MATLAB中的Robotics Toolbox工
具箱对所求结果进行验证,所得结果正确快速,为之后的机械臂运动控制奠定了基础。
【总页数】6页(P1191-1196)
【作者】高春艳;唐家豪;吕晓玲;张明路
【作者单位】河北工业大学机械工程学院
【正文语种】中文
【中图分类】TP241
【相关文献】
1.构形平面方法求解冗余机械臂逆运动学
2.超冗余移动机械臂逆运动学快速求解的两种方法比较
3.超冗余移动机械臂逆运动学快速求解的两种方法比较
4.一种求解
冗余机械臂逆运动学的自适应动态差分进化算法
因版权原因,仅展示原文概要,查看原文内容请购买。

解释机器人运动学方程的正解和逆解
机器人运动学方程是研究机器人运动规律的一种数学工具。
机器人运动由位置、速度和加速度三部分组成,而机器人运动学方程便是描述这三部分关系的方程。
机器人运动学方程分为正解和逆解。
正解是指根据机器人关节角度、长度等参数,推导出机器人末端执行器的位置、速度和加速度等运动学参数的过程。
在机器人运动学分析中,正解一般使用解析法、几何法和向量法等方法。
通常我们会在正解中借助三角函数和向量函数,对机械臂的运动主体进行数学建模,推导出机器人最终执行器的位置和末端的速度、加速度等参数,完成机器人运动学方程的正解。
而逆解则是指在已知机器人末端执行器的位置、速度和加速度等参数的基础上,求出机器人关节角度,这样机器人才能达到需要执行的动作。
逆解是机器人指令控制中的核心技术之一,一般采用数值计算的方法来求解。
逆解方法有直接法和迭代法两种,直接法一般应用于计算复杂的工业机器人,而迭代法则更适用于机场搬运、医疗康复等关节数较少的应用场景。
机器人运动学方程的正解和逆解都涉及高等数学和工程数学的知识,需要对机器人的运动学规律有一定的理解和掌握。
随着人工智能和机器人技术的不断发展,机器人运动学方程的应用将得到更广泛的推广和应用,成为未来机器人研究和应用的重要工具。

六自由度机器人逆向运动学解题过程
六自由度机器人逆向运动学主要是通过求解机器人末端执行器的位姿,从而得到关节的角度。
逆向运动学求解的过程如下:
1. 了解机器人运动学模型:首先需要了解六自由度机器人的运动学模型,包括机器人臂部的结构、关节类型和运动学参数。
常见的运动学模型有DH(Denavit-Hartenberg)模型和旋量法。
2. 建立运动学方程:根据机器人臂部的结构,建立运动学方程。
对于DH模型,运动学方程为:
θ1 * A1 + θ2 * A2 + θ3 * A3 + θ4 * A4 + θ5 * A5 + θ6 * A6 = T
其中,θ1-θ6为六个关节的角度,A1-A6为相邻两个关节之间的变换矩阵。
3. 初始化关节角度:给定一个初始的关节角度序列,作为求解逆向运动学的输入。
4. 求解位姿:利用运动学方程,将关节角度序列代入,计算出末端
执行器的位姿。
5. 评价求解结果:根据实际应用需求,评价求解结果的精度和实用性。
如果结果不满足要求,可以调整初始关节角度序列,重复步骤2-4,直至得到满意的解。
6. 应用:将求解得到的关节角度序列应用于机器人控制系统,实现机器人的运动。
在求解过程中,可以使用一些优化算法,如牛顿法、梯度下降法等,以提高求解速度和精度。
同时,为了减少计算复杂度,可以采用一些技巧,如LU分解、QR分解等。
需要注意的是,六自由度机器人逆向运动学求解过程依赖于机器人运动学模型的精确性、运动学方程的稳定性和求解算法的性能。
在实际应用中,可能需要根据具体情况调整模型和算法,以获得更优的求解结果。

基于TMS320F206 DSP的冗余度TT-VGT机器人的运动学求解
作者:成都四川大学电气信息学院(610065)雷勇成都四川大学机械系徐礼钜
来源:《电子技术应用》
摘要:提供了采用TMS320F206 DSP芯片进行冗余度TT-VGT机器人运动学计算方案。
该方案充分利用DSP并行特性进行机器人位姿逆解计算,在程序设计中采用了多种技巧以实现优化计算,并对四重四面体变几何桁架(TT-VGT)机器人进行了仿真计算。
关键词:DSP 并行计算 TT-VGT机器人运动学
20世纪90年代以来,数字信号处理器(DSP)在自动控制中得到越来越广泛的应用。
这主要是因为它具有以下优点:(1)并行体系结构和专用的硬件乘法器使得DSP运算能力极强;(2)高速特性使得DSP能实现实时处理和实时控制。
据调查,目前将DSP应用于机器人控制系统的方案,通常是将机器人位置控制中运动学计算任务交给PC机完成,PC机将计算结果(机器人各关节的转角)下载到以DSP芯片为核心的电机控制器,实现机器人控制[2]。
本文提出将机器人运动学计算任务直接交给DSP的控制方案,利用DSP的并行性计算特点,提高了计算速度,缩小了控制系统的体积。
仿真结果表明,该方案计算精度和实时性都较好。
1 TMS320F206 DSP结构特点
TMS320F206DSP基本结构特点包括:①哈佛结构;②流水线操作;③专用的硬件乘法器;④特殊的DSP指令;⑤快速的指令周期(25ns);⑥芯片内部集成了4.5KRAM和32K FLASH RAM,大多数程序及数据可存放在DSP芯片内。
这些特点使得该芯片可以实现快速的DSP计算,并能使大部分运算能够在一个指令周期内完成。
TMS320F206的并行性表现在以下两方面:
(1)哈佛结构是不同于传统的冯诺曼结构的并行体系结构,其主要特点是将程序和数据存储在不同的存储空间,因此取指令和执行能完全重叠运行。
(2)DSP芯片广泛采用流水线以减少指令执行时间。
指令流水线由一系列总线操作组成。
TMS320F206流水线具有4个独立的操作阶段:取指令、译码、取操作数和执行,如图1所示。
由于4个操作阶段是独立的,因此,这些操作可交叠地进行。
2 TT-VGT机器人的位姿逆解
TT-VGT(Tetrahedron-Tetrahedron-Variable Geometry Truss)机器人是由多个四面体组成的变几何桁架机器人,平面ABC为机器人的基础平台,基本单元中各杆之间由球校连接,通过可伸缩构件
li(i=1,2,…n)的长度,来改变机构的构形,如图2所示。
设冗余度TT-VGT机器人操作手由N个伸缩关节组成,图3所示为两个单元的TT-VGT构成。
设变量qi(i=1,2,…N)为平面ACB和平面BCD的夹角,其相应的速度和加速度分别为qi,qi(i=1,2,…N)。
它们与li,li,li(i=1,2,…N)的关系如下[1]:
式中,d表示TT-VGT中不可伸缩构件的长度
li,l'i,l''I分别表示机器人可缩构件的长度、速度和加速度
相邻两个四面体单元的坐标系的建立如图3所示。
坐标系XiYiZi相对于坐标系Xi-1Yi-1的变换矩阵可表示为:
对于机构自由度为N、任务自由度为L的冗余度TT-VGT机器人,其余四面体单元的结构与坐标系的建立与图3所示的相似。
由文献[1]可知,其末端位姿X是中间变量qi(i=1,2,…,N)的函数,有:
X=f(q) (3)
对式(3)求导,可得如下的运动学方程式:
X=Jq (4)
式中,X=(x1,x2,…,xL) T∈R L
q=(q1,q2,…,qN)T∈R N
L<N
J为机器人的雅可比矩阵,
由式(4)可得:
q=J + X (6)
式中,J+为雅可比矩阵的伪逆,
J+=J T(JJT)-1 (7)
将式(6)离散化,可得机器人运动轨迹上第k点各关节中间变量的dqk及位置qk:
dqk=J+dXk (8)
q k=q (k-1)+dq k (9)
将q k代入式(1),可求得TT-VGT机器人各伸缩构件的长度li。
3 TMS320F206 DSP运动学程序设计
对于TT-VGT机器人的位姿逆解,采用DSP汇编语言设计的程序流程进行求解,如图4所示。
为了保证该程序的执行速度和计算精度,采取了以下算法:
(1)由于汇编语言指令系统中没有三角函数等数学函数指令,这些函数的计算只有通过级数展开算法实现,但计算量太大。
考虑到三角函数的周期性,建立了一人1024点的正弦函数和余弦函数表,其分辨率完全能满足精度要求。
(2)由于TMS320F206 DSP芯片为定点运算器
件,因此需要将浮点运算转换为定点运算。
为保证计
算精度,将数据定标设定为可动态调节,数据表达能
力为从Q13(-4~+3.9998779)到Q0(-32768~
+32767)。
(3)采用并行指令,充分利用TMS320F206四级流水线操作,来提高程序运行速度。
如:
MAC ;乘并累加
APAC ;累加
SACH +,3,AR2 ;将计算结果左移3位后,存于当前辅助寄存器(AR)所指的存储器单元中,并将AR内容加1,最后,将AR2设定为当有AR。
(4)对运算过程进行优化,
既要减少计算量,又要防止计算溢
出;在混合运算中采用“先除后
加”、“加减交叉”的方法。
(5)尽量采用移位运算代替
乘除运算,以提高运行速度和计算
精度。
通过以上方法,实现了机器
人运行学计算的实时性和准确性。
4 仿真计算
以四重四面体为例,建立如图5所示的基础坐标系XYZ,末端参考点H位于末端平台EFG的中点。
设参考点H在基础坐标系中从点(0.522689,-0.818450,0.472752)直线运动到点(0.771439,-0.965700,0.721502),只实现空间的位置运动,不实现姿态。
动态的整个时间T设为5秒,运动轨迹分为等时间间隔的100个区间。
设各定长构件长度为1m。
中间变量q曲线和中间变量q误差曲线如图6和图7所示。
从误差曲线可看出,采用
TMS329F206DSP芯片进行的运动学计算精度较高。
经过实测,该计算程序运行时间为34ms。
(TMS320F206芯片指令周期为25ns),可见其实时性较强。
本文提出的采用TMS320F206 DSP的芯片进行冗余度TT-VGT机器人运动学计算方案,充分利用了DSP 并行特性进行机器人位姿逆解计算,在程序设计中采用了多种技巧优化计算。
仿真结果表明,该方案计算误差较小,实时性强。
因此,可将其应用于机器人控制系统,实现机器人计算和控制任务一体化,从而大大缩小机器人体积、降低成本、增强灵活性、具有较强的先进性和实用性。