小波去噪和小波包去噪的对比
- 格式:doc
- 大小:120.50 KB
- 文档页数:5

⼩波分解和⼩波包分解这篇⽂章介绍了⼩波分解和⼩波包分解。
⼩波分解(wavelet transform )⼩波傅⾥叶变换的基本⽅程是sin 和cos ,⼩波变换的基本⽅程是⼩波函数(basic wavelet),不同的⼩波在波形上有较⼤的差异,相似的⼩波构成⼀个⼩波族(family)。
⼩波具有这样的局部特性:只有在有限的区间内取值不为0。
这个特性可以很好地⽤于表⽰带有尖锐, 不连续的信号。
⼩波变换其中 表⽰变换得到的⼩波系数,W 是正交矩阵。
是输⼊信号。
正交矩阵构造特定的⼩波函数(basic wavelet )由⼀组特定的⼩波滤波系数(wavelet filter coefficients)构成。
当选定了⼩波函数,其对应的那组⼩波滤波器系数就知道。
⽤⼩波滤波器系数构造不同维度的低通滤波器和⾼通滤波器(下⾯的例⼦中W 就是由这些系数构造出来的)。
低通滤波器可以看作为⼀个平滑滤波器(smoothing filter)。
这两个滤波器,低通和⾼通滤波器,⼜分别被称为尺度(scaling)和⼩波滤波器(wavelet filter)。
⼀旦定义好了这两个滤波器,通过递归分解算法(也称为⾦字塔算法(pyramid algorithm),树算法(tree algorithm)将得到⽔平多分辨率表⽰的信号。
树算法原始信号通过低通滤波器得到低频系数 (approximate coefficients), 通过⾼通滤波器得到⾼频系数(detail coefficients )。
把第⼀层的低频系数作为信号输⼊,⼜得到⼀组approximate coefficients 和detail coefficients 。
再把得到的approximate coefficients 作为信号输⼊,得到第⼆层的approximate coefficients 和detail coefficients 。
以此类推,直到满⾜设定的分级等级。

小波去噪阈值处理小波去噪是一种非常有效的信号处理方法,可以用于降低信号噪声对信号质量的影响,在很多应用场景中得到了广泛的应用,例如图像处理、语音处理、生物信号处理等。
而阈值处理是小波去噪过程中的一个关键环节,它决定了去除噪声的效果和保留信号细节的程度。
本文将详细介绍小波去噪和阈值处理的原理、方法和应用。
一、小波去噪原理小波去噪的基本原理是利用小波变换将信号分解成不同频率的子信号,然后通过对不同频率子信号进行阈值处理来去除噪声。
具体步骤如下:1. 将原始信号进行小波分解,得到多个尺度和频带的子信号。
2. 对每个子信号进行阈值处理,将小于某个阈值的系数置为0,大于阈值的系数保留。
3. 将处理后的子信号进行小波重构,得到去噪后的信号。
小波去噪的实现可以采用基于硬阈值或软阈值的方法。
硬阈值法:当小波系数绝对值小于阈值时,将其置为0。
软阈值法:当小波系数绝对值小于阈值时,将其置为0;当小波系数绝对值大于阈值时,用系数减去阈值的符号函数乘以阈值得到新的系数。
二、阈值确定方法阈值处理的成功与否取决于选择适当的阈值。
阈值的确定是小波去噪的核心问题之一,以下是几种比较常见的阈值确定方法:1. 固定阈值法:直接将固定的阈值应用到所有子带中。
缺点是不同信号质量和性质的信号适用的阈值不同,固定阈值法不灵活。
2. 聚类阈值法:将小波系数按大小排序,按固定的步长确定一定数量的阈值。
计算每个子带中小于阈值的系数的平均值和标准差,再将它们作为该子带的阈值参数。
缺点是对于每个信号,都需要多次试验选择最优的步长。
3. 利用样本特征值确定阈值:对于多种不同性质的样本,提取其中一定的特征值,如样本的均值或中值,并将其作为阈值对待。
缺点是对于不同的信号,需要多次测试阈值的灵敏度。
4. 神经网络法:利用神经网络的训练能力,让神经网络自己学习适合某种类型信号的阈值算法。
神经网络法带有较强的自适应性和实时性,但缺点是需要大量的样本数据和更高的计算复杂度。



第21卷第5期海军航空工工程学院学报报Vol.21No.52006年9月JOURNAL OF NA VAL AERONAUTICAL ENGINEERING INSTITUTE Sep.2006收稿日期2006-05-25作者简介史贤俊1968男副教授硕士.基于最优小波包基的信号去噪算法及其应用史贤俊1林飒2李瑞亮31海军航空工程学院控制工程系山东烟台2640012海装驻北京地区军事代表室北京100854392840部队山东胶南266405摘要提出了一种基于Shannon 熵准则的最优小波包基信号去噪算法并将其应用于某型导弹惯导系统陀螺仪信号的去噪处理中该算法在最优小波包基的基础上针对不同频段采用不同的阈值算法用量化后的系数重构得到去噪后的信号仿真结果表明该算法具有良好的去噪性能并且消噪效果明显优于基于小波变换的去噪算法因而将具有更为广泛的应用前景关键词最优小波包变换去噪陀螺仪中图分类号TP 277文献标识码A小波变换被认为是傅立叶分析的突破性进展它具有良好的时频局部特性和多尺度分辨能力目前已经成为国际上极为活跃的研究领域它特别适用于非平稳信号的分析基于小波分解的信号去噪方法是通过浮动阈值将大部分噪声及接近噪声强度的小波系数均视为零而舍去已经在许多实际应用中得到了较好的效果[1-4]而小波包变换则是对小波分解中所得到的高频部分再继续细分为一些子频带并且每个子频带提取各自的阈值具有更精细的信噪分离能力陀螺仪是惯性导航系统中的关键元件其精度在很大程度上决定了系统的性能因此有效地消除陀螺漂移误差是保证惯性导航系统精度的关键尤其是消除随机漂移误差成为陀螺仪信号处理中亟待解决的问题于是本文提出了一种基于Shannon 熵准则的最优小波包基信号去噪算法并将其应用于某型导弹惯导系统陀螺仪信号的消噪该算法在最优小波包基的基础上针对不同频段采用不同的阈值算法用量化后的系数重构得到去噪后的信号仿真结果表明该方法具有良好的去噪性能能够识别和确定陀螺信号所包含的频率成分保留了所需的信号达到了滤波去噪的目的而且由仿真结果比较可见该方法消噪效果明显优于基于小波变换的去噪算法将具有更为广泛的应用前景1信号的小波包分解1.1小波变换与小波包分析定义1设函数)()()(21R L R L t ,∈ψ且0)0(=ψ即∫+∞∞=0d )(t tψ则称)(t ψ为一个基本小波或母小波对母小波)(t ψ进行伸缩和平移可得,,,1)(,≠∈=a Rb a abt at b a ψψ(1)称)(,t b a ψ为小波函数简称小波其中a 为尺度因子b为平移因子对于)()(2R L t f∈其连续小波变换可定义为()b a f f t a bt t f ab a W T ,*,d )(1),(ψψ==∫+∞∞(2)式中ab t均为连续变量且0≠a )(*t ψ表示)(t ψ的复共轭小波包是由C oi f man M eye r 及W i ckha us er 引入的与小波变换相比它能对信号的高频部分进行更精细的分解是小波函数的推广定义下列递推关系==∑∑∈+∈Zk n kn Z k nk n k tgt k th t )2(2)()2(2)(122(3)则由上面定义的函数集合Zn n t ∈)}({为由正交尺度总第89期史贤俊等基于最优小波包基的信号去噪算法及其应用507函数φ=0确定的小波包可见小波包Zn n t ∈)}({是包括尺度函数)(0t 和小波母函数)(1t 在内的一个具有一定联系的函数集合定义2空间nj U 为由小波包)(t n 在j 尺度下的二进伸缩和平移Z k k t j nj ∈),2(22/的线性组合生成的L 2(R )的闭子空间因此{}Z k k t j n j ∈),2(22/为子空间n j U 的一组规范正交基定义3从小波库{}Z k j k t j nj ∈,),2(22/中抽取的能组成L 2(R )的一组规范正交基为L 2(R )的小波包基[5]1.2最优小波包基的选取根据上面的定义可知小波库中有很多小波包基而不同的小波包基一般具有不同的时频局部化能力反映不同的信号特性因此对于一个给定的信号希望依照一定的准则称为代价函数来选择一个最优的小波包基在一个正交小波包基下可以把信号f (t )展开使得f (t )与一个小波包系数序列}{k x x =对应在序列}{k x 上定义一个信息代价函数M 它满足如下两个条件1可加性条件即0)0(,)(})({==∑∈M x M x M Zk kk (4)2信息代价函数M 的取值应反映系数的集中程度对于一个给定的信息代价函数M L 2(R )的小波包基B 称为信号f (t )相对于代价函数M的最优基如果在L 2(R )的所有小波包基中f (t )在小波包基B下对应的小波包系数序列具有最小的信息代价函数值采用工程上常用的基于Shannon 信息熵的代价函数即定义序列}{k x x =的熵为∑=jjj PP x M lg )((5)式中22xx P j j =且P =0时0lg =PP由于信息是半可加的所以引入了可加函数∑=kkkx xx 22lg )(λ则)(x M可表示为22lg )()(xx x x M +=λ(6)这样)(x λ最小时)(x M也最小有了上面的信息代价函数就可以求出使信息代价函数最小的小波包序列从而求出最优基当基库是一个二叉树时可以采用自底向顶的快速搜索法选择最优小波包基2基于最优小波包基的信号去噪算法2.1阈值的选择阈值化处理的关键问题是选择合适的阈值若阈值太小去噪后的信号仍然有噪声存在相反地若阈值太大重要信号特征将被滤掉引起偏差由于小波包分解系数在不同频带反映信号的不同特征很难找到一个特别有效的统一的阈值算法对各个频带进行处理因此本文对于小波包分解在不同频带上的系数采用不同的阈值选择算法对于高频系数采用基于史坦St ei n无偏似然估计原理的自适应阈值选择[6]对于一个给定的阈值t得到它的似然估计再将似然t最小化就得到了所选的阈值它是一种软件阈值估计器具体算法如下设信号)(k x 为一个离散时间序列nk ,,2,1/=令信号)(k y 为)(k x 的升序序列再令21)()(k y k y=(7)则阈值1thr的计算公式如下∑==ki i y k y 112)()((8)nk y k nk y k nk r )()()(2)(12++=(9))min(th 1r r=(10)对于低频系数则采用一种以信号能量为判据的浮动阈值选择[7]由公式n n T /)ln(2σ=来计算阈值其中n为信号长度σ为噪声能量对于噪声能量的计算首先根据各个系数携带信号能量的大小计算其权值然后根据这个权值和各细节小波包系数v 的中位数来估计各频段的噪声能量即6745.0median =σ2.2基于最优小波包基的信号去噪算法一般地一个含有噪声的信号模型可表示为)()()(n e n f n s +=σ(11)式中s (n )为含有噪声的信号f (n )为有用信号e (n )为噪声n为等间隔的时间为噪声能量传统的基于傅立叶变换的信号去噪要使信号与噪声的频带重叠得尽可能的少这样就可在频域通过时不变滤波法将信号与噪声分离开来但海海军军航空工程程学学院学报2006年第5期508是当信号和噪声的频域大量重叠时这种方法就不太适用了小波分析作为一种新的时频分析方法以其具有良好的时频局部化特性为解决上述问题提供了极其有效的工具由于信号可以用其小波系数来刻画小波系数较大者携带的信号能量较多而小波系数较小者携带的信号能量较少因此可以用携带信号能量的多少作为衡量小波系数在信号中的权重大小与小波变换相比小波包提供了一种更为复杂更为灵活的分析手段因为它对上一层的低频部分和高频部分同时进行分解具有更加精确的局部分析能力基于最优小波包的信号去噪算法具体步骤1信号的小波包分解选择一个小波并确定所需分解的层次N 然后对含噪信号进行N 层小波包分解2对于给定的Shannon 熵标准选择最优小波包基3对分解的各个频段根据不同的阈值选择方法选择阈值对最优小波包基每个节点上的分解系数进行阈值量化阈值量化采用软阈值方法4只利用阈值量化以后的最优小波包基的分解系数进行信号的重构重构得到的信号就是经过最优小波包基去噪后的信号3应用实例3.1陀螺仪漂移的数学模型一般来说陀螺漂移主要由常值分量和周期分量组成但是由于各种电路的噪声等外部环境因素的影响实际观察到的信号还包括噪声即白噪声和色噪声在短时间内比如在初始对准时间内可以将漂移模型描述为[8])()()2sin()(00t w t n ft A t ++++=δθπεε(12)式中0ε为陀螺常值零偏A 为周期分量的幅值F为周期分量的频率0θ为初始相位)(t n 为高斯白噪声其强度为δ)(t w为有色噪声3.2仿真实验下面以某型导弹惯导系统上的陀螺仪为例采用基于最优小波包基的信号去噪算法对其测试信号进行处理图1为陀螺仪刚刚上电时的零偏采样值选用具有良好相位特性的紧支撑正交小波D a ubechi es小波对该原始信号进行5层小波包分解-3-2-10123采样点数陀螺输出值V图1陀螺零偏信号采样值图2为采用相同分解层数和阈值选取方法的db4小波进行去噪处理的效果图而图3为采用本文提出的基于Shannon 熵准则的db4最优小波包基去噪算法处理后的效果图1002003004005006007008009001000-3-2-10123采样点数陀螺输出值V 图2db4小波5层分解去噪效果图100200300400500600700800900100000.10.20.30.40.50.60.70.80.91采样点数陀螺输出值V 图3db4最优小波包基5层分解去噪效果图从图2和图3仿真结果比较可得在采用相同的小波母函数分解层数和阈值选取方法的情况下基于Sha nnon 熵准则的最优小波包基陀螺信号去噪算法效果明显优于基于小波变换的去噪算法具有更精细的信噪分离能力4结论本文提出了一种基于Shannon 熵准则的最优小波包基信号去噪算法并将其应用于某型导弹惯导陀螺输出值/V 陀螺输出值/V 陀螺输出值/V总第89期史贤俊等基于最优小波包基的信号去噪算法及其应用509系统陀螺仪信号的消噪该算法在最优小波包基的基础上针对不同频段采用不同的阈值算法用量化后的系数重构得到去噪后的信号仿真结果表明该方法具有良好的去噪性能能够识别和确定陀螺信号所包含的频率成分根据Sha nnon 熵准则选择一个最优的小波包基来滤除陀螺信号的周期分量和噪声保留了所需的信号达到了滤波去噪的目的并且由仿真结果比较可见该方法消噪效果明显优于基于小波变换的去噪算法将具有更为广泛的应用前景参考文献[1]L ang M ,G uo H .N oi s er educt i on usi ng anundeci m at ed di scr et e w avel et t ransf orm [J].I EE E Si gnal Proces s i ng Let t er s,1996,3:613-627[2]K ar i m G O ,D avi d J A .N oi se r educt i on i nm ul t i channel neur al recor di ngs usi ng a new ar r ay w avel et denoi s i ng al gor i t hm[J ].N eur ocom put i ng,2001,38(4):1687-1693[3]Thom as T L ,A nt ony C S.D et ect i on of t rans i ent si n 1/f noi s e w i t h t he undeci m at ed di s cr et e w avel ett r ans f or m [J].I E EE Tr ans act i onsonSi gnal Pr ocess i ng,2000,48(5):1458-1462[4]袁瑞铭,韦锡华,李自,等.基于小波阈值滤波的光纤陀螺信号消噪算法[J].中国惯性技术学报,2003,10(5):43-47[5]简涛,何友,苏峰,等.小波变换在雷达信号检测中的应用[J ].海军航空工程学院学报,2006,21(1):121-126[6]杨建国.小波分析及其工程应用[M ].北京:机械工业出版社,2005:216-217[7]魏云冰,黄进,黄建华.基于小波包变换的电机测试信号去噪处理[J].电工技术学报,2001,16(5):64-67[8]郭秀中.惯导系统陀螺仪理论[M ].北京:国防工业出版社,1996:195-196Si gnal denoi si ng al gor i t hm and i t s appl i cat i onba sed on best w avel et packe t basi sSH I X i anj un 1LI N Sa 2LI R ui l i ang 31D epar t m ent of C ont r ol Engi neer ingN AEIY ant aiShandong2640012M i l i t ar y Repr esent at i ves O ff i ce of N E D i n B ei j i ngB ei j i ng1000833T he 92840t hof PLA J i aonan Shandong266405A r act :bs t ract :In t hi s paper,a new si gnal denoi si ng al gor i t hmbas ed on bes t w avel et packet bas i sw hi ch adopt s Shannon ent ropy i s di scuss ed,and i s appl i ed i n t he gyro s i gnal denoi s i ng of t he i nert i al navi gat i on sys t emof t he m i ss i l e.The al gor i t hmt hat i s bas ed on bes t w avel et packet bas i s adopt s di ff erent m et hods of deal i ng coef f i ci ent for hi gh f r equency and l ow er f requency coeff i ci ent s ,and t he denoi s ed si gnal i s got w i t h t hes e coef fi ci ent s.Fi nal l y,t he s i m ul at i on res ul t s s how t hat t he al gor i t hm has t he favor abl e char act er i st i cs and t he bet t er s i gnal denoi s i ng eff ect com par ed w i t h s i gnal denoi si ng al gor i t hmbas ed on w avel et t rans for m .So,i t w i l l be appl i ed i n m or e f i el ds w i del y.ey K ey or ds w ords :bes t w avel et packet t r ans f or m ;denoi si ng;gyr o。

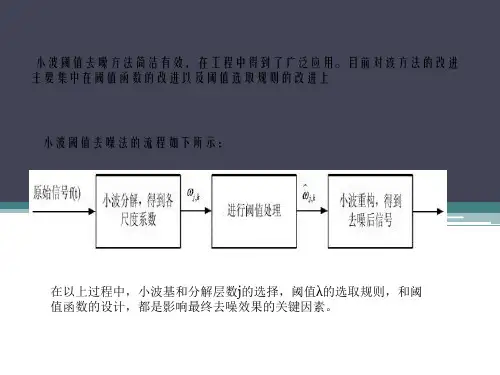
小波滤波去噪原理
小波滤波是一种常用的信号处理方法,用于解决信号中存在的噪声问题。
小波滤波的原理是通过选取小波基函数,将原始信号从时域转换到小波域,对小波系数进行处理,再将处理后的小波系数从小波域转换回时域,得到去噪后的信号。
原始信号可能存在多种类型的噪声,例如高斯噪声、椒盐噪声、周期性噪声等。
对于不同类型的噪声,小波滤波的处理方法也不同。
对于高斯噪声,小波滤波使用高斯小波作为基函数,通过去除小波系数中较低的能量分量,实现去噪。
高斯小波函数具有连续性和平滑性,能够刻画信号的较低频成分。
对于周期性噪声,小波滤波使用第三种小波函数,例如Daubechies小波、Symlets小波等。
这些小波函数具有可扩展性和对称性,能够有效地描述信号的周期成分。
小波滤波通过将信号进行分解,并对分解后的小波系数进行处理,将噪声从信号中去除。
分解层数可以根据信号的特点和去噪效果进行选择。
一般而言,信号特征较明显时,可以选择较少的层数;信号含有较多噪声时,可以选择较多的层数,以获取更好的去噪效果。
小波滤波在信号处理和图像处理领域得到了广泛的应用。
通过选择不同的小波基函数和分解层数,可以处理多种类型的信号和噪声。
因此,小波滤波成为了数字信号处理必不可少的组成部分之一。

小波阈值去噪的基本原理_小波去噪阈值如何选取小波阈值去噪是利用小波变换的频率分析特性,将信号分解到不同的频带中进行处理并去除噪声的一种方法。
其基本原理是通过小波变换将原始信号分解为不同频带的子信号,然后对每个子信号进行阈值处理,将低幅值的信号置为零,最后通过反变换将处理后的信号恢复到原始信号的时域上。
小波去噪阈值如何选取:小波去噪的核心是选择合适的阈值来判断信号频带中的噪声与信号成分。
有许多常用的阈值函数可供选择,常见的有软阈值和硬阈值。
1.软阈值:对于一些频带的子信号,如果其绝对值小于一个特定的阈值,则将其置为零;如果绝对值大于阈值,则将其保留。
软阈值能有效地抑制较小的噪声,但可能会损失一些信号的微弱成分。
2.硬阈值:对于一些频带的子信号,如果其绝对值小于一个特定的阈值,则将其置为零;如果绝对值大于阈值,则将其保留。
与软阈值相比,硬阈值能更彻底地去除噪声,但可能会导致信号的失真。
选取合适的阈值是小波去噪的关键,一般来说1.基于固定阈值的去噪方法:根据经验或实验数据设定一个固定的阈值对信号进行去噪处理。
这种方法简单直观,但需要根据具体问题和实际情况选取合适的阈值。
2.基于百分比阈值的去噪方法:将小波系数按大小排序,并根据百分比选取阈值。
常用的方法有能量百分比法和极大值百分比法。
能量百分比法选择固定能量百分比并将小波系数按能量大小进行排序,然后选取对应百分位的小波系数作为阈值。
极大值百分比法选择相对于整个小波系数序列的极大值进行百分比计算,选取对应百分位的极大值作为阈值。
3. 基于信息准则的去噪方法:利用统计学原理,通过最大化似然函数或最小化信息准则(如Akaike信息准则、最小描述长度准则等)来选择最优的阈值。
这种方法较为复杂,但具有更好的理论依据。
综上所述,小波去噪阈值的选择需要根据具体情况和实际需求进行,可以根据经验、百分比法或信息准则等方法选取合适的阈值,以达到较好的去噪效果。


基于小波变换的信号特征提取研究一、引言信号特征提取是信号处理中的重要环节,对于准确地分析信号具有重要的作用。
而小波变换是一种非常有效的信号分析方法,被广泛地应用于信号特征提取领域。
本文将介绍基于小波变换的信号特征提取研究,并探讨其在实际应用中的优缺点。
二、小波变换简介小波变换是一种信号处理技术,其特点是可以将信号分解成不同时间和频率尺度下的小波基函数。
与傅里叶变换不同的是,小波变换拥有更好的时间特性,可以分析信号在时间上的局部特征。
因此,小波变换在某些信号上的应用要比傅里叶变换更加优秀。
小波变换的算法包含离散小波变换(DWT)和连续小波变换(CWT)两种,其中DWT是一种可以离散处理信号的方法,被广泛地应用于工业控制、医学检测等领域。
三、小波变换在信号特征提取中的应用小波变换具有很多优越的特性,因此在信号特征提取中被广泛地应用。
下面将介绍几种常见的应用方式。
1.小波包分析小波包分析是对小波分析的一种扩展,它可以将小波分解得更加细致,使分析结果更加准确。
小波包分析通常用于高精度的信号处理中,如地震信号分析、人脑磁图信号分析等。
2.小波包特征提取小波包特征提取是在小波包分析的基础上,提取出信号的一些重要特征,如能量、熵等。
这些特征对于信号的识别和分类非常重要,可以帮助我们建立高精度的模型。
3.小波自适应滤波小波自适应滤波是指利用小波变换对信号进行去噪处理的一种方法。
它可以根据信号的局部特性进行滤波,保留信号的有用信息,同时去除噪声。
小波自适应滤波通常用于图像处理、语音识别等领域。
四、小波变换在实际应用中的优缺点小波变换作为一种先进的信号分析方法,具有很多优越性质。
但是,在实际应用中,小波变换也存在一些局限性,下面将对其做出分析。
优点:1.小波变换具有很好的时间局部性,可以对信号的瞬态和突变进行有效的分析,有助于识别信号中的关键特征。
2.小波变换采用多分辨率分析方法,能够有效地处理非平稳信号,提高了信号处理的精度。
第六章 小波变换的几个典型应用6.1 小波变换与信号处理小波变换作为信号处理的一种手段,逐渐被越来越多领域的理论工作者和工程技术人员所重视和应用,并在许多应用中取得了显著的效果。
同传统的处理方法相比,小波变换取得了质的飞跃,在信号处理方面具有更大的优势。
比如小波变换可以用于电力负载信号的分析与处理,用于语音信号的分析、变换和综合,还可以检测噪声中的未知瞬态信号。
本部分将举例说明。
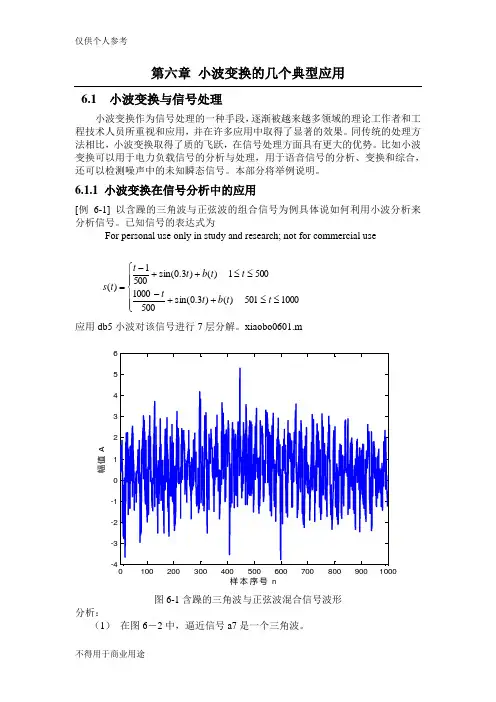
6.1.1 小波变换在信号分析中的应用[例6-1] 以含躁的三角波与正弦波的组合信号为例具体说如何利用小波分析来分析信号。
已知信号的表达式为For personal use only in study and research; not for commercial use⎪⎪⎩⎪⎪⎨⎧≤≤++-≤≤++-=1000501)()3.0sin(50010005001)()3.0sin(5001)(t t b t t t t b t t t s应用db5小波对该信号进行7层分解。
xiaobo0601.m1002003004005006007008009001000-4-3-2-10123456样本序号 n幅值 A图6-1含躁的三角波与正弦波混合信号波形分析:(1) 在图6-2中,逼近信号a7是一个三角波。
(2) 在图6-3中细节信号d1和d2是与噪声相关的,而d3(特别是d4)与正弦信号相关。
01002003004005006007008009001000-101a 701002003004005006007008009001000-202a 601002003004005006007008009001000-202a 501002003004005006007008009001000-202a 401002003004005006007008009001000-505a 301002003004005006007008009001000-505a 2010*******4005006007008009001000-505a 1样本序号 n图6-2 小波分解后各层逼近信号01002003004005006007008009001000-101d 701002003004005006007008009001000-101d 601002003004005006007008009001000-101d 501002003004005006007008009001000-202d 401002003004005006007008009001000-202d 301002003004005006007008009001000-202d 2010*******4005006007008009001000-505d 1样本序号 n图6-3 小波分解后各层细节信号6.1.2 小波变换在信号降躁和压缩中的应用一、信号降躁1.工程中,有用信号一般是一些比较平稳的信号,噪声通常表现为高频信号。
小波分析知识点总结小波分析的基本思想是利用小波函数对信号进行分解,得到不同尺度和频率的成分,然后对这些成分进行分析。
小波函数通常具有局部化特性,能够反映信号的局部特征,在时域和频域上都具有一定的分辨率,因此可以更准确地描述信号的时频特性。
小波分析主要包括小波变换、小波系数的选择、小波包分析、小波域滤波等内容。
下面将从这些方面对小波分析进行介绍。
1. 小波变换小波变换是小波分析的核心内容,它将信号分解成不同尺度和频率的成分。
小波变换包括连续小波变换和离散小波变换两种形式。
连续小波变换将信号分解成不同尺度和频率的成分,并且可以实现任意精细程度的分解。
但是由于小波函数是连续的,计算复杂度较高,因此应用较为有限。
离散小波变换是将连续小波变换进行离散化处理,从而降低计算复杂度。
离散小波变换可以通过小波分解和小波重构过程来实现信号的分解和重构,具有较好的实用性和计算效率。
小波变换具有多重分辨率分析的特点,可以在不同尺度和频率上对信号进行分析,具有较好的时频局部化特性。
2. 小波系数的选择小波系数对信号的分解和重构效果具有重要影响。
通常情况下,小波系数是由小波函数的形状和尺度决定的,不同的小波函数对信号的分解和重构效果有一定的影响。
常用的小波函数包括哈尔小波、Daubechies小波、Meyer小波、Gabor小波等。
这些小波函数具有不同的形状和尺度特性,可以适用于不同类型的信号。
在选择小波系数时,需要考虑信号的特点和分析的目的,选择合适的小波函数和尺度参数,以实现更好的分解效果。
3. 小波包分析小波包分析是小波变换的一种扩展形式,它能够对信号进行更为细致的分解。
小波包分析将信号进行逐层分解,得到更为丰富的频率成分,能够更准确地描述信号的时频特性。
小波包分析通常采用二叉树结构进行信号分解,在每层分解中都能够获得更为细致的频率分量。
小波包分析可以实现任意精细程度的频率分解,能够更充分地利用小波函数的局部化特性,对信号进行更为全面的时频分析。
小波阈值去噪法是一种有效的信号去噪方法,它通过选取合适的小波基对信号进行小波分解,并对分解的各层系数进行阈值处理,以实现去噪效果。
该方法的原理是将含有噪声的信号分解成近似分量和细节分量。
在小波分解的每一尺度下,近似分量表示信号的低频部分,细节分量表示信号的高频部分。
由于噪声主要集中在高频部分,因此通过对小波系数进行阈值处理,可以抑制信号中的无用部分,增强有用部分。
在阈值去噪过程中,首先需要选择合适的小波基。
由于没有任何一种小波基可以对不同类型的信号达到最优的分解效果,因此如何选择小波基成为小波分解的一个重点。
另外,阈值函数的选取也是阈值去噪法的关键之一。
常用的阈值函数包括硬阈值函数和软阈值函数。
硬阈值函数在处理时可能会产生震荡,而软阈值函数虽然连续性好,但存在恒定偏差,直接影响重构信号的性质。
总的来说,小波阈值去噪法是一种有效的信号去噪方法,但在实际应用中需要根据具体的情况选择合适的小波基和阈值函数,以达到最佳的去噪效果。
信号去噪中的小波阈值去噪法处理流程如下:对信号进行小波分解,选择合适的小波基和分解层次。
对小波分解的各层系数进行阈值处理,可以选择默认阈值或根据经验公式获得阈值。
对处理后的小波系数进行重构,得到去噪后的信号。
其中,阈值处理是小波阈值去噪法的关键步骤之一。
常用的阈值函数包括硬阈值函数和软阈值函数。
硬阈值函数将小于阈值的系数置为零,大于等于阈值的系数保留;软阈值函数将小于阈值的系数置为零,大于等于阈值的系数进行收缩。
需要注意的是,小波阈值去噪法在处理过程中可能会产生一些副作用,如信号失真和边缘效应等。
因此,在实际应用中需要根据具体的情况选择合适的小波基和阈值函数,以达到最佳的去噪效果。
小波包分解原理
小波包分解是一种在信号处理中常用的方法,用于将信号分解成频率成分不同的近似信号和细节信号。
其原理是将信号分成不同的频带,每个频带中的信号频率范围是不同的,然后对每个频带进行小波分解。
小波包分解是小波分析的一种扩展形式,可以更加精细地分解信号,以便更好地理解和处理信号。
其主要步骤包括选择小波基函数和频带数目,计算小波包系数,以及对系数进行阈值处理和重构。
在小波包分解中,不同的频带可以选择不同的小波基函数,以适应不同类型的信号。
同时,可以根据需要选择不同的频带数目,以便更好地分解信号。
小波包分解常用于信号去噪、特征提取和数据压缩等领域,其优点是能够提供更加精细的频域信息,以及更好的时域和频域局部化性质。
- 1 -。
小波分析作业 学生姓名:柴凯
问题1:试生成一个含噪声信号,利用matlab中的小波去噪和小波
包去噪函数去除噪声,比较两者的性能差异。
程序如下:
clc
clear all
load noisdopp
x=noisdopp;
subplot(311)
plot(x);
title('原始信号的波形图')
axis tight;
[thr,sorh,keepapp]=ddencmp('den','wv',x);
xwd=wden(x,'rigrsure','s','one',4,'sym4');
subplot(312)
plot(xwd)
title('小波降噪信号')
axis tight
[thr1,sorh1,keepapp1,crit]=ddencmp('den','wp',x);
xwpd=wpdencmp(x,'h',4,'sym4','sure',thr1,1);
subplot(313)
plot(xwpd)
title('小波包降噪信号')
axis tight
运行结果如下:
1002003004005006007008009001000
-5
0
5
原始信号的波形图
1002003004005006007008009001000
-5
0
5
小波降噪信号
1002003004005006007008009001000
-5
0
5
小波包降噪信号
区别:小波变换在低信噪比情况下的去噪效果较好,小波包分解去噪后信号更加
的平滑;小波分解主要是针对细节成分全置0或者给定软(硬)阈值去噪,容易
丢失信号中的有用信息。
小波分析作业 学生姓名:柴凯
问题2:研究小波包分解树中各节点的重构系数,给出其频谱分布,
讨论波包分解的频带划分
程序如下:
clc
clear all
load noisdopp;
s=noisdopp;
wpt=wpdec(s,3,'sym1');
plot(wpt);
r20=wprcoef(wpt,[2 0]);
subplot(621)
plot(r20)
title('r20')
subplot(623)
hua_fft(r20,10000,1)
title('r20的FFT')
r21=wprcoef(wpt,[2 1]);
subplot(622)
plot(r21)
title('r21')
subplot(624)
hua_fft(r21,10000,1)
title('r21的FFT')
r22=wprcoef(wpt,[2 2]);
subplot(625)
plot(r22)
title('r22')
subplot(627)
hua_fft(r22,10000,1)
title('r22的FFT')
r23=wprcoef(wpt,[2 3]);
subplot(626)
plot(r23)
title('r23')
subplot(628)
hua_fft(r23,10000,1)
title('r23的FFT')
r10=wprcoef(wpt,[1 0]);
subplot(629)
plot(r10)
title('r10')
subplot(6,2,11)
小波分析作业 学生姓名:柴凯
hua_fft(r10,10000,1)
title('r10的FFT')
r11=wprcoef(wpt,[1 1]);
subplot(6,2,10)
plot(r11)
title('r11')
subplot(6,2,12)
hua_fft(r11,10000,1)
title('r11的FFT')
程序运行结果如下:
Tree Decomposition(0,0)(1,0)(1,1)(2,0)(2,1)(2,2)(2,3)(3,0)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(3,7)2004006008001000-10-8-6-4-20246810data for node: (0) or (0,0).
小波分析作业 学生姓名:柴凯
问题3:生成最优树结构,给出其熵值
程序如下:
clc
clear all
load noisdopp;
x=noisdopp;
wpt=wpdec(x,3,'sym4');
wpt=wpsplt(wpt,[3 0]);
plot(wpt)
bt=besttree(wpt);
plot(bt)
ent=read(wpt,'ent',allnodes(wpt))
T=entrupd(bt,'shannon');
ent=read(wpt,'ent',allnodes(bt))
(0,0)(1,0)(1,1)(2,0)(2,1)(2,2)(2,3)(3,0)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(3,7)(4,0)(4,1)2004006008001000-10-8-6-4-202468
10
图1 小波包树
Tree Decomposition(0,0)(1,0)(1,1)(2,0)(2,1)(2,2)(2,3)(3,0)(3,1)(3,2)(3,3)(4,0)(4,1)2004006008001000-10-8-6-4-20246810data for node: (0) or (0,0).
图2 最优小波包树
小波分析作业 学生姓名:柴凯
表1 小波包树中各节点的熵值
00 10 11 20 21 22 23 30 31
-3.3195 -3.8687
-0.0128 -4.4528 -0.0194 -0.0068 -0.0071 -5.0345 -0.0406
32 33 34 35 36 37 40 41
-0.0041 -0.0374 -0.0033 -0.0026 -0.0049 -0.0014 -5.3961 -0.2270
表2 最优小波包树中各节点的熵值
00 10 11 20 21 22 23 30 31
-3.3195 -3.8687
-0.0128 -4.4528 -0.0194 -0.0068 -0.0071 -5.0345 -0.0406
32 33 40 41
-0.0041 -0.0374 -5.3961 -0.2270