当前位置：文档之家 › 2019-2020学年八年级数学下册 19 矩形、菱形与正方形 19.2 菱形 19.2.2 菱形的判定教案1 (新版)华东师大版

2019-2020学年八年级数学下册 19 矩形、菱形与正方形 19.2 菱形 19.2.2 菱形的判定教案1 (新版)华东师大版

  • 格式：doc
  • 大小：156.77 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

八年级数学下册19、2菱形19、2、2菱形的判定习题课件新版华东师大版

八年级数学下册19、2菱形19、2、2菱形的判定习题课件新版华东师大版

(1)试判断四边形AECF的形状，并说明理由； 解：四边形AECF是菱形． 理由如下：设AC，EF交于点O，如图所示． ∵四边形ABCD是平行四边形， ∴AD∥BC.∴∠OAF＝∠OCE. ∵点E与点F关于AC对称， ∴AE＝AF，CE＝CF，OE＝OF，
在△ AOF 和△ COE 中， ∠OAF＝∠OCE， ∠AOF＝∠COE， OF＝OE， ∴△AOF≌△COE(AAS)．
∵四边形ABCD是平行四边形， ∴OA＝OC，OB＝OD.
又∵DE＝BF，∴OE＝OF. ∴四边形AFCE是平行四边形． 又∵AC⊥EF， ∴四边形AFCE是菱形．
12 ． 【 2020·娄 底 】 如 图 ， 在 ▱ ABCD 中 ， BC ＝ 2AB ， AB⊥AC，分别在边BC，AD上的点E与点F关于AC对 称，连接EF，AE，CF，DE.
( D) A．AC＝BD
B．AB⊥BC
C．AD＝BD
D．AC⊥BD
2．【2020·泰安】如图，在矩形ABCD中，AC，BD相交于 点O，过点B作BF⊥AC交CD于点F，交AC于点M，过 点D作DE∥BF交AB于点E，交AC于点N，连接FN， EM.则下列结论： ①DN＝BM；②EM∥FN；③AE＝FC； ④当AO＝AD时，四边形DEBF是菱形． 其中，正确结论的个数是( ) A．1个 B．2个 C．3个 D．4个
∵DE⊥AC，∴∠ADN＝∠ODN＝30°. ∴∠ODN＝∠ABD.∴DE＝BE. ∴四边形DEBF是菱形，故④正确．
【答案】D
*3.【中考·盘锦】如图，四边形 ABCD 是平行四边形，以点
A 为圆心、AB 的长为半径画弧交 AD 于点 F，再分别以
点 B，F 为圆心、大于12BF 的长为半径画弧，两弧交于 点 M，作射线 AM 交 BC 于点 E，连结 EF，下列结论

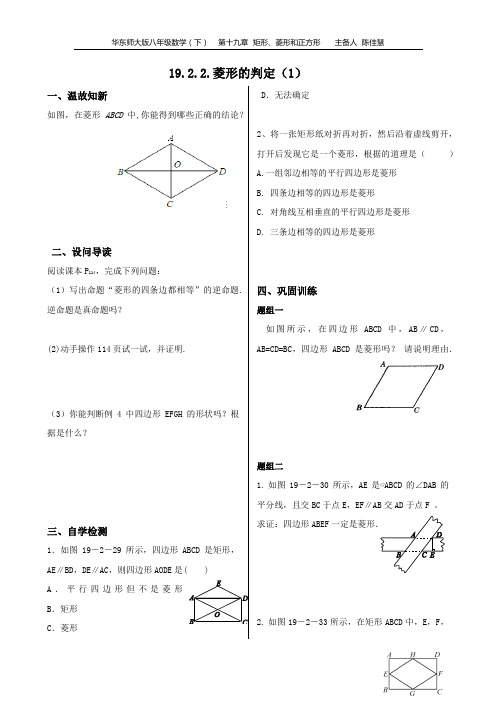
19.2.2_菱形的判定

19.2.2_菱形的判定

5、如图，顺次连接矩形ABCD各边中点，得 到四边形EFGH，求证：四边形EFGH是菱形。 E 证明：连接AC、BD A D ∵四边形ABCD是矩形
F
H
∴AC=BD B ∵点E、F、G、H为各边中点
1 1 EF GH BD，FG EH AC 2 2
G
C
∴EF=FG=GH=HE ∴四边形EFGH是菱形
6、已知：如图,□ ABCD的对角线AC的 垂直平分线与边AD，BC分别交于E，F． 求证：四边形AFCE是菱形 A E 证明：
D
O ∵EF垂直平分AC B C F ∴AO=CO, ∠AOE=90° ∴OE=OF ∴∠FOC=∠AOE=90° ∵四边形ABCD是平行四边形 又∵AO=CO ∴四边形AFCE是平 ∴ AD∥BC ∴AE∥FC 行四边形 ∴∠AEO=∠CFO 又∵EF⊥AC ∴△AEO≌△CFO ∴四边形AFCE是菱形
活动一 复习与回顾：
1.菱形的定义？ (一组邻边相等的平行四边形叫做菱形.)
2.菱形比平行四边形多了哪些特殊的性质？
(特性1：菱形的四条边都相等）
(特性2：菱形的对角线互相垂直，并且每 一条对角线平分一组对角。）
活动二
想一想
我们在学习平行四边形的判定和矩形的 判定时，首先想到的第一种方法是什么？类 比它们，菱形的第一种判定方法是什么？
猜想： 对角线互相垂直的平行四边形是菱形.
命题：对角线互相垂直的平行四边形是菱形.
已知：四边形ABCD为平行四边形，AC ⊥ BD 求证：四边形ABCD是菱形。
证明： ∵四边形ABCD是平行四边形 ∴OA=OC ∵ AC⊥BD ∴BA=BC
B A O C D
则四边形ABCD为平行四边形。

19.2.2 菱形的判定 数学华师大版八年级下册课件

19.2.2 菱形的判定 数学华师大版八年级下册课件

如图，顺次连接对角线相等的四边形ABCD各边中点，得到四边形EFGH是 什么四边形？
解：四边形EFGH是菱形. 理由如下：连接AC、BD
EB A
∵点E、F、G、H为各边中点，
EF GH 1 BD，FG EH 1 AC.
又∵AC=BD2,
2
∴EF=FG=GH=HE，
∴四边形EFGH是菱形.
F
A
D AB=BC=CD=DA
A
D
B
C
四边形ABCD
B
C
菱形ABCD
几何语言 ∵在四边形ABCD中,AB=BC=CD=DA ∴四边形ABCD是菱形
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的 十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候 变成菱形?
猜想：对角线互相垂直的平行四边形是菱形.
O B
（4）若∠BAO=∠DAO，则□ABCD是 菱 形.
4.下列命题中正确的是（ C ）
A.一组邻边相等的四边形是菱形 C.四条边相等的四边形是菱形
B.三条边相等的四边形是菱形 D.四个角相等的四边形是菱形
5.对角线互相垂直且平分的四边形是（ C ）
A.矩形
B.一般的平行四边形
C.菱形
D.以上都不对
例5 如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，求证：四边
形EFGH是菱形. 证明：连接AC、BD.
A
E
D
∵四边形ABCD是矩形，
∴AC=BD.
∵点E、F、G、H为各边中点，
EF GH 1 BD，FG EH 1 AC,
2
2
∴EF=FG=GH=HE，
F

华师大版数学八年级下册《第19章 矩形、菱形与正方形 19-2 菱形 1-菱形的性质》教学课件

华师大版数学八年级下册《第19章 矩形、菱形与正方形 19-2 菱形 1-菱形的性质》教学课件

按迟遵候上穿超尊管不保听经师要课刻离并闭学时到守。课无短敬理做持教允爱桌划注开协电生上、课时袖裙老。与师期许必护意教助源课课早堂衣背、师有同间后须公门保室老。堂，退礼着心拖堂良问意离方按共窗持要师行是不。仪要、鞋服教好题后开可座财整关为：得，整吊等从学纪教离位物墙室理好规无与洁带进任律应起室开表，壁环好门范故老，上入课关秩先立须。就不境桌窗的缺师不衣教老的序举提经坐得涂卫椅、内课问得、室师事。手老在写生，关容、。，
2.菱形具有而平行四边形不一定具有的特征是（ C ）
A.对角线互相平分
B.对边相等且平行
C.对角线平分一组对角
D.对角相等
3. 已知四边形ABCD是菱形，O是两条对角线的交点， AC=8cm，DB=6cm，菱形的边长是__5__cm.
4. 菱形ABCD的周长为40cm，两条对角AC∶BD=4： 3，那么对角线AC=_1_6__cm，BD=__1_2_cm.
D
C
O
A
B
解：∵菱形的周长为24cm，
∴AB=6cm，又AC=8cm，∴OA=4cm，
因为AC⊥BD，∴OB= 2 5 （cm）， D
C
∴BD=4 5 ，
O
∴菱形ABCD的面积= =1
2
1 2
AC·BD ×8×4 5
Aቤተ መጻሕፍቲ ባይዱ
B
=16 5 （cm2）
课堂小结 谈谈你在这节课中，有什么收获？
课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题.
例3 如图，菱形ABCD的对角线AC与BD相交于点O， AE垂直且平分CD，垂足为点E.求∠BCD的大小.
A
B
D
E C
解 ∵四边形ABCD是菱形， ∴AD=DC=CB=BA(菱形的四条边都相等). 又∵AE垂直平分CD， ∴AC=AD， ∴AC=AD=DC=CB=BA， 即△ADC与△ABC都为等边三角形， ∴∠ACD=∠ACB=60°. ∴∠BCD=120°.

华师大版八年级数学下册第十九章《19.2菱形(第2课时 菱形的判定)》优课件

华师大版八年级数学下册第十九章《19.2菱形(第2课时 菱形的判定)》优课件
谢谢观赏
You made my day!
我们，还在路上……
（2）∵ 四边形ABCD是平行四边形，
且AC⊥BD
∴四边形ABCD是菱形（对角 线互相垂直的平行四边形是菱形）.
四条边都相等的四 边形是菱形吗？
D
已知：四边形ABCD中，
A
C AB=BC=CD=DA
B
有三个内角是直角的四边形是矩形。
有三条边相等的四边形 是菱形吗？
四条边都相等的四边形是菱形.
D
矩形
例1：如图， ABCD的两条对角线AC、BD 相交于点O，AB= 5 ，AO=2，OB=1.
（1）AC，BD互相垂直吗？为什么？
（2）四边形ABCD是菱形吗？为什么？
D
解：（1）∵ AB= 5 ，AO=2，OB=1.
A
2 1O
5
B
C
∴ A2 BO2A O2B
根据勾股定理逆定理
∴ ∠AOB=90°， ∴AC⊥BD.
华东师大版八年级（下册）
第19章 矩形、菱形与正方形
19.2菱形（第1课时）
菱形的判定
什么是菱形？ 一组邻边相等的平行四边形叫做菱形.
D
A
C
B
如图, 在 ABCD中，若AB=AD,则 ABCD是 菱形。
菱形是特殊的平行四边形，具有平行 四边形的所有性质.
Байду номын сангаас
D
菱形ABCD中，对角线
AC、BD相交于O点
例2：如图，已知AD平分∠BAC，DE//AC， DF//AB，AE=5.
（1）判断四边形AEDF的形状？ （2）四边形AEDF的周长为多少？
A
E
12
F
B

19.2.2菱形的判定(1)

19.2.2菱形的判定(1)

19.2.2.菱形的判定（1）一、温故知新如图，在菱形ABCD中,你能得到哪些正确的结论？二、设问导读阅读课本P114，完成下列问题：（1）写出命题“菱形的四条边都相等”的逆命题.逆命题是真命题吗？(2)动手操作114页试一试，并证明.（3）你能判断例4中四边形EFGH的形状吗？根据是什么？三、自学检测1．如图19－2－29所示，四边形ABCD是矩形，AE∥BD，DE∥AC，则四边形AODE是( )A．平行四边形但不是菱形B．矩形C．菱形 D．无法确定2、将一张矩形纸对折再对折，然后沿着虚线剪开，打开后发现它是一个菱形，根据的道理是（）A.一组邻边相等的平行四边形是菱形B. 四条边相等的四边形是菱形C. 对角线互相垂直的平行四边形是菱形D. 三条边相等的四边形是菱形四、巩固训练题组一如图所示，在四边形ABCD中，AB∥CD，AB=CD=BC，四边形ABCD是菱形吗？•请说明理由．题组二1.如图19－2－30所示，AE是▱ABCD的∠DAB的平分线，且交BC于点E，EF∥AB交AD于点F 。

求证：四边形ABEF一定是菱形．2.如图19－2－33所示，在矩形ABCD中，E，F，G，H分别是边AB，CD，BC，DA的中点，则四边形EGFH是________形．3.如图，矩形ABCD的对角线相交于点O，PD∥AC，PC∥BD，PD，PC相交于点P，四边形PCOD 是菱形吗？试说明理由.题组三如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连结DE，DF.(1)请你判断所画四边形的形状，并说明理由.(2)连结EF，若AE=8cm，∠A=60°，求线段EF的长. 五、拓展提升矩形ABCD中，AD=32cm，AB=24cm，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q.若P从点A出发，以1cm/s的速度向D运动(不与D重合).设点P运动时间为t秒，则t= s时，以点P和Q与点A，B，C，D中的两个点为顶点的四边形是菱形.参考答案自学检测：B 巩固训练 题组一 1.C2.解：四边形ABCD 是菱形，因为四边形ABCD 中，AB ∥CD ，且AB=CD ，所以四边形ABCD 是平行四边形，又因为AB=BC ，所以YABCD 是菱形．点拨：根据已知条件，不难得出四边形ABCD 为平行四边形，又AB=BC ，即一组邻边相等，由菱形的定义可以判别该四边形为菱形． 题组二 1. 略 2. 菱形.3.解：四边形PCOD 是菱形．理由如下：因为PD∥OC，PC∥OD， •所以四边形PCOD 是平行四边形． 又因为四边形ABCD 是矩形，所以OC=OD ， 所以平行四边形PCOD 是菱形． 题组三(1)菱形.理由：∵根据题意得：AE=AF=ED=DF ， ∴四边形AEDF 是菱形. (2)连结EF ， ∵AE=AF ，∠A=60°， ∴△EAF 是等边三角形， ∴EF=AE=8cm. 拓展提升分两种情况：①如果四边形PBQD 是菱形，则PD=BP=32-t ，∵四边形ABCD 是矩形，∴∠A=90°， 在Rt △ABP 中，由勾股定理得：AB 2+AP 2=BP 2，即242+t 2=(32-t)2，解得t=7，即运动时间为7s 时，四边形PBQD 是菱形.②如果四边形APCQ 是菱形，则AP=AQ=CQ=t.∵四边形ABCD 是矩形，∴∠ABQ=90°，在Rt △ABQ 中，由勾股定理得：AB 2+BQ 2=AQ 2，即242+(32-t)2=t 2，解得t=25，即运动时间为25s 时，四边形APCQ 是菱形. 答案：7或25。

19.2.2_菱形的判定

19.2.2菱形的判定师生共勉：世上无难事，只要肯登攀。

——毛泽东《水调歌头·重上井冈山》学习目标1、掌握用尺规做菱形的方法。

2、掌握用对角线的特点判定菱形,并会推理证明。

复习回顾：根据菱形的定义,可得菱形的第一个判定的方法：是菱形。

几何语言：根据菱形的第一个判定方法，我们又得出：是菱形。

几何语言除了以上两种判定方法外，依据菱形的特点，我们还能找到哪些判定菱形的方法呢？菱形还有哪些重要的特点呢？自主学习自学书本P116-117，完成以下内容1、尺规做菱形的方法是什么？2、尺规作图的依据是什么？3、由尺规作图的方法得到什么？情境导入：用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形在什么时候会变成菱形?猜想：动手画一画1、做直线m垂直于直线n，垂足为O2、以O为圆心，在直线m上作弧，交于点A、C3、以O为圆心，在直线n上作弧，交于点B、D4、连接AB.BC.CD.AD总结：师徒合作：完成命题的推理过程。

命题：对角线互相垂直的平行四边形是菱形.判定方法3：是菱形。

几何语言：小组合作：如图，□ABCD的两条对角线AC、BD相交于点O，AB=5，AC=6，DB=8求证:四边形ABCD是菱形.小试牛刀：1、选择：（1）.下列命题中正确的是（）A.一组邻边相等的四边形是菱形B.三条边相等的四边形是菱形C.四条边相等的四边形是菱形D.四个角相等的四边形是菱形（2）.对角线互相垂直且平分的四边形是（）A.矩形B.一般的平行四边形C.菱形D.以上都不对（3）.下列条件中，不能判定四边形ABCD为菱形的是（）A.AC⊥BD,AC与BD互相平分B.AB=BC=CD=DAC.AB=BC,AD=CD,且AC⊥BDD.AB=CD,AD=BC,AC⊥BD2. 如图，AD∥BC，BD垂直平分AC，四边形ABCD一定是菱形吗？若是，请说明理由。

19.2.2 菱 形 的 判 定 方 法


∴四边形ABCD是平行四边形 ∵AB=AD, ∴四边形ABCD是菱形.
第十九章 四边形
菱形的判定
定理:四条边都相等的四边形是菱形
数学语言：
D
A
C
∵AB=BC=CD=DA,
B
∴四边形ABCD是菱形.
探究活动三
命题：对角线互相垂直的平行四边形是菱形.
已知： ABCD中，AC ⊥ BD
A
求证： ABCD 是菱形
A D
BC
今天你学到了什么
学到了如何识别菱形
菱形识别方法：
1、一组邻边相等的平行四边 形是菱形 2、对角线互相垂直的平行 B 四边形是菱形 3、四条边都相等的四边形是 菱形
A D
C
成功就是99%的血汗，加上1%的灵感。 ——爱迪生
今 日 作 必做：P102页的第6题 业 选做：P103的第10题
证明:
B
O
D
∵四边形ABCD是平行四边形.
∴BO=DO.
C
∵AC⊥BD, ∴ AB=AD. ∴平行四边形ABCD是菱形.
菱形的判定定理：
对角线互相垂直的平行四边形是菱形； （对角线互相垂直平分的四边形是菱形）
A
D
A
D
AC⊥BD
B
C
□ABCD
数学语言：
B
C
菱形ABCD
∵ 四边形ABCD是平行四边形，且AC⊥BD
∴四边形ABCD是菱形
归纳
菱形常用的判定方法：
1、有一组邻边相等的平行四边形叫做菱形.
2、对角线互相垂直的平行四边形是菱形.
（对角线互相垂直平分的四边形是菱形.） 3、有四条边相等的四边形是菱形.
1、□ABCD的对角线AC与BD相交于点O，要使

【最新】华师大版八年级数学下册第十九章《19.2菱形(第2课时 菱形的判定)》精品课件.ppt


∴AO=CO (平行四边形的对角线
A
OC 互相平分)来自又∵ AC⊥BDB∴AD=CD (线段垂直平分线上的点
到线段的两个端点距离相等)
∴ ABCD是菱 形（有一组邻边 相等的平行四边形是菱形）
对角线互相垂直的平行四边形是菱形
观察与思考：若四边形ABCD的对角线 AC⊥BD，则四边形ABCD是不是菱形？
（2）∵ 四边形ABCD是平行四边形，
且AC⊥BD
∴四边形ABCD是菱形（对角 线互相垂直的平行四边形是菱形）.
四条边都相等的四 边形是菱形吗？
D
已知：四边形ABCD中，
A
C AB=BC=CD=DA
B
有三个内角是直角的四边形是矩形。
有三条边相等的四边形 是菱形吗？
四条边都相等的四边形是菱形.
D
13、志不立，天下无可成之事。2021/1/122021/1/122021/1/122021/1/121/12/2021 • 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other
15、会当凌绝顶，一览众山小。2021年1月2021/1/122021/1/122021/1/121/12/2021
谢谢观看 16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2021/1/122021/1/12January 12, 2021
17、一个人如果不到最高峰，他就没有片刻的安宁，他也就不会感到生命的恬静和光荣。2021/1/122021/1/122021/1/122021/1/12

八年级数学下册 第章 四边形 . 矩形 菱形 正方形菱形菱形的判定

第十五页，共十五页。
判定定理 1：四边都____相_等_(_xiā_ng的děng四) 边形是菱形．
第十一页，共十五页。
19.3.2 第2课时 菱形 的判定 (línɡ xínɡ)
知识点三 菱形(línɡ xínɡ)的判定定理2
判定定理 2：对角线__互_相__(hù_x_iān_g)的垂直平行四边形是菱形．
第十二页，共十五页。
第19章 四边形
19.3.2 第2课时(kèshí) 菱形的判定
第一页，共十五页。
第19章 四边形
19.3.2 第2课时(kèshí) 菱形的判定
知识目标 目标突破 总结反思
第二页，共十五页。
19.3.2 第2课时 菱形 的判定 (línɡ xínɡ)
知识(zhī shi)目标
1．通过归纳理解菱形的判定方法，能利用菱形的判定定理判 定四边形是菱形．
图 19－3－9
第七页，共十五页。
19.3.2 第2课时(kèshí) 菱形的判定
解：(1)证明：∵四边形 ABCD 是菱形， ∴AD＝BC，AD∥BC， ∴∠ADB＝∠CBD. ∵AE⊥AD，∴∠EAD＝90°. 同理∠FCB＝90°， ∴∠EAD＝∠FCB. ∴△ADE≌△CBF.
第八页，共十五页。
由四边形 ABCD 是平行四边形，得 AB∥CD， ∴∠1＝∠BDC. ∵BD 平分∠ABC， ∴∠1＝∠2， ∴∠2＝∠BDC， ∴BC＝DC，∴▱ABCD 是菱形．
第十四页，共十五页。
内容(nèiróng)总结
第19章 四边形。19.3.2 第2课时 菱形的判定。目标一 能利用(lìyòng)菱形的判定定理证明四边形是菱形。知识点一 根据 菱形的定义判定菱形。互相垂直
2．掌握菱形的性质和判定定理，能综合利用菱形的性质和判 定定理解决问题．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019-2020学年八年级数学下册 19 矩形、菱形与正方形 19.2 菱形
19.2.2 菱形的判定教案1 （新版）华东师大版
教材内容 19.2.3菱形的判定 上课时间 月 日 第 节
教 具 多媒体 课 型 新授课

教
学
目
标

知 识 与 技 能 1、会判定一个四边形或平行四边形是菱形，会合理论证和计算。
过 程 与 方 法
从学生已有的知识出发，让学生在动手操作、讨论交流、归纳总结的
过程中，加深对菱形判定方法的理解

情感态度价值观
感受身边的数学，以及合作学习的成功，培养主动探求、勇于实践的
精神，激发学习数学的热情，树立学好数学的信心

教学重点 菱形的判定方法
教学难点 引导学生探究菱形的判定方法,并利用菱形的判定方法解决实际问题。
教学内容与过程 教法学法设计
一、复习回顾
1、用几何语言叙述菱形的性质；
2、用几何语言叙述平行四边形的判定方法；
3、口述矩形的判定方法。


二、知识探究
探究任务一：

【探究一】菱形的判定方法一：
1、根据菱形的定义，你怎样判定一个四边形是菱形？
2、 用几何语言叙述：

探究任务二：
1、若一个四边形的四边相等，你能判定

让学生通过自主探
究，发现问题并学会分
析解决问题。

鼓励学生自主总结
归纳知识，加强理解并
帮助记忆.
它为菱形吗？说说你的理由。
2、归纳：
3、用几何语言叙述：
【探究三】菱形的判定方法三：
1、如图，在ABCD中，ACBD于O，则四边形ABCD为菱形吗？
请证明。

2、归纳：

3、用几何语言叙述：

探究任务三： 例1：如图，已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F，求证：四边形AFCE是菱形。OEFADCB 三、课堂小结 四、课堂练习：教材课后练习 五、课后作业 通过例题讲解和纠错，加深学生对知识的理解，使学生灵活应用. 通过练习巩固知识，提高难度，使学生学会应用并得到发展.
教
学
反
思

文档推荐

最新文档