2013年浙江高考自选模块测试(数学部分)

秘密★启用前2013年普通高等学校招生全国统一考试（浙江卷）模拟卷二 数学（理科）本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分，考试时间120分钟． 参考公式：如果事件A 、B 互斥，那么()()()P A B P A P B +=+如果事件A 、B 相互独立，那么()()()P A B P A P B ⋅=⋅如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率(1)k kn k n n P C P P -=-（k=0，1，2，…，n ）球的表面积公式24R S π=，球的体积公式334R V π=，其中R 表示球的半径棱柱的体积公式V Sh =，其中S 表示棱柱的底面积，h 表示棱柱的高 棱锥的体积公式13V Sh=，其中S 表示棱锥的底面积，h 表示棱锥的高棱台的体积公式11221()3V h S S S S =++，其中12,S S 分别表示棱台的上、下底面积，h 表示棱台的高 第Ⅰ卷（选择题 共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.请在答题卡指定区域内作答1．设集合A={x|1≤|x －1|≤2}，集合B ={x|0322≤-+x x }, 则C R A ∩（C R B ）=（） A ．（2，3）B ．[-3，3]C ．(]3,-∞-∪[)+∞,3D ．（－∞，－3）∪（3，+∞）2．已知i 是虚数单位，ai i-+131的共轭复数是－3i ，则实数a=（） A ．3 B ．－3 C ．31 D ．－313．设a ∈R ，则“a ＝－415”是“直线l ：ax+2y －1=0与圆C ：x 2+（y －a ）2=4相切”的（）A ． 充分不必要条件B ． 必要不充分条件C ． 充分必要条件D ． 既不充分也不必要条件 4．把函数y=cos （2x －1）的图象向左平移21，再横向伸长2倍后可得函数（）A ．y=cos （x+2π）B ．y=sin （x+2π）C ．y=sinx D ．y=cos （x+23π）5．设a ，b 是两个非零向量， ①.若|a +b |=|a |+|b |，则a ∥b ②.若a ∥b ，则|a +b |=|a |+|b |③若|a +b |=|a |+|b |，则存在实数λ，使得b =λa ④若存在实数λ，使得b =λa ，则|a +b |=|a |+|b |则正确命题是（）A ．①② Ｂ．①③ Ｃ．②③ Ｄ．②④6．从1，2，3，…，9这9个整数中同时取4个不同的数，其积为偶数，则不同的取法共有（）A ．65B ．66C ．121D ．917．若正数x ，y ，a 满足x+3y=axy ，且3x+4y 的最小值为25，则a 为（） A ．1 B ．2 C ．3 D ．48．F 1，F 2分别是双曲线C ：22a x －22by =1（a ，b ＞0）的左、右焦点，B 是虚轴的端点，直线F 1B 与C 的两条渐近线分别交于P ，Q 两点，线段PQ 的垂直平分线与x 轴交于点M ，若△OBM 的面积为△OBF 1的面积的三倍，则C 的离心率是（） A.23 B ．6C ．2D ．3 9．设实数a>1，b>1，①若lna+2a=lnb+3b ，则a ＞b ②若lna+2a=lnb+3b ，则a ＜b ③若lna －2a=lnb －3b ，则a ＞b ④若lna －2a=lnb －3b 则a ＜b 则下列命题成立的是（）A ．①②B ．②③C ．③④D ．①③10．已知矩形ABCD ，AB=1，BC=2，将△ABD 沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中（）A.存在某个位置，使得直线AC 与平面ABD 垂直.B.存在某个位置，使得直线AB 与平面ACD 垂直.C.存在某个位置，使得直线AD 与平面ABC 垂直.D.对任意位置，三对直线与平面“AC 与平面ABD ”，“AB 与平面ACD ”，“AD 与平面ABC ”均不垂直第Ⅱ卷（非选择题 共100分）二、填空题 ：本大题共7小题，每小题4分，共28分，请在答题卡指定区域内作答（第13题图）11．直角三角形△ABC 两直角边为AB=3和AC=2，△ABC 围绕AC 所在直线旋转到某一位置△AB 1C ，构成一个三棱锥C —ABB 1（单位：cm ），则该三棱锥的体积的最大值为________cm 3. 12．设公差为d 的等差数列{a n }的前n 项和为S n ， 若S 2=3a 2+2，S 4=3a 4+2，则d=_______13．如右上图，如果执行它的程序框图，输入正整数48==m n 、，那么输出的p 等于14．若将函数f （x ）=x 5表示为f （x ）=a 0＋a 1（1＋x ）＋a 2（1＋x ）2＋……＋a 5（1＋x ）5，其中a 0，a 1，a 2，…a 5为实数，则a 1+a 5=_________15．实数x ，y 满足平面区域⎪⎩⎪⎨⎧≥≥≤-+≥+-0,00201y x y x y x ，则覆盖此平面区域的最小圆的方程是______16．设函数f （x ）是定义在R 上的周期为2的偶函数，当x∈[0，1]时，f （x ）=x ＋1，则 f （0.5）+f （1.5）+f （2.5）+…+f （2013.5）=_____17．如图，AB 为单位圆的直径，E ，F 为半圆上点，弧BE 是弧的三分之一，若AB ·AF=1，则·的值是三、解答题 ：本大题共5小题，共72分,解答应写出文字说明、证明过程或演算过程，请在答题卡指定区域内作答 18．(本小题满分14分)已知函数f （x ）=2asin 2x+2sinxcosx －a （a 为常数）在x=83π处取得最大值 （1）求a 值；（2）求函数f （x ）的最小正周期和单调递增区间； （3）若f （θ）=51，0＜θ＜83π，求cos θ 19． (本小题满分14分)单位正方体ABCD —A 1B 1C 1D 1中，E ，F 分别是BC ，CD 中点，平面A 1EF 交BB 1于M ，交DD 1于N（1）画出几何体A 1MEFN —ABEFD 的直观图与三视图； （2）设AC 中点为O ，在CC 上存在一点G ，使CG =λ1CC ，且OG ⊥平面A 1EF ，求λ；（3）求A 1C 与平面A 1EF 所成角的正弦值20． (本小题满分14分) 设单调递增等比数列{a n }满足a 1+a 2+a 3=7，且a 3是a 1，a 2+5的等差中项，（1）求数列{a n }的首项； （2）数列{c n }满足：对任意正整数n ，11a c +22a c +…+n n a c =22+12112--n n 均成立，求数列{c n }的通项FEADBC 1B1D 1A1BOEF21．(本小题满分15分) 已知椭圆C 的方程是12222=+by a x )0(>>b a .（1）如果椭圆C 左焦点为（－2，0），且经过点)2,2(--，求椭圆C 的方程（2）设斜率为k 的直线l ，交椭圆C 于A B 、两点，AB 的中点为M. 证明：当直线l 平行移动时，动点M 在一条过原点的定直线上； 22．(本小题满分15分) 已知函数f(x)=21(x －1)2+lnx ，g(x)=kx －k ． （1）若23=k ，求函数F(x)=f(x)－g(x)的极值； （2）若对任意的)3,1(∈x ，都有f(x)＞g(x)成立，求k 的取值范围．感谢您的阅读，祝您生活愉快。

2013年普通高等学校夏季招生全国统一考试数学理工农医类(浙江卷)选择题部分(共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2013浙江，理1)已知i是虚数单位，则(－1＋i)(2－i)＝()．A．－3＋i B．－1＋3iC．－3＋3i D．－1＋i答案：B解析：(－1＋i)(2－i)＝－2＋i＋2i－i2＝－1＋3i，故选B．2．(2013浙江，理2)设集合S＝{x|x＞－2}，T＝{x|x2＋3x－4≤0}，则(R S)∪T＝()．A．(－2,1] B．(－∞，－4]C．(－∞，1] D．[1，＋∞)答案：C解析：由题意得T＝{x|x2＋3x－4≤0}＝{x|－4≤x≤1}．又S＝{x|x＞－2}，∴(R S)∪T＝{x|x≤－2}∪{x|－4≤x≤1}＝{x|x≤1}，故选C．3．(2013浙江，理3)已知x，y为正实数，则()．A．2lg x＋lg y＝2lg x＋2lg y B．2lg(x＋y)＝2lg x·2lg yC．2lg x·lg y＝2lg x＋2lg y D．2lg(xy)＝2lg x·2lg y答案：D解析：根据指数与对数的运算法则可知，2lg x＋lg y＝2lg x·2lg y，故A错，B错，C错；D中，2lg(xy)＝2lg x＋lg y＝2lg x·2lg y，故选D．4．(2013浙江，理4)已知函数f(x)＝A cos(ωx＋φ)(A＞0，ω＞0，φ∈R)，则“f(x)是奇函数”是“π2ϕ=”的()．A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件答案：B解析：若f(x)是奇函数，则φ＝kπ＋π2，k∈Z；若π2ϕ=，则f(x)＝A cos(ωx＋φ)＝－A sin ωx，显然是奇函数．所以“f(x)是奇函数”是“π2ϕ=”的必要不充分条件．5．(2013浙江，理5)某程序框图如图所示，若该程序运行后输出的值是95，则()．A ．a ＝4B ．a ＝5C ．a ＝6D ．a ＝7 答案：A解析：该程序框图的功能为计算1＋112⨯＋123⨯＋…＋11a a (+)＝2－11a +的值，由已知输出的值为95，可知当a ＝4时2－11a +＝95.故选A ．6．(2013浙江，理6)已知α∈R ，sin α＋2cos αtan 2α＝( )． A ．43 B ．34 C ．34- D ．43- 答案：C解析：由sin α＋2cos αsin α2cos α.①把①式代入sin 2α＋cos 2α＝1中可解出cos α＝10或10，当cos α＝10sin α＝10；当cos α时，sin α＝.∴tan α＝3或tan α＝13-，∴tan 2α＝34-.7．(2013浙江，理7)设△ABC ，P 0是边AB 上一定点，满足P 0B ＝14AB ，且对于边AB 上任一点P ，恒有PB ·PC ≥0P B ·0P C，则( )． A ．∠ABC ＝90° B ．∠BAC ＝90°C ．AB ＝ACD ．AC ＝BC 答案：D解析：设PB ＝t AB(0≤t ≤1)，∴PC ＝PB ＋BC ＝t AB ＋BC，∴PB ·PC ＝(t AB )·(t AB ＋BC )＝t 22AB ＋t AB ·BC .由题意PB ·PC ≥0P B ·0P C， 即t 22AB ＋t AB ·BC ≥14AB 14AB BC ⎛⎫+ ⎪⎝⎭＝214⎛⎫ ⎪⎝⎭2AB ＋14AB ·BC ，即当14t =时PB·PC 取得最小值． 由二次函数的性质可知：2142AB BC AB ⋅-=， 即：AB - ·BC＝122AB ， ∴AB ·12AB BC ⎛⎫+ ⎪⎝⎭＝0.取AB 中点M ，则12AB ＋BC＝MB ＋BC ＝MC ，∴AB ·MC＝0，即AB ⊥MC ． ∴AC ＝BC ．故选D ．8．(2013浙江，理8)已知e 为自然对数的底数，设函数f (x )＝(e x －1)(x －1)k (k ＝1,2)，则( )．A ．当k ＝1时，f (x )在x ＝1处取到极小值B ．当k ＝1时，f (x )在x ＝1处取到极大值C ．当k ＝2时，f (x )在x ＝1处取到极小值D ．当k ＝2时，f (x )在x ＝1处取到极大值 答案：C解析：当k ＝1时，f (x )＝(e x －1)(x －1)，f ′(x )＝x e x －1， ∵f ′(1)＝e －1≠0，∴f (x )在x ＝1处不能取到极值；当k ＝2时，f (x )＝(e x －1)(x －1)2，f ′(x )＝(x －1)(x e x ＋e x －2)， 令H (x )＝x e x ＋e x －2，则H ′(x )＝x e x ＋2e x ＞0，x ∈(0，＋∞)． 说明H (x )在(0，＋∞)上为增函数， 且H (1)＝2e －2＞0，H (0)＝－1＜0，因此当x 0＜x ＜1(x 0为H (x )的零点)时，f ′(x )＜0，f (x )在(x 0,1)上为减函数． 当x ＞1时，f ′(x )＞0，f (x )在(1，＋∞)上是增函数． ∴x ＝1是f (x )的极小值点，故选C ．9．(2013浙江，理9)如图，F 1，F 2是椭圆C 1：24x ＋y 2＝1与双曲线C 2的公共焦点，A ，B 分别是C 1，C 2在第二、四象限的公共点．若四边形AF 1BF 2为矩形，则C 2的离心率是( )．A B C ．32D 答案：D解析：椭圆C 1中，|AF 1|＋|AF 2|＝4，|F 1F 2|＝又因为四边形AF 1BF 2为矩形， 所以∠F 1AF 2＝90°.所以|AF 1|2＋|AF |2＝|F 1F 2|2，所以|AF 1|＝2|AF 2|＝2所以在双曲线C 2中，2c ＝2a ＝|AF 2|－|AF 1|＝2e ==，故选D ． 10．(2013浙江，理10)在空间中，过点A 作平面π的垂线，垂足为B ，记B ＝f π(A )．设α，β是两个不同的平面，对空间任意一点P ，Q 1＝f β[f α(P )]，Q 2＝f α[f β(P )]，恒有PQ 1＝PQ 2，则( )．A ．平面α与平面β垂直B ．平面α与平面β所成的(锐)二面角为45°C ．平面α与平面β平行D ．平面α与平面β所成的(锐)二面角为60° 答案：A非选择题部分(共100分)二、填空题：本大题共7小题，每小题4分，共28分．11．(2013浙江，理11)设二项式5的展开式中常数项为A ，则A ＝__________. 答案：－10解析：T r ＋1＝553255C C (1)rr rr r r r x x ---⎛⋅=⋅-⋅ ⎝＝515523655(1)C (1)C r rr rrrr xx----=-.令15－5r ＝0，得r ＝3， 所以A ＝(－1)335C ＝25C -＝－10.12．(2013浙江，理12)若某几何体的三视图(单位：cm)如图所示，则此几何体的体积等于__________cm 3.答案：24解析：由三视图可知该几何体为如图所示的三棱柱割掉了一个三棱锥．11111111A EC ABC A B C ABC E A B C V V V ---=-＝12×3×4×5－13×12×3×4×3＝30－6＝24.13．(2013浙江，理13)设z ＝kx ＋y ，其中实数x ，y 满足20,240,240.x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩若z 的最大值为12，则实数k ＝__________.答案：2解析：画出可行域如图所示．由可行域知，最优解可能在A (0,2)或C (4,4)处取得． 若在A (0,2)处取得不符合题意；若在C (4,4)处取得，则4k ＋4＝12，解得k ＝2，此时符合题意．14．(2013浙江，理14)将A ，B ，C ，D ，E ，F 六个字母排成一排，且A ，B 均在C 的同侧，则不同的排法共有__________种(用数字作答)．答案：480解析：如图六个位置.若C 放在第一个位置，则满足条件的排法共有55A 种情况；若C 放在第2个位置，则从3,4,5,6共4个位置中选2个位置排A ，B ，再在余下的3个位置排D ，E ，F ，共24A ·33A 种排法；若C 放在第3个位置，则可在1,2两个位置排A ，B ，其余位置排D ，E ，F ，则共有22A ·33A 种排法或在4,5,6共3个位置中选2个位置排A ，B ，再在其余3个位置排D ，E ，F ，共有23A ·33A 种排法；若C 在第4个位置，则有22A 33A ＋23A 33A 种排法；若C 在第5个位置，则有24A 33A 种排法；若C 在第6个位置，则有55A 种排法．综上，共有2(55A ＋24A 33A ＋23A 33A ＋22A 33A )＝480(种)排法．15．(2013浙江，理15)设F 为抛物线C ：y 2＝4x 的焦点，过点P (－1,0)的直线l 交抛物线C 于A ，B 两点，点Q 为线段AB 的中点，若|FQ |＝2，则直线l 的斜率等于__________．答案：±1解析：设直线l 的方程为y ＝k (x ＋1)，A (x 1，y 1)，B (x 2，y 2)．由24,1y x y k x ⎧=⎨=(+)⎩联立，得k 2x 2＋2(k 2－2)x＋k 2＝0，∴x 1＋x 2＝2222k k (-)-，∴212222212x x k k k +-=-=-+，1222y y k+=，即Q 2221,k k ⎛⎫-+ ⎪⎝⎭.又|FQ |＝2，F (1,0)，∴22222114k k ⎛⎫⎛⎫-+-+= ⎪ ⎪⎝⎭⎝⎭，解得k ＝±1.16．(2013浙江，理16)在△ABC 中，∠C ＝90°，M 是BC 的中点．若sin ∠BAM ＝13，则sin ∠BAC ＝__________.答案：3解析：如图以C 为原点建立平面直角坐标系，设A (0，b )，B (a,0)，则M ,02a ⎛⎫ ⎪⎝⎭，AB ＝(a ，－b )，AM ＝,2a b ⎛⎫- ⎪⎝⎭，cos ∠MAB ＝AB AMAB AM ⋅22a b +.又sin ∠MAB ＝13，∴cos ∠MAB=.∴22222222894a b aa b b ⎛⎫+ ⎪⎝⎭=⎛⎫(+)+ ⎪⎝⎭， 整理得a 4－4a 2b 2＋4b 4＝0，即a 2－2b 2＝0，∴a 2＝2b 2，sin ∠CAB3===. 17．(2013浙江，理17)设e 1，e 2为单位向量，非零向量b ＝x e 1＋y e 2，x ，y ∈R .若e 1，e 2的夹角为π6，则||||x b 的最大值等于__________．答案：2解析：|b |2＝(x e 1＋y e 2)2＝x 2＋y 2＋2xy e 1·e 2＝x 2＋y 2xy .∴||||x =b x ＝0时，||0||x =b ； 当x ≠0时，||2||x ==≤b .三、解答题：本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤．18．(2013浙江，理18)(本题满分14分)在公差为d 的等差数列{a n }中，已知a 1＝10，且a 1,2a 2＋2,5a 3成等比数列．(1)求d ，a n ；(2)若d ＜0，求|a 1|＋|a 2|＋|a 3|＋…＋|a n |. 解：(1)由题意得5a 3·a 1＝(2a 2＋2)2， 即d 2－3d －4＝0， 故d ＝－1或d ＝4.所以a n ＝－n ＋11，n ∈N *或a n ＝4n ＋6，n ∈N *. (2)设数列{a n }的前n 项和为S n .因为d ＜0，由(1)得d ＝－1，a n ＝－n ＋11.则当n ≤11时，|a 1|＋|a 2|＋|a 3|＋…＋|a n |＝S n ＝212122n n -+. 当n ≥12时，|a 1|＋|a 2|＋|a 3|＋…＋|a n |＝－S n ＋2S 11＝212122n n -＋110.综上所述，|a 1|＋|a 2|＋|a 3|＋…＋|a n |＝22121,11,22121110,12.22n n n n n n ⎧-+≤⎪⎪⎨⎪-+≥⎪⎩19．(2013浙江，理19)(本题满分14分)设袋子中装有a 个红球，b 个黄球，c 个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．(1)当a ＝3，b ＝2，c ＝1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此2球所得分数之和，求ξ的分布列；(2)从该袋子中任取(每球取到的机会均等)1个球，记随机变量η为取出此球所得分数．若Eη＝53，Dη＝59，求a ∶b ∶c . 解：(1)由题意得ξ＝2,3,4,5,6.故P (ξ＝2)＝331664⨯=⨯， P (ξ＝3)＝2321663⨯⨯=⨯，P (ξ＝4)＝2312256618⨯⨯+⨯=⨯，P (ξ＝5)＝2211669⨯⨯=⨯， P (ξ＝6)＝1116636⨯=⨯， 所以ξ的分布列为(2)由题意知η所以E (η)＝3a a b c a b c a b c ++=++++++，D (η)＝22255551233339a b c a b c a b c a b c ⎛⎫⎛⎫⎛⎫-⋅+-⋅+-⋅= ⎪ ⎪ ⎪++++++⎝⎭⎝⎭⎝⎭， 化简得240,4110.a b c a b c --=⎧⎨+-=⎩解得a ＝3c ，b ＝2c ，故a ∶b ∶c ＝3∶2∶1.20．(2013浙江，理20)(本题满分15分)如图，在四面体A －BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD ＝2，BD ＝M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ ＝3QC ．(1)证明：PQ ∥平面BCD ；(2)若二面角C －BM －D 的大小为60°，求∠BDC 的大小．方法一：(1)证明：取BD 的中点O ，在线段CD 上取点F ，使得DF ＝3FC ，连结OP ，OF ，FQ ，因为AQ ＝3QC ，所以QF ∥AD ，且QF ＝14AD ．因为O ，P 分别为BD ，BM 的中点， 所以OP 是△BDM 的中位线， 所以OP ∥DM ，且OP ＝12DM .又点M 为AD 的中点，所以OP ∥AD ，且OP ＝14AD ． 从而OP ∥FQ ，且OP ＝FQ ，所以四边形OPQF 为平行四边形，故PQ ∥OF . 又PQ ⊄平面BCD ，OF ⊂平面BCD ， 所以PQ ∥平面BCD ．(2)解：作CG ⊥BD 于点G ，作CH ⊥BM 于点H ，连结CH . 因为AD ⊥平面BCD ，CG ⊂平面BCD ， 所以AD ⊥CG ，又CG ⊥BD ，AD ∩BD ＝D ，故CG ⊥平面ABD ，又BM ⊂平面ABD ， 所以CG ⊥BM .又GH ⊥BM ，CG ∩GH ＝G ，故BM ⊥平面CGH ， 所以GH ⊥BM ，CH ⊥BM .所以∠CHG 为二面角C －BM －D 的平面角，即∠CHG ＝60°. 设∠BDC ＝θ.在Rt △BCD 中，CD ＝BD cos θ＝θ，CG ＝CD sin θ＝θsin θ，BG ＝BC sin θ＝2θ.在Rt △BDM 中，23BG DM HG BM θ⋅==.在Rt △CHG 中，tan ∠CHG ＝3cos sin CG HG θθ==所以tan θ从而θ＝60°.即∠BDC ＝60°.方法二：(1)证明：如图，取BD 的中点O ，以O 为原点，OD ，OP 所在射线为y ，z 轴的正半轴，建立空间直角坐标系Oxyz .由题意知A (0，2)，B (0，0)，D (00)． 设点C 的坐标为(x 0，y 0,0)．因为3AQ QC = ，所以Q 00331,,4442x y ⎛⎫+ ⎪ ⎪⎝⎭.因为M 为AD 的中点，故M (01)． 又P 为BM 的中点，故P 10,0,2⎛⎫ ⎪⎝⎭，所以PQ ＝0033,044x y ⎛⎫+ ⎪ ⎪⎝⎭. 又平面BCD 的一个法向量为u ＝(0,0,1)，故PQ·u ＝0. 又PQ ⊄平面BCD ，所以PQ ∥平面BCD ．(2)解：设m ＝(x ，y ，z )为平面BMC 的一个法向量．由CM ＝(－x 00y ,1)，BM＝(0,1)，知000,0.x x y y z z ⎧-+)+=⎪⎨+=⎪⎩取y ＝－1，得m＝00,1,y x ⎛- ⎝. 又平面BDM 的一个法向量为n ＝(1,0,0)，于是|cos 〈m ，n 〉|＝||1||||2⋅==m n m n，即200y x ⎛= ⎝⎭① 又BC ⊥CD ，所以CB ·CD＝0， 故(－x 0，0y ,0)·(－x 00y ,0)＝0，即x 02＋y 02＝2.②联立①，②，解得000,x y =⎧⎪⎨=⎪⎩(舍去)或0022x y ⎧=±⎪⎪⎨⎪=⎪⎩所以tan ∠BDC=又∠BDC 是锐角，所以∠BDC ＝60°.21．(2013浙江，理21)(本题满分15分)如图，点P (0，－1)是椭圆C 1：22221x y a b+=(a ＞b ＞0)的一个顶点，C 1的长轴是圆C 2：x 2＋y 2＝4的直径，l 1，l 2是过点P 且互相垂直的两条直线，其中l 1交圆C 2于A ，B 两点，l 2交椭圆C 1于另一点D ．(1)求椭圆C 1的方程；(2)求△ABD 面积取最大值时直线l 1的方程． 解：(1)由题意得1,2.b a =⎧⎨=⎩所以椭圆C 的方程为24x ＋y 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，D (x 0，y 0)．由题意知直线l 1的斜率存在，不妨设其为k ， 则直线l 1的方程为y ＝kx －1.又圆C 2：x 2＋y 2＝4，故点O 到直线l 1的距离d =，所以||AB==.又l2⊥l1，故直线l2的方程为x＋ky＋k＝0.由220,44,x ky kx y++=⎧⎨+=⎩消去y，整理得(4＋k2)x2＋8kx＝0，故0284kx=-.所以|PD|＝24k+.设△ABD的面积为S，则S＝12|AB|·|PD|＝24k+，所以S＝32=当且仅当k=时取等号．所以所求直线l1的方程为y＝x－1.22．(2013浙江，理22)(本题满分14分)已知a∈R，函数f(x)＝x3－3x2＋3ax－3a＋3.(1)求曲线y＝f(x)在点(1，f(1))处的切线方程；(2)当x∈[0,2]时，求|f(x)|的最大值．解：(1)由题意f′(x)＝3x2－6x＋3a，故f′(1)＝3a－3.又f(1)＝1，所以所求的切线方程为y＝(3a－3)x－3a＋4.(2)由于f′(x)＝3(x－1)2＋3(a－1)，0≤x≤2，故①当a≤0时，有f′(x)≤0，此时f(x)在[0,2]上单调递减，故|f(x)|max＝max{|f(0)|，|f(2)|}＝3－3a.②当a≥1时，有f′(x)≥0，此时f(x)在[0,2]上单调递增，故|f(x)|max＝max{|f(0)|，|f(2)|}＝3a－1.③当0＜a＜1时，设x1＝1－x2＝1则0＜x1＜x2＜2，f′(x)＝3(x－x1)(x－x2)．由于f(故f(x1)＋f(x2)＝2＞0，f(x1)－f(x2)＝4(1－a0，从而f(x1)＞|f(x2)|.所以|f(x)|max＝max{f(0)，|f(2)|，f(x1)}．当0＜a＜23时，f(0)＞|f(2)|.又f(x1)－f(0)＝2(1－a(2－3a)2＞0，故|f(x)|max＝f(x1)＝1＋2(1－a当23≤a＜1时，|f(2)|＝f(2)，且f(2)≥f(0)．又f(x1)－|f(2)|＝2(1－a(3a－2)2，所以当23≤a＜34时，f(x1)＞|f(2)|.故f(x)max＝f(x1)＝1＋2(1－a当34≤a＜1时，f(x1)≤|f(2)|.故f(x)max＝|f(2)|＝3a－1. 综上所述，|f(x)|max＝33,0,3 121,4331,.4a aa aa a⎧⎪-≤⎪⎪+(-<<⎨⎪⎪-≥⎪⎩。

浙江理科选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2013浙江,理1)已知i是虚数单位,则(-1+i)(2-i)=().A.-3+iB.-1+3iC.-3+3iD.-1+i答案:B解析:(-1+i)(2-i)=-2+i+2i-i2=-1+3i,故选B.2.(2013浙江,理2)设集合S={x|x>-2},T={x|x2+3x-4≤0},则(∁R S)∪T=().A.(-2,1]B.(-∞,-4]C.(-∞,1]D.[1,+∞)答案:C解析:由题意得T={x|x2+3x-4≤0}={x|-4≤x≤1}.又S={x|x>-2},∴(∁R S)∪T={x|x≤-2}∪{x|-4≤x≤1}={x|x≤1},故选C.3.(2013浙江,理3)已知x,y为正实数,则().A.2lg x+lg y=2lg x+2lg yB.2lg(x+y)=2lg x·2lg yC.2lg x·lg y=2lg x+2lg yD.2lg(xy)=2lg x·2lg y答案:D解析:根据指数与对数的运算法则可知,2lg x+lg y=2lg x·2lg y,故A错,B错,C错;D中,2lg(xy)=2lg x+lg y=2lg x·2lg y,故选D.”的().4.(2013浙江,理4)已知函数f(x)=A cos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ=π2A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案:B解析:若f(x)是奇函数,则φ=kπ+π2,k∈Z;若φ=π2,则f(x)=A cos(ωx+φ)=-A sinωx,显然是奇函数.所以“f(x)是奇函数”是“φ=π2”的必要不充分条件.5.(2013浙江,理5)某程序框图如图所示,若该程序运行后输出的值是95,则().A.a=4B.a=5C.a=6D.a=7答案:A解析:该程序框图的功能为计算1+11×2+12×3+…+1a(a+1)=2-1a+1的值,由已知输出的值为95,可知当a=4时2-1a+1=95.故选A.6.(2013浙江,理6)已知α∈R,sinα+2cosα=√102,则tan2α=().A.43B.34C.-34D.-43答案:C解析:由sin α+2cos α=√102得,sin α=√102-2cos α.①把①式代入sin 2α+cos 2α=1中可解出cos α=√1010或3√1010, 当cos α=√1010时,sin α=3√1010; 当cos α=3√1010时,sin α=-√1010. ∴tan α=3或tan α=-13,∴tan 2α=-34.7.(2013浙江,理7)设△ABC ,P 0是边AB 上一定点,满足P 0B=14AB ,且对于边AB 上任一点P ,恒有PB⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗⃗ ≥P 0B ⃗⃗⃗⃗⃗⃗⃗ ·P 0C ⃗⃗⃗⃗⃗⃗ ,则( ). A.∠ABC=90° B.∠BAC=90° C.AB=AC D.AC=BC答案:D解析:设PB⃗⃗⃗⃗⃗ =t AB ⃗⃗⃗⃗⃗ (0≤t ≤1), ∴PC⃗⃗⃗⃗⃗ =PB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =t AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ , ∴PB⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗⃗ =(t AB ⃗⃗⃗⃗⃗ )·(t AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )=t 2AB ⃗⃗⃗⃗⃗ 2+t AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ . 由题意PB ⃗⃗⃗⃗⃗ ·PC ⃗⃗⃗⃗⃗ ≥P 0B ⃗⃗⃗⃗⃗⃗⃗ ·P 0C ⃗⃗⃗⃗⃗⃗ ,即t 2AB ⃗⃗⃗⃗⃗ 2+t AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ ≥14AB ⃗⃗⃗⃗⃗ (14AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ ) =(14)2AB⃗⃗⃗⃗⃗ 2+14AB ⃗⃗⃗⃗⃗ ·BC , 即当t=14时PB ⃗⃗⃗⃗⃗ ·PC⃗⃗⃗⃗⃗ 取得最小值.由二次函数的性质可知:-AB ⃗⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ 2AB⃗⃗⃗⃗⃗⃗ 2=14,即:-AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =12AB⃗⃗⃗⃗⃗ 2, ∴AB ⃗⃗⃗⃗⃗ ·(12AB⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )=0. 取AB 中点M ,则12AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =MB ⃗⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =MC ⃗⃗⃗⃗⃗⃗ , ∴AB⃗⃗⃗⃗⃗ ·MC ⃗⃗⃗⃗⃗⃗ =0,即AB ⊥MC. ∴AC=BC.故选D .8.(2013浙江,理8)已知e 为自然对数的底数,设函数f (x )=(e x -1)(x-1)k (k=1,2),则( ). A.当k=1时,f (x )在x=1处取到极小值 B.当k=1时,f (x )在x=1处取到极大值 C.当k=2时,f (x )在x=1处取到极小值 D.当k=2时,f (x )在x=1处取到极大值 答案:C解析:当k=1时,f (x )=(e x -1)(x-1),f'(x )=x e x -1,∵f'(1)=e -1≠0,∴f (x )在x=1处不能取到极值;当k=2时,f (x )=(e x -1)(x-1)2,f'(x )=(x-1)(x e x +e x -2), 令H (x )=x e x +e x -2,则H'(x )=x e x +2e x >0,x ∈(0,+∞). 说明H (x )在(0,+∞)上为增函数, 且H (1)=2e -2>0,H (0)=-1<0,因此当x 0<x<1(x 0为H (x )的零点)时,f'(x )<0,f (x )在(x 0,1)上为减函数. 当x>1时,f'(x )>0,f (x )在(1,+∞)上是增函数.∴x=1是f(x)的极小值点,故选C.9.(2013浙江,理9)如图,F1,F2是椭圆C1:x 24+y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是().A.√2B.√3C.32D.√62答案:D解析:椭圆C1中,|AF1|+|AF2|=4,|F1F2|=2√3.又因为四边形AF1BF2为矩形,所以∠F1AF2=90°.所以|AF1|2+|AF2|2=|F1F2|2,所以|AF1|=2-√2,|AF2|=2+√2.所以在双曲线C2中,2c=2√3,2a=|AF2|-|AF1|=2√2,故e=ca =√3√2=√62,故选D.10.(2013浙江,理10)在空间中,过点A作平面π的垂线,垂足为B,记B=fπ(A).设α,β是两个不同的平面,对空间任意一点P,Q1=fβ[fα(P)],Q2=fα[fβ(P)],恒有PQ1=PQ2,则().A.平面α与平面β垂直B.平面α与平面β所成的(锐)二面角为45°C.平面α与平面β平行D.平面α与平面β所成的(锐)二面角为60°答案:A非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分.11.(2013浙江,理11)设二项式(√x -√x3)5的展开式中常数项为A ,则A= .答案:-10解析:T r+1=C 5r (√x )5-r·(√x3)r =C 5r x5-r2·(-1)r·x -r3=(-1)r C 5rx5-r 2-r 3=(-1)r C 5rx15-5r 6.令15-5r=0,得r=3,所以A=(-1)3C 53=-C 52=-10.12.(2013浙江,理12)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于 cm 3.答案:24解析:由三视图可知该几何体为如图所示的三棱柱割掉了一个三棱锥.V A 1EC 1-ABC =V A 1B 1C 1-ABC −V E -A 1B 1C 1=12×3×4×5-13×12×3×4×3=30-6=24.13.(2013浙江,理13)设z=kx+y ,其中实数x ,y 满足{x +y -2≥0,x -2y +4≥0,2x -y -4≤0.若z 的最大值为12,则实数k= . 答案:2解析:画出可行域如图所示.由可行域知,最优解可能在A(0,2)或C(4,4)处取得.若在A(0,2)处取得不符合题意;若在C(4,4)处取得,则4k+4=12,解得k=2,此时符合题意.14.(2013浙江,理14)将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有种(用数字作答).答案:480解析:如图六个位置若C放在第一个位置,则满足条件的排法共有A55种情况;若C放在第2个位置,则从3,4,5,6共4个位置中选2个位置排A,B,再在余下的3个位置排D,E,F,共A42·A33种排法;若C放在第3个位置,则可在1,2两个位置排A,B,其余位置排D,E,F,则共有A22·A33种排法或在4,5,6共3个位置中选2个位置排A,B,再在其余3个位置排D,E,F,共有A32·A33种排法;若C在第4个位置,则有A22A33+A32A33种排法;若C在第5个位置,则有A42A33种排法;若C在第6个位置,则有A55种排法.综上,共有2(A55+A42A33+A32A33+A22A33)=480(种)排法.15.(2013浙江,理15)设F为抛物线C:y2=4x的焦点,过点P(-1,0)的直线l交抛物线C于A,B两点,点Q 为线段AB的中点,若|FQ|=2,则直线l的斜率等于.答案:±1解析:设直线l的方程为y=k(x+1),A(x1,y1),B(x2,y2).由{y2=4x,y=k(x+1)联立,得k2x2+2(k2-2)x+k2=0,∴x1+x2=-2(k 2-2)k2,∴x1+x22=-k2-2k2=-1+2k2,y1+y22=2k,即Q(-1+2k2,2 k ).又|FQ|=2,F(1,0),∴(-1+2k 2-1)2+(2k)2=4,解得k=±1.16.(2013浙江,理16)在△ABC 中,∠C=90°,M 是BC 的中点.若sin ∠BAM=13,则sin ∠BAC= .答案:√63解析:如图以C 为原点建立平面直角坐标系,设A (0,b ),B (a ,0),则M (a 2,0),AB ⃗⃗⃗⃗⃗ =(a ,-b ),AM ⃗⃗⃗⃗⃗⃗ =(a2,-b),cos ∠MAB=AB ⃗⃗⃗⃗⃗⃗ ·AM ⃗⃗⃗⃗⃗⃗⃗ |AB ⃗⃗⃗⃗⃗⃗||AM⃗⃗⃗⃗⃗⃗⃗ |=a 22+b2√a 2+b 2·√a 4+b 2.又sin ∠MAB=13,∴cos ∠MAB=√1-(13)2=√89.∴(a 22+b2)2(a 2+b 2)(a 24+b 2)=89,整理得a 4-4a 2b 2+4b 4=0, 即a 2-2b 2=0,∴a 2=2b 2, sin ∠CAB=a√a 2+b =a√3b 2=√2b √3b=√63.17.(2013浙江,理17)设e 1,e 2为单位向量,非零向量b =x e 1+y e 2,x ,y ∈R .若e 1,e 2的夹角为π6,则|x ||b |的最大值等于 . 答案:2解析:|b |2=(x e 1+y e 2)2=x 2+y 2+2xy e 1·e 2=x 2+y 2+√3xy.∴|x ||b |=√x 2+y 2+√3xy,当x=0时,|x ||b |=0;当x ≠0时,|x ||b |=√(y x)2+√3yx +1=√(y x+√32)2+14≤2.三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.18.(2013浙江,理18)(本题满分14分)在公差为d 的等差数列{a n }中,已知a 1=10,且a 1,2a 2+2,5a 3成等比数列. (1)求d ,a n ;(2)若d<0,求|a 1|+|a 2|+|a 3|+…+|a n |. 解:(1)由题意得5a 3·a 1=(2a 2+2)2,即d 2-3d-4=0, 故d=-1或d=4.所以a n =-n+11,n ∈N *或a n =4n+6,n ∈N *. (2)设数列{a n }的前n 项和为S n . 因为d<0,由(1)得d=-1,a n =-n+11.则当n ≤11时,|a 1|+|a 2|+|a 3|+…+|a n |=S n =-12n 2+212n.当n ≥12时,|a 1|+|a 2|+|a 3|+…+|a n |=-S n +2S 11=12n 2-212n+110.综上所述,|a 1|+|a 2|+|a 3|+…+|a n |={-12n 2+212n ,n ≤11,12n 2-212n +110,n ≥12.19.(2013浙江,理19)(本题满分14分)设袋子中装有a 个红球,b 个黄球,c 个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列;(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E η=53,D η=59,求a ∶b ∶c.解:(1)由题意得ξ=2,3,4,5,6.故P (ξ=2)=3×36×6=14,P (ξ=3)=2×3×26×6=13,P (ξ=4)=2×3×1+2×26×6=518, P (ξ=5)=2×2×16×6=19,P (ξ=6)=1×16×6=136, 所以ξ的分布列为(2)由题意知η的分布列为所以E (η)=aa+b+c +2ba+b+c +3ca+b+c =53,D (η)=(1-53)2·aa+b+c +(2-53)2·ba+b+c +(3-53)2·c a+b+c =59, 化简得{2a -b -4c =0,a +4b -11c =0.解得a=3c ,b=2c ,故a ∶b ∶c=3∶2∶1.20.(2013浙江,理20)(本题满分15分)如图,在四面体A-BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD=2,BD=2√2.M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ=3QC.(1)证明:PQ ∥平面BCD ;(2)若二面角C-BM-D 的大小为60°,求∠BDC 的大小.方法一:(1)证明:取BD 的中点O ,在线段CD 上取点F ,使得DF=3FC ,连结OP ,OF ,FQ ,因为AQ=3QC ,所以QF ∥AD ,且QF=14AD.因为O ,P 分别为BD ,BM 的中点, 所以OP 是△BDM 的中位线,所以OP ∥DM ,且OP=12DM.又点M 为AD 的中点,所以OP ∥AD ,且OP=14AD. 从而OP ∥FQ ,且OP=FQ ,所以四边形OPQF 为平行四边形,故PQ ∥OF.又PQ⊄平面BCD,OF⊂平面BCD,所以PQ∥平面BCD.(2)解:作CG⊥BD于点G,作CH⊥BM于点H,连结CH.因为AD⊥平面BCD,CG⊂平面BCD,所以AD⊥CG,又CG⊥BD,AD∩BD=D,故CG⊥平面ABD,又BM⊂平面ABD,所以CG⊥BM.又GH⊥BM,CG∩GH=G,故BM⊥平面CGH,所以GH⊥BM,CH⊥BM.所以∠CHG为二面角C-BM-D的平面角,即∠CHG=60°.设∠BDC=θ.在Rt△BCD中,CD=BD cosθ=2√2cosθ,CG=CD sinθ=2√2cosθsinθ,BG=BC sinθ=2√2sin2θ.在Rt△BDM中,HG=BG·DMBM =2√2sin2θ3.在Rt△CHG中,tan∠CHG=CGHG =3cosθsinθ=√3.所以tanθ=√3.从而θ=60°.即∠BDC=60°.方法二:(1)证明:如图,取BD的中点O,以O为原点,OD,OP所在射线为y,z轴的正半轴,建立空间直角坐标系Oxyz.由题意知A (0,√2,2),B (0,-√2,0),D (0,√2,0). 设点C 的坐标为(x 0,y 0,0).因为AQ⃗⃗⃗⃗⃗ =3QC ⃗⃗⃗⃗⃗ ,所以Q (34x 0,√24+34y 0,12). 因为M 为AD 的中点,故M (0,√2,1). 又P 为BM 的中点,故P (0,0,12),所以PQ ⃗⃗⃗⃗⃗ =(34x 0,√24+34y 0,0). 又平面BCD 的一个法向量为u =(0,0,1),故PQ ⃗⃗⃗⃗⃗ ·u =0. 又PQ ⊄平面BCD ,所以PQ ∥平面BCD. (2)解:设m =(x ,y ,z )为平面BMC 的一个法向量. 由CM ⃗⃗⃗⃗⃗⃗ =(-x 0,√2-y 0,1),BM ⃗⃗⃗⃗⃗⃗ =(0,2√2,1), 知{-x 0x +(√2-y 0)y +z =0,2√2y +z =0.取y=-1,得m =(y 0+√2x 0,-1,2√2).又平面BDM 的一个法向量为n =(1,0,0),于是|cos <m ,n >|=|m ·n ||m ||n |=|y 0+√2x |√9+(y 0+√2x 0)2=12,即(y 0+√2x 0)2=3.①又BC ⊥CD ,所以CB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =0, 故(-x 0,-√2-y 0,0)·(-x 0,√2-y 0,0)=0,即x 02+y 02=2.②联立①,②,解得{x 0=0,y 0=-√2,(舍去)或{x 0=±√62,y 0=√22.所以tan ∠BDC=|√2-y 0|=√3.又∠BDC 是锐角,所以∠BDC=60°.21.(2013浙江,理21)(本题满分15分)如图,点P (0,-1)是椭圆C 1:x 2a2+y 2b 2=1(a>b>0)的一个顶点,C 1的长轴是圆C 2:x 2+y 2=4的直径,l 1,l 2是过点P 且互相垂直的两条直线,其中l 1交圆C 2于A ,B 两点,l 2交椭圆C 1于另一点D.(1)求椭圆C 1的方程;(2)求△ABD 面积取最大值时直线l 1的方程. 解:(1)由题意得{b =1,a =2.所以椭圆C 的方程为x 24+y 2=1. (2)设A (x 1,y 1),B (x 2,y 2),D (x 0,y 0).由题意知直线l 1的斜率存在,不妨设其为k , 则直线l 1的方程为y=kx-1.又圆C 2:x 2+y 2=4,故点O 到直线l 1的距离d=√k +1,所以|AB|=2√4-d 2=2√4k 2+3k 2+1.又l 2⊥l 1,故直线l 2的方程为x+ky+k=0.由{x +ky +k =0,x 2+4y 2=4,消去y ,整理得(4+k 2)x 2+8kx=0, 故x 0=-8k4+k 2.所以|PD|=8√k 2+14+k 2.设△ABD 的面积为S ,则S=12|AB|·|PD|=8√4k 2+34+k 2, 所以S=√4k +3+134k 2+3≤2√√4k 2+3·13√4k 2+3=16√1313, 当且仅当k=±√102时取等号.所以所求直线l 1的方程为y=±√102x-1.22.(2013浙江,理22)(本题满分14分)已知a ∈R ,函数f (x )=x 3-3x 2+3ax-3a+3. (1)求曲线y=f (x )在点(1,f (1))处的切线方程; (2)当x ∈[0,2]时,求|f (x )|的最大值. 解:(1)由题意f'(x )=3x 2-6x+3a ,故f'(1)=3a-3.又f (1)=1,所以所求的切线方程为y=(3a-3)x-3a+4. (2)由于f'(x )=3(x-1)2+3(a-1),0≤x ≤2,故①当a ≤0时,有f'(x )≤0,此时f (x )在[0,2]上单调递减,故|f (x )|max =max{|f (0)|,|f (2)|}=3-3a.②当a ≥1时,有f'(x )≥0,此时f (x )在[0,2]上单调递增, 故|f (x )|max =max{|f (0)|,|f (2)|}=3a-1. ③当0<a<1时,设x 1=1-√1-a ,x 2=1+√1-a , 则0<x 1<x 2<2,f'(x )=3(x-x 1)(x-x 2). 列表如下:由于f (x 1)=1+2(1-a )√1-a ,f (x 2)=1-2(1-a )√1-a , 故f (x 1)+f (x 2)=2>0,f (x 1)-f (x 2)=4(1-a )√1-a >0, 从而f (x 1)>|f (x 2)|.所以|f (x )|max =max{f (0),|f (2)|,f (x 1)}. 当0<a<23时,f (0)>|f (2)|.又f (x 1)-f (0)=2(1-a )√1-a -(2-3a )=22(1-a )√1-a+2-3a>0,故|f (x )|max =f (x 1)=1+2(1-a )√1-a . 当23≤a<1时,|f (2)|=f (2),且f (2)≥f (0).又f (x 1)-|f (2)|=2(1-a )√1-a -(3a-2)=22(1-a )√1-a+3a -2,所以当23≤a<34时,f (x 1)>|f (2)|. 故f (x )max =f (x 1)=1+2(1-a )√1-a .当34≤a<1时,f(x1)≤|f(2)|.故f(x)max=|f(2)|=3a-1.综上所述,|f(x)|max={3-3a,a≤0,1+2(1-a)√1-a,0<a<34,3a-1,a≥34.。

浙江省2013届高三考前全真模拟考试自选模块试题考试须知：1．本试卷18题，全卷满分为60分，考试时间为90分钟。

2．答卷前，考生务必将自己的姓名和准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。

3．将选定的题号按规定要求先用2B铅笔填写在答题纸上的“题号”框内，确定后再用签字笔或钢笔描黑，否则答题视作无效。

4．考生可任选6道题作答；所答试题应与题号一致；多答视作无效。

题号：01 科目：语文“中国古代诗歌散文欣赏”模块(10分)阅读下面的文章，回答问题。

习惯说（清）刘蓉蓉少时，读书养晦堂①之西偏一室，俛而读，仰而思，思有弗得，辄起绕室以旋。

室有洼，径尺，浸淫②日广。

每履之，足若踬焉。

既久而遂安之。

一日，先君子来室中坐，语之，顾而笑曰：“一室之不治，何以天下家国为？”顾谓童子取土平之。

后蓉复履其地，蹶然以惊，如土忽隆起者。

俯视，坦然，则既平矣。

已而复然，又久而后安之。

噫！习之中人③甚矣哉！足之履平地，而不与洼适也；及其久，则洼者若平；至使久而即乎其故，则反窒焉而不宁。

故君子之学，贵乎慎始。

【注】①养晦堂：刘蓉居室名，在湖南湘乡。

②浸淫：渐渐扩展。

③中(zhòng)人：这里是影响人的意思。

中，深入影响。

（1）文章第一段写到“仰而思，思有弗得，辄起绕室以旋”，后人评价本文“以思为经，贯穿始末”，你是如何理解的？（4分）（2）本文写作上有何特色？阐发了什么道理？（6分）题号：02 科目：语文“中国现代诗歌散文欣赏”模块(10分)阅读下面的诗歌，回答问题。

窗外康白情窗外的闲月，紧恋着窗内蜜也似的相思。

相思都恼了，她还涎着脸儿在墙上相窥。

回头月也恼了，一抽身就没了。

月倒没了：相思倒觉着舍不得了。

（1）请简析这首诗歌的语言特色。

（3分）（2）诗歌讲究创作新奇，请就这首诗歌所选的意象和表现手法，分析作者创作的新颖别致之处。

(7分)题号：03 科目：数学“数学史与不等式选讲”模块（10分）03．在平面直角坐标系xoy 中，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C l 的极坐标方程为3ρ2=12ρcos θ－1 0（ρ>0） （1）求曲线C l 的直角坐标方程；（2）曲线C 2的方程为4222y x +=1，设P ，Q 分别为曲线C l 与曲线C 2上的任意一点，求|PQ|的最小值。

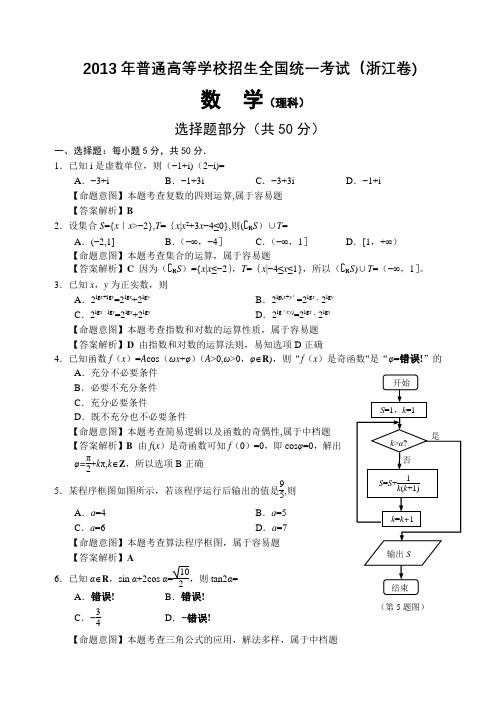
2013年普通高等学校招生全国统一考试（浙江卷)数 学（理科）选择题部分（共50分）一、选择题：每小题5分，共50分． 1．已知i 是虚数单位，则（−1+i)（2−i)=A ．−3+iB ．−1+3iC ．−3+3iD ．−1+i【命题意图】本题考查复数的四则运算,属于容易题【答案解析】B2．设集合S ={x ｜x >−2},T =｛x |x 2+3x −4≤0},则( R S ）∪T =A ．(−2,1]B ．（−∞，−4］C ．（−∞，1］D ．[1，+∞） 【命题意图】本题考查集合的运算，属于容易题 【答案解析】C 因为（ R S ）={x |x ≤−2｝，T =｛x |−4≤x ≤1}，所以（ R S )∪T =（−∞，1］。

3．已知x ，y 为正实数，则A ．2lg x +lg y =2lg x +2lg yB ．2lg(x +y ）=2lg x ∙ 2lg yC ．2lg x ∙ lg y =2lg x +2lg yD ．2lg（xy )=2lg x ∙ 2lg y【命题意图】本题考查指数和对数的运算性质，属于容易题【答案解析】D 由指数和对数的运算法则，易知选项D 正确 4．已知函数f （x ）=A cos （ωx +φ）（A >0,ω>0，φ∈R )，则“f （x ）是奇函数"是“φ=错误!”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【命题意图】本题考查简易逻辑以及函数的奇偶性,属于中档题 【答案解析】B 由f (x ）是奇函数可知f （0）=0，即cos φ=0，解出φ=π2+k π,k ∈Z ，所以选项B 正确 5．某程序框图如图所示，若该程序运行后输出的值是95,则A ．a =4B ．a =5C ．a =6D ．a =7【命题意图】本题考查算法程序框图，属于容易题【答案解析】A 6．已知α∈R ，sin α+2cos α=102，则tan2α= A ．错误! B ．错误!C ．−34D ．−错误! 【命题意图】本题考查三角公式的应用，解法多样，属于中档题（第5题图）【答案解析】C 由(sin α+2cos α）2=错误!可得错误!=错误!，进一步整理可得3tan 2α−8tan α−3=0，解得tan α=3或tan α=−错误!，于是tan2α=错误!=−错误!。

2013年数学高考模拟试卷（理科）三本试卷分卷I 和卷II 两部分.考试时间120分钟.满分120分.请考生按规定用笔将所有试题的答案涂、写在答题卡上。

卷1选择题部分 (共50分)一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)(原创)已知集合{}{}21,,1,M y y x x R N y y x x R ==+∈==+∈，则M N =（ ）(A)[1,)+∞ (B)[1,)-+∞ (C)[1,2) (D)[1,2)-(2) (原创)已知i 是虚数单位，则12i 1i+-的值为 （ ）(A)12i 2-+ (B)3-i 2(C)-1+3i 2(D) 3＋i(3)(如图所示某程序框图，则输出的n 的值是（ ）(A) 13 (B)15 (C) 16 (D)14 (4)(原创)已知命题22:90,:60p x q x x -<+->，则q p ⌝⌝是的（ ） (A)充分不必要条件 (B)既不充分也不必要条件(C)充要条件(D)必要不充分条件(5)（原创）用a ，b ，c 表示三条不同的直线，γ表示平面，给出下列命题： ①若//,//,//;a b b c a c 则 ②若,,a b b c a c ⊥⊥⊥则； ③若//,//,a b γγ则a//b ；④若,,//.a b a b γγ⊥⊥则参考公式：如果事件A ，B 互斥，那么 P (A +B )=P (A )+P (B )如果事件A ，B 相互独立，那么 P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率P n (k )=C k n p k (1-p )n -k(k =0,1,2,…，n ) 台体的体积公式V=)(312211S S S S h ++其中S 1,S 2分别表示台体的上、下底面积， h 表示台体的高柱体的体积公式Sh V =其中S 表示柱体的底面积，h 表示柱体的高 锥体的体积公式Sh V 31=其中S 表示锥体的底面积，h 表示锥体的高 球的表面积公式 S =4πR 2球的体积公式3π34R V =其中R 表示球的半径开始p ＝0，n ＝20p=p+np p n=+P ＞100?输出n 结束 (第3题)是 否n=n-1432 2 正视侧视俯视（第13题）（第9题）其中真命题的序号是（ ）(A) ①③ (B) ①④ (C) ②③ (D) ②④(6)原创）若实数x,y 满足不等式组⎪⎩⎪⎨⎧≥-+≤+-≤,01,032,5y x y x y 则y x z 2+=的最大值是 （ ）(A)10 (B) 11 (C)15 (D) 14(7)(原创)若25(21)x +=24100125a a x a x a x +++ ，则135a a a ++的值为( )(A) 121 (B)122 (C)124 (D)120(8)已知六个相同的盒子里各放了一本书，其中三本是语文书，三本是数学书，现在一次打开一个盒子，直到弄清哪三个盒子里放了语文书，则打开的盒子为4个的概率为（ ） (A)0.15 (B)0.4 (C)0.3 (D)0.6 （9）(原创)如图，直角梯形ABCD 中，AD ⊥AB, AB//DC , AB=4,AD=DC=2,设点N 是DC 边的中点，点M 是梯形ABCD 内或边界上的一个动点，则AM AN ⋅的最大值是( )（A ）4 （B ） 6 （C ） 8 （D ）10（10）把已知正整数n 表示为若干个正整数（至少3个，且可以相等）之和的形式，若这几个正整数可以按一定顺序构成等差数列，则称这些数为n 的一个等差分拆．将这些正整数的不同排列视为相同的分拆．如：（1，4，7）与（7，4，1）为12的相同等差分拆．问正整数36的不同等差分拆的个数是（ ）．（A ）20 （B ）18 （C ）19 （D ）21卷II 非选择题部分 (共100分)二、 填空题: 本大题共7小题, 每小题4分, 共28分。

2013年浙江省高考数学（理科）试题校对版（word 版）（含答案）数学（理科）试题选择题部分（共50分）一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知i 是虚数单位，则(1)(2)i i -+-=A ．3i -+B ．13i -+C ．33i -+D ．1i -+2．设集合{|2}S x x =>-，2{|340}T x x x =+-≤，则()R C S T ⋃=A ．(21]-，B ．(4]-∞-，C ．(1]-∞，D ．[1)+∞， 3．已知x ，y 为正实数，则 A ．lg lg lg lg 222x yx y +=+ B ．lg()lg lg 222x y x y +=⋅C ．lg lg lg lg 222x yx y ⋅=+ D ．lg()lg lg 222xy x y =⋅4．已知函数()cos()(0f x A x A ωϕ=+>，0ω>，)R ϕ∈，则“()f x 是 奇函数”是“2πϕ=”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 5．某程序框图如图所示，若该程序运行后输出的值是95，则 A ．4a = B ．5a = C ．6a = D ．7a =6．已知R α∈，sin 2cos αα+=tan 2α= A ．43 B ．34 C ．34- D ．43- 7．设ABC ∆，0P 是边AB 上一定点，满足014P B AB =，且对于边AB 上任一点P ，恒有00PB PC P B PC ⋅≥⋅ ．则A ．90ABC ∠=︒B ．30BAC ∠=︒ C ．AB AC =D ．AC BC = 8．已知e 为自然对数的底数，设函数()(1)(1)(12)xkf x e x k =--=，，则A ．当1k =时，()f x 在1x =处取到极小值B ．当1k =时，()f x 在1x =处取到极大值C ．当2k =时，()f x 在1x =处取到极小值D ．当2k =时，()f x 在1x =处取到极大值9．如图，1F ，2F 是椭圆221:14x C y +=与双曲线2C 的公共焦 点，A ，B 分别是1C ，2C 在第二、四象限的公共点．若四边形12AF BF 为矩形，则2C 的离心率是ABC ．32 D．210．在空间中，过点A 作平面π的垂线，垂直为B ，记()B f A π=．设α，β是两个不同的平面，对空间任意一点P ，1[()]Q f f P βα=，2[()]Q f f P αβ=，恒有12PQ PQ =，则 A ．平面α与平面β垂直 B ．平面α与平面β所成的（锐）二面角为45︒ C ．平面α与平面β平行 D ．平面α与平面β所成的（锐）二面角为60︒非选择题部分（共100分）二、填空题：本大题共7小题，每小题4分，共28分。

2013年普通高等学校招生全国统一考试（浙江卷）数学理一.选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.(5分)已知i是虚数单位，则(-1+i)(2-i)=( )A. -3+iB. -1+3iC. -3+3iD. -1+i解析：(-1+i)(2-i)=-2+i+2i+1=-1+3i，答案：B.2.(5分)设集合S={x|x＞-2}，T={x|x2+3x-4≤0}，则(C R S)∪T=( )A. (-2，1]B. (-∞，-4]C. (-∞，1]D. [1，+∞)解析：∵集合S={x|x＞-2}，∴C R S={x|x≤-2}，由x2+3x-4≤0得：T={x|-4≤x≤1}，故(C R S)∪T={x|x≤1}.答案：C.3.(5分)已知x，y为正实数，则( )A. 2lgx+lgy=2lgx+2lgyB. 2lg(x+y)=2lgx·2lgyC. 2lgx·lgy=2lgx+2lgyD. 2lg(xy)=2lgx·2lgy解析：因为a s+t=a s·a t，lg(xy)=lgx+lgy(x，y为正实数)，所以2lg(xy)=2lgx+lgy=2lgx·2lgy，满足上述两个公式.答案：D.4.(5分)已知函数f(x)=Acos(ωx+φ)(A＞0，ω＞0，φ∈R)，则“f(x)是奇函数”是“φ=”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件解析：若φ=，则f(x)=Acos(ωx+)⇒f(x)=-Asin(ωx)(A＞0，ω＞0，x∈R)是奇函数；若f(x)是奇函数⇒f(0)=0，∴f(0)=Acos(ω×0+φ)=Acosφ=0.∴φ=kπ+，k∈Z，不一定有φ=，“f(x)是奇函数”是“φ=”必要不充分条件.答案：B.5.(5分)某程序框图如图所示，若该程序运行后输出的值是，则( )A. a=4B. a=5D. a=7解析：由已知可得该程序的功能是计算并输出S=1++…+=1+1-=2-.若该程序运行后输出的值是，则 2-=.∴a=4，答案：A.6.(5分)已知，则tan2α=( )A.B.C.D.解析：∵，又sin2α+cos2α=1，联立解得，或，故tanα==，或tanα=3，代入可得tan2α===-，或tan2α===.答案：C7.(5分)设△ABC，P0是边AB上一定点，满足，且对于边AB上任一点P，恒有则( )A. ∠ABC=90°B. ∠BAC=90°D. AC=BC解析：以AB所在的直线为x轴，以AB的中垂线为y轴建立直角坐标系，设AB=4，C(a，b)，P(x，0)，则BP0=1，A(-2，0)，B(2，0)，P0(1，0)，∴=(1，0)，=(2-x，0)，=(a-x，b)，=(a-1，b)，∵恒有，∴(2-x)(a-x)≥a-1恒成立，整理可得x2-(a+2)x+a+1≥0恒成立，令f(x)=x2-(a+2)x+a+1，当a+2＜-2，必有f(-2)≥0，无解；当a+2＞2，必有f(2)≥0，无解；当-2≤a+2≤2，必有△=(a+2)2-4(a+1)≤0，即△=a2≤0，∴a=0，即C在AB的垂直平分线上，∴AC=BC，故△ABC为等腰三角形.答案：D8.(5分)已知e为自然对数的底数，设函数f(x)=(e x-1)(x-1)k(k=1，2)，则( )A. 当k=1时，f(x)在x=1处取得极小值B. 当k=1时，f(x)在x=1处取得极大值C. 当k=2时，f(x)在x=1处取得极小值D. 当k=2时，f(x)在x=1处取得极大值解析：当k=1时，函数f(x)=(e x-1)(x-1).求导函数可得f'(x)=e x(x-1)+(e x-1)=(xe x-1)，f'(1)=e-1≠0，f'(2)=2e2-1≠0，则f(x)在在x=1处与在x=2处均取不到极值，当k=2时，函数f(x)=(e x-1)(x-1)2.求导函数可得f'(x)=e x(x-1)2+2(e x-1)(x-1)=(x-1)(xe x+e x-2)，∴当x=1，f'(x)=0，且当x＞1时，f'(x)＞0，当x0＜x＜1时(x0为极大值点)，f'(x)＜0，故函数f(x)在(1，+∞)上是增函数；在(x0，1)上是减函数，从而函数f(x)在x=1取得极小值.对照选项.答案：C.9.(5分)如图F1、F2是椭圆C1：+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是( )A.B.C.D.解析：设|AF1|=x，|AF2|=y，∵点A为椭圆C1：+y2=1上的点，∴2a=4，b=1，c=；∴|AF1|+|AF2|=2a=4，即x+y=4；①又四边形AF1BF2为矩形，∴+=，即x2+y2=(2c)2==12，②由①②得：，解得x=2-，y=2+，设双曲线C2的实轴长为2a，焦距为2c，则2m=|AF2|-|AF1|=y-x=2，2n=2=2，∴双曲线C2的离心率e===. 答案：D.10.(5分)在空间中，过点A作平面π的垂线，垂足为B，记B=fπ(A).设α，β是两个不同的平面，对空间任意一点P，Q1=fβ[fα(P)]，Q2=fα[fβ(P)]，恒有PQ1=PQ2，则( )A. 平面α与平面β垂直B. 平面α与平面β所成的(锐)二面角为45°C. 平面α与平面β平行D. 平面α与平面β所成的(锐)二面角为60°解析：设P1=fα(P)，则根据题意，得点P1是过点P作平面α垂线的垂足，∵Q1=fβ[fα(P)]=fβ(P1)，∴点Q1是过点P1作平面β垂线的垂足，同理，若P2=fβ(P)，得点P2是过点P作平面β垂线的垂足，因此Q2=fα[fβ(P)]表示点Q2是过点P2作平面α垂线的垂足，∵对任意的点P，恒有PQ1=PQ2，∴点Q1与Q2重合于同一点，由此可得，四边形PP1Q1P2为矩形，且∠P1Q1P2是二面角α-l-β的平面角，∵∠P1Q1P2是直角，∴平面α与平面β垂直.答案：A二、填空题：本大题共7小题，每小题4分，共28分.11.(4分)设二项式的展开式中常数项为A，则A= .解析：二项式的展开式的通项公式为 T r+1=··(-1)r·=(-1)r··.令=0，解得r=3，故展开式的常数项为-=-10，答案：-10.12.(4分)若某几何体的三视图(单位：cm)如图所示，则此几何体的体积等于cm3.解析：几何体为三棱柱去掉一个三棱锥后的几何体，底面是直角三角形，直角边分别为3，4，侧面的高为5，被截取的棱锥的高为3.如图：V棱柱==16(cm3).故答案为：1613.(4分)设z=kx+y，其中实数x，y满足，若z的最大值为12，则实数k= .解析：可行域如图：由得：A(4，4)，同样地，得B(0，2)，①当k＞-时，目标函数z=kx+y在x=4，y=4时取最大值，即直线z=kx+y在y轴上的截距z最大，此时，12=4k+4，故k=2.②当k时，目标函数z=kx+y在x=0，y=2时取最大值，即直线z=kx+y在y轴上的截距z最大，此时，12=0×k+2，故k不存在.综上，k=2.答案：2.14.(4分)将A，B，C，D，E，F六个字母排成一排，且A，B均在C的同侧，则不同的排法共有种(用数字作答)解析：按C的位置分类，在左1，左2，左3，或者在右1，右2，右3，因为左右是对称的，所以只看左的情况最后乘以2即可.当C在左边第1个位置时，有A，当C在左边第2个位置时A A，当C在左边第3个位置时，有A A+A A，共为240种，乘以2，得480.则不同的排法共有 480种.答案：480.15.(4分)设F为抛物线C：y2=4x的焦点，过点P(-1，0)的直线l交抛物线C于两点A，B，点Q为线段AB的中点，若|FQ|=2，则直线l的斜率等于.解析：由题意设直线l的方程为my=x+1，联立得到y2-4my+4=0，△=16m2-16=16(m2-1)＞0.设A(x1，y1)，B(x2，y2)，Q(x0，y0).∴y1+y2=4m，∴=2m，∴x0=my0-1=2m2-1.∴Q(2m2-1，2m)，由抛物线C：y2=4x得焦点F(1，0).∵|QF|=2，∴，化为m2=1，解得m=±1，不满足△＞0. 故满足条件的直线l不存在.答案：不存在.16.(4分)△ABC中，∠C=90°，M是BC的中点，若，则sin∠BAC= . 解析：如图，设AC=b，AB=c，CM=MB=，∠MAC=β，在△ABM中，由正弦定理可得=，代入数据可得=，解得sin∠AMB=，故cosβ=cos(-∠AMC)=sin∠AMC=sin(π-∠AMB)=sin∠AMB=，而在RT△ACM中，cosβ==，故可得=，化简可得a4-4a2b2+4b4=(a2-2b2)2=0，解之可得a=b，再由勾股定理可得a2+b2=c2，联立可得c=，故在RT△ABC中，sin∠BAC====，答案：17.(4分)设、为单位向量，非零向量=x+y，x、y∈R.若、的夹角为30°，则的最大值等于.解析：∵、为单位向量，和的夹角等于30°，∴=1×1×cos30°= .∵非零向量=x+y，∴||===，∴====，故当=-时，取得最大值为2，答案： 2.三、解答题：本大题共5小题，共72分.解答应写出文字说明、证明过程或演算步骤.18.(14分)在公差为d的等差数列{a n}中，已知a1=10，且a1，2a2+2，5a3成等比数列. (Ⅰ)求d，a n；(Ⅱ)若d＜0，求|a1|+|a2|+|a3|+…+|a n|.解析：(Ⅰ)直接由已知条件a1=10，且a1，2a2+2，5a3成等比数列列式求出公差，则通项公式a n可求；(Ⅱ)利用(Ⅰ)中的结论，得到等差数列{a n}的前11项大于等于0，后面的项小于0，所以分类讨论求d＜0时|a1|+|a2|+|a3|+…+|a n|的和.答案：(Ⅰ)由题意得，即，整理得d2-3d-4=0.解得d=-1或d=4.当d=-1时，a n=a1+(n-1)d=10-(n-1)=-n+11.当d=4时，a n=a1+(n-1)d=10+4(n-1)=4n+6.所以a n=-n+11或a n=4n+6；(Ⅱ)设数列{a n}的前n项和为S n，因为d＜0，由(Ⅰ)得d=-1，a n=-n+11.则当n≤11时，.当n≥12时，|a1|+|a2|+|a3|+…+|a n|=-S n+2S11=.综上所述，|a1|+|a2|+|a3|+…+|a n|=.19.(14分)设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球2分，取出蓝球得3分.(1)当a=3，b=2，c=1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此2球所得分数之和.求ξ分布列；(2)从该袋子中任取(且每球取到的机会均等)1个球，记随机变量η为取出此球所得分数.若，求a：b：c.解析：(1)ξ的可能取值有：2，3，4，5，6，求出相应的概率可得所求ξ的分布列；(2)先列出η的分布列，再利用η的数学期望和方差公式，即可得到结论.答案：(1)由题意得ξ=2，3，4，5，6，P(ξ=2)==；P(ξ=3)==；P(ξ=4)==；P(ξ=5)==；P(ξ=6)==.故所求ξ的分布列为(2)由题意知η的分布列为Eη==Dη=(1-)2+(2-)2+(3-)2=.得，解得a=3c，b=2c，故a：b：c=3：2：1.20.(15分)如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2.M是AD 的中点，P是BM的中点，点Q在线段AC上，且AQ=3QC.(1)证明：PQ∥平面BCD；(2)若二面角C-BM-D的大小为60°，求∠BDC的大小.解析：(1)取BD的中点O，在线段CD上取点F，使得DF=3CF，连接OP、OF、FQ.根据平行线分线段成比例定理结合三角形的中位线定理证出四边形OPQF是平行四边形，从而PQ∥OF，再由线面平行判定定理，证出PQ∥平面BCD；(2)过点C作CG⊥BD，垂足为G，过G作GH⊥BM于H，连接CH.根据线面垂直的判定与性质证出BM⊥CH，因此∠CHG是二面角C-BM-D的平面角，可得∠CHG=60°.设∠BDC=θ，用解直角三角形的方法算出HG和CG关于θ的表达式，最后在Rt△CHG中，根据正切的定义得出tan∠CHG==，从而得到tanθ=，由此可得∠BDC.答案：(1)取BD的中点O，在线段CD上取点F，使得DF=3CF，连接OP、OF、FQ.∵△ACD中，AQ=3QC且DF=3CF，∴QF∥AD且QF=AD，∵△BDM中，O、P分别为BD、BM的中点，∴OP∥DM，且OP=DM，结合M为AD中点得：OP∥AD且OP=AD，∴OP∥QF且OP=QF，可得四边形OPQF是平行四边形，∴PQ∥OF，∵PQ⊄平面BCD且OF⊂平面BCD，∴PQ∥平面BCD；(2)过点C作CG⊥BD，垂足为G，过G作GH⊥BM于H，连接CH，∵AD⊥平面BCD，CG⊂平面BCD，∴AD⊥CG，又∵CG⊥BD，AD、BD是平面ABD内的相交直线，∴CG⊥平面ABD，结合BM⊂平面ABD，得CG⊥BM，∵GH⊥BM，CG、GH是平面CGH内的相交直线，∴BM⊥平面CGH，可得BM⊥CH，因此，∠CHG是二面角C-BM-D的平面角，可得∠CHG=60°，设∠BDC=θ，可得，Rt△BCD中，CD=BDcosθ=2cosθ，CG=CDsinθ=sinθcosθ，BG=BCsinθ=2sin2θ，Rt△BMD中，HG==；Rt△CHG中，tan∠CHG==，∴tanθ=，可得θ=60°，即∠BDC=60°.21.(15分)如图，点P(0，-1)是椭圆C1：+=1(a＞b＞0)的一个顶点，C1的长轴是圆C2：x2+y2=4的直径，l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A、B 两点，l2交椭圆C1于另一点D.(1)求椭圆C1的方程；(2)求△ABD面积的最大值时直线l1的方程.解析：(1)由题意可得b=1，2a=4，即可得到椭圆的方程；(2)设A(x1，y1)，B(x2，y2)，D(x0，y0).由题意可知：直线l1的斜率存在，设为k，则直线l1的方程为y=kx-1.利用点到直线的距离公式和弦长公式即可得出圆心O到直线l1的距离和弦长|AB|，又l2⊥l1，可得直线l2的方程为x+kx+k=0，与椭圆的方程联立即可得到点D的横坐标，即可得出|PD|，即可得到三角形ABD的面积，利用基本不等式的性质即可得出其最大值，即得到k的值.答案：(1)由题意可得b=1，2a=4，即a=2.∴椭圆C1的方程为；(2)设A(x1，y1)，B(x2，y2)，D(x0，y0).由题意可知：直线l1的斜率存在，设为k，则直线l1的方程为y=kx-1.又圆的圆心O(0，0)到直线l1的距离d=.∴|AB|== .又l2⊥l1，故直线l2的方程为x+ky+k=0，联立，消去y得到(4+k2)x2+8kx=0，解得，∴.∴三角形ABD的面积.∴=，当且仅当时取等号，故所求直线l1的方程为.22.(14分)已知a∈R，函数f(x)=x3-3x2+3ax-3a+3.(1)求曲线y=f(x)在点(1，f(1))处的切线方程；(2)当x∈[0，2]时，求|f(x)|的最大值.解析：(1)求出原函数的导函数，求出函数取x=1时的导数值及f(1)，由直线方程的点斜式写出切线方程；(2)求出原函数的导函数，分a≤0，0＜a＜1，a≥1三种情况求|f(x)|的最大值.特别当0＜a＜1时，仍需要利用导数求函数在区间(0，2)上的极值，然后在根据a的范围分析区间端点值与极值绝对值的大小.答案：(1)因为f(x)=x3-3x2+3ax-3a+3，所以f′(x)=3x2-6x+3a，故f′(1)=3a-3，又f(1)=1，所以所求的切线方程为y=(3a-3)x-3a+4；(2)由于f′(x)=3(x-1)2+3(a-1)，0≤x≤2.故当a≤0时，有f′(x)≤0，此时f(x)在[0，2]上单调递减，故|f(x)|max=max{|f(0)|，|f(2)|}=3-3a.当a≥1时，有f′(x)≥0，此时f(x)在[0，2]上单调递增，故|f(x)|max=max{|f(0)|，|f(2)|}=3a-1.当0＜a＜1时，由3(x-1)2+3(a-1)=0，得，.所以，当x∈(0，x1)时，f′(x)＞0，函数f(x)单调递增；当x∈(x1，x2)时，f′(x)＜0，函数f(x)单调递减；当x∈(x2，2)时，f′(x)＞0，函数f(x)单调递增.所以函数f(x)的极大值，极小值.故f(x 1)+f(x2)=2＞0，.从而f(x1)＞|f(x2)|.所以|f(x)|max=max{f(0)，|f(2)|，f(x1)}.当0＜a＜时，f(0)＞|f(2)|.又=故.当时，|f(2)|=f(2)，且f(2)≥f(0).又=.所以当时，f(x1)＞|f(2)|.故.当时，f(x1)≤|f(2)|.故f(x)max=|f(2)|=3a-1.综上所述|f(x)|max=.考试高分秘诀是什么？试试这四个方法，特别是中考和高考生谁都想在考试中取得优异的成绩，但要想取得优异的成绩，除了要掌握好相关的知识定理和方法技巧之外，更要学会一些考试技巧。

自选模块测试试题题号：03 科目：数学“数学史与不等式选将”模块（10分）（1） 解不等式丨x-1丨+丨x-4丨≥5（2） 求函数y=丨x-1丨+丨x-4丨+2x -4x 的最小值题号：04 科目：数学“矩阵与变换和坐标系与参数方程“模块（10分）（1）以极坐标Ox 为x 轴建立平面直角坐标系xOy ，并在两种坐标系中取相同的长度单位，把极坐标方程 2cos sin 1p θθ+=化成直角坐标方程2cos x θ=（3） 在直角坐标系xOy 中，曲线C: （θ为参数），过点P （2，1）的sin y θ=直线与曲线交与A,B 两点，若丨PA 丨·丨PB 丨=83，求丨AB 丨的值 题号：05 科目：英语阅读理解（分两节，共5小题；每小题2分，共10分）阅读下面短文，并根据短文后的要求答题。

Our cultural backgrounds influence how we make choices in nearly every area of our lives. Form early on, members of individualist societies are taught the importance of choice. As soon as children cantalk,or perhaps as soon as they can accurately point,they are asked, “Which one of these would you like?” By the age of four ,he may well be expected to bothUnderstand and respced to the challenging question, “what do you want to be when you grow up?”Fromthis children learn that they should be able to figure out what they like and dislike , what will make themhappy and what won`t ①By contrast, members of collectivist societies place greater emphasis on duty .Children are oftentold, :If you`re a good child , you`ll do what your parents tell you. “ ② As you grow older , instead ofbeing asked what you want , you may be asked ,”How will you take care of your pareents` needs and wants? How will you make them proud?’’ It is believed that your parents, and olders in general, will show you theright way to live your life so that you will be paotected from a costly mistake.③ Get a piece of paper and the from write down all the aspects of your life in which youlike having choice .On the back , list all the aspects in which you would prefer not to have choice , or tohave someone clse choose for you ,Take a few extra minutes to make sure you have`t left anyching outWhen I had 100 American and Japanese college students do this exercise , the front sides ofthe American` pages were often completely filled with answers such as “my job ” “where Ilive “ and “who I vote for “In contrast , the backs , without exception, were either completelyblank or contained only a single item , most commomly “when I like or “when my loved ones die “The Japanese a very different pattern of results , with not a single one wishing to have choice all or nearly all of the times ④Comparing responses between the two ,Americans destred personal choice in four as many domains of life as the Japanese第一节根据短文内容。

2013年浙江省高考数学试卷（理科）参考答案与试题解析一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）（2013•浙江）已知i是虚数单位，则（﹣1+i）（2﹣i）=（）A．﹣3+i B．﹣1+3i C．﹣3+3i D．﹣1+i考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：直接利用两个复数代数形式的乘法法则，以及虚数单位i的幂运算性质，运算求得结果．解答：解：（﹣1+i）（2﹣i）=﹣2+i+2i+1=﹣1+3i，故选B．点评：本题主要考查两个复数代数形式的乘法，虚数单位i的幂运算性质，属于基础题．2．（5分）（2013•浙江）设集合S={x|x＞﹣2}，T={x|x2+3x﹣4≤0}，则（∁R S）∪T=（）A．（﹣2，1]B．（﹣∞，﹣4]C．（﹣∞，1]D．[1，+∞）考点：交、并、补集的混合运算；全集及其运算．专题：集合．分析：先根据一元二次不等式求出集合T，然后求得∁R S，再利用并集的定义求出结果．解答：解：∵集合S={x|x＞﹣2}，∴∁R S={x|x≤﹣2}，T={x|x2+3x﹣4≤0}={x|﹣4≤x≤1}，故（∁R S）∪T={x|x≤1}故选C．点评：此题属于以一元二次不等式的解法为平台，考查了补集及并集的运算，是高考中常考的题型．在求补集时注意全集的范围．3．（5分）（2013•浙江）已知x，y为正实数，则（）A．2lgx+lgy=2lgx+2lgy B．2lg（x+y）=2lgx•2lgyC．2lgx•lgy=2lgx+2lgy D．2lg（xy）=2lgx•2lgy考点：有理数指数幂的化简求值；对数的运算性质．专题：函数的性质及应用．分析：直接利用指数与对数的运算性质，判断选项即可．解答：解：因为a s+t=a s•a t，lg（xy）=lgx+lgy（x，y为正实数），所以2lg（xy）=2lgx+lgy=2lgx•2lgy，满足上述两个公式，故选D．点评：本题考查指数与对数的运算性质，基本知识的考查．4．（5分）（2013•浙江）已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，φ∈R），则“f（x）是奇函数”是“φ=”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：三角函数的图像与性质．分析：φ=⇒f（x）=Acos（ωx+）⇒f（x）=Asin（ωx）（A＞0，ω＞0，x∈R）是奇函数．f （x）为奇函数⇒f（0）=0⇒φ=kπ+，k∈Z．所以“f（x）是奇函数”是“φ=”必要不充分条件．解答：解：若φ=，则f（x）=Acos（ωx+）⇒f（x）=﹣Asin（ωx）（A＞0，ω＞0，x∈R）是奇函数；若f（x）是奇函数，⇒f（0）=0，∴f（0）=Acos（ω×0+φ）=Acosφ=0．∴φ=kπ+，k∈Z，不一定有φ=“f（x）是奇函数”是“φ=”必要不充分条件．故选B．点评：本题考查充分条件、必要条件和充要条件的判断，解题时要认真审题，仔细解答，注意三角函数性质的灵活运用．5．（5分）（2013•浙江）某程序框图如图所示，若该程序运行后输出的值是，则（）A．a=4 B．a=5 C．a=6 D．a=7考点：程序框图．专题：算法和程序框图．分析：根据已知流程图可得程序的功能是计算S=1++…+的值，利用裂项相消法易得答案．解答：解：由已知可得该程序的功能是计算并输出S=1++…+=1+1﹣=2﹣．若该程序运行后输出的值是，则2﹣=．∴a=4，故选A．点评：本题考查的知识点是程序框图，其中分析出程序的功能是解答的关键．6．（5分）（2013•浙江）已知，则tan2α=（）A．B．C．D．考点：二倍角的正切；同角三角函数间的基本关系．专题：三角函数的求值．分析：由题意结合sin2α+cos2α=1可解得sinα，和cosα，进而可得tanα，再代入二倍角的正切公式可得答案．解答：解：∵，又sin2α+cos2α=1，联立解得，或故tanα==，或tanα=3，代入可得tan2α===﹣，或tan2α===故选C点评：本题考查二倍角的正切公式，涉及同角三角函数的基本关系，属中档题．7．（5分）（2013•浙江）设△ABC，P0是边AB上一定点，满足，且对于边AB 上任一点P，恒有则（）A．∠ABC=90°B．∠BAC=90°C．A B=AC D．A C=BC考点：平面向量数量积的运算．专题：平面向量及应用．分析：设||=4，则||=1，过点C作AB的垂线，垂足为H，在AB上任取一点P，设HP0=a，则由数量积的几何意义可得||2﹣（a+1）||+a≥0恒成立，只需△=（a+1）2﹣4a=（a﹣1）2≤0即可，由此能求出△ABC是等腰三角形，AC=BC．解答：解：设||=4，则||=1，过点C作AB的垂线，垂足为H，在AB上任取一点P，设HP0=a，则由数量积的几何意义可得，=||•||=||﹣（a+1））||，•=﹣a，于是•≥••恒成立，整理得||2﹣（a+1）||+a≥0恒成立，只需△=（a+1）2﹣4a=（a﹣1）2≤0即可，于是a=1，因此我们得到HB=2，即H是AB的中点，故△ABC是等腰三角形，所以AC=BC．故选：D．点评：本题主要考查了平面向量的运算，向量的模及向量的数量积的概念，向量运算的几何意义的应用，还考查了利用向量解决简单的几何问题的能力8．（5分）（2013•浙江）已知e为自然对数的底数，设函数f（x）=（e x﹣1）（x﹣1）k（k=1，2），则（）A．当k=1时，f（x）在x=1处取得极小值B．当k=1时，f（x）在x=1处取得极大值C．当k=2时，f（x）在x=1处取得极小值D．当k=2时，f（x）在x=1处取得极大值考点：函数在某点取得极值的条件．专题：导数的综合应用．分析：通过对函数f（x）求导，根据选项知函数在x=1处有极值，验证f'（1）=0，再验证f （x）在x=1处取得极小值还是极大值即可得结论．解答：解：当k=1时，函数f（x）=（e x﹣1）（x﹣1）．求导函数可得f'（x）=e x（x﹣1）+（e x﹣1）=（xe x﹣1），f'（1）=e﹣1≠0，f'（2）=2e2﹣1≠0，则f（x）在在x=1处与在x=2处均取不到极值，当k=2时，函数f（x）=（e x﹣1）（x﹣1）2．求导函数可得f'（x）=e x（x﹣1）2+2（e x﹣1）（x﹣1）=（x﹣1）（xe x+e x﹣2），∴当x=1，f'（x）=0，且当x＞1时，f'（x）＞0，当x0＜x＜1时（x0为极大值点），f'（x）＜0，故函数f（x）在（1，+∞）上是增函数；在（x0，1）上是减函数，从而函数f（x）在x=1取得极小值．对照选项．故选C．点评：本题考查了函数的极值问题，考查学生的计算能力，正确理解极值是关键．9．（5分）（2013•浙江）如图F1、F2是椭圆C1：+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（）A．B．C．D．考点：椭圆的简单性质．专题：圆锥曲线的定义、性质与方程．分析：不妨设|AF1|=x，|AF2|=y，依题意，解此方程组可求得x，y的值，利用双曲线的定义及性质即可求得C2的离心率．解答：解：设|AF1|=x，|AF2|=y，∵点A为椭圆C1：+y2=1上的点，∴2a=4，b=1，c=；∴|AF1|+|AF2|=2a=4，即x+y=4；①又四边形AF1BF2为矩形，∴+=，即x2+y2=（2c）2==12，②由①②得：，解得x=2﹣，y=2+，设双曲线C2的实轴长为2m，焦距为2n，则2m=|AF2|﹣|AF1|=y﹣x=2，2n=2=2，∴双曲线C2的离心率e===．故选D．点评：本题考查椭圆与双曲线的简单性质，求得|AF1|与|AF2|是关键，考查分析与运算能力，属于中档题．10．（5分）（2013•浙江）在空间中，过点A作平面π的垂线，垂足为B，记B=fπ（A）．设α，β是两个不同的平面，对空间任意一点P，Q1=fβ[fα（P）]，Q2=fα[fβ（P）]，恒有PQ1=PQ2，则（）A．平面α与平面β垂直B．平面α与平面β所成的（锐）二面角为45°C．平面α与平面β平行D．平面α与平面β所成的（锐）二面角为60°考点：空间中直线与平面之间的位置关系；平面与平面之间的位置关系；二面角的平面角及求法．专题：空间位置关系与距离．分析：设P1是点P在α内的射影，点P2是点P在β内的射影．根据题意点P1在β内的射影与P2在α内的射影重合于一点，由此可得四边形PP1Q1P2为矩形，且∠P1Q1P2是二面角α﹣l﹣β的平面角，根据面面垂直的定义可得平面α与平面β垂直，得到本题答案．解答：解：设P1=fα（P），则根据题意，得点P1是过点P作平面α垂线的垂足∵Q1=fβ[fα（P）]=fβ（P1），∴点Q1是过点P1作平面β垂线的垂足同理，若P2=fβ（P），得点P2是过点P作平面β垂线的垂足因此Q2=fα[fβ（P）]表示点Q2是过点P2作平面α垂线的垂足∵对任意的点P，恒有PQ1=PQ2，∴点Q1与Q2重合于同一点由此可得，四边形PP1Q1P2为矩形，且∠P1Q1P2是二面角α﹣l﹣β的平面角∵∠P1Q1P2是直角，∴平面α与平面β垂直故选：A点评：本题给出新定义，要求我们判定平面α与平面β所成角大小，着重考查了线面垂直性质、二面角的平面角和面面垂直的定义等知识，属于中档题．二、填空题：本大题共7小题，每小题4分，共28分．11．（4分）（2013•浙江）设二项式的展开式中常数项为A，则A=﹣10．考点：二项式系数的性质．专题：排列组合．分析：先求出二项式展开式的通项公式，再令x的系数等于0，求得r的值，即可求得展开式中的常数项的值．解答：解：二项式的展开式的通项公式为T r+1=••（﹣1）r•=（﹣1）r••．令=0，解得r=3，故展开式的常数项为﹣=﹣10，故答案为﹣10．点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．12．（4分）（2013•浙江）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积等于24cm3．考点：由三视图求面积、体积．专题：立体几何．分析：先根据三视图判断几何体的形状，再利用体积公式计算即可．解答：解：几何体为三棱柱去掉一个三棱锥后的几何体，底面是直角三角形，直角边分别为3，4，侧面的高为5，被截取的棱锥的高为3．如图：V=V棱柱﹣V棱锥==24（cm3）故答案为：24．点评：本题考查几何体的三视图及几何体的体积计算．V椎体=Sh，V柱体=Sh．考查空间想象能力．13．（4分）（2013•浙江）设z=kx+y，其中实数x，y满足，若z的最大值为12，则实数k=2．考点：简单线性规划．专题：不等式的解法及应用．分析：先画出可行域，得到角点坐标．再对k进行分类讨论，通过平移直线z=kx+y得到最大值点A，即可得到答案．解答：解：可行域如图：由得：A（4，4），同样地，得B（0，2），z=kx+y，即y=﹣kx+z，分k＞0，k＜0两种情况．当k＞0时，目标函数z=kx+y在A点取最大值，即直线z=kx+y在y轴上的截距z最大，即12=4k+4，得k=2；当k＜0时，①当k＞﹣时，目标函数z=kx+y在A点（4，4）时取最大值，即直线z=kx+y在y轴上的截距z最大，此时，12=4k+4，故k=2．②当k时，目标函数z=kx+y在B点（0，2）时取最大值，即直线z=kx+y在y轴上的截距z最大，此时，12=0×k+2，故k不存在．综上，k=2．故答案为：2．点评：本题主要考查简单线性规划．解决此类问题的关键是正确画出不等式组表示的可行域，将目标函数赋予几何意义．14．（4分）（2013•浙江）将A，B，C，D，E，F六个字母排成一排，且A，B均在C的同侧，则不同的排法共有480种（用数字作答）考点：排列、组合及简单计数问题．专题：排列组合．分析：按C的位置分类，在左1，左2，左3，或者在右1，右2，右3，因为左右是对称的，所以只看左的情况最后乘以2即可．解答：解：按C的位置分类，在左1，左2，左3，或者在右1，右2，右3，因为左右是对称的，所以只看左的情况最后乘以2即可．当C在左边第1个位置时，有A，当C在左边第2个位置时，A和B有C右边的4个位置可以选，有A A，当C在左边第3个位置时，有A A+A A，共为240种，乘以2，得480．则不同的排法共有480种．故答案为：480．点评：本题考查排列、组合的应用，关键在于明确事件之间的关系，同时要掌握分类讨论的处理方法．15．（4分）（2013•浙江）设F为抛物线C：y2=4x的焦点，过点P（﹣1，0）的直线l交抛物线C于两点A，B，点Q为线段AB的中点，若|FQ|=2，则直线l的斜率等于不存在．考点：直线与圆锥曲线的关系；直线的斜率．专题：圆锥曲线的定义、性质与方程．分析：由题意设直线l的方程为my=x+1，联立得到y2﹣4my+4=0，△=16m2﹣16=16（m2﹣1）＞0．设A（x1，y1），B（x2，y2），Q（x0，y0）．利用根与系数的关系可得y1+y2=4m，利用中点坐标公式可得=2m，x0=my0﹣1=2m2﹣1．Q（2m2﹣1，2m），由抛物线C：y2=4x得焦点F（1，0）．再利用两点间的距离公式即可得出m及k，再代入△判断是否成立即可．解答：解：由题意设直线l的方程为my=x+1，联立得到y2﹣4my+4=0，△=16m2﹣16=16（m2﹣1）＞0．设A（x1，y1），B（x2，y2），Q（x0，y0）．∴y1+y2=4m，∴=2m，∴x0=my0﹣1=2m2﹣1．∴Q（2m2﹣1，2m），由抛物线C：y2=4x得焦点F（1，0）．∵|QF|=2，∴，化为m2=1，解得m=±1，不满足△＞0．故满足条件的直线l不存在．故答案为不存在．点评：本题综合考查了直线与抛物线的位置关系与△的关系、根与系数的关系、中点坐标关系、两点间的距离公式等基础知识，考查了推理能力和计算能力．16．（4分）（2013•浙江）△ABC中，∠C=90°，M是BC的中点，若，则sin∠BAC=．考点：正弦定理．专题：解三角形．分析：作出图象，设出未知量，在△ABM中，由正弦定理可得sin∠AMB=，进而可得cosβ=，在RT△ACM中，还可得cosβ=，建立等式后可得a=b，再由勾股定理可得c=，而sin∠BAC═=，代入化简可得答案．解答：解：如图设AC=b，AB=c，CM=MB=，∠MAC=β，在△ABM中，由正弦定理可得=，代入数据可得=，解得sin∠AMB=，故cosβ=cos（﹣∠AMC）=sin∠AMC=sin（π﹣∠AMB）=sin∠AMB=，而在RT△ACM中，cosβ==，故可得=，化简可得a4﹣4a2b2+4b4=（a2﹣2b2）2=0，解之可得a=b，再由勾股定理可得a2+b2=c2，联立可得c=，故在RT△ABC中，sin∠BAC====，故答案为：点评： 本题考查正弦定理的应用，涉及三角函数的诱导公式以及勾股定理的应用，属难题．17．（4分）（2013•浙江）设、为单位向量，非零向量=x+y，x 、y ∈R ．若、的夹角为30°，则的最大值等于 2 ．考点：数量积表示两个向量的夹角． 专题： 平面向量及应用． 分析：由题意求得 =，||==，从而可得===，再利用二次函数的性质求得的最大值．解答：解：∵、 为单位向量，和的夹角等于30°，∴=1×1×cos30°=．∵非零向量=x +y，∴||===，∴====， 故当=﹣时，取得最大值为2，故答案为 2．点评： 本题主要考查两个向量的数量积的运算，求向量的模，利用二次函数的性质求函数的最大值，属于中档题．三、解答题：本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤．18．（14分）（2013•浙江）在公差为d的等差数列{a n}中，已知a1=10，且a1，2a2+2，5a3成等比数列．（Ⅰ）求d，a n；（Ⅱ）若d＜0，求|a1|+|a2|+|a3|+…+|a n|．考点：数列的求和；等差数列的通项公式；等比数列的性质．专题：等差数列与等比数列．分析：（Ⅰ）直接由已知条件a1=10，且a1，2a2+2，5a3成等比数列列式求出公差，则通项公式a n可求；（Ⅱ）利用（Ⅰ）中的结论，得到等差数列{a n}的前11项大于等于0，后面的项小于0，所以分类讨论求d＜0时|a1|+|a2|+|a3|+…+|a n|的和．解答：解：（Ⅰ）由题意得，即，整理得d2﹣3d﹣4=0．解得d=﹣1或d=4．当d=﹣1时，a n=a1+（n﹣1）d=10﹣（n﹣1）=﹣n+11．当d=4时，a n=a1+（n﹣1）d=10+4（n﹣1）=4n+6．所以a n=﹣n+11或a n=4n+6；（Ⅱ）设数列{a n}的前n项和为S n，因为d＜0，由（Ⅰ）得d=﹣1，a n=﹣n+11．则当n≤11时，．当n≥12时，|a1|+|a2|+|a3|+…+|a n|=﹣S n+2S11=．综上所述，|a1|+|a2|+|a3|+…+|a n|=．点评：本题考查了等差数列、等比数列的基本概念，考查了等差数列的通项公式，求和公式，考查了分类讨论的数学思想方法和学生的运算能力，是中档题．19．（14分）（2013•浙江）设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球2分，取出蓝球得3分．（1）当a=3，b=2，c=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量ξ为取出此2球所得分数之和．求ξ分布列；（2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量η为取出此球所得分数．若，求a：b：c．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分析：（1）ξ的可能取值有：2，3，4，5，6，求出相应的概率可得所求ξ的分布列；（2）先列出η的分布列，再利用η的数学期望和方差公式，即可得到结论．解答：解：（1）由题意得ξ=2，3，4，5，6，P（ξ=2）==；P（ξ=3）==；P（ξ=4）==；P（ξ=5）==；P（ξ=6）==．故所求ξ的分布列为ξ 2 3 4 5 6P（2）由题意知η的分布列为η 1 2 3PEη==Dη=（1﹣）2+（2﹣）2+（3﹣）2=．得，解得a=3c，b=2c，故a：b：c=3：2：1．点评：本题主要考查随机事件的概率和随机变量的分布列、数学期望等概念，同时考查抽象概括、运算能力，属于中档题．20．（15分）（2013•浙江）如图，在四面体A﹣BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2．M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ=3QC．（1）证明：PQ∥平面BCD；（2）若二面角C﹣BM﹣D的大小为60°，求∠BDC的大小．考点：二面角的平面角及求法；直线与平面平行的判定．专题：空间位置关系与距离；空间角；立体几何．分析：（1）取BD的中点O，在线段CD上取点F，使得DF=3CF，连接OP、OF、FQ．根据平行线分线段成比例定理结合三角形的中位线定理证出四边形OPQF是平行四边形，从而PQ∥OF，再由线面平行判定定理，证出PQ∥平面BCD；（2）过点C作CG⊥BD，垂足为G，过G作GH⊥BM于H，连接CH．根据线面垂直的判定与性质证出BM⊥CH，因此∠CHG是二面角C﹣BM﹣D的平面角，可得∠CHG=60°．设∠BDC=θ，用解直角三角形的方法算出HG和CG关于θ的表达式，最后在Rt△CHG中，根据正切的定义得出tan∠CHG==，从而得到tanθ=，由此可得∠BDC．解答：（1）取BD的中点O，在线段CD上取点F，使得DF=3CF，连接OP、OF、FQ ∵△ACD中，AQ=3QC且DF=3CF，∴QF∥AD且QF=AD∵△BDM中，O、P分别为BD、BM的中点∴OP∥DM，且OP=DM，结合M为AD中点得：OP∥AD且OP=AD∴OP∥QF且OP=QF，可得四边形OPQF是平行四边形∴PQ∥OF∵PQ⊄平面BCD且OF⊂平面BCD，∴PQ∥平面BCD；（2）过点C作CG⊥BD，垂足为G，过G作GH⊥BM于H，连接CH∵AD⊥平面BCD，CG⊂平面BCD，∴AD⊥CG又∵CG⊥BD，AD、BD是平面ABD内的相交直线∴CG⊥平面ABD，结合BM⊂平面ABD，得CG⊥BM∵GH⊥BM，CG、GH是平面CGH内的相交直线∴BM⊥平面CGH，可得BM⊥CH因此，∠CHG是二面角C﹣BM﹣D的平面角，可得∠CHG=60°设∠BDC=θ，可得Rt△BCD中，CD=BDcosθ=2cosθ，CG=CDsinθ=sinθcosθ，BG=BCsinθ=2sin2θRt△BMD中，HG==；Rt△CHG中，tan∠CHG==∴tanθ=，可得θ=60°，即∠BDC=60°点评：本题在底面为直角三角形且过锐角顶点的侧棱与底面垂直的三棱锥中求证线面平行，并且在已知二面角大小的情况下求线线角．着重考查了线面平行、线面垂直的判定与性质，解直角三角形和平面与平面所成角求法等知识，属于中档题．21．（15分）（2013•浙江）如图，点P（0，﹣1）是椭圆C1：+=1（a＞b＞0）的一个顶点，C1的长轴是圆C2：x2+y2=4的直径，l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A、B两点，l2交椭圆C1于另一点D．（1）求椭圆C1的方程；（2）求△ABD面积的最大值时直线l1的方程．考点：直线与圆锥曲线的关系；椭圆的标准方程．专题：圆锥曲线的定义、性质与方程；圆锥曲线中的最值与范围问题．分析：（1）由题意可得b=1，2a=4，即可得到椭圆的方程；（2）设A（x1，y1），B（x2，y2），D（x0，y0）．由题意可知：直线l1的斜率存在，设为k，则直线l1的方程为y=kx﹣1．利用点到直线的距离公式和弦长公式即可得出圆心O到直线l1的距离和弦长|AB|，又l2⊥l1，可得直线l2的方程为x+kx+k=0，与椭圆的方程联立即可得到点D的横坐标，即可得出|PD|，即可得到三角形ABD的面积，利用基本不等式的性质即可得出其最大值，即得到k的值．解答：解：（1）由题意可得b=1，2a=4，即a=2．∴椭圆C1的方程为；（2）设A（x1，y1），B（x2，y2），D（x0，y0）．由题意可知：直线l1的斜率存在，设为k，则直线l1的方程为y=kx﹣1．又圆的圆心O（0，0）到直线l1的距离d=．∴|AB|==．又l2⊥l1，故直线l2的方程为x+ky+k=0，联立，消去y得到（4+k2）x2+8kx=0，解得，∴|PD|=．∴三角形ABD 的面积S △==，令4+k 2=t ＞4，则k 2=t ﹣4， f （t ）===，∴S △=，当且仅，即，当时取等号，故所求直线l 1的方程为．点评：本题主要考查了椭圆的几何性质、直线与圆及椭圆的位置关系等基础知识，同时考查了推理能力和计算能力及分析问题和解决问题的能力． 22．（14分）（2013•浙江）已知a ∈R ，函数f （x ）=x 3﹣3x 2+3ax ﹣3a+3． （1）求曲线y=f （x ）在点（1，f （1））处的切线方程； （2）当x ∈[0，2]时，求|f （x ）|的最大值．考点：利用导数研究曲线上某点切线方程；利用导数求闭区间上函数的最值． 专题：导数的综合应用． 分析： （1）求出原函数的导函数，求出函数取x=1时的导数值及f （1），由直线方程的点斜式写出切线方程；（2）求出原函数的导函数，分a ≤0，0＜a ＜1，a ≥1三种情况求|f （x ）|的最大值．特别当0＜a ＜1时，仍需要利用导数求函数在区间（0，2）上的极值，然后在根据a 的范围分析区间端点值与极值绝对值的大小． 解答： 解：（1）因为f （x ）=x 3﹣3x 2+3ax ﹣3a+3，所以f ′（x ）=3x 2﹣6x+3a ， 故f ′（1）=3a ﹣3，又f （1）=1，所以所求的切线方程为y=（3a ﹣3）x ﹣3a+4；（2）由于f ′（x ）=3（x ﹣1）2+3（a ﹣1），0≤x ≤2．故当a ≤0时，有f ′（x ）≤0，此时f （x ）在[0，2]上单调递减，故 |f （x ）|max =max{|f （0）|，|f （2）|}=3﹣3a ．当a ≥1时，有f ′（x ）≥0，此时f （x ）在[0，2]上单调递增，故 |f （x ）|max =max{|f （0）|，|f （2）|}=3a ﹣1．当0＜a ＜1时，由3（x ﹣1）2+3（a ﹣1）=0，得，．所以，当x ∈（0，x 1）时，f ′（x ）＞0，函数f （x ）单调递增； 当x ∈（x 1，x 2）时，f ′（x ）＜0，函数f （x ）单调递减； 当x ∈（x 2，2）时，f ′（x ）＞0，函数f （x ）单调递增． 所以函数f （x ）的极大值，极小值．故f （x 1）+f （x 2）=2＞0，．从而f （x 1）＞|f （x 2）|． 所以|f （x ）|max =max{f （0），|f （2）|，f （x 1）}． 当0＜a ＜时，f （0）＞|f （2）|． 又=故．当时，|f （2）|=f （2），且f （2）≥f （0）．又=．所以当时，f （x 1）＞|f （2）|．故．当时，f （x 1）≤|f （2）|．故f （x ）max =|f （2）|=3a ﹣1．综上所述|f （x ）|max =．点评： 本题考查了利用导数研究曲线上某点处的切线方程，考查了利用导数求闭区间上的最值，考查了分类讨论的数学思想方法，正确的分类是解答（2）的关键，此题属于难题．。