流体力学连续性方程微分形式

微分形式的连续性方程连续方程是流体力学的基本方程之一，流体运动的连续方程，反映流体运动和流体质量分布的关系，它是在质量守恒定律在流体力学中的应用。

重点讨论不同表现形式的流体连续方程。

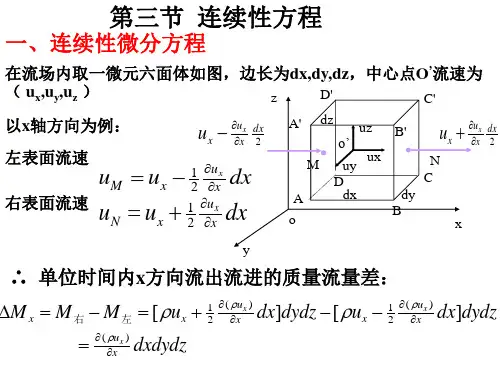
用一个微六面体元控制体建立微分形式的连续性方程。

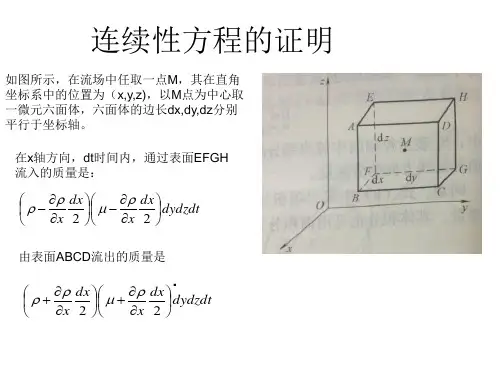
设在流场中取一固定不动的微平行六面体（控制体），在直角坐标系oxyz 中，六面体的边长取为dx ，dy ，dz 。

先看x 轴方向的流动，流体从ABCD 面流入六面体，从EFGH 面流出。

在x 轴方向流出与流入质量之差()()[]x x x x u u u dx dydzdt u dydzdt dxdydzdt x xρρρρ∂∂+-=∂∂用同样的方法，可得在y 轴方向和z 轴方向的流出与流入质量之差分别为()y u dxdydzdt y ρ∂∂()z u dxdydzdt z ρ∂∂这样，在dt 时间内通过六面体的全部六个面净流出的质量为：()()()[]y x z u u udxdydzdt x x x ρρρ∂∂∂++∂∂∂在dt 的时间内，六面体内的质量减少了 ， 根据质量守恒定律，净流出六面体的质量必等于六面体内所减少的质量()dxdydzdt t ρ∂-∂()()()[]y x z u u u dxdydzdt dxdydzdt x y z tρρρρ∂∂∂∂++=-∂∂∂∂()()()0y x z u u u x y z tρρρρ∂∂∂∂+++=∂∂∂∂这就是直角坐标系中流体运动的微分形式的连续性方程。

这就是直角坐标系中流体运动的微分形式的连续性方程。

代表单位时间内，单位体积的质量变化代表单位时间内，单位体积内质量的净流出利用散度公式：得到利用矢量场基本运算公式和随体导数公式：得到 )()()()div(z y x u z u y u x u ρρρρ∂∂+∂∂+∂∂= 0)div(=+∂∂u tρρ()()()0y x z u u u x y z tρρρρ∂∂∂∂+++=∂∂∂∂在连续方程中 div()div u u u ρρρ=+⋅∇ρρρ∇⋅+∂∂=u tDt D 0div =+u Dt D ρρdiv 0u u tρρρ∂++⋅∇=∂讨论*表明对不可压流体，体积在随体运动中保持不变。

理解流体力学中的连续性方程流体力学是研究流体静力学和流体动力学的学科，涵盖了许多重要的基本方程。

其中，连续性方程是流体力学中的基础之一，用于描述流体在宏观尺度上的连续性。

理解连续性方程对于研究流体运动和分析流体现象具有重要意义。

本文将介绍连续性方程的定义、推导与应用，并探讨其中的物理意义。

一、连续性方程的定义与推导连续性方程描述了流体运动时，质量守恒的性质。

在宏观尺度上，流体的质量保持不变，由此可以得到连续性方程的数学表达式。

假设流体流动方向为坐标轴方向，流体通过某一截面的流量为Q，流动截面面积为A，则单位时间内通过截面的质量为Δm。

根据质量守恒原理，Δm应保持不变。

考虑时间间隔Δt内，流体运动导致流量Q发生变化。

根据定义，Δt时刻通过截面的质量为Δm1，Δt+Δt时刻通过截面的质量为Δm2。

根据质量守恒原理，Δm1+Δm2应等于Δm。

Δm1+Δm2 = ρ1QΔt + ρ2QΔt (1)其中，ρ1和ρ2分别为Δt时刻和Δt+Δt时刻的流体密度。

将流体密度表示为单位体积的质量，即ρ = m/V。

在Δt时间间隔内，流体的体积可以表示为：Δt时刻的体积为V1 = QΔt (2)Δt+Δt时刻的体积为V2 = QΔt + AΔx (3)其中，Δx为流体运动方向上的位移。

将公式（2）和（3）代入公式（1），得到：ρ1QΔt + ρ2QΔt = ρ1V1 + ρ2V2 (4)根据密度的定义，可以将公式（4）进一步推导为：ρ1Q + ρ2Q = ρ1Q + ρ2(Q + AΔx) (5)化简后可简化为：d(ρQ)/dt + A(ρv) = 0 (6)其中，v为流体的流速。

以上就是连续性方程的定义与推导过程。

连续性方程的表达形式可以用偏微分方程来表示，常被称为连续性方程的微分形式。

二、连续性方程的物理意义连续性方程描述了流体在运动过程中的连续性。

通过分析连续性方程，我们可以进一步理解其中的物理意义。

在连续性方程中，d(ρQ)/dt表示单位时间内流体质量的变化率，A(ρv)表示单位时间内流体通过截面边界的质量变化率。

《流体力学与流体机械》(下)主要公式及方程式1．流体力学常用准数： (1) 雷诺准数 μρlu =Re (2) 欧拉准数 2Eu u p ρ= (3) 牛顿准数 22Ne l u F ρ=(4) 付鲁德准数 lg u 2Fr = (5) 马赫准数 a u=M (6) 斯特罗哈准数 l u τ=St(7) 阿基米德准数 TTu l g ∆=2Ar (8) 格拉晓夫准数23G r νβt l g ∆= (9) 韦伯准数 σρl u 2We =2．气体等压比热和等容比热计算式：1p -=k Rk C ； 1v -=k R C 3．完全气体比焓定义式：T C RT e pe i p =+=+=ρ4．完全气体状态方程式：T R p ρ= 状态方程微分式：TT p p d d d +=ρρ 5．完全气体等熵过程方程式：C p=kρ等熵过程方程微分式：ρρd d kp p = 气体压力p 、密度ρ和温度T 之间的等熵关系：1k k12k 1212)()(-==T Tp p ρρ6．气体熵增计算式：)]()ln[(ln ln 211k k121212p 12p pT T R p p R T T C s s -=-=-7．热力学第一定律的能量方程式：we u z g p q e u z g p ++++=++++22222212111122ρρ 可压缩理想流体绝热流动能量方程式： 022221122i u i u i =+=+ 以温度和流速表述： 0p 222p 211p 22T C u T C u T C =+=+ 以温度和流速表述：022221112121T R k k u T R k k u T R k k -=+-=+-以压力、密度和流速表述： 002222211112121ρρρp k k u p k k u p k k -=+-=+- 以音速和流速表述： 121212022222121-=+-=+-k a u k a u k a 8．完全气体的音速公式：T R k pk pa ===ρρd d9．理想流体一维稳定流动连续性方程式：C uA Q ==ρ 连续性方程微分式：0d d d =++AA u u ρρ10．欧拉运动方程的积分式：C u z g p=++⎰2d 2ρ 或简化为 C u p=+⎰2d 2ρ 欧拉运动方程的微分式：0d d d =++u u z g pρ或简化为0d d =+u u pρ11．理想流体稳定流动的动量方程式： ⎪⎭⎪⎬⎫-=∑-=∑-=∑)()()(z1z2z y 1y 2y x1x2x u u Q F u u Q F u u Q F ρρρ一维稳定流动动量方程微分式：0d d x=++AR u u pρδρ12．气体极限速度及临界速度计算式：120m ax -=k T kR u ； 120*+=k kRT u 13．流动参量与滞止参量间的关系：20211M k T T -+=； 1k k20)211(--+=M k p p 1k 120)211(--+=M k ρρ； 2120)211(M k a a -+= 14．无因次速度Λ与马赫数M 间的关系： 222)1()1(2ΛΛ--+=k k M15．流速的计算式： ])(1[12k1k 00---=p pRT k k u ； 或 ])(1[12k1k 000---=p pp k k u ρ无因次速度计算式：k1k 00max)(11--=-=p p T T u u16．质量流量的计算式： ])()[(12k1k 0k 2000+--=p pp p p k k AG ρ1)2(k 1k 200)211(-+--+=M k M p k A G ρ 最大质量流量计算式：00*1)2(k 1k max )12(ρp k A k G -++= 或 00*1)2(k 1k max )12(T P A k R k G -++= 17．喷管出口马赫数计算式： ]1)[(12k 1k e0e --=-p p k M 18．正激波在静止气体中传播速度计算式： 121212w ρρρρ⋅--=p p u 19．正激波后气流速度计算式： 211212)()(ρρρρ--=p p u20．正激波前后速度关系式： 2*21a u u =21．正激波前后马赫数间的关系式： )1(2)1(2212112121212122---+=---+=k M k M k k M k M k M 22．正激波前后气流参量比与波前M 1数的关系式：2121212112)1(2)1(21121M k M k M k M k -++=-++=ρρ11122112+--+=k k M k k p p]1)1(2)[112()11(2121212+---+-=M k M k k k k T T11)1(22112+-++=k k M k u u1k 1211k k21210102)1112(])1(2)1([--+--+-++=k k M k k M k M k p p23．范诺流极限管长计算式： ])1(2)1(ln 211[21212121max M k M k k k M k M D L -++++-=λ24．范诺流参量变化关系式：2*)1(21M k k T T -++=； 2122*])1(2)1([Mk M k u u -++= 2122*])1()1(2[Mk M k +-+=ρρ； 212*])1(21[1M k k M p p -++= 1)2(k 1k 2*00)1112(1-++-++=M k k k M p p 25．瑞利流参量变化关系式：2*11M k k p p ++=；222*)11(M k k M T T ++= )11(122*kM k M ++=ρρ； )11(22*M k k M u u ++= ]1)1(2[)11(2222*00+-+++=k M k Mk k M T T 1k k 22*00]1)1(2[11-+-+++=k M k M k k p p 26．瑞利流能量方程式： 22222211u i q u i +=++ 27．等温流能量方程式： 0201i q i =+ 或 222221u q u =+ 28．等温流压降计算式：)ln2(1212112221Dl u u p u p p λρ+=- 等温流压降近似计算式：211211211M k Dlp T R u D l p p λλ-=-= 29．等温流质量流量计算式：)(16222152p p TR l D G -=λπ 30．等温流极限管长计算式： )]ln(1[212121maxM k M k M k D L +-=λ 31．等温流参量变化关系式：M k u u =∆； Mk p p 1==∆∆ρρ； T R u =∆32．等温流可能的最小压力： 11min M p k p p ==∆ 33．紊流射流主要参量计算式：35．阿基米德准数：对圆截面射流a 0200Ar T T u R g ∆=，对平面射流a200Ar T T u B g ∆=。

流体力学中的连续性方程与守恒流体力学中的连续性方程与守恒流体力学是研究流体运动及其力学性质的学科，而连续性方程和守恒定律是流体力学中的两个基本理论。

连续性方程描述了流体在运动过程中质量守恒的原理，而守恒定律则描述了流体力学中不同物理量的守恒规律。

连续性方程是描述流体质量守恒的基本方程。

它表明，对于一个封闭的流体系统，在任何给定的时间和空间点上，质量的净流入和净流出量应该是相等的。

换句话说，流体在任何一个点上的流入质量等于流出质量。

这个原理可以通过考虑流体的密度和速度来解释。

连续性方程的数学表达式是：∂ρ/∂t + ∇·(ρv) = 0其中，ρ是流体的密度，t是时间，v是流体的速度矢量，∇·表示散度运算符。

这个方程可以解释为：流体质量的变化率等于流体质量通过单位面积的流入和流出速度的散度之和。

守恒定律是流体力学中描述物理量守恒的基本定律。

根据这个定律，对于一个封闭的流体系统，在任何给定的时间和空间点上，某一物理量的净流入和净流出量应该是相等的。

常见的守恒定律包括质量守恒、动量守恒和能量守恒。

这些守恒定律可以用微分形式和积分形式表示。

对于质量守恒定律，可以根据连续性方程推导出质量守恒方程：∂(ρA)/∂t + ∇·(ρAv) = 0其中，A是流体系统中的任意闭合面积，其边界为∂A，ρ是流体的密度，t是时间，v是流体的速度矢量。

这个方程表示了质量的变化率等于通过边界∂A的质量流入和质量流出之差。

对于动量守恒定律，可以根据牛顿第二定律推导出动量守恒方程。

对于一个封闭的流体系统，动量守恒方程可以表示为：∂(ρv)/∂t + ∇·(ρvv) = -∇p + ∇·τ + ρg其中，ρ是流体的密度，t是时间，v是流体的速度矢量，p是流体的压力，τ是流体的应力张量，g是重力加速度。

能量守恒定律是描述能量守恒的基本定律。

根据能量守恒定律，对于一个封闭的流体系统，在任何给定的时间和空间点上，能量的净流入和净流出量应该是相等的。