一次函数第二课时
- 格式:ppt
- 大小:1.75 MB
- 文档页数:8

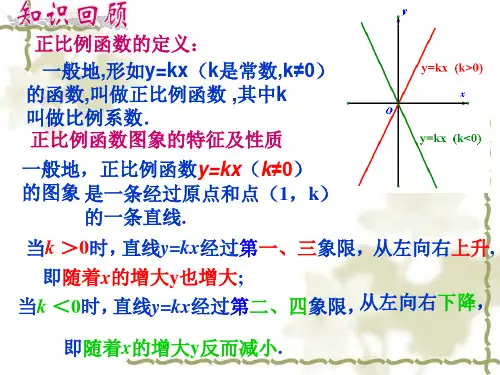

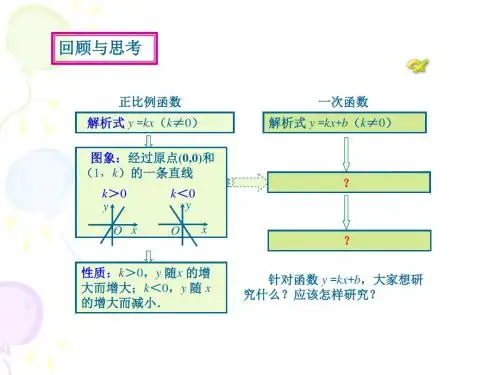






19.2.2一次函数的图象和性质第二课时一次函数图象的位置(说明:本节课是19.2.2学习一次函数图象和性质后安排的一节探究课, 探究一次函数图象的位置,目的是进一步把握一次函数的图象和性质.)教学目标1.掌握直线y=kx+b 位置的四种情况,并会进行简单应用.2.体会数形结合、分类思想、特殊到一般等思想方法解决数学问题.3.培养学生的探索精神,提高学习数学兴趣. 教学重难点重点是直线y=kx+b 位置的四种情况及应用.难点是理解一次函数y=kx+b 中k 、b 的值与直线y=kx+b 位置的关系. 教学设计 一、复习引入 回忆一次函数y=kx+b 的图象和性质是什么? 1.图象:经过(0,b)和( kb-,0)的直线; 2.性质:(1)当k>0时,y 随x 的增大而增大. (2)当k<0时,y 随x 的增大而减小. 思考1.用描点法画一次函数的图象怎样画最简单? 用两点画图象,一般选(0,b)和(kb-,0) 2.一次函数的图象是经过几个象限的直线?一次函数的图象是经过三个象限的直线. 探究k 、b 与直线y=kx+b 经过的三个象限的关系 二、探究新知体会:分别用两点法在直角坐标系上画出下列一次函数的图象, 并观察k 和b 的值与直线所在象限的联系.(1) y=x+2 (2) y=2x-1 (3) y=-2x+1 (4) y=-x-2探究:学生讨论k 、b 的值与直线y=kx+b 位置的关系探究1:k>0,b>0经过哪三个象限? 学生甲:由b>0知直线与y 轴交点(0,b)在正半轴上; 由k>0知直线从左至右斜向上.由此,当k>0,b>0时,直线经过一、二、三象限. 学生乙:探究2:k>0,b<0经过哪三个象限?由b<0知直线与y 轴交点(0,b)在负半轴上; 由k>0知直线从左至右斜向上.由此,当k>0,b<0时,直线经过一、三、四象限. 学生丙:探究3:k<0,b>0经过哪三个象限? 由b>0知直线与y 轴交点(0,b)在正半轴上; 由k<0知直线从左至右斜向下.由此,当k<0,b>0,时直线经过一、二、四象限.学生丁:探究4:k<0,b<0经过哪三个象限?由b<0知直线与y 轴交点(0,b)在负半轴上; 由k<0知直线从左至右斜向下.由此,当k<0,b<0时,直线经过二、三、四象限. 归纳1.k >0,b >0⇔一、二、三象限.2.k >0,b <0⇔一、三、四象限.3.k <0,b >0⇔一、二、四象限.4.k <0,b <0⇔二、三、四象限. 试试1.直线y=3x-2经过 象限.2.直线y=-4x-2不经过 象限.3.一次函数y=kx+b (k ≠0)在平面直角坐标系内的图象如图所示,则k 和b 的取值范围是( ) A .k >0,b >0B .k <0,b <0{32m m C .k <0,b >0 D .k >0,b <0三、应用迁移例:已知一次函数y=(3-m)x-(2m-4)经过二、三、四象限,求m 的取值范围. 分析:由一次函数经过二、三、四象限 知k<0, b<0解:由题意,得解得所以m 的取值范围是m>3 变式抽学生上黑板完成:已知一次函数y=3(4-m)x-(2m-5)的位置如图,求整数m 的值 并写出一次函数解析式. 小结本节课里你学到了什么??? 学生讨论后回答:函数知识:k 、b 与直线y=kx+b 经过三个象限的关系. 思想方法:(1)数形结合. (2)分类思想.(3)特殊到一般.练练{030)42( m m ---1.直线y=kx+b经过一、二、四象限,则k、b应满足()A.k>0, b<0B.k>0, b>0C.k<0, b<0D.k<0, b>02.已知一次函数y=kx+b, y随着x的增大而减小,且kb<0,则在直角坐标系内它的图象大致为()巩固1.当k+b<0且kb>0时,一次函数y=kx+b的图象一定经过象限是.2.在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限3.已知一次函数y=(a+8)x+(6-b).(1)a,b为何值时,是正比例函数且y随x的增大而增大?(2)a,b为何值时,图象过第一、二、四象限?4.已知一次函数y=(m+2)x+m+3的图象与y轴交点在x轴上方,且y随x的增大而减小,求m的取值范围.5.已知一次函数y=(m+2)x-3(m+4)的图象不经过一象限,且m为整数,求一次函数解析式.。