同步时序逻辑电路的分析方法
- 格式:docx
- 大小:31.07 KB
- 文档页数:4
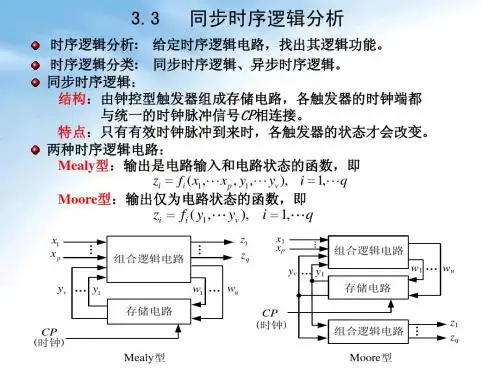


时序逻辑电路的分析方法时序逻辑电路的分析:根据给定的电路,写出它的方程、列出状态转换真值表、画出状态转换图和时序图,而后得出它的功能。
同步时序逻辑电路的分析方法同步时序逻辑电路的主要特点:在同步时序逻辑电路中,由于所有触发器都由同一个时钟脉冲信号CP来触发,它只控制触发器的翻转时刻,而对触发器翻转到何种状态并无影响,所以,在分析同步时序逻辑电路时,可以不考虑时钟条件。
1、基本分析步骤1)写方程式:输出方程:时序逻辑电路的输出逻辑表达式,它通常为现态和输入信号的函数。
驱动方程:各触发器输入端的逻辑表达式。
状态方程:将驱动方程代入相应触发器的特性方程中,便得到该触发器的状态方程。
2)列状态转换真值表:将电路现态的各种取值代入状态方程和输出方程中进行计算,求出相应的次态和输出,从而列出状态转换真值表。
如现态的起始值已给定时,则从给定值开始计算。
如没有给定时,则可设定一个现态起始值依次进行计算。
3)逻辑功能的说明:根据状态转换真值表来说明电路的逻辑功能。
4)画状态转换图和时序图:状态转换图:是指电路由现态转换到次态的示意图。
时序图:是在时钟脉冲CP作用下,各触发器状态变化的波形图。
5)检验电路能否自启动关于电路的自启动问题和检验方法,在下例中得到说明。
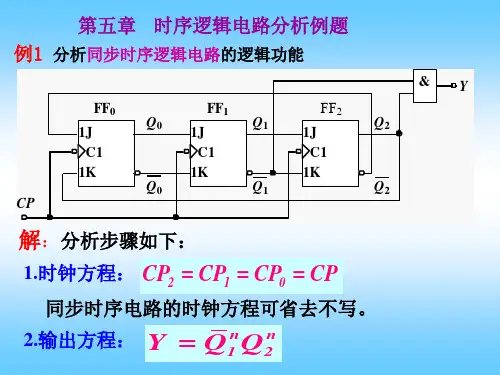
2、分析举例例、试分析下图所示电路的逻辑功能,并画出状态转换图和时序图。
解:由上图所示电路可看出,时钟脉冲CP加在每个触发器的时钟脉冲输入端上。
因此,它是一个同步时序逻辑电路,时钟方程可以不写。
①写方程式:输出方程:驱动方程:状态方程:②列状态转换真值表:状态转换真值表的作法是:从第一个现态“000”开始,代入状态方程,得次态为“001”,代入输出方程,得输出为“0”。
把得出的次态“001”作为下一轮计算的“现态”,继续计算下一轮的次态值和输出值。
依次类推,直到次态值又回到了第一个现态值“000”。
现态次态输出Y00101000110110010100010010101010001③逻辑功能说明:电路在输入第6个计数脉冲CP后,返回原来的状态,同时输出端Y 输出一个进位脉冲。







实验八同步时序逻辑电路的分析一、实验目的⑴熟悉同步时序逻辑电路的一般分析、设计方法⑵熟悉移位寄存器和同步计数器的逻辑功能二、实验预习复习触发器的功能、特点和应用三、实验器材⑴直流稳压电源、数字逻辑实验箱⑵ 74LS00、74LS08、74LS10、74LS86、74LS74、74LS76四、实验内容和步骤1.移位寄存器型计数器⑵将集成D型触发器74LS74按图8-2接线。
电路的脉冲输入端CP接单脉冲,四个输出端Q4、Q3、Q2、Q1分别接发光二极管。
用触发器的异步清除端CLR将触发器初始状态复位为“0000”,Q4Q3Q2Q1=0000。
(同样,可以用各触发器的预置端将触发器的初始状态置为某个状态。
)逐次按动单脉冲按钮,观察在CP脉冲作用下,计数器输出端的变化状态,将结果填入自制的表中。
分析电路输出端状态变化的规律,画出状态转换图,并说明电路的功能。
实验结果:五、思考题总结同步时序逻辑电路的一般分析方法。
(1) 根据逻辑电路写出各个触发器的驱动方程,即写出每个触发器输入端的逻辑函数表达式。
(2) 根据所给触发器,将得到的驱动方程代入触发器特性方程,得到时钟脉冲作用下的状态方程。
(3) 从逻辑电路中写出输出端的逻辑函数表达式。
(4) 将任何一组输入变量的取值及电路的初始状态,代入状态转移方程中和输出函数表达式中,得到时钟信号作用下的存储电路的次态逻辑值;再以得到的次态逻辑值为初始状态,和此时的输入变量的取值,再次代入状态转移方程中和输出函数表达式中,又得到新的次态逻辑值以及电路的输出值,如此循环代入逻辑值,直到所有输入变量的取值和所有逻辑状态值全部代入。
将存储电路的状态转换以及电路的输出用表格的形式来描述它们之间的关系,称为状态转移表。
将存储电路状态之间的转换关系用图形的方式来描述,就是状态转换图。
(5) 检查状态转换图(状态转移表),如果在时钟信号和输入信号的作用下,各个状态之间能够建立联系,则说明该时序逻辑电路能够自启动,否则不能自启动。
时序逻辑电路的分析方法
时序逻辑电路的分析:根据给定的电路,写出它的方程、列出状态转换真值表、画出状态转换图和时序图,而后得出它的功能。
同步时序逻辑电路的分析方法
同步时序逻辑电路的主要特点:在同步时序逻辑电路中,由于所有触发器都由同一个时钟脉冲信号CP来触发,它只控制触发器的翻转时刻,而对触发器翻转到何种状态并无影响,所以,在分析同步时序逻辑电路时,可以不考虑时钟条件。
1、基本分析步骤
1)写方程式:
输出方程:时序逻辑电路的输出逻辑表达式,它通常为现态和输入信号的函数。
驱动方程:各触发器输入端的逻辑表达式。
状态方程:将驱动方程代入相应触发器的特性方程中,便得到该触发器的状态方程。
2)列状态转换真值表:
将电路现态的各种取值代入状态方程和输出方程中进行计算,求出相应的次态和输出,从而列出状态转换真值表。
如现态的起始值已给定时,则从给定值开始计算。
如没有给定时,则可设定一个现态起始值依次进行计算。
3)逻辑功能的说明:
根据状态转换真值表来说明电路的逻辑功能。
4)画状态转换图和时序图:
状态转换图:是指电路由现态转换到次态的示意图。
时序图:是在时钟脉冲CP作用下,各触发器状态变化的波形图。
5)检验电路能否自启动
关于电路的自启动问题和检验方法,在下例中得到说明。
2、分析举例
例、试分析下图所示电路的逻辑功能,并画出状态转换图和时序图。
解:由上图所示电路可看出,时钟脉冲CP加在每个触发器的时钟脉冲输入端上。
因此,它是一个同步时序逻辑电路,时钟方程可以不写。
①写方程式:
输出方程:
驱动方程:
状态方程:
②列状态转换真值表:
状态转换真值表的作法是:
从第一个现态“000”开始,代入状态方程,得次态为“001”,代入输出方程,得输出为“0”。
把得出的次态“001”作为下一轮计算的“现态”,继续计算下一轮的次态值和输出值。
依次类推,直到次态值又回到了第一个现态值“000”。
③逻辑功能说明:
电路在输入第6个计数脉冲CP后,返回原来的状态,同时输出端Y 输出一个进位脉冲。
因此,上图所示电路为同步六进制计数器。
④画状态转换图和时序图:
状态转换图和时序图如下图所示
状态转换图的圆圈内表示电路的一个状态,即三个触发器的状态,箭头表示电路状态的转换方向。
箭头线上方标注的X/Y为转换条件,X为电路状态转换前输入变量的取值,Y为输出值,由于本例没有输入变量,故X未标数值。