抛物线的几何性质
- 格式:doc
- 大小:4.69 KB
- 文档页数:5

一、 第一讲: 抛物线标准方程 二、 考点、热点回顾一、定义: 在平面内,及一个定点F 和一条定直线l(l 不经过点F)的距离相等的点的轨迹叫抛物线.即:的轨迹是抛物线。
则点若M MNMF,1 三、 (定点F 叫做抛物线的焦点, 定直线l 叫做抛物线的准线。
)标准方程:设定点F 到定直线l 的距离为p(p 为已知数且大于0).取过焦点F 且垂直于准线l 的直线为x 轴, x 轴及l 交于K, 以线段KF 的垂直平分线为y 轴, 建立直角坐标系抛物线上的点M(x, y)到l的距离为d, 抛物线是集合p={M||MF|=d}.化简后得: y2=2px(p>0).由于焦点和准线在坐标系下的不同分布情况, 抛物线的标准方程有四种情形(列表如下):二、典型例题(2)例1.(1)已知抛物线的标准方程是y2=6x, 求它的焦点坐标和准线方程;已知抛物线的焦点坐标是F(0, -2), 求它的标准方程.方程是x2=-8y.例2.根据下列所给条件, 写出抛物线的标准方程:(1)焦点是F(3, 0);(3)焦点到准线的距离是2.答案是:(1)y2=12x;(2)y2=-x;(3)y2=4x, y2=-4x, x2=4y, x2=-4y.三、课堂练习1.抛物线y2=4x的焦点到准线的距离是________答案:2解析: 解析: 抛物线y2=4x的焦点F(1,0), 准线x=-1.∴焦点到准线的距离为2.2.分别求适合下列条件的抛物线的标准方程:(1)过点(-3,2);(2)焦点在直线x-2y-4=0上.答案:解析: 解: (1)设抛物线方程为y2=-2px或x2=2py(p>0), 则将点(-3,2)代入方程得2p=或2p=, 故抛物线方程为y2=-x或x2=y.(2)①令x=0, 由方程x-2y-4=0, 得y=-2.∴抛物线的焦点为F(0, -2).设抛物线方程为x2=-2py(p>0), 则由=2, 得2p=8. ∴所求抛物线方程为x2=-8y.②令y=0,由方程x-2y-4=0,得x=4.∴抛物线的焦点为F(4,0).设抛物线方程为y2=2px(p>0), 则由=4, 得2p=16.∴所求抛物线方程为y2=16x.综上, 所求抛物线方程为y2=16x或x2=-8y.3.已知抛物线的顶点在原点, 对称轴是x轴, 抛物线上的点M(-3, m)到焦点的距离等于5, 求抛物线的方程和m的值解法一: 由焦半径关系, 设抛物线方程为y2=-2px(p>0), 则准线方因为抛物线上的点M(-3, m)到焦点的距离|MF|及到准线的距离得p=4.因此, 所求抛物线方程为y2=-8x.又点M(-3, m)在此抛物线上, 故m2=-8(-3).解法二: 由题设列两个方程, 可求得p和m. 由学生演板. 由题意在抛物线上且|MF|=5, 故四、课后作业1.分别求适合下列条件的抛物线的标准方程:(1)过点(-3,2);(2)焦点在直线x-2y-4=0上.答案:解析: (1)设抛物线方程为y2=-2px或x2=2py(p>0), 则将点(-3,2)代入方程得2p=或2p=, 故抛物线方程为y2=-x或x2=y.(2)①令x=0, 由方程x-2y-4=0, 得y=-2.∴抛物线的焦点为F(0, -2).设抛物线方程为x2=-2py(p>0), 则由=2, 得2p=8. ∴所求抛物线方程为x2=-8y.②令y=0,由方程x-2y-4=0,得x=4.∴抛物线的焦点为F(4,0).设抛物线方程为y2=2px(p>0), 则由=4, 得2p=16.∴所求抛物线方程为y2=16x.综上, 所求抛物线方程为y2=16x或x2=-8y.2.若抛物线y2=-2px(p>0)上有一点M, 其横坐标为-9, 它到焦点的距离为10, 求抛物线方程和M点的坐标.解析: 解: 由抛物线的定义, 设焦点F(-, 0). 则准线为x=.设M到准线的距离为|MN|,则|MN|=|MF|=10, 即-(-9)=10, ∴p=2. 故抛物线方程为y2=-4x.将M(-9,y),代入抛物线方程得y=±6. 故M(-9,6)或M(-9,-6).3.已知抛物线C的焦点F在x轴的正半轴上, 点A(2, )在抛物线内. 若抛物线上一动点P到A.F两点距离之和的最小值为4, 求抛物线C的方程.解析: 解: 设抛物线方程为y2=2px(p>0), 其准线为x=-, 过P点作抛物线准线的垂线, 垂足为H(图略), 由定义知, |PH|=|PF|.∴|PA|+|PF|=|PA|+|PH|, 故当H、P、A三点共线时, |PA|+|PF|最小. ∴|PA|+|PF|的最小值为+2=4, p=4, 即抛物线C的方程为y2=8x.4.动圆M经过点A(3,0)且及直线l: x=-3相切, 求动圆圆心M的轨迹方程.解:设圆M及直线l相切于点N. ∵|MA|=|MN|, ∴圆心M到定点A(3,0)和定直线x=-3的距离相等.根据抛物线的定义, M在以A为焦点, l为准线的抛物线上.∵=3,∴p=6. ∴圆心M的轨迹方程为y2=12x.第二讲: 抛物线简单几何性质一、考点、热点回顾定义: 在平面内,及一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.补充:1.通径: 通过焦点且垂直对称轴的直线, 及抛物线相交于两点, 连接这两点的线段叫做抛物线的通径。


《抛物线的几何性质》讲义一、抛物线的定义在平面内,到一个定点 F 和一条定直线 l 的距离相等的点的轨迹叫做抛物线。
点 F 叫做抛物线的焦点,定直线 l 叫做抛物线的准线。
例如,我们常见的喷泉喷出的水形成的曲线,篮球投篮时的运动轨迹,都可以近似地看作是抛物线。
二、抛物线的标准方程抛物线的标准方程有四种形式:1、当焦点在 x 轴正半轴上时,抛物线的标准方程为\(y^2 =2px (p>0)\),此时焦点坐标为\((\frac{p}{2}, 0)\),准线方程为\(x =\frac{p}{2}\)。
2、当焦点在 x 轴负半轴上时,抛物线的标准方程为\(y^2 =-2px (p>0)\),焦点坐标为\((\frac{p}{2}, 0)\),准线方程为\(x =\frac{p}{2}\)。
3、当焦点在 y 轴正半轴上时,抛物线的标准方程为\(x^2 =2py (p>0)\),焦点坐标为\((0, \frac{p}{2})\),准线方程为\(y =\frac{p}{2}\)。
4、当焦点在 y 轴负半轴上时,抛物线的标准方程为\(x^2 =-2py (p>0)\),焦点坐标为\((0, \frac{p}{2})\),准线方程为\(y =\frac{p}{2}\)。
这里的\(p\)表示焦点到准线的距离,它决定了抛物线的开口大小。
\(p\)值越大,抛物线的开口就越宽;\(p\)值越小,抛物线的开口就越窄。
三、抛物线的几何性质1、范围对于抛物线\(y^2 = 2px (p>0)\),\(y\)可以取任意实数,\(x\geq 0\);对于抛物线\(y^2 =-2px (p>0)\),\(y\)可以取任意实数,\(x\leq 0\);对于抛物线\(x^2 = 2py (p>0)\),\(x\)可以取任意实数,\(y\geq 0\);对于抛物线\(x^2 =-2py (p>0)\),\(x\)可以取任意实数,\(y\leq 0\)。
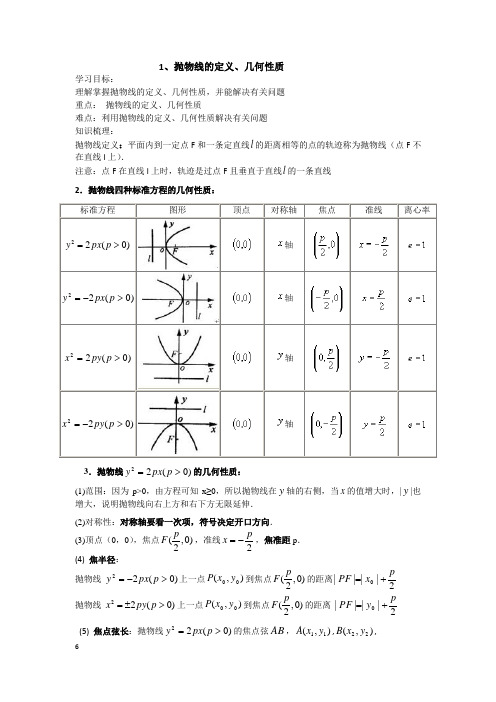
1、抛物线的定义、几何性质学习目标:理解掌握抛物线的定义、几何性质,并能解决有关问题 重点: 抛物线的定义、几何性质难点:利用抛物线的定义、几何性质解决有关问题 知识梳理:抛物线定义:平面内到一定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线(点F 不在直线l 上). 注意:点F 在直线l 上时,轨迹是过点F 且垂直于直线l 的一条直线 2.抛物线四种标准方程的几何性质:轴)轴轴)轴3.抛物线)0(22>=p px y 的几何性质:(1)范围:因为p>0,由方程可知x ≥0,所以抛物线在y 轴的右侧,当x 的值增大时,|y |也增大,说明抛物线向右上方和右下方无限延伸. (2)对称性:对称轴要看一次项,符号决定开口方向. (3)顶点(0,0),焦点(,0)2p F ,准线2px -=,焦准距p . (4) 焦半径:抛物线 )0(22>-=p px y 上一点),(00y x P 到焦点(,0)2p F 的距离2||||0px PF += 抛物线 )0(22>±=p py x 上一点),(00y x P 到焦点(,0)2p F 的距离 2||||0py PF +=(5) 焦点弦长:抛物线)0(22>=p px y 的焦点弦AB ,),(11y x A ,),(22y x B ,则p x x AB ++=21||.4.焦点弦的相关性质:焦点弦AB ,),(11y x A ,),(22y x B , 焦点(,0)2p F (1)以抛物线的焦点弦为直径的圆和抛物线的准线相切(2) 221p y y -=,4221p x x =(3)pBF AF 211=+ (4)通径:过焦点垂直于焦点所在的轴的焦点弦叫做通径.抛物线的通径长:2p . 5.弦长公式:),(11y x A ,),(22y x B 是抛物线上两点,则221212()()AB x x y y =-+-||11||1212212y y kx x k -+=-+= 分类例析: 一、 抛物线的定义、几何性质及应用 例1(1)过抛物线x y 82=的焦点F 作倾斜角是π43的直线,交抛物线于A,B 两点,则||AB = A .8B .28C .216D .16(2)(2020新课标1理4)已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =A .2B .3C .6D .9(3)经过抛物线)0(22>=p px y 的焦点作一直线l 交抛物线 于),(11y x A ,),(22y x B ,则2121x x y y 的值为__________。


教学设计板书:§8.6 抛物线的简单几何性质抛物线的几何性质 例题 练习 课时小结 教 学 过 程教学内容 教师导拨与学生活动 设计意图 一、知识回顾1、 抛物线的定义:平面内与一个点F 和一条定直线L 的距离相等的点的轨迹叫做抛物线。
点F →焦点,直线L →准线。
2、 抛物线的标准方程。
图形 标准方程焦点坐标准线方程抛物线的定义及标准方程由学生口述,老师展示结论提出这一问题的研究方法——对比、数形结合二、引入课题若大桥的桥拱为抛物线型,其水面宽度为8米,拱顶离水面4米,方形货船宽4米,高2.6米. 问:能安全通过大桥吗?提出问题由学生完成,引导学生由“数学模型”到“数学问题”通过“过桥”事件模型引发学生探究问题本质的)0(22>=p px y )0,2(p2p x -=)0(22>-=p px y )0,2(p-2p x =)0(22>=p py x )2,0(p2p y -=)0(22>-=p py x )2,0(p -2p y =的解决问题的方法。
并思考抛物线的几何性质。
热情,同时巩固抛物线方程的知识并提出本节课的标题,起着承上启下的自然过度。
三、讲授新课我们根据抛物线的标准方程)0(22 p px y =来研究它的几何性质。
1、 范围:0≥x2、 对称性:关于x 轴对称抛物线的对称轴叫做抛物线的轴3、 顶点:(0,0)抛物线和它的轴的交点叫做抛物线的的顶点。
4、 离心率:e=1抛物线上的点M 与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e 表示。
标准 方程图形范围 0≥x 0≤x0≥y0≤y对称 轴 关于x 轴对称 关于x 轴对称关于y 轴对称关于y 轴对称顶点 (0,0) 离心率e=1补充说明:1、抛物线只位于半个平面坐标内,虽然他可以无通过类比椭圆与双曲线的几何性质,从范围、对称性、顶点、离心率方面研究抛物线的几何性质,并由学生归纳总结出其他三种标准方程的几何性质。
2.3.2抛物线的简单几何性质
(一)教学目标:
1.掌握抛物线的范围、对称性、顶点、离心率等几何性质;
2.能根据抛物线的几何性质对抛物线方程进行讨论,在此基础上列表、描点、画抛
物线图形;
3.在对抛物线几何性质的讨论中,注意数与形的结合与转化 .
(二)教学重点:抛物线的几何性质及其运用
(三)教学难点:抛物线几何性质的运用
(四)教学过程:
一、复习引入:(学生回顾并填表格)
1.抛物线定义:平面内与一个定点F和一条定直线 的距离相等的点的轨迹叫做抛物
线. 定点F叫做抛物线的焦点,定直线 叫做抛物线的准线.
图形
方程
焦点
准线
2.抛物线的标准方程:
相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂直,垂足与
焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的 ,即 .
不同点:(1)图形关于x轴对称时,x为一次项,y为二次项,方程右端为 、左端为 ;
图形关于y轴对称时,x为二次项,y为一次项,方程右端为 ,左端为 . (2)开口方向在x
轴(或y轴)正向时,焦点在x轴(或y轴)的正半轴上,方程右端取正号;开口在x轴(或y轴)
负向时,焦点在x轴(或y轴)负半轴时,方程右端取负号.
二、讲解新课:
类似研究双曲线的性质的过程,我们以 为例来研究一下抛物线的简单几何性质:
1.范围
因为p0,由方程 可知,这条抛物线上的点M的坐标(x,y)满足不等式x0,所以这
条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限
延伸.
2.对称性
以-y代y,方程 不变,所以这条抛物线关于x轴对称,我们把抛物线的对称轴叫做
抛物线的轴.
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程 中,当y=0时,x=0,因此抛物线
的顶点就是坐标原点.
4.离心率
抛物线上的点M与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e
表示.由抛物线的定义可知,e=1.
对于其它几种形式的方程,列表如下:(学生通过对照完成下表)
标准方程 图形 顶点 对称轴 焦点 准线 离心率
注意强调 的几何意义:是焦点到准线的距离.
思考:抛物线有没有渐近线?(体会抛物线与双曲线的区别)
三、例题讲解:
例1 已知抛物线关于x轴为对称,它的顶点在坐标原点,并且经过点 ,求它的标
准方程,并用描点法画出图形.
分析:首先由已知点坐标代入方程,求参数p.
解:由题意,可设抛物线方程为 ,因为它过点 ,
所以 ,即
因此,所求的抛物线方程为 .
将已知方程变形为 ,根据 计算抛物线在 的范围内几个点的坐标,得
x 0 1 2 3 4
y 0 2 2.8 3.5 4
描点画出抛物线的一部分,再利用对称性,就可以画出抛物线的另一部分
点评:在本题的画图过程中,如果描出抛物线上更多的点,可以发现这条抛物线虽
然也向右上方和右下方无限延伸,但并不能像双曲线那样无限地接近于某一直线,也就是说,
抛物线没有渐近线.
例2斜率为1的直线经过抛物线y2=4x的焦点,与抛物线交于两点A、B,求线段AB
的长.
解法1:如图所示,由抛物线的标准方程可知,焦点F(1,0),准线方程x=1.
由题可知,直线AB的方程为y=x1
代入抛物线方程y2=4x,整理得:x26x+1=0
解上述方程得x1=3+2 ,x2=32
分别代入直线方程得y1=2+2 ,y2=22
即A、B的坐标分别为(3+2 ,2+2 ),(32 ,22 )
|AB|=
解法2:设A(x1,y1)、B(x2,y2),则x1+x2=6,x1x2=1
|AB|= |x1x2|
解法3:设A(x1,y1)、B(x2,y2),由抛物线定义可知,
|AF|等于点A到准线x=1的距离|AA|
即|AF|=|AA|=x1+1
同理|BF|=|BB|=x2+1
|AB|=|AF|+|BF|=x1+x2+2=8
点评:解法2是利用韦达定理根与系数的关系,设而不求,是解析几何中求弦长的
一种普遍适用的方法;解法3充分利用了抛物线的定义,解法简洁,值得引起重视。
变式训练:过抛物线 的焦点 作直线,交抛物线于 , 两点,若 ,求 。
解: , , 。
点评:由以上例2以及变式训练可总结出焦点弦弦长: 或 。
四、达标练习:
1.过抛物线 的焦点作直线交抛物线于 , 两点,如果 ,那么 =( )
(A)10 (B)8 (C)6 (D)4
2.已知 为抛物线 上一动点, 为抛物线的焦点,定点 ,则 的最小值为( )
(A)3 (B)4 (C)5 (D)6
3.过抛物线 焦点 的直线 它交于 、 两点,则弦 的中点的轨迹方程是 ______
4.定长为 的线段 的端点 、 在抛物线 上移动,求 中点 到 轴距离的最小值,并
求出此时 中点 的坐标.
参考答案:1. B 2. B 3. 4. , M到 轴距离的最小值为 .
五、小结 :抛物线的离心率、焦点、顶点、对称轴、准线、中心等.
六、课后作业:
1.根据下列条件,求抛物线的方程,并画出草图.
(1)顶点在原点,对称轴是x轴,顶点到焦点的距离等于8.
(2)顶点在原点,焦点在y轴上,且过P(4,2)点.
(3)顶点在原点,焦点在y轴上,其上点P(m,-3)到焦点距离为5.
2.过抛物线焦点F的直线与抛物线交于A、B两点,若A、B在准线上的射影是A2、
B2,则A2FB2等于 .
3.抛物线顶点在原点,以坐标轴为对称轴,过焦点且与y轴垂直的弦长为16,求抛
物线方程.
4.以椭圆 的右焦点,F为焦点,以坐标原点为顶点作抛物线,求抛物线截椭圆在准
线所得的弦长.
5.有一抛物线型拱桥,当水面距拱顶4米时,水面宽40米,当水面下降1米时,水
面宽是多少米?
习题答案:
1.(1)y2=32x (2)x2=8y (3)x2=-8y
2.90 3.x2=16 y 4. 5. 米
七、板书设计(略)