当前位置：文档之家 › 高等数学微积分 第三章 一元函数导数与微分 ppt课件

高等数学微积分 第三章 一元函数导数与微分 ppt课件

  • 格式：ppt
  • 大小：2.79 MB
  • 文档页数：92

下载文档原格式

  / 92

合集下载

高等数学 第三章 一元函数微积分学及其应用

高等数学 第三章 一元函数微积分学及其应用

x x0
x0
x
xx0
x x0
存在，则称该极限为 y f x 在点 x0 处的导数，记为
dy
df (x)
f x0 ， y xx0 ， dx xx0 或
dx xx0
10
二、导数的定义
第三章 一元函数微分学及其应用
这时也称函数 y f x 在点 x0 处可导.
如果该极限不存在，称函数 y f x 在点 x0处不可导 .
例1 求函数 y ln x 在点 x e 处的切线斜率.
解
k lim f (x) f (x0 ) = lim ln x ln e
x x0
x x0
xe x e
ln x = lim e
xe x e
lim
ln 1
xe e
xe
xe
所以
xe lim e 1
xe x e e
第三章 一元函数微分学及其应用
y
此刻切线的斜率即为 k lim y y0 lim f (x) f (x0 )
x x xx0
0
x x0
x x0
y f x
N Δy T
从上面的例子可以看出， 在求切线斜率的过
程中， 需要用到极限
lim f (x) f (x0 )
x x0
x x0
M C
α
Δx
O
x0
xx
7
二、导数的定义
故 y x2
在 x=0处导数为零，即
dy dx
x x0
0.
O
x
图 3-7
12
二、导数的定义
第三章 一元函数微分学及其应用
例3 求函数 y | x |,在点 x 0 处（见图2-8）的导数.

(优选)一元函数微分学ppt讲解

(优选)一元函数微分学ppt讲解

x0 x
1
(二)导数的运算 • 基本初等函数的导数公式
导数的四则运算法则
设u=u(x),v=v(x)都可导，则
反函数的求导法则
复合函数的求导法则
隐函数求导法则
设y=f(x)由方程F(x,y)=0确定，求y′,只需直接由方 程F(x,y)=0关于x求导，将y当做中间变量，依复 合函数链式法则求之。
★ f (x)在开区间(a,b)内的导函数为f '(x)
f '(a ) lim f '(x) xa
f '(b ) lim f '(x) xb
称为导函数的右极限 称为导函数的左极限
★ 设f (x)在闭区间[a,b]连续， 开区间(a,b)内的可导，记导函数为f '(x) 若f '(a 0)存在，则f (x)在a点右可导， 若f '(b 0)存在，则f (x)在b点左可导
记为y
，dy xx0 dx
或 df (x)
x x0
Hale Waihona Puke dxx x0关于导数的说明：
★ 导数是因变量在点x0处的变化率，它反映了 因变量随自变量的变化而变化的快慢程度. ★ 如果函数 y f (x)在开区间I内的每点
处都可导，就称函数f (x)在开区间I内可导.
★ 对于任一x I ,都对应着f (x)的一个确定的
2.右导数:
f( x0 )
lim
x x0 0
f (x) x
f (x0 ) x0
lim
x 0
f (x0
x) x
f (x0 );
★ 函数 f ( x)在点 x0处可导 左导数 f( x0 )和右导数 f( x0 )都存在且相等.

高等数学(微积分)ppt课件

高等数学(微积分)ppt课件
，且f'(x0)=0，则可通过二阶导数 f''(x0)的符号来判断f(x)在x0处取得极大值还是极小值。
曲线的凹凸性与拐点
凹凸性
若函数f(x)在区间I上二阶可导，且 f''(x)>0（或<0），则称曲线y=f(x)在 I上是凹的（或凸的）。
拐点
拐点的判定
若函数f(x)在点x0处二阶可导，且 f''(x0)=0，则可通过三阶导数f'''(x0) 的符号来判断点(x0,f(x0))是否为曲线 的拐点。
THANKS
感谢观看
非线性微分方程
通过变量替换、积分等方法求解，或 利用数值方法近似求解
级数的概念与性质
级数的定义 无穷序列的部分和序列
级数的性质 加法、减法、乘法、除法、重排等性
质
级数的收敛与发散 部分和序列有极限则级数收敛，否则 发散
常见级数及其敛散性 等差级数、等比级数、调和级数、交 错级数等，通过比较法、比值法、根 值法等方法判断其敛散性
VS
极限的性质
唯一性、局部有界性、保号性、保不等式 性、迫敛性等。
极限的运算法则
极限的四则运算法则
若两个函数的极限存在，则它们的和、差、积、商（分母不为零）的极限也存在，且等于这两 个函数极限的和、差、积、商。
复合函数的极限运算法则
设函数$y=f[g(x)]$是由函数$u=g(x)$与函数$y=f(u)$复合而成，若$lim_{x
无穷小量的定义
如果函数$f(x)$当$x to x_0$(或$x to infty$)时的极限为零，那么称函数$f(x)$为当$x to x_0$(或$x to infty$)时 的无穷小量。

微积分课件(导数与微分2)资料

微积分课件(导数与微分2)资料

设函数 f ( x)在点x0可导,即
lim y x0 x
f ( x0 )
y x

f ( x0 )
0 (x 0) y f ( x0 )x x
lim
x 0
y

lim [
x 0
f
(
x0
)x

x]
0
函数 f ( x)在点 x0连续 .

1
11
x2
2
1. 2x
( x 1 ) (1) x 11


1 x2
.
第一节 导数的概念
例3 设函数 f ( x) sin x,求(sin x)及(sin x) x . 3
解 (sin x) lim sin( x h) sin x
h0
h
h
lim cos( x h) sin 2
k y x1 2

( 1 ) x
x1 2


1 x2
x1 2
4
所求切线方程为 y 2 4( x 1), 即 4x y 4 0.
2
法线方程为
y 2 1 ( x 1), 42
即 2x 8 y 15 0.
第一节 导数的概念
四、函数可导性与连续性的关系
h0
2h
cos x
2
即 (sin x) cos x
(sin x) x cos x x
3
3
1 2
第一节 导数的概念
例4 求函数 f ( x) a x (a 0, a 1)的导数.
解 (a x ) lim a xh a x

大学微积分第三章函数的求导法则ppt课件

大学微积分第三章函数的求导法则ppt课件
x0
f( x) f(0)
x0
lim
x0
xe x 0 1 x
f ( 0 ) 1
f
(x)
e x
xex
,
x0
1,
x0
（讨论分断点的可导性用定义）
24
小结
(1) 掌握求导数的四则运算法则 (2) 熟记16个求导数公式
两条经验
(1).一般函数的求导用公式 (2).求分断点的导数用定义
25
作业 P82 1单 2单 3
h0
h
u( x h ) u( x )
v( x h ) v( x )
lim
v( x h ) lim
u( x )
h0
h
h0
h
u(x) v(x) u(x) v(x)
即 [u(x) v(x)] u(x) v(x) u(x) v(x)
7
3、商的导数
设函数 u u(x), v v(x)在点 x 处可导，(v(x) 0) 则
3x2 cos x ln x x3 sin x ln x x2 cos x
x
11
例4. y tan x 求 y
解
y
(tan
x)
sin
x
cos x
(sin
x)cos x sin cos2 x
x(cos
x)
cos2 x sin 2 cos2 x
x
1 cos2
x
sec2
x
即 (tan x) sec2 x (cot x) csc2 x
x sin y
在
Iy
2
,
2
内单调、可导，且 (sin y) cos y 0

微分ppt课件

微分ppt课件
微分PPT课件
目录
微分的定义与性质导数的概念与性质导数在研究函数中的应用微分中值定理微分的应用
01
CHAPTER
微分的定义与性质
总结词
微分是一种数学运算，表示函数在某一点的局部变化率。
详细描述
微分是微积分的基本概念之一，它表示函数在某一点的切线的斜率。具体来说，如果函数在某一点的导数存在，那么这个导数就是函数在该点的微分。微分可以看作是函数值的增量与自变量增量的比的极限。
极值点是函数的重要特征点，利用导数研究函数的极值有助于找到这些关键点。
1
2
3
4
通过求二阶导数，可以找到函数的拐点。
二阶导数为0的点可能是拐点，需要进一步判断三阶导数的符号来确定是向上凸还是向下凸。
对于函数$f(x) = x^4$，其二阶导数$f''(x) = 12x^2$，令其为0得到拐点$x=0$，进一步求三阶导数$f'''(x) = 24x$，在$x=0$处为非正值，因此$x=0$为向下凸的拐点。
举例
单调性是函数的一个重要性质，利用导数研究函数的单调性有助于理解函数的述
举例
应用
通过求导数，可以找到函数的极值点。
一阶导数为0的点可能是极值点，需要进一步判断二阶导数的符号来确定是极大值还是极小值。
对于函数$f(x) = x^3$，其一阶导数$f'(x) = 3x^2$，令其为0得到极值点$x=0$，进一步求二阶导数$f''(x) = 6x$，在$x=0$处为非负值，因此$x=0$为极小值点。
罗尔定理是数学分析中的一个基本定理，由法国数学家罗尔发现。该定理在微分学、积分学等领域有着广泛的应用。它提供了一个判断函数是否存在导数为零的点的方法，对于研究函数的极值和拐点等问题具有重要的意义。

第3章 一元函数积分学


( 9 ) csc 2 xdx cot x C
(10 )
1 dx arcsin 1 x2
xC
(11
)
1
1 x
2
dx
arctan
xC
2020/10/29
12
不定积分性质
1. (f(x)dx) f(x) 或 df(x)dx f(x)dx 2. F (x)dx F(x)C 或 dF(x) F(x)C
1 d (cc2 x o ) x o ssc d (2 o c x x ) s 1 o令 sco x u s
ud2u112lnuu 11C
1ln1cosx 2 1cosx
C
12ln(11ccoo2xssx)2
C
lncsxccoxtC
2020/10/29
29
解4 sexcd xln |ta2 xn (4)|C
1 cosx
dx
d x
2
sin x
2
lntan1x C
2 2
lntanx C
2 4
2020/10/29
30
总结如下：
f(a x b )d xa 1f(a x b )d (a x b ) x(fx2)d x1 f(x2)d(x2)
2
f(xlxn )d xf(lxn )d(lxn ) exf(ex)d xf(ex)d(ex)
f(sx)icno xs d x f(sx)id ( nsx)in f(arx c)s1d in xx 2f(arx c)ds(ianrx c)sin
fc(to 2a x xs)n d xf(tax)d n(tax)n
2020/10/29
31
二、第二类换元积分法

人大四版微积分第3章导数与微分

微积分 第三章 导数与微分

瞬时速度 切线斜率
两个问题的共性:
o
y
f (t0 )
f (t )
t0
t
s
y f ( x)
N
C
M
T
o x0
x x
所求量为函数增量与自变量增量之比的极限 . 类似问题还有: 加速度 是速度增量与时间增量之比的极限 角速度 是转角增量与时间增量之比的极限 变 化 率 问 题
即 log a
x

1 x ln a
特别地，当 a e 时，有
微积分 第三章
l n x

1 x
导数与微分
5．指数函数的导数
a
x

a x ln a
a 0, a 1,
特别地，当 a e 时，有
e
x
ex
微积分
第三章
导数与微分
(二)导数的四则运算法则
f ( x0 ) f ( x) x x0
第三章

d f ( x0 ) dx
微积分
导数与微分
导数的定义式: f (x0 x) f (x0 ) y f (x0 ) lim lim x 0 x x 0 x f (x) f (x0 ) f (x0 h) f (x0 ) f (x0 ) lim lim h0 h x x0 x x0
若上述极限不存在 , 就说函数 在点 x0不可导. y 若 lim 在 的导数为无穷大 . , 也称 x 0 x 若函数在开区间 I 内每点都可导, 就称函数在 I 内可导.
此时导数值构成的新函数称为导函数. d y d f ( x) . ; 记作: y ; f ( x ) ; dx dx 注意:

导数及其应用定积分与微积分基本定理课件理ppt

求法
求函数的导数有多种方法，例如，利用求导公式求导；利用求导法则求导；利用复合函数求导法则求复合函数 的导数；利用微分学基本定理求高阶导数等。
02
定积分
定积分的定义与性质
定积分的定义
定积分是函数在区间[a,b]上的积分，表示 为∫abf(x)dx，其中f(x)是待积函数，a和b 是积分的下限和上限。
定积分的性质
定积分具有一些基本性质，如线性性质、 可加性、可减性、可正可负性等。这些性 质在解决定积分问题时非常重要。
定积分的几何与物理应用
定积分的几何应用
定积分可以用于计算曲线下面积、旋转体体积等问题。例如，计算圆、椭圆 等图形的面积，或求圆柱、圆锥等旋转体的体积。
定积分的物理应用
定积分在物理中有广泛的应用，如计算变力沿直线所做的功、计算液体对平 面所施加的力等。
最优问题求解
导数可以用于求解最优问题，例如在投资组合理论中，通过求解收益率关于资产配置的导数，可以找到最优的资产配置比 例。
动态最优化
导数可以用于建立动态最优化模型，例如在宏观经济学中，通过求解一阶导数和二阶导数，可以研究经济的稳定性和增长 问题。
定积分在物理学中的应用案例
面积和体积计算
定积分可以用于计算曲线下包围的面积和曲线的长度，以及计算立体的体积。例如，在计 算旋转体的体积时，可以将旋转体表面展开成一系列的小圆环，然后利用定积分计算每个 小圆环的面积并求和得到总体积。
微积分基本定理可以用于求解一些方 程，例如在求解一些涉及到多个变量 的方程时，可以通过微积分基本定理 将方程转化为一个易于求解的方程并 求解。
THANKS
感谢观看
物理应用
导数可以描述物理量随时间的变化率，例如速度是位移对时间的导数。导数 在物理中有广泛的应用，例如牛顿第二定律、欧姆定律等。

一元函数微分学课件

将详细讲解一元函数微分学的内容。包括导数和微分的基本概念、计 算方法以及应用，以及如何应用高阶导数和高阶微分进行函数的近似计算。
第一部分：导数
1
基本概念
导数的定义、几何意义和物理意义。
2
导数的计算
一阶导数、高阶导数和导数的性质。
3
导数的应用
极值与最值、凹凸性和曲线的拐点。
第二部分：微分
学习资源推荐
推荐一些优质的教材和在线学习 资源，帮助学生进一步学习一元 函数微分学。
问题与讨论
留下时间回答学生的问题，进行 问题讨论，加深对一元函数微分 学的理解。
基本概念
微分的定义和几何意义。
微分的计算
一阶微分、高阶微分和微分 的性质。
微分的应用
近似计算和误差估计。
第三部分：应用
1
反函数
反函数的导数、微分和应用。
2
高阶导数与高阶微分的应用
泰勒公式、麦克劳林公式和函数的近似。
结束语
总结
一元函数微分学是数学中重要且 基础的一部分，良好的掌握将有 助于理解更高级的数学概念。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

则在 I 上定义了一个新的函数, 称这个新的函数
为 f(x)的 导函数 ,简称 导数 :
f(x)lim f(x x)f(x), xI .
x 0
x
注意: f (x0) f(x) x x0，但 f(x0) f(x0).
二. 函数不可导的情况
函数f(x)在x0 不可导，有以下况 三： 种情
1.若f(x)在x0 不连则 续f， (x)在x0 不可.导
v S S(t0t)S(t0)
t
t
v 质点在 t0 的瞬时速: 度
limS(t0t)S(t0).
t 0
t
定义 1 设函 yf(数 x )在 U (x 0)有定 ,
给自x变 在x量 0处一改 x,相变 应地量 ，有
yf(x0 x)f(x0)， （ x0xU(x0)）
若 lim y lim f(x0x)f(x0) 存在,
T
在点P( x0, f(x0)) 处的
P
切线的斜, 率 即
o
x0
x
f(x0)tan, (是切线x轴 法线方程为:
1 yy0 f(x0)(xx0).
定义 2（单侧导数，左右导数）
f(x0)
l
x
im
0
y x
lim f(x0x)f(x0)
x 0
切线 PT ktanlim f(x0x)f(x0).
的斜率为：
x 0
x
2. 瞬时速度
设一质点作变速直线运动, 其运动方程为 ：
S S(t)，若 t0 为某一确定的时,刻求质点在时
v 刻t0 的瞬时速度（距离对时间的变化率 ）.
.
.
t0
t0 t
t
质 点 在[t时 0,t0间 t]中 的 平 均 速 度 ：
x0, 在x0处不可.导
0, x0
事实上, f(0)
y
f(0x)f(0)
lim
1
x 0
x
xsin 1
lim
x
x0
x
－1/π
0
1/π
x
lim sin 1 不存在,
x0
x
f(x)在x0不可 . 导
3. limy 为无穷的情况 x0 x
定义 1 设f(x)在x0 连续，
o
x
x lim
lim x 1,
右可导
x0 x x0 x
f (0) lx i0 m f(0 x x )f(0)
lim
x 0
x x
lim x 1, 左可导
x0 x
但 f (0)f (0), f(0)不存在 . 证毕
定理 2 若f(x)在x0 不连续则 ，f(x)在x0
不可导 . 函 数 f(x ) 在 x 0 点 :
可导
连续
不连续
左右可导 左右导数不一定相等
不可导 连续
定义 3 若f(x)在(a,b)内每一 x处 点 都可
即x(a,b), f(x)都存则 在称 f， (x)在
(a,b) 内可导； 若 f(x)在 (a,b)内 可 f (导 a),
f(b)都存,在则称 f(x)在[a,b]上可 . 导
若f(x)在区I间 可导 则， xI, f(x)都存在 即xI,都对应唯一确值 定f的 (x)导 ，数
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
2. 由定理 1，知
( 定理 2 )
( i ) 若f(x0)与f(x0)都存在但值不相
则f(x)在x0 不可.导 例如f： (x)x，
f (0 ) 1 1f (0 )， f(0)不存在 .
( ii ) 若f(x0)与f(x0)中至少有一个不存
则f(x)在x0 不可.导
例:
f
(x) xsi
n1 , x
证 lxi m 0 xyf(x0), xyf(x0),
0( x 0), yf(x 0) x x,
limy x0
lx i0 [m f(x0) x x]
0
,
即f(x)在点 x0连续 .
但反之不然， 例如： f(x) x 在x0处连续，
但f(0)不 存.在 事 实 上 ,
y y x
f (0 ) lx i0 m f(0 x x )f(0 )
1.切线问题 割线的极限位置——切线位置
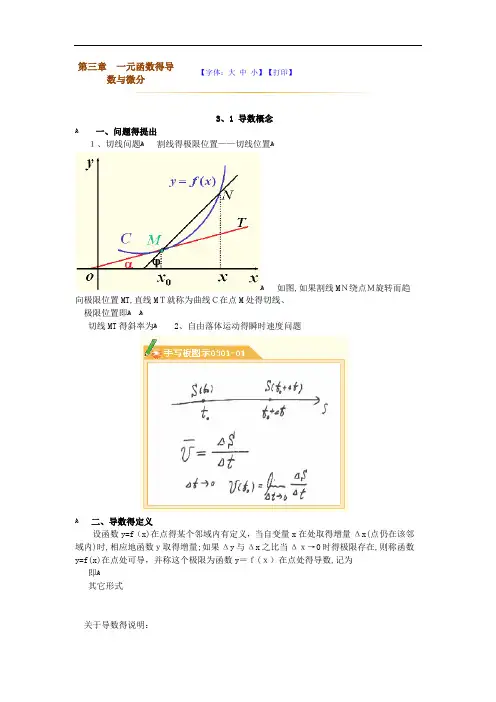
如,图 在曲 C:线 yf(x) y 上 取 一P(定 x0,y0点 ),
yf(x)
Q
Q(x, y)是 曲线 上 P附 点
T
近 的一 点 当， 动点 Q沿
CP
曲线趋于 P 时, 割线PQ o
x
x0
xx
的极限位置 PT, 称为曲线P在处点的切线.
的割 当 斜Q 线率 P为Q沿 :曲 C ta 线 nP时 ,f(xxx)xfx0(0x,0)xf (x00, xx)f(x0),
x x0
x 0
x
则y称 f(x)在x 点 0处 可 , 并称导 这个极
限y为 f(x)在点 x0处的, 导 记作 数 :
f (x0) 或 y xx0
或 dy dx xx0
或 df dx
, x x0
即
f(x0)lxi m0xy
lim f(x0x)f(x0).
x 0
x
导数的几何意义
y
yf(x)
f(x0)表示曲线 y f(x)
x
(令 xx0x)xl ixm 0 f(xx)xf0(x0) 存在,
则f称 (x)在 x0处 右 左 可,导 并称此极限
为 f(x)在x 点 0处右左的 导.数
定理 1（双侧导数与单侧导数的关系）
f(x0)存在 f(x0)与f(x0)都存在且 . 相
定理 2（可导与连续的关系）若f(x)在 x0
可导 ， 则f(x)在x0必 连, 但续 反之不然！
导数的概念起源于几何学中的切线问题 及 力学中 速度的 问题 ， 这是由莱布尼兹Le（ibniz,
16 4167,德 16国）N 和 ew 牛 ,1t6o 顿 41 n27（ ,27 英国）分别在研学 究和 几力 何学过程中建 来的.
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
第二章 一元函数导数与微分
2.1 导数的概念 2.2 导数的计算 2.3 2.4 几种类型函数的求导方法 2.5 函数的微分与线性逼近
2.1 导 数 的 概 念
一. 导数的定义 问题的提出
导数的思想最初 尔是 马F由 （ er费 m,1a6t 01 166,法 5 国为 ）研究极值问题 的.而引入