CHAPTER
03
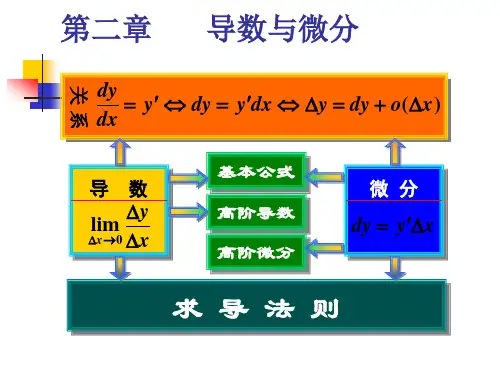
第3章 导数与 微分
PART
03
3.1
导数
导数是数学中的一个分支——微积分的两个基本概念之一,它
表示一个函数的因变量相对于自变量的变化的快慢程度,即因变 量关于自变量的变化率.事物总是在不断地运动和变化的,而描述 这种运动和变化离不开变化率,导数就是对现实生活中各种各样 的变化率的一种统一的数学抽象.导数是微积分以及实际生活中 应用极其广泛的概念,其应用范围包括函数性态的描述、曲线的 描绘、最优化问题的讨论以及变化率的分析等.
,
即函数在点x=0处的右导数不存在,所以函数f(x)在点x=0处的导
数不存在.
3. 1. 5
高阶导数
在本小节中,我们将讨论一个量的变化率的变化率.这样的变化率 有很多种,例如,汽车的加速度是它的速度关于时间的变化率,而 速度本身又是路程关于时间的变化率.如果路程的单位是千米,时 间的单位是小时,那么速度(路程关于时间的变化率)的单位是千 米/小时,而加速度(速度的变化率)的单位则是千米/小时2.
上述有关变化率的变化率的问题,在经济上是常用的.例如,在通 货膨胀时期,你可以听到经济部门的报告指出,“尽管通货膨胀率 在增长,但其增长速度在减缓”,就是指物价在上涨,但已经不比 以前那样增长得快了.
3. 1. 5
高阶导数
1) 高阶导数的概念 ➢ 设函数y=f(x)关于x的变化率由其导函数f '(x)给出.类似地,函数f
3.2 1 微分的定义
关于微分定义的几点说明: ➢ (1)函数的微分dy是Δx的一次函数,它不仅与Δx有关,而且与x也
有关.函数的微分dy与Δy只差一个比Δx高阶的无穷小,它是Δy的 主要部分,所以也称微分dy是函数改变量Δy的线性主部. ➢ (2)若函数y=f(x)在x处的改变量Δy可以表示成Δx的线性函数 k(x)Δx与一个比Δx高阶的无穷小之和Δy=k(x)Δx+o(Δx),则称 函数y=f(x)在点x处可微. ➢ (3)由于自变量x的微分dx=(x)'Δx=Δx,故dx可理解为自变量x的 改变量Δx.于是dy=f '(x)Δx=f '(x)dx,即函数的微分等于函数的 导数乘上自变量的微分.