四川师范大学附属中学数学平面图形的认识(一)专题练习(解析版)

一、选择题1．如图，点C 是线段AB 的中点，点D 是线段CB 上任意一点，则下列表示线段关系的式子不正确的是（ ）A ．AB=2ACB ．AC+CD+DB=ABC ．CD=AD-12ABD ．AD=12（CD+AB ） 2．已知点P 是CD 的中点，则下列等式中正确的个数是（ ）①PC CD =；②12PC CD =；③2PC PD =；④PC PD CD += A ．1个 B ．2个C ．3个D ．4个 3．如图，O 是直线AC 上一点，OB 是一条射线，OD 平分∠AOB ，OE 在∠BOC 内，且∠DOE ＝60°，∠BOE ＝13∠EOC ，则下列四个结论正确的个数有（ ） ①∠BOD ＝30°；②射线OE 平分∠AOC ；③图中与∠BOE 互余的角有2个；④图中互补的角有6对．A ．1个B ．2个C ．3个D ．4个4．已知∠α与∠β互补，且∠α＞∠β，则∠β的余角可以表示为（ ）A ．12α∠B ．12β∠C ．()12αβ∠-∠ D ．()1+2αβ∠∠ 5．“枪挑一条线，棍扫一大片”，从数学的角度解释为（ ）． A ．点动成线，线动成面B ．线动成面，面动成体C ．点动成线，面动成体D ．点动成面，面动成线 6．如图，CD 是直角三角形ABC 的高，将直角三角形ABC 按以下方式旋转一周可以得到右侧几何体的是（ ）．A ．绕着AC 旋转B ．绕着AB 旋转C ．绕着CD 旋转 D ．绕着BC 旋转 7．如图．已知//AB CD ．直线EF 分别交,AB CD 于点,,EF EG 平分BEF ∠．若1 50∠=︒．则2∠的度数为（ ）A ．50︒B ．65︒C ．60︒D ．70︒8．某正方体的平面展开图如下图所示，这个正方体可能是下面四个选项中的（ ）．A ．B ．C ．D ． 9．已知α∠和β∠互补，且αβ∠>∠，则有下列式子：①90β︒-∠；②90α∠-︒；③()12αβ∠+∠；④()12αβ∠-∠；⑤()1902α∠-︒；其中，表示β∠的余角的式子有( ) A ．4个 B ．3个 C ．2个 D ．1个10．下列说法正确的是（ ）A ．射线PA 和射线AP 是同一条射线B ．射线OA 的长度是3cmC ．直线,AB CD 相交于点 P D ．两点确定一条直线11．如图，点A 、B 、C 是直线l 上的三个定点，点B 是线段AC 的三等分点，AB ＝BC +4m ，其中m 为大于0的常数，若点D 是直线l 上的一动点，M 、N 分别是AD 、CD 的中点，则MN 与BC 的数量关系是（ ）A．MN＝2BC B．MN＝BC C．2MN＝3BC D．不确定12．一个小立方块的六个面分别标有字母A，B，C，D，E，F，从三个不同的方向看形如图所示，则字母D的对面是( )A．字母A B．字母F C．字母E D．字母B13．若射线OA与射线OB是同一条射线，下列画图正确的是（）A．B．C．D．14．用一个平面去截正方体，所得截面是三角形，留下较大的几何体一定有（）A．7个面B．15条棱C．7个顶点D．10个顶点15．下列说法不正确的是（）A．两条直线相交，只有一个交点B．两点之间，线段最短C．两点确定一条直线D．过平面上的任意三点，一定能作三条直线二、填空题16．如图，能用O，A，B，C中的两个字母表示的不同射线有____条．17．如图所示，填空：∠=∠+_________；（1）AOB AOC∠=∠-_________=_________-_________；（2）COB COD∠+∠-∠=_________.（3）AOB COD AOD18．用一个平面截三棱柱，最多可以截得________边形；用一个平面截四棱柱，最多可以截得________边形；用一个平面截五棱柱，最多可以截得________边形.试根据以上结论，猜测用一个平面去截n棱柱，最多可以截得________边形.19．把棱长为1cm的四个正方体拼接成一个长方体，则在所得长方体中，表面积最大等于________2cm.20．把一条长为20厘米的线段分成三段，如果中间一段长为8厘米，那么第一段中点到第三段中点间的距离等于________厘米．21．8点15分，时针与分针的夹角是______________。

一、选择题1．已知圆224x y +=与圆22260x y y +--=，则两圆的公共弦长为（ ）A ．3B ．23C ．2D ．12．P 为⊙C ：22220x y x y +--=上一点，Q 为直线l ：40x y --=上一点，则线段PQ 长度的最小值（ ） A ．2B ．23C ．26 D ．223．已知圆C 与直线30x y ++=相切，直线10mx y ++=始终平分圆C 的面积，则圆C 方程为（ ） A ．2222x y y +-= B ．2222x y y ++= C ．2221x y y +-=D ．2221x y y ++=4．已知圆221:2410C x y x y ++-+=，圆222:(3)(1)1C x y -++=，则这两个圆的公切线条数为（ ） A ．1条B ．2条C ．3条D ．4条5．已知两个不相等的实数a ，b 满足以下关系式：2sin cos 02a a πθθ+-=，2sin cos 02b b πθθ+-=，则连接()2,A a a ，()2,B b b 两点的直线与圆心在原点的单位圆的位置关系为（） A ．相交B ．相切C ．相离D ．相切或相交6．已知动直线:20(0,0)l ax by c a c ++-=>>恒过点(1,)P m 且(4,0)Q 到动直线l 的最大距离为3，则122a c+的最小值为( ) A ．92 B ．94C ．1D ．97．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为正方形，PA AB =，E 为AP 的中点，则异面直线PC 与DE 所成的角的正弦值为（ ）．A 2B 5C 15D 108．正方体1111ABCD A BC D -的棱长为2，E 是1CC 的中点，则点1C 到平面EBD 的距离为（ ） A ．34B ．63C ．52D ．2239．已知正三棱柱111ABC A B C -，的体积为163，底面积为43，则三棱柱111ABC A B C -的外接球表面积为（ ）A ．1123π B ．563π C ．2243π D ．28π10．某几何体的三视图如图所示，其中网格纸的小正方形的边长是1，则该几何体外接球的体积为（ ）A ．323πB ．48πC ．323π D ．643π 11．一个底面为正三角形的棱柱的三视图如图所示，若在该棱柱内部放置一个球，则该球的最大体积为（ ）A ．6πB ．12πC ．43πD ．83π12．已知四面体ABCD 中，二面角A BC D --的大小为60，且2AB =，4CD =，120CBD ∠=，则四面体ABCD 体积的最大值是（ ）A ．43B ．23C ．83D ．43二、填空题13．在空间直角坐标系O xyz -中，若点(1,2,3)A ，(1,1,4)B -，点C 是点A 关于平面yOz 的对称点，则点B 与C 的距离为_________.14．已知点()2,2A --，()4,2，点P 在圆224x y +=上运动，则22PA PB +的最小值是______.15．在平面直角坐标系xOy 中，过点(0,3)M -的直线l 与圆223x y +=交于A ，B 两点，且2MB MA =，则直线l 的方程为________.16．已知直线0x y a -+=与圆心为C 的圆222440x y x y ++--=相交于,A B 两点，且AC BC ⊥，则实数a 的值为_________．17．在平面直角坐标系xOy 中,A 的坐标为(2,0),B 是第一象限内的一点,以C 为圆心的圆经过O ､A ､B 三点,且圆C 在点A ,B 处的切线相交于P ,若P 的坐标为(4,2),则直线PB 的方程为_____. 18．已知圆22(1)16x y ++=，点(1,0),(1,0)E F -，过(1,0)E -的直线1l 与过(1,0)F 的直线2l 垂直且圆相交于,A C 和,B D ，则四边形ABCD 的面积的取值范围是_________.19．如图所示，Rt A B C '''∆为水平放置的ABC ∆的直观图，其中AC B C ''''⊥，2B O O C ''''==，则ABC ∆的面积是________________.20．四棱锥V ABCD -中，底面ABCD 是正方形，各条棱长均为2.则异面直线VC 与AB 所成角的大小为______.21．如图，平面四边形ABCD 中，1AB AD ==，2,3,BD CD BD CD ==⊥将其沿对角线BD 折成四面体A BCD '-，使平面A BD '⊥平面BCD ，则四面体A BCD '-的外接球的球心到平面ACD '的距离等于__________．22．已知正四棱锥的体积为18，侧棱与底面所成的角为45，则该正四棱锥外接球的表面积为___________.23．如图，正二十面体是由20个等边三角形组成的正多面体，共有12个顶点，30条棱，20个面，是五个柏拉图多面体之一.如果把sin 36按35计算，则棱长为6的正二十面体的外接球半径等于___________.24．如图在菱形ABCD 中，2AB =，60A ∠=，E 为AB 中点，将AED 沿DE 折起使二面角A ED C '--的大小为90，则空间A '、C 两点的距离为________；三、解答题25．如图，四边形ABCD 为正方形，QA ⊥平面ABCD ，PD//QA ，112QA AB PD ===.（1）证明：直线PQ ⊥平面DCQ ； （2）求二面角D QB A --的余弦值.26．如图，在四棱锥P ABCD -中，底面ABCD 为菱形，M 是棱PD 的中点.（1）求证：//PB 平面AMC ；（2）若PD ⊥平面ABCD ，2AD PD ==，3BAD π∠=，求点B 到平面AMC 的距离．27．如图，在五面体ABCDEF 中，四边形ABCD 是平行四边形.（1）求证：//AB EF ；（2）若CF AE ⊥，AB AE ⊥，求证：平面ABFE ⊥平面CDEF .28．如图，四边形ABCD 为矩形，且4=AD ，22AB =PA ⊥平面ABCD ，2PA =，E 为BC 的中点.（1）求证：PC DE ⊥；（2）若M 为PC 的中点，求三棱锥M PAB -的体积.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】把两个圆的方程相减可得相交弦所在直线方程，通过半弦长，半径，弦心距的直角三角形，求出半弦长，即可得到公共弦长. 【详解】圆224x y +=与圆22260x y y +--=的方程相减可得公共弦所在的直线方程为1y =-，由于圆224x y +=的圆心到直线1y =-的距离为1，且圆224x y +=的半径为2， 故公共弦的长为224123-= 故选：B . 【点睛】本题考查两圆的位置关系，相交弦所在的直线方程，弦长，重点考查计算能力，属于基础题型.2．A解析：A 【分析】将圆的一般方程化为标准方程，求解出圆心和半径，然后根据圆上一点到圆外直线的距离最小值等于圆心到直线的距离减去半径求解出结果.【详解】因为圆22:220C x y x y +--=，即()()22:112C x y -+-=，所以圆心()1,1C ，半径r =又因为PQ 长度的最小值为圆心到直线的距离减去半径，且圆心到直线距离d ==所以min PQ d r =-== 故选：A. 【点睛】结论点睛：圆上点到一条与圆相离直线的距离最值（圆心到直线的距离为d ，圆的半径为r ）：（1）最大值：圆心到直线的距离加上半径，即d r +； （2）最小值：圆心到直线的距离减去半径，即d r -.3．D解析：D 【分析】计算出直线10mx y ++=所过定点的坐标，由题意得出定点是圆C 的圆心，然后利用点到直线的距离公式计算出圆C 的半径长，即可得出圆C 的方程. 【详解】在直线10mx y ++=的方程中，令0x =，则1y =-，则直线10mx y ++=过定点()0,1-.由于直线10mx y ++=始终平分圆C 的面积，则点()0,1-是圆C 的圆心，又圆C 与直线30x y ++=相切，则圆C 的半径r ==.因此，圆C 的方程为()2212x y ++=，即2221x y y ++=.故选D. 【点睛】本题考查圆的方程的求解，同时也考查了直线过定点问题，求出圆的圆心坐标为解题的关键，考查运算求解能力，属于中等题.4．D解析：D 【分析】根据题意，分析两圆的圆心与半径，进而分析两圆的位置关系，据此分析可得答案． 【详解】根据题意，圆221:2410C x y x y ++-+=，即22+1+24x y -=（）（）其圆心为12-（，），半径12r =， 圆222:(3)(1)1C x y -++=，其圆心为31-（，），半径21r =，则有12125C C r r ==>+，两圆外离，有4条公切线；故选D ． 【点睛】本题考查圆与圆的位置关系以及两圆的公切线，关键是分析两圆的位置关系，属于基础题．5．C解析：C 【分析】由题意可得直线AB 的方程为sin cos 02x y πθθ⋅+⋅-=，由点到直线的距离公式可得圆心()0,0到直线AB 的距离，即可得解. 【详解】因为实数a 满足关系式2sin cos 02a a πθθ+-=，实数b 满足关系式2sin cos 02b b πθθ+-=，且实数a ，b 不相等，所以点()2,A a a ，()2,B b b 为直线sin cos 02x y πθθ⋅+⋅-=上的两点，所以直线AB 的方程为sin cos 02x y πθθ⋅+⋅-=，因为圆心()0,0到直线AB的距离12d π==>，所以直线AB 与圆心在原点的单位圆的位置关系为相离. 故选：C. 【点睛】本题考查了直线方程的应用及直线与圆位置关系的应用，考查了运算求解能力与转化化归思想，属于中档题.6．B解析：B 【分析】由题意可得：可得20a bm c ++-=．又(4,0)Q 到动直线l 的最大距离为3，可得3=，解得0m =，从而得到2a c +=．再利用“乘1法”与基本不等式的性质即可得出． 【详解】动直线:20(0,0)l ax by c a c ++-=>>恒过点(1,)P m ，20a bm c ∴++-=． 又(4,0)Q 到动直线l 的最大距离为3，∴22(41)3m -+=，解得0m =．2a c ∴+=．则121121521529()()()(2)2222222224c a c a a c a c a c a c a c +=++=+++=，当且仅当423c a ==时取等号． 故选：B ． 【点睛】本题考查直线方程、点到直线的距离公式、两点之间的距离公式、基本不等式的性质，考查推理能力与计算能力，属于中档题．7．D解析：D 【分析】先取正方形的中心O ，连接OE ，由PC //OE 知OED ∠为异面直线PC 与DE 所成的角，再在OED 中求OED ∠的正弦即可. 【详解】连AC ，BD 相交于点O ，连OE 、BE ，因为E 为AP 的中点，O 为AC 的中点，有PC //OE ，可得OED ∠为异面直线PC 与DE 所成的角，不妨设正方形中，2AB =，则2PA =，由PA ⊥平面ABCD ，可得,PA AB PA AD ⊥⊥， 则145BE DE ==+=1122222OD BD ==⨯= 因为BE DE =，O 为BD 的中点，所以90EOD ∠=︒，210sin 5OD OED DE ∠===故选：D. 【点睛】 方法点睛：求空间角的常用方法：（1）定义法，由异面直线所成角、线面角、二面角的定义，结合图形，作出所求空间角，再结合题中条件，解对应三角形，即可求出结果；（2）向量法：建立适当的空间直角坐标系，通过计算向量夹角（直线方向向量与直线方向向量、直线方向向量与平面法向量，平面法向量与平面法向量）余弦值，即可求出结果.8．B解析：B 【分析】利用等体积法11C EBD D C EB V V --=，设点1C 到平面EBD 的距离为d ，利用三棱锥的体积公式代入面积即求得d . 【详解】如图，利用等体积法，11C EBD D C EB V V --=，设点1C 到平面EBD 的距离为d ，正方体1111ABCD A BC D -的棱长为2，故22,5BD BE ED ===，如图，2215232h ED BD ⎛⎫=-=- ⎪⎝⎭11223622EBDSBD h =⨯⨯=⨯= 又点D 到平面1C EB 的距离，即D 到平面11C CBB 的距离，为CD =2，111212EBC S=⨯⨯=， 由11C EBD D C EB V V --=得，1161233d =⨯⨯，故636d ==. 故选：B. 【点睛】 方法点睛：空间中求点到平面的距离的常见方法：（1）定义法：直接作垂线，求垂线段长；（2）等体积法：利用三棱锥换底求体积，结合两个面积和另一个高求未知高，即得距离；（3）向量法：过点的一个斜线段对应的向量a，平面法向量n，则a n dn⋅=.9．A解析：A【分析】由面积和体积可得三棱柱的底面边长和高，根据特征可知外接球的球心为上下底面中心连线的中点，再由勾股定理可得半径及球的表面积.【详解】依题意，1163443AA==，而213sin432ABCS AB AC A AB=⨯⨯==，解得4AB=，记ABC的中心为О，111A B C△的中心为О1，则114OA OA==，取1OO的中点D，因为AO CO=，90AOD COD∠=∠=，由勾股定理得AD CD=，同理可得111AD BD A D B D C D====，所以正三棱柱的外接球的球心为即D，AD为外接球的半径，由正弦定理得432sin60ABAO==，故2221628433A ODD O A=+=+=，故三棱柱111ABC A B C-的外接球表面积2281124433S Rπππ==⨯=，故选：A．【点睛】本题考查了正三棱柱外接球的表面积的求法，关键点是确定球心的位置和球的半径的长度，考查了学生的空间想象力和计算能力.10．A解析：A 【分析】由三视图可知，该几何体是四棱锥，其中四棱锥底面是边长为4的正方形，将四棱锥补成棱长为4的正方体，则该几何体的外接球就是正方体的外接球，进而可得答案. 【详解】由三视图可知，该几何体是如图所示的四棱锥P ABCD -， 其中四棱锥底面是边长为4的正方形，四棱锥的一条侧棱与底面垂直，四棱锥的高为4， 将四棱锥补成棱长为4的正方体， 则该几何体的外接球就是正方体的外接球， 外接球的直径2R 等于正方体的对角线长， 即24323R R =⇒=，所以该几何体外接球的体积为()34233π⨯=323π，故选：A.【点睛】方法点睛：三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响，对简单组合体三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状.11．C解析：C 【分析】先由三视图计算底面正三角形内切圆的半径，内切圆的直径和三棱柱的高比较大小，确定球的半径的最大值，计算球的最大体积. 【详解】由三视图知该直三棱柱的高为4，底面正三角形的高为33半径为高的三分之一，即3r =234，所以该棱柱内部可放置球的半径的最大343V π==.故选：C 【点睛】关键点点睛：本题的第一个关键是由三视图确定底面三角形的高是定球的最大半径.12．D解析：D 【分析】在BCD △中，利用余弦定理和基本不等式可得163BC BD ⋅≤，由三角形的面积公式可得BCDS≤，由二面角A BC D --的大小为60，可得A 到平面BCD 的最大距离为2sin 603h ==ABCD 体积的最大值.【详解】在BCD △中，由余弦定理可得2222cos120CD BC BD BC BD =+-⋅22BC BD BC BD =++⋅因为222BC BD BC BD +≥，所以23CD BC BD ≥⋅， 所以163BC BD ⋅≤，当且仅当BC BD =时等号成立，1116sin120223BCDSBC BD =⋅≤⨯= 因为二面角A BC D --的大小为60，所以点A 到平面BCD 的最大距离为2sin 603h ==所以114333A BCD BCDV S h -=⋅≤=， 所以四面体ABCD 体积的最大值是43， 故选：D 【点睛】关键点点睛：本题解题的关键点是利用余弦定理和基本不等式、三角形面积公式求出BCD S △最大值，再由二面角求出高的最大值. 二、填空题13．【分析】求出的坐标由空间中两点间的距离公式即可计算与的距离【详解】由题意知则故答案为：【点睛】关键点点睛：该题考查了空间中两点间的距离计算解题的关键点是正确求出的坐标【分析】求出C 的坐标，由空间中两点间的距离公式即可计算B 与C 的距离. 【详解】由题意知，()1,2,3C -，则BC ==【点睛】关键点点睛：该题考查了空间中两点间的距离计算，解题的关键点是正确求出C 的坐标.14．28【分析】设则由表示圆上的点与点间的距离的平方可得答案【详解】设则表示圆上的点与点间的距离的平方所以所以所以故的最小值是28故答案为：28【点睛】关键点睛：本题考查圆中的相关距离的最值问题解答本题解析：28 【分析】设(),P x y ,则22PA PB +()222113x y ⎡⎤=-++⎣⎦，由()221x y -+表示圆224x y +=上的点(),P x y 与点()10B ,间的距离的平方，可得答案. 【详解】设(),P x y ，则()()()()2222222242x y x y PA PB =++++--++2222428x y x =+-+()222214x y x =+-+()222113x y ⎡⎤=-++⎣⎦()221x y -+表示圆224x y +=上的点(),P x y 与点()10B ,间的距离的平方. 所以211PB R OB ≥-=-=，所以()2211x y -+≥所以()()22211321+1328x y ⎡⎤-++≥⨯=⎣⎦故22PA PB +的最小值是28 故答案为：28 【点睛】关键点睛：本题考查圆中的相关距离的最值问题，解答本题的关键是22PA PB +()222113x y ⎡⎤=-++⎣⎦，又()221x y -+表示圆224x y +=上的点(),P x y 与点()10B ,间的距离的平方，根据211PB R OB ≥-=-=，可求解，属于中档题. 15．【分析】根据题意知点为的中点设再由得利用韦达定理建立方程解得即可【详解】由题知点为的中点设直线设将直线带入圆的方程得则由得即所以解得故直线方程为：故答案为：【点睛】本题考查直线和圆的位置关系属于基础题解析：3y =-【分析】根据题意知，点A 为MB 的中点，设()11,A x y ，()22,B x y ，再由2MB MA =得122x x =，利用韦达定理建立方程，解得即可.【详解】由题知，点A 为MB 的中点，设直线:3l y kx =-，设()11,A x y ，()22,B x y ，将直线带入圆的方程得()221660k x kx +-+=，则12261k x x k +=+，12261x x k ⋅=+， 由2MB MA =，得122x x =，即2221k x k =+，1241kx k =+， 所以，21222246111k k x x k k k ⋅=⨯=+++，解得k =3y =-.故答案为：3y =-. 【点睛】本题考查直线和圆的位置关系，属于基础题.16．0或6【分析】计算得到圆心半径根据得到利用圆心到直线的距离公式解得答案【详解】即圆心半径故圆心到直线的距离为即故或故答案为：或【点睛】本题考查了根据直线和圆的位置关系求参数意在考查学生的计算能力和转解析：0或6 【分析】计算得到圆心()1,2C -，半径3r =，根据AC BC ⊥得到2d =，利用圆心到直线的距离公式解得答案. 【详解】222440x y x y ++--=，即()()22129x y ++-=，圆心()1,2C -，半径3r =.AC BC ⊥，故圆心到直线的距离为2d =2d ==，故6a =或0a =. 故答案为：0或6. 【点睛】本题考查了根据直线和圆的位置关系求参数，意在考查学生的计算能力和转化能力。

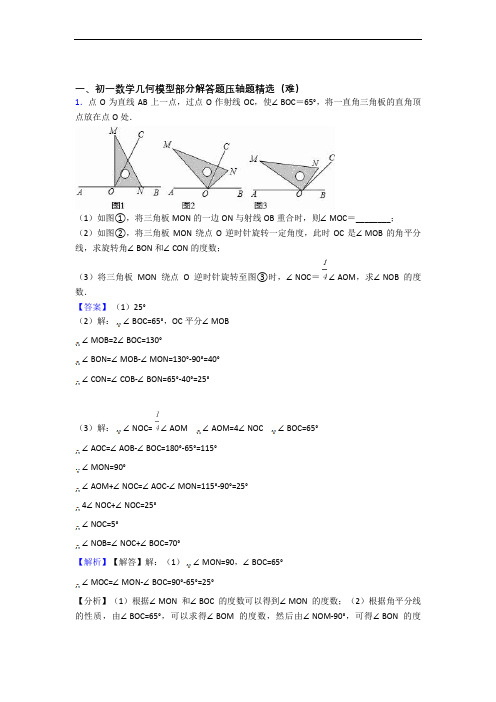
一、初一数学几何模型部分解答题压轴题精选（难）1．点O为直线AB上一点，过点O作射线OC，使∠BOC＝65°，将一直角三角板的直角顶点放在点O处．（1）如图①，将三角板MON的一边ON与射线OB重合时，则∠MOC＝________；（2）如图②，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数；（3）将三角板MON绕点O逆时针旋转至图③时，∠NOC＝∠AOM，求∠NOB的度数．【答案】（1）25°（2）解：∠BOC=65°，OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°（3）解：∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解：（1）∠MON=90，∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】（1）根据∠MON和∠BOC的度数可以得到∠MON的度数；（2）根据角平分线的性质，由∠BOC=65°，可以求得∠BOM的度数，然后由∠NOM-90°，可得∠BON的度数，从而得解；（3）由∠BOC=65°，∠NOM=90°，∠NOC= ∠AOM，从而可求得∠NOC的度数，然后由∠BOC=65°，从而得解.2．如图1，点A、B分别在数轴原点O的左右两侧，且 OA+50=OB，点B对应数是90．（1）求A点对应的数；（2）如图2，动点M、N、P分别从原点O、A、B同时出发，其中M、N均向右运动，速度分别为2个单位长度/秒，7个单位长度/秒，点P向左运动，速度为8个单位长度/秒，设它们运动时间为t秒，问当t为何值时，点M、N之间的距离等于P、M之间的距离；（3）如图3，将（2）中的三动点M、N、P的运动方向改为与原来相反的方向，其余条件不变，设Q为线段MN的中点，R为线段OP的中点，求22RQ﹣28RO﹣5PN的值．【答案】（1）解：如图1，∵点B对应数是90，∴OB=90．又∵ OA+50=OB，即 OA+50=90，∴OA=120．∴点A所对应的数是﹣120（2）解：依题意得，MN=|（﹣120+7t）﹣2t|=|﹣120+5t|，PM=|2t﹣（90﹣8t）|=|10t﹣90|，又∵MN=PM，∴|﹣120+5t|=|10t﹣90|，∴﹣120+5t=10t﹣90或﹣120+5t=﹣（10t﹣90）解得t=﹣6或t=14，∵t≥0，∴t=14，点M、N之间的距离等于点P、M之间的距离（3）解：依题意得RQ=（ 45+4t）﹣（﹣60﹣4.5t）=105+8.5t，RO=45+4t，PN=（90+8t）﹣（﹣120﹣7t）=210+15t，则22RQ﹣28RO﹣5PN=22（105+8.5t）﹣28（45+4t）﹣5（210+15t）=0【解析】【分析】（1）根据点B对应的数求得OB的长度，结合已知条件和图形来求点A 所对应的数；（2）由M、N之间的距离等于P、M之间的距离列式为，列方程求出t；（3）由M、N之间的距离等于P、M之间的距离列式为，列方程求出t，并求出RQ，RO 及PN，再求出22RQ﹣28RO﹣5PN的值．3．将一副直角三角板如图1摆放在直线AD上（直角三角板OBC和直角三角板MON，∠OBC=90°，∠BOC=45°，∠MON=90°，∠MNO=30°），保持三角板OBC不动，将三角板MON绕点O以每秒10°的速度顺时针旋转，旋转时间为t秒（1）当t=________秒时，OM平分∠AOC？如图2，此时∠NOC﹣∠AOM=________°；（2）继续旋转三角板MON，如图3，使得OM、ON同时在直线OC的右侧，猜想∠NOC 与∠AOM有怎样的数量关系？并说明理由；（3）若在三角板MON开始旋转的同时，另一个三角板OBC也绕点O以每秒5°的速度顺时针旋转，当OM旋转至射线OD上时同时停止，（自行画图分析）①当t=________秒时，OM平分∠AOC？（4）②请直接写出在旋转过程中，∠NOC与∠AOM的数量关系．【答案】（1）2.25；45（2）解：∠NOC﹣∠AOM=45°，∵∠AON=90°+10t，∴∠NOC=90°+10t﹣45°=45°+10t，∵∠AOM=10t，∴∠NOC﹣∠AOM=45°（3）3（4）解：②∠NOC﹣∠AOM=45°．∵∠AOB=5t，∠AOM=10t，∠MON=90°，∠BOC=45°，∵∠AON=90°+∠AOM=90°+10t，∠AOC=∠AOB+∠BOC=45°+5t，∴∠NOC=∠AON﹣∠AOC=90°+10t﹣45°﹣5t=45°+5t，∴∠NOC﹣∠AOM=45°．【解析】【解答】解：（1）∵∠AOC=45°，OM平分∠AOC，∴∠AOM= =22.5°，∴t=2.25秒，∵∠MON=90°，∠MOC=22.5°，∴∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°；故答案为：2.25，45；·（3）①∵∠AOB=5t，∠AOM=10t，∴∠AOC=45°+5t，∵OM平分∠AOC，∴∠AOM= AOC，∴10t= （45°+5t），∴t=3秒，故答案为：3．【分析】（1）根据角平分线的定义得到∠AOM= =22.5°，于是得到t=2.25秒，由于∠MON=90°，∠MOC=22.5°，即可得到∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°；（2）根据题意得∠AON=90°+10t，求得∠NOC=90°+10t﹣45°=45°+10t，即可得到结论；（3）①根据题意得∠AOB=5t，∠AOM=10t，求得∠AOC=45°+5t，根据角平分线的定义得到∠AOM= AOC，列方程即可得到结论；（4）②根据角的和差即可得到结论．4．如图1，已知，点A、B在直线a上，点C、B在直线b上，且于E.（1）求证：；（2）如图2，平分交于点F，平分交于点G，求的度数；（3）如图3，P为线段上一点，I为线段上一点，连接，N为的角平分线上一点，且，则、、之间的数量关系是________. 【答案】（1）证明：过作 ,∴∴∴∴∴（2）解：作，，设，，由（1）知：，，，∴，∴，同理：，∴（3）【解析】【解答】解：（3）结论：或，I.∠NCD在∠BCD内部时，过I点作，过N点作，设∠IPN=∠BPN=x， =y，∴∠BCD=3y.∵a∥b，∴∴，，，∴，，∴，∴∴II. 在外部时,如图3（2）：过I点作，过N点作，设∠IPN=∠BPN=x， =y，∴∠BCD=y.∵a∥b，∴IG∥a∥∴，，，∴，，∴，∴∴.故答案为：.【分析】(1) 过作EF∥a,由BC⊥AD可知,由平行可知，,从而可得 = + = ；(2)作，，设，，由平行线性质和邻补角定义可得，，进而计算出即可解答;（3）分两种情况解答：I.∠NCD在∠BCD内部，II 外部，仿照（2）解答即可.5．如图，已知DC∥FP，∠1=∠2，∠FED=28°，∠AGF=80°，FH平分∠EFG.（1）说明：DC∥AB；（2）求∠PFH的度数.【答案】（1）证明:∵DC∥FP，∴∠3=∠2，又∵∠1=∠2，∴∠3=∠1，∴DC∥AB（2）解:∵DC∥FP，DC∥AB，∠DEF=30°，∴∠DEF=∠EFP=30°，AB∥FP，又∵∠AGF=80°，∴∠AGF=∠GFP=80°，∴∠GFE=∠GFP+∠EFP=80°+30°=110°，又∵FH平分∠EFG，∴∠GFH= ∠GFE=55°，∴∠PFH=∠GFP﹣∠GFH=80°﹣55°=25°【解析】【分析】（1）根据二直线平行，同位角相等得出，又∠1=∠2，故∠1=∠3，根据同位角相等，两直线平行得出DC∥AB；（2）根据平行于同一直线的两条直线互相平行得出AB∥FP，根据二直线平行，内错角相等得出，，根据角的和差，由算出∠GFE的度数，根据角平分线的定义得出∠GFH的度数，最后根据即可算出答案。

一、初一数学几何模型部分解答题压轴题精选（难）1．如图 1，CE 平分∠ACD，AE 平分∠BAC，且∠EAC＋∠ACE=90°．（1）请判断 AB 与 CD 的位置关系，并说明理由；（2）如图2，若∠E=90°且AB 与CD 的位置关系保持不变，当直角顶点E 移动时，写出∠BAE 与∠ECD 的数量关系，并说明理由；（3）如图 3，P 为线段 AC 上一定点，点 Q 为直线 CD 上一动点，且 AB 与 CD 的位置关系保持不变，当点 Q 在射线 CD 上运动时(不与点 C 重合)，∠PQD，∠APQ 与∠ BAC 有何数量关系？写出结论，并说明理由．【答案】（1），理由如下：CE 平分，AE 平分，；（2），理由如下：如图，延长AE交CD于点F，则由三角形的外角性质得：；（3），理由如下：，即由三角形的外角性质得：又，即即．【解析】【分析】（1）根据角平分线的定义、平行线的判定即可得；（2）根据平行线的性质（两直线平行，内错角相等）、三角形的外角性质即可得；（3）根据平行线的性质（两直线平行，同旁内角互补）、三角形的外角性质、邻补角的定义即可得．2．（1）问题发现：如图 1，已知点 F，G 分别在直线 AB，CD 上，且 AB∥CD，若∠BFE=40°，∠CGE=130°，则∠GEF 的度数为________；（2）拓展探究：∠GEF，∠BFE，∠CGE 之间有怎样的数量关系？写出结论并给出证明；答：∠GEF=▲ .证明：过点 E 作 EH∥AB，∴∠FEH=∠BFE（▲），∵AB∥CD，EH∥AB，（辅助线的作法）∴EH∥CD（▲），∴∠HEG=180°-∠CGE（▲），∴∠FEG=∠HFG+∠FEH=▲ .（3）深入探究：如图 2，∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P，试探究∠GPQ 与∠GEF 之间的数量关系，请直接写出你的结论.【答案】（1）90°（2）解：∠GEF＝∠BFE＋180°−∠CGE，证明：过点 E 作 EH∥AB，∴∠FEH=∠BFE（两直线平行，内错角相等），∵AB∥CD，EH∥AB，（辅助线的作法）∴EH∥CD（平行线的迁移性），∴∠HEG=180°-∠CGE（两直线平行，同旁内角互补），∴∠FEG=∠HFG+∠FEH=∠BFE＋180°−∠CGE ，故答案为：∠BFE＋180°−∠CGE；两直线平行，内错角相等；平行线的迁移性；两直线平行，同旁内角互补；∠BFE＋180°−∠CGE；（3）解：∠GPQ＋∠GEF＝90°，理由是：如图2，∵FQ平分∠BFE，GP平分∠CGE，∴∠BFQ＝∠BFE，∠CGP＝∠CGE，在△PMF中，∠GPQ＝∠GMF−∠PFM＝∠CGP−∠BFQ，∴∠GPQ＋∠GEF＝∠CGE− ∠BFE＋∠GEF＝ ×180°＝90°.即∠GPQ＋∠GEF＝90°.【解析】【解答】（1）解：如图1，过E作EH∥AB，∵AB∥CD，∴AB∥CD∥EH，∴∠HEF＝∠BFE＝40°，∠HEG＋∠CGE＝180°，∵∠CGE＝130°，∴∠HEG＝50°，∴∠GEF＝∠HEF＋∠HEG＝40°＋50°＝90°；故答案为：90°；【分析】（1）如图1，过E作EH∥AB，根据平行线的性质可得∠HEF＝∠BFE＝40 ，∠HEG＝50 ，相加可得结论；（2）由①知：∠HEF＝∠BFE，∠HEG＋∠CGE＝180°，则∠HEG＝180°−∠CGE，两式相加可得∠GEF＝∠BFE＋180°−∠CGE；（3）如图2，根据角平分线的定义得：∠BFQ＝∠BFE，∠CGP＝∠CGE，由三角形的外角的性质得：∠GPQ＝∠GMF−∠PFM＝∠CGP−∠BFQ，计算∠GPQ＋∠GEF并结合②的结论可得结果.3．将一副三角板放在同一平面内，使直角顶点重合于点O（1）如图①，若∠AOB=155°，求∠AOD、∠BOC、∠DOC的度数.（2）如图①，你发现∠AOD与∠BOC的大小有何关系？∠AOB与∠DOC有何关系？直接写出你发现的结论.（3）如图②，当△AOC与△BOD没有重合部分时，（2）中你发现的结论是否还仍然成立，请说明理由.【答案】（1）解：∵而同理：∴∴（2）解：∠AOD与∠BOC的大小关系为：∠AOB与∠DOC存在的数量关系为：（3）解：仍然成立.理由如下：∵又∵∴【解析】【分析】（1）先计算出再根据（2）根据(1)中得出的度数直接写出结论即可.（3）根据即可得到利用周角定义得∠AOB+∠COD+∠AOC+∠BOD=360°，而∠AOC=∠BOD=90°，即可得到∠AOB+∠DOC=180°．4．在数轴上、两点分别表示有理数和，我们用表示到之间的距离；例如表示7到3之间的距离.（1）当时，的值为________.（2）如何理解表示的含义？（3）若点、在0到3（含0和3）之间运动，求的最小值和最大值.【答案】（1）5或-3（2）解：∵ = ，∴表示到-2的距离（3）解：∵点、在0到3（含0和3）之间运动，∴0≤a≤3, 0≤b≤3,当时， =0+2=2，此时值最小，故最小值为2；当时， =2+5=7，此时值最大，故最大值为7【解析】【解答】（1）∵，∴a=5或-3；故答案为：5或-3；【分析】（1）此题就是求表示数a的点与表示数1的点之间的距离是4，根据表示数a的点在表示数1的点的右边与左边两种情况考虑即可得出答案；（2）此题就是求表示数b的点与表示数-2的点之间的距离;（3）此题就是求表示数a的点与表示数2的点之间的距离及表示数b的点与表示数-2的点之间的距离和，而0≤a≤3, 0≤b≤3, 借助数轴当时，的值最小；当时，的值最大.5．如图1，点为直线上一点，过点作射线，使，将一直角三角板的直角顶点放在点处，一边在射线上，另一边在直线的下方.（1）将图1中的三角板绕点逆时针旋转至图，使一边在的内部，且恰好平分，问：此时直线是否平分？请直接写出结论：直线 ________（平分或不平分） .（2）将图1中的三角板绕点以每秒的速度沿逆时针方向旋转一周，在旋转的过程中，第秒时，直线恰好平分锐角，则的值为________.（直接写出结果）（3）将图1中的三角板绕点顺时针旋转，请探究：当始终在的内部时（如图3），与的差是否发生变化？若不变，请求出这个差值；若变化，请举例说明.【答案】（1）平分（2）或49（3）解：不变，设，，，【解析】【解答】（1）直线平分；（2）或【分析】（1）根据图形得到直线ON平分∠AOC ；（2）由三角板绕点 O 以每秒 5 °的速度沿逆时针方向旋转一周，在旋转的过程中，第t 秒时，直线ON恰好平分锐角∠AOC，求出t的值；（3）根据题意得到∠AON=50°−y，∠AOM−∠NOC=x−y=40°.6．如图（1），将两块直角三角尺的直角顶点C叠放在一起，（1）若∠DCE=25°，∠ACB=？；若∠ACB=150°，则∠DCE=？；（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；（3）如图（2），若是两个同样的直角三角尺60°锐角的顶点A重合在一起，则∠DAB与∠CAE的大小又有何关系，请说明理由．【答案】（1）【解答】∵∠ECB=90°，∠DCE=25°∴∠DCB=90°﹣25°=65°∵∠ACD=90°∴∠ACB=∠ACD+∠DCB=155°．∵∠ACB=150°，∠ACD=90°∴∠DCB=150°﹣90°=60°∵∠ECB=90°∴∠DCE=90°﹣60°=30°．故答案为：155°，30°（2）【解答】猜想得：∠ACB+∠DCE=180°（或∠ACB与∠DCE互补）理由：∵∠ECB=90°，∠ACD=90°∴∠ACB=∠ACD+∠DCB=90°+∠DCB∠DCE=∠ECB﹣∠DCB=90°﹣∠DCB∴∠ACB+∠DCE=180°（3）【解答】∠DAB+∠CAE=120°理由如下：∵∠DAB=∠DAE+∠CAE+∠CAB故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°．【解析】【分析】（1）本题已知两块直角三角尺实际就是已知三角板的各个角的度数，根据角的和差就可以求出∠ACB，∠DCE的度数；（2）根据前个小问题的结论猜想∠ACB与∠DCE的大小关系，结合前问的解决思路得出证明．（3）根据（1）（2）解决思路确定∠DAB与∠CAE的大小并证明．7．如图，已知点，且，满足 .过点分别作轴、轴，垂足分别是点A、C.（1）求出点B的坐标；（2）点M是边上的一个动点（不与点A重合），的角平分线交射线于点N，在点M运动过程中，的值是否变化？若不变，求出其值；若变化，说明理由. （3）在四边形的边上是否存在点，使得将四边形分成面积比为1：4的两部分？若存在，请直接写出点的坐标；若不存在，说明理由.【答案】（1）解：由得：,解得：∴点的坐标为（2）解：不变化∵轴∴BC∥x轴∴∵平分∴∴∴（3）解：点P可能在OC,OA边上，如下图所示，由（1）可知，BC=5，AB=3，故矩形的面积为15若点P在OC边上，可设P点坐标为，则三角形BCP的面积为，剩余部分面积为，所以，解得，P点坐标为；若点P在OA边上，可设P点坐标为，则三角形BAP的面积为，剩余部分面积为，所以，解得，P点坐标为 .综上,点的坐标为， .【解析】【分析】（1）由绝对值和算术平方根的非负性可知由两个非负数的和为0，则这两个数都为0，由此可列出关于，的二元一次方程组，解之即可得出B点坐标；（2）根据平行线和角平分线的性质可证明，所以比值不变化；（3）点P只能在OC,OA边上，表示出两部分的面积，依比值求解即可.8．在△ABC中，∠A=60°，BD，CE是△ABC的两条角平分线，且BD，CE交于点F，如图所示，用等式表示BE，BC，CD这三条线段之间的数量关系，并证明你的结论；晓东通过观察，实验，提出猜想：BE+CD=BC，他发现先在BC上截取BM，使BM=BE，连接FM，再利用三角形全等的判定和性质证明CM=CD即可．（1）下面是小东证明该猜想的部分思路，请补充完整；①在BC上截取BM，使BM=BE，连接FM，则可以证明△BEF与________全等，判定它们全等的依据是________；②由∠A=60°，BD，CE是△ABC的两条角平分线，可以得出∠EFB=________°；（2）请直接利用①，②已得到的结论，完成证明猜想BE+CD=BC的过程．【答案】（1）△BMF；SAS；60（2）证明：由①知，∠BFE=60°，∴∠CFD=∠BFE=60°∵△BEF≌△BMF，∴∠BFE=∠BFM=60°，∴∠CFM=∠BFC-∠BFM=120°-60°=60°，∴∠CFM=∠CFD=60°，∵CE是∠ACB的平分线，∴∠FCM=∠FCD，在△FCM和△FCD中，，∴△FCM≌△FCD（ASA），∴CM=CD，∴BC=CM+BM=CD+BE，∴BE+CD=BC．【解析】【解答】解：（1）解：①在BC上取一点M，使BM=BE，连接FM，如图所示：∵BD、CE是△ABC的两条角平分线，∴∠FBE=∠FBM= ∠ABC，在△BEF和△BMF中，，∴△BEF≌△BMF（SAS），故答案为：△BMF，SAS；②∵BD、CE是△ABC的两条角平分线，∴∠FBC+FCB= （∠ABC+∠ACB），在△ABC中，∠A+∠ABC+∠ACB=180°，∵∠A=60°，∴∠ABC+∠ACB=180°-∠A=180°-60°=120°，∴∠BFC=180°-（∠FBC+∠FCB）=180°- （∠ABC+∠ACB）=180°- ×120°=120°，∴∠EFB=60°，故答案为：60；【分析】（1）①由BD，CE是△ABC的两条角平分线知∠FBE=∠FBC= ∠ABC，结合BE=BM，BF=BF，依据“SAS”即可证得△BEF≌△BMF；②利用三角形内角和求出∠ABC+∠ACB=120°，进而得出∠FBC+∠FCB=60°，得出∠BFC=120°，即可得出结论；（2）利用角平分线得出∠EBF=∠MBF，进而得出△BEF≌△BMF，求出∠BFM，即可判断出∠CFM=∠CFD，即可判断出△FCM≌△FCD，即可得出结论．9．己知AB∥CD，点E在直线AB，CD之间。

一、初一数学几何模型部分解答题压轴题精选（难）1．已知：如图1，点M是线段AB上一定点，AB=12cm，C、D两点分别从M、B出发以1cm/s、2cm/s的速度沿直线BA向左运动，运动方向如箭头所示（C在线段AM上，D在线段BM上）（1）若AM=4cm，当点C、D运动了2s，此时AC=________，DM=________；（直接填空）（2）当点C、D运动了2s，求AC+MD的值．（3）若点C、D运动时，总有MD=2AC，则AM=________（填空）（4）在（3）的条件下，N是直线AB上一点，且AN﹣BN=MN，求的值．【答案】（1）2；4（2）解：当点C、D运动了2 s时，CM=2 cm，BD=4 cm∵AB=12 cm，CM=2 cm，BD=4 cm∴AC+MD=AM﹣CM+BM﹣BD=AB﹣CM﹣BD=12﹣2﹣4=6 cm（3）4（4）解：①当点N在线段AB上时，如图1，∵AN﹣BN=MN，又∵AN﹣AM=MN∴BN=AM=4∴MN=AB﹣AM﹣BN=12﹣4﹣4=4∴ = = ；②当点N在线段AB的延长线上时，如图2，∵AN﹣BN=MN，又∵AN﹣BN=AB∴MN=AB=12∴ = =1；综上所述 = 或1【解析】【解答】解：（1.）根据题意知，CM=2cm，BD=4cm，∵AB=12cm，AM=4cm，∴BM=8cm，∴AC=AM﹣CM=2cm，DM=BM﹣BD=4cm，故答案为：2，4；（3.）根据C、D的运动速度知：BD=2MC，∵MD=2AC，∴BD+MD=2（MC+AC），即MB=2AM，∵AM+BM=AB，∴AM+2AM=AB，∴AM= AB=4，故答案为：4；【分析】（1）根据运动速度和时间分别求得CM、BD的长，根据线段的和差计算可得；（2）由题意得CM=2 cm、BD=4 cm，根据AC+MD=AM﹣CM+BM﹣BD=AB﹣CM﹣BD可得答案；（3）根据C、D的运动速度知BD=2MC，再由已知条件MD=2AC求得MB=2AM，所以AM= AB；（4）分点N在线段AB上时和点N在线段AB的延长线上时分别求解可得．2．如图1，点O为直线AB上一点，过O点作射线OC，使∠AOC：∠BOC=1：2，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图1中的三角板绕点O按逆时针方向旋转至图2的位置，使得ON落在射线OB 上，此时三角板旋转的角度为________度；（2）继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置，使得ON在∠AOC的内部．试探究∠AOM与∠NOC之间满足什么等量关系，并说明理由；（3）在上述直角三角板从图1逆时针旋转到图3的位置的过程中，若三角板绕点O按15°每秒的速度旋转，当直角三角板的直角边ON所在直线恰好平分∠AOC时，求此时三角板绕点O的运动时间t的值．【答案】（1）90（2）解：如图3，∠AOM﹣∠NOC=30°．设∠AOC=α，由∠AOC：∠BOC=1：2可得∠BOC=2α．∵∠AOC+∠BOC=180°，∴α+2α=180°．解得α=60°．即∠AOC=60°．∴∠AON+∠NOC=60°．①∵∠MON=90°，∴∠AOM+∠AON=90°．②由②﹣①，得∠AOM﹣∠NOC=30°；（3）（ⅰ）如图4，当直角边ON在∠AOC外部时，由OD平分∠AOC，可得∠BON=30°．因此三角板绕点O逆时针旋转60°．此时三角板的运动时间为：t=60°÷15°=4（秒）．（ⅱ）如图5，当直角边ON在∠AOC内部时，由ON平分∠AOC，可得∠CON=30°．因此三角板绕点O逆时针旋转240°．此时三角板的运动时间为：t=240°÷15°=16（秒）．【解析】【解答】解：（1）由旋转的性质知，旋转角∠MON=90°．故答案是：90；【分析】（1）根据旋转的性质知，旋转角是∠MON；（2）如图3，利用平角的定义，结合已知条件“∠AOC：∠BOC=1：2”求得∠AOC=60°；然后由直角的性质、图中角与角间的数量关系推知∠AOM﹣∠NOC=30°；（3）需要分类讨论：（ⅰ）当直角边ON在∠AOC外部时，旋转角是60°；（ⅱ）当直角边ON在∠AOC内部时，旋转角是240°．3．如图，已知，在的右侧，平分，平分，，所在直线交于点.（1）求的度数.（2）若，求的度数(用含的代数式表示).（3）将线段沿方向平移，使得点在点的右侧，其他条件不变，在图中画出平移后的图形，并判断的度数是否发生改变?若改变，求出它的度数(用含的式子表示)；若不改变，请说明理由.【答案】（1）解：∵平分，，.（2）解：如图，过点作∵，，， .∵平分，平分，，，，，..（3）解：如图2为平移后的图形.的度数发生了改变.过点作，平分，平分，，，， .∵，，，，.【解析】【分析】（1）根据角平分线的定义即可求∠EDC的度数；（2）过点E作EF∥AB，根据平行于同一直线的两条直线互相平行得出AB∥CD∥EF，然后根据两直线平行内错角相等，即可求∠BED的度数；（3）∠BED的度数改变.过点E作EF∥AB，先由角平分线的定义可得：∠ABE=∠ABC，∠CDE=∠ADC，然后根据两直线平行内错角相等及同旁内角互补可得：，进而可由求得答案.4．已知：如图1，在平面直角坐标系中，点A，B，E分别是x轴和y轴上的任意点．BD是∠ABE的平分线，BD的反向延长线与∠OAB的平分线交于点C．（1）探究：求∠C的度数．（2）发现：当点A，点B分别在x轴和y轴的正半轴上移动时，∠C的大小是否发生变化？若不变，请直接写出结论；若发生变化，请求出∠C的变化范围．（3）应用：如图2在五边形ABCDE中，∠A+∠B+∠E＝310°，CF平分∠DCB，CF的反向延长线与∠EDC外角的平分线相交于点P，求∠P的度数．【答案】（1）解：∵∠ABE＝∠OAB+∠AOB，∠AOB＝90°，∴∠ABE＝∠OAB+90°，∵BD是∠ABE的平分线，AC平分∠OAB，∴∠ABE＝2∠ABD，∠OAB＝2∠BAC，∴2∠ABD＝2∠BAC+90°，∴∠ABD＝∠BAC+45°，又∵∠ABD＝∠BAC+∠C，∴∠C＝45°（2）解：不变．理由如下：∵∠ABE＝∠OAB+∠AOB，∠AOB＝90°，∴∠ABE＝∠OAB+90°，∵BD是∠ABE的平分线，AC平分∠OAB，∴∠ABE＝2∠ABD，∠OAB＝2∠BAC，∴2∠ABD＝2∠BAC+∠AOB，∴∠ABD＝∠BAC+ ∠AOB，又∵∠ABD＝∠BAC+∠C，∴∠C＝∠AOB＝45°（3）解：延长ED，BC相交于点G．在四边形ABGE中，∵∠G＝360°﹣（∠A+∠B+∠E）＝50°，∴∠P＝∠FCD﹣∠CDP＝（∠DCB﹣∠CDG）＝∠G＝ ×50°＝25°【解析】【分析】（1）（2）根据三角形外角的性质和角平分线的性质进行解答；（3）延长ED，BC相交于点G，根据四边形形内角和为360°求得∠G的度数，再根据三角形外角的性质和角平分线的性质求∠P的度数.5．如图四边形ABCD中，AD∥BC，∠BCD=90°，∠BAD的平分线AG交BC于点G．（1）求证：∠BAG=∠BGA；（2）如图2，∠BCD的平分线CE交AD于点E，与射线GA相交于点F，∠B=50°．①若点E在线段AD上，求∠AFC的度数；②若点E在DA的延长线上，直接写出∠AFC的度数；（3）如图3，点P在线段AG上，∠ABP=2∠PBG，CH∥AG，在直线AG上取一点M，使∠PBM=∠DCH，请直接写出∠ABM：∠PBM的值．【答案】（1）证明：∵AD∥BC，∴∠GAD=∠BGA，∵AG平分∠BAD，∴∠BAG=∠GAD，∴∠BAG=∠BGA；（2）解：①∵CF平分∠BCD，∠BCD=90°，∴∠GCF=45°，∵AD∥BC，∠ABC=50°，∴∠AEF=∠GCF=45°；∠DAB=180°﹣50°=130°，∵AG平分∠BAD，∴∠BAG=∠GAD=65°，∴∠AFC=65°﹣45°=20°；②如图：∵∠AGB=65°，∠BCF=45°，∴∠AFC=∠CGF+∠BCF=115°+45°=160°；（3）解：有两种情况：①当M在BC的下方时，如图：∵∠ABC=50°，∠ABP=2∠PBG，∴∠ABP=（）°，∠PBG=（）°，∵AG∥CH，∴∠BCH=∠AGB=65°，∵∠BCD=90°，∴∠DCH=∠PBM=90°﹣65°=25°，∴∠ABM=∠ABP+∠PBM=（ +25）°=（）°，∴∠ABM：∠PBM=（）°：25°= ；②当M在BC的上方时，如图：同理得：∠ABM=∠ABP﹣∠PBM=（﹣25）°=（）°，∴∠ABM：∠PBM=（）°：25°= ；综上，∠ABM：∠PBM的值是或．【解析】【分析】（1）根据AD//BC可知∠GAD=∠BGA，由AG平分∠BAD可知∠BAG=∠GAD，即可得答案.（2）①根据CF平分∠BCD，∠BCD=90°，可求出∠GCF的度数，由AD//BC可求出∠AEF和∠DAB的度数，根据三角形外角的性质求出∠AFC的度数即可；②根据三角形外角性质求出即可；（3）根据M点在BP的上面和下面两种情况讨论，分别求出∠PBM和∠ABM的值即可.6．如图，P是定长线段AB上一点，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上）（1）若C、D运动到任一时刻时，总有PD＝2AC，请说明P点在线段AB上的位置：（2）在（1）的条件下，Q是直线AB上一点，且AQ﹣BQ＝PQ，求的值.（3）在（1）的条件下，若C、D运动5秒后，恰好有，此时C点停止运动，D 点继续运动（D点在线段PB上），M、N分别是CD、PD的中点，下列结论：①PM﹣PN的值不变；② 的值不变，可以说明，只有一个结论是正确的，请你找出正确的结论并求值.【答案】（1）解：由题意：BD=2PC∵PD=2AC，∴BD+PD=2（PC+AC），即PB=2AP.∴点P在线段AB上的处（2）解：如图：∵AQ-BQ=PQ，∴AQ=PQ+BQ，∵AQ=AP+PQ，∴AP=BQ，∴PQ= AB，∴（3）解：② 的值不变.理由：如图，当点C停止运动时，有CD= AB，∴CM= AB，∴PM=CM-CP= AB-5，∵PD= AB-10，∴PN= AB-10）= AB-5，∴MN=PN-PM= AB，当点C停止运动，D点继续运动时，MN的值不变，所以【解析】【分析】（1）根据C、D的运动速度知BD=2PC，再由已知条件PD=2AC求得PB=2AP，所以点P在线段AB上的处；（2）由题设画出图示，根据AQ-BQ=PQ求得AQ=PQ+BQ；然后求得AP=BQ，从而求得PQ与AB的关系；（3）当点C停止运动时，有CD＝ AB，从而求得CM与AB的数量关系；然后求得以AB表示的PM与PN的值，所以MN＝PN−PM＝ AB.7．如图，三角形ABC，直线，CD、BD分别平分和．（1）图中，，，求的度数，说明理由．（2）图中，，直接写出 ________．（3）图中，， ________．【答案】（1）解：，，如图1过D点作，，，，，即又、BD分别平分和．，同理（2）（3）【解析】【解答】如图2过D点作，，，，，即又、BD分别平分和．，同理，，，即，，，，，故答案为．如图3过D点作，，，，，即又、BD分别平分和．，同理，，，即，，，，，故答案为．【分析】（1）过点作，根据平行线的性质，得出，，则，再根据、分别平分和，得出，同理，即可解答；（2）根据（1）的思路即可解答；（3）根据（2）的思路即可解答.8．直线MN与直线PQ相交于O，∠POM＝60°，点A在射线OP上运动，点B在射线OM 上运动.（1）如图1，∠BAO=70°,已知AE、BE分别是∠BAO和∠ABO角的平分线，试求出∠AEB 的度数.（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE 分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值.（3）在（2）的条件下，在△CDE中，如果有一个角是另一个角的2倍，请直接写出∠DCE的度数.【答案】（1）解：∵∠POM＝60°，∠BAO=70°，∴∠ABO=50°.∵AE、BE分别是∠BAO和∠ABO的角平分线，∴∠EAB= ∠OAB=35°，∠EBA= ∠OBA=25°，∴∠AEB=180°-35°-25°=120°（2）解：不发生变化，理由如下：如图，延长BC、AD交于点F，∵点D、C分别是∠PAB和∠ABM的角平分线上的两点，∴∠FAB= ∠PAB= （180°-∠OAB），∠FBA= ∠MBA= （180°-∠OBA），∴∠FAB+∠FBA= （180°-∠OAB）+ （180°-∠OBA）= （180°+∠AOB）=90°+ ∠AOB，∵∠AOB=60°，∴∠F=180°-（∠FAB+∠FBA）=90°- ∠AOB=60°，同理可求∠CED =90°- ∠F=60°；（3）∠DCE的度数40°或80°【解析】【解答】解：（3）①当∠DCE=2∠E时，显然不符合题意；②当∠DCE=2∠CDE时，∠DCE= =80°；③当∠DCE= ∠CDE时，∠DCE= =40°，综上可知，∠DCE的度数40°或80°.【分析】（1）由∠POM＝60°，∠BAO=70°，可求出∠ABO的值，根据AE、BE分别是∠BAO和∠ABO的角平分线，可得∠EAB和∠EBA的值，在△EAB中，根据三角形内角和即可得出∠AEB的大小；（2）不发生变化，延长BC、AD交于点F，根据角平分线的定义以及三角形内角和可得∠F =90°- ∠AOB，∠CED =90°- ∠F，即可得出∠CED的度数；（3）分三种情况求解即可.9．如（图1），在平面直角坐标系中，，，，且满足，线段交轴于点.（1）填空： ________， ________；（2）点为轴正半轴上一点，若，，且分别平分，如（图2），求的度数；（3）求点的坐标；（4）如（图3），在轴上是否存在一点，使三角形的面积和三角形的面积相等？若存在，求出点坐标，若不存在，说明理由.【答案】（1）-3；3（2）解：∵AB∥DE，∴∠ODE＋∠DFB＝180°，∵，∴∠DFB＝∠AFO＝180°-140°=40°，∴∠FAO＝50°，∵分别平分，∴∠OAN＝∠FAO=25°，∠NDM＝∠ODE=70°，∴∠DNM=∠ANO=90°-25°=65°，∴∠AMD=180°−∠DNM-∠NDM＝45°（3）解：连结OB，如图，设F（0，t），∵△AOF的面积＋△BOF的面积＝△AOB的面积，∴ ×3×t＋ ×t×3＝ ×3×3，解得t＝，∴F点坐标为（0，）；（4）解：存在，∵，∴△的面积= ，设Q（0，y），∵△ABQ的三角形＝△AQF的面积＋△BQF的面积，∴•|y− |•3＋•|y− |•3＝，解得y＝5或y＝−2，∴此时Q点坐标为（0，5）或（0，−2）；【解析】【解答】解：（1）∵（a＋b）2＋|b-a-6|＝0，∴a＋b＝0，b-a-6＝0，∴a＝−3，b＝3，故答案为：-3，3；【分析】（1）根据非负数的性质得a＋b＝0，b-a-6＝0，然后解方程组求出a和b即可得到点A和B的坐标；（2）由AB∥DE可知∠ODE＋∠DFB＝180°，得到∠DFB＝∠AFO＝180°-140°=40°，所以∠FAO＝50°，再根据角平分线定义得∠OAN＝∠FAO=25°，∠NDM＝∠ODE=70°，得到∠DNM=∠ANO=90°-25°=65°，然后根据三角形内角和定理得∠AMD=180°−∠DNM-∠NDM＝45°；（3）①连结OB，如图3，设F（0，t），根据△AOF的面积＋△BOF的面积＝△AOB的面积得到 ×3×t＋ ×t×3＝ ×3×3，解得t＝，则可得到F点坐标为（0，）；（4）先计算△ABC的面积＝，利用△ABQ的三角形＝△AQF的面积＋△BQF的面积得到•|y− |•3＋•|y− |•3＝，解出y即可.10．（1）①如图1，已知，，可得 ________.②如图2，在①的条件下，如果平分，则 ________.③如图3，在①、②的条件下，如果，则 ________.（2）尝试解决下面问题：已知如图4，，，是的平分线，，求的度数.【答案】（1）60°；30°；60°（2）解：∵，∴，∵，∴ .∵是的平分线，∴∵，∴ .【解析】【解答】解：(1)①由两直线平行，内错角相等得到∠BCD=60°；②如果平分，则 =30°；③如果，则 90°－ 60°.【分析】(1) ①根据两直线平行,内错角相等即可求解;②根据角平分线的定义求解即可;③根据互余的两个角的和等于90°,计算即可;(2)先根据两直线平行,同旁内角互补和角平分线的定义求出∠BCN的度数,再利用互余的两个角的和等于90°即可求出.11．如图所示，O为一个模拟钟面圆心，M、O、N 在一条直线上，指针OA、OB 分别从OM、ON 出发绕点 O 转动，OA 运动速度为每秒 30 ，OB 运动速度为每秒10 ，当一根指针与起始位置重合时，运动停止，设转动的时间为 t 秒，试解决下列问题：（1）如图①，若OA顺时针转动，OB逆时针转动， =________秒时，OA与OB第一次重合；（2）如图②，若OA、OB同时顺时针转动，①当 =3秒时，∠AOB=________ ；②当为何值时，三条射线OA、OB、ON其中一条射线是另两条射线夹角的角平分线？________【答案】（1）4.5（2）；解：由题意知，∴∠BON＝10t ，∠AON＝180－30t (0≤t≤6)，∠AON＝30t－180(6<t≤12).当ON为∠AOB的角平分线时，有180－30t ＝10t ，解得：t ＝4.5；当OA为∠BON的角平分线时，10t ＝2(30t －180)，解得：t ＝7.2；当OB为∠AON的角平分线时，30t －180＝2×10t ，解得：t ＝18（舍去）；∴经过4.5，7.2秒时，射线OA、OB、ON其中一条射线是另外两条射线夹角的平分线【解析】【解答】（1）解：若OA顺时针转动，OB逆时针转动，∴∠AOM+∠BON=180 ,∴，解得：；∴秒，OA与OB第一次重合；故答案为：4.52）解：①若OA、OB同时顺时针转动，∴，，∴；故答案为：120；【分析】（1）设t秒后第一次重合．根据题意，列出方程，解方程即可；（2）①利用180 减去OA转动的角度，加上OB转动的角度，即可得到答案；②先用t的代数式表示∠BON和∠AON，然后分为三种情况进行讨论：当ON、OA、OB为角平分线时，分别求出t的值，即可得到答案.12．我们知道，|a|表示数a在数轴上的对应点与原点的距离．如：|5|表示5在数轴上的对应点到原点的距离。

2022-2023学年四川师大附中八年级（上）入学数学试卷学校:___________姓名：___________班级：___________考号：___________一、选择题（本大题共10小题，共30.0分。

在每小题列出的选项中，选出符合题目的一项）1.下列计算正确的是( )A. a2+a2=a4B. 2x⋅3x2=6x3C. (−a2b)2=a4bD. (−6x6)÷2x=5x52.如果一个角的余角是60°，那么这个角的补角的度数是( )A. 150°B. 140°C. 120°D. 30°3.下面4个图案，其中不是轴对称图形的是( )A. B. C. D.4.生物学家发现了一种病毒，其长度约为0.00000032mm，数据0.00000032用科学记数法表示正确的是( )A. 3.2×107B. 3.2×108C. 3.2×10−7D. 3.2×10−85.已知(x+3)(x−2)=x2+bx+c，那么b、c的值分别是( )A. b=1，c=−6B. b=1，c=6C. b=5，c=−6D. b=5，c=66.如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为( )A. 15°B. 17.5°C. 20°D. 22.5°7.如图，AB//CD，∠BED=110°，BF平分∠ABE，DF平分∠CDE，则∠BFD=( )A. 110°B. 115°C. 125°D. 130°8.一列火车由甲市驶往相距600km的乙市，火车的速度是200km/时，火车离乙市的距离s(单位：km)随行驶时间t(单位：小时)变化的关系用图表示正确的是( )A. B. C. D.9.已知：如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1=∠2.图中全等的三角形共有( )A. 4对B. 3对C. 2对D. 1对10.如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB.若BE=2，则AE的长为( )A.√3B. 1C. √2D. 2二、填空题（本大题共10小题，共30.0分）11.81的平方根是______，27的立方根是______．12.(−2m+3)(______)=4m2−9，(−2ab+3)2=______．13.若a+b=8，ab=5，则a2+b2=______．14.如图，∠BAC=30°，AM是∠BAC的平分线，过M作ME//BA交AC于E，作MD⊥BA，垂足为D，ME=10cm，则MD=______ ．15.(2x+3y+5)(2x+3y−5)=______．16.若(a−2)a+1=1，则a=______．17.若x m=4，x n=8，则x3m−n=______ ．18.若a2+2ka+9是一个完全平方式，则k等于______．19.拖拉机工作时，油箱中的余油量Q(升)与工作时间t(时)的关系式为Q=40−6t.当t=4时，Q=______，从关系式可知道这台拖拉机最多可工作______小时．20.在Rt△ABC中，BC=2，AC=5，作AB边上的垂线交AC于F点，交BC的延长线于E点，连接AE，若刚好EF=AB，AE=______．三、解答题（本大题共7小题，共60.0分。

一、多选题1．题目文件丢失！2．已知ABC 的面积为3，在ABC 所在的平面内有两点P ，Q ，满足20PA PC +=，2QA QB =，记APQ 的面积为S ，则下列说法正确的是（ ）A ．//PB CQ B ．2133BP BA BC =+ C ．0PA PC ⋅<D ．2S =3．已知在平面直角坐标系中，点()10,1P ，()24,4P .当P 是线段12PP 的一个三等分点时，点P 的坐标为（ ） A ．4,23⎛⎫⎪⎝⎭B ．4,33⎛⎫⎪⎝⎭C ．()2,3D ．8,33⎛⎫ ⎪⎝⎭4．已知向量a =(2，1)，b =(1，﹣1)，c =(m ﹣2，﹣n )，其中m ，n 均为正数，且(a b -)∥c ，下列说法正确的是（ ） A ．a 与b 的夹角为钝角B ．向量a 在bC ．2m +n =4D ．mn 的最大值为25．已知向量()1,0a =，()2,2b =，则下列结论正确的是（ ） A ．()25,4a b += B ．2b = C ．a 与b 的夹角为45°D ．()//2a a b +6．ABC 中，2AB =，30ACB ∠=︒，则下列叙述正确的是（ ） A ．ABC 的外接圆的直径为4.B ．若4AC =，则满足条件的ABC 有且只有1个 C ．若满足条件的ABC 有且只有1个，则4AC =D ．若满足条件的ABC 有两个，则24AC <<7．在ABC 中，内角,,A B C 所对的边分别为,,a b c .根据下列条件解三角形，其中有两解的是（ ）A ．10,45,70b A C ==︒=︒B ．45,48,60b c B ===︒C ．14,16,45a b A ===︒D ．7,5,80a b A ===︒8．已知a 、b 是任意两个向量，下列条件能判定向量a 与b 平行的是（ ） A ．a b =B ．a b =C ．a 与b 的方向相反D ．a 与b 都是单位向量9．在下列结论中，正确的有（ ）A ．若两个向量相等，则它们的起点和终点分别重合B ．平行向量又称为共线向量C ．两个相等向量的模相等D ．两个相反向量的模相等10．设a 、b 、c 是任意的非零向量，则下列结论不正确的是（ ） A ．00a ⋅= B ．()()a b c a b c ⋅⋅=⋅⋅ C ．0a b a b ⋅=⇒⊥D ．()()22b b a b a a +-=⋅-11．已知实数m ，n 和向量a ，b ，下列说法中正确的是（ ） A ．()m a b ma mb -=- B ．()m n a ma na -=-C ．若ma mb =，则a b =D ．若()0ma na a =≠，则m n =12．某人在A 处向正东方向走xkm 后到达B 处,他向右转150°,然后朝新方向走3km 到达C处,,那么x 的值为( )A B ．C ．D ．313．下列命题中正确的是( )A ．对于实数m 和向量,a b ,恒有()m a b ma mb -=-B ．对于实数,m n 和向量a ,恒有()m n a ma na -=-C ．若()ma mb m =∈R ,则有a b =D ．若(,,0)ma na m n a =∈≠R ,则m n =14．题目文件丢失！15．题目文件丢失！二、平面向量及其应用选择题16．在△ABC 中，AB ＝a ，BC ＝b ，且a b ⋅>0，则△ABC 是（ ） A ．锐角三角形B ．直角三角形C ．等腰直角三角形D ．钝角三角形17．已知ABC 所在平面内的一点P 满足20PA PB PC ++=，则::PAB PAC PBC S S S =△△△（ ）A ．1∶2∶3B ．1∶2∶1C ．2∶1∶1D ．1∶1∶218．若O 为ABC 所在平面内任意一点，且满足()20BC OB OC OA ⋅+-=，则ABC 一定为（ ）A ．锐角三角形B ．直角三角形C ．等腰三角形D ．钝角三角形19．已知向量OA 与OB 的夹角为θ，2OA =，1OB =，=OP tOA ，()1OQ t OB =-，PQ 在t t =0时取得最小值，则当0105t <<时，夹角θ的取值范围为（ ）A ．0,3π⎛⎫ ⎪⎝⎭B ．,32ππ⎛⎫ ⎪⎝⎭C ．2,23ππ⎛⎫⎪⎝⎭D ．20,3π⎛⎫ ⎪⎝⎭ 20．在ABC ∆中，角A ，B ，C 所对的边分别是a ，b ，c ，设S 为ABC ∆的面积，满足cos cos b A a B =，且角B 是角A 和角C 的等差中项，则ABC ∆的形状为（ ）A ．不确定B ．直角三角形C ．钝角三角形D ．等边三角形21．设θ为两个非零向量,a b →→的夹角，已知对任意实数t ，||b t a →→-的最小值为1，则（ ）A ．若θ确定，则||a →唯一确定 B ．若θ确定，则||b →唯一确定 C ．若||a →确定，则θ唯一确定D ．若||b →确定，则θ唯一确定22．在△ABC 中，内角A 、B 、C 所对边分别为a 、b 、c ，若2cosA 3cosB 5cosCa b c==，则∠B 的大小是（ ） A ．12πB ．6π C ．4π D ．3π23．在三角形ABC 中，若三个内角,,A B C 的对边分别是,,a b c ，1a =，c =45B =︒，则sin C 的值等于（ ）A ．441B ．45C ．425D ．4124．若点G 是ABC 的重心，,,a b c 分别是BAC ∠，ABC ∠，ACB ∠的对边，且303aGA bGB cGC ++=.则BAC ∠等于（ ） A ．90°B ．60°C ．45°D ．30°25．著名数学家欧拉提出了如下定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半．此直线被称为三角形的欧拉线，该定理则被称为欧拉线定理．设点O ，H 分别是△ABC 的外心、垂心，且M 为BC 中点，则 （ ）A ．33AB AC HM MO +=+ B ．33AB AC HM MO +=- C ．24AB AC HM MO +=+D ．24AB AC HM MO +=-26．在ABC ∆中，8AB =，6AC =，60A ∠=，M 为ABC ∆的外心，若AM AB AC λμ=+，λ、R μ∈，则43λμ+=（ ）A ．34B ．53C ．73D ．8327．在△ABC 中，M 为BC 上一点，60,2,||4ACB BM MC AM ∠=︒==，则△ABC 的面积的最大值为（ ）A ．123B ．63C ．12D ．18328．在ABC 中，CB a =，CA b =，且sin sin a b OP OC m a B b A ⎛⎫⎪=++ ⎪⎝⎭，m R ∈，则点P 的轨迹一定通过ABC 的（ ） A ．重心B ．内心C ．外心D ．垂心29．在△ABC 中，M 是BC 的中点．若AB ＝a ，BC ＝b ，则AM ＝( ) A ．1()2a b + B ．1()2a b - C ．12a b + D ．12a b +30．在ABC 中，角A 、B 、C 所对的边分别是a 、b 、c ，若1c =，45B =︒，3cos 5A =，则b 等于（ ） A ．35 B ．107C ．57D ．521431．如图，在ABC 中，点D 在线段BC 上，且满足12BD DC =，过点D 的直线分别交直线AB ，AC 于不同的两点M ，N 若AM mAB =，AN nAC =，则（ ）A ．m n +是定值，定值为2B ．2m n +是定值，定值为3C ．11m n +是定值，定值为2 D ．21m n+是定值，定值为3 32．若两个非零向量a ，b 满足2a b a b b +=-=，则向量a b +与a 的夹角为( ) A ．3π B ．23π C ．56π D ．6π 33．已知D ，E ，F 分别是△ABC 的边BC ，CA ，AB 的中点，且BC a CA b ==，，AB c =，则①AD ＝－b －12a ；②BE ＝a ＋12b ；③CF ＝－12a ＋12b ；④AD ＋BE ＋CF ＝0.其中正确的等式的个数为( ) A ．1 B ．2 C ．3 D ．434．已知点O 是ABC ∆内一点，满足2OA OB mOC +=，47AOB ABC S S ∆∆=，则实数m 为（ ） A ．2B ．-2C ．4D ．-435．在ABC 中，若A B >，则下列结论错误的是（ ）A ．sin sin AB > B ．cos cos A B <C ．sin2sin2A B >D ．cos2cos2A B <【参考答案】***试卷处理标记，请不要删除一、多选题 1．无 2．BCD 【分析】本题先确定B 是的中点，P 是的一个三等分点，判断选项A 错误，选项C 正确； 再通过向量的线性运算判断选项B 正确；最后求出，故选项D 正确. 【详解】 解：因为，，所以B 是的中点，P 是的 解析：BCD 【分析】本题先确定B 是AQ 的中点，P 是AC 的一个三等分点，判断选项A 错误，选项C 正确； 再通过向量的线性运算判断选项B 正确；最后求出2APQ S =△，故选项D 正确. 【详解】解：因为20PA PC +=，2QA QB =，所以B 是AQ 的中点，P 是AC 的一个三等分点，如图：故选项A 错误，选项C 正确；因为()121333BP BA AP BA BC BA BA BC =+=+-=+，故选项B 正确； 因为112223132APQ ABCAB hS S AB h ⨯⨯==⋅△△，所以，2APQ S =△，故选项D 正确. 故选：BCD 【点睛】本题考查平面向量的线性运算、向量的数量积、三角形的面积公式，是基础题.3．AD 【分析】设，则，然后分点P 靠近点，靠近点两种情况，利用平面向量的线性运算求解. 【详解】 设，则，当点P 靠近点时，， 则， 解得， 所以，当点P 靠近点时，， 则， 解得， 所以， 故选：解析：AD 【分析】设(),P x y ，则()()12,1,4,4=-=--PP x y PP x y ，然后分点P 靠近点1P ，靠近点2P 两种情况，利用平面向量的线性运算求解. 【详解】设(),P x y ，则()()12,1,4,4=-=--PP x y PP x y ， 当点P 靠近点1P 时，1212PPPP =， 则()()1421142x x y y ⎧=-⎪⎪⎨⎪-=-⎪⎩，解得432x y ⎧=⎪⎨⎪=⎩，所以4,23P ⎛⎫⎪⎝⎭， 当点P 靠近点2P 时，122PP PP =， 则()()24124x x y y ⎧=-⎪⎨-=-⎪⎩，解得833xy⎧=⎪⎨⎪=⎩，所以8,33P⎛⎫ ⎪⎝⎭，故选：AD【点睛】本题主要考查平面向量的线性运算，还考查了运算求解的能力，属于基础题.4．CD【分析】对于A，利用平面向量的数量积运算判断；对于B，利用平面向量的投影定义判断；对于C，利用()∥判断；对于D，利用C 的结论，2m+n=4，结合基本不等式判断.【详解】对于A，向量(解析：CD【分析】对于A，利用平面向量的数量积运算判断；对于B，利用平面向量的投影定义判断；对于C，利用(a b-)∥c判断；对于D，利用C的结论，2m+n=4，结合基本不等式判断.【详解】对于A，向量a =(2，1)，b =(1，﹣1)，则2110a b⋅=-=>，则,a b的夹角为锐角，错误；对于B，向量a =(2，1)，b =(1，﹣1)，则向量a在b 方向上的投影为22a bb⋅=，错误；对于C，向量a=(2，1)，b=(1，﹣1)，则a b-=(1，2)，若(a b-)∥c，则(﹣n)=2(m ﹣2)，变形可得2m+n=4，正确；对于D，由C的结论，2m+n=4，而m，n均为正数，则有mn12= (2m•n)12≤(22m n+)2=2，即mn的最大值为2，正确；故选：CD.【点睛】本题主要考查平面向量的数量积运算以及基本不等式的应用，属于基础题.5．AC【分析】利用向量线性的坐标运算可判断A；利用向量模的坐标求法可判断B；利用向量数量积的坐标运算可判断C ；利用向量共线的坐标表示即可求解. 【详解】 由向量，， 则，故A 正确； ，故B 错误；解析：AC 【分析】利用向量线性的坐标运算可判断A ；利用向量模的坐标求法可判断B ；利用向量数量积的坐标运算可判断C ；利用向量共线的坐标表示即可求解. 【详解】由向量()1,0a =，()2,2b =，则()()()21,022,25,4a b +=+=，故A 正确；222b =+=，故B 错误；2cos ,21a b a b a b⋅<>===⋅+，又[],0,a b π<>∈，所以a 与b 的夹角为45°，故C 正确； 由()1,0a =，()25,4a b +=，140540⨯-⨯=≠，故D 错误. 故选：AC 【点睛】本题考查了向量的坐标运算，考查了基本运算能力，属于基础题.6．ABD 【分析】根据正弦定理，可直接判断的对错，然后，，三个选项，都是已知两边及一边的对角，判断解得个数的问题，做出图象，构造不等式即可． 【详解】解：由正弦定理得，故正确； 对于，，选项：如图解析：ABD 【分析】根据正弦定理，可直接判断A 的对错，然后B ，C ，D 三个选项，都是已知两边及一边的对角，判断解得个数的问题，做出图象，构造不等式即可． 【详解】解：由正弦定理得224sin sin30AB R ACB ===∠︒，故A 正确；对于B ，C ，D 选项：如图：以A 为圆心，2AB =为半径画圆弧，该圆弧与射线CD 的交点个数，即为解得个数． 易知当122x =，或即4AC =时，三角形ABC 为直角三角形，有唯一解； 当2AC AB ==时，三角形ABC 是等腰三角形，也是唯一解；当AD AB AC <<，即122x x <<，24x ∴<<时，满足条件的三角形有两个．故B ，D 正确，C 错误． 故选：ABD ．【点睛】本题考查已知两边及一边的对角的前提下，三角形解得个数的判断问题．属于中档题．7．BC 【分析】根据题设条件和三角形解的个数的判定方法，逐项判定，即可求解，得到答案. 【详解】对于选项A 中：由，所以，即三角形的三个角是确定的值，故只有一解； 对于选项B 中：因为，且，所以角有两解析：BC 【分析】根据题设条件和三角形解的个数的判定方法，逐项判定，即可求解，得到答案. 【详解】对于选项A 中：由45,70A C =︒=︒，所以18065B A C =--=︒，即三角形的三个角是确定的值，故只有一解； 对于选项B 中：因为csin 83sin 115B C b ==<，且c b >，所以角C 有两解； 对于选项C 中：因为sin 2sin 17b A B a ==<，且b a >，所以角B 有两解； 对于选项D 中：因为sin sin 1b AB a=<，且b a <，所以角B 仅有一解. 故选：BC . 【点睛】本题主要考查了三角形解得个数的判定，其中解答中熟记三角形解得个数的判定方法是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.8．AC【分析】根据共线向量的定义判断即可.【详解】对于A选项，若，则与平行，A选项合乎题意；对于B选项，若，但与的方向不确定，则与不一定平行，B选项不合乎题意；对于C选项，若与的方向相反，解析：AC【分析】根据共线向量的定义判断即可.【详解】对于A选项，若a b=，则a与b平行，A选项合乎题意；=，但a与b的方向不确定，则a与b不一定平行，B选项不合乎题对于B选项，若a b意；对于C选项，若a与b的方向相反，则a与b平行，C选项合乎题意；对于D选项，a与b都是单位向量，这两个向量长度相等，但方向不确定，则a与b不一定平行，D选项不合乎题意.故选：AC.【点睛】本题考查向量共线的判断，考查共线向量定义的应用，属于基础题.9．BCD【分析】根据向量的定义和性质依次判断每个选项得到答案.【详解】A. 若两个向量相等，它们的起点和终点不一定不重合，故错误；B. 平行向量又称为共线向量，根据平行向量定义知正确解析：BCD【分析】根据向量的定义和性质依次判断每个选项得到答案.【详解】A. 若两个向量相等，它们的起点和终点不一定不重合，故错误；B. 平行向量又称为共线向量，根据平行向量定义知正确；C. 相等向量方向相同，模相等，正确；D. 相反向量方向相反，模相等，故正确；故选：BCD【点睛】本题考查了向量的定义和性质，属于简单题.【分析】利用平面向量数量积的定义和运算律可判断各选项的正误. 【详解】对于A 选项，，A 选项错误；对于B 选项，表示与共线的向量，表示与共线的向量，但与不一定共线，B 选项错误； 对于C 选项，解析：AB 【分析】利用平面向量数量积的定义和运算律可判断各选项的正误. 【详解】对于A 选项，00a ⋅=，A 选项错误；对于B 选项，()a b c ⋅⋅表示与c 共线的向量，()a b c ⋅⋅表示与a 共线的向量，但a 与c 不一定共线，B 选项错误；对于C 选项，0a b a b ⋅=⇒⊥，C 选项正确；对于D 选项，()()2222a b a b a b a b +⋅-=-=-，D 选项正确. 故选：AB. 【点睛】本题考查平面向量数量积的应用，考查平面向量数量积的定义与运算律，考查计算能力与推理能力，属于基础题.11．ABD 【分析】根据向量数乘运算判断AB 选项的正确性，通过的特殊情况判断C 选项的正确性，根据向量运算判断D 选项的正确性. 【详解】根据向量数乘的运算可知A 和B 正确；C 中，当时，，但与不一定相等，解析：ABD 【分析】根据向量数乘运算判断AB 选项的正确性，通过m 的特殊情况判断C 选项的正确性，根据向量运算判断D 选项的正确性. 【详解】根据向量数乘的运算可知A 和B 正确；C 中，当0m =时，0ma mb ==，但a 与b 不一定相等，故C 不正确；D 中，由ma na =，得()0m n a -=，因为0a ≠，所以m n =，故D 正确. 故选：ABD本小题主要考查向量数乘运算，属于基础题.12．AB 【分析】由余弦定理得，化简即得解. 【详解】由题意得,由余弦定理得, 解得或. 故选：AB. 【点睛】本题主要考查余弦定理的实际应用，意在考查学生对这些知识的理解掌握水平.解析：AB 【分析】由余弦定理得293cos306x x︒+-=，化简即得解.【详解】由题意得30ABC ︒∠=,由余弦定理得293cos306x x︒+-=,解得x =x 故选：AB. 【点睛】本题主要考查余弦定理的实际应用，意在考查学生对这些知识的理解掌握水平.13．ABD 【详解】解：对于：对于实数和向量、，根据向量的数乘满足分配律，故恒有：，故正确．对于：对于实数，和向量，根据向量的数乘运算律，恒有，故 正确． 对于：若，当 时，无法得到，故不正确． 对解析：ABD 【详解】解：对于A ：对于实数m 和向量a 、b ，根据向量的数乘满足分配律，故恒有：()m a b ma mb -=-，故A 正确．对于B ：对于实数m ，n 和向量a ，根据向量的数乘运算律，恒有()m n a ma na -=-，故 B 正确．对于C ：若()ma mb m =∈R ，当 0m =时，无法得到a b =，故C 不正确．对于D ：若(,,0)ma na m n a =∈≠R ，则m n =成立，故D 正确． 故选：ABD ． 【点睛】本题考查相等的向量，相反的向量的定义，向量的数乘法则以及其几何意义，注意考虑零向量的情况．14．无 15．无二、平面向量及其应用选择题16．D 【分析】由数量积的定义判断B 角的大小，得三角形形状． 【详解】由题意cos()0a b a b B π⋅=->，∴cos()0B π->，cos 0B ->，cos 0B <，又B 是三角形内角，∴2B ππ<<．∴ABC 是钝角三角形． 故选：D ． 【点睛】本题考查考查三角形形状的判断，解题关键是掌握数量积的定义．向量夹角的概念． 17．B 【分析】延长PB 至D ，可得出点P 是ADC 的重心，再根据重心的性质可得出结论。

数学平面图形的认识试题答案及解析1.过一点可以画出（）条直线与已知直线垂直．A．一条B．两条C．三条D．无数条【答案】A【解析】过直线外一点有并且只有一条直线与已知直线垂直．据此解答．解：过直线外一点只有一条直线与已知直线垂直．故选：A．点评：本题考查了学生过直线外一点有并且只有一条直线与已知直线垂直的知识．2.在同一个平面内，一条直线用a 表示，另一条直线用b 表示．如果直线a 和直线b是不相交的，那么下面说法正确的是（）A．a 是平行线B．a和b互相平行C．b是平行线D．a和b互相垂直【答案】B【解析】因为在同一个平面内，两条直线只有两种位置关系，相交和平行，据此判断即可．解：因为在同一个平面内，两条直线只有两种位置关系，相交和平行，如果直线a 和直线b是不相交的，那么这两条直线一定平行．所以a和b互相平行．故选：B．点评：解决本题的关键是明确：在同一个平面内，两条直线只有两种位置关系，相交和平行．3.画一条线段，把这个梯形分成一个三角形和一个平行四边形．【答案】【解析】利用过直线外一点作已知直线的平行线的方法，过梯形的上底的一个端点A，作腰CD的平行线AE即可．解：如图所示，AE即为所要求作的线段：．点评：此题主要考查过直线外一点作已知直线的平行线的方法．4.判断：读数时，只要从高位起，依次读出每级的数字就行．10cm的直线比8cm的射线长2cm．三位数乘两位数，积可能是五位数，也可能是两位数．两条直线同时垂直于第三条直线，那么这两条直线互相平行．．【答案】错误；错误；错误；正确【解析】（1）根据整数的读法：从高位到低位，一级一级地读，每一级末尾的0都不读出来，其他数位连续几个0都只读一个零．即读多位数时，应先读亿级，再读万级，最后读个级，万级和亿级的数要按照个级的数的读法来读，再在后面加读“万或亿”字．（2）直线没有端点，它向两方无限延伸，无法量得其长度；射线只有一个端点，它向一方无限延伸，也无法量得其长度；据此解答即可．（3）根据题意，可以假设这个两位数和三位数都是最小的数，然后再进行判断即可；（4）由垂直和平行的特征和性质可知：平面内，垂直于同一条直线的两条直线互相平行；据此判断即可．解：（1）解：读多位数时，应先读亿级，再读万级，最后读个级，万级和亿级的数要按照个级的数的读法来读，再在后面加读“万或亿”字．所以读数时，只要从高位起，依次读出每级的数字就行．是错误的；（2）因为直线没有端点，它向两方无限延伸，无法量得其长度；射线只有一个端点，它向一方无限延伸，也无法量得其长度；所以10cm的直线比8cm的射线长2cm，是错误的；（3）根据题意，假设这个两位数和三位数都是最小的数，即分别是10、100，那么，10×100=1000，因为1000是四位数，与题意不符，所以，三位数乘两位数，积可能是五位数，也可能是两位数，是错误的；（4）由垂直和平行的特征和性质可知：平面内，垂直于同一条直线的两条直线互相平行；所以两条直线同时垂直于第三条直线，那么这两条直线互相平行．是正确的．故答案为：错误；错误；错误；正确．点评：本题主要考查整数的读法，注意读亿级和万级数时要按照个级数的读法去读，区别是最后再加读“万或亿”字．此题主要考查直线和射线的含义，应注意基础知识的灵活运用．三位数乘两位数，积是几位数取决于两个因数的大小．三位数乘两位数的积最少是四位数，最多是五位数．此题考查了垂直和平行的特征和性质，应注意理解和灵活运用．5.在如图的平行线中画一个最大的正方形．【答案】【解析】先在两条平行线中画出一条垂线段，量出长度，然后以这条垂线段的两个端点为正方形的两个顶点，在两条平行线上分别截取和垂线段相等的两条线段，连接截取的另两个端点即可得出平行线里最大的正方形．解：由分析作图如下：点评：解答此题应明确：所作出的正方形的边长等于这两条平行线之间的垂线段的长度．6.和如图的直线相距1cm的平行线你能画几条？试着画一画吧．【答案】【解析】与已知直线相距1厘米的点能找出2个，在直线的两侧各一个，因为过直线外一点画已知直线答平行线只能画一条，所以经过这两个点可以画出两条平行线，据此回答即可．解：如图，距离已知直线的距离为1厘米的点能找出两个，所以能画出两条平行线，如下图：点评：此题主要考查点到直线的距离以及平行线的画法．7.画出图形指定底的高．【答案】【解析】根据梯形的高的意义，梯形的上下底之间的距离叫做梯形的高．由此解答．解：作梯形上下底的垂线段即可．如下图：点评：此题的解答主要明确梯形的高的意义，根据作垂线的方法解决问题．8.画出两个图形的一条高．【答案】【解析】在平行四边形中，从一条边上的任意一点向对边作垂线，这点与垂足间的距离叫做以这条边为底的平行四边形的高．习惯上作平行四边形的高时都从一个顶点出发作一边的垂线；同样在梯形中，从一底的任一点作另一底的垂线，这点与垂足间的距离叫做梯形的高．习惯上作梯形的高时都从上底（较短的底）一个顶点出发作下底的垂线．解：如图所示：．点评：本题主要是考查作平行四边形和梯形的高．很多同学作高时画不垂直，可以用两个三角板来完成．高一般用虚线来表示，要标出垂足．9.想一想，选一选．A．互相平行 B．互相垂直 C．都有可能（1）在同一平面内两条直线都平行于一条直线，这两条直线的位置关系是．（2）在同一平面内两条直线都垂直于一条直线，这两条直线的位置关系是．【答案】A，A【解析】（1）根据平行线的定义，在同一平面内，不相交的两条直线叫做平行线，有两条直线都和一条直线平行，这两条直线互相平行，据此解答．（2）根据垂直定义得出∠CMB=∠ENB=90°，根据平行线的判定求出即可．解：（1）由分析可知：在同一平面内，有两条直线都和一条直线平行，这两条直线互相平行；（2）因为CD⊥AB，EF⊥AB，所以∠CMB=∠ENB=90°，所以CD∥EF．所以在同一平面内两条直线都垂直于一条直线，这两条直线的位置关系是平行；故答案为：A，A．点评：此题考查了垂直于平行的特征及性质，应注意基础知识的积累．10.两条笔直的铁轨互相．【答案】平行【解析】根据平行的含义：在同一平面内，不相交的两条直线叫做平行线；据此判断即可．解：根据平行的含义可知：两条笔直的铁轨互相平行；故答案为：平行．点评：此题考查了平行的含义，应注意理解和应用．11. x的3倍与4的差是非负数，列不等式是．【答案】3x﹣4≥0【解析】关键描述语是：差是非负数．最后算的差应大于或等于0．解：根据题意，得3x﹣4≥0．点评：读懂题意，抓住关键词语，弄清运算的先后顺序和不等关系，才能把文字语言的不等关系转化为用数学符号表示的不等式．12.已知不等式3（x﹣2）+5＜4（x﹣1）+6的最小整数解为方程2x﹣ax=3的解，则代数式4a﹣的值为．【答案】代入代数式4a﹣=4×﹣=14﹣4=10【解析】先求得不等式3（x﹣2）+5＜4（x﹣1）+6的解集，可求得x的最小整数解是﹣2，也就是方程2x﹣ax=3的解是x=﹣2，把x=﹣2代入2x﹣ax=3，求出a=，代入代数式4a﹣即可求解．解：因为3（x﹣2）+5＜4（x﹣1）+6，去括号得3x﹣6+5＜4x﹣4+6移项得3x﹣4x＜﹣4+6+6﹣5合并同类项得﹣x＜3系数化为1得x＞﹣3，所以x的最小整数解是﹣2，也就是方程2x﹣ax=3的解是x=﹣2，把x=﹣2代入2x﹣ax=3，得到a=，代入代数式4a﹣=4×﹣=14﹣4=10．点评：注意理解最小整数既可以是正整数，0，也可以是负整数．解题关键是先求出不等式的解，再代入方程求出a的值，最后把a的值代入代数式求值．13.在同一平面内的两条直线不平行就一定垂直．．【答案】错误【解析】因为在同一平面内的两条直线不平行就相交，垂直只是相交情况中的一种，据此判断即可．解：由分析可知：在同一平面内，不平行的两条直线一定垂直．…，说法错误；故答案为：×．点评：此题主要考查在同一平面内的两条直线的位置关系，明确垂直只是相交的一种特殊情况．14.过P点画出AB的平行线，画出BC的垂线．【答案】【解析】（1）把三角板的一条直角边与已知直线AB重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和AB重合的直角边和P点重合，过P点沿三角板的直角边画直线即可．（2）把三角板的一条直角边与已知直线BC重合，沿直线移动三角板，使三角板的另一条直角边和P点重合，过P点沿三角板的直角边向已知直线画直线即可．解：据分析作图如下：点评：本题考查了学生作平行线和垂线的方法，培养学生的作图能力．15.过B点画出角两边的平行线．【答案】【解析】把三角板的一条直角边与已知直线重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和B点重合，过B点沿三角板的直角边画直线即可．解：由分析画图如下：点评：本题考查了学生画平行线的能力．16.过点A分别画直线的平行线．【答案】【解析】把三角板的一条直角边与已知直线重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和A点重合，过A点沿三角板的直角边画直线即可．解：作图如下：点评：本题考查了学生利用直尺和三角板作平行线的能力．17.要划船从A点到河的对岸，把最短的线路画出来，然后过B点画出与河流平行的直线．【答案】【解析】（1）把河的对岸看做一条直线，依据垂线段最短，作出A点到直线的垂线段即可解答．（2）将河岸的一条边当作已知直线，B点是已知直线外一点，根据过直线外一点画已知直线的平行线的方法画出过B点与河流平行的直线即可．解：如图所示：，红色垂线段即为所求最短路线；过B点的直线即为所求与河流平行的直线．点评：本题考查了学生对点到直线距离知识的掌握和画垂线段、平行线的能力．18.过顶点C作AB的平行线，再过B点作AC的垂线．【答案】【解析】（1）把三角板的一条直角边与AB重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和AB重合的直角边和C点重合，过C点沿三角板的直角边画直线即可．（2）用三角板的一条直角边的AC重合，沿AC平移三角板，使三角板的另一条直角边和B点重合，过B沿直角边向AC画直线即可．解：根据分析：（1）过C点画AB的平行线，（2）过B点画AC的垂线．画图如下：点评：本题考查了学生画垂线和平行线的作图能力．19.你能在下面的平行线里画一个最大的正方形吗？【答案】【解析】先在两条平行线中画出一条垂线段，量出长度，然后以这条垂线段的两个端点为正方形的两个顶点，在两条平行线上分别截取和垂线段相等的两条线段，连接截取的另两个端点即可得出平行线里最大的正方形．解：由分析作图如下：点评：解答此题应明确：所作出的正方形的边长等于这两条平行线之间的垂线段的长度．20.请你用画平行线的方法，把图形画成一个长方形．【答案】【解析】把三角板的一条直角边与已知直线重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和顶点重合，过顶点沿三角板的直角边画直线即可．解：作图如下：点评：本题考查了学生利用平行线作长方形的能力．21.画出下面图形指定底的高．【答案】【解析】在图形中标上字母，如下图，从A点做AE⊥BC，交BC于E，则AE即为所求．解：从A点做AE⊥BC，交BC于E，则AE即为所求．点评：此题考查了学生作图能力，考查了画出图形指定底的高．22.作一个长3厘米、宽2厘米的长方形．【答案】【解析】已知长方体的长为3厘米，宽2厘米，据已知条件用直尺及三角尺作图即可．解：点评：作正方形及长方形要用到直尺及三角尺．23.（2013•华亭县模拟）过已知直线外的一点A（1）作直线的平行线（2）作直线的垂线．【答案】【解析】（1）用三角板的一条直角边的已知直线重合，沿重合的直线平移三角板，使三角板的另一条直角边和A点重合，过A沿直角边向已知直线画直线即可．（2）把三角板的一条直角边与已知直L重合，用直尺靠紧三角板的另一条直角边，沿直尺移动三角板，使三角板的原来和已知直线重合的直角边和A点重合，过A点沿三角板的直角边画直线即可．解：画图如下：点评：本题考查了学生过直线外一点作已知直线的平行线和垂线的画图能力．24.下列各组直线，组互相平行，组互相垂直．【答案】②，③【解析】根据平行线和垂线的定义：在同一平面内不相交的两条直线叫做平行线；当两条直线相交成90度时，这两条直线就互相垂直；据此解答即可．解：下列各组直线，②组互相平行，③组互相垂直；故答案为：②，③．点评：此题考查了平行和垂直的定义．25.小明绕水池边走一圈，走了多少米？【答案】小明绕水池边走一圈，走了210米【解析】依据平面图形的周长的意义，将组成这个图形的所有线段加在一起即可得解．解：60+30+15+60+30+15=（60+30+15）×2=105×2=210（米）；答：小明绕水池边走一圈，走了210米．点评：解答此题的主要依据是：平面图形的周长的意义．26.平行四边形的高有（）条．A．1B．2C．8D．无数条【答案】D【解析】根据平行四边形高的含义：平行四边形的高是指对边之间的距离，那么，两组对边之间都可以画无数条垂直线段，所以，有无数条高，即可选择．解：由分析可知，平行四边形有无数条高，故选：D．点评：此题考查了平行四边形高的含义．27.用两个边长为3厘米的正方形拼成一个长方形，这个长方形的周长是（）A.24厘米B.18厘米C.12厘米【答案】B【解析】用2个边长3厘米的小正方形拼成一个长方形，方法只有一种，拼成后的长方形的长是（3×2）厘米，宽是3厘米，然后根据长方形的周长公式求出它的周长．据此解答．解：拼成后长方形的长是：3×2=6（厘米），拼成后长方形的宽是3厘米，拼成后长方形的周长是：（6+3）×2，=9×2，=18（厘米），答：它的周长是18厘米．故答案选：B．点评：本题的关键是求出拼成后长方形的长和宽，再根据长方形的周长公式进行计算．28.一个长方形的周长是24厘米，如把它平均分成两个正方形，每个正方形的周长是12cm．．【答案】错误【解析】如图所示，先依据长方形的周长公式求出其长和宽的和，由题意可知，长方形的长应等于其宽的2倍，从而依据正方形的周长公式即可求解．解：设长方形的宽为a，则其长为2a，a+2a=24÷2，3a=12，a=4，4×4=16（厘米）；答：每个正方形的周长是16厘米．故答案为：错误．点评：此题主要考查长方形和正方形的周长的计算方法的灵活应用．29.（2012•通川区模拟）长方形、正方形和梯形都是特殊的平行四边形．．【答案】错误【解析】根据平行四边形的特征：两组对边平行且相等；则得出：长方形、正方形是特殊的平行四边形，而梯形是只有一组对边平行的四边形，另一组对边不平行；进行解答即可．解：长方形、正方形是特殊的平行四边形，而梯形是只有一组对边平行的四边形，另一组对边不平行；故答案为：错误．点评：此题考查了平行四边形的特征和性质，应注意基础知识的积累．30.如图，用2条线段可以把一个边长为10厘米的正方形分割成面积相等的4部分，这两条分割线的长度总和是20厘米（如图），现在请你用不超过4条的线段将一个边长为10厘米的正方形分割成面积相等的5部分，要求找出3种不同的分割方法，其分割线的长度总和必须小于40厘米，在图中画分割线并在每个图下面的横线上写上分割线的长度总和．【答案】【解析】首先一个一个边长10厘米的正方形面积为100平方厘米，分成相等的五份，每份面积应为20平方厘米；第一种方法：把它分为一个长为10厘米，宽为2厘米的长方形和四个长为5厘米，宽为4厘米的长方形；第二种方法：把它分为一个长为10厘米，宽为2厘米的长方形和四个底边为5厘米，高为8厘米直角三角形；第三种方法：把它分成中间一个正方形和四个角上四个直角三角形，如下图所示．解：根据分析画图如下：点评：本题先把每一个正方形的两条对边都5等分是解答的关键确定分割线长度总和最短是难点．31.一块长方形布料长5米，宽比长短2米，这块布料的周长是多少米？【答案】这块布料的周长是16米【解析】首先求出它的宽，再根据长方形的周长公式：c=（a+b）×2，把数据代入公式解答即可．解：（5+5﹣2）×2，=8×2，=16（米）；答：这块布料的周长是16米．点评：此题主要考查长方形的公式的灵活运用．32.农业科技小组有块劳动基地（如图），他们要在四周扎上围栏，他们需要扎多长的围栏？【答案】他们需要扎104米长的围栏【解析】由题意得出：四周扎上围栏的长度等于正方形的周长，根据正方形周长=边长×4即可解答．解：26×4=104（米），答：他们需要扎104米长的围栏．点评：此题主要考查正方形周长的计算．33.如图是中心小学操场示意图．小刚绕操场周边跑一圈，跑多少米？【答案】90.84米【解析】由题意得操场一周是由长方形和圆周组成的，圆的直径为30﹣24=6米，半径为6÷2=3米，长方形的长是24米，宽为18﹣3×2=12米，根据圆的周长=πd，长方形周长=长×2+宽×2，把圆周的长和长方形四条边相加即可求出操场的长度．解：圆的半径为：（30﹣24）÷2=3（米），所以操场的周长为：（18﹣2×3）×2+24×2+3.14×（30﹣24），=24+48+18.84，=90.84（米）．答：跑90.84米．点评：解决本题的关键是分析得出整个操场的组成部分．34.下面的图形有周长吗？如果有请用彩笔描出来．【答案】【解析】封闭图形一周的长度，叫做这个图形的周长，只有封闭的平面图形才有周长，据此判断出哪些图形有周长，再用彩笔沿图形的一周描出图形的周长即可．解：围成一个图形的所有边长的总和叫做这个图形的周长，由此可知，从左数1、2、3、4、6、8、9有周长，用彩笔描出如下：点评：此题考查了周长的定义，要注意掌握判断什么图形有周长的方法．35.一块正方形菜地边长为40米，把它的边长缩小为原来的一千分之一，缩小后的图形周长是多少？【答案】0.16米【解析】根据比例尺，先求出缩小后的边长，再利用正方形的周长公式计算即可．解：40×=0.04（米），0.04×4=0.16（米），答：缩小后的图形的周长是0.16米．点评：此题主要考查正方形的周长以及利用比例尺的计算应用．36.一个正方形果园，边长是340米，如果要用篱笆把果园的四周围起来，求篱笆的长是多少米？【答案】1360米【解析】此题要求四周篱笆的长度，就是求这个边长为340米的正方形果园的周长，根据正方形的周长公式即可列式求篱笆长．解：340×4=1360（米）．答：篱笆的长是1360米．点评：本题考查了正方形的周长=边长×4的应用，是基础题型．37.周长是80厘米的长方形，它的长是28厘米，宽是多少厘米？【答案】12【解析】因为长方形周长=（长+宽）×2，所以周长除以2就是一条长和宽的长度之和，再减去长就是宽的长度．解：80÷2﹣28，=40﹣28，=12（厘米）．答：宽是12厘米．点评：此题主要考查长方形周长公式的灵活运用．38.先测量，再算出他们的周长．【答案】长方形的周长是8.8厘米，平行四边形的周长是7.4厘米【解析】首先测量出长方形的长和宽，平行四边形的底和它的邻边的长度，根据长方形（平行四边形）的周长公式：c=（a+b）×2，把数据代入公式解答．解：（2.4+2）×2，=4.4×2，=8.8（厘米）；（2.1+1.6）×2，=3.7×2，=7.4（厘米）；答：长方形的周长是8.8厘米，平行四边形的周长是7.4厘米．点评：此题考查的目的在掌握长度测量方法以及长方形、平行四边形的周长的计算方法．39.用两个长8厘米、宽4厘米的长方形，分别拼成一个长方形和一个正方形．（1）计算这个长方形的周长．（2）计算这个正方形的周长．【答案】拼成后长方形的周长是36厘米，拼成后正方形的周长是32厘米【解析】用两个长8厘米，宽4厘米的长方形，拼成一个大长方形这个大长方形的长是（8+8）厘米，宽是2厘米，拼成正方形的边长是（4+4）厘米，然后根据它们的周长公式进行计算．据此解答．解：拼成长方形的周长是：（8+8+2）×2，=18×2，=36（厘米）．拼成后正方形的周长是：（4+4）×4，=8×4，=32（厘米）．答：拼成后长方形的周长是36厘米，拼成后正方形的周长是32厘米．点评：本题的关键是先求出拼成后图形的边长，再根据它们的周长公式进行计算．40.已知一个长方形的周长和圆的周长相等，长方形的长是10厘米，宽比长少43%，则圆的面积是多少？【答案】圆的面积是78.5平方厘米【解析】根据“宽比长少43%”，知道宽是长的（1﹣43%），由此先求出长方形的宽，再根据长方形的周长公式，C=（a+b）×2，求出长方形的周长，即圆的周长；再由圆的周长公式的变形，求出圆的半径，最后根据圆的面积公式，S=πr2，求出面积即可．解：长方形的宽：10×（1﹣43%）=5.7（厘米），圆的周长：（10+5.7）×2，=15.7×2，=31.4（厘米），圆的半径：31.4÷3.14÷2=5（厘米），面积是：3.14×5×5，=15.7×5，=78.5（平方厘米），答：圆的面积是78.5平方厘米．点评：解答此题的关键是，根据要求问题，一步一步的确定要求的量，分别根据相应的公式和公式的变形，列式解决问题．41.有两个同样的长方形，长是8分米，宽是4分米．如果把它们拼成一个长方形，这个长方形的周长是多少分米？如果拼成一个正方形，这个正方形的周长是多少分米？【答案】这个长方形的周长是40分米；这个正方形的周长是32分米【解析】（1）要拼成一个长方形，必须两个同样的长方形的宽重合在一起，如下图，再根据长方形的周长公式C=（a+b）×2，即可求出拼成的长方形的周长；（2）要拼成一个正方形，必须两个同样的长方形的长重合在一起，如下图，再根据正方形的周长公式C=4a，即可求出拼成的正方形的周长．解：（1）拼成的长方形的长是：8+8=16（分米），拼成的长方形的周长：（16+4）×2，=20×2，=40（分米）；（2）拼成的正方形的边长是8分米，拼成的正方形的周长是：8×4=32（分米）；答：这个长方形的周长是40分米；这个正方形的周长是32分米．点评：关键是知道如何将两个同样的长方形拼成一个长方形或正方形，再根据相应的公式解决问题．42.足球场是一个长方形，长100米，宽75米，小明沿着足球场跑了2圈，跑了多少米？【答案】700【解析】根据长方形的周长公式C=（a+b）×2，先求出小明沿着足球场跑了1圈的米数，再乘2即可求出小明沿着足球场跑了2圈的米数．解：（100+75）×2×2，=175×2×2，=175×4，=700（米）；答：小明沿着足球场跑了2圈，跑了700米．点评：此题主要考查了长方形的周长公式C=（a+b）×2的实际应用．43.下面都是由边长1厘米的正方形组成的图形，数一数这些图形的周长是多少？（1）厘米；（2）厘米；（3）厘米．【答案】14、12、10【解析】数清楚每个图形的周长由多少个小正方形的边长组成，问题即可得解．解：（1）1×14=14（厘米）；（2）1×12=12（厘米）；（3）1×10=10（厘米）；答：三个图形的周长分别是14厘米、12厘米和10厘米．故答案为：14、12、10．点评：解答此题的关键是：数清楚每个图形的周长由多少个小正方形的边长组成．。

一、选择题1．如图，把一长方形纸片ABCD 沿EG 折叠后，AEG A EG '∠=∠，点A ､B 分别落在A '､B ′的位置，EA '与BC 相交于点F ，已知1125∠=︒，则2∠的度数是（ ）A ．55°B ．60°C ．70°D ．75°2．如图，若180A ABC ∠+∠=︒，则下列结论正确的是（ ）A ．12∠=∠B ．24∠∠=C ．13∠=∠D ．23∠∠= 3．下列图中的“笑脸”，由如图平移得到的是（ ）A ．B ．C ．D ． 4．对于命题“如果∠1+∠2＝90°，那么∠1≠∠2”，能说明它是假命题的反例是（ ） A ．∠1＝50°，∠2＝40°B ．∠1＝50°，∠2＝50°C ．∠1＝∠2＝45°D ．∠1＝40°，∠2＝40° 5．下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容，则回答正确的是（ ） 已知：如图，∠BEC ＝∠B+∠C ，求证：AB ∥CD证明：延长BE 交__※__于点F ，则∠BEC ＝__⊙__+∠C又∵∠BEC ＝∠B+∠C ，∴∠B ＝▲∴AB ∥CD （__□__相等，两直线平行）A ．⊙代表∠FECB ．□代表同位角C ．▲代表∠EFCD ．※代表AB 6．如图，A 是直线l 外一点，过点A 作AB l ⊥于点B ，在直线l 上取一点C ，连接AC ，使2AC AB =，P 在线段BC 上，连接AP ．若3AB =，则线段AP 的长不可能是（ ）A ．4B ．5C ．2D ．5.57．如图，直线l 与直线AB 、CD 分别相交于点E 、点F ，EG 平分BEF ∠交直线CD 与点G ，若168BEF ∠=∠=︒，则EGF ∠的度数为（ ）．A ．34°B ．36°C ．38°D ．68°8．如图，下列条件：13241804523623∠=∠∠+∠=∠=∠∠=∠∠=∠+∠①，②，③，④，⑤中能判断直线12l l 的有( )A ．5个B ．4个C ．3个D ．2个9．如图所示，已知 AB ∥CD ，下列结论正确的是（ ）A ．∠1=∠2B ．∠2=∠3C ．∠1=∠4D ．∠3=∠4 10．如图，下列说法错误的是( )A ．若a ∥b ，b ∥c ，则a ∥cB ．若∠1＝∠2，则a ∥cC ．若∠3＝∠2，则b ∥cD ．若∠3＋∠5＝180°，则a ∥c11．下列命题中，属于假命题的是（ ） A ．如果三角形三个内角的度数比是1:2:3，那么这个三角形是直角三角形B ．内错角不一定相等C ．平行于同一直线的两条直线平行D ．若数a 使得a a >-，则a 一定小于012．在如图所示的四个汽车标识图案中，能用平移变换来分析其形成过程的是（ ） A ． B ． C ． D ．二、填空题13．已知A ∠与B （A ∠，B 都是大于0°且小于180°的角）的两边一边平行，另一边垂直，且227A B ∠-∠=︒，则A ∠的度数为_________．14．两个角的两边两两互相平行，且一个角的12等于另一个角的13，则这两个角中较小角的度数为____︒．15．如图，长8米宽6米的草坪上有一条弯折的小路（小路进出口的宽度相等，且每段小路均为平行四边形），小路进出口的宽度均为1米，则绿地的面积为__平方米．16．如图，长方形ABCD 的周长为30，则图中虚线部分总长为____________．17．如图，点О为直线AB 上一点，,,135OC OD OE AB ⊥⊥∠=︒．（1）EOD ∠= °，2∠= °；（2）1∠的余角是_ ，EOD ∠的补角是__ ．18．命题“若a 2＞b 2则a ＞b ”是_____命题（填“真”或“假”），它的逆命题是_____． 19．如图，AB ∥CD ，∠β=130°，则∠α=_______°．20．如图，直角△ABC 中，AC=3，BC=4，AB=5，则内部五个小直角三角形的周长为_____．三、解答题21．在一张地图上有、、A B C 三地，但地图被墨迹污染，C 地具体位置看不清楚，但知道C 地在A 地的北偏东30°方向，在B 地南偏东45°方向．（1）根据以上条件，在地图上画出C 地的位置；（2）直接写出ACB ∠的度数．22．在如图所示的方格纸中，每个小正方形的顶点称为格点，点,,A B C 都在格点上． ()1找一格点D ，使得直线//CD AB ，画出直线CD ；()2找一格点E ，使得直线AE BC ⊥于点F ，画出直线AE ，并注明垂足F ； ()3找一格点G ，使得直线BG AB ⊥，画出直线BG ；()4连接AG ，则线段,,AB AF AG 的大小关系是 (用“<”连接)．23．如图，AE //CF ，∠A =∠C ．（1）若∠1=35°，求∠2的度数；（2）判断AD 与BC 的位置关系，并说明理由．24．如图，DE 平分∠ADF ，DF ∥BC ，点E ，F 在线段AC 上，点A ，D ，B 在一直线上，连接BF ．（1）若∠ADF ＝70°，∠ABF ＝25°，求∠CBF 的度数；（2）若BF 平分∠ABC 时，求证：BF ∥DE ．25．如图，在△ABC 中，CD ⊥AB ，垂足为D ，点E 在BC 上，EF ⊥AB ，垂足为F ． （1）CD 与EF 平行吗？为什么？（2）如果∠1=∠2，且∠3=115°，∠A=30°，求∠B 的度数．26．如图，已知12∠=∠，C D ∠=∠，求证：A F ∠=∠．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】先根据平行线的性质可得55AEG ∠=︒，再根据平角的定义可得70∠︒=DEF ，然后根据平行线的性质即可得．【详解】由题意得：//AD BC ，1125∠=︒，180155AEG ∴∠=︒-∠=︒，AEG A EG '∠=∠，55A EG '∴∠=︒，18070DEF AEG A EG '∴∠=︒-∠-∠=︒，又//AD BC ，270DEF ∴∠=∠=︒，故选：C ．【点睛】本题考查了平角的定义、平行线的性质，熟练掌握平行线的性质是解题关键． 2．C解析：C【分析】由∠A+∠ABC=180°可得到AD ∥BC ，再根据平行线的性质判断即可得答案．【详解】∵180A ABC ∠+∠=︒，∴//AD BC （同旁内角互补，两直线平行），∴13∠=∠（两直线平行，内错角相等）．故选：C．【点睛】本题考查的是平行线的判定与性质，同旁内角互补，两直线平行；两直线平行内错角相等；熟知平行线的判定定理是解答此题的关键．3．D解析：D【分析】根据平移的性质，不改变图形的形状和大小，经过平移，对应点所连的线段平行且相等，对应线段平行且相等．【详解】解：A、B、C都是由旋转得到的，D是由平移得到的．故选：D．【点睛】本题考查平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．4．C解析：C【分析】能说明是假命题的反例就是能满足已知条件，但不满足结论的例子．【详解】A、满足条件∠1＋∠2＝90°，也满足结论∠1≠∠2，故A选项错误；B、不满足条件，故B选项错误；C、满足条件，不满足结论，故C选项正确；D、不满足条件，也不满足结论，故D选项错误．故选：C．【点睛】此题考查了命题与定理的知识，理解能说明它是假命题的反例的含义是解决本题的关键．5．C解析：C【分析】延长BE交CD于点F，利用三角形外角的性质可得出∠BEC＝∠EFC+∠C，结合∠BEC＝∠B+∠C可得出∠B＝∠EFC，利用“内错角相等，两直线平行”可证出AB∥CD，找出各符号代表的含义，再对照四个选项即可得出结论．【详解】证明：延长BE交CD于点F，则∠BEC＝∠EFC+∠C．又∵∠BEC＝∠B+∠C，∴∠B＝∠EFC，∴AB∥CD（内错角相等，两直线平行）．∴※代表CD ，⊙代表∠EFC ，▲代表∠EFC ，□代表内错角．故选：C ．【点睛】本题考查了平行线的判定以及三角形外角的性质，利用各角之间的关系，找出∠B ＝∠EFC 是解题的关键．6．C解析：C【分析】根据题意计算出AC 的长度，由垂线段最短得出AP 的范围，选出AP 的长度不可能的选项即可．【详解】3AB =，26AC AB cm ∴==，结合垂线段最短，得：36AP ≤≤．故选：C ．【点睛】本题主要考查直线外一点与直线上各点连接的所有线段中，垂线段最短，熟记概念并求出对应线段的范围是解题关键．7．A解析：A【分析】由角平分线的性质可得∠GEB=12∠BEF=34°，由同位角相等，两直线平行可得CD ∥AB ，即可求解．【详解】∵EG 平分∠BEF ， ∴∠GEB=12∠BEF=34°， ∵∠1=∠BEF=68°，∴CD ∥AB ，∴∠EGF=∠GEB=34°，故选：A ．【点睛】 本题考查了平行线的判定和性质,角平分线的定义，灵活运用这些性质进行推理是本题的关键．8．B解析：B【分析】根据平行线的判定定理对各小题进行逐一判断即可．【详解】解：①∵∠1=∠3，∴l1∥l2，故本小题正确；②∵∠2+∠4=180°，∴l1∥l2，故本小题正确；③∵∠4=∠5，∴l1∥l2，故本小题正确；④∠2=∠3不能判定l1∥l2，故本小题错误；⑤∵∠6=∠2+∠3，∴l1∥l2，故本小题正确．故选B．【点睛】本题考查的是平行线的判定，熟记平行线的判定定理是解答此题的关键．9．C解析：C【分析】根据平行线的性质即可得到结论．【详解】∵AB∥CD，∴∠1=∠4，故选 C．【点睛】本题考查了平行线的性质，熟练掌握平行线的性质是解题的关键．10．C解析：C【解析】试题分析：根据平行线的判定进行判断即可．解：A、若a∥b，b∥c，则a∥c，利用了平行公理，正确；B、若∠1=∠2，则a∥c，利用了内错角相等，两直线平行，正确；C、∠3=∠2，不能判断b∥c，错误；D、若∠3+∠5=180°，则a∥c，利用同旁内角互补，两直线平行，正确；故选C．考点：平行线的判定．11．D解析：D【分析】利用三角形内角和对A进行判断；根据内错角的定义对B进行判断；根据平行线的判定方法对C进行判断；根据绝对值的意义对D进行判断．【详解】解：A、如果三角形三个内角的度数比是1：2：3，则三个角的度数分别为30°，60°，90°，所以这个三角形是直角三角形，所以A选项为真命题；B、内错角不一定相等，所以B选项为真命题；C、平行于同一直线的两条直线平行，所以C选项为真命题；D 、若数a 使得|a|＞-a ，则a 为不等于0的实数，所以D 选项为假命题．故选：D ．【点睛】本题考查了命题与定理：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．12．D解析：D【分析】根据平移作图是一个基本图案按照一定的方向平移一定的距离，连续作图设计出的图案进行分析即可．【详解】解：A 、不能用平移变换来分析其形成过程，故此选项错误；B 、不能用平移变换来分析其形成过程，故此选项错误；C 、不能用平移变换来分析其形成过程，故此选项正确；D 、能用平移变换来分析其形成过程，故此选项错误；故选：D ．【点睛】本题考查利用平移设计图案，解题关键是掌握图形的平移只改变图形的位置，而不改变图形的形状、大小和方向．二、填空题13．或【分析】分两种情况：①如图1作EF ∥BD 由BD ∥AC 推出EF ∥AC 得到∠B=∠BEF ∠A=∠AEF 根据∠A+∠B=求出∠A=；②如图2作EF ∥BD 由BD ∥AC 推出EF ∥AC 得到∠B+∠BEF=∠A解析：39︒或99︒．【分析】分两种情况：①如图1，作EF ∥BD ，由BD ∥AC 推出EF ∥AC ，得到∠B=∠BEF ，∠A=∠AEF ，根据∠A+∠B=90︒，227A B ∠-∠=︒，求出∠A=39︒；②如图2，作EF ∥BD ，由BD ∥AC 推出EF ∥AC ，得到∠B+∠BEF=180︒，∠A+∠AEF=180︒，根据∵∠AEB=∠AEF+∠BEF=90︒，227A B ∠-∠=︒，计算得出答案．【详解】分两种情况：①如图1，作EF ∥BD ，∴∠B=∠BEF ，∵EF ∥BD ，BD ∥AC ，∴EF ∥AC ，∴∠A=∠AEF ，∴∠A+∠B=∠AEF+∠BEF=90︒，∵227A B ∠-∠=︒，∴∠A=39︒；②如图2，作EF ∥BD ，∴∠B+∠BEF=180︒，∵EF ∥BD ，BD ∥AC ，∴EF ∥AC ，∴∠A+∠AEF=180︒，∴∠A+∠AEB+∠B=360︒，∵∠AEB=∠AEF+∠BEF=90︒，∴∠A+∠B=270︒，∵227A B ∠-∠=︒，∴∠A=99︒；故答案为：39︒或99︒．．【点睛】此题考查平行线的性质，平行公理的推论，根据题意作出图形，引出恰当的辅助线解决问题是解题的关键．14．72【分析】如果两个角的两边互相平行则这两个角相等或互补根据题意这两个角只能互补然后列方程求解即可【详解】解：设其中一个角是x°则另一个角是(180-x)°根据题意得解得x=72∴180-x=108解析：72【分析】如果两个角的两边互相平行，则这两个角相等或互补．根据题意，这两个角只能互补，然后列方程求解即可．【详解】解：设其中一个角是x°，则另一个角是(180-x)°，根据题意，得11(180)23x x =-， 解得x=72，∴180-x=108°；∴较小角的度数为72°．故答案为：72．【点睛】本题考查了平行线的性质，一元一次方程的应用，运用“若两个角的两边互相平行，则两个角相等或互补”，而此题中显然没有两个角相等这一情况是解决此题的突破点． 15．42【分析】利用平移表示出草坪的长和宽然后根据长方形的面积公式列式计算即可得解【详解】解：由平移的性质得:草坪的长为8﹣1＝7（米）宽为6米草坪的面积＝7×6＝42（平方米）故答案为：42【点睛】本解析：42【分析】利用平移表示出草坪的长和宽，然后根据长方形的面积公式列式计算即可得解．【详解】解：由平移的性质，得:草坪的长为8﹣1＝7（米），宽为6米，草坪的面积＝7×6＝42（平方米）．故答案为：42．【点睛】本题考查了平移的性质，熟记性质并理解求出与草坪的面积相当的长方形的长和宽是解题的关键．16．15【分析】由长方形的性质和平移的性质即可求出答案【详解】解：根据题意虚线部分的总长为：故答案为：15【点睛】本题考查了长方形的性质平移变换等知识解题的关键是理解题意灵活运用所学知识解决问题属于中考 解析：15【分析】由长方形的性质和平移的性质，即可求出答案．【详解】解：根据题意， 虚线部分的总长为：130152AB BC +=⨯=． 故答案为：15．【点睛】本题考查了长方形的性质，平移变换等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型． 17．（1）3555；（2）与【分析】（1）由可得所以所以已知的度数即可得出与的度数；（2）由（1）可得的余角是与要求的补角即要求的补角的补角是【详解】（1）；（2）由（1）可得的余角是与的补角是的补角是解析：（1）35，55；（2）COE ∠与2∠，COB ∠【分析】（1）由OC OD ⊥，OE AB ⊥可得=90COD ∠︒，=90AOE ∠︒，所以1290∠+∠=︒，190COE ∠+∠=︒，90EOD COE ∠+∠=︒，所以1=EOD ∠∠，已知1∠的度数，即可得出2∠与EOD ∠的度数；（2）由（1）可得1∠的余角是COE ∠与2∠，要求EOD ∠的补角，即要求1∠的补角，1∠的补角是COB ∠．【详解】（1）OC OD ⊥，OE AB ⊥，∴=90COD ∠︒，=90AOE ∠︒，∴1290∠+∠=︒，190COE ∠+∠=︒，90EOD COE ∠+∠=︒，∴1=EOD ∠∠，135∠=︒，∴255∠=︒，35=EOD ∠︒；（2）由（1）可得1∠的余角是COE ∠与2∠，1180COB =∠∠+︒，∴1∠的补角是COB ∠，∴EOD ∠的补角是COB ∠．故答案为：（1）35，55；（2）COE ∠与2∠，COB ∠．【点睛】本题主要考查余角、补角以及垂直的定义，熟记补角、余角以及垂直的定义是解题关键． 18．假若a ＞b 则a2＞b2【分析】a2大于b2则a 不一定大于b 所以该命题是假命题它的逆命题是若a ＞b 则a2＞b2【详解】①当a ＝－2b ＝1时满足a2＞b2但不满足a ＞b 所以是假命题；②命题若a2＞b2则解析：假 若a ＞b 则a 2＞b 2【分析】a 2大于b 2则a 不一定大于b ，所以该命题是假命题，它的逆命题是“若a ＞b 则a 2＞b 2”．【详解】①当a ＝－2，b ＝1时，满足a 2＞b 2，但不满足a ＞b ，所以是假命题；②命题“若a 2＞b 2则a ＞b ”的逆命题是若“a ＞b 则a 2＞b 2”；故答案为：假；若a ＞b 则a 2＞b 2．【点睛】本题主要考查判断命题真假、逆命题的概念以及平方的计算，熟记相关概念取特殊值代入是解题关键．19．50【分析】根据平行线的性质解答即可【详解】解：∵AB ∥CD ∴=∠1∵∠1+=180°∠=130°∴∠1=180°-=180°-130°=50°∴=50°故答案为：50【点睛】本题考查了平行线的性质解析：50【分析】根据平行线的性质解答即可．【详解】解：∵AB∥CD，∠ =∠1，∴α∵∠1+β∠=180°，∠β=130°，∴∠1=180°-β∠=180°-130°=50°，∴α∠=50°，故答案为：50．【点睛】本题考查了平行线的性质和平角的定义，解题的关键掌握平行线的性质和平角的定义．20．12【解析】分析：由图形可知内部小三角形直角边是大三角形直角边平移得到的故内部五个小直角三角形的周长为大直角三角形的周长详解：由图形可以看出：内部小三角形直角边是大三角形直角边平移得到的故内部五个小解析：12【解析】分析：由图形可知，内部小三角形直角边是大三角形直角边平移得到的，故内部五个小直角三角形的周长为大直角三角形的周长．详解：由图形可以看出：内部小三角形直角边是大三角形直角边平移得到的，故内部五个小直角三角形的周长为AC+BC+AB=12．故答案为12．点睛：本题主要考查了平移的性质，需要注意的是：平移前后图形的大小、形状都不改变．三、解答题21．（1）见详解；（2）105°．【分析】（1）过点A、B作正北方向，再据方位角的含义画射线BX和AY，两射线之交点即是C 地；（2）记过点A的正北方向线与射线BX之交点为D，先求得∠CDA的度数，最后由三角形内角和为180°计算得∠ACB的度数．【详解】（1）如下图，第一步过B作m的平行线BS，以B为顶点作射线BX，使∠SBX=45°；第二步过A作m的平行线AN交BX于点D，以A为顶点作射线AY，使∠NAY=30°；则射线BX与射线AY的交点就是C地．（2）如上图，由C地在B地南偏东45°方向得∠SBX=45°∵SB∥m，AN∥m∴SB∥AN∴∠ADC=∠SBX=45°由C地在A地的北偏东30°方向得∠NAY=30°，∴∠ACB=180°-∠ADC-∠NAY=180°-45°-30°=105°．【点睛】此题考查方位角、平行线等知识，其中理解方位角正确画出图形是关键．<< 22．（1）见解析；（2）见解析；（3）见解析；（4）AF AB AG 【分析】（1）将AB沿着BC方向平移，使其过点C，此时经过的格点即为所求；（2）延长CB，作AE与CB交于F点，此时E点即为所求；（3）过B点作AB的垂线，经过的格点即为所求；（4）在两个直角三角形中比较即可得出结论．【详解】（1）如图所示，符合题意的格点有D1，D2两个，画出其中一个即可；（2）如图所示：E点即为所求，垂足为F点；（3）如图所示，点G即为所求；（4）如图所示，显然，在Rt ABF 中，AB AF >；在Rt ABG 中，AG AB >， 故答案为：AF AB AG <<．【点睛】本题考查应用与设计作图，平行线的判定与性质以及垂线的定义，熟练掌握基本性质定理是解题关键．23．（1）∠2=145°；（2）BC ∥AD ，理由见解析．【分析】（1）由平行线的性质求得∠BDC=∠1=35°，再根据邻补角的定义即可求得∠2； （2）由平行线的性质可知：∠A+∠ADC=180°，然后根据∠A=∠C ，可证得∠C+∠ADC=180°，从而可证得BC ∥AD ．【详解】解：（1）∵AE ∥CF ，∴∠BDC=∠1=35°，又∵∠2+∠BDC=180°，∴∠2=180°-∠BDC=180°-35°=145°；（2）BC ∥AD ．理由：∵AE ∥CF ，∴∠A+∠ADC=180°，又∵∠A=∠C ，∴∠C+∠ADC=180°，∴BC ∥AD ．【点睛】本题考查平行线的性质和判定．在本题中能正确识图找出同位角和同旁内角是解题关键． 24．（1）∠CBF ＝45°；（2）见解析．【分析】（1）根据平行线的性质和已知条件即可求出∠CBF 的度数；（2）根据平行线的性质可得∠ABC ＝∠ADF ，再根据BF 平分∠ABC ，DE 平分∠ADF ，可得∠ADE ＝∠ABF ，再根据同位角相等，两直线平行即可证明BF ∥DE ．【详解】解：（1）∵DF ∥BC ，∴∠ABC ＝∠ADF ＝70°，∵∠ABF ＝25°，∴∠CBF ＝70°﹣25°＝45°；（2）证明：∵DF ∥BC ，∴∠ABC ＝∠ADF ，∵BF 平分∠ABC ，DE 平分∠ADF ，∴∠ADE 12=∠ADF ，∠ABF 12=∠ABC ， ∴∠ADE ＝∠ABF ，∴BF ∥DE ．【点睛】 本题考查了平行线的判定与性质，解决本题的关键是掌握平行线的判定与性质． 25．（1）CD 与EF 平行．理由见解析；（2）∠B=35°【分析】（1）先根据垂直的定义得到∠CDB=∠EFB=90°，然后根据同位角相等，两直线平行可判断EF ∥CD ；（2）由EF ∥CD ，根据平行线的性质得∠2=∠BCD ，而∠1=∠2，所以∠1=∠BCD ，根据内错角相等，两直线平行得到DG ∥BC ，所以∠ACB=∠3=115°，根据三角形的内角和即可得到结论．【详解】（1）CD 与EF 平行．理由如下：∵CD ⊥AB ，EF ⊥AB ，∴∠CDB=∠EFB=90°，∴EF ∥CD ；（2）∵EF ∥CD ，∴∠2=∠BCD ，∵∠1=∠2，∴∠1=∠BCD ，∴DG ∥BC ，∴∠ACB=∠3=115°，∵∠A=30°，∴∠B=35°．【点评】本题考查了平行线的判定与性质，注意：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等．26．证明见解析【分析】根据平行线的判定与性质即可得证．【详解】∠=∠，解：∵12BD CE，∴//∠=∠，∴C ABD∠=∠，∵C D∠=∠，∴D ABDAC DF，∴//∠=∠．∴A F【点睛】本题考查平行线的判定与性质，熟练运用平行线的判定与性质定理是解题的关键．。