高一数学人教a版必修二 习题 第二章 点、直线、平面之间的位置关系 2.2.4 含答案

2.2.4 平面与平面平行的性质选题明细表基础巩固1.已知平面α∥平面β,过平面α内的一条直线a的平面γ,与平面β相交,交线为直线b,则a,b的位置关系是( A )(A)平行 (B)相交(C)异面 (D)不确定解析:由面面平行的性质定理可知选项A正确.故选A.2.若不在同一直线上的三点A,B,C到平面α的距离相等,则( B )(A)平面α∥平面ABC(B)△ABC中至少有一边平行于平面α(C)△ABC中至多有两边平行于α(D)△ABC中只可能有一边与平面α相交解析:若三点在平面α的同侧,则平面α∥平面ABC,有三边平行于α.若一点在平面α的一侧,另两点在平面α的另一侧,则有两边与平面α相交,有一边平行于α,故△ABC中至少有一边平行于平面α.故选B.3.设平面α∥平面β,A∈α,B∈β,C是AB的中点,当点A,B分别在平面α,β内运动时,动点C( D )(A)不共面(B)当且仅当点A,B分别在两条直线上移动时才共面(C)当且仅当点A,B分别在两条给定的异面直线上移动时才共面(D)无论点A,B如何移动都共面解析:无论点A,B如何移动,点C到α,β的距离都相等,故点C在到α,β距离相等且与两平面都平行的平面上.故选D.4.过正方体ABCDA1B1C1D1的顶点A1,C1,B的平面与底面ABCD所在的平面的交线为l,则l与A1C1的位置关系是.解析:由于平面ABCD∥平面A1B1C1D1,平面A1B1C1D1∩平面A1C1B=A1C1,平面ABCD∩平面A1C1B=l,所以l∥A1C1.答案:平行5.正方体ABCDA1B1C1D1的棱长为3,点E在A1B1上,且B1E=1,平面α∥平面BC1E,若平面α∩平面AA1B1B=A1F,则AF的长为.解析:因为平面α∥平面BC1E,所以A1FBE,所以Rt△A1AF≌Rt△BB1E,所以FA=B1E=1.答案:16.如图,S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,且=,求证:MN∥平面SBC.证明:在AB上取一点P,使=,连接MP,NP,则MP∥SB.因为SB⊂平面SBC,MP⊄平面SBC,所以MP∥平面SBC.又=,所以=,所以NP∥AD.因为AD∥BC,所以NP∥BC.又BC⊂平面SBC,NP⊄平面SBC,所以NP∥平面SBC.又MP∩NP=P,所以平面MNP∥平面SBC,而MN⊂平面MNP,所以MN∥平面SBC.能力提升7.已知a,b表示直线,α,β,γ表示平面,下列推理正确的是( D )(A)α∩β=a,b⊂α⇒a∥b(B)α∩β=a,a∥b⇒b∥α,且b∥β(C)a∥β,b∥β,a⊂α,b⊂α⇒α∥β(D)α∥β,α∩γ=a,β∩γ=b⇒a∥b解析:A项中,α∩β=a,b⊂α,则a,b可能平行也可能相交;B项中,α∩β=a,a∥b,则可能b ∥α,且b∥β,也可能b在平面α或β内;C项中,a∥β,b∥β,a⊂α,b⊂α,根据面面平行的判定定理,若再加上条件a∩b=A,才能得出α∥β;D项为面面平行的性质定理的符号语言,正确.8.如图,在多面体ABC-DEFG中,平面ABC∥平面DEFG,EF∥DG,且AB= DE,DG=2EF,则( A )(A)BF∥平面ACGD(B)CF∥平面ABED(C)BC∥FG(D)平面ABED∥平面CGF解析:取DG的中点为M,连接AM,FM,如图所示.则由已知条件易证四边形DEFM是平行四边形.所以DEFM.因为平面ABC∥平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,所以AB∥DE,所以AB∥FM.又AB=DE,所以AB=FM,所以四边形ABFM是平行四边形,即BF∥AM.又BF⊄平面ACGD,所以BF∥平面ACGD.故选A.9.如图所示,平面α∥平面β,△ABC,△A′B′C′分别在α,β内,线段AA′,BB′,CC′共点于O,O在α,β之间,若AB=2,AC=1,∠BAC = 90°, OA∶OA′=3∶2,则△A′B′C′的面积为.解析:由题意可知,AB∥A′B′,AC∥A′C′,BC∥B′C′,所以△ABC∽△A′B′C′,且==.=()2,因为S△ABC=AB·AC=1,所以S△A′B′C′=.答案:10.如图所示,过正方体ABCD-A1B1C1D1的对角线BD1作一截面分别交棱AA1,CC1于点M,Q,O为底面A B C D的中心,P是D D1的中点,若截面BQD1M∥平面PAO,求的值.解:因为平面AA1D1D∥平面BB1C1C,平面BQD1M∩平面ADD1A1=D1M,平面BQD1M∩平面BCC1B1=BQ,所以D1M∥BQ.因为平面BQD1M∥平面PAO,PA⊂平面PAO,所以PA∥平面BQD1M,又因为AP⊂平面ADD1A1,平面ADD1A1∩平面BQD1M=D1M,所以AP∥D1M,又因为D1M∥BQ,所以AP∥BQ.又因为点P为DD1中点,所以点Q为CC1的中点,所以=1.探究创新11.如图所示:ABC-A1B1C1中,平面ABC∥平面A1B1C1,若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1?证明你的结论.解:当点E为棱AB的中点时,DE∥平面AB1C1.证明如下:如图,取BB1的中点F,AB的中点E.连接EF,FD,DE,因为D,E,F分别为CC1,AB,BB1的中点,所以EF∥AB1,因为AB1⊂平面AB1C1,EF⊄平面AB1C1,所以EF∥平面AB1C1.同理可证FD∥平面AB1C1.因为EF∩FD=F,所以平面EFD∥平面AB1C1.因为DE⊂平面EFD.所以DE∥平面AB1C1.。

千思兔在线教育平面与平面平行的判断【课时目标】 1．理解平面与平面平行的判断定理的含义． 2．能运用平面与平面平行的判断定理，证明一些空间面面平行的简单问题．1．平面α与平面β平行是指两平面________公共点．若α∥ β，直线a?α，则a与β的地点关系为 ________．2．下边的命题在“ ________处”缺乏一个条件，补上这个条件，使其组成真命题(M ， n 为直线，α，β为平面 )，则此条件应为________．m? αn? αm∥ β? α∥ βn∥ β一、选择题1．经过平面α外的两个点作该平面的平行平面，能够作出( )A．0 个B．1 个C．0个或 1个D．1个或 2个2．α和β是两个不重合的平面，在以下条件中，可判断α∥ β的是 ( )A ．α内有无数条直线平行于βB．α内不共线三点到β的距离相等C．l 、M 是平面α内的直线，且 l ∥ α， M∥ βD． l 、M 是异面直线且 l ∥ α， M∥ α， l∥ β， M∥ β3．给出以下结论，正确的有( )①平行于同一条直线的两个平面平行；②平行于同一平面的两个平面平行；③过平面外两点，不可以作一个平面与已知平面平行；④若 a， b 为异面直线，则过 a 与 b 平行的平面只有一个．A．1 个B．2 个C．3 个D．4个4．若不在同向来线上的三点A、 B、 C 到平面α的距离相等，且AD/∈ α，则 ( )A ．α∥平面 ABCB．△ ABC 中起码有一边平行于αC．△ ABC 中至多有两边平行于αD．△ ABC 中只可能有一边与α订交5．正方体 EFGH — E1F1G1H1中，以下四对截面中，相互平行的一对截面是( ) A ．平面 E1FG 1与平面 EGH1B．平面 FHG 1与平面 F1H 1GC．平面 F1H1H 与平面 FHE 1D．平面 E1HG 1与平面 EH 1G6．两个平面平行的条件是()A．一个平面内一条直线平行于另一个平面B．一个平面内两条直线平行于另一个平面C．一个平面内的随意一条直线平行于另一个平面D．两个平面都平行于同一条直线二、填空题7．已知直线a、 b，平面α、β，且 a∥ b， a∥ α，α∥β，则直线 b 与平面β的地点关系为______ ．8．有以下几个命题：①平面α内有无数个点到平面β的距离相等，则α∥β；② α∩ γ＝ a，α∩ β＝ b，且 a∥ b(α，β，γ分别表示平面，a， b 表示直线 )，则γ∥ β；③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边，则α∥ β；④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行，则α∥ β．此中正确的有 ________． (填序号 )9．如下图，在正方体 ABCD — A1B1C1D 1中， E、F 、G、H 分别是棱 CC1、C1D 1、D1D 、CD 的中点， N 是 BC 的中点，点 M 在四边形 EFGH 及其内部运动，则 M 知足 ________时，有 MN ∥平面 B1BDD 1．三、解答题10．如下图，在正方体ABCD － A1B1C1D1中，S 是 B1D 1的中点，E、 F、G 分别是 BC、 DC 和 SC 的中点．求证：平面 EFG∥平面BDD 1B1．11．如下图， B 为△ ACD 所在平面外一点， M，N，G 分别为△ ABC，△ ABD，△ BCD 的重心．(1)求证：平面MNG ∥平面 ACD ；(2)求 S△MNG∶S△ADC．能力提高12．三棱柱ABC－A1B1C1， D 是 BC 上一点，且A1B∥平面 AC1D ，D 1是 B1C1的中点．求证：平面A1BD1∥平面 AC1D ．13．如下图，在正方体 ABCD —A1B1C1D1中， O 为底面ABCD 的中心， P 是 DD 1的中点，设 Q 是 CC1上的点，问：当点 Q 在什么地点时，平面 D 1BQ∥平面 PAO?判断或证明面面平行的方法(1)面面平行的定义；(2)面面平行的判断定理：假如一个平面内有两条订交直线平行于另一个平面，那么这两个平面平行；(3)两个平面同时平行于第三个平面，那么这两个平面平行．2．2．2 平面与平面平行的判断答案知识梳理1．无a∥ β2． M， n 订交作业设计1．C 2．D 3．B 4． B 5． A 6． C 7． b∥β或b? β8．③分析① 不正确，当两平面订交时，在一个平面双侧分别有无数点知足条件；②不正确，当平面β与γ订交时也可知足条件；③ 正确，知足平面平行的判断定理；④ 不正确，当两平面订交时，也可知足条件．9． M ∈线段 FH分析∵ HN ∥ BD ，HF∥ DD 1，HN∩HF＝H，BD ∩DD1＝D，∴平面 NHF ∥平面 B 1BDD 1，故线段 FH 上随意点M 与 N 连结，有 MN ∥平面 B1BDD1．10．证明如下图，连结 SB， SD，∵ F、 G 分别是 DC 、 SC 的中点，∴ FG∥ SD．又∵ SD? 平面 BDD 1 B1， FG?平面 BDD 1B1，∴直线 FG∥平面 BDD 1B 1．同理可证 EG∥平面 BDD 1B1，又∵ EG? 平面 EFG，FG? 平面 EFG，EG∩ FG＝ G，∴平面 EFG∥平面 BDD 1B1．11． (1)证明 (1)连结 BM ， BN ，BG 并延伸分别交AC ，AD ，CD 于 P，F， H．∵M，N，G 分别为△ ABC ，△ABD ，△BCD 的重心，则有BMMP＝BNNF＝BGGH＝ 2，且 P，H ，F 分别为 AC ， CD ， AD 的中点．连结 PF， FH， PH，有 MN ∥PF．又 PF? 平面 ACD ， MN ?平面 ACD ，∴MN ∥平面 ACD ．同理 MG ∥平面 ACD ，MG ∩MN ＝M ，∴平面 MNG ∥平面 ACD ．千思兔在线教育MG ＝ BG ＝2，(2)解 由(1)可知 PH BH 32∴MG ＝ PH ．31 1AD ． 又 PH ＝ AD ，∴MG ＝32同理 NG ＝ 1AC ，MN ＝ 1CD ．3 3 ∴△ MNG ∽△ ACD ，其相像比为 1∶3． ∴ S △ MNG ∶ S △ACD ＝ 1∶ 9． 12．证明连结 A 1C 交 AC 1于点 E ，∵ 四边形 A 1ACC 1 是平行四边形， ∴ E 是 A 1C 的中点，连结 ED ，∵ A 1B ∥平面 AC 1D ，ED? 平面 AC 1D ， ∴ A 1B 与 ED 没有交点，又 ∵ ED? 平面 A 1BC ，A 1B? 平面 A 1BC ， ∴ ED ∥ A 1B ．∵ E 是 A 1C 的中点， ∴D 是 BC 的中点．又 ∵ D 1 是 B 1C 1 的中点，∴ BD 1∥C 1D ，A 1D 1∥ AD ，∴ BD 1∥ 平面 AC 1D ，A 1D 1∥ 平面 AC 1D ．又 A 1D 1∩ BD 1＝D 1，∴平面 A 1BD 1∥平面 AC 1D ．13． 解 当 Q 为 CC 1 的中点时， 平面 D 1BQ ∥ 平面 PAO ．∵Q 为 CC 1的中点， P 为 DD 1 的中点， ∴ QB ∥PA ．∵ P 、O 为 DD 1、 DB 的中点， ∴ D 1B ∥ PO ．又 PO ∩ PA ＝ P ， D 1B ∩ QB ＝ B ， D 1B ∥ 平面 PAO ，QB ∥ 平面 PAO ，∴ 平面 D 1BQ ∥ 平面 PAO ．。

数学人教A版必修2第二章点、直线、平面之间的位置关系单元检测(时间：90分钟，满分：100分)一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若直线a和b没有公共点，则a与b的位置关系是()A．相交B．平行C．异面D．平行或异面2．下列推理错误的是()A．A∈l，A∈α，B∈l，B∈αlαB．A∈α，A∈β，B∈α，B∈βα∩β＝ABC．l⊄α，A∈l A∉αD．A∈l，lαA∈α3．长方体ABCD-A1B1C1D1中，异面直线AB，A1D1所成的角等于()A．30°B．45°C．60°D．90°4．对两条不相交的空间直线a与b，必存在平面α，使得()A．aα，bαB．aα，b∥αC．a⊥α，b⊥αD．aα，b⊥α5．下面四个命题：①若直线a，b异面，b，c异面，则a，c异面；②若直线a，b相交，b，c相交，则a，c相交；③若a∥b，则a，b与c所成的角相等；④若a⊥b，b⊥c，则a∥c.其中真命题的个数为()A．4 B．3 C．2 D．16．在正方体ABCD-A1B1C1D1中，E，F分别是线段A1B1，B1C1上的不与端点重合的动点，如果A1E＝B1F，有下面四个结论：①EF⊥AA1; ②EF∥AC；③EF与AC异面；④EF∥平面ABCD．其中一定正确的是()A．①②B．②③C．②④D．①④7．设a，b为两条不重合的直线，α，β为两个不重合的平面，下列命题中为真命题的是()A．若a，b与α所成的角相等，则a∥b B．若a∥α，b∥β，α∥β，则a∥bC．若aα，bβ，a∥b，则α∥βD．若a⊥α，b⊥β，α⊥β，则a⊥b8．已知平面α⊥平面β，α∩β＝l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是()A．AB∥m B．AC⊥m C．AB∥βD．AC⊥β9．若m，n为两条不重合的直线，α，β为两个不重合的平面，则下列命题中的真命题的个数是()①若m，n都平行于平面α，则m，n一定不是相交直线；②若m，n都垂直于平面α，则m，n一定是平行直线；③已知α，β互相垂直，m，n互相垂直，若m⊥α，则n⊥β；④m，n在平面α内的射影互相垂直，则m，n互相垂直．A．1 B．2 C．3 D．410．设平面α∥平面β，A∈α，B∈β，C是AB的中点，当A，B分别在α，β内运动时，那么所有的动点C()A．不共面B．当且仅当A，B在两条相交直线上移动时才共面C．当且仅当A，B在两条给定的平行直线上移动时才共面D．不论A，B如何移动都共面二、填空题(本大题共5小题，每小题5分，共25分．把答案填在题中的横线上)11．下列图形可用符号表示为__________．12．正方体ABCD-A1B1C1D1中，二面角C1-AB-C的平面角等于________．13．设平面α∥平面β，A，C∈α，B，D∈β，直线AB与CD交于点S，且点S位于平面α，β之间，AS＝8，BS＝6，CS＝12，则SD＝__________.14．如图，正方体ABCD-A1B1C1D1中，若过A，C，B1三点的平面与底面A1B1C1D1的交线为l，则l与AC的关系是________．15．如图，P A⊥平面ABC，∠ACB＝90°，EF∥P A，则图中直角三角形的个数是________．三、解答题(本大题共2小题，共25分．解答时应写出文字说明、证明过程或演算步骤)16．(10分)如图，在底面为正三角形且侧棱垂直于底面的三棱柱ABC-A1B1C1中，F，F1分别是AC，A1C1的中点．求证：(1)平面AB1F1∥平面C1BF；(2)平面AB1F1⊥平面ACC1A1.17．(15分)如图，△ABC中，AC＝BC＝AB，ABED是边长为1的正方形，平面ABED2⊥底面ABC，若G，F分别是EC，BD的中点．(1)求证：GF∥平面ABC；(2)求证：AC⊥平面EBC；(3)求几何体ADEBC的体积V.参考答案1.答案：D2.答案：C3.答案：D4.答案：B5.答案：D6.答案：D7.答案：D8.答案：D9.答案：A10. 答案：D11. 答案：α∩β＝AB12. 答案：45°13. 答案：914．答案：平行15. 答案：616.证明：(1)在底面为正三角形且侧棱垂直于底面的三棱柱ABC-A1B1C1中，∵F，F1分别是AC，A1C1的中点，∴B1F1∥BF，AF1∥C1F.又∵B1F1∩AF1＝F1，C1F∩BF＝F，∴平面AB1F1∥平面C1BF.(2)在底面为正三角形且侧棱垂直于底面的三棱柱ABC-A1B1C1中，AA1⊥平面A1B1C1，∴B1F1⊥AA1.又∵B1F1⊥A1C1，A1C1∩AA1＝A1，∴B1F1⊥平面ACC1A1，而B1F1平面AB1F1，∴平面AB1F1⊥平面ACC1A1.17. 解：(1)证明：连接AE，如图所示，∵ADEB为正方形，∴AE∩BD＝F，且F是AE的中点．又G是EC的中点，∴GF∥AC，又AC平面ABC，GF平面ABC，∴GF∥平面ABC．(2)证明：∵ADEB为正方形，∴EB⊥AB，又∵平面ABED ⊥平面ABC ，平面ABED ∩平面ABC ＝AB ，EB 平面ABED ， ∴BE ⊥平面ABC ，∴BE ⊥AC ．又∵AC ＝BC AB ，∴CA 2＋CB 2＝AB 2， ∴AC ⊥BC ．又∵BC ∩BE ＝B ，∴AC ⊥平面BCE .(3)取AB 的中点N ，如图所示，∵AC ＝BC ，∴CN ⊥AB ．又平面ABED ⊥平面ABC ， CN 平面ABC ，平面ABED ∩平面ABC ＝AB ，∴CN ⊥平面ABED ．∵△ABC 是等腰直角三角形，∴CN ＝12AB ＝12， ∴V C -ABED ＝13S ABED ·CN ＝13×1×12＝16.。

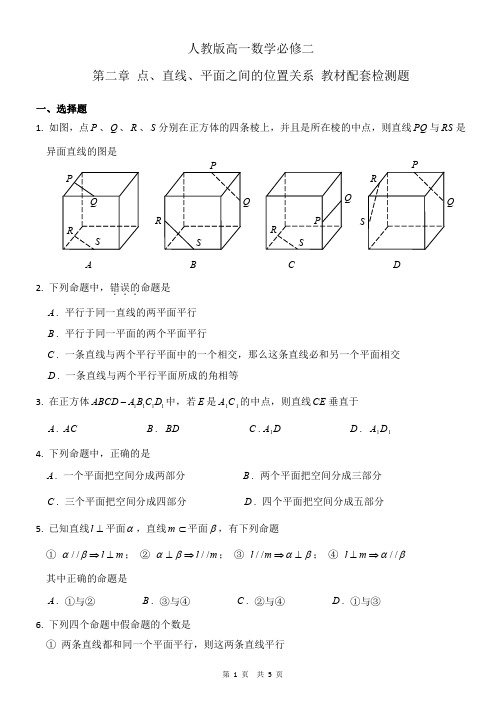
人教版高一数学必修二第二章点、直线、平面之间的位置关系教材配套检测题一、选择题1.如图，点P 、Q 、R 、S 分别在正方体的四条棱上，并且是所在棱的中点，则直线PQ 与RS 是异面直线的图是2.下列命题中，错误的．．．命题是.A 平行于同一直线的两平面平行.B 平行于同一平面的两个平面平行.C 一条直线与两个平行平面中的一个相交，那么这条直线必和另一个平面相交.D 一条直线与两个平行平面所成的角相等3.在正方体1111ABCD A B C D -中，若E 是11A C 的中点，则直线CE 垂直于.A AC.B BD.C 1A D.D 11A D 4.下列命题中，正确的是.A 一个平面把空间分成两部分.B 两个平面把空间分成三部分.C 三个平面把空间分成四部分.D 四个平面把空间分成五部分5.已知直线l ⊥平面α，直线m ⊂平面β，有下列命题①//l m αβ⇒⊥；②//l m αβ⊥⇒；③//l m αβ⇒⊥；④//l m αβ⊥⇒其中正确的命题是.A ①与②.B ③与④.C ②与④.D ①与③6.下列四个命题中假命题的个数是①两条直线都和同一个平面平行，则这两条直线平行PABCDQ PQP QPQRRRRSS SS②两条直线没有公共点，则这两条直线平行③两条直线都和第三条直线垂直，则这两条直线平行④一条直线和一个平面内的无数条直线没有公共点，则这条直线和这个平面平行.A 4.B 3.C 2.D 17.平面α与β平行，且a α⊂，下列四个命题中①a 与β内的所有直线平行②a 与β内的无数条直线平行③a 与β内的任何一条直线都不垂直④a 与β无公共点其中真命题的个数是.A 1.B 2.C 3.D 48.若a 、b 是异面直线，b 、c 是异面直线，则a 、c 的位置关系是.A 相交、平行或异面.B 相交或平行.C 异面.D 平行或异面二、填空题9.如图所示，在正方体1111ABCD A B C D -中，与对角线1DB 成异面直线的棱共条.10.若点M 在直线a 上，a 在平面α上，则M 、a 、α间的关系可用集合语言表示为：。

第 1 页 共 10 页 高中数学人教新课标A版必修2 第二章 点、直线、平面之间的位置关系 2.2.4平面与平面平行的性质A卷

姓名:________ 班级:________ 成绩:________ 一、 选择题 (共8题；共16分) 1. （2分） 已知直线a和两个平面 ， 给出下列两个命题： 命题p：若a∥,a⊥ ， 则⊥； 命题q：若a∥,a∥,则∥。 那么下列判断正确的是（ ） A . p为假 B . 为假 C . p∧q为真 D . p∨q为真 2. （2分） (2018·凯里模拟) 若 ， 表示空间中两条不重合的直线， ， 表示空间中两个不重合的平面，则下列命题中正确的是（ ）

A . 若 ， ，则 B . 若 ， ， ，则 C . 若 ， ， ，则 D . 若 ， ， ，则 3. （2分） 四棱锥中,底面是平行四边形,,,若平面,则的值为 （ ） 第 2 页 共 10 页

A . 1 B . 3 C . 2 D . 4 4. （2分） 已知平面α∥平面β，m⊂α，n⊂β，且直线m与n不平行．记平面α、β的距离为d1 ， 直线m、n的距离为d2 ， 则（ ）

A . d1＜d2 B . d1=d2 C . d1＞d2 D . d1与d2大小不确定 5. （2分） (2019高一上·蒙山月考) 如图，平面 平面 ，过平面 ， 外一点 引直线 分别交平面 ，平面 于 、 两点， ， ，引直线 分别交平面 ，平面 于 、 两点，已知 ，则 的长等于（ ）

A . 9 B . 10 第 3 页 共 10 页

C . 8 D . 7 6. （2分） 设为两两不重合的平面，为两两不重合的直线，给出下列四个命题： ①若 ， ， 则； ②若 ， ， ， ， 则； ③若 ， ， 则； ④若 ， ， ， ， 则 其中真命题的个数是 （ ） A . 1 B . 2 C . 3 D . 4 7. （2分） 下列四个正方体图形中，为正方体的两个顶点，分别为其所在棱的中点，能得出平面的图形的序号是（ ）

数学人教A版必修2第二章点、直线、平面之间的位置关系单元检测(时间：90分钟，满分：100分)一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若直线a和b没有公共点，则a与b的位置关系是()A．相交B．平行C．异面D．平行或异面2．下列推理错误的是()A．A∈l，A∈α，B∈l，B∈αlαB．A∈α，A∈β，B∈α，B∈βα∩β＝AB C．l⊄α，A∈l A∉αD．A∈l，lαA∈α3．长方体ABCD-A1B1C1D1中，异面直线AB，A1D1所成的角等于()A．30°B．45°C．60°D．90°4．对两条不相交的空间直线a与b，必存在平面α，使得()A．aα，bαB．aα，b∥αC．a⊥α，b⊥αD．aα，b⊥α5．下面四个命题：①若直线a，b异面，b，c异面，则a，c异面；②若直线a，b相交，b，c相交，则a，c相交；③若a∥b，则a，b与c所成的角相等；④若a⊥b，b⊥c，则a∥c.其中真命题的个数为()A．4 B．3 C．2 D．16．在正方体ABCD-A1B1C1D1中，E，F分别是线段A1B1，B1C1上的不与端点重合的动点，如果A1E＝B1F，有下面四个结论：①EF⊥AA1; ②EF∥AC；③EF与AC异面；④EF∥平面ABCD．其中一定正确的是()A．①②B．②③C．②④D．①④7．设a，b为两条不重合的直线，α，β为两个不重合的平面，下列命题中为真命题的是()A．若a，b与α所成的角相等，则a∥b B．若a∥α，b∥β，α∥β，则a∥bC．若aα，bβ，a∥b，则α∥βD．若a⊥α，b⊥β，α⊥β，则a⊥b8．已知平面α⊥平面β，α∩β＝l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是()A．AB∥m B．AC⊥m C．AB∥βD．AC⊥β9．若m，n为两条不重合的直线，α，β为两个不重合的平面，则下列命题中的真命题的个数是()①若m，n都平行于平面α，则m，n一定不是相交直线；②若m，n都垂直于平面α，则m，n一定是平行直线；③已知α，β互相垂直，m，n互相垂直，若m⊥α，则n⊥β；④m，n在平面α内的射影互相垂直，则m，n互相垂直．A．1 B．2 C．3 D．410．设平面α∥平面β，A∈α，B∈β，C是AB的中点，当A，B分别在α，β内运动时，那么所有的动点C()A．不共面B．当且仅当A，B在两条相交直线上移动时才共面C．当且仅当A，B在两条给定的平行直线上移动时才共面D．不论A，B如何移动都共面二、填空题(本大题共5小题，每小题5分，共25分．把答案填在题中的横线上)11．下列图形可用符号表示为__________．12．正方体ABCD-A1B1C1D1中，二面角C1-AB-C的平面角等于________．13．设平面α∥平面β，A，C∈α，B，D∈β，直线AB与CD交于点S，且点S位于平面α，β之间，AS＝8，BS＝6，CS＝12，则SD＝__________.14．如图，正方体ABCD-A1B1C1D1中，若过A，C，B1三点的平面与底面A1B1C1D1的交线为l，则l与AC的关系是________．15．如图，P A⊥平面ABC，∠ACB＝90°，EF∥P A，则图中直角三角形的个数是________．三、解答题(本大题共2小题，共25分．解答时应写出文字说明、证明过程或演算步骤)16．(10分)如图，在底面为正三角形且侧棱垂直于底面的三棱柱ABC-A1B1C1中，F，F1分别是AC，A1C1的中点．(2)平面AB1F1⊥平面ACC1A1.2⊥底面ABC，若G，F分别是EC，BD的中点．(1)求证：GF∥平面ABC；(2)求证：AC⊥平面EBC；(3)求几何体ADEBC的体积V.参考答案1.答案：D2.答案：C3.答案：D4.答案：B5.答案：D6.答案：D7.答案：D8.答案：D9.答案：A10. 答案：D11. 答案：α∩β＝AB12. 答案：45°13. 答案：914．答案：平行15. 答案：616.证明：(1)在底面为正三角形且侧棱垂直于底面的三棱柱ABC-A1B1C1中，∵F，F1分别是AC，A1C1的中点，∴B1F1∥BF，AF1∥C1F.又∵B1F1∩AF1＝F1，C1F∩BF＝F，∴平面AB1F1∥平面C1BF.(2)在底面为正三角形且侧棱垂直于底面的三棱柱ABC-A1B1C1中，AA1⊥平面A1B1C1，∴B1F1⊥AA1.又∵B1F1⊥A1C1，A1C1∩AA1＝A1，∴B 1F1⊥平面ACC1A1，而B1F1平面AB1F1，∴平面AB1F1⊥平面ACC1A1.17. 解：(1)证明：连接AE，如图所示，∵ADEB 为正方形，∴AE ∩BD ＝F ，且F 是AE 的中点．又G 是EC 的中点，∴GF ∥AC ，又AC 平面ABC ，GF 平面ABC ，∴GF ∥平面ABC ．(2)证明：∵ADEB 为正方形，∴EB ⊥AB ，又∵平面ABED ⊥平面ABC ，平面ABED ∩平面ABC ＝AB ，EB 平面ABED ， ∴BE ⊥平面ABC ，∴BE ⊥AC ．又∵AC ＝BC ＝22AB ，∴CA 2＋CB 2＝AB 2，∴AC ⊥BC ．又∵BC ∩BE ＝B ，∴AC ⊥平面BCE .(3)取AB 的中点N ，如图所示，∵AC ＝BC ，∴CN ⊥AB ．又平面ABED ⊥平面ABC ，CN 平面ABC ，平面ABED ∩平面ABC ＝AB ，∴CN ⊥平面ABED ．∵△ABC 是等腰直角三角形，∴CN ＝12AB ＝12，1 3S ABED·CN＝13×1×12＝16.∴V C-ABED＝。