高斯滤波器和2RC滤波器
- 格式:docx
- 大小:192.79 KB
- 文档页数:10

高斯滤波器的作用在数字图像处理中,高斯滤波器是一种常用的平滑滤波器,它可以有效地去除图像中的噪声,使图像更加清晰和平滑。
高斯滤波器的作用主要是通过对图像中的像素值进行加权平均来实现的。
高斯滤波器通过在图像上滑动一个小的窗口来处理每个像素。
在窗口内,每个像素的值会与高斯函数中的权重相乘,并求和得到新的像素值。
这样可以使图像中每个像素的值受到周围像素的影响,从而减少噪声的影响,使图像更加清晰。
高斯滤波器的主要作用之一是平滑图像。
在图像处理中,噪声是不可避免的,特别是在低光照条件下拍摄的图像中。
噪声会导致图像细节模糊,影响图像质量。
通过使用高斯滤波器,可以有效地去除图像中的噪声,使图像更加平滑,细节更加清晰。
高斯滤波器还可以用于边缘检测。
边缘是图像中像素值变化较大的地方,通常表示物体之间的分界线或者物体的轮廓。
高斯滤波器可以通过平滑图像来减少噪声的影响,从而更容易检测图像中的边缘。
通过边缘检测,可以帮助我们更好地理解图像内容,进行目标识别和分割。
除了平滑和边缘检测,高斯滤波器还可以用于图像增强和特征提取。
在一些图像处理任务中,我们需要突出图像中的某些特征或者增强图像的对比度。
通过适当调整高斯滤波器的参数,可以实现对图像的增强和特征提取,从而更好地满足不同应用的需求。
总的来说,高斯滤波器在数字图像处理中起着至关重要的作用。
它不仅可以帮助我们去除图像中的噪声,使图像更加清晰和平滑,还可以用于边缘检测、图像增强和特征提取等任务。
因此,熟练掌握高斯滤波器的原理和应用是每个图像处理工程师都应该具备的基本技能。
通过合理地使用高斯滤波器,我们可以更好地处理图像数据,实现各种图像处理任务,提高图像处理的效果和质量。
图像滤波之⾼斯滤波介绍1 ⾼斯滤波简介 了解⾼斯滤波之前,我们⾸先熟悉⼀下⾼斯噪声。
⾼斯噪声是指它的服从(即)的⼀类噪声。
如果⼀个噪声,它的幅度分布服从⾼斯分布,⽽它的⼜是均匀分布的,则称它为⾼斯⽩噪声。
⾼斯⽩噪声的⼆阶矩不相关,⼀阶矩为,是指先后信号在时间上的相关性,包括和。
⾼斯滤波器是⼀类根据⾼斯函数的形状来选择权值的线性平滑滤波器。
⾼斯平滑滤波器对于抑制服从正态分布的噪声⾮常有效。
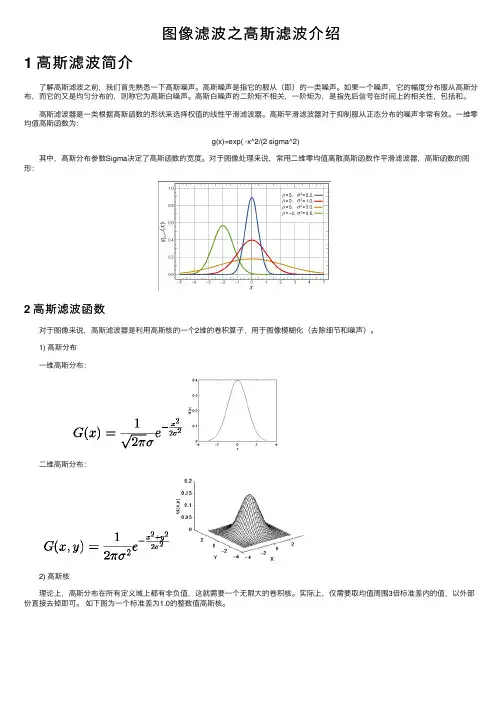
⼀维零均值⾼斯函数为: g(x)=exp( -x^2/(2 sigma^2) 其中,⾼斯分布参数Sigma决定了⾼斯函数的宽度。
对于图像处理来说,常⽤⼆维零均值离散⾼斯函数作平滑滤波器,⾼斯函数的图形:2 ⾼斯滤波函数 对于图像来说,⾼斯滤波器是利⽤⾼斯核的⼀个2维的卷积算⼦,⽤于图像模糊化(去除细节和噪声)。
1) ⾼斯分布 ⼀维⾼斯分布: ⼆维⾼斯分布: 2) ⾼斯核 理论上,⾼斯分布在所有定义域上都有⾮负值,这就需要⼀个⽆限⼤的卷积核。
实际上,仅需要取均值周围3倍标准差内的值,以外部份直接去掉即可。
如下图为⼀个标准差为1.0的整数值⾼斯核。
3 ⾼斯滤波性质 ⾼斯函数具有五个重要的性质,这些性质使得它在早期图像处理中特别有⽤.这些性质表明,⾼斯平滑滤波器⽆论在空间域还是在频率域都是⼗分有效的低通滤波器,且在实际图像处理中得到了⼯程⼈员的有效使⽤.⾼斯函数具有五个⼗分重要的性质,它们是: (1)⼆维⾼斯函数具有旋转对称性,即滤波器在各个⽅向上的平滑程度是相同的.⼀般来说,⼀幅图像的边缘⽅向是事先不知道的,因此,在滤波前是⽆法确定⼀个⽅向上⽐另⼀⽅向上需要更多的平滑.旋转对称性意味着⾼斯平滑滤波器在后续边缘检测中不会偏向任⼀⽅向. (2)⾼斯函数是单值函数.这表明,⾼斯滤波器⽤像素邻域的加权均值来代替该点的像素值,⽽每⼀邻域像素点权值是随该点与中⼼点的距离单调增减的.这⼀性质是很重要的,因为边缘是⼀种图像局部特征,如果平滑运算对离算⼦中⼼很远的像素点仍然有很⼤作⽤,则平滑运算会使图像失真. (3)⾼斯函数的傅⽴叶变换频谱是单瓣的.正如下⾯所⽰,这⼀性质是⾼斯函数付⽴叶变换等于⾼斯函数本⾝这⼀事实的直接推论.图像常被不希望的⾼频信号所污染(噪声和细纹理).⽽所希望的图像特征(如边缘),既含有低频分量,⼜含有⾼频分量.⾼斯函数付⽴叶变换的单瓣意味着平滑图像不会被不需要的⾼频信号所污染,同时保留了⼤部分所需信号. (4)⾼斯滤波器宽度(决定着平滑程度)是由参数σ表征的,⽽且σ和平滑程度的关系是⾮常简单的.σ越⼤,⾼斯滤波器的频带就越宽,平滑程度就越好.通过调节平滑程度参数σ,可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(⽋平滑)之间取得折衷. (5)由于⾼斯函数的可分离性,较⼤尺⼨的⾼斯滤波器可以得以有效地实现.⼆维⾼斯函数卷积可以分两步来进⾏,⾸先将图像与⼀维⾼斯函数进⾏卷积,然后将卷积结果与⽅向垂直的相同⼀维⾼斯函数卷积.因此,⼆维⾼斯滤波的计算量随滤波模板宽度成线性增长⽽不是成平⽅增长.4 ⾼斯滤波应⽤ ⾼斯滤波后图像被平滑的程度取决于标准差。


加噪去噪的方法与引用场景
加噪和去噪是数字图像处理中的重要概念。
以下是几种加噪和去噪的方法,以及它们的引用场景:
加噪的方法:
1. 添加高斯噪声:在图像中添加高斯噪声可以模拟图像在传输或记录过程中受到的随机误差。
高斯噪声是一种以正态分布形式出现的随机噪声。
2. 添加椒盐噪声:椒盐噪声是一种由图像传感器、传输信道等引起的随机误差,表现为图像中突然出现的白点或黑点。
添加椒盐噪声可以模拟这种情况。
去噪的方法:
1. 中值滤波:中值滤波器是一种非线性滤波器,可以将图像中的噪声去除。
中值滤波器对某个区域内的所有像素值进行排序,并将中值作为输出,对于去除椒盐噪声特别有效。
2. 高斯滤波:高斯滤波器是一种线性滤波器,通过将每个像素的值替换为其邻域内像素的加权平均值来去除噪声。
高斯滤波适用于去除高斯噪声。
3. 傅里叶变换:傅里叶变换可以将图像从空间域转换到频率域,通过在频率域中进行滤波操作,再反变换回空间域,可以达到去除噪声的效果。
傅里叶变换可以用于去除各种类型的噪声。
引用场景:
1. 医学图像处理:在医学领域,图像处理技术广泛应用于诊断、治疗和手术导航等方面。
去噪算法可以用于提高医学图像的清晰度和可读性,帮助医生更准确地诊断病情。
2. 遥感图像处理:遥感图像经常受到噪声的干扰,影响其质量和解译效果。
去噪算法可以提高遥感图像的信噪比,从而提高遥感数据的可利用性和可靠性。
3. 通信系统:在通信系统中,噪声是影响信号传输质量的重要因素之一。
通过去噪算法可以降低噪声对信号的影响,提高通信系统的性能和可靠性。

iir 递归高斯滤波IIR递归高斯滤波高斯滤波是一种常用的图像处理方法,可以有效地平滑图像并去除噪声。
在高斯滤波中,通过对像素周围的邻域进行加权平均来计算滤波后的像素值,其中权值是根据高斯函数确定的。
传统的高斯滤波方法通常使用卷积运算来实现,但是这种方法需要进行大量的乘法和加法运算,计算复杂度较高。
为了提高高斯滤波的效率,可以使用递归方法来实现。
IIR(Infinite Impulse Response)滤波器是一种递归滤波器,其输出值不仅依赖于当前输入值,还依赖于过去的输入值和输出值。
在递归高斯滤波中,使用了递归的思想来实现高斯滤波。
递归高斯滤波器的核心思想是将高斯滤波的过程分解为两个一维滤波器的级联。
具体来说,递归高斯滤波器通过两个一维低通滤波器来逼近二维高斯滤波器的效果。
递归高斯滤波的一维低通滤波器是一个IIR滤波器,其传递函数为一个有理函数。
传递函数的分子和分母是两个多项式,其中分母是一个一阶差分方程,分子是一个与分母相同阶数的多项式。
通过不断迭代这个差分方程,可以逼近高斯函数的效果。
递归高斯滤波器的参数由高斯函数的标准差决定,标准差越大,滤波器的阶数越大,滤波效果越好,但计算复杂度也会增加。
递归高斯滤波器的实现可以使用直接递归或者平移递归的方法。
直接递归方法将滤波器的差分方程直接应用于输入序列和输出序列,计算复杂度较高。
平移递归方法通过引入延迟线来降低计算复杂度,具有较高的运行效率。
在平移递归方法中,输入序列和输出序列通过延迟线连接,每个延迟线上的延迟元素表示一个时刻的输入或输出值。
通过不断更新延迟元素的值,可以实现滤波器的运算。
递归高斯滤波器的实现可以使用多种编程语言来实现,如C++、Python等。
在实现时,需要注意选择适当的数据类型和算法,以提高运行效率和滤波质量。
同时,为了避免边界效应,可以对输入图像进行扩展或者使用边界处理方法来处理。
递归高斯滤波器在图像处理中有着广泛的应用。

常见的滤波器类型及其特点滤波器是一种用于处理信号的电子设备或电路元件,它可以通过选择特定频率范围内的信号来增强或抑制信号。
在电子通信、音频处理、图像处理和数据处理等领域中,滤波器起着至关重要的作用。
本文将介绍几种常见的滤波器类型及其特点。
一、低通滤波器(Low-pass filter)低通滤波器允许低频信号通过,同时抑制高频信号。
常见的低通滤波器包括RC低通滤波器、RL低通滤波器和Butterworth低通滤波器等。
1. RC低通滤波器:RC低通滤波器由电阻(R)和电容(C)组成,可以通过调整RC的数值来改变滤波效果。
该滤波器主要用于对音频信号和直流信号进行滤波,具有简单、成本低、频率响应平滑的特点。
2. RL低通滤波器:RL低通滤波器由电阻(R)和电感(L)组成,主要用于信号的衰减和频率分析。
相较于RC低通滤波器,RL滤波器具有更好的频率稳定性和阻尼特性。
3. Butterworth低通滤波器:Butterworth低通滤波器为典型的滤波器设计,具有平坦的幅频响应曲线和最小幅度损失,但转折点的陡度较低。
常用于音频信号和通信信号的滤波。
二、高通滤波器(High-pass filter)高通滤波器允许高频信号通过,同时抑制低频信号。
常见的高通滤波器包括RC高通滤波器、RL高通滤波器和Butterworth高通滤波器等。
1. RC高通滤波器:RC高通滤波器与RC低通滤波器相似,但输入和输出信号的位置交换。
该滤波器可以保留高频信号,并适用于去除直流信号。
2. RL高通滤波器:RL高通滤波器也与RL低通滤波器类似,具有良好的阻抗匹配和频率特性。
常用于音频处理和电信号分离。
3. Butterworth高通滤波器:Butterworth高通滤波器与Butterworth 低通滤波器相似,但是其功能相反。
它可用于音频信号的滤波和高频噪声去除。
三、带通滤波器(Band-pass filter)带通滤波器可以选择特定的频率范围内的信号,并抑制其他频率的信号。

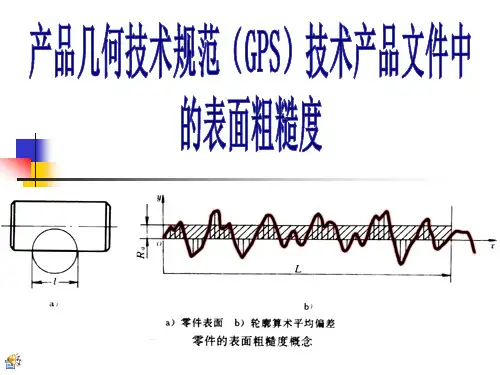
粗糙度相关参数1、表明面轮廓:表面粗糙度R、表面波纹度W和表面结构P的总称。
RProfile-粗糙度轮廓波距小于1mmWProfile-波纹度轮廓波距在1~10mm之间。
PProfile-原始轮廓波距大于10mm2、仪器可以选的两个粗糙度定义标准。
默认选择ISO国际标准。
AMSE B46.1:American Society of Mechanical Engineers美国机械工程协会2002制定的标准。
ISO 4287 :(International Organization for Standardization)标准是指由国际标准化组织, ISO 制订的标准4287用于确认描述表面粗糙度的不规则变化的参照线的长度.Cutoff:传输频带的切断值。
R轮廓仅使用两种两种不同的取样长度(长波过滤器和短波过滤器)在ISO 4287默认切断值波长=0.8mm=0.03in短波滤波器:确定存在于表面上的粗糙度与比它更短的波的成分之间相交界限的滤波器。
Dektak仪器的短波滤波器最长波长为25um长波滤波器:确定粗糙度与波纹度成分之间相交界限的滤波器。
Dektak仪器的长波滤波器最短波长是0.08mm。
3、高斯滤波器和2RC滤波。
对于ISO 4287标准的过滤器是Gaussian:高斯滤波器实质上是一种信号的滤波器,其用途为信号的平滑处理,数字图像用于后期应用,其噪声是最大的问题,因为误差会累计传递等原因。
ASME B46.1标准(美国机械工程协会2002)对2RC(2 Resistance Capacitance)滤波器有所提及,但是国际标准ISO中并没有涉及该滤波器。
不选择2RC滤波器一些原因:(a)在粗糙度轮廓中它有一个相位的失真;(b)粗糙度滤波器和波纹度滤波器需要分开处理;(c)最后它有边缘失真现象;对于同一种表面,高斯滤波器测出的值比以2RC过滤方式测得的值至少少了37%。
高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。

高斯滤波器在通信上的应用
高斯滤波器在通信领域有多种应用,以下是一些常见的应用:
1.图像处理:高斯滤波器常用于图像处理中的平滑操作,它可以消除图像中的噪声,为进一步的处理提供更准确的图像数据。
2.语音处理:在语音识别和语音合成中,高斯滤波器可以用于改善语音信号的质量,特别是在消除背景噪声方面效果显著。
3.通信系统中的信号处理:在通信系统中,高斯滤波器可以用于信号的预处理和后处理,以提高信号的传输质量和降低误码率。
例如,在数字信号的调制解调过程中,高斯滤波器可以用于提高信号的抗干扰能力。
4.雷达和声呐信号处理:在雷达和声呐信号处理中,高斯滤波器可以用于提取目标的特征信息,如速度、距离等。
5.频域分析:高斯滤波器在频域分析中也具有应用价值,例如在频谱分析中用于提取特定频率范围内的信号成分。
总之,高斯滤波器在通信领域中的应用广泛,它能够提高信号的传输质量和处理效果,为通信系统的稳定运行提供了有力支持。

表面结构的图样表示法加工零件时,由于刀具在零件表面上留下刀痕和切削分裂时表面金属的塑性变形等影响,使零件表面存在着间距较小的轮廓峰谷。
这种表面上具有较小间距的峰谷所组成的微观几何形状特性,称为表面粗糙度。
机器设备对零件各个表面的要求不一样,如配合性质、耐磨性、抗腐蚀性、密封性、外观要求等,因此,对零件表面粗糙度的要求也各有不同。
一般说来,凡零件上有配合要求或有相对运动的表面,表面粗糙度参数值小。
因此,应在满足零件表面功能的前提下,合理选用表面粗糙度参数。
1.评定表面结构常用的轮廓参数①算术平均偏差Ra是指在一个取样长度内纵坐标值Z(x)绝对值的算术平均值② 轮廓的最大高度Rz是指在同一取样长度内,最大轮廓峰高和最大轮廓谷深之和的高度图9-27 评定表面结构常用的轮廓参数2.有关检验规范的基本术语检验评定表面结构参数值必须在特定条件下进行。
国家标准规定,图样中注写参数代号及其数值要求的同时,还应明确其检验规范。
有关检验规范方面的基本术语有取样长度、评定长度、滤波器和传输带以及极限值判断规则。
本有关检验规范仅介绍取样长度与评定长度和极限值判断规则。
(1)取样长度和评定长度以粗糙度高度参数的测量为例,由于表面轮廓的不规则性,测量结果与测量段的长度密切相关,当测量段过短,各处的测量结果会产生很大差异,但当测量段过长,则测得的高度值中将不可避免地包含了波纹度的幅值。
因此,在X轴上选取一段适当长度进行测量,这段长度称为取样长度。
但是,在每一取样长度内的测得值通常是不等的,为取得表面粗糙度最可靠的值,一般取几个连续的取样长度进行测量,并以各取样长度内测量值的平均值作为测得的参数值。
这段在X轴方向上用于评定轮廓的并包含着一个或几个取样长度的测量段称为评定长度。
当参数代号后未注明时,评定长度默认为5 个取样长度,否则应注明个数。
例如:Rz0.4、Ra30.8、Rz13.2分别表示评定长度为5个(默认)、3个、1个取样长度。
高斯滤波器和2RC滤波器第五章高斯滤波器5.1介绍高斯滤波器被广泛应用于表面轮廓分析。
美国标准(美国机械工程师协会2002)和国际标准(国际标准化组织1996)都对它进行了阐述。
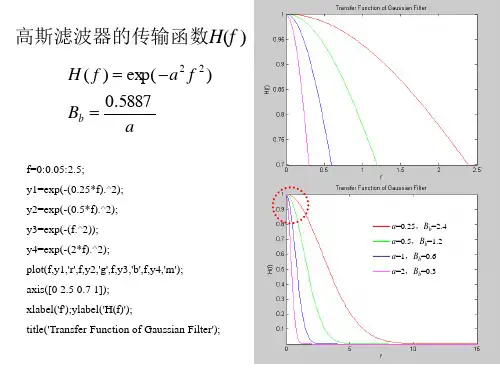
高斯滤波器的权重函数(滤波器在时域和空间域的定义)如下:S x =αλcexp[−π(αλc2] 5.1 式子中α= =0.4697,x是权重函数距离原点的位置,λc是粗糙度中长波波长的截止频率。
通过对连续函数S x 进行傅里叶变换可以得到函数的传递特性,变化如下: Sf λ=∞ −∞1xS x eiλxdx=∞1 −∞αλce[−π(x2)]αλceiλxdx=e[−π(αλc2)]λ 5.2 从等式5.2,能够看出该正弦波振幅有衰减,其波长截止波长(λ=λc)是0.5,因此在截止处,滤波器传递了50%。
下面的例子展示了,在给定权重函数下,其高斯滤波器传递曲线的样子。
范例5.1 在给定空间域λc≤x≤λc下,描绘高斯滤波器S。
其中让λc=0.8mm,采样间隔∆x=1μm。
下面是MATLAB生成的代码,并且其所描述的图展示在(图5.1 a)。
图5.1 a绘制高斯滤波器;λc=0.8mm,b高斯滤波器传递特性lambdac=0.8; % in mmdx=0.001; % in mmx=(-lambdac:dx:lambdac)’;alpha=0.4697;S=(1/(alpha*lambdac)).*exp(-pi*(x/(alpha*lambdac)).^2);% generate the Gaussian filterS=S/sum(S); % normalize to unit sumplot(x,S);xlabel(’Distance (mm)’);ylabel(’Weighting function’);范例5.2 产生高斯滤波器S的振幅传输特性,并且评估正弦波的振幅传输特性,其截止波长(λc=0.8mm)。
高斯滤波器的传递特性能够同样获得,通过借助第四章4.4范例所示的矩形滤波器例程。
高斯滤波器原理高斯滤波器是一种常用的图像处理滤波器,它利用高斯函数对图像进行平滑处理,能够有效去除图像中的噪声,保留图像的细节信息。
在数字图像处理领域,高斯滤波器被广泛应用于图像去噪、边缘检测、图像增强等方面。
本文将介绍高斯滤波器的原理及其在图像处理中的应用。
高斯滤波器的原理基于高斯函数,高斯函数是数学中的一种特殊函数,其形状呈钟型曲线。
高斯函数具有以下形式:\[G(x, y) = \frac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2}\]其中,\(G(x, y)\)表示高斯函数在点\((x, y)\)处的取值,\(\sigma\)表示高斯函数的标准差。
高斯函数的特点是中心点取值最大,随着距离中心点的增加,取值逐渐减小。
这种特性使得高斯函数在图像处理中能够实现平滑效果,同时保留图像的整体特征。
在图像处理中,高斯滤波器利用高斯函数对图像进行卷积操作,以实现图像的平滑处理。
卷积操作的数学表达式为:\[I'(x, y) = \sum_{s=-a}^{a}\sum_{t=-b}^{b}I(x+s, y+t) \cdot G(s, t)\]其中,\(I(x, y)\)表示原始图像在点\((x, y)\)处的灰度值,\(I'(x, y)\)表示经过高斯滤波器处理后的图像在点\((x, y)\)处的灰度值,\(G(s, t)\)表示高斯函数在点\((s, t)\)处的取值。
通过对图像中的每个像素点进行卷积操作,即可得到经过高斯滤波器处理后的图像。
高斯滤波器在图像处理中有着广泛的应用。
首先,高斯滤波器能够有效去除图像中的高频噪声,如椒盐噪声、高斯噪声等,使图像更加清晰。
其次,高斯滤波器还可以用于图像的边缘检测,通过调节高斯函数的标准差,可以实现不同程度的平滑效果,从而影响图像的边缘检测效果。
此外,高斯滤波器还可以用于图像的增强处理,通过对图像进行适当的平滑处理,可以突出图像的细节特征,使图像更加鲜明。
高斯滤波器和2RC滤波器第五章高斯滤波器5.1介绍高斯滤波器被广泛应用于表面轮廓分析。
美国标准(美国机械工程师协会2002)和国际标准(国际标准化组织1996)都对它进行了阐述。
高斯滤波器的权重函数(滤波器在时域和空间域的定义)如下:S x =αλcexp[−π(αλc2] 5.1 式子中α= =0.4697,x是权重函数距离原点的位置,λc是粗糙度中长波波长的截止频率。
通过对连续函数S x 进行傅里叶变换可以得到函数的传递特性,变化如下: Sf λ=∞ −∞1xS x eiλxdx=∞1 −∞αλce[−π(x2)]αλceiλxdx=e[−π(αλc2)]λ 5.2 从等式5.2,能够看出该正弦波振幅有衰减,其波长截止波长(λ=λc)是0.5,因此在截止处,滤波器传递了50%。
下面的例子展示了,在给定权重函数下,其高斯滤波器传递曲线的样子。
范例5.1 在给定空间域λc≤x≤λc下,描绘高斯滤波器S。
其中让λc=0.8mm,采样间隔∆x=1μm。
下面是MATLAB生成的代码,并且其所描述的图展示在(图5.1 a)。
图5.1 a绘制高斯滤波器;λc=0.8mm,b高斯滤波器传递特性lambdac=0.8; % in mmdx=0.001; % in mmx=(-lambdac:dx:lambdac)’;alpha=0.4697;S=(1/(alpha*lambdac)).*exp(-pi*(x/(alpha*lambdac)).^2);% generate the Gaussian filterS=S/sum(S); % normalize to unit sumplot(x,S);xlabel(’Distance (mm)’);ylabel(’Weighting function’);范例5.2 产生高斯滤波器S的振幅传输特性,并且评估正弦波的振幅传输特性,其截止波长(λc=0.8mm)。
高斯滤波器的传递特性能够同样获得,通过借助第四章4.4范例所示的矩形滤波器例程。
一、图像噪声由于图像采集、处理、传输等过程不可避免的会受到噪声的污染,妨碍人们对图像理解及分析处理。
常见的图像噪声有高斯噪声、椒盐噪声等。
1、椒盐噪声2、高斯噪声高斯噪声是指噪声的密度服从高斯分布的一类噪声,由于高斯噪声在空间和频域中数学上的易处理性,这种噪声(也称为正态噪声)模型经常被用于实践中。
高斯噪声随机变量z的概率密度函数由下式给出:加入高斯噪声后的效果:二、图像平滑图像平滑从信号处理的角度看就是去除其中的高频信息,保留低频信息。
因此我们可以对图像实施低通滤波。
低通滤波可以去除图像中的噪声,对图像进行平滑。
根据滤波器的不同可以分为:均值滤波、高斯滤波、中值滤波、双边滤波我们认为高频信息就是噪声,低频信息就是有用的内容。
1、均值滤波(1)api介绍(2)实例分析import cv2 as cvimport numpy as npimport matplotlib.pyplot as pltfrom matplotlib import font_manager#字体设置my_font = font_manager.fontproperties(fname="c:/windows/fonts/sthupo.ttf")#1、读取图像img = cv.imread("./images/girl.jpg")#2、均值滤波blur = cv.blur(img, (5,5))#3、图像显示plt.figure(figsize=(10,8), dpi=100)# subplot中的121代表[1,2,1],表示在本区域里显示1行2列个图像,最后的1表示本图像显示在第一个位置。
plt.subplot(121)plt.imshow(img[:,:,::-1])plt.title("原图", fontproperties=my_font)plt.xticks([]), plt.yticks([])plt.subplot(122)plt.imshow(blur[:,:,::-1])plt.title("均值滤波后的结果", fontproperties=my_font)plt.xticks([]), plt.yticks([])plt.show()2、高斯滤波图像是二维的,所以使用二维高斯分布。
第五章 高斯滤波器5.1介绍高斯滤波器被广泛应用于表面轮廓分析。
美国标准(美国机械工程师协会2002)和国际标准(国际标准化组织1996)都对它进行了阐述。
高斯滤波器的权重函数(滤波器在时域和空间域的定义)如下:S (x )=1αλc exp[−π(x αλc )2] 5.1 式子中α=√ln2/π=0.4697,x 是权重函数距离原点的位置,λc 是粗糙度中长波波长的截止频率。
通过对连续函数S (x )进行傅里叶变换可以得到函数的传递特性,变化如下: Sf (λ)=∫S (x )e iλx dx ∞−∞=∫1αλc e [−π(x αλc )2]∞−∞e iλx dx =e [−π(αλc λ)2] 5.2从等式5.2,能够看出该正弦波振幅有衰减,其波长截止波长(λ=λc )是0.5,因此在截止处,滤波器传递了50%。
下面的例子展示了,在给定权重函数下,其高斯滤波器传递曲线的样子。
范例5.1 在给定空间域λc ≤x ≤λc 下,描绘高斯滤波器S 。
其中让λc =0.8mm ,采样间隔∆x =1μm 。
下面是MATLAB 生成的代码,并且其所描述的图展示在(图5.1 a)。
图5.1 a 绘制高斯滤波器;λc =0.8mm ,b 高斯滤波器传递特性lambdac=0.8; % in mmdx=0.001; % in mmx=(-lambdac:dx:lambdac)’;alpha=0.4697;S=(1/(alpha *lambdac)).*exp(-pi *(x/(alpha *lambdac)).^2);% generate the Gaussian filterS=S/sum(S); % normalize to unit sumplot(x,S);xlabel(’Distance (mm)’);ylabel(’Weighting function’);范例5.2 产生高斯滤波器S的振幅传输特性,并且评估正弦波的振幅传输特性,其截止波长(λc=0.8mm)。
高斯滤波器的传递特性能够同样获得,通过借助第四章4.4范例所示的矩形滤波器例程。
传递特性如图5.1b所示。
该正弦波由0.8mm波长组成,其振幅衰减为0.5(Sf的阵列元素有11个)。
因此高斯滤波器在截止频率处,传输量为50%。
注意在图5.1b所示的传递特性中,可以清楚的看到,在其截止频率处有一个坡度过程,并没有直上直下的锋利过渡。
这意味着滤波器不能立刻抑制所有波长小于截止频率的波长,而是在截止频率处使它们逐渐变弱。
这个传递特性也能够被描述通过直接对等式5.2采样。
m=size(S,1); % length of Gaussian filterl=8; % length of a profile is assumed to be 8 mmn=l/dx; % number of profile pointsS=[zeros(n/2-floor(m/2),1); S; zeros(n/2-floor(m/2)-1,1)];% center the filter and zero-pad to 8000 longSf=fft(S); % DFT of Sj=(2:1:floor(n/2)+1)’;% generate wavelength array for X axis of% transmission plotwave=n*dx./(j-1);semilogx(wave,100*abs(Sf(2:floor(n/2)+1,1)));xlabel(’Wavelength (mm)’);ylabel(’Amplitude (%)’);5.2高通和低通滤波器迄今为止描述的滤波器都是低通滤波器,因为它只能传递低频部分(波长大于截止波长)。
第3章和第4章所描述的矩形滤波器和步进滤波器也都是低通滤波器。
低通滤波器是一个平均滤波器因为它能产生一个光滑的轮廓。
一个滤波器也能够被设计成只传输高频的信号。
这种滤波器是众所知周的高通滤波器。
高斯高通滤波器的传递特性如下Sf(λ)=1−e(−π(αλcλ)2) 5.3这个高通高斯滤波器在截止波长处也传递50%。
这是很重要的,因为它阐释了高斯低通和高通在传递上的互补性。
这可以表明高频信号与低频信号的差异仅仅表现在原始轮廓。
因此用两种不同滤波器同时捕捉高频和低频信号是没有必要的。
5.3用高斯滤波器量化粗糙度、波纹度和形状滤波器的输出是粗糙度,波纹度还是形状(三者为专业术语),取决于滤波器的类型(高通或者低通)和截止波长的阈值。
如之前第3章所述,因为粗糙度,波纹度还是形状都有自己明确定义的带宽范围,所以构造带宽的上限和下限截止波长要符合各自要求。
ASME B46.1标准中定义截止波长λcw作为波纹度的长波截止波长,λsw作为波纹度的短波截止波长,λc作为粗糙度的长波截止波长,λs 作为粗糙度的短波截止波长。
λc的选择等于λsw。
ASME B46.1与ISO 11562两者都已经给出了截止波长的推荐阈值。
除此之外,他们也提供了进一步的指导对于截止比率的选择。
例如,选择λc与一个适当的λc/λs比率将限制探针的大小(美国机械工程师协会2002)。
滤波器与截止波长λs相关联构成低通滤波器,与此相对应滤波器与截止波长λc相关联,则构成一个高通滤波器。
上述这对滤波器应用到轮廓上输出的是粗糙度。
如果想获得波纹度需要调整到λsw(低通)λcw(高通)。
形状通常包含了所有大尺寸波长,因此下端的截止波长为λf,通常来说这样就足够了。
但值得注意的是在ASME B46.1标准中并没有定义λf。
图5.2举例说明了上述滤波器的不同。
图5.2划分粗糙度轮廓、波纹度轮廓、形状轮廓的五种滤波器的传递特性(λs=25um,λc=0.8mm,λsw=0.8mm,λcw=8mm,λf=8mm)综上所述,很显然根据粗糙度或者波纹度的定义,我们需要两个滤波器同时操作来获得。
然而事实上有些简单化的公共认可,这样通过一个信号的滤波操作也可以简单的获得粗糙度或者波纹度。
首先,截止波长为λs的低通滤波器有时可以被忽略,或者用自动滤波器仪器的初始数据。
其次一种情况是,轮廓长度通常并没有足够的长度去捕捉形状,因此截止波长λcw的高通滤波器并没有用到。
最后一种状况是,在第5.2部分已经有所提及,利用高斯低通和高通滤波器的互补定义,可以用一个滤波器来评估粗糙度和波纹度(截止波长λc的高通或者低通)。
总的来说,粗糙度轮廓能够通过用一个截止波长为λc的高通滤波器去过滤原始轮廓来获得。
波纹度轮廓与原始轮廓和粗糙度轮廓的区别是很简单的。
在原始轮廓上应用高斯低通滤波器λsw就以获得波纹度的表面轮廓。
同样的这也是粗糙度轮廓与波纹轮廓和原始轮廓之间的区别。
无论怎么做,两者产生的结果是一样的。
5.4截止波长的影响当λc增加,粗糙度轮廓的带宽将变大,因此应该增加振幅参数,例如Ra,来计算粗糙度轮廓。
另一方面,同样的截止波长将导致波纹度轮廓中的一些波长被移除,作为这个结果应该在计算波纹度轮廓时,减小振幅参数Wa5.5相位特性我们已经非常详细的研究了高斯滤波器的振幅传递特性,但是对于相位特性我们还没有提及。
高斯滤波器并不会使两个不同波长的正弦波产生相对的相位改变。
换句话说,每一个进入滤波器的正弦波形都会复现它进入时的相位特性,并不会发生相位改变。
这种相位不变的特性,也正是高斯滤波器的最大优点。
5.6总结高斯滤波器可能是今天被用的最广泛的滤波器。
我们本章复习了它的定义和实现方法。
我也讨论了高通和低通滤波器的定义。
而且我们还讨论了高斯高通和低通滤波器是如何互补的,因此用两个滤波器操作获得粗糙度和波纹度是多余的。
高斯滤波器的相位不变性,使得它的输出不会扭曲变形。
练习5.1通过对公式5.2的连续采样生成一个高斯低通滤波器曲线。
假设λc=0.8mm ,采样间隔∆x =1μm 。
和图5.1 b 对比两者相同吗?5.2生成一个如图5.2所示的图,假设轮廓长度是1,000mm ,采样间隔为∆x =1μm ,截止波长参考图5.2所示。
5.3写一个高斯函数文件 myGaussian.m ,调用该函数需要给两个参数——间隔和截止波长(两者单位相同),然后函数产生一个高斯低通滤波器,这个高斯函数是经过归一化的,为了使所有的权重统一。
5.4用截止波长0.8mm 的高斯低通滤波器滤波2mm 波长振幅为1μm 的曲线z 1, 利用高斯滤波器的振幅传递曲线观察振幅衰减情况。
采样间隔参数为∆x =1μm 。
用同样的滤波器滤波0.5mm 波长振幅为0.5μm 的曲线z 2,观察其振幅衰减状况。
5.5根据练习5.4和已知高斯滤波器的相位特性,计算并绘制滤波输出,高斯滤波器的滤波轮廓为练习5.4讨论的两个正弦波之和。
5.6用空间卷积验证练习5.4的结果。
并用5.3制作的高斯滤波函数生成这个滤波器。
5.7用频域积分验证练习5.4的结果。
为了这个窗口能均匀排放这8000长度的数组,需要在高斯滤波器的空间域填补零点。
然后对滤波器和轮廓执行DFTs ,进行逐项积分。
用反向DFT 进行评估并提取相关部分补偿相位(看4.6的例子)。
这个波纹度轮廓一定是和5.5与5.6中产生的轮廓相同,除了在边缘上可能有少许差别。
5.8用空间卷积方法过滤练习3.1中的轮廓z ,用三种不同截止波长的低通高斯滤波器,分别是0.5mm,0.8mm 和2mm 。
从波纹度轮廓w 上截取截止长度的一半。
计算波纹度轮廓w 中的Wa 。
其中Wa 被定义为Wa =∑|w(i)|n i=1n ,w(i)是波纹度数组的第i 个元素,n 是数组w 的长度。
随着截止波长的增加是Wa 增加还是减小,为什么?参考文献美国机械工程协会2002,ASME B46.1-2002,表面纹理(表面粗糙度,波纹度和花纹),ASME.美国.纽约国际标准化组织1996,ISO11562:1996,几何产品规格(GPS)-表面纹理:轮廓方式-滤波器相位调整特性,ISO,瑞士,日内瓦第6章2RC滤波器6.1引言最早用于表面测量的滤波器是2RC滤波器。
这种滤波器早期由硬件构成,现在已经可以方便使用软件执行。
2RC滤波器并不是一个线性相位的滤波器,并且对粗糙度和波纹度两个滤波器需要区分来看待。
尽管2RC滤波器很早就被应用于表面轮廓滤波,但是却在高斯滤波器之后来讨论它,是因为这种滤波器在执行时更具有挑战性的问题存在。
ASME B46.1标准(美国机械工程协会2002)对2RC滤波器有所提及,但是国际标准中并没有涉及该滤波器。
6.2 2RC高通滤波器从历史上来看,2RC滤波器仅仅被用于从原始轮廓中提取粗错度轮廓,因此文献报道中一般仅提供了2RC的粗糙度滤波器的权重函数。