(完整word版)高斯滤波器理解

高斯滤波器的原理及其实现过程（附模板代码）来源：网络素材本文主要介绍了高斯滤波器的原理及其实现过程高斯滤波器是一种线性滤波器，能够有效的抑制噪声，平滑图像。

其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。

其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1;而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。

所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。

什么是高斯滤波器既然名称为高斯滤波器，那么其和高斯分布(正态分布)是有一定的关系的。

一个二维的高斯函数如下：其中(x,y)(x,y)为点坐标，在图像处理中可认为是整数;σσ是标准差。

要想得到一个高斯滤波器的模板，可以对高斯函数进行离散化，得到的高斯函数值作为模板的系数。

例如：要产生一个3×33×3的高斯滤波器模板，以模板的中心位置为坐标原点进行取样。

模板在各个位置的坐标，如下所示(x轴水平向右，y轴竖直向下)这样，将各个位置的坐标带入到高斯函数中，得到的值就是模板的系数。

对于窗口模板的大小为(2k+1)×(2k+1)，模板中各个元素值的计算公式如下：这样计算出来的模板有两种形式：小数和整数。

•小数形式的模板，就是直接计算得到的值，没有经过任何的处理;•整数形式的，则需要进行归一化处理，将模板左上角的值归一化为1，下面会具体介绍。

使用整数的模板时，需要在模板的前面加一个系数，系数为也就是模板系数和的倒数。

高斯模板的生成知道模板生成的原理，实现起来也就不困难了•••••••••••••••••••••••••void generateGaussianTemplate(double window[][11], int ksize, double sigma){ static const double pi = 3.1415926; int center = ksize / 2; // 模板的中心位置，也就是坐标的原点 doublex2, y2; for (int i = 0; i < ksize; i++) { x2 = pow(i - center, 2); for (int j = 0; j < ksize; j++) { y2 = pow(j - center, 2); double g = exp(-(x2 + y2) / (2 * sigma * sigma));g /= 2 * pi * sigma; window[i][j] = g; } } double k= 1 / window[0][0]; // 将左上角的系数归一化为1 for (int i = 0; i< ksize; i++) { for (int j = 0; j < ksize; j++) { window[i][j] *= k; } }}需要一个二维数组，存放生成的系数(这里假设模板的最大尺寸不会超过11);第二个参数是模板的大小(不要超过11);第三个参数就比较重要了，是高斯分布的标准差。

图像滤波之⾼斯滤波介绍1 ⾼斯滤波简介 了解⾼斯滤波之前，我们⾸先熟悉⼀下⾼斯噪声。

⾼斯噪声是指它的服从（即）的⼀类噪声。

如果⼀个噪声，它的幅度分布服从⾼斯分布，⽽它的⼜是均匀分布的，则称它为⾼斯⽩噪声。

⾼斯⽩噪声的⼆阶矩不相关，⼀阶矩为，是指先后信号在时间上的相关性，包括和。

⾼斯滤波器是⼀类根据⾼斯函数的形状来选择权值的线性平滑滤波器。

⾼斯平滑滤波器对于抑制服从正态分布的噪声⾮常有效。

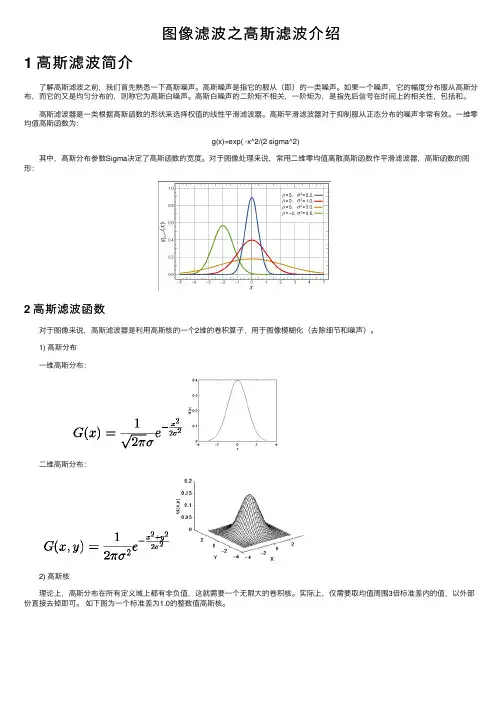
⼀维零均值⾼斯函数为： g(x)=exp( -x^2/(2 sigma^2) 其中，⾼斯分布参数Sigma决定了⾼斯函数的宽度。

对于图像处理来说，常⽤⼆维零均值离散⾼斯函数作平滑滤波器，⾼斯函数的图形：2 ⾼斯滤波函数 对于图像来说，⾼斯滤波器是利⽤⾼斯核的⼀个2维的卷积算⼦，⽤于图像模糊化（去除细节和噪声）。

1) ⾼斯分布 ⼀维⾼斯分布： ⼆维⾼斯分布： 2) ⾼斯核 理论上，⾼斯分布在所有定义域上都有⾮负值，这就需要⼀个⽆限⼤的卷积核。

实际上，仅需要取均值周围3倍标准差内的值，以外部份直接去掉即可。

如下图为⼀个标准差为1.0的整数值⾼斯核。

3 ⾼斯滤波性质 ⾼斯函数具有五个重要的性质，这些性质使得它在早期图像处理中特别有⽤．这些性质表明，⾼斯平滑滤波器⽆论在空间域还是在频率域都是⼗分有效的低通滤波器，且在实际图像处理中得到了⼯程⼈员的有效使⽤．⾼斯函数具有五个⼗分重要的性质，它们是： （1）⼆维⾼斯函数具有旋转对称性，即滤波器在各个⽅向上的平滑程度是相同的．⼀般来说，⼀幅图像的边缘⽅向是事先不知道的，因此，在滤波前是⽆法确定⼀个⽅向上⽐另⼀⽅向上需要更多的平滑．旋转对称性意味着⾼斯平滑滤波器在后续边缘检测中不会偏向任⼀⽅向． （2）⾼斯函数是单值函数．这表明，⾼斯滤波器⽤像素邻域的加权均值来代替该点的像素值，⽽每⼀邻域像素点权值是随该点与中⼼点的距离单调增减的．这⼀性质是很重要的，因为边缘是⼀种图像局部特征，如果平滑运算对离算⼦中⼼很远的像素点仍然有很⼤作⽤，则平滑运算会使图像失真． （3）⾼斯函数的傅⽴叶变换频谱是单瓣的．正如下⾯所⽰，这⼀性质是⾼斯函数付⽴叶变换等于⾼斯函数本⾝这⼀事实的直接推论．图像常被不希望的⾼频信号所污染(噪声和细纹理)．⽽所希望的图像特征（如边缘），既含有低频分量，⼜含有⾼频分量．⾼斯函数付⽴叶变换的单瓣意味着平滑图像不会被不需要的⾼频信号所污染，同时保留了⼤部分所需信号． （4）⾼斯滤波器宽度(决定着平滑程度)是由参数σ表征的，⽽且σ和平滑程度的关系是⾮常简单的．σ越⼤，⾼斯滤波器的频带就越宽，平滑程度就越好．通过调节平滑程度参数σ，可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(⽋平滑)之间取得折衷． （5）由于⾼斯函数的可分离性，较⼤尺⼨的⾼斯滤波器可以得以有效地实现．⼆维⾼斯函数卷积可以分两步来进⾏，⾸先将图像与⼀维⾼斯函数进⾏卷积，然后将卷积结果与⽅向垂直的相同⼀维⾼斯函数卷积．因此，⼆维⾼斯滤波的计算量随滤波模板宽度成线性增长⽽不是成平⽅增长．4 ⾼斯滤波应⽤ ⾼斯滤波后图像被平滑的程度取决于标准差。

白噪声英文名称：white noise定义1：在感兴趣的频率范围内，每单位带宽内有相等功率的噪声或振动。

应用学科：机械工程（一级学科）；振动与冲击（二级学科）；机械振动（三级学科）定义2：在所考虑的频带内具有连续频谱和恒定的功率谱密度的随机噪声。

应用学科：通信科技（一级学科）；通信原理与基本技术（二级学科）以上内容由全国科学技术名词审定委员会审定公布求助编辑百科名片白噪声白噪声是指功率谱密度在整个频域内均匀分布的噪声。

所有频率具有相同能量的随机噪声称为白噪声。

从我们耳朵的频率响应听起来它是非常明亮的“咝”声（每高一个八度，频率就升高一倍。

因此高频率区的能量也显著增强）。

目录编辑本段概述白噪声是指在较宽的频率范围内，各等带宽的频带所含的噪声能量相等的噪声。

一般在物理上把它翻译成白噪声（white noise）。

白噪声或白杂讯，是一种功率频谱密度为常数的随机信号或随机过程。

换句话说，此信号在各个频段上的功率是一样的，由于白光是由各种频率（颜色）的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是“白色的”，此信号也因此被称作白噪声。

相对的，其他不具有这一性质的噪声信号被称为有色噪声。

理想的白噪声具有无限带宽，因而其能量是无限大，这在现实世界是不可能存在的。

实际上，我们常常将有限带宽的平整讯号视为白噪音，因为这让我们在数学分析上更加方便。

然而，白噪声在数学处理上比较方便，因此它是系统分析的有力工具。

一般，只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，就可以把它作为白噪声来处理。

例如，热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度，通常可以认为它们是白噪声。

当你需要专心工作，而周遭总是有繁杂的声音时，就可以选用这两种声音来加以遮蔽。

一般来说，通常的情况下你可以选用白色噪音，而粉红色噪音则是特别针对说话声的遮蔽材料。

粉红色噪音又被称做频率反比(1/f) 噪音，因为它的能量分布与频率成反比，或者说是每一个八度音程(Octave) 能量就衰退3 dB。

高斯滤波原理高斯滤波是一种常见的图像处理技术，它可以有效地去除图像中的噪声，使图像更加清晰和平滑。

高斯滤波的原理是利用高斯函数对图像中的每个像素点进行加权平均，从而达到去除噪声的效果。

在本文中，我们将详细介绍高斯滤波的原理及其在图像处理中的应用。

首先，我们来了解一下高斯函数的定义。

高斯函数又称为正态分布函数，它的数学表达式为：\[ G(x,y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} \]其中，\( (x,y) \) 表示图像中的像素坐标，\( \sigma \) 表示高斯函数的标准差。

高斯函数的特点是中心点权重最大，随着距离中心点的增大，权重逐渐减小。

这种权重分布的特性使得高斯滤波能够有效地去除图像中的高频噪声，同时保留图像的细节信息。

在图像处理中，高斯滤波的原理是将图像中的每个像素点与一个高斯模板进行卷积运算。

高斯模板是一个二维的矩阵，它的大小和标准差决定了滤波的效果。

对于图像中的每个像素点，通过与高斯模板进行卷积运算，可以得到一个加权平均的结果，从而达到去除噪声的目的。

在实际应用中，高斯滤波常常用于图像的预处理阶段，以减少图像中的噪声对后续图像处理算法的影响。

除此之外，高斯滤波还可以用于图像的平滑处理，使图像更加柔和和自然。

需要注意的是，高斯滤波虽然能够有效地去除高斯噪声，但对于椒盐噪声等其他类型的噪声效果并不明显。

因此，在实际应用中，需要根据图像的特点选择合适的滤波算法。

总结一下，高斯滤波是一种常见的图像处理技术，它利用高斯函数对图像中的每个像素点进行加权平均，从而去除图像中的噪声，使图像更加清晰和平滑。

在实际应用中，高斯滤波常常用于图像的预处理阶段，以减少噪声对后续图像处理算法的影响。

希望本文对您理解高斯滤波原理有所帮助。

高斯滤波引入的振铃现象
高斯滤波器在图像处理中能够有效地抑制噪声，但引入了“振铃”现象。

振铃现象是指在图像处理过程中，图像的边缘或细节出现了剧烈的震荡，就像钟被敲击后产生的空气震荡一样。

高斯滤波器是一种平滑滤波器，其系统函数是平滑的，避免了振铃现象的产生。

相比之下，理想型滤波器（如理想低通滤波器）在傅里叶变换后会产生陡峭的变化，这种变化在逆变换后会产生“振铃”现象。

为了解决这个问题，可以采用巴特沃斯型滤波器。

巴特沃斯型滤波器的阶数越高，其边缘越平滑，振铃现象越不明显。

另外，高斯滤波器由于其傅里叶变换仍然是高斯函数，所以不会产生振铃现象。

总的来说，虽然高斯滤波器会引入一些振铃现象，但是通过合理选择滤波器的阶数或者采用其他合适的滤波器类型，可以有效地减轻或避免振铃现象的产生。

matlab 高斯滤波的点数-概述说明以及解释1.引言1.1 概述高斯滤波是一种常用的图像滤波方法，其基本原理是通过对图像中的每个像素点周围的像素值进行加权平均，从而达到平滑图像的效果。

与其他滤波方法相比，高斯滤波具有较好的平滑效果和保持图像细节的能力。

因此，在图像处理、计算机视觉和模式识别等领域被广泛应用。

本文旨在探讨高斯滤波中滤波器的点数对滤波效果的影响。

高斯滤波器的点数是指滤波器的大小，即滤波器矩阵的行列数。

常见的滤波器大小有3x3、5x5、7x7等不同的尺寸。

不同的滤波器大小会使高斯滤波的平滑效果和处理速度有所变化，因此选择合适的滤波器大小对于实际应用非常重要。

在正文部分，我们将介绍高斯滤波的原理及其应用领域。

随后，我们将着重探讨高斯滤波中滤波器大小的参数设置以及其对滤波效果的影响。

进一步地，我们将总结高斯滤波的优点，并提出改进高斯滤波算法的建议。

最后，展望高斯滤波的未来发展，希望为读者提供一个全面了解高斯滤波的视角。

通过本文的阅读，读者将能够了解到高斯滤波的基本原理、应用领域以及它在图像处理中的参数设置及其影响。

希望本文能够对读者在实际应用中选择合适的滤波器大小提供一定的参考和指导。

1.2文章结构文章结构主要包括引言、正文和结论三个部分。

引言部分旨在简要介绍文章的研究背景和目的，为读者提供对文章后续内容的预期。

正文部分是文章的主体部分，详细介绍了高斯滤波的原理、应用和参数设置等内容。

结论部分对前文进行总结，总结高斯滤波的优点，并提出改进高斯滤波算法的建议，并展望高斯滤波的未来发展趋势。

为了让读者更好地理解文章的结构，以下是各部分的详细内容概述：1. 引言1.1 概述在引言的概述部分，可以简要介绍高斯滤波的概念和在图像处理中的重要性。

可以提及高斯滤波是一种常用的线性平滑滤波器，可用于去除图像中的噪声和平滑图像。

1.2 文章结构在引言的文章结构部分，将详细介绍文章的组织结构。

可以指出文章分为引言、正文和结论三个部分，并简要介绍各部分的内容概述。

均值滤波、中值滤波、高斯滤波的公式如下：
1.均值滤波：使用邻域平均法，用均值代替原图像中的各个像素值。

设有一个滤波
模板，该模板由其近邻的若干像素组成，求模板中所有像素的均值，再把该均值赋予当前像素点（x，y），作为处理后图像在该点上的灰度g（x，y），即g（x，y）=∑f（x，y）/m m为该模板中包含当前像素在内的像素总个数。

2.中值滤波：其数学公式为y[n]=median(x[n-k],…,x[n],…,x[n+k]) 其中x xx是原始
信号，y yy是滤波后的信号，n nn是当前位置，k kk是窗口大小。

3.高斯滤波：高斯函数可以用来模拟存在噪声的图像。

假设有一幅大小为N×N像
素的图像f(x,y)，那么任意一点(x,y)上的像素值可以用高斯函数来描述：
f(x,y)=∫∫f(u,v)exp[-{(u-x)^2+(v-y)^2}/2σ^2]dudv 其中，f(u,v)是原始图像上(u,v)点的像素值，σ是高斯滤波参数，表示高斯函数的“宽度”。

以上信息仅供参考，如有需要，建议咨询专业人士。

高斯滤波器傅里叶变换推导高斯滤波器是一种常用的图像平滑滤波器，通过对图像进行高斯模糊处理，可以有效地去除图像中的噪声和细节，使图像变得更加平滑。

傅里叶变换是一种将信号从时域转换到频域的数学方法，它可以将信号表示为一系列不同频率的正弦和余弦函数的叠加。

下面是高斯滤波器的傅里叶变换推导过程。

假设原始图像为f(x, y)，高斯滤波器为g(x, y)，则滤波后的图像h(x, y)可以表示为它们的卷积：h(x, y) = f(x, y) g(x, y)。

其中，表示卷积操作。

根据卷积定理，卷积在频域中等于两个函数的傅里叶变换的乘积。

因此，我们可以将上式转换到频域进行计算。

首先，对原始图像f(x, y)和高斯滤波器g(x, y)分别进行二维离散傅里叶变换（DFT），得到它们的频域表示F(u, v)和G(u, v)： F(u, v) = DFT[f(x, y)]G(u, v) = DFT[g(x, y)]然后，根据卷积定理，滤波后的图像的频域表示H(u, v)等于原始图像频域表示和滤波器频域表示的乘积：H(u, v) = F(u, v) G(u, v)。

最后，将H(u, v)进行逆傅里叶变换（IDFT），得到滤波后的图像h(x, y)：h(x, y) = IDFT[H(u, v)]综上所述，高斯滤波器的傅里叶变换推导过程如上所示。

通过将原始图像和高斯滤波器分别转换到频域，并进行频域上的乘积和逆变换，可以得到滤波后的图像。

需要注意的是，上述推导过程是基于离散傅里叶变换（DFT）的，实际应用中可能会使用快速傅里叶变换（FFT）等更高效的算法来进行计算。

此外，高斯滤波器的具体参数（如标准差）会影响滤波效果，需要根据实际需求进行选择。

高斯滤波器的应用原理1. 介绍高斯滤波器是一种常用的图像处理方法，它可以有效地去除图像中的噪声，平滑图像并减小图像的细节。

本文将介绍高斯滤波器的应用原理，并探讨其在图像处理领域中的应用。

2. 高斯滤波器的原理高斯滤波器基于高斯函数进行滤波操作。

高斯函数是一种连续的概率分布函数，其形状呈钟形曲线。

在图像处理中，高斯函数被应用于滤波操作中，用于对图像进行平滑处理。

高斯滤波器将图像中的每一个像素点与其周围的邻近像素点进行加权平均。

每个邻域的像素点被加权平均后的值赋予给中心像素点，从而达到减少图像噪声和平滑图像的效果。

3. 高斯滤波器的计算公式高斯滤波器通常使用二维高斯函数进行计算。

其计算公式如下：G(x,y) = (1 / (2πσ^2)) * exp(-(x^2+y^2) / (2σ^2))其中，G(x,y)表示二维高斯函数的值，(x,y)表示像素点的坐标，σ表示高斯函数的标准差。

4. 高斯滤波器的应用高斯滤波器在图像处理领域中有广泛的应用，主要包括以下几个方面：•图像去噪：由于高斯滤波器的平滑效果，可以有效地去除图像中的噪声，提高图像的质量。

•图像平滑：高斯滤波器可以对图像进行平滑处理，减小图像的细节。

这在一些特定的应用场景中很有用，例如股票走势图的平滑处理。

•边缘检测前的预处理：在进行边缘检测之前，通常会对图像进行平滑处理，以减少噪声干扰。

高斯滤波器能够对图像进行有效的平滑，为边缘检测提供更好的输入。

•图像模糊效果：通过调整高斯函数的标准差，可以实现不同程度的图像模糊效果。

这在一些特定的美化效果中被广泛使用，如光晕效果等。

5. 高斯滤波器的参数选择在使用高斯滤波器时，需要选择合适的参数，包括滤波器的大小和高斯函数的标准差。

•滤波器的大小：滤波器的大小决定了邻域的大小，它会影响到滤波效果。

通常情况下，选择较大的滤波器可以获得更平滑的图像，但也会导致图像细节的丢失。

•高斯函数的标准差：标准差决定了高斯函数的分布范围，它会影响到滤波器对图像的平滑程度。

高斯滤波器是一种线性平滑滤波器，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。

通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。

高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

高斯滤波器是一个低通滤波器，其用途是信号的平滑处理，用于得到信噪比SNR较高的图像（反应真实信号）。

以上内容仅供参考，如需更具体全面的信息，建议查阅高斯滤波器相关的文献资料或咨询数学和物理领域专业人士。

高斯滤波器的作用高斯滤波器是一种常见的线性平滑滤波器，它的作用是对图像进行平滑处理，减少图像中的噪声，使图像更加清晰和平滑。

在数字图像处理中，噪声是一个常见的问题，噪声会影响图像的质量和清晰度，降低图像的信息量。

因此，对图像进行滤波处理是非常重要的，而高斯滤波器正是其中一种有效的滤波方法。

高斯滤波器的原理是利用高斯函数对图像进行加权平均处理，通过改变高斯函数的标准差来控制滤波器的尺度，从而实现对图像的平滑处理。

在滤波过程中，像素点的值会被周围像素的值加权平均，这样可以有效地消除图像中的噪声，使图像变得更加清晰。

与其他滤波器相比，高斯滤波器具有平滑效果好、边缘保持能力强等优点，因此被广泛应用于图像处理领域。

在实际应用中，高斯滤波器常常用于图像去噪、图像平滑、边缘检测等方面。

在图像去噪方面，高斯滤波器可以有效地去除图像中的高斯噪声、椒盐噪声等常见噪声，提高图像的质量和清晰度。

在图像平滑方面，高斯滤波器可以使图像变得更加柔和和自然，减少图像中的锯齿和颗粒感。

在边缘检测方面，高斯滤波器可以帮助减少边缘检测算法的误检率，提高边缘检测的准确性。

除了在图像处理领域，高斯滤波器还被广泛应用于信号处理、模式识别、机器学习等领域。

在信号处理中，高斯滤波器可以用来平滑信号、滤除噪声，提高信号的质量和可靠性。

在模式识别和机器学习中，高斯滤波器常常用来对特征进行平滑处理，降低特征之间的冗余性，提高分类和识别的准确性。

总的来说，高斯滤波器作为一种常见的线性平滑滤波器，在图像处理和信号处理领域有着重要的应用价值。

它可以帮助去除图像和信号中的噪声，提高图像和信号的质量和清晰度，从而更好地满足人们对图像和信号处理的需求。

通过合理地选择高斯滤波器的参数，可以实现不同场景下的滤波效果，使图像和信号处理更加高效和准确。

希望通过本文的介绍，读者能够更加深入地了解高斯滤波器的作用和原理，为今后的图像处理和信号处理工作提供参考和帮助。

高斯滤波器原理高斯滤波器是一种常用的图像处理滤波器，它利用高斯函数对图像进行平滑处理，能够有效去除图像中的噪声，保留图像的细节信息。

在数字图像处理领域，高斯滤波器被广泛应用于图像去噪、边缘检测、图像增强等方面。

本文将介绍高斯滤波器的原理及其在图像处理中的应用。

高斯滤波器的原理基于高斯函数，高斯函数是数学中的一种特殊函数，其形状呈钟型曲线。

高斯函数具有以下形式：\[G(x, y) = \frac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2}\]其中，\(G(x, y)\)表示高斯函数在点\((x, y)\)处的取值，\(\sigma\)表示高斯函数的标准差。

高斯函数的特点是中心点取值最大，随着距离中心点的增加，取值逐渐减小。

这种特性使得高斯函数在图像处理中能够实现平滑效果，同时保留图像的整体特征。

在图像处理中，高斯滤波器利用高斯函数对图像进行卷积操作，以实现图像的平滑处理。

卷积操作的数学表达式为：\[I'(x, y) = \sum_{s=-a}^{a}\sum_{t=-b}^{b}I(x+s, y+t) \cdot G(s, t)\]其中，\(I(x, y)\)表示原始图像在点\((x, y)\)处的灰度值，\(I'(x, y)\)表示经过高斯滤波器处理后的图像在点\((x, y)\)处的灰度值，\(G(s, t)\)表示高斯函数在点\((s, t)\)处的取值。

通过对图像中的每个像素点进行卷积操作，即可得到经过高斯滤波器处理后的图像。

高斯滤波器在图像处理中有着广泛的应用。

首先，高斯滤波器能够有效去除图像中的高频噪声，如椒盐噪声、高斯噪声等，使图像更加清晰。

其次，高斯滤波器还可以用于图像的边缘检测，通过调节高斯函数的标准差，可以实现不同程度的平滑效果，从而影响图像的边缘检测效果。

此外，高斯滤波器还可以用于图像的增强处理，通过对图像进行适当的平滑处理，可以突出图像的细节特征，使图像更加鲜明。

图像的高斯滤波原理
高斯滤波是一种常用的图像处理技术，它可以有效地平滑图像并减小图像中的噪声。

该滤波器基于高斯函数的理念，对图像中的每个像素进行加权平均，使得每个像素的值都与其周围像素的值有关。

高斯函数是一种钟形曲线，其具有一个均值和一个标准差，用于描述数据的分布。

在图像处理中，高斯函数常用于计算与每个像素相关的权重。

权重越高，该像素对平均值的贡献越大。

高斯滤波的原理是在图像中使用一个特定大小的卷积核，该卷积核通过对图像进行卷积运算来计算每个像素的新值。

卷积运算是指将卷积核与图像的每个像素及其相邻像素进行逐元素相乘，并将乘积求和得到新的像素值。

使用高斯函数计算的权重将应用于卷积运算中，以加权平均的方式融合周围像素的信息。

为了使图像平滑并降低噪声，高斯滤波器会使得图像的每个像素值都由其周围像素的值加权平均得到。

由于高斯函数模拟了自然界中很多事物的分布规律，因此该滤波器可以在保留图像主要特征的同时，减少噪声的影响。

不同的卷积核大小和标准差值会导致不同程度的平滑效果。

尽管高斯滤波对图像平滑和噪声减少很有效，但也会导致图像细节的丢失。

较大的卷积核和较大的标准差会导致更明显的平滑效果，但可能会以牺牲图像细节为代价。

因此，在使用高斯滤波器时需要权衡滤波器参数的选择，以达到最佳的平滑效果和细节保留。

数字信号高斯滤波数字信号是一种通过离散的数值来表示连续信号的方法。

在数字信号处理中，为了降低噪声和增强信号的质量，常常需要对信号进行滤波处理。

而高斯滤波是一种常用的信号滤波方法，其原理是通过卷积运算来消除信号中的高频成分。

高斯滤波在图像处理领域尤为常见。

在数字图像中，每个像素点都可以表示为一个灰度值或者RGB值。

这些值构成了图像的亮度、颜色等信息。

但是，在图像获取和传输过程中，往往会受到噪声的干扰，导致图像质量下降。

为了解决这个问题，可以使用高斯滤波器来平滑图像。

高斯滤波的核心思想是通过将每个像素点与其周围像素点进行加权平均，从而减少噪声的影响。

这里的权值是根据高斯函数来计算的，距离中心像素点越远的像素点，其权值越小。

这样，通过对整个图像进行卷积运算，可以使图像变得更加平滑，同时保留图像的细节。

在实际应用过程中，高斯滤波具有一些重要的特性。

首先，高斯滤波是线性的，也就是说多次使用高斯滤波和一次使用高斯滤波的结果是相同的。

其次，高斯滤波可以有效地降低图像的噪声，并能够较好地保持图像的边缘信息。

这是因为高斯函数的性质决定了它在空域中的平滑性和频域中的带通特性。

然而，高斯滤波也存在一些限制。

由于高斯滤波使用了卷积操作，因此对于噪声信号和图像信号的频率分布区别不大的情况下，会导致图像细节丢失和模糊化。

此外，如果高斯窗口的大小选择不当，会导致滤波效果不佳，无法达到预期的去噪和平滑效果。

因此，在使用高斯滤波进行图像处理时，需要根据具体情况来选择滤波窗口的大小和权值分布。

一般情况下，较小的窗口可以保留更多图像细节，但容易保留一些噪声。

而较大的窗口可以更好地去除噪声，但也会损失一些图像细节。

因此，需要在平衡去噪和保持图像细节之间进行权衡。

总之，高斯滤波是一种常用的数字信号滤波方法，尤其在图像处理领域具有重要意义。

通过对图像进行卷积运算，可以显著降低图像的噪声，提高图像质量。

然而，高斯滤波也存在一些限制，需要根据具体情况选择滤波窗口的大小和权值分布。

高斯滤波器原理高斯滤波器是一种常用的图像滤波器，可以实现图像的平滑处理和噪声的去除。

它的原理是基于高斯函数的卷积运算，通过不同的参数设置，可以实现不同程度的平滑和去噪效果。

一、高斯函数高斯函数是一种常用的数学函数，它的形式如下：G(x,y) = 1/(2πσ^2) * e^(-((x-x0)^2 + (y-y0)^2)/(2σ^2)) 其中，x、y为坐标，x0、y0为中心点坐标，σ为标准差，e为自然对数的底数。

高斯函数的图像呈现出一种钟形曲线的形状，中心点处取得最大值，随着距离的增加逐渐减小。

二、高斯滤波器的卷积运算高斯滤波器的卷积运算是将图像中每个像素点的值与高斯函数进行卷积，得到一个新的像素值。

卷积运算的公式如下：I(x,y) = ∑∑ K(i,j) * G(x-i,y-j)其中，I(x,y)为卷积后的像素值，K(i,j)为原图像中的像素值，G(x-i,y-j)为高斯函数在(i,j)处的值。

通过对整个图像进行卷积运算，可以得到一张新的图像，其中每个像素的值都是通过周围像素的加权平均计算得到的。

三、高斯滤波器的应用高斯滤波器广泛应用于图像处理领域，主要用于平滑处理和噪声去除。

在图像平滑处理中，高斯滤波器可以有效地去除图像中的细节和噪声，使图像更加平滑和连续。

在噪声去除中，高斯滤波器可以通过调整标准差的大小来控制去噪的程度，不同的标准差对应不同的滤波半径，即卷积核的大小，从而实现不同程度的去噪效果。

四、高斯滤波器的优缺点高斯滤波器具有以下几个优点：1. 可以有效地平滑图像，去除噪声，使图像更加清晰。

2. 通过调整标准差的大小，可以实现不同程度的平滑和去噪效果。

3. 高斯滤波器的卷积核是对称的，可以保持图像的几何形状不变。

4. 高斯滤波器的卷积运算可以通过快速傅里叶变换等算法实现，计算速度较快。

但是，高斯滤波器也存在一些缺点：1. 高斯滤波器会使图像失去细节和锐度，对于一些需要保留细节和边缘的图像处理任务可能不适用。

高斯泼溅算法解读
高斯泼溅算法（Gaussian Splash）是一种图像处理中的算法，主要用于模拟水滴在图像表面上的扩散过程。

该算法通过高斯滤波器来实现，可以生成逼真的水滴扩散效果。

下面是对高斯泼溅算法的基本解读：
1.算法原理：高斯泼溅算法基于随机过程，通过在图像上随机生成水滴，并模拟水滴在图像表面的扩散过程，从而达到模拟真实水滴的效果。

高斯滤波器在这个过程中起到关键作用，它可以根据设定的参数（如标准差、核大小等）来控制水滴的扩散范围和速度。

2.参数设置：在高斯泼溅算法中，用户需要设置一些参数来控制算法的运行，如扩散速度、扩散范围、水滴数量等。

这些参数可以通过实验和调整来获得最佳效果。

3.算法流程：高斯泼溅算法的基本流程如下：
a. 初始化水滴位置和大小。

b. 对每个水滴应用高斯滤波器，模拟水滴在图像表面的扩散过程。

c. 更新水滴位置和大小，并检查是否满足停止条件（如水滴扩散到图像边界或其他水滴）。

d. 重复步骤b和c，直到达到预设的扩散程度或水滴数量。

4.应用领域：高斯泼溅算法在许多领域都有广泛应用，如影视
特效、游戏开发、艺术创作等。

通过调整算法参数，可以实现不同效果的水滴扩散现象，为图像增添逼真的湿润感。



总之，高斯泼溅算法是一种基于随机过程的图像处理方法，可以模拟水滴在图像表面的扩散过程。

通过合理设置参数和高斯滤波器，可以生成逼真的水滴效果，应用于各种领域。