克-克方程

习题解答(第二章)一、选择题1．25℃时，0.01mol/kg的糖水的渗透压为π1，而0.01 mol/kg的尿素水溶液的渗透压π2，则___ B _。

（A）π1＜π2（B）π1 =π2（C）π1＞π2（D）无法确定2．应用克-克方程回答问题：当物质由固相变为气相时，平衡压力随温度降低而__ C__。

（A）不变（B）升高（C）降低（D）视不同物质升高或降低3．通常称为表面活性剂的物质，是指当其加入少量后就能__ C的物质。

（A）增加溶液的表面张力（B）改变溶液的导电能力（C）显著降低溶液的表面张力（D）使溶液表面发生负吸附4．兰格缪尔（Langmuir）等温吸附理论中最重要的基本假设是_ D___。

（A）气体为理想气体（B）多分子层吸附（C）固体表面各吸附位置上的吸附能力是不同的（D）单分子层吸附5．溶胶的基本特征之一是___D__。

（A）热力学上和动力学上皆稳定的系统（B）热力学上和动力学上皆不稳定的系统（C）热力学上稳定而动力学上不稳定的系统（D）热力学上不稳定而动力学上稳定的系统6．下列各性质中，属于溶胶的动力学性质的是___A___。

（A）布朗运动（B）电泳（C）丁达尔现象（D）流动电势7．引起溶胶聚沉的诸因素中，最重要的是___D__。

（A）温度的变化（B）溶胶浓度的变化（C）非电解质的影响（D）电解质的影响8．用KBr加入浓的AgNO3溶液中，制备得AgBr溶胶，再向其中加入下列不同的电解质，能使它在一定时间内完全聚沉所需电解质最少的是__ C _。

（A）Na2SO4（B）NaNO3 （C）K3[Fe(CN)6] （D）KCl9．等体积0.10mol/dm3 KI和0.12mol/dm3的AgNO3溶液混合制成的AgI溶胶，下列电解质中，聚沉能力最强的是___D__。

（A ）Na 2SO 4 （B ）MgSO 4 （C ）K 3[Fe(CN)6] （D ）FeCl 3二、简答题1．理想气体存在吗？真实气体的pVT 行为在何种条件下可用pV=nRT 来描述？答：事实上，理想气体不存在。

克劳修斯-克拉伯龙方程
克劳修斯-克拉伯龙方程（Clausius-Clapeyron Equation）是热力学学科中一个重要的方程式，用来表达物质受热后汽化压力（或汽化温度）关于温度（或汽化压力）随温度变化的关系。

该方程式由德国物理学家克劳修斯于1830年提出，后来法国物理学家克拉伯重新推导并于1834年发表。

克劳修斯—克拉伯龙方程的具体表达形式为：
$$ \frac{\mathrm{d}P}{\mathrm{d}T} = \frac{L}{T\cdot V_m} $$
其中$P$为汽化压力，$T$为温度，$L$为某一物质的汽化吸热，$V_m$为某一物质的摩尔容积。

根据克劳修斯—克拉伯龙方程，可以得出当温度变化时，汽化压力也会根据它们之间的关系发生变化。

克劳修斯—克拉伯龙方程可以应用于各种物质的汽化过程，例如水，甲烷，氧气等。

在水的汽化过程中，当温度变化时，由于汽化压力变化，极大地影响了大气中水汽的增减，从而影响着气候。

克劳修斯—克拉伯龙方程可以预测水蒸发和凝结的规律，有助于我们理解气候变化的本质。

克劳修斯—克拉伯龙方程在化学及物理学中也有重要的技术意义，它可以用来研究其它物质的汽化过程，以及汽液不完全稳定的熵，协同弛豫和热力学状态的变化等。

总之，克劳修斯-克拉伯龙方程是一个重要的物理学方程式，它提供了关于物质汽化压力与温度之间关系的重要结论，为我们理解气候变化提供了重要的科学支持，并且也在化学及物理学中发挥了重要的技术作用。

二水..磷酸氢钙二水..磷酸二氢钙二水..硫酸氢钙磷酸二氢钙磷酸二氢钙，无机化合物，是无色三斜片状、粒状或结晶性粉末，广泛用于水产养殖动物及畜禽养殖动物的饲料添加剂，用作膨松剂、面团调节剂、缓冲剂、营养增补剂、乳化剂、稳定剂等品质改良剂。

物化性质性状：磷酸二氢钙是无色三斜片状、粒状或结晶性粉末。

有强酸味。

纯品时不吸潮，但含有微量杂质，如含有磷酸时能潮解。

100℃时失去结晶水，200℃时分解。

溶解性：溶于稀盐酸、稀硝酸和稀乙酸，略溶于水，几乎不溶于乙醇。

密度：相对密度(d184)2.220。

保存：密封保存。

毒性：中毒。

可燃性：不燃。

沸点：158 °C at 760 mmHg。

水中溶解度：1.8g/100ml（20°C）根据不同的精度要求，可以用不同的公式表达压强和沸点关系。

以理想气体假设为基础的克劳修斯-克拉贝龙方程在理论上有重要的意义，也可以很方便的表达饱和蒸汽压和沸点的关系。

ln(p2/p1)=-ΔvapHm/R·(1/T2-1/T1)其中ΔvapHm是液体的摩尔汽化焓。

对任意温度下的饱和蒸汽压，克-克方程可以变为2参数形式：lnp=a/T+b其中a、b是依赖于液体的参数。

但克-克方程只能用于很接近理想气体的实际气体，对非理想性较强的气体偏离严重。

安托因方程是在实际计算中广泛应用的经验方程。

lgp=A-B/(C+T)其中A、B、C是经验参数。

相比于形式上类似的克-克方程，多一个参数的安托因方程实用性明显提高了。

但一个方程不足以描述一种气体。

在实际应用中，一种气体有在正常沸点以下以及正常沸点到临界点间的2套参数。

对精度要求较高并且参数不齐全的计算，李-凯斯勒方程是一个可行的方法。

lnpr=f0-ωf1其中pr是对比压强，ω是气体的偏心因子，f0和f1是2个关于对比温度Tr的函数，对各种气体有同样的形式。

如果知道临界压强，就能由对比压强得到饱和蒸汽压。

在较高温度和正常气压下，李-凯斯勒方程的误差可以控制在2%以内。

克拉伯龙—克劳修斯方程克拉伯龙—克劳修斯方程（Clausius-Clapeyron equation）是描述气体相变时蒸气压与温度之间的关系的方程。

该方程由克勞修斯 (Benjamin Paul Émile Clapeyron)和克拉伯龙 (Rudolf Clausius) 两位物理学家分别于1834年和1864年独立提出。

克拉伯龙—克劳修斯方程的基本形式为：ln(P2/P1) = (ΔHvap/R) \left(\frac{1}{T1}-\frac{1}{T2}\right)其中，P1和P2分别为相变前和相变后的蒸气压，ΔHvap为相变的摩尔焓变，R为气体常数，T1和T2分别为相变前和相变后的温度。

该方程的推导基于理想气体状态方程和热力学第二定律，假设相变前和相变后的气体均为理想气体。

克拉伯龙—克劳修斯方程可以用来计算蒸气压关于温度的变化。

利用该方程，可以推导出不同物质的蒸气压随温度变化的特征曲线。

一种常见的应用是计算液体的沸点。

根据该方程，当蒸气压等于环境大气压（常常为标准大气压）时，液体开始沸腾。

因此，通过测量液体在不同温度下的蒸气压，可以得到该液体的沸点。

该方程也可用于预测物质的气化和凝结条件。

当两个物质的蒸气压相等时，它们处于饱和状态，蒸气和液体达到动态平衡。

根据克拉伯龙—克劳修斯方程，可以计算出不同温度下两种物质的蒸气压，从而判断它们是否会发生气化或凝结。

在气候学和大气科学中，克拉伯龙—克劳修斯方程也被用于计算水的饱和水汽压和相对湿度之间的关系。

通过测量气温和精确的水汽压力，可以使用克拉伯龙—克劳修斯方程来计算相对湿度。

这对于气象预测、大气湿度监测和气候研究非常重要。

总结而言，克拉伯龙—克劳修斯方程是物理化学中非常重要的一种方程。

它描述了气体相变时蒸气压与温度之间的关系，并可以应用于计算沸点、预测气化和凝结条件，以及研究大气湿度等相关问题。

克雷姆塞尔方程的推导摘要：一、引言二、克雷姆塞尔方程的定义三、克雷姆塞尔方程的推导过程四、克雷姆塞尔方程的应用五、结论正文：一、引言克雷姆塞尔方程是数学物理中的一个重要方程，主要用于描述强耦合系统的动力学行为。

它的发现者克雷姆塞尔（Kramers）在20 世纪20 年代提出了这个方程，从而为解决许多实际问题提供了理论依据。

在本文中，我们将详细探讨克雷姆塞尔方程的推导过程及其应用。

二、克雷姆塞尔方程的定义克雷姆塞尔方程是一个描述两自由度强耦合系统的动力学方程，其表达式为：$$frac{d动物}{dt} = -(omega_1^2 + omega_2^2) 动物+ frac{1}{2} left(frac{1}{omega_1^2} + frac{1}{omega_2^2}ight) frac{d^2动物}{domega_1^2} - frac{1}{2}left(frac{1}{omega_1^2} + frac{1}{omega_2^2}ight) frac{d^2动物}{domega_2^2}$$其中，$omega_1$和$omega_2$分别表示系统的两个角频率，$动物$表示相位差。

三、克雷姆塞尔方程的推导过程为了推导克雷姆塞尔方程，我们首先需要了解强耦合系统的基本概念。

强耦合系统是指两个或多个系统通过相互作用而形成的一个整体。

在这个整体中，各个子系统的动力学行为会相互影响。

考虑一个具有两个角频率的强耦合系统，我们可以用拉格朗日方程来描述这个系统的动力学行为。

通过对拉格朗日方程进行求导和化简，我们可以得到克雷姆塞尔方程。

具体的推导过程较为复杂，涉及到较高的数学技巧，这里不再赘述。

四、克雷姆塞尔方程的应用克雷姆塞尔方程在实际应用中有着广泛的应用，例如在天文学、地球物理学、生物学等领域。

它可以用来描述两个或多个物体之间的相互作用，以及它们之间的相对运动。

此外，克雷姆塞尔方程还可以用于解决许多实际问题，如分析系统的稳定性、求解系统的周期解等。

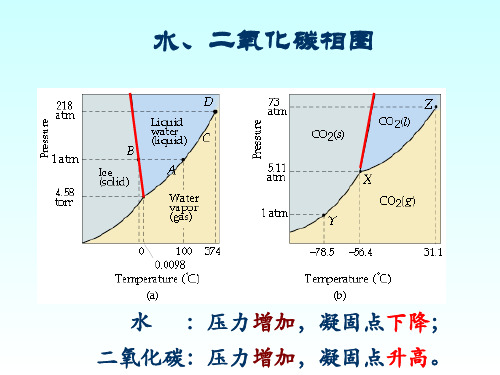
相图一、是非题下述各题中的说法是否正确?正确的在题后括号内画“√”,错的画“⨯”。

1.相是指系统处于平衡时,系统中物理性质及化学性质都均匀的部分。

( )2.依据相律,纯液体在一定温度下,蒸气压应该是定值。

( )3.依据相律,恒沸温合物的沸点不随外压的改变而改变。

( )二、选择题选择正确答案的编号，填在各题题后的括号内。

1NH4HS(s)和任意量的NH3(g)及H2 S(g)达平衡时有：( )。

(A)C=2，φ=2，f =2；(B) C=1，φ=2，f =1；(C) C=1，φ=3，f =2；(D) C=1，φ=2，f =3。

2已知硫可以有单斜硫，正交硫，液态硫和气态硫四种存在状态。

硫的这四种状态____稳定共存。

(A) 能够；(B) 不能够；(C) 不一定。

3硫酸与水可形成H2SO4⋅H2O(s)，H2SO4⋅2H2O(s)，H2SO4⋅4H2O(s)三种水合物，问在101 325Pa的压力下，能与硫酸水溶液及冰平衡共存的硫酸水合物最多可有多少种？( )(A) 3种；(B) 2种；(C) 1种；(D) 不可能有硫酸水合物与之平衡共存。

4将固体NH4HCO3(s) 放入真空容器中，恒温到400 K，NH4HCO3按下式分解并达到平衡：NH4HCO3(s) === NH3(g) + H2O(g) + CO2(g) 系统的组分数C和自由度数f为：( )(A) Ｃ＝2，f ＝2；(B) Ｃ＝2，f ＝2；(C) Ｃ＝2，f ＝0；(D) Ｃ＝3，f ＝2。

5某系统存在C(s)、H2O(g)、CO(g)、CO2(g)、H2(g)五种物质，相互建立了下述三个平衡：H2O(g)+C(s) H2(g) + CO(g)CO2(g)+H2(g) H2O + CO(g)CO2(g) + C(s) 2CO(g)则该系统的独立组分数C为：( )。

(A) 3；(B) 2；(C) 1；(D) 4。

三、计算题习题1A，B二组分在液态完全互溶，已知液体B在80︒C下蒸气压力为101.325 kPa，汽化焓为30.76 kJ·mol-1。

两相平衡范特霍夫方程的应用范森;朱元海【摘要】应用相平衡常数讨论了范特霍夫方程在简化一些两相平衡热力学公式推导时的应用.%The applications of Van't Hoff equation of phase equilibrium,a special case of chemical equilibrium, in simplifying the deduction of some relevant thermodynamic equations are discussed in the paper.【期刊名称】《大学化学》【年(卷),期】2018(033)003【总页数】4页(P70-73)【关键词】范特霍夫方程;相平衡常数;热力学公式推导【作者】范森;朱元海【作者单位】东北石油大学石油工程学院,黑龙江大庆 163318;东北石油大学化学化工学院,黑龙江大庆 163318【正文语种】中文【中图分类】G642;O642物理化学中存在一类与两相平衡相关的热力学公式，诸如克劳修斯-克拉佩龙方程，沸点升高和凝固点下降公式，吸附热和溶解热公式等，尽管这些公式形式上不尽相同，但物理实质其实是一样的。

常见教材受限于教学内容对这些公式的推导都是逐一进行，篇幅冗长，过程繁复[1,2]。

两相平衡通用关系式覆盖面宽[3]，有理论价值，但无论是论证过程和公式形式都较复杂，难以在教学中推广。

把相平衡作为化学平衡的特例处理可有效简化一些两相平衡关系式的推导[4,5]，该方法最有价值的应该是范特霍夫方程的应用，但远没有在各物理化学教材中推广。

本文介绍范特霍夫方程对相平衡的应用实例，希望对物理化学教学有所帮助。

把物质B在两相间转移关系表示为。

达到平衡时物质B在两相的化学势相等，这与单一物种间相互转化的化学平衡条件是一样的。

若把相平衡看成化学平衡的特例，则标准相平衡常数可表示为：式中aB为物质B的活度。

对理想气体，aB = pB/py，pB为B的分压，py是标准态压力；对于理想稀溶液溶质，aB = xB；对于稀溶液溶剂，aA = xA，A表示溶剂。

芬斯克方程
芬斯克方程是指相对挥发度恒定时，计算二元精馏所需的最小理论板数的方程。

芬斯克方程（英语：Fenske equation）用于计算双成分连续分馏，于全回流操作条件下，蒸馏塔所需的最小理论板（英语：Theoretical plate）数。

这对于蒸馏塔设计非常实用。

芬斯克方程系由梅里尔·芬斯克（Merrell Fenske）于1932年推导而来；他曾于1959至1969年间担任宾州州立大学化学工程学系主任。

在设计大尺度连续工业精馏塔时，经常以芬斯克方程初步估算产出理想塔顶产品组成所需的最小理论板数。

通常计算最少理论板数用芬斯克方程。

对于一定的分离要求，减少回流比，所需的理论塔板数增加，当减到某一回流比时，需要无穷多个理论板才能达到分离要求，这一回流比称为最小回流比Rm。