当前位置：文档之家 › 8.3 扩散和单相传质

8.3 扩散和单相传质

  • 格式：doc
  • 大小：392.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

化工原理1-7章习题答案

化工原理1-7章习题答案

目录第一章流体流动与输送机械 (2)第二章非均相物系分离 (32)第三章传热 (42)第四章蒸发 (69)第五章气体吸收 (73)第六章蒸馏 (95)第七章固体干燥 (119)第一章 流体流动与输送机械1. 某烟道气的组成为CO 2 13％，N 2 76％，H 2O 11％（体积％），试求此混合气体在温度500℃、压力101.3kPa 时的密度。

解：混合气体平均摩尔质量kg/mol 1098.2810)1811.02876.04413.0(33--⨯=⨯⨯+⨯+⨯=∑=i i m M y M ∴ 混合密度333kg/m 457.0)500273(31.81098.28103.101=+⨯⨯⨯⨯==-RT pM ρm m2．已知20℃时苯和甲苯的密度分别为879 kg/m 3和867 kg/m 3,试计算含苯40％及甲苯60％（质量％）的混合液密度。

解：8676.08794.012211+=+=ρρρa a m混合液密度 3kg/m 8.871=m ρ3．某地区大气压力为101.3kPa ，一操作中的吸收塔塔内表压为130kPa 。

若在大气压力为75 kPa 的高原地区操作该吸收塔，且保持塔内绝压相同，则此时表压应为多少？解：''表表绝＋p p p p p a a =+=∴kPa 3.15675)1303.101)(''=-==＋（－＋真表a a p p p p4．如附图所示，密闭容器中存有密度为900 kg/m 3的液体。

容器上方的压力表读数为42kPa ，又在液面下装一压力表，表中心线在测压口以上0.55m ，其读数为58 kPa 。

试计算液面到下方测压口的距离。

解：液面下测压口处压力 gh p z g p p ρρ+=∆+=10题4 附图m 36.255.081.990010)4258(30101=+⨯⨯-=+ρ-=ρ-ρ+=∆∴h g p p g p gh p z5. 如附图所示，敞口容器内盛有不互溶的油和水，油层和水层的厚度分别为700mm 和600mm 。

传质过程(化工基础,化学)汇总

传质过程(化工基础,化学)汇总

②填料塔内的流体力学状况
在设计填料塔时，首先要考虑填料塔的流 体力学性能：包括气体通过填料层的压降、 液泛气速、持液量（单位体积填料所持有的 液体体积）、气液分布等。
例如，确定动力消耗需知压降；确定塔径 以液泛速度为依据；持液量关系着填料支承 装置的强度；气液分布情况影响着传质效率 等。
L =0（当没有液体喷淋 时），即气体通过干填料 层时，Δp/H～u呈直线关 系，直线的斜率为1.8～ 2.O，表明H与u的1.8～2 次方成比例，气流状态为 湍流。
• ③若物质在A相实际浓度等于B相实际浓度 所要求的平衡浓度，则无传质过程发生，体系 处于平衡状态。
对于空气中的氨向水中传 递的过程，若以氨的分压p表 示气相中氨的实际浓度，p* 表示液相实际浓度所要求的 气相平衡分压，则：
p＞p*时，氨从气相向液相传递； p＜p*时，氨由液相向气相转移； p= p*时，体系达到平衡状态。
无论哪种类型的均相混合物，要将 其分离成纯净或几乎为纯态物质，必 须造成一个两相物系，利用原物系中 各组分间某种特性的差异，使其中某 个组分在两相间进行传质。
物质在两相中的传质历程
物质首先从一相主体扩散到两 相界面的该相一侧，然后通过相 界面进入另一相，最后从此相的 界面向主体扩散。
例如气体吸收，气相主体中溶 质扩散经过气相到达气液相界面， 溶解进入液相，然后扩散进入液 相主体。
以混合物中吸收质摩尔数与惰性物质摩尔数的比 来表示气相中吸收质的含量，称为气相摩尔比，用Y 表示；
以液相中吸收质摩尔数与纯吸收剂摩尔数的比来 表示液相中吸收质的含量，称为液相摩尔比，用X表 示。
摩尔比与摩尔分数的关系是： Y=y/(1-y) X=x/(1-x)
• 吸收计算中，有时需要在亨利定律 各系数之间进行变换。

扩散与单相传质

扩散与单相传质
（2）溶质A在相界面上的溶解，由气相转入液相， 即界面发生的溶解过程；
（3）溶质A自界面被传递至液相主体，即液相内的 物质传递。
武汉工程大学化工原理课件
单相内传递方式：分子扩散，对流传质 。
(1) 分子扩散：在静止或滞流流体内部，若某一 组分存在温度梯度、压强梯度及浓度梯度，则因分子 无规则的热运动而导致的物质传递现象。类似于间壁 换热过程的热传导。

ln CB2 C B1

D cM
cBM
(c A1 cA2 )
cBM

cB2 cB1 ln cB2
cB1
武汉工程大学化工原理课件 讨论
(1) 组分的浓度与扩散距离z成指数关系。
(2) 漂流因子：其大小反映了总体流动对传质速率
的影响程度，其值为总体流动使传质速率较单纯分子
扩散通量：单位时间内通过垂直于扩散方向的单 位截面积扩散的物质量，以J表示， kmol/(m2·s)。
传质速率：任一固定的空间位置上， 单位时间 内通过单位面积的物质量，以N表示, kmol/(m2·s) 。
费克定律：温度、总压一定，组分A在扩散方向上 任一点处的扩散通量与该处A的浓度梯度成正比。
武汉工程大学化工原理课件 恒温恒压的一维定态扩散
武汉工程大学化工原理课件 问题：如何保持组分B在界面处浓度恒定？
可能的措施：
① 由液相提供（液相能以速率JA通过界面向气相 提供组分）——等分子反向扩散
等分子反向扩散的前提：界面能等速率地向气相提 供组分B.
② 由气相提供(混合气体产生宏观的流动，混合物 流动时向界面将提供的组分B的量正好等于组分的反向 扩散量，从而保持cAi定态)——单向扩散
JA NM
气 液 界 面

中国石油大学化工原理第二讲扩散与单向传质

中国石油大学化工原理第二讲扩散与单向传质

第二节 扩散与单相传质
二、双组分混合物中的一维稳定分子扩散[412-414]
1.等分子反向扩散
p、T相同
p A1 > p A 2 pB1 < p B 2
气
NA
=
JA
=
D
RTδ
( p A1 −
) p A 2
相
NB
=
JB
=
D
RTδ
( pB1 −
) p B 2
N = NA + NB = 0
液
NA
=
JA
=
N BL = J BL
N AL = − N BL J AL = − J BL N =0
( ) N AL
=
⎛ ⎜⎝
D
δ
⎞ ⎟⎠ L
c cSm
cA1 − cA2 L
N AL
=
J AL
+
NM
⋅ cA c
N AL ≠ − N BL
J AL = − J BL
N = N AL
N BL = 0
第八章 传质过程概论
气相
液相
p
pi ci c
δG δL
第一节 概述
一、分离过程及其分类
分离过程——将混合物分离成组成不同的两种或多种产物的过 程。
分离的目的： ① 分离 ② 提取和回收 ③ 纯化 ④ 浓缩
第一节 概述
一、分离过程及其分类
分离过程
机械分离过程 （非均相）
传质分离过程 （均 相）
——过滤、沉降、离心分离等
——液体吸附、结晶 、浸取
第一节 概述
二、混合物组成的表示方法[409]
1.质量分率与摩尔分率

化工原理8.03

化工原理8.03

9
在上述吸收过程中，组分 A 不断被界面液体吸收，组分 B 则被界面阻留， 故组分 B 在界面处的浓度高于气相主体。 这样， 尽管液相不能向界面提供组分 B，组分 B 的反向扩散流依然存 在。组分 A 被液体吸收及组分 B 的反向扩散, 都将导致界面处 气体总压降低，使气相主体与界面之间产生微小压差。这一压 差必促使混合气体向界面流动，此流动称为主体流动。 主体流动不同于扩散流。扩散流是分子微观运动的宏观结 果，它所传递的是纯组分 A 或纯组分 B。 主体流动系宏观运动， 它同时携带组分 A 与 B 流向界面。在定态条件下，主体流动所 带组分 B 的量必恰好等于组分 B 的反向扩散，以使 CBi 保持定 态。 由此可见，即使液相主体不能向界面提供组分 B，但由于 主体流动的存在，组分 B 仍有反向扩散且 CBi 仍可保持定态。
对双组分混合物
dCB dz
（8-11）
D AB = DBA = D
代入（8-11）可得
（8-12）
即在同一物系中，组分 A 在 B 中的扩散系数等于组分 B 在 A 中的扩散系数。于是，将式（8-10）
J A = −J B
此式表明，组分 B 的扩散流 JB 与组分 A 的扩散流 JA 大小相等，方向相反。 分子扩散与主体流动
一般地说，对双组分物系，净物流速率 N 既包括组分 A 也包括组分 B，即
N = NA + NB
故
N A = J A + (N A + NB )
CA CM
（8-16）
由于主体流动乃因分子扩散而引起的一种伴生流动， 因而包括主体流动在内的组分 A 的传递速 率 NA 仍可理解为分子扩散所造成的总的宏观结果，故式（8-16）称为组分 A 的分子扩散速率方程。 分子扩散速率的积分式 上述分子扩散速率微分式中包含 NA 和 NB 两个未知数，只有已知 NB 和

单相传质

单相传质

（3）单相对流传质速率——有效膜模型; 传质系数k
31
32
作业：p245 7题
25
1）层流内层：分子扩散，A的浓度梯度较大 2）湍流主体：主要是涡流扩散，A浓度均一化 3）过渡区：分子扩散+涡流扩散
（2）有效膜模型 单相对流传质的传质阻力全部集中在一层虚拟
的膜层内，膜层内的传质形式仅为分子扩散 。 δG ≠δL
26
三、单相对流传质速率方程
速率 = 推动力 = 传质系数 ×传质推动力 阻力
2
分子扩散：在静止或层流流体内部，若某一组分存 在浓度差，则因分子无规则的热运动使 该组分由浓度较高处传递至浓度较低处。
扩散通量：单位时间内通过垂直于扩散方向的单位截 面积扩散的物质量。
J
单位 : kmol m2 ⋅s
4
二、菲克定律
总T、p一定
JA
=
− DAB
dcA dz
JA——A扩散速率（扩散通量）
=
D'c δ LcSm
⇒ N A = kL (cAi − cA )
以液相摩尔浓度差表示推动力的液相传质分系数 m / s
其他形式： N A = k x ( xi − x)
以液相摩尔分数差
kmol m 2 .s
29
NA = kX (Xi − X)
以液相摩尔比差
kmol m 2 .s
相互关系： k x = ckL
形式：等分子反向扩散、单向扩散 一、等分子反向扩散
Tp pA1 pB1
p A1 > p A2
7
JA 1
Tp
pA2 pB2 2
JB
A：1 ⇒ 2扩散 B： 2 ⇒1 扩散
等分子反向扩散：任一截面处两个组分的扩散速率 大小相等，方向相反。

化工原理-第8章 气体吸收


8.3 扩散和单相传质
① 溶质由气相主体传递到两相界面，即气相内的物质传递；
② 溶质在相界面上的溶解，由气相转入液相，即界面上发生 的溶解过程
③ 溶质自界面被传递至液相主体，即液相内的物质传递。 通常，第②步即界面上发生的溶解过程很容易进行，其阻力很小
( 传质速率 小，
=
传质推动力 传质阻力
)故认为相界面上的溶解推动力亦很
8.1概述
①溶剂应对被分离组分（溶质）有较大的溶解度，或者说在 一定的温度与浓度下，溶质的平衡分压要低。这样，从平衡角度 来说，处理一定量混合气体所需溶剂量较少，气体中溶质的极限 残余浓度亦可降低；就过程数率而言，溶质平衡分压↓，过程推 动力大，传质数率快，所需设备尺寸小。
②溶剂对混合气体中其他组分的溶解度要小，即溶剂应具备 较高的选择性。若溶剂的选择性不高，将同时吸收混合物中的其 他组分，只能实现组分间某种程度的增浓而不能实现较为完全的 分离。
⑷工业吸收流程（见旧讲稿） 由流程图可见，采用吸收操作实现气体混合物的分离必须解决下 列问题： ①选择合适的溶剂，使能选择性比溶解某个（或某些）被分离组 分； ②提供适当的传质设备（多位填料塔，也有板式塔）以实现气液 两相的接触，使被分离组分得以从气相转移到液相（吸收）或气相 (解吸)；
8.1概述
注意：此时并非没有溶质分子继续进入液相，只是任何瞬间 进入液相的溶质分子数与从液相逸出的溶质分子数恰好相等，在 宏观上过程就象是停止了。这种状态称为相际动平衡，简称相平 衡。
8.2.1平衡溶解度
⑴溶解度曲线
对 单 组 分 物 理 吸 收 的 物 系 ， 根 据相律 ，自 由度数F 为F=CΦ+2=3-2+2=3(C=3,溶质A，惰性组分B,溶剂S，Φ＝2，气、液两 相)，即在温度 t ，总压 p ，气、液相组成共4个变量中，由3个自 变量（独立变量），另1个是它们的函数，故可将平衡时溶质在气

分子扩散与单向传.


nA 3 c A ，kmol / m V
对于气体混合物：当总压p<1MPa,可 按照理想气体处理，其 摩尔浓度： 质量浓度：
nA pA cA V RT
mA M AnA M A p A CA V V RT
由道尔顿分压定律 摩尔分率：
nA p A yA , n p
气体混合物： 摩尔比：
分子扩散现象：
ABΒιβλιοθήκη 2.费克定律现以双组分气体（A+B），为例： 气体分子A,B处于不停地杂乱、 无规运动中，A与B及其自身相互碰 撞，改变速度大小和运动方向。
组分A的某个分子可能 在碰撞中由(1)处到达 (2)处。(2)处的A分子 可能到达(1)处。 1）若各处A的浓度相 等,则1-2与2-1的扩 散量相等，净传质=0 2）若A的浓度(1)>(2), 则1-2的A要多于2-1的A，净传质量>0
三.浓度：单位体积的物质的质量 或物质的量(摩尔数) 。 1.质量浓度： 2.摩尔浓度： 对于均相物系： CA CB CC ... Ci
m A wA m CA wA V V nA xAn cA x AC V V
mA 3 CA ，kg / m V
nA p A y A y Y nB pB yB 1 y
第二节：扩散原理 8-3 费克定律 1.相际传质概念： 当流体静止或作平行于相界面的层 流流动时，传质只能借助于分子的 热运动引起的扩散来进行。 分子扩散：流体内某一组分存 在浓度差时，则由于分子运动使组 分从浓度高处传递至浓度低处。
第一节 概述 8-1 化工生产中的传质过程 1.研究对象:均相物系的相际传质 2.常见的传质单元操作: 吸收—物质由气相进入液相 液液萃取—溶质由一液相进入另一液相 固液萃取—浸取，溶质由固相进入液相 结晶—溶质液相变为固相 干燥—液体经过气化，脱离固体 精馏—不同物质在气液两相间的转移

8.2_传质过程导论

A
C
D
NA z
c c cAB11
A2
cA1
NB
DcB2 z
cB1 cB2
气相：
NA
D 0
RTz
pA1 pA2 扩散距离 z
NB
zcAR2 DTz
pB1 pB2
等分子反向扩散
二、等摩尔相互扩散及速率方程 长江大学机械工程学院 School of Mechanical Engineering
讨论：
D N A z cA1 cA2
NA
D RTz
p
A1
pA2
(1) NA∝(cA1-cA2) NA∝(pA1-pA2)
（2）组分的浓度与扩散距离z成直线关系。
（3）等分子反向扩散发生在蒸馏过程中。
汽 相(A+B) A
B
液 相(A+B)
三、单向扩散及速率方程
1.单相扩散
总体流动：气相主体中的 溶质A扩散到界面并溶解 于溶剂中，造成的空位由 混合气体填补，致使气相 主体与界面产生一小压差， 促使混合气体由气相主体 向界面处的流动。
NA
Nb
cB c
Nb
cA c
Nb
cB
cA c
Nb
NA
JA
Nb
cA c
D
dcA dz
NA
cA c
NA
Dc c cA
dcA dz
气相扩散:
cA
pA RT
c p RT
N
A
RT
D p
pA
dpA dz
D dpA 长江大学机械工程学院
School of Mechanical Engineering
三、单向扩散及速率方程 N A

第8章 化工原理气体吸收


8.3.1双组分混合物中的分子扩散
⑴费克定律 温度、总压一定，组分A在扩散方向上任 一点处的扩散通量与该处A的浓度梯度成正比。
dCA J A DAB d
JA——组分A扩散速率（扩散通量）， kmol/（m2· s）；
dCA ——组分A在扩散方向z上的浓度梯度（kmol/m3）/m； d DAB——组分A在B组分中的扩散系数，m2/s。
பைடு நூலகம்G L
8.3.5对流传质理论
②数学模型
DG p DG 1 ( pA pAi ) p ( y yi ) 气膜 N A RT G pBm RT G yBm
式中：
pBm yBm (1 y ) m p DG DG 1 DG p 1 kG RT G pBm RT G yBm RT G (1 y )m
pB1 pA1 pA2
0 扩散距离z
z
3）等分子反方向扩散发生在蒸馏过程中。
2．单向扩散及速率方程
JA
（1）总体流动：因溶质Ａ扩散到界面溶 解于溶剂中，造成界面与主体的微小压差， NMcA/c 使得混合物向界面处的流 动。 总体流 动NM NMcB/c （2）总体流动的特点： JB 1）因分子本身扩散引起的宏观流动。 2）A、B在总体流动中方向相同，流动 速度正比于摩尔分率。 1 2
负号：表示扩散方向与浓度梯度方向相反，扩散沿 着浓度降低的方向进行。 理想气体：
pA cA RT
dc A 1 dp A = dz RT dz
DAB dpA JA RT dz
8.3.1双组分混合物中的分子扩散
对双组分混合物，总浓度 CM CA CB ＝常数
dC A dC B d d
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

8.3 扩散和单相传质在分析任一化工过程时都需要解决两个基本问题：过程的极限和过程的数率。

吸收过程的极限决定于吸收的相平衡常数，在8.2节中作了讨论。

本节将讨论吸收的速率问题。

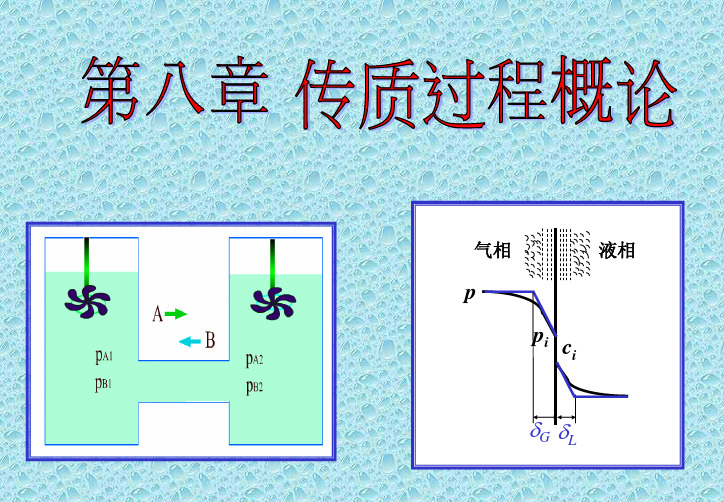
吸收过程涉及两相间的物质传递，它包括三个步骤：① 溶质由气相主体传递到两相界面，即气相内的物质传递；② 溶质在相界面上的溶解，由气相转入液相，即界面上发生的溶解过程③ 溶质自界面被传递至液相主体，即液相内的物质传递。

通常，第②步即界面上发生的溶解过程很容易进行，其阻力很小（传质阻力传质推动力传质速率=）故认为相界面上的溶解推动力亦很小，小至可认为其推动力为零，则相界面上气、液组成满足相平衡关系，这样总过程的速率将由两个单相即①步气相和③步液相内的传质速率所决定。

无论是气相还是液相，物质传递的机理包括以下两种。

（1）分子扩散。

类似于传热中的热传导，是分子微观运动的宏观统计结果。

混合物中存在温度梯度、压强梯度及浓度梯度都会产生分子扩散，本章仅讨论因浓度梯度而造成的分子扩散速率。

发生在静止或层流流体里的扩散就是分子扩散。

（2）对流传质。

是凭藉流体质点的湍流和漩涡而引起的扩散称为对流传质。

发生在湍流流体里的传质除分子扩散外更主要的是对流传质。

将一勺砂糖投于杯水中，片刻后整杯的水都会变甜，这就是分子扩散的结果。

若用勺搅动杯中水，则将甜得更快更均匀，那便是对流传质的结果。

以下仅讨论定态条件下双组分物系的分子扩散和对流传质。

8.3.1双组分混合物中的分子扩散（1）费克定律只要流体内部有浓度梯度，就会产生分子扩散，在恒温恒压下，一维分子扩散速率可用费克定律表达如下：δd dC D J A ABA -= 浓度梯度δd dC A 指向浓度增加的方向，而扩散向浓度降低的方向进行，故式中加－负号。

AB D 为组分A 在双组分混合物A 、B 中的扩散系数。

对双组分混合物，在总浓度（对气相也可说总压）各处相等及B A M C C C +=＝常数的前提下，也有δδd d d d B A C C -= B A J J -=(前提M C 为常数，对气压为总压P 不变)也就是说费克定律中的“2m ”为“分子对称面”，A 、B 两组分的分子扩散速率大小相等，方向相反，否则就不能保证总浓度M C （或总压P ）不变。

δδd d )d d (A BA B AB B A C D C D J J -=--=-= D D D BA AB ==∴（2）分子扩散与主体流动气液相界面只允许溶质A 溶解穿过，惰性气体B 不能溶解穿过，也不允许溶剂S 逆向汽化通过。

由于界面处A 组分不断被溶解吸收，i C C A A >，A 组分存在浓度梯度 δd d A C ,其方向指向A 组分浓度高的方向为正，而A 组分的分子扩散方向与其相反，朝界面扩散→A J 惰性气体B 组分由于不能被液体吸收，故B 组分在相界处的浓度高于气相主体B B i c c >，B 组分存在浓度梯度B d d c z，其方向指向B 组分浓度高的方向为正，而B 组分的分子扩散方向与其相反，朝气相主体扩散。

当液相能以同一速率向界面供应B 组分时，界面处B i c 保持恒定，则A B J J =-，这种情况属于等分子反向扩散（下一章精馏属于这种情况）。

吸收过程液相不存在B 组分，不可能向截面提供B 组分，故吸收过程所发生的是组分A 的单向扩散，而不是等分子反向扩散。

由于界面处组分A 被液体吸收及组分B 反向扩散离开界面，都将导致截面处气体总压降低，使气相主体与界面之间产生微小压差，这一压差必然促使混合气体向界面流动，此流动称为主体流动。

主体流动不同于扩散流（A J 或B J ），扩散流是分子微观运动的宏观结果，它所传递的是纯组分A 或纯组分B 。

主体流动系宏观运动，它同时携带组分A 与B 流向界面。

在定态条件下，主体流动所带组分B 的量必恰好等于组分B 反向扩散的量，以使B i c 保持恒定。

因气相主体与界面间的微小压差便足以造成必要的主体流动，因此气相各处的总压（或M c ）仍可认为基本上是相等的，即A B J J =-的前提依然成立。

（3）分子扩散的速率方程通过静止或层流气膜中与界面平行的任一静止平面PQ 的物流由三个：两个扩散流A J 和B J ，及一个主体流动M N 。

设通过静止考擦平面PQ 的净物流为N ，对平面PQ 作总物料衡算可得()M A B M A B N N J J N J J =++==-式中：N ——2kmol m s⋅ M N ——2kmol m s⋅ A J ——2kmol m s⋅ B J ——2kmol m s ⋅ 上式说明，尽管主体流动与净物流的含义不同，但主体流动的速率M N 与净物流速率N 必相等。

为了求出组分A 因分子扩散和主体流动而造成的传质速率A N ,可在平面PQ 处组分A 作物料衡算得：A A A A MA M M c c N J N J N c c =+=+ 式中： A J ——因组分A 存在浓度梯度引起的分子扩散速率；A M Mc N c ——主体流动中A 所占的传递速率。

一般情况下，对双组分物系，净物流速率N 即包括组分A 也包括组分B ，即A B N N N =+ 故： A A A A B M()c N J N N c =++ (8-16) A J 与Ad d c z 有关（4）分子扩散速率的积分式上式分子扩散速率微分式中包含A N 和B N 两个未知数，只有已知A N 和B N 之间的关系时，才能积分求解A N ，下面讨论两种常见的情况。

① 等分子反向扩散（精馏）等分子反向扩散时没有净物流0N =（因而也无主体流动M N ＝0），则A B N N =-，故 A A A d dzc N J D ==- 2211A Ad d A A z c z c J z D c =-⎰⎰令21z z δ-=，δ为扩散距离，积分上式得()A A1A2DJ c c δ=-此式表明等分子反向扩散时组分A 的浓度分布为一直线。

如图8-11所示。

对气相 A A A n p c V RT== A A1A2()D J p p RT δ=- ② 单向扩散（吸收）前已述及，吸收过程主体流动所带组分B 的量必等于组分B 反向分子扩散的量，故惰性组分B 的净传递速率A B A A A M0,c N N J N c ==+，可改写为： 2A21A1A A A M A A M M A M M A2M B2A 21M A1B1d (1)d d d ln ln z c z c c c N D c z c N z Dc c c Dc c c Dc c N z z c c c δ-=-=---==--⎰⎰令 B2B1Bm B2B1ln c c c c c -= 则 B 2B 2B 1A 1A 2B 1B m B mln c c c c c c c c --== M A 1B 1A 2B 2B 1A 1A 2c c c c c c c c c =+=+-=- 故 M A A 1A 2Bm ()c D N c c c δ=- 此式表面单向扩散时组分A 的浓度分布为一对数函数，如图8-12所示。

对气相B2B2A1A2M B1B1BM,ln ln c p p p p c RT c p p -=== B2A A1A2Bm B1()()ln p D p Dp N p p RT p RT p δδ=-= 与等分子反向扩散速率方程相比，单向扩散时多了一个因子MBm cc或Bmp p ， M Bm Bm 1(1)c p c p >>，我们称之为漂流因子（数），它反映了主体流动对传质速率的影响，Bm p p ↑，主体流动作用↑，对吸收愈好，这就如顺水推舟，水流使船速加大，故称之为漂流因子。

若A c ↓↓,Bm Bm ,1p p p p ≈≈，主体流动的影响可略去。

8.3.2扩散系数扩散系数是物质的一种传递性质。

它在传质中的作用与导热系数在传热中的作用相类似，但比导热系数更为复杂：一种物质的扩散总是相对于其他物质而言的，所以它至少要涉及两种物质，同一组分在不同混合物中的扩散系数是不一样的；扩散系数还与体系体系的温度、总压（气相）或浓度（液相有关）。

目前，扩散系数可由以下3种途径获得：① 试验测得。

试验测定是求物质扩散系数的根本途径，后面通过例8-2说明试验测定扩散系数的方法，当然还有其他的试验测定法。

② 有的手册中查得。

③ 借助某些经验的或半经验的公式进行估算（查不到D 又缺乏进行试验测定的条件时）。

（1） 组分在气体中的扩散系数表8-1列出总压在101.3kpa 下某些气体在空气中的扩散系数数值，由表可见气体扩散系数的值约为12101/cm s - 。

经分子运动论的理论推导与试验修正，可以得到估算气体扩散系数的半经验式，如式（8-23）所示。

该式形式复杂不须记住，只要能正确使用即可。

由该式可知气体扩散系数D 与A 、B 两组分的性质、体系和温度、压强有关。

对一定物系气体D 与绝对温度T 的1.81次方成正比，与压强p 成反比，式（8-24）须记住。

例8-2，解：4CCl 通过静止气体层的扩散为单向扩散，且为一非定态过程，但因扩散距离z 的变化缓慢，故可作为拟定态处理。

扩散速率可用式（8-22）表示B2A B1ln p Dp N RTz p = A1A2101.3,37.6,0p kpa p kpa p ==≈B1A1101.337.663.7p p p kpa =-=-=8.314KJ/(KmolgK),321K R T ==为求D 必须知道A N ,设汽化时间为τ，则4CCl 的汽化速率也可用液面高度变化的速率表示，即L L A A A d d d d A z z N M A M ρρττ== 3L A 1540Kg/m 154Kg/KmolM ρ== 所以 L B2A B1d ln d p z Dp M RTz p ρτ=0A B20L B1d ln d zz M p Dp z z RT p ττρ=⎰⎰ ()2A B220L B11ln 2M p DP z z RT p τρ-= ()220LB2A B12ln z z RT D p M p p ρτ-= =3223315408.314103210.060.01101.3154210910101.310ln 63.7⨯⨯-⨯⨯⨯⨯⨯ =9.12×10-6m 2/s注意：①本题的难点在何处？（A N ）②本解法与书本解法的区别在何处？（2） 组分在液体中的扩散系数表8-3列出了某些物质在液体中的扩散系数，由于液体中的分子要比气体中的分子密集的多，可以预计其扩散系数要比气体中的扩散系数小的多，由表8-3知，液体中的扩散系数的数量级约为10-5cm 2/s ，为气相中的万分之一（气相约10-1～1cm 2/s ）。