二次函数-因动点产生的面积问题典型例题

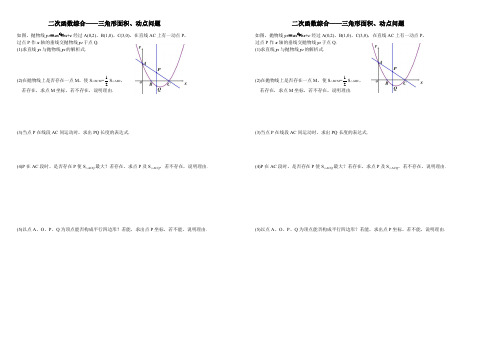
二次函数综合——三角形面积、动点问题 二次函数综合——三角形面积、动点问题
如图，抛物线y 2＝ax 2
+bx+c 经过A(0,2)、B(1,0)、C(3,0)，在直线AC 上有一动点P ， 过点P 作x 轴的垂线交抛物线y 2于点Q. (1)求直线y 1与抛物线y 2的解析式.
(2)在抛物线上是否存在一点M ，使S △BCM =
21
S △ABC ， 若存在，求点M 坐标，若不存在，说明理由.
(3)当点P 在线段AC 间运动时，求出PQ 长度的表达式.
(4)P 在AC 段时，是否存在P 使S △ACQ 最大？若存在，求点P 及S △ACQ ，若不存在，说明理由.
(5)以点A 、O 、P 、Q 为顶点能否构成平行四边形？若能，求出点P 坐标，若不能，说明理由. 如图，抛物线y 2＝ax 2
+bx+c 经过A(0,2)、B(1,0)、C(3,0)，在直线AC 上有一动点P ， 过点P 作x 轴的垂线交抛物线y 2于点Q. (1)求直线y 1与抛物线y 2的解析式.
(2)在抛物线上是否存在一点M ，使S △BCM =
2
1
S △ABC ， 若存在，求点M 坐标，若不存在，说明理由.
(3)当点P 在线段AC 间运动时，求出PQ 长度的表达式.
(4)P 在AC 段时，是否存在P 使S △ACQ 最大？若存在，求点P 及S △ACQ ，若不存在，说明理由.
(5)以点A 、O 、P 、Q 为顶点能否构成平行四边形？若能，求出点P 坐标，若不能，说明理由.。

考向3.10 二次函数-面积问题例1、（2021·四川雅安·中考真题）已知二次函数223y x bx b =+-． （1）当该二次函数的图象经过点1,0A 时，求该二次函数的表达式；（2）在(1) 的条件下，二次函数图象与x 轴的另一个交点为点B ，与y 轴的交点为点C ,点P 从点A 出发在线段AB 上以每秒2个单位长度的速度向点B 运动，同时点Q 从点B 出发，在线段BC 上以每秒1个单位长度的速度向点C 运动，直到其中一点到达终点时，两点停止运动，求△BPQ 面积的最大值;（3）若对满足1≥x 的任意实数x ，都使得0y ≥成立，求实数b 的取值范围．解：（1）把1,0A 代入223y x bx b =+-， 得：20123b b =+-，解得：b =1，∴该二次函数的表达式为：223y x x =+-； （2）令y =0代入223y x x =+-， 得：2023x x =+-， 解得：11x =或23x =-，令x =0代入223y x x =+-得：y =-3， ∴A (1，0)，B (-3，0)，C (0，-3)， 设运动时间为t ，则AP =2t ，BQ =t ， ∴BP =4-2t ，过点M 作MQ ⊥x 轴， ∵OB =OC =3， ∴∠OBC =45°，∴BMQ 是等腰直角三角形，∴MQ =22BQ =22t ， ∴△BPQ 的面积=()11222242BP MQ t t -⋅=⋅=()222122t --+，∴当t =1时，△BPQ 面积的最大值=22；（3）抛物线223y x bx b =+-的对称轴为：直线x =-b ，开口向上， 设2()23y f x x bx b ==+-，∵对1≥x 的任意实数x ，都使得0y ≥成立，∴()110b f -≤⎧⎨≥⎩或()10b f b ->⎧⎨-≥⎩，∴-1≤b ≤1或-3≤b ＜-1， ∴-3≤b ≤1．1、二次函数面积问题的几种形式（1）直接用面积公式；（2）三角形的面积等于铅直高度与水平宽度积的一半；(3)平行线等面积法（通过做平行线辅助线完成）。

二次函数综合大题面积最大问题1(东城二模).如图，在平面直角坐标系xOy 中，已知二次函数2+2y ax ax c =+的图像与y 轴交于(0,3)C ，与x 轴交于A 、B 两点，点B 的坐标为(-3,0) （1） 求二次函数的解析式及顶点D 的坐标；（2） 点P 是第二象限内抛物线上的一动点，问：点P 在何处时△CPB 的面积最大？最大面积是多少？并求出 此时点P 的坐标.2.如图，抛物线经过(40)(10)(02)A B C -，，，，，三点．（1）求出抛物线的解析式；（2）在直线AC 上方的抛物线上有一点D ，使得DCA △的面积最大，求出点D 的坐标C-241y xA BO3.如图所示，在平面直角坐标系中，Rt △OBC 的两条直角边分别落在x 轴、y 轴上， 且OB=1,OC=3,将△OBC 绕原点O 顺时针旋转90°得到△OAE ，将△OBC 沿y 轴翻折得到△ODC ，AE 与CD 交于点F.（1）若抛物线过点A 、B 、C, 求此抛物线的解析式;（2）求△OAE 与△ODC 重叠的部分四边形ODFE 的面积; （3）点M 是第三象限内抛物线上的一动点，点M 在何处时△AMC 的面积最大？最大面积是多少？求出此时点M 的坐标.4.已知关于x 的一元二次方程242(1)0x x k -+-=有两个不相等的实数根． （1）求k 的取值范围；（2）如果抛物线242(1)y x x k =-+-与x 轴的两个交点的横坐标为整数，求正整数k 的值；（3）直线y =x 与（2）中的抛物线在第一象限内的交点为点C ，点P 是射线OC 上的一个动点（点P 不与点O 、点C 重合），过点P 作垂直于x 轴的直线，交抛物线于点M ，点Q 在直线PC 上，距离点P 为2个单位长度，设点P 的横坐标为t ，△PMQ 的面积为S ，求出S 与t 之间的函数关系式．12345–1–2–3–412345–1–2xy O5.在平面直角坐标系中，已知抛物线经过A(4,0)-，B(0,4)-，C(2,0)三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S 关于m的函数关系式，并求出S的最大值．AB CMyx O。

2023年九年级数学中考专题：二次函数综合压轴题（面积问题）1．如图，二次函数25y ax bx =++的图象经过点(1,8)，且与x 轴交于A 、B 两点，与y 轴交于点C ，其中点(1,0)A -，M 为抛物线的顶点．(1)求二次函数的解析式； (2)求MCB △的面积；(3)在坐标轴上是否存在点N ，使得BCN △为直角三角形？若存在，求出点N 的坐标；若不存在，请说明理由．2．如图，抛物线212y x bx c =-++（b 、c 为常数）经过()4,0A 和()0,4B 两点，其顶点为C ．(1)求该抛物线的表达式及其顶点坐标；(2)若点M 是拋物线上第一象限的一个动点．设ABM 的面积为S ，试求S 的最大值； (3)若抛物线222y mx mx m =-++与线段AB 有两个交点，直接写出m 的取值范围． 3．如图，抛物线22(0)y ax ax c a =-+>与y 轴交于点C ，与x 轴交于A ，B 两点，点A 在点B 左侧．点A 的坐标为(1,0),3OC OA -=．(1)求抛物线的解析式；(2)在直线BC 下方的抛物线上是否存在一点P ，使得PBC 的面积等于ABC 面积的三分之二？若存在，求出此时OP 的长；若不存在，请说明理由．(3)将直线AC 绕着点C 旋转45︒得到直线l ，直线l 与抛物线的交点为M （异于点C ），求M 点坐标．4．如图1，抛物线24y ax bx a =+-经过()10A -，，()04C ，两点，与x 轴交于另一点B ．(1)求抛物线和直线BC 的解析式；(2)如图2，点P 为第一象限抛物线上一点，是否存在使四边形PBOC 面积最大的点P ？若存在，求出点P 的坐标；若不存在，请说明理由；(3)如图3，若抛物线的对称轴EF （E 为抛物线顶点）与直线BC 相交于点F ，M 为直线BC 上的任意一点，过点M 作MN EF ∥交抛物线于点N ，以E ，F ，M ，N 为顶点的四边形能否为平行四边形？若能，请求出点N 的坐标；若不能，请说明理由． 5．如图，抛物线24y ax bx =+-与x 轴交于点()2,0A -，()4,0B ，与y 轴交于点C ，顶点为D ．(1)求抛物线的解析式和顶点D 的坐标；(2)动点P ，Q 以相同的速度从点O 同时出发，分别在线段,OB OC 上向点B ，C 方向运动，过点P 作x 轴的垂线，交抛物线于点E ． ①当四边形OQEP 为矩形时，求点E 的坐标；①过点E 作EM BC ⊥于点M ，连接,PM QM ，设BPM △的面积为1S ，CQM 的面积为2S ，当PE 将BCE 的面积分成1:3两部分时，请直接写出12S S 的值． 6．如图，抛物线2(0)y ax bx c a =++≠与x 轴相交于A ，B 两点，抛物线的对称轴为直线=1x -，其中点A 的坐标为(3,0)-．(1)求点B 的坐标；(2)已知1a =，C 为抛物线与y 轴的交点，求抛物线的解析式； (3)若点P 在抛物线上，且4POCBOCSS=，求点P 的坐标；(4)设点Q 是线段AC 上的动点，过点Q 作QD y 轴交抛物线于点D ，求线段QD 长度的最大值．7．如图，在平面直角坐标系中，二次函数22y ax bx =++的图象与x 轴交于()30A -,，()10B ,两点，与y 轴交于点C ．(1)求二次函数的解析式；(2)点P 是直线AC 上方的抛物线上一动点，当ACP △的面积最大时，求点P 的坐标；(3)Q 是x 轴上一动点，M 是第二象限内抛物线上一点，若以A ，C ，M ，Q 为顶点的四边形是平行四边形，直接写出点Q 的坐标．8．如图，直线132y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c =-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出点A ，点B ，点C 的坐标及抛物线的解析式；(2)在直线AC 上方的抛物线上有一点M ，求四边形ABCM 面积的最大值及此时点M 的坐标；(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请结合函数图象，求m 的取值范围．9．如图，已知抛物线与x 轴交于()1,0A - 、()4,0B 两点，与y 轴交于点()0,3C ．(1)求抛物线的解析式； (2)求直线BC 的函数解析式；(3)在抛物线上，是否存在一点P ，使PAB 的面积等于ABC 的面积？若存在，求出点P 的坐标；若不存在，请说明理由．10．如图，抛物线26y ax bx =++与x 轴交于点()6,0B ，()2,0C -，与y 轴交于点A ，点P 是线段AB 上方抛物线上的一个动点．(1)求抛物线的解析式；(2)当点P 运动到什么位置时，PAB 的面积最大？(3)过点P 作x 轴的垂线，交线段AB 于点D ，再过点P 作PE x ∥轴交抛物线于点E ，连接DE ．是否存在点P ，使PDE △为等腰直角三角形？若存在，求点P 的坐标；若不存在，请说明理由．11．如图，直线l ：112y x =-+与x 轴，y 轴分别交于点B ，C ，经过B ，C 两点的抛物线2y x bx c =++与x 轴的另一个交点为A ．(1)求该抛物线的解析式；(2)若点P 在直线l 下方的抛物线上，过点P 作PD ①x 轴交l 于点D ，PE ①y 轴交l 于点E ，求PD PE +的最大值；(3)若点P 在直线l 下方的抛物线上，F 为直线l 上的点，以A ，B ，P ，F 为顶点的四边形能否构成平行四边形？若能，直接写出点F 的坐标；若不能，请说明理由． 12．已知顶点为()1,5A 的抛物线2y ax bx c =++经过点()5,1B ，(1)求抛物线的解析式；(2)设C ，D 分别是x 轴、y 轴上的两个动点．①当四边形ABCD 的周长最小时，在图1中作直线CD ，保留作图痕迹并直接写出直线CD 的解析式；①点()(),>0P m n m 是直线y x =上的一个动点，Q 是OP 的中点，以PQ 为斜边按图2所示构造等腰Rt PQR △．在①的条件下，记PQR 与COD △的公共部分的面积为S ，求S 关于m 的函数关系式，并求S 的最大值．13．抛物线24y x x =-与直线y x =交于原点O 和点B ， 与x 轴交于另一点A ， 顶点为D ．(1)填空： 点B 的坐标为___________， 点D 的坐标为___________．(2)如图1 ， 连结OD P ，为x 轴上的动点， 当以O D P ，，为顶点的三角形是等腰三角形时， 请直接写出点P 的坐标；(3)如图2， M 是点B 关于拋物线对称轴的对称点， Q 是拋物线上的动点， 它的横坐标为 (05)m m <<， 连结MQ BQ MQ ，，与直线OB 交于点E ． 设BEQ 和BEM △的面积分别为1S 和2S ， 设12S t s =， 试求t 关于m 的函数解析式并求出t 的最值． 14．如图，二次函数的图象经过点()10A -，，()30B ，，()03C -，，直线22y x =-与x 轴、y 轴交于点D ，E ．(1)求该二次函数的解析式(2)点M 为该二次函数图象上一动点．①若点M 在图象上的B ，C 两点之间，求DME 的面积的最大值． ①若MED EDB ∠∠=，求点M 的坐标．15．如图，在平面直角坐标系中，抛物线24y ax bx =+-与x 轴交于()2,0A -，B 两点，其对称轴直线2x =与x 轴交于点D ．(1)求该抛物线的函数表达式为______；(2)如图1，点P 为抛物线上第四象限内的一动点，连接CD ，PB ，PC ，求四边形BDCP 面积最大值和点P 此时的坐标；(3)如图2，将该抛物线向左平移得到抛物线y '，当抛物线y '经过原点时，与原抛物线的对称轴相交于点E ，点F 为抛物线y '对称轴上的一点，点M 是平面内一点，若以点A ，E ，F ，M 为顶点的四边形是以AE 为边的菱形，请直接写出满足条件的点M 的坐标______．16．如图，已知抛物线2y x bx c =++与x 轴交于点()21,0A m -和点()2,0B m +，与y 轴交于点C ，对称轴轴为直线=1x -．(1)求抛物线的解析式；(2)点P 是直线AC 上一动点，过点P 作PQ y ∥轴，交抛物线于点Q ，以P 为圆心，PQ 为半径作P ，当P 与坐标轴相切时，求P 的半径；(3)直线()340y kx k k =++≠与抛物线交于M ，N 两点，求AMN 面积的最小值．17．如图，在平面直角坐标系中，抛物线23y ax bx =+-与x 轴交于两点()1,0A -和()3,0B ，与y 轴交于点C ，抛物线上有一动点P ，抛物线的对称轴交x 轴于点E ，连接EC ，作直线BC ．(1)求抛物线的解析式；(2)若点P 为直线BC 上方抛物线上一动点时，连接,PB PC ，当23EBC PBC S S =△△时，求点P 坐标；(3)如果抛物线的对称轴上有一动点Q ，x 轴上有一动点N ，是否存在四边形PQCN 是矩形？若存在，在横线上直接写出点N 的坐标，若不存在，请说明理由． 18．如图，直线122y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c=-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出点A ，点B ，点C 的坐标及抛物线的解析式；(2)在直线AC 上方的抛物线上有一点M ，求三角形ACM 面积的最大值及此时点M 的坐标；(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90︒得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请结合函数图象，求m 的取值范围（直接写出结果即可）．参考答案：1．(1)245y x x =-++； (2)15(3)存在，点N 的坐标为(5,0)-或(0,5)-或(0,0)．2．(1)2142y x x =-++，91,2⎛⎫⎪⎝⎭(2)S 的最大值为4 (3)2m ≥或1249m -<≤-3．(1)抛物线的解析式为2=23y x x -- (2)不存在这样的点P ， (3)M 点坐标是(45)，或315()24-，4．(1)抛物线的解析式：234y x x =-++；直线BC 的解析式为4y x =-+；(2)当()26P ，时，四边形PBOC 面积最大； (3)能，点N 的坐标为52124⎛⎫ ⎪⎝⎭，或724⎛- ⎝或724⎛- ⎝．5．(1)2142y x x =--，91,2D ⎛⎫- ⎪⎝⎭．(2)①(-；①1215S S =或1279S S =6．(1)(1,0) (2)223y x x =+- (3)(4,21)或()4,5- (4)947．(1)224233y x x =--+(2)3(2P -，5)2(3)(5,0)-或(1,0)-8．(1)03A （，），20B -（，），60C （，），抛物线解析式为：2134y x x =-++； (2)3a =时，四边形ABCM 面积最大，其最大值为754，此时M 的坐标为153,4⎛⎫⎪⎝⎭；(3)当3m -≤≤-33m ≤≤时，线段O A ''与抛物线只有一个公共点．9．(1)239344y x x =-++(2)334y x =-+(3)存在，点P 的坐标为：()13,3P ，23P ⎫-⎪⎪⎝⎭，33P ⎫-⎪⎪⎝⎭10．(1)21262y x x =-++(2)153,2P ⎛⎫ ⎪⎝⎭(3)点P 坐标为()46，或()55．11．(1)2512y x x =-+ (2)3(3)13,2⎛⎫- ⎪⎝⎭或1(1,)212．(1)21119424y x x =-++(2)①4y x =-+；①当02m <≤时，218PQRSm =；当823m <≤时，27448S m m =-+-；当843m ≤≤时，21244S m m =-+；S 的最大值为：47答案第3页，共3页 13．(1)()5,5；()2,4-；(2)点P的坐标为()或()-或()4,0或()5,0； (3)()2150566t m m m =-+<<，当52m =时，t 的最大值为2524．14．(1)该二次函数的解析式是()()21323y x x x x =+-=--；(2)①DME 的面积的最大值为52；①点M的坐标为⎝⎭或()12--．15．(1)214433y x x =-- (2)PBDC S 四边形的最大值为17，此时点P 的坐标为()3,5-(3)⎛ ⎝⎭或⎛ ⎝⎭或⎛- ⎝⎭或8,⎛- ⎝⎭16．(1)223y x x =+-(2)2或4(3)817．(1)2=23y x x --(2)⎝⎭或⎝⎭ (3)存在，⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭18．(1)()0,2A ，()2,0B -，()4,0C ，211242y x x =-++ (2)2，()2,2(3)34m -≤≤-或32m -+≤。

专题9：由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题，而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路，而后“以静制动”、“转化求解”. 即把动态问题变为静态问题，变为我们所熟知的模型来解。

基本模型一利用“铅垂高、水平宽”求三角形面积.面积公式：S =12ah 基本模型二CABD其中：:ACD BCD S S AD BD =△△： ，:ACD BCA S S AD BA =△△： 基本模型三OB()12AOB ACB AOBC S S S a h OA =+=+△△四边形 类型一、一次函数由动点问题引出的面积问题例1. 如图例1-1，在平面直角坐标系中，直线121y x =+和直线2443y x =-+交于点A . 直线y n =从x 轴出发以每秒2个单位的速度向上运动，至通过A 点时停止. 在运动过程中，直线y n =分别交y 1、y 2两条直线于C 、B 两点，交y 轴于点D . 连接OC 、OB .（1）设运动时间为t （s ），求t 的取值范围.（2）求出△OBC 的面积S 与t 的函数关系式，并求出S 的最大值及此时n 的值.y=n类型二、二次函数由动点问题引出的面积问题例2. 如图例2-1，二次函数y =ax 2+bx +c 的图像与x 轴的交点为A 、D (A 在D 的右侧），与y 轴的交点为C ，且A (4，0)，C (0，－3)，对称轴是直线x =1． (1)求二次函数的解析式；(2)若M 是第四象限抛物线上一动点，且横坐标为m ，设四边形OCMA 的面积为S ．请写出S 与m 之间的函数关系式，并求出当m 为何值时，四边形OCMA 的面积最大.图例2-1图例2-2类型三、反比例函数由动点问题引出的面积问题例3. 如图例3-1，直线y＝2x＋6与反比例函数kyx(k＞0)的图象交于点A(1，m)，与x轴交于点B，平行于x轴的直线y＝n(0＜n＜6)交反比例函数的图象于点M，交AB于点N，连接BM.(1)求m的值和反比例函数的表达式；(2)直线y＝n沿y轴方向平移，当n为何值时，△BMN的面积最大？图例3-1类型四、利用三角函数求解由动点问题引出的面积问题例4. 如图例4-1，在矩形OABC中，点O为原点，边OA的长度为8，对角线AC＝10，抛物线y ＝－49x 2＋bx ＋c 经过点A 、C ，与AB 交于点D .(1)求抛物线的解析式；(2)点P 为线段BC 上一个动点(不与点C 重合)，点Q 为线段AC 上一个动点，AQ ＝CP ，连接PQ ，设CP ＝m ，△CPQ 的面积为S . 求S 关于m 的函数表达式并求出S 最大时的m 值.图例4-1.类型五、由动点问题引出的面积存在性问题例5. 如图例5-1，在平面直角坐标系中，△ABC 是等腰直角三角形，∠BAC =90°，A （1，0），B （0，2），C （3，1）抛物线2122y x bx =+-的图象过C 点，交y 轴于点D ． （1）在后面的横线上直接写出点D 的坐标及b 的值： ，b = ；（2）平移该抛物线的对称轴所在直线l ，设l 与x 轴交于点G （x ，0），当OG 等于多少时，恰好将△ABC的面积分为相等的两部分？AOxyBCGF H E图例5-1 图例5-2类型六、利用转化思想解决由动点问题引出的面积问题如图例6-1，在平面直角坐标系中，抛物线24 5y ax x c=++与直线2255y x=--交于A、B两点，已知点B的横坐标是4，直线2255y x=--与x、y轴的交点分别为A、C，点P是抛物线上一个动点.（1）求抛物线的解析式；（2）若点P在直线2255y x=--上方，求△P AC的最大面积.OxyPACBGEH 图例6-1专题9：由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题，而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路，而后“以静制动”、“转化求解”. 即把动态问题变为静态问题，变为我们所熟知的模型来解。

二次函数面积问题专题练习1. 如图，抛物线2y x bx c =++交x 轴于A ，()3,0B 两点，交y 轴于点()0,3C -．点P 是抛物线上动点．(1)求该抛物线的函数表达式；(2)当点P 的坐标为()1,4-时，求四边形BACP 的面积；(3)当动点P 在直线BC 上方时，在平面直角坐标系是否存在点Q ，使得以B ，C ，P ，Q 为顶点的四边形是矩形？若存在，请求出点Q 的坐标；若不存在，请说明理由；2. 如图1，抛物线23y ax bx =++经过()()1,0,3,0A B 两点，交y 轴于点C ．(1)求抛物线的函数解析式．(2)在抛物线的对称轴上是否存在一点M ，使得ACM △的周长最小？若存在，求出点M 的坐标；若不存在，请说明理由．(3)如图2，连接BC ，若在BC 下方的抛物线上存在一点P ，使得12BCP BCA S S =△△，请直接写出点P 的横坐标．3.如图，在平面直角坐标系中，点A 的坐标为()m m -，，点B 的坐标为()n n ，，抛物线经过A ，O ，B 三点，连接OA ，OB ，AB ，线段AB 交y 轴于点C ，实数m ，n （m n <）分别是方程2230x x +-=两根．(1)求抛物线的解析式；(2)若点P 为线段OA 上的一个动点（不与点O ，A 重合），直线PC 与抛物线交于D ，E 两点（点D 在y 轴左侧），连接OD ，AD ．①求AOD △面积的最大值，并求出此时点D 的坐标；①当OPC 为等腰三角形时，请直接写出点P 的坐标．4.如图，抛物线y ＝﹣x 2+bx +c 与x 轴交于点A （﹣2，0）和B （1，0），与y 轴交于点C ．（1）求抛物线的表达式；（2）作射线AC ，将射线AC 绕点A 顺时针旋转90°交抛物线于另一点D ，在射线AD 上是否存在一点H ，使△CHB 的周长最小．若存在，求出点H 的坐标；若不存在，请说明理由；（3）在（2）的条件下，点Q 为抛物线的顶点，点P 为射线AD 上的一个动点，且点P 的横坐标为t ，过点P 作x 轴的垂线l ，垂足为E ，点P 从点A 出发沿AD 方向运动，直线l 随之运动，当﹣2＜t ＜1时，直线l 将四边形ABCQ 分割成左右两部分，设在直线l 左侧部分的面积为S ，求S 关于t 的函数表达式．5．已知抛物线y＝ax2+bx﹣4经过点A（2，0）、B（﹣4，0），与y轴交于点C．（1）求这条抛物线的解析式；（2）如图1，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点P的坐标；（3）如图2，线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，求出点G的坐标；若不存在，请说明理由．6．在平面直角坐标系xOy中，顶点为A的抛物线与x轴交于B、C两点，与y轴交于点D，已知A（1，4），B（3，0）．（1）求抛物线对应的二次函数表达式；（2）探究：如图1，连接OA，作DE∥OA交BA的延长线于点E，连接OE交AD于点F，M是BE的中点，则OM是否将四边形OBAD分成面积相等的两部分？请说明理由；（3）应用：如图2，P（m，n）是抛物线在第四象限的图象上的点，且m+n＝﹣1，连接PA、PC，在线段PC上确定一点N，使AN平分四边形ADCP的面积，求点N的坐标．。

专题一：二次函数中的面积问题（一）利用割补：将图形割（补）成三角形或梯形面积的和差，其中需使三角形的底边在坐标轴上或平行于坐标轴；（例如以下4、5两图中，连结BD 解法不简便。

）例1：如图抛物线与轴交于两点，与轴交于点, （1）k=___-3_____,点的坐标为___(-1,0)___，点的坐标为____(3,0)____； （2）设抛物线的顶点为，求的面积；（3）在轴下方的抛物线上是否存在一点，使四边形的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；解：（2）M （1，-4）；(3)设,,当m =52时，四边形ABDC 面积最大，为52。

练习1、如图，抛物线与轴交于A 、B 两点，与轴交于点C ，抛物线的对称轴交轴于点D ，已知A （﹣1，0），C （0，2）． （1）求抛物线的表达式；（2）点E 是线段BC 上的一个动点，过点E 作轴的垂线与抛物线相交于点F ，当点E 运动到什么位置时，四边形CDBF 的面积最大？求出四边形CDBF 的最大面积及此时E 点的坐标．解：（1）y =-12x 2+32x +2(2)对称轴x =-b 2a =32,\D (32,0)， 令-12x 2+32x +2=0,x 1=-1,x 2=4,\B (4,0) ,设F (a ,-12a 2+32a +2),y =x 2-2x +k x A ,B y C (0,-3)A B M D BCM x D ABDC S D BCM =S D OCM +S D BOM -S D BOC =12´3´1+12´3´4-12´3´3=3D (m ,m 2-2m -3) S 四边形ABDC =S D AOC +S D BOD +S D COD=12´1´3+12´|m 2-2m -3|´3+12´m ´3=-12m 2+52m +3-b 2a =-522´(-12)=52,0<m <3y =-12x 2+mx +n x y xxS四边形CDBF =SD COF+SD BOF-SD COD=12´2´a+12´4´(-12a2+32a+2)-12´2´32=-a2+4a+52∵-42´(-1)=2,0<a<4,-1<0,\当a=2时，S四边形CDBF最大，为132此时，直线BC解析式可求得y=-12x+2,\E(2,1)练习2：已知：抛物线的顶点坐标为C（1，4），抛物线交x轴于点A，交y轴于点B（0，3）．点P是在第一象限内的抛物线上的一个动点，过点P作y轴的平行线，交AB于点D．是否存在点P，使S△PAB=S△CAB？若存在，求出P点的坐标；若不存在，请说明理由．解：设抛物线解析式为y=a(x-1)2+4,将B(0,3)代入得a=-1\y=-(x-1)2+4=-x2+2x+3,令y=0得x1=-1,x2=3,\A(3,0)连结OC，SD ABC =SD CBO+SD ACO-SD ABO=3,\SD PAB=54×SD ABC=54´3=154设P(m,-m2+2m+3),连结OP、BP,SD PAB =SD BPO+SD APO-SD AOB=12´3´m+12´3´(-m2+2m+3)-12´3´3=-32m2+92m-32m2+92m=154,整理得2m2-6m+0,D=(-6)2-4´2´5=-4<0,所以不存在这样的点P。

专题10 二次函数中面积问题方法1 割补法求面积1．如图，直线l ：33y x =-+与x 轴、y 轴分别相交于A 、B 两点，抛物线()2240y ax ax a a =-++<经过点B ．(1)求该抛物线的函数表达式：(2)已知点M 是抛物线上的一个动点，并且点M 在第一象限内，连接AM 、BM ，设点M 的横坐标为m ，△ABM 的面积为S ，求S 与m 的函数表达式，并求出S 的最大值．【答案】（1）2y x 2x 3=-++；（2）21252528S m ⎛⎫=--+ ⎪⎝⎭;当52m =时，S 取得最大值258．【解析】 【分析】（1）根据题意先求出点B 的坐标，然后代入二次函数解析式求解即可；（2）由题意可求点A 坐标，连接OM ，由题意知，点M 的坐标为2(,23)m m m -++，则有03m <<，然后根据割补法求面积即可．【详解】解：（1）把0x =代入33y x =-+得3y =， △(0,3)B ．把(0,3)B 代入224y ax ax a =-++， 得34a =+，△1a =-．△抛物线的解析式为2y x 2x 3=-++；（2）令0y =，则2230x x -++=，解得1x =-或3， △抛物线与x 轴的交点横坐标分别为1-和3． △点M 在抛物线上，且在第一象限内， △03m <<．将0y =代入33y x =-+，得033x =-+，解得1x =， △(1,0)A ．如解图，连接OM ，由题意知，点M 的坐标为2(,23)m m m -++，则2111(31)2223132AOBOBMOAMAOBOAMB S S SSSSm m m =-=+-=⨯⨯+⨯-⨯-++⨯⨯四边形 2215122522528m m m ⎛⎫=-+=--+⎪⎝⎭， △102-<，且03m <<， △当52m =时，S 取得最大值258． 【点睛】本题主要考查二次函数的综合，熟练掌握二次函数的性质是解题的关键．方法2 铅锤高水平宽求面积2．如图，抛物线y ＝ax 2+bx+c 经过A （0，3）、B （﹣1，0）、D （2，3），抛物线与x 轴的另一交点为E,点P 为直线AE 上方抛物线上一动点，设点P 的横坐标为t ． （1）求抛物线的表达式；（2）当t 为何值时，△PAE 的面积最大？并求出最大面积；解：（1）由题意得：4233a b ca b cc-+=⎧⎪++=⎨⎪=⎩，解得：123abc=-⎧⎪=⎨⎪=⎩，△抛物线解析式为y＝﹣x2+2x+3；（2）△A（0，3），D（2，3），△抛物线对称轴为x＝1，△E（3，0），设直线AE的解析式为y＝kx+3，△3k+3＝0，解得，k＝﹣1，△直线AE的解析式为y＝﹣x+3，如图1，作PM△y轴，交直线AE于点M，设P（t，﹣t2+2t+3），M（t，﹣t+3），△PM＝﹣t2+2t+3+t﹣3＝﹣t2+3t，△12PAE PMA PMES S S PM OE=+=⋅＝()21332t t⨯⨯-+＝23327228t⎛⎫--+⎪⎝⎭，△t＝32时，△PAE的面积最大，最大值是278．方法3 △=0时求面积最大3．如图，二次函数的图象与轴交于、两点，与轴交于点，已知点（－1，0），点C(0，－2)．（1）求抛物线的函数解析式； （2）若点是线段下方的抛物线上的一个动点，求面积的最大值以及此时点的坐标．（1）将A （－1，0）、点C(0，－2)．代入232y ax x c =-+ 求得：213222y x x =-- （2）已求得：B （4，0）、C （0，-2），可得直线BC 的解析式为：y=12x -2； 设直线l△BC ，则该直线的解析式可表示为：y=12x+b ， 当直线l 与抛物线只有一个交点时，可列方程：12x+b=12x 2-32x -2，即：12x 2-2x -2-b=0，且△=0； △4-4×12（-2-b ）=0，即b=-4； △直线l ：y=12x -4．所以点M 即直线l 和抛物线的唯一交点，有： 213222{142y x x y x =--=-，解得：2{3x y ==-即 M （2，-3）．过M 点作MN△x 轴于N ，S△BMC=S 梯形OCMN+S△MNB -S△OCB=12×2×（2+3）+12×2×3-12×2×4=4． △点M （2，﹣3），△MBC 面积最大值是4. 考点：二次函数综合题．类型拓展1 求四边形面积4．如图1，在平面直角坐标系中，一次函数y ＝12x ﹣2的图象与x 轴交于点B ，与y 轴交于点C ，抛物线y ＝12x 2＋bx ＋c 的图象经过B 、C 两点，且与x 轴的负半轴交于点A ． （1）求二次函数的表达式；（2）若点D 在直线BC 下方的抛物线上，如图1，连接DC 、DB ，设四边形OCDB 的面积为S ，求S 的最大值；解：（1）对于y ＝12x ﹣2，令y ＝12x ﹣2＝0， 解得：x ＝4； 令x ＝0，则y ＝﹣2，故点B 、C 的坐标分别为（4，0）、（0，﹣2）；将点B 、C 的坐标代入抛物线表达式得2116402c b c =-⎧⎪⎨⨯++=⎪⎩，解得：322b c ⎧=-⎪⎨⎪=-⎩， 故抛物线的表达式为213222y x x =--①； （2）连接OD ，点D 的坐标为（x ，213222x x --），则S ＝S △ODC ＋S △ODB ＝12×OC ×D x ＋12×BO ×（﹣D y ）＝12×2×x ＋12×4×（213222x x -++）＝﹣x 2＋4x ＋4，△﹣1＜0，故S 有最大值， 当x ＝2时，S 有最大值8；5．如图，抛物线2y x bx c =-++与x 轴交于A （-1，0），B （3，0）两点，与y 轴交于点C ，直线3y x =-+经过B ，C 两点，连接AC ．(1)求抛物线的表达式；(2)点E 为直线BC 上方的抛物线上的一动点（点E 不与点B ，C 重合），连接BE ，CE ，设四边形BECA 的面积为S ，求S 的最大值； (1)解：（1）将(1A -，0)(3B ，0)代入2y x bx c =-++，∴10930b c b c --+=⎧⎨-++=⎩，解得：23b c =⎧⎨=⎩，223y x x ∴=-++；(2)（2）过E 作EF x ⊥轴于点F ，与BC 交于点H ，(1A -，0)(3B ，0)，4AB ∴=当0x =时，3y =，(0,3)C ∴，3OC ∴=，设2(,23)F a a a -++，则(,3)H a a -+，222333EH a a a a a ∴=-+++-=-+，ABC BCE BECA S S S ∆∆=+四边形，21143(3)322S a a ∴=⨯⨯+-+⨯ 236(3)2a a =+-+23375()228a =--+，∴当32a =时，S 的最大值为758；类型拓展2 抛物线上有且只有三个点6．如图1，已知抛物线y ＝ax 2+2x +c （a ≠0），与y 轴交于点A （0，6），与x 轴交于点B （6，0）．（1）求这条抛物线的表达式及其顶点坐标；（2）设点P 是抛物线上的动点，若在此抛物线上有且只有三个P 点使得△P AB 的面积是定值S ，求这三个点的坐标及定值S ．解：(1)△抛物线y＝ax2+2x+c（a≠0），与y轴交于点A（0，6），与x轴交于点B（6，0）．△603612ca c=⎧⎨=++⎩△126 ac⎧=-⎪⎨⎪=⎩△抛物线解析式为：y＝﹣12x2+2x+6，△y＝﹣12x2+2x+6＝﹣12（x﹣2）2+8，△顶点坐标为（2，8）(2)△点A（0，6），点B（6，0），△直线AB解析式y＝﹣x+6，当x＝2时，y＝4，△点D（2，4）如图1，设AB上方的抛物线上有点P，过点P作AB的平行线交对称轴于点C，且与抛物线只有一个交点为P，设直线PC解析式为y＝﹣x+b，△﹣12x2+2x+6＝﹣x+b，且只有一个交点，△△＝9﹣4×12×（b﹣6）＝0△b ＝212， △直线PC 解析式为y ＝﹣x +212， △当x ＝2，y ＝172， △点C 坐标（2，172）， △CD ＝92，△﹣12x 2+2x +6＝﹣x +92，△x ＝3， △点P （3，152） △在此抛物线上有且只有三个P 点使得△P AB 的面积是定值S ，△另两个点所在直线与AB ，PC 都平行，且与AB 的距离等于PC 与AB 的距离， △DE ＝CD ＝92，△点E （2，﹣12），设P 'E 的解析式为y ＝﹣x +m ， △﹣12＝﹣2+m ， △m ＝32△P 'E 的解析式为y ＝﹣x +32，△﹣12x 2+2x +6＝﹣x +32，△x ＝△点P '（，﹣32﹣，P ''（3﹣，﹣32，△S ＝12×6×（152﹣3）＝272．7．如图，直线334y x =-+与 x 轴交于点 C ，与 y 轴交于点 B ，抛物线 234y ax x c =++经过 B 、C 两点．（1）求抛物线的解析式；（2）如图，点 E 是抛物线上的一动点（不与 B ，C 两点重合），△BEC 面积记为 S ，当 S 取何值时，对应的点 E 有且只有三个？【答案】（1）233384y x x =-++；（2）3【解析】 【分析】（1）先利用一次函数解析式确定B （0，3），C （4，0），然后利用待定系数法求抛物线解析式；（2）由于E 点在直线BC 的下方的抛物线上时，存在两个对应的E 点满足△BEC 面积为S ，则当E 点在直线BC 的上方的抛物线上时，只能有一个对应的E 点满足△BEC 面积为S ，所以过E 点的直线与抛物线只有一个公共点，设此时直线解析式为34y x b =-+，利用方程组23433384y x b y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩只有一组解求出b 得到E 点坐标，然后计算此时S △BEC ． 【详解】（1）当x=0时，y=-34x+3=3，则B （0，3），当y=0时，-34x+3=0，解得x=4，则C （4，0），把B （0，3），C （4，0）代入y=ax 2+34x+c 得383a c ⎧=-⎪⎨⎪=⎩， 所以抛物线解析式为233384y x x =-++；（2）当E 点在直线BC 的下方的抛物线上时，一定有两个对应的E 点满足△BEC 面积为S ， 所以当E 点在直线BC 的上方的抛物线上时，只能有一个对应的E 点满足△BEC 面积为S ， 即此时过E 点的直线与抛物线只有一个公共点，设此时直线解析式为34y x b =-+， 方程组23433384y x b y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩只有一组解， 方程23333844x x x b -++=-+有两个相等的实数解， 则△=122-4×3×（-24+8b ）=0，解得b=92，解方程得x 1=x 2=2， E 点坐标为（2，3）， 此时1343322BEC S ⎛⎫=⨯⨯-= ⎪⎝⎭， 所以当S=1时，对应的点E 有且只有三个．【点睛】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x 轴有两个交点时，可选择设其解析式为交点式来求解．8．如图，直线4y x =-+与x 轴交于点C ，与y 轴交于点B ，抛物线223y x bx c =-++经过B 、C 两点．（1）求抛物线的解析式；（2）如图，点E 是抛物线上的一动点(不与B ，C 两点重合)，当14BEC BOC S S =△时，求点E 的坐标；（3）若点F 是抛物线上的一动点，当BFC S △为什么取值范围时，对应的点F 有且只有两个？【答案】（1）225433y x x =-++；（2）1E ⎝⎭，2E ⎝⎭，34222E ⎛-+ ⎝⎭，44222E ⎛+- ⎝⎭；（3）当163BFC S >△时，对应的点F 有且只有两个．【解析】【分析】（1）根据待定系数法，即可求解；（2）过点E 作x 轴的垂线交BC 于点N ，设点225,433E a a a ⎛⎫-++ ⎪⎝⎭，点(,4)N a a -+，根据12BEC B C S EN x x =-△，14BEC BOC S S =△，列出方程，即可求解； （3）当F 点在直线BC 的下方的抛物线上时，一定有两个对应的F 点满足BCF △面积为S ，当F 点在直线BC 的上方的抛物线上时，无F 点满足BCF △面积为S 才符合题意，故只需要求出当点F 在直线BC 的上方时，BFC S △的最大值，即可得到结论 ．【详解】（1）△直线4y x =-+与x 轴交于点C ，与y 轴交于点B ，△(0,4)B ，(4,0)C ，将(0,4)B ，(4,0)C 代入223y x bx c =-++， 可得2424403c b c =⎧⎪⎨-⨯++=⎪⎩，解得534b c ⎧=⎪⎨⎪=⎩， △225433y x x =-++； （2）如图，过点E 作x 轴的垂线交BC 于点N ， 设点225,433E a a a ⎛⎫-++ ⎪⎝⎭，则点(,4)N a a -+， △2212541624423333BEC B C S EN x x a a a a a =-=-+++-=-+△， △182BOC S BO OC =⋅=△，14BEC BOC S S =△， △2416233a a -+=，解得：1x =2x =3x =4x = 将1x ，2x ，3x ，4x代入抛物线解析式，可得：1y =，2y =3y =4y =△1E ⎝⎭，2E ⎝⎭，34222E ⎛ ⎝⎭，44222E ⎛ ⎝⎭； （3）当点F 在直线BC 上方的抛物线上时，设点225,433F m m m ⎛⎫-++ ⎪⎝⎭， 由（2）同理可得：22416416(2)3333BFC S m m m =-+=--+△， △当2m =时，BFC S △的最大值为163， △当BFC S △＞163时，在直线BC 的上方的抛物线上无法找到F 点， 综上所述：当163BFC S >△时，对应的点F 有且只有两个．【点睛】本题主要考查二次函数与一次函数的综合，掌握待定系数法，函数图像上的点的坐标特征以及三角形的面积=铅垂高×水平宽，是解题的关键．类型拓展3 综合运用9．综合与实践 如图，二次函数234y x bx c =++的图象与x 轴交于点A 和B ，点B 的坐标是()4,0，与y 轴交于点()0,3C -，点D 在抛物线上运动．(1)求抛物线的表达式；(2)如图2，当点D 在第四象限的抛物线上运动时，连接BD ，CD ，BC ，当BCD △的面积最大时，求点D 的坐标及BCD △的最大面积；(1)解：点B ()4,0和点()0,3C -代入二次函数234y x bx c =++， 得：01243b c c=++⎧⎨-=⎩ 解得943b c ⎧=-⎪⎨⎪=-⎩． △抛物线的表达式是239344y x x =--． (2) 解：如图，连接OD ，过点D 作DM x ⊥轴，作DN y ⊥轴．设点D 的坐标是239,344m m m ⎛⎫-- ⎪⎝⎭．△239344DM m m =-++，DN m =． △()4,0B ，()0,3C -，△4OB =，3OC =．△BCD OCD OBD OBC S S S S =+-△△△△111222OC DN OB DM OB OC =⋅+⋅-⋅ 2113913434322442m m m ⎛⎫=⨯+⨯-++-⨯⨯ ⎪⎝⎭ 2362m m =-+ 23(2)62m =--+． △302-<， △当2m =时，BCD △的面积最大且为6．当2m =时，2239399322344442m m --=⨯-⨯-=-． △点D 的坐标是92,2⎛⎫- ⎪⎝⎭，BCD △的最大面积是6． 10．如图，抛物线2y x bx c =-++与x 轴相交于A 、B 两点，与y 轴相交于点C ，且点B 与点C 的坐标分别为()()3,0,0,3B C ，点M 是抛物线的顶点．(1)求二次函数的关系式；(2)点P 为线段MB 上一个动点，过点P 作PD x ⊥轴于点D ，若OD m =，PCD 的面积为S ，求S 与m 的函数关系式，并求当S 取得最大值时，点P 的坐标；(1)解：将点B （3，0），C （0，3）代入y =-x 2+bx +c ，得09333b c =-++⎧⎨=⎩；解得23b c =⎧⎨=⎩， △二次函数的解析式为y =-x 2+2x +3；(2)△y =-x 2+2x +3=-（x -1）2+4，△顶点M （1，4），设直线BM 的解析式为y =kx +b ，将点B （3，0），M （1，4）代入，得304k b k b +=⎧⎨+=⎩， 解得26k b =-⎧⎨=⎩， △直线BM 的解析式为y =-2x +6，△PD △x 轴且OD =m ，△P （m ，-2m +6），△S =S △PCD =12PD •OD =12m （-2m +6）=-m 2+3m ，即S =-m 2+3m ，△当点P 与点B 重合时，不存在以P 、C 、D 为顶点的三角形，△1≤m <3，△S =-m 2+3m =-（m -32）2+94， △-1＞0，△当m =32时，S 取最大值94；此时点P 的坐标为332⎛⎫ ⎪⎝⎭，. 11．如图，在平面直角坐标系中，抛物线2y ax bx c =++的对称轴为2x =，与y 轴交于点A 与x 轴交于点E 、B ，且点(0,5)A ，(5,0)B ，过点A 作AC 平行于x 轴，交抛物线于点C ，点P 为抛物线上的点，且在AC 的上方，作PD 平行于y 轴交AB 于点D ．(1)求二次函数的解析式；(2)当点P 在何位置时，四边形APCD 的面积最大？并求出最大面积；(1) 解：抛物线2y ax bx c =++的对称轴为2x =， △22b a-=， 4b a ∴=-，∴抛物线解析式为24y ax ax c =-+，点(0,5)A ，(5,0)B ，∴52550c a b c =⎧⎨-+=⎩， ∴15a c =-⎧⎨=⎩， ∴二次函数的解析式为245y x x =-++；(2)解：//AC x 轴，点(0,5)A ，当5y =时，2455x x -++=，10x ∴=，24x =，(4,5)C ∴，4AC ∴=，设直线AB 的解析式为y mx n =+，(0,5)A ，(5,0)B ，由点A 、B 的坐标得，直线AB 的解析式为5y x =-+；设2(,45)P m m m -++，,5()D m m ∴-+，224555PD m m m m m ∴=-+++-=-+，4AC =， △()221525252222APCD S AC PD m m m ⎛⎫=⋅=-+=--+ ⎪⎝⎭四边形 ∴当52m =时，四边形APCD 的面积最大， ∴即点5(2P ，35)4时，四边形APCD 的面积最大为252； 12．如图，在平面直角坐标系中，二次函数y ＝﹣x 2＋bx ＋c 的图象与坐标轴交于A ，B ，C 三点，其中点B 的坐标为（1，0），点C 的坐标为（0，4），点D 的坐标为（0，2），点P 为二次函数图象上的动点．（1）求二次函数的解析式和直线AD 的解析式；（2）当点P 位于第二象限内二次函数的图象上时，连接AD ，AP ，以AD ，AP 为邻边作平行四边形APED ，设平行四边形APED 的面积为S ，求S 的最大值．【答案】（1）y ＝－x 2－3x ＋4，122y x =+；（2）814【解析】【分析】 （1）利用待定系数法将B （1，0），C （0，4）代入二次函数y ＝﹣x 2＋bx ＋c 即可求出二次函数的解析式，令y ＝0，可求出A 点坐标，然后设直线AD 的解析式为y ＝kx ＋b ，利用待定系数法将A 点坐标和D 点坐标代入y ＝kx ＋b 即可求出直线AD 的解析式；（2）连接PD ，作PG y 轴交AD 于点G ，根据题意设出点P 和点G 的坐标，然后表示出线段PG 的长度，进而根据2APD S S ∆=表示出平行四边形APED 的面积，最后根据二次函数的性质求解即可．【详解】解：（1）将B （1，0），C （0，4）代入y ＝－x 2＋bx ＋c 中，得014b c c =-++⎧⎨=⎩，解得34b c =-⎧⎨=⎩， △二次函数的解析式为y ＝－x 2－3x ＋4在y ＝－x 2－3x ＋4中，令y ＝0，即2340x x --+=，解得x 1＝－4，x 2＝1，△A （－4，0）．设直线AD 的解析式为y ＝kx ＋b'．△D （0，2），△04'2'k b b =-+⎧⎨=⎩， 解得：12'2k b ⎧=⎪⎨⎪=⎩ △直线AD 的解析式为122y x =+． （2）连接PD ，作PG y 轴交AD 于点G ，如图所示．设P （t ，－t 2－3t ＋4）（－4＜t ＜0），则G （t ，122t +）， △2217342222PG t t t t t =--+--=--+， △2122||41482APD D A S S PG x x t t ∆==⨯⋅-=--+， 27814()44t =-++． △－4＜0，－4＜t ＜0，△当74t =-时，S 有最大值814．【点睛】此题考查了待定系数法求二次函数和一次函数表达式，二次函数中有关面积的综合题，解题的关键是熟练掌握待定系数法求函数表达式，根据题意设出点的坐标表示出平行四边形APED的面积．。