习题集-02 数字信号处理习题答案

习题及答案 4一、填空题（每空1分, 共10分）1．序列()sin(3/5)x n n π=的周期为 。

2．线性时不变系统的性质有 律、 律、 律。

3．对4()()x n R n =的Z 变换为 ，其收敛域为 。

4．抽样序列的Z 变换与离散傅里叶变换DFT 的关系为 。

5．序列x(n)=(1，-2，0，3；n=0，1，2，3), 圆周左移2位得到的序列为 。

6．设LTI 系统输入为x(n) ，系统单位序列响应为h(n)，则系统零状态输出y(n)= 。

7．因果序列x(n)，在Z →∞时，X(Z)= 。

二、单项选择题（每题2分, 共20分）1．δ(n)的Z 变换是 （ ）A.1 B.δ(ω) C.2πδ(ω) D.2π2．序列x 1（n ）的长度为4，序列x 2（n ）的长度为3，则它们线性卷积的长度是 （ ）A. 3 B. 4 C. 6 D. 73．LTI 系统，输入x （n ）时，输出y （n ）；输入为3x （n-2），输出为 （ ） A. y （n-2） B.3y （n-2） C.3y （n ） D.y （n ）4．下面描述中最适合离散傅立叶变换DFT 的是 （ ） A.时域为离散序列，频域为连续信号B.时域为离散周期序列，频域也为离散周期序列C.时域为离散无限长序列，频域为连续周期信号D.时域为离散有限长序列，频域也为离散有限长序列5．若一模拟信号为带限，且对其抽样满足奈奎斯特条件，理想条件下将抽样信号通过 即可完全不失真恢复原信号 （ ）A.理想低通滤波器 B.理想高通滤波器 C.理想带通滤波器 D.理想带阻滤波器6．下列哪一个系统是因果系统 （ ）A.y(n)=x (n+2) B. y(n)= cos(n+1)x (n) C. y(n)=x (2n) D.y(n)=x (- n)7．一个线性时不变离散系统稳定的充要条件是其系统函数的收敛域包括 （ ） A. 实轴B.原点C.单位圆D.虚轴8．已知序列Z 变换的收敛域为｜z ｜>2，则该序列为 （ ）A.有限长序列 B.无限长序列 C.反因果序列 D.因果序列9．若序列的长度为M ，要能够由频域抽样信号X(k)恢复原序列，而不发生时域混叠现象，则频域抽样点数N 需满足的条件是 ( ) A.N≥M B.N≤M C.N≤2M D.N≥2M10．设因果稳定的LTI 系统的单位抽样响应h(n)，在n<0时，h(n)= ( ) A.0 B .∞ C. -∞ D.1 三、判断题（每题1分, 共10分）1．序列的傅立叶变换是频率ω的周期函数，周期是2π。

数字信号处理（姚天任江太辉）第三版课后习题答案第二章2.1判断下列序列是否是周期序列。

若是，请确定它的最小周期(1)x(n)二Acos( 5 n86)(2)x(n )= e j(- 8 )(3) x(n )=Asi n(3 n4 3)解(1)对照正弦型序列的-般公式x(n)二 Acos( n )，得出5。

因此82 16是有理数，所以是周期序列。

5 最小周期等于N=^k 16(k取5)。

5(2)对照复指数序列的般公式x(n)二exp[ j ]n,得出1。

因此2168是无理数，所以不是周期序列。

(3)对照正弦型序列的般公式x(n)二 Acos( 3n )，又x(n)二Asin( n ) =Acos(— .门—)=Acos( —n 丄)，得出3。

因此2 8是有理数，所以2 434 6 4 3是周期序列。

最小周期等于N=-k38(k 取3)2.2在图2.2中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。

计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。

解利用线性卷积公式y(n )= x(k)h( n k)k按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值(a) y(0)=x(0)h(0)=1y(l)=x(0)h(1)+x(1)h(0)=3y(n)=x(O)h( n)+x(1)h( n-1)+x(2)h( n-2)=4,n (b) x(n )=2 (n)- (n-1)h(n)=- (n)+2 (n-1)+ (n-2)y(n)=-2(n )+5(n-1)= (n-3)(c) y(n )=u(k)kn ka u(n k)：n k 1 a n 1/ \=a = . a u(n)k i a2.3计算线性线性卷积(1) y(n )=u( n)*u( n)(2) y(n)= n u(n)*u(n)解：(1) y(n)二u(k)u(n k)ku(k)u(n k)=(n+1),n >0 k 0 即y(n)=(n+1)u(n)(2) y(n )=kku(k)u( n k)2.4图P2.4所示的是单位取样响应分别为 九(n)和h 2(n)的两个线性非移变系统的级联，已知 x(n)=u(n), h ^n)二(n)-(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出 y(n).解(n)=x( n)*h Jn)u(k)[(n-k)- (n-k-4)]k=u( n)-u( n-4)y(n)= (n)*h 2 (n)a k u(k)[u( n-k)-u( n-k-4)]k算线性卷积的方法，求系统的单位阶跃响应即 y(n)二ku(k)u(n1n 1——,n >n 1—u(n)2.5已知一个线性非移变系统的单位取样响应为h(n)二a n u(-n),0<a<1 用直接计2.6 试证明线性卷积满足交换率、结合率和加法分配率。

数字信号处理习题(xítí)解答第1-2章：1. 判断下列(xiàliè)信号是否为周期信号，若是，确定其周期。

若不是，说明(shuōmíng)理由（1）f1(t) = sin2t + cos3t（2）f2(t) = cos2t + sinπt2、判断下列序列是否为周期(zhōuqī)信号，若是，确定其周期。

若不是(bùshi)，说明理由（1）f1(k) = sin(3πk/4) + cos(0.5πk)（2）f2(k) = sin(2k)(3)若正弦序列x(n)=cos(3πn /13)是周期的, 则周期是N=3、判断下列信号是否为周期信号，若是，确定其周期; 若不是，说明理由（1）f(k) = sin(πk/4) + cos(0.5πk)（2）f2(k) = sin(3πk/4) + cos(0.5πk)解1、解β1 = π/4 rad，β2 = 0.5π rad 由于2π/ β1 = 8 N1 =8，N2 = 4，故f(k) 为周期序列，其周期为N1和N2的最小公倍数8。

（2）β1 = 3π/4 rad，β2 = 0.5π rad由于2π/ β1 = 8/3 N1 =8， N2 = 4，故f1(k) 为周期序列，其周期为N1和N2的最小公倍数8。

4、画出下列函数的波形(1).(2).解5、画出下列函数的波形x(n)=3δ(n+3)+δ(n+1)-3δ(n-1)+2δ(n-2)6. 离散线性时不变系统单位阶跃响应，则单位响应=?7、已知信号(xìnhào)，则奈奎斯特取样(qǔyàng)频率为( 200 )Hz。

8、在已知信号(xìnhào)的最高频率为100Hz(即谱分析范围(fànwéi))时，为了避免频率(pínlǜ)混叠现象，采样频率最少要200 Hz：9. 若信号的最高频率为20KHz，则对该信号取样，为使频谱不混叠，最低取样频率是40KHz10、连续信号：用采样频率采样，写出所得到的信号序列x(n)表达式，求出该序列x(n) 的最小周期解：，11、连续信号：用采样频率100s f Hz = 采样，写出所得到的信号序列x(n)表达式，求出该序列x(n) 的最小周期长度。

第一章数字信号处理概述简答题：1．在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器，它们分别起什么作用？答：在A/D变化之前为了限制信号的最高频率，使其满足当采样频率一定时，采样频率应大于等于信号最高频率2倍的条件。

此滤波器亦称为“抗混叠”滤波器。

在D/A变换之后为了滤除高频延拓谱，以便把抽样保持的阶梯形输出波平滑化，故又称之为“平滑”滤波器。

判断说明题：2．模拟信号也可以与数字信号一样在计算机上进行数字信号处理，自己要增加一道采样的工序就可以了。

（）答：错。

需要增加采样和量化两道工序。

3．一个模拟信号处理系统总可以转换成功能相同的数字系统，然后基于数字信号处理理论，对信号进行等效的数字处理。

（）答：受采样频率、有限字长效应的约束，与模拟信号处理系统完全等效的数字系统未必一定能找到。

因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析，再考虑幅度量化及实现过程中有限字长所造成的影响。

故离散时间信号和系统理论是数字信号处理的理论基础。

第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理计算题：1．过滤限带的模拟数据时，常采用数字滤波器，如图所示，图中T 表示采样周期（假设T 足够小，足以防止混叠效应），把从)()(t y t x 到的整个系统等效为一个模拟滤波器。

（a ） 如果kHz rad n h 101,8)(=π截止于，求整个系统的截止频率。

（b ） 对于kHz T 201=，重复（a ）的计算。

解 （a ）因为当0)(8=≥ωπωj e H rad 时，在数 — 模变换中)(1)(1)(Tj X Tj X Te Y a a j ωω=Ω=所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ，因此对T8π没有影响，故整个系统的截止频率由)(ωj e H 决定，是625Hz 。

数字信号处理课后习题答案数字信号处理课后习题答案数字信号处理是一门重要的学科，它研究如何对数字信号进行处理和分析。

在学习过程中，我们经常会遇到一些习题，通过解答这些习题可以帮助我们更好地理解和掌握数字信号处理的知识。

本文将为大家提供一些数字信号处理课后习题的答案，希望对大家的学习有所帮助。

一、离散时间信号和系统1. 什么是离散时间信号？答：离散时间信号是在离散时间点上取值的信号，它可以用数学上的序列表示。

2. 什么是离散时间系统？答：离散时间系统是对离散时间信号进行处理的系统，它可以用差分方程或差分方程组来描述。

3. 离散时间信号和连续时间信号有何区别？答：离散时间信号是在离散时间点上取值的信号，而连续时间信号是在连续时间上取值的信号。

二、离散时间信号的表示和运算1. 如何表示离散时间信号？答：离散时间信号可以用数学上的序列表示，例如x(n)表示离散时间信号x在时间点n上的取值。

2. 离散时间信号的运算有哪些？答：离散时间信号的运算包括加法、减法、乘法和卷积等。

3. 什么是离散时间信号的卷积？答：离散时间信号的卷积是指两个离散时间信号之间的一种数学运算，它可以表示两个信号之间的线性叠加关系。

三、离散时间系统的性质和稳定性1. 离散时间系统有哪些常见的性质？答：离散时间系统常见的性质包括线性性、时不变性、因果性和稳定性等。

2. 什么是离散时间系统的稳定性？答：离散时间系统的稳定性是指当输入信号有界时，输出信号也有界。

3. 如何判断离散时间系统的稳定性？答：可以通过判断系统的冲激响应的绝对可和性来判断离散时间系统的稳定性。

四、离散傅里叶变换1. 什么是离散傅里叶变换（DFT）？答：离散傅里叶变换是将离散时间信号转换为离散频率信号的一种数学变换。

2. 离散傅里叶变换有何作用？答：离散傅里叶变换可以将时域的信号转换为频域的信号，从而方便对信号的频谱进行分析。

3. 如何计算离散傅里叶变换？答：可以通过对离散时间信号进行离散傅里叶变换公式的计算来得到离散傅里叶变换的结果。

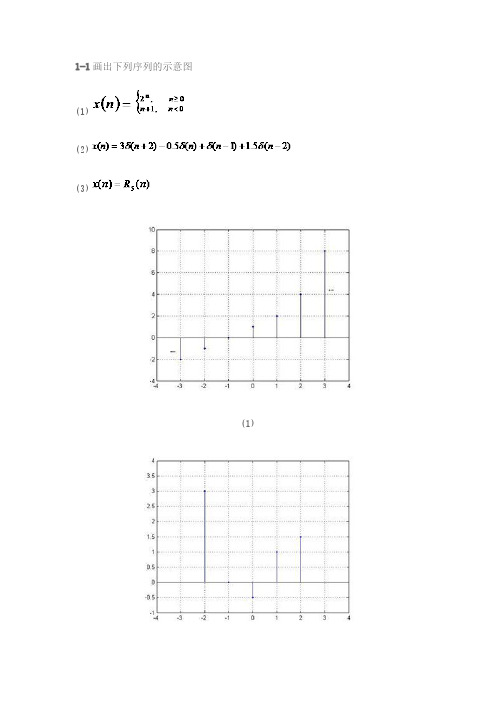
1-1画出下列序列的示意图(1)(2)(3)(1)(2)(3)1-2已知序列x(n)的图形如图1.41，试画出下列序列的示意图。

图1.41 信号x(n)的波形(1) (2)(3) (4)(5) (6)(修正：n=4处的值为0，不是3）（修正：应该再向右移4个采样点）1-3判断下列序列是否满足周期性，若满足求其基本周期(1)解：非周期序列;(2)解：为周期序列，基本周期N=5;(3)解：，，取为周期序列，基本周期。

(4)解：其中，为常数，取，，取则为周期序列，基本周期N=40。

1-4 判断下列系统是否为线性的？是否为移不变的？(1)非线性移不变系统(2) 非线性移变系统（修正：线性移变系统）(3) 非线性移不变系统(4) 线性移不变系统(5) 线性移不变系统（修正：线性移变系统）1-5判断下列系统是否为因果的？是否为稳定的？(1) ，其中因果非稳定系统(2) 非因果稳定系统(3) 非因果稳定系统(4) 非因果非稳定系统(5) 因果稳定系统1-6已知线性移不变系统的输入为x(n)，系统的单位脉冲响应为h(n)，试求系统的输出y(n)及其示意图(1)(2)(3)解：（1）（2）（3）1-7若采样信号m(t)的采样频率fs=1500Hz，下列信号经m(t)采样后哪些信号不失真？(1)(2)(3)解：(1)采样不失真(2)采样不失真(3)，采样失真1-8已知,采样信号的采样周期为。

(1) 的截止模拟角频率是多少？(2)将进行A/D采样后，的数字角频率与的模拟角频率的关系如何？(3)若，求的数字截止角频率。

解：(1)(2)(3)1-9计算下列序列的Z变换，并标明收敛域。

(1) (2)(3) (4)(5)解：(1)(2)(3)(4) ，，收敛域不存在(5)1-10利用Z变换性质求下列序列的Z变换。

(1)(2)(3)(4)解：(1) ,(2) ,(3),(4) , 1-11利用Z变换性质求下列序列的卷积和。

(1)(2)(3)(4)(5)(6)解：(1) ，,，,(2) ,，,(3) , ，,(4) ，,(5) ,，，(6) ，，，1-12利用的自相关序列定义为，试用的Z 变换来表示的Z变换。

第2章时域离散信号和系统的频域分析2.1学习要点与重要公式2.2FT和ZT的逆变换2.3分析信号和系统的频率特性 2.4例题2.5习题与上机题解答2.1学习要点与重要公式数字信号处理中有三个重要的数学变换工具，即傅里叶变换（FT）、Z变换（ZT）和离散傅里叶变换（DFT）。

利用它们可以将信号和系统在时域空间和频域空间相互转换，这方便了对信号和系统的分析和处理。

三种变换互有联系，但又不同。

表征一个信号和系统的频域特性是用傅里叶变换。

Z 变换是傅里叶变换的一种推广，单位圆上的Z变换就是傅里叶变换。

在z域进行分析问题会感到既灵活又方便。

离散傅里叶变换是离散化的傅里叶变换，因此用计算机分析和处理信号时，全用离散傅里叶变换进行。

离散傅里叶变换具有快速算法FFT，使离散傅里叶变换在应用中更加方便与广泛。

但是离散傅里叶变换不同于傅里叶变换和Z变换，它将信号的时域和频域，都进行了离散化，这是它的优点。

但更有它自己的特点，只有掌握了这些特点，才能合理正确地使用DFT。

本章只学习前两种变换，离散傅里叶变换及其FFT将在下一章学习。

2.1.1学习要点（1）傅里叶变换的正变换和逆变换定义，以及存在条件。

（2）傅里叶变换的性质和定理：傅里叶变换的周期性、移位与频移性质、时域卷积定理、巴塞伐尔定理、频域卷积定理、频域微分性质、实序列和一般序列的傅里叶变换的共轭对称性。

（3）周期序列的离散傅里叶级数及周期序列的傅里叶变换表示式。

（4）Z变换的正变换和逆变换定义，以及收敛域与序列特性之间的关系。

（5）Z变换的定理和性质：移位、反转、z域微分、共轭序列的Z变换、时域卷积定理、初值定理、终值定理、巴塞伐尔定理。

（6）系统的传输函数和系统函数的求解。

（7）用极点分布判断系统的因果性和稳定性。

（8）零状态响应、零输入响应和稳态响应的求解。

（9）用零极点分布定性分析并画出系统的幅频特性。

2.1.2重要公式（1）这两式分别是傅里叶变换的正变换和逆变换的公式。