《数字信号处理》课后习题答案111

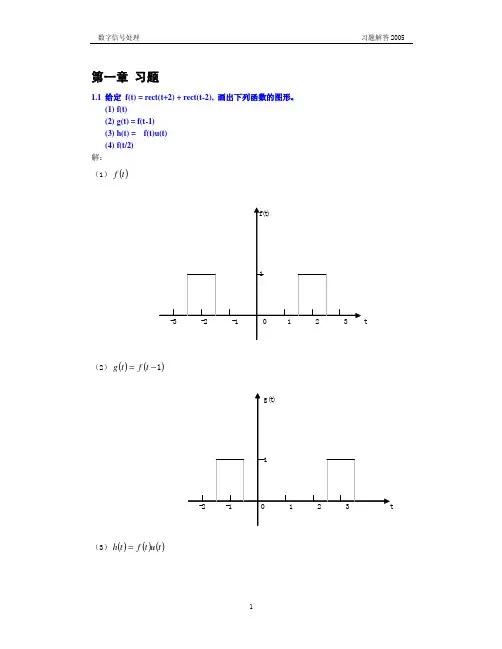
习 题1-1 有一个连续信号)2cos()(ψπ+=ft t x a ，式中Hz f 20=，2πψ=，（１） 求出)(t x a 的周期；（２） 用采样间隔s T 02.0=对)(t x a 进行采样，写出采样信号)(ˆt xa 的表达式； （３） 画出对应)(ˆt xa 的时域离散信号（序列）)(n x 的波形，并求出)(n x 的周期。

解：（1）)(t x a 的周期是s fT a 05.01==（2）∑∞-∞=-+=n a nT t fnT t x)()2cos()(ˆδψπ∑∞-∞=-+=n nT t nT )()40cos(δψπ（3）)(n x 的数字频率为πω8.0=，252=ωπ周期5=N 。

)28.0cos()(ππ+=n n x ，画出其波形如题1-1图所示。

题1-1图 1-2 设)sin()(t t x a π=，()()sin()a s s x n x nT nT π==，其中s T 为采样周期。

（1）)(t x a 信号的模拟频率Ω为多少？ （2）Ω和ω的关系是什么？（3）当s T s 5.0=时，)(n x 的数字频率ω为多少？ 解：（1）)(t x a 的模拟频率s rad /π=Ω。

（2）Ω和ω的关系是：s T ⋅Ω=ω。

（3）当s T s 5.0=时，rad πω5.0=。

1-3 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）)873cos()(ππ-=n A n x ，A 为常数；（2）)81()(π-=n j e n x 。

解： （1）πω73=，3142=ωπ，这是有理数，因此是周期序列，周期是14=T ； （2）81=ω，πωπ162=，这是无理数，因此是非周期序列。

1-4 研究一个线性时不变系统，其单位脉冲响应为指数序列)()(n u a n h n =，10<<a 。

对于矩阵输入序列，1,01()0N n N R n ≤≤-⎧=⎨⎩,其他 求出输出序列，并用MA TLAB 计算，比较其结果。

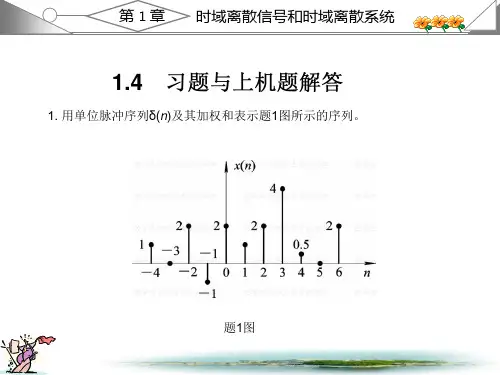
数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的， 确定其周期。

（1）A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= （2）)81(j e )(π-=n n x 解： （1） 因为ω=73π, 所以314π2=ω, 这是有理数， 因此是周期序列， 周期T =14。

（2） 因为ω=81, 所以ωπ2=16π, 这是无理数， 因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法乘法序列{2，3，2，1}与序列{2，3，5，2，1}相加为__{4，6，7，3，1}__，相乘为___{4，9，10，2} 。

移位翻转：①已知x(n)波形，画出x(-n)的波形图。

②尺度变换：已知x(n)波形，画出x(2n)及x(n/2)波形图。

卷积和：①h(n)*求x(n)，其他02n 0n 3，h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤= }23,4,7,4，23{0,h(n)*答案：x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5}，则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案：x(n)=4.如果输入信号为，求下述系统的输出信号。

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

答案很详细，考试前或者平时作业的时候可以好好研究，祝各位考试成功！！电子科技大学微电子与固体电子学陈钢教授著数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如 5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-； （3）0()()y n x n n =-，0n 为整常数； （5）2()()y n x n =； （7）0()()nm y n x m ==∑。

数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理（姚天任江太辉）第三版课后习题答案第二章判断下列序列是否是周期序列。

若是，请确定它的最小周期。

（1）x(n)=Acos(685ππ+n )（2）x(n)=)8(π-ne j（3）x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，得出=ω85π。

因此5162=ωπ是有理数，所以是周期序列。

最小周期等于N=)5(16516取k k =。

（2）对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。

因此πωπ162=是无理数，所以不是周期序列。

（3）对照正弦型序列的一般公式x(n)=Acos(ϕω+n )，又x(n)=Asin(343ππ+n )＝Acos(-2π343ππ-n )＝Acos(6143-n π)，得出=ω43π。

因此382=ωπ是有理数，所以是周期序列。

最小周期等于N=)3(838取k k =在图中，x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。

计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n)，并画出y(n)的图形。

解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法，计算y(n)的每一个取样值。

(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解：(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联，已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法，求系统的单位阶跃响应。

数字信号处理智慧树知到期末考试答案章节题库2024年温州医科大学1.设系统的单位抽样响应为h(n)，则系统因果的充要条件为（）答案:当n<0时，h(n)=02.已知FIR滤波器的冲激响应函数H(z)=1+2z-1+4z-2+3z-3+2z-4，则该滤波器h(n)的特点是（）答案:非对称3.序列x(n)=sin(11n/3)的周期为（）答案:∞4.平稳各台态遍历随机序列的功率谱密度可以通过单一样本的时间平均得到。

（）答案:对5.循环卷积运算可以由DFT运算实现、由于DFT存在快速算法FFT，因此对于所有卷积运算均可大幅度增加运算效率。

（）答案:错6.x[k]的循环位移特性可由除法运算来实现。

（）答案:错7.一个有限长的常数序列，其DFT也是一个有限长的常数序列。

（）答案:错8.频域信号的采样可以通过时域信号的周期化实现。

（）答案:对9.信号的内插会引起频谱的混叠。

（）答案:错10.DFT的变换矩阵由序列点数完全决定（）答案:对11.现代功率谱估计也成为参数模型法。

（）答案:对12.离散序列的抽取表示每隔M个点抽取原序列汇中的一点。

（）答案:错13.平稳随机序列统计特性与时间七点的选取无关。

（）答案:对14.各态遍历的随机序列一定是平稳随机序列。

（）答案:对15.基2时间算法与基2频率算法处理信号时，需将信号按照二进制翻转方法重新进行排列（）答案:错16.答案:1017.当遇到长序列和短序列进行循环卷积时，可使用重叠相加法与重叠保留法，则下列说法错误的是（）答案:重叠相加法一般须在第一段开头补零而重叠保留法需在最后一段末尾补零18.冲激响应不变法设计数字滤波器的特点是（）答案:有混频，线性相位19.已知x[k]为一个6点序列，则其DFT为对其DTFT哪些频率点的采样（）答案:20.当x[k]为实序列时，下列说法正确的是（）答案:DFT幅度为偶函数、相位为奇函数21.下列关于用冲激响应不变法设计IIR滤波器的说法中错误的是（）答案:可以用于设计低通、高通和带阻等各类滤波器22.已知FIR数字滤波器的系统函数H(z)=0.5(1-z-1)，试该滤波器的类型为（）答案:高通23.对于循环位移，下列说法错误的是（）。